Carbonaceous Materials Investigated by Small-Angle X-ray and Neutron Scattering
Abstract
:1. Introduction
2. Analysis of Carbons by Small-Angle Scattering: Evaluation of the Data
3. Discussion of the Structural Features and Calculated Characteristics of Different Carbonaceous Materials
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zhang, J.; Terrones, M.; Park, C.R.; Mukherjee, R.; Monthioux, M.; Koratkar, N.; Kim, Y.S.; Hurt, R.H.; Frackowiak, E.; Enoki, T.; et al. Carbon science in 2016: Status, challenges and perspectives. Carbon 2016, 98, 708–732. [Google Scholar] [CrossRef]
- Korenblit, Y.; Rose, M.; Kockrick, E.; Borchardt, L.; Kvit, A.; Kaskel, S.; Yushin, G. High-Rate Electrochemical Capacitors Based on Ordered Mesoporous Silicon Carbide-Derived Carbon. ACS Nano 2010, 4, 1337–1344. [Google Scholar] [CrossRef] [PubMed]
- Oschatz, M.; Kockrick, E.; Rose, M.; Borchardt, L.; Klein, N.; Senkovska, I.; Freudenberg, T.; Korenblit, Y.; Yushin, G.; Kaskel, S. A cubic ordered, mesoporous carbide-derived carbon for gas and energy storage applications. Carbon 2010, 48, 3987–3992. [Google Scholar] [CrossRef]
- Dash, R.; Chmiola, J.; Yushin, G.; Gogotsi, Y.; Laudisio, G.; Singer, J.; Fischer, J.; Kucheyev, S. Titanium carbide derived nanoporous carbon for energy-related applications. Carbon 2006, 44, 2489–2497. [Google Scholar] [CrossRef] [Green Version]
- Portet, C.; Yushin, G.; Gogotsi, Y. Electrochemical performance of carbon onions, nanodiamonds, carbon black and multiwalled nanotubes in electrical double layer capacitors. Carbon 2007, 45, 2511–2518. [Google Scholar] [CrossRef]
- Härmas, R.; Palm, R.; Härmas, M.; Pohl, M.; Kurig, H.; Tallo, I.; Tee, E.; Vaas, I.; Väli, R.; Romann, T.; et al. Influence of porosity parameters and electrolyte chemical composition on the power densities of non-aqueous and ionic liquid based supercapacitors. Electrochim. Acta 2018, 283, 931–948. [Google Scholar] [CrossRef]
- Wang, Q.; Yan, J.; Fan, Z. Carbon materials for high volumetric performance supercapacitors: Design, progress, challenges and opportunities. Energy Environ. Sci. 2016, 9, 729–762. [Google Scholar] [CrossRef]
- Vatamanu, J.; Bedrov, D. Capacitive Energy Storage: Current and Future Challenges. J. Phys. Chem. Lett. 2015, 6, 3594–3609. [Google Scholar] [CrossRef]
- Ciszewski, M.; Koszorek, A.; Radko, T.; Szatkowski, P.; Janas, D. Review of the Selected Carbon-Based Materials for Symmetric Supercapacitor Application. J. Electron. Mater. 2018, 48, 717–744. [Google Scholar] [CrossRef] [Green Version]
- Fang, R.; Zhao, S.; Sun, Z.; Wang, D.-W.; Cheng, H.-M.; Li, F. More Reliable Lithium-Sulfur Batteries: Status, Solutions and Prospects. Adv. Mater. 2017, 29, 1606823–1606847. [Google Scholar] [CrossRef]
- Komaba, S.; Murata, W.; Ishikawa, T.; Yabuuchi, N.; Ozeki, T.; Nakayama, T.; Ogata, A.; Gotoh, K.; Fujiwara, K. Electrochemical Na Insertion and Solid Electrolyte Interphase for Hard-Carbon Electrodes and Application to Na-Ion Batteries. Adv. Funct. Mater. 2011, 21, 3859–3867. [Google Scholar] [CrossRef]
- Renault, S.; Mihali, V.A.; Edström, K.; Brandell, D. Stability of organic Na-ion battery electrode materials: The case of disodium pyromellitic diimidate. Electrochem. Commun. 2014, 45, 52–55. [Google Scholar] [CrossRef]
- Wu, L.; Hu, X.; Qian, J.; Pei, F.; Wu, F.; Mao, R.; Ai, X.; Yang, H.; Cao, Y. Sb–C nanofibers with long cycle life as an anode material for high-performance sodium-ion batteries. Energy Environ. Sci. 2014, 7, 323–328. [Google Scholar] [CrossRef]
- Seidlmayer, S.; Hattendorff, J.; Buchberger, I.; Karge, L.; Gasteiger, H.A.; Gilles, R. In Operando Small-Angle Neutron Scattering (SANS) on Li-Ion Batteries. J. Electrochem. Soc. 2015, 162, A3116–A3125. [Google Scholar] [CrossRef]
- Bresser, D.; Passerini, S.; Scrosati, B. Recent progress and remaining challenges in sulfur-based lithium secondary batteries—A review. Chem. Commun. 2013, 49, 10545–10562. [Google Scholar] [CrossRef]
- Dhawa, T.; Chattopadhyay, S.; Sreemany, M.; De, G.; Mahanty, S. Influence of C–S interactions on the electrochemical performance of –COOH functionalized MWCNT/S composites as lithium-sulfur battery cathode. J. Chem. Sci. 2018, 130, 109. [Google Scholar] [CrossRef] [Green Version]
- Schuster, J.; He, G.; Mandlmeier, B.; Yim, T.; Lee, K.T.; Bein, T.; Nazar, L.F. Spherical Ordered Mesoporous Carbon Nanoparticles with High Porosity for Lithium-Sulfur Batteries. Angew. Chem. Int. Ed. 2012, 51, 3591–3595. [Google Scholar] [CrossRef]
- Kondrat, S.; Pérez, C.R.; Presser, V.; Gogotsi, Y.; Kornyshev, A.A. Effect of pore size and its dispersity on the energy storage in nanoporous supercapacitors. Energy Environ. Sci. 2012, 5, 6474–6479. [Google Scholar] [CrossRef]
- Merlet, C.; Péan, C.; Rotenberg, B.; Madden, P.A.; Simon, P.; Salanne, M. Simulating Supercapacitors: Can We Model Electrodes As Constant Charge Surfaces? J. Phys. Chem. Lett. 2013, 4, 264–268. [Google Scholar] [CrossRef]
- Pean, C.; Daffos, B.; Rotenberg, B.; Levitz, P.; Haefele, M.; Taberna, P.-L.; Simon, P.; Salanne, M. Confinement, Desolvation, And Electrosorption Effects on the Diffusion of Ions in Nanoporous Carbon Electrodes. J. Am. Chem. Soc. 2015, 137, 12627–12632. [Google Scholar] [CrossRef]
- Simon, P.; Gogotsi, Y. Capacitive Energy Storage in Nanostructured Carbon–Electrolyte Systems. Accounts Chem. Res. 2013, 46, 1094–1103. [Google Scholar] [CrossRef] [PubMed]
- Chmiola, A.J.; Yushin, G.; Gogotsi, Y.; Portet, C.; Simon, P.; Taberna, P.L. Anomalous Capacitance Less Than Increase in Carbon at Pore Sizes. Science 2015, 313, 1760–1763. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- He, L.; Chathoth, S.M.; Melnichenko, Y.B.; Presser, V.; McDonough, J.; Gogotsi, Y. Small-angle neutron scattering characterization of the structure of nanoporous carbons for energy-related applications. Microporous Mesoporous Mater. 2012, 149, 46–54. [Google Scholar] [CrossRef]
- Leis, J.; Arulepp, M.; Käärik, M.; Perkson, A. The effect of Mo2C derived carbon pore size on the electrical double-layer characteristics in propylene carbonate-based electrolyte. Carbon 2010, 48, 4001–4008. [Google Scholar] [CrossRef]
- Jänes, A.; Thomberg, T.; Kurig, H.; Lust, E. Nanoscale fine-tuning of porosity of carbide-derived carbon prepared from molybdenum carbide. Carbon 2009, 47, 23–29. [Google Scholar] [CrossRef]
- Thomberg, T.; Jänes, A.; Lust, E. Energy and power performance of electrochemical double-layer capacitors based on molybdenum carbide derived carbon. Electrochim. Acta 2010, 55, 3138–3143. [Google Scholar] [CrossRef]
- Eikerling, M.; Kornyshev, A.A.; Lust, E. Optimized Structure of Nanoporous Carbon-Based Double-Layer Capacitors. J. Electrochem. Soc. 2005, 152, E24–E33. [Google Scholar] [CrossRef]
- Borchardt, L.; Oschatz, M.; Paasch, S.; Kaskel, S.; Brunner, E. Interaction of electrolyte molecules with carbon materials of well-defined porosity: Characterization by solid-state NMR spectroscopy. Phys. Chem. Chem. Phys. 2013, 15, 15177–15184. [Google Scholar] [CrossRef]
- Tallo, I.; Thomberg, T.; Kontturi, K.; Jänes, A.; Lust, E. Nanostructured carbide-derived carbon synthesized by chlorination of tungsten carbide. Carbon 2011, 49, 4427–4433. [Google Scholar] [CrossRef]
- Presser, V.; Heon, M.; Gogotsi, Y. Carbide-Derived Carbons—From Porous Networks to Nanotubes and Graphene. Adv. Funct. Mater. 2011, 21, 810–833. [Google Scholar] [CrossRef]
- Ishikawa, S.; Saito, T.; Kuwahara, K. Carbon materials with nano-sized pores derived from carbides. SEI Tech. Rev. 2016, 82, 152–157. [Google Scholar]
- Jäckel, N.; Simon, P.; Gogotsi, Y.; Presser, V. Increase in Capacitance by Subnanometer Pores in Carbon. ACS Energy Lett. 2016, 1, 1262–1265. [Google Scholar] [CrossRef] [Green Version]
- Heimböckel, R.; Hoffmann, F.; Fröba, M. Insights into the influence of the pore size and surface area of activated carbons on the energy storage of electric double layer capacitors with a new potentially universally applicable capacitor model. Phys. Chem. Chem. Phys. 2019, 21, 3122–3133. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kim, H.S.; Singer, J.P.; Gogotsi, Y.; Fischer, J.E. Molybdenum carbide-derived carbon for hydrogen storage. Microporous Mesoporous Mater. 2009, 120, 267–271. [Google Scholar] [CrossRef]
- Chmiola, J.; Largeot, C.; Taberna, P.-L.; Simon, P.; Gogotsi, Y. Monolithic Carbide-Derived Carbon Films for Micro-Supercapacitors. Science 2010, 328, 480–483. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jäckel, N.; Rodner, M.; Schreiber, A.; Jeongwook, J.; Zeiger, M.; Aslan, M.; Weingarth, D.; Presser, V. Anomalous or regular capacitance? The influence of pore size dispersity on double-layer formation. J. Power Sources 2016, 326, 660–671. [Google Scholar] [CrossRef]
- Stoeckli, F.; Centeno, T.A. Pore size distribution and capacitance in microporous carbons. Phys. Chem. Chem. Phys. 2012, 14, 11589–11591. [Google Scholar] [CrossRef]
- García-Gómez, A.; Moreno-Fernández, G.; Lobato, B.; Centeno, T.A. Constant capacitance in nanopores of carbon monoliths. Phys. Chem. Chem. Phys. 2015, 17, 15687–15690. [Google Scholar] [CrossRef] [Green Version]
- Salitra, G.; Soffer, A.; Eliad, L.; Cohen, Y.; Aurbach, D. Carbon Electrodes for Double-Layer Capacitors I. Relations Between Ion and Pore Dimensions. J. Electrochem. Soc. 2000, 147, 2486–2493. [Google Scholar] [CrossRef]
- Thommes, M.; Kaneko, K.; Neimark, A.V.; Olivier, J.P.; Rodriguez-Reinoso, F.; Rouquerol, J.; Sing, K.S.W. Physisorption of gases, with special reference to the evaluation of surface area and pore size distribution (IUPAC Technical Report). Pure Appl. Chem. 2015, 87, 1051–1069. [Google Scholar] [CrossRef] [Green Version]
- Landers, J.; Gor, G.Y.; Neimark, A.V. Density functional theory methods for characterization of porous materials. Colloids Surf. A Physicochem. Eng. Asp. 2013, 437, 3–32. [Google Scholar] [CrossRef]
- Sing, K. The use of nitrogen adsorption for the characterisation of porous materials. Colloids Surf. A Physicochem. Eng. Asp. 2001, 187, 3–9. [Google Scholar] [CrossRef]
- Radlinski, A.P.; Mastalerz, M.; Hinde, A.L.; Hainbuchner, M.; Rauch, H.; Baron, M.; Lin, J.S.; Fan, L.; Thiyagarajan, P. Application of SAXS and SANS in evaluation of porosity, pore size distribution and surface area of coal. Int. J. Coal Geol. 2004, 59, 245–271. [Google Scholar] [CrossRef]
- Calo, J.M.; Hall, P.J. The application of small angle scattering techniques to porosity characterization in carbons. Carbon 2004, 42, 1299–1304. [Google Scholar] [CrossRef]
- Calo, J.M.; Hall, P.J.; Antxustegi, M. Carbon porosity characterization via small angle neutron scattering. Colloids Surf. A Physicochem. Eng. Asp. 2001, 219–232. [Google Scholar] [CrossRef]
- Perret, R.; Ruland, W. X-ray small-angle scattering of glassy carbon. J. Appl. Crystallogr. 1972, 5, 183–187. [Google Scholar] [CrossRef]
- Diduszko, R.; Swiatkowski, A.; Trznadel, B.J.J. On surface of micropores and fractal dimension of activated carbon determined on the basis of adsorption and SAXS investigations. Carbon 2000, 38, 1153–1162. [Google Scholar] [CrossRef]
- Laudisio, G.; Dash, R.K.; Singer, J.P.; Yushin, G.; Gogotsi, Y.; Fischer, J.E. Carbide-Derived Carbons: A Comparative Study of Porosity Based on Small-Angle Scattering and Adsorption Isotherms. Langmuir 2006, 22, 8945–8950. [Google Scholar] [CrossRef]
- Braun, A.; Huggins, F.E.; Seifert, S.; Ilavsky, J.; Shah, N.; Kelly, K.E.; Sarofim, A.; Huffman, G.P. Size-range analysis of diesel soot with ultra-small angle X-ray scattering. Combust. Flame 2004, 137, 63–72. [Google Scholar] [CrossRef]
- Perret, R.; Ruland, W. X-ray small-angle scattering of non-graphitizable carbons. J. Appl. Crystallogr. 1968, 1, 308–313. [Google Scholar] [CrossRef]
- Prehal, C.; Koczwara, C.; Jäckel, N.; Schreiber, A.; Burian, M.; Amenitsch, H.; Hartmann, M.A.; Presser, V.; Paris, O. Quantification of ion confinement and desolvation in nanoporous carbon supercapacitors with modelling and in situ X-ray scattering. Nat. Energy 2017, 2, 1–8. [Google Scholar] [CrossRef]
- Smarsly, B.; Antonietti, M.; Wolff, T. Evaluation of the small-angle x-ray scattering of carbons using parametrization methods. J. Chem. Phys. 2002, 116, 2618–2627. [Google Scholar] [CrossRef]
- Weth, M.; Mathias, J.; Emmerling, A.; Kuhn, J.; Fricke, J. The Structure of Carbon Blacks Measured with (Ultra)-Small Angle X-ray Scattering. J. Porous Mater. 2001, 8, 319–325. [Google Scholar] [CrossRef]
- Prehal, C.; Koczwara, C.; Jäckel, N.; Amenitsch, H.; Presser, V.; Paris, O. A carbon nanopore model to quantify structure and kinetics of ion electrosorption with in situ small-angle X-ray scattering. Phys. Chem. Chem. Phys. 2017, 19, 15549–15561. [Google Scholar] [CrossRef]
- Gibaud, A.; Xue, J.S.; Dahn, J.R. A small angle X-ray scattering study of carbons made from pyrolyzed sugar. Carbon 1996, 34, 499–503. [Google Scholar] [CrossRef]
- Avdeev, M.A.; Blagoveshchenskiĭ, N.M.; Martynov, P.N.; Mel’nikov, V.P.; Novikov, A.G.; Puchkov, A.V. Investigation of the microstructure of activated carbons by the small-angle slow neutron scattering method. Phys. Solid State 2010, 52, 985–987. [Google Scholar] [CrossRef]
- Hoinkis, E.; Lima, E.B.F.; Schubert-Bischoff, P. A Study of Carbon Black Corax N330 with Small-Angle Scattering of Neutrons and X-rays. Langmuir 2004, 20, 8823–8830. [Google Scholar] [CrossRef]
- Hoinkis, E.; Allen, A. A small angle neutron scattering study of porous graphitic materials before and after adsorption and condensation of C6D6 within the accessible pores. J. Colloid Interface Sci. 1991, 145, 540–556. [Google Scholar] [CrossRef]
- Biscoe, J.; Warren, B.E. An X-ray Study of Carbon Black. J. Appl. Phys. 1942, 13, 364–371. [Google Scholar] [CrossRef]
- Franklin, R.E. The structure of graphitic carbons. Acta Crystallogr. 1951, 4, 253–261. [Google Scholar] [CrossRef]
- Warren, B.E. X-ray Diffraction Study of Carbon Black. J. Chem. Phys. 1934, 2, 551–555. [Google Scholar] [CrossRef]
- Ruland, W.; Smarsly, B. research papers X-ray scattering of non-graphitic carbon: An improved method of evaluation. J. Appl. Crystallogr. 2002, 35, 624–633. [Google Scholar] [CrossRef]
- Faber, K.; Badaczewski, F.; Ruland, W.; Smarsly, B.M. Investigation of the Microstructure of Disordered, Non-graphitic Carbons by an Advanced Analysis Method for Wide-Angle X-ray Scattering. Z. Anorg. Allg. Chem. 2014, 640, 3107–3117. [Google Scholar] [CrossRef]
- Loeh, M.O.; Badaczewski, F.; Faber, K.; Hintner, S.; Bertino, M.F.; Mueller, P.; Metz, J.; Smarsly, B.M. Analysis of thermally induced changes in the structure of coal tar pitches by an advanced evaluation method of X-ray scattering data. Carbon 2016, 109, 823–835. [Google Scholar] [CrossRef]
- Faber, K.; Badaczewski, F.; Oschatz, M.; Mondin, G.; Nickel, W.; Kaskel, S.; Smarsly, B.M. In-Depth Investigation of the Carbon Microstructure of Silicon Carbide-Derived Carbons by Wide-Angle X-ray Scattering. J. Phys. Chem. C 2014, 118, 15705–15715. [Google Scholar] [CrossRef]
- Badaczewski, F.; Loeh, M.O.; Pfaff, T.; Dobrotka, S.; Wallacher, D.; Clemens, D.; Metz, J.; Smarsly, B.M. Peering into the structural evolution of glass-like carbons derived from phenolic resin by combining small-angle neutron scattering with an advanced evaluation method for wide-angle X-ray scattering. Carbon 2019, 141, 169–181. [Google Scholar] [CrossRef]
- Harris, P.J.F. Structure of non-graphitising carbons. Int. Mater. Rev. 1997, 42, 206–218. [Google Scholar] [CrossRef]
- Urbonaite, S.; Juarez-Galán, J.M.; Leis, J.; Rodríguez-Reinoso, F.; Svensson, G. Porosity development along the synthesis of carbons from metal carbides. Microporous Mesoporous Mater. 2008, 113, 14–21. [Google Scholar] [CrossRef]
- Oschatz, M.; Pré, P.; Dörfler, S.; Nickel, W.; Beaunier, P.; Rouzaud, J.-N.; Fischer, C.; Brunner, E.; Kaskel, S. Nanostructure characterization of carbide-derived carbons by morphological analysis of transmission electron microscopy images combined with physisorption and Raman spectroscopy. Carbon 2016, 105, 314–322. [Google Scholar] [CrossRef]
- De Tomas, C.; Suarez-Martinez, I.; Vallejos-Burgos, F.; López, M.J.; Kaneko, K.; Marks, N.A. Structural prediction of graphitization and porosity in carbide-derived carbons. Carbon 2017, 119, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Daniels, H.; Brydson, R.; Rand, B.; Brown, A. Investigating carbonization and graphitization using electron energy loss spectroscopy (EELS) in the transmission electron microscope (TEM). Philos. Mag. 2007, 87, 4073–4092. [Google Scholar] [CrossRef]
- Petzold, A.; Juhl, A.; Scholz, J.; Ufer, B.; Goerigk, G.; Fröba, M.; Ballauff, M.; Mascotto, S.; Goerigk, G.J. Distribution of Sulfur in Carbon/Sulfur Nanocomposites Analyzed by Small-Angle X-ray Scattering. Langmuir 2016, 32, 2780–2786. [Google Scholar] [CrossRef] [PubMed]
- Jafta, C.J.; Petzold, A.; Risse, S.; Clemens, D.; Wallacher, D.; Goerigk, G.J.; Ballauff, M. Correlating pore size and shape to local disorder in microporous carbon: A combined small angle neutron and X-ray scattering study. Carbon 2017, 123, 440–447. [Google Scholar] [CrossRef]
- Härk, E.; Petzold, A.; Goerigk, G.J.; Ballauff, M.; Kent, B.; Keiderling, U.; Palm, R.; Vaas, I.; Lust, E. The effect of a binder on porosity of the nanoporous RP-20 carbon. A combined study by small angle X-ray and neutron scattering. Microporous Mesoporous Mater. 2019, 275, 139–146. [Google Scholar] [CrossRef]
- Härk, E.; Petzold, A.; Goerigk, G.J.; Risse, S.; Tallo, I.; Härmas, R.; Lust, E.; Ballauff, M. Carbide derived carbons investigated by small angle X-ray scattering: Inner surface and porosity vs. graphitization. Carbon 2019, 11, 398–408. [Google Scholar] [CrossRef]
- Mascotto, S.; Wallacher, D.; Brandt, A.; Hauss, T.; Thommes, M.; Zickler, G.A.; Funari, S.S.; Timmann, A.; Smarsly, B.M. Analysis of Microporosity in Ordered Mesoporous Hierarchically Structured Silica by Combining Physisorption With in Situ Small-Angle Scattering (SAXS and SANS). Langmuir 2009, 25, 12670–12681. [Google Scholar] [CrossRef]
- Mascotto, S.; Kuźmicz, D.; Wallacher, D.; Siebenbürger, M.; Clemens, D.; Risse, S.; Yuan, J.; Antonietti, M.; Ballauff, M. Poly(ionic liquid)-derived nanoporous carbon analyzed by combination of gas physisorption and small-angle neutron scattering. Carbon 2015, 82, 425–435. [Google Scholar] [CrossRef]
- Härk, E.; Kardjilov, N.; Hilger, A.; Petzold, A.; Risse, S.; Vaas, I.; Goerigk, G.J.; Jafta, C.J.; Ballauff, M.; Lust, E. The Nanoporous RP-20 Carbon Electrode as a Model for Energy Storage and Conversion Systems—Studied with µCT, SAXS and SANS Techniques. ECS Trans. 2017, 77, 1133–1144. [Google Scholar] [CrossRef]
- Porod, G. Die Röntgenkleinwinkelstreuung von dichtgepackten kolloiden Systemen. Kolloid Z. 1951, 124, 83–114. [Google Scholar] [CrossRef]
- Glatter, O.; Kratky, O. Small Angle X-ray Scattering; Academic Press: London, UK, 1982; pp. 1–515. [Google Scholar] [CrossRef]
- Cohaut, N.; Blanche, C.; Dumas, D.; Guet, J.M.; Rouzaud, J.N. A small angle X-ray scattering study on the porosity of anthracites. Carbon 2000, 38, 1391–1400. [Google Scholar] [CrossRef]
- Ruland, W. Apparent fractal dimensions obtained from small-angle scattering of carbon materials. Carbon 2001, 39, 323–324. [Google Scholar] [CrossRef]
- Nguyen, T.X.; Bhatia, S.K. Characterization of accessible and inaccessible pores in microporous carbons by a combination of adsorption and small angle neutron scattering. Carbon 2012, 50, 3045–3054. [Google Scholar] [CrossRef]
- Mileeva, Z.; Ross, D.K.; Wilkinson, D.; King, S.M.; Ryan, T.A.; Sharrock, H. The use of small angle neutron scattering with contrast matching and variable adsorbate partial pressures in the study of porosity in activated carbons. Carbon 2012, 50, 5062–5075. [Google Scholar] [CrossRef] [Green Version]
- Jänes, A.; Kurig, H.; Lust, E. Characterisation of activated nanoporous carbon for supercapacitor electrode materials. Carbon 2007, 45, 1226–1233. [Google Scholar] [CrossRef]
- Kurig, H.; Russina, M.; Tallo, I.; Siebenbürger, M.; Romann, T.; Lust, E. The suitability of infinite slit-shaped pore model to describe the pores in highly porous carbon materials. Carbon 2016, 100, 617–624. [Google Scholar] [CrossRef]
- Ruch, P.W.; Hahn, M.; Cericola, D.; Menzel, A.; Kötz, R.; Wokaun, A. A dilatometric and small-angle X-ray scattering study of the electrochemical activation of mesophase pitch-derived carbon in non-aqueous electrolyte solution. Carbon 2010, 8, 2–10. [Google Scholar] [CrossRef]
- Kalliat, M.; Kwak, C.Y.; Schmidt, P.W. Small-Angle X-ray Investigation of the Porosity in Coals. New Approaches Coal Chem. 1981, 3–22. [Google Scholar] [CrossRef] [Green Version]
- Debye, P.; Anderson, H.R.; Brumberger, H. Scattering by an Inhomogeneous Solid. II. The Correlation Function and Its Application. J. Appl. Phys. 1957, 28, 679–683. [Google Scholar] [CrossRef]
- Schiller, C.; Mering, J. Diffusion centrale des rayons X par des carbones graphitables. Déviation de la loi de Porod. C. R. Acad. Sci. Paris Ser. B 1967, 264, 247–250. [Google Scholar]
- Ruland, W. Carbon Fibers. Adv. Mater. 1990, 2, 528–536. [Google Scholar] [CrossRef]
- Stoeckel, D.; Wallacher, D.; Zickler, G.A.; Perlich, J.; Tallarek, U.; Smarsly, B.M. Coherent analysis of disordered mesoporous adsorbents using small angle X-ray scattering and physisorption experiments. Phys. Chem. Chem. Phys. 2014, 16, 6583–6592. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Méring, J.; Tchoubar, D. Interprétation de la diffusion centrale des rayons X par les systèmes poreux. I. J. Appl. Crystallogr. 1968, 1, 153–165. [Google Scholar] [CrossRef]
- Bacon, G.E. The interlayer spacing of graphite. Acta Crystallogr. 1951, 4, 558–561. [Google Scholar] [CrossRef]
- Palm, R.; Härmas, R.; Härk, E.; Kent, B.; Kurig, H.; Koppel, M.; Russina, M.; Tallo, I.; Romann, T.; Mata, J.P.; et al. Study of the Structural Curvature in Mo2C Derived Carbons with Contrast Matched Small-Angle Neutron Scattering. Carbon 2021, 171, 695–703. [Google Scholar] [CrossRef]
- Keiderling, U. The new ’BerSANS-PC’software for reduction and treatment of small angle neutron scattering data. Appl. Phys. A 2002, 74, 1455–1457. [Google Scholar] [CrossRef]
- Keiderling, U.; Wiedenmann, A. New SANS instrument at the BER II reactor in Berlin, Germany. Phys. B Condens. Matter 1995, 213, 895–897. [Google Scholar] [CrossRef]
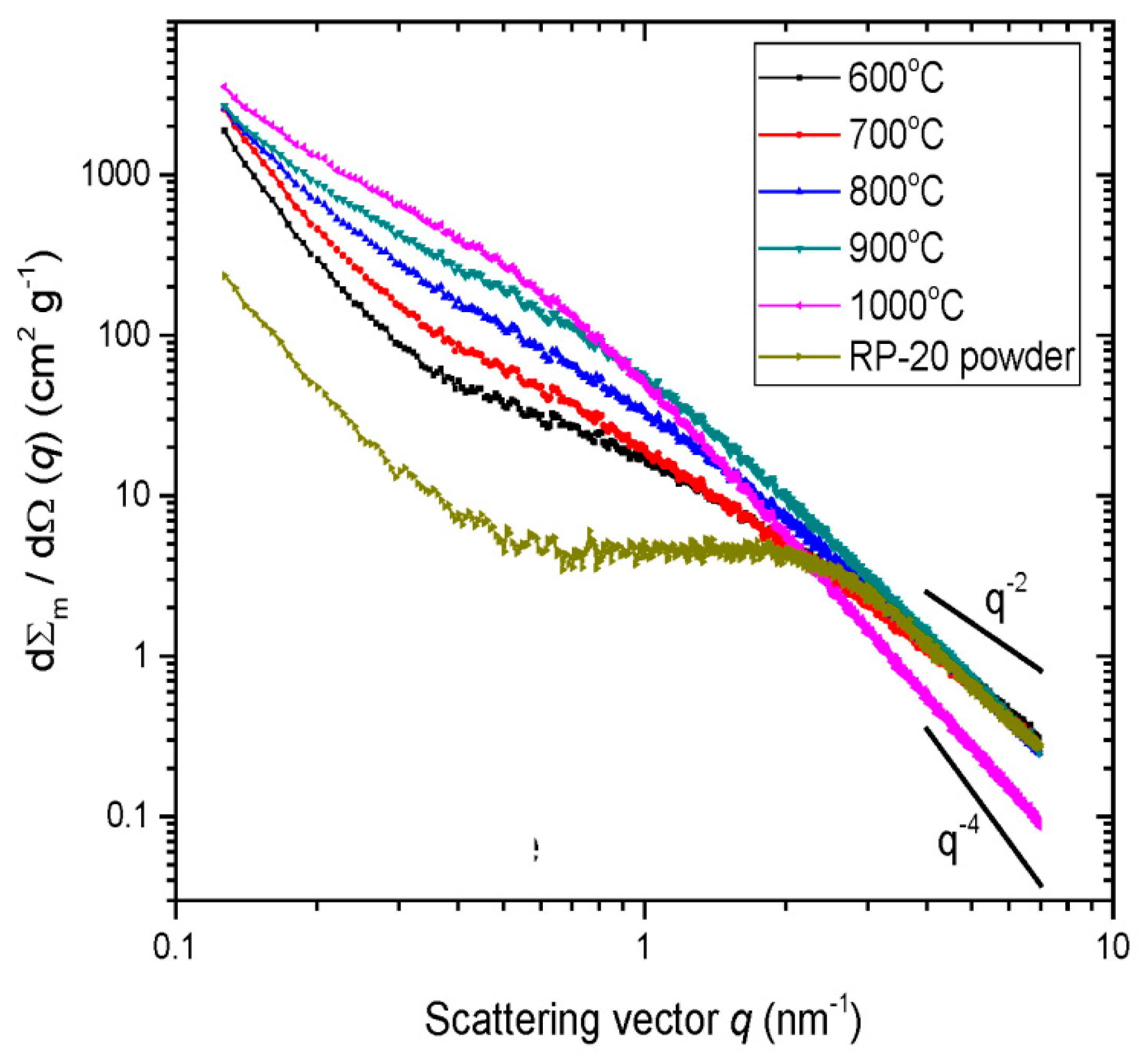

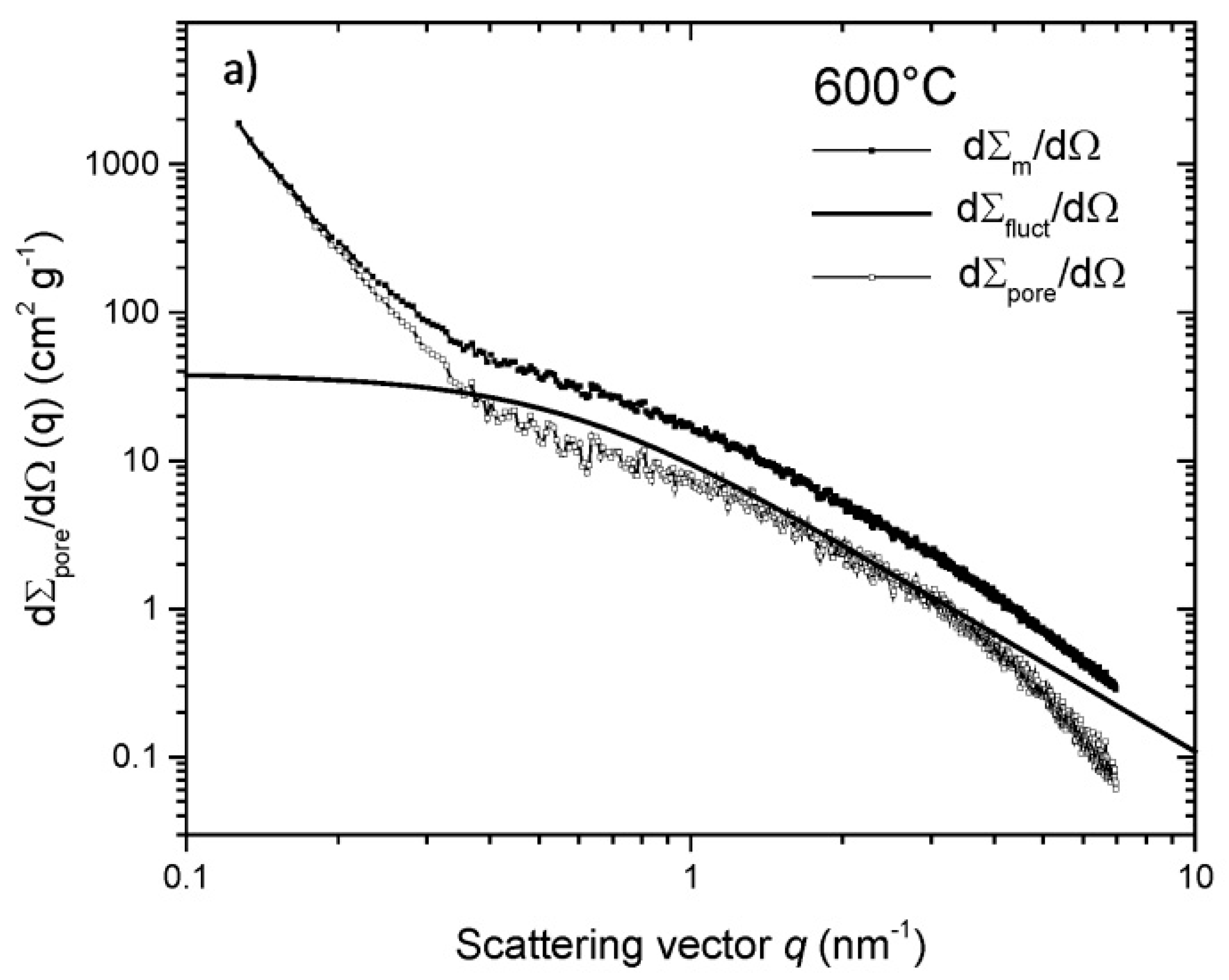
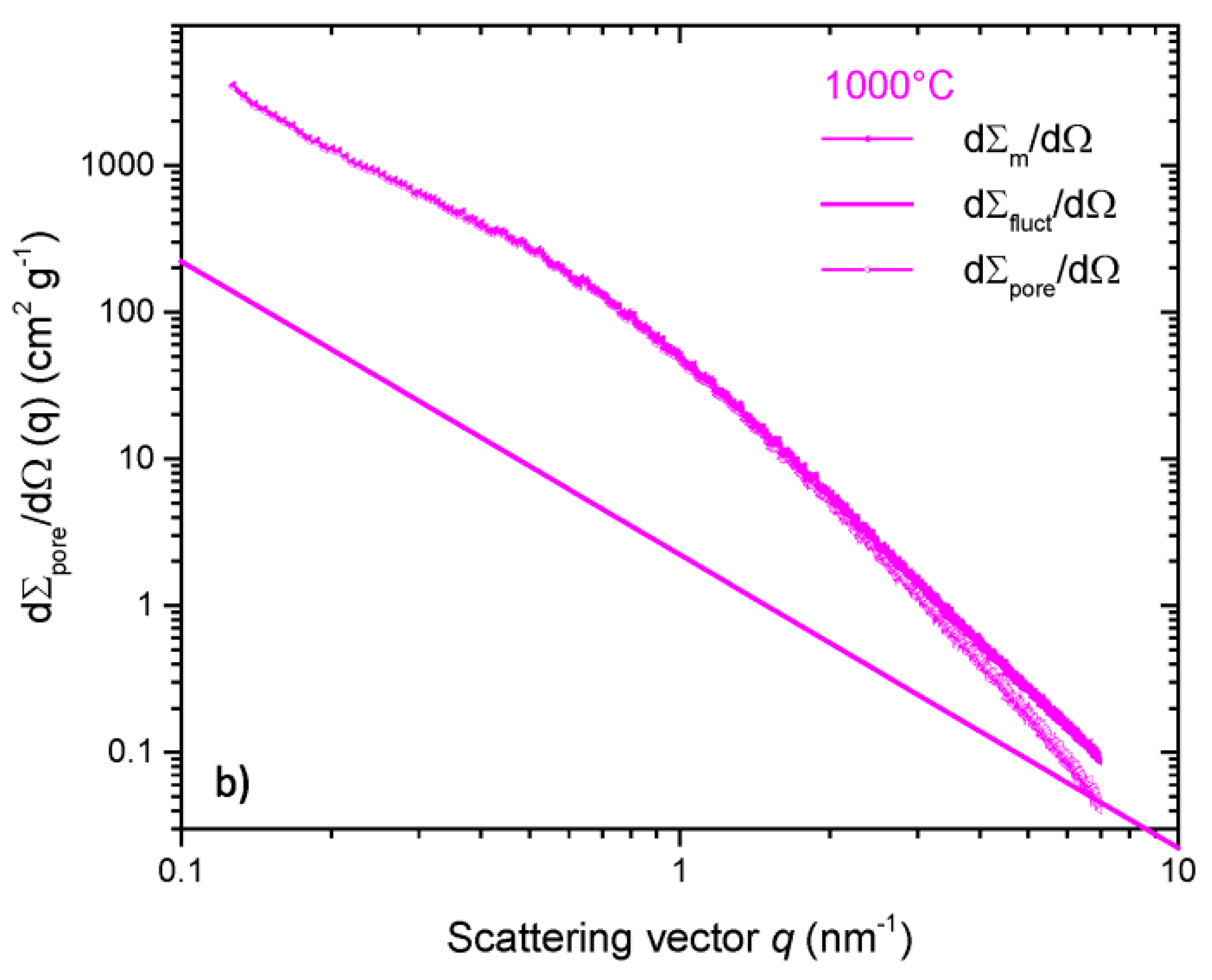

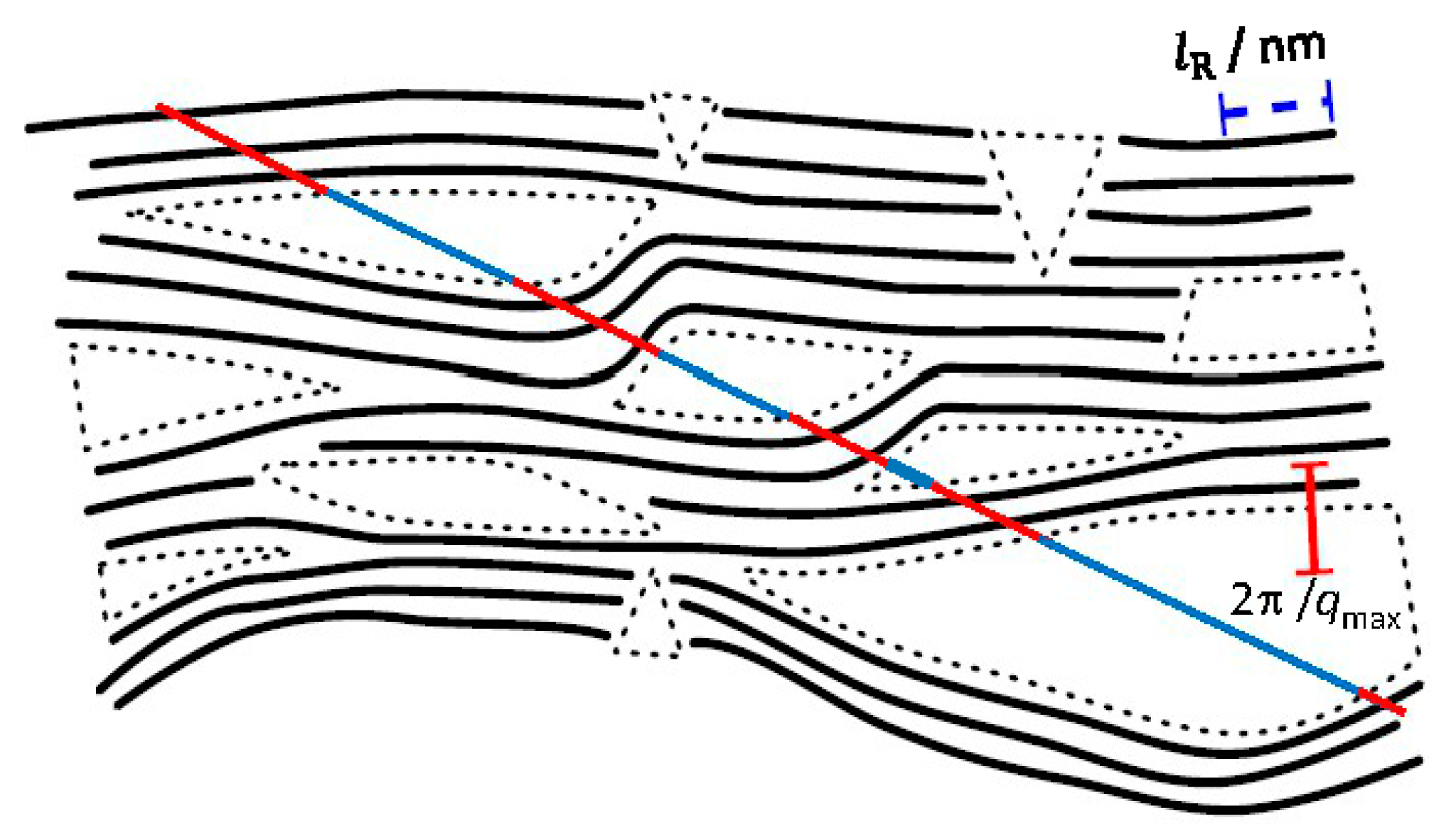
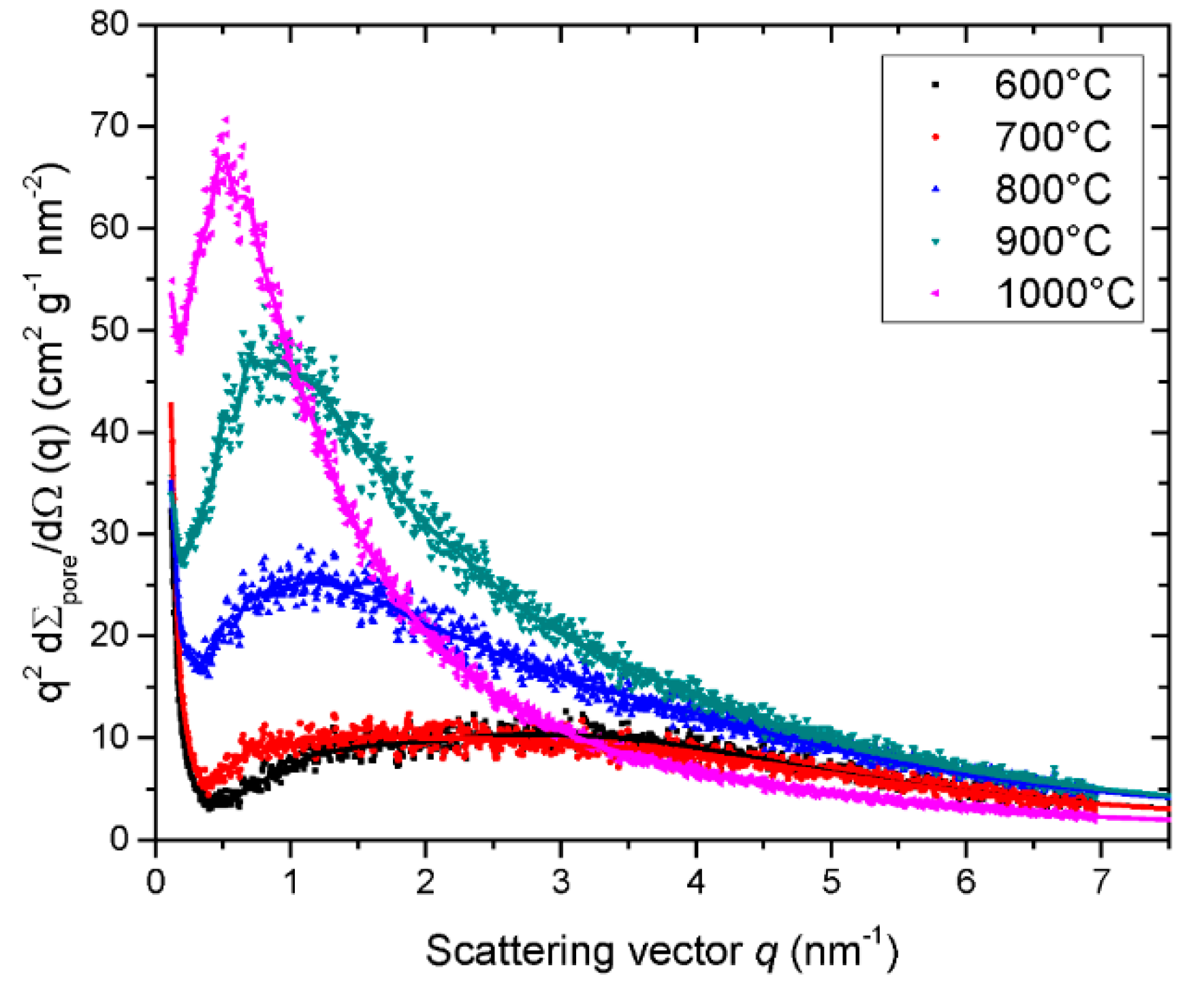
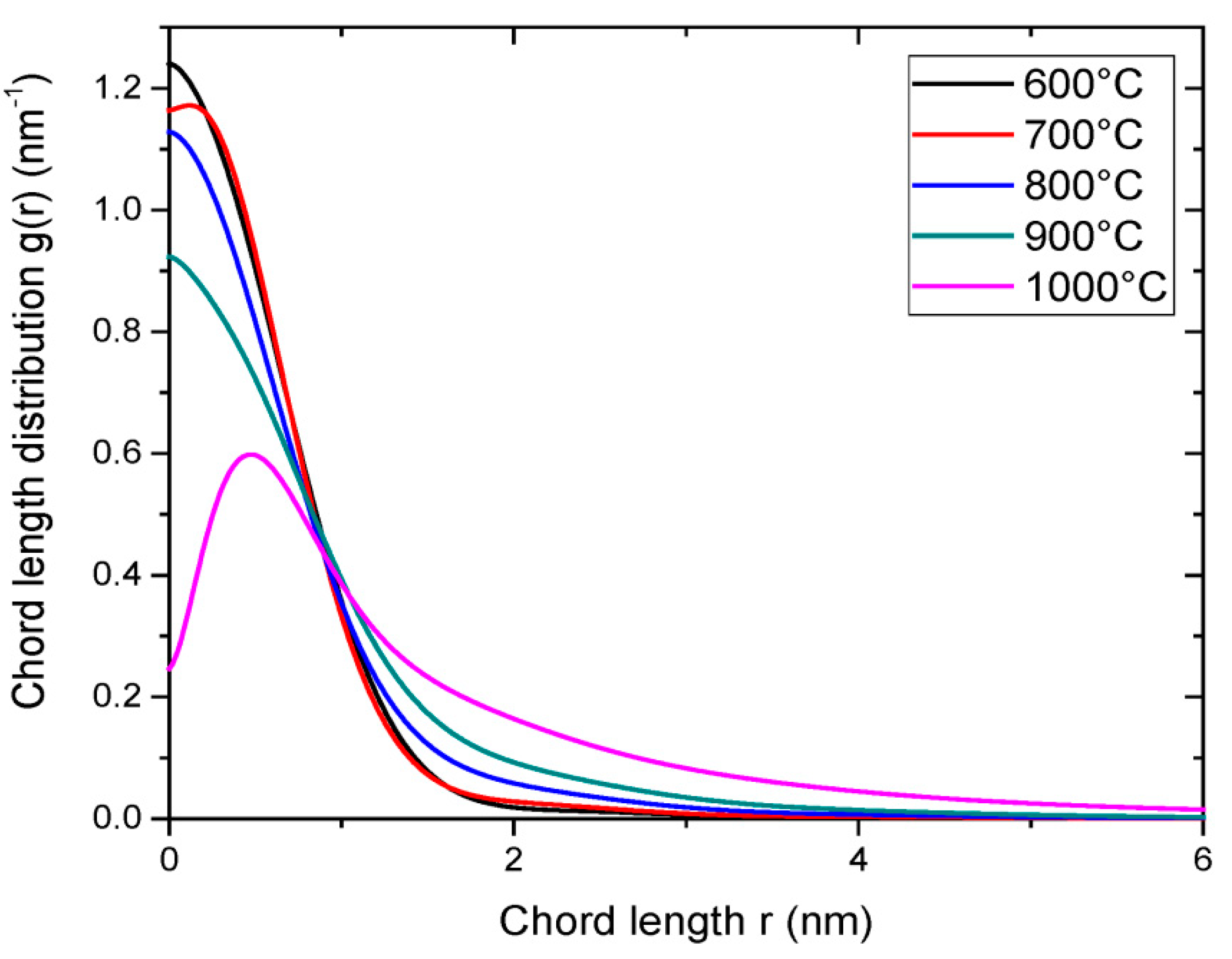
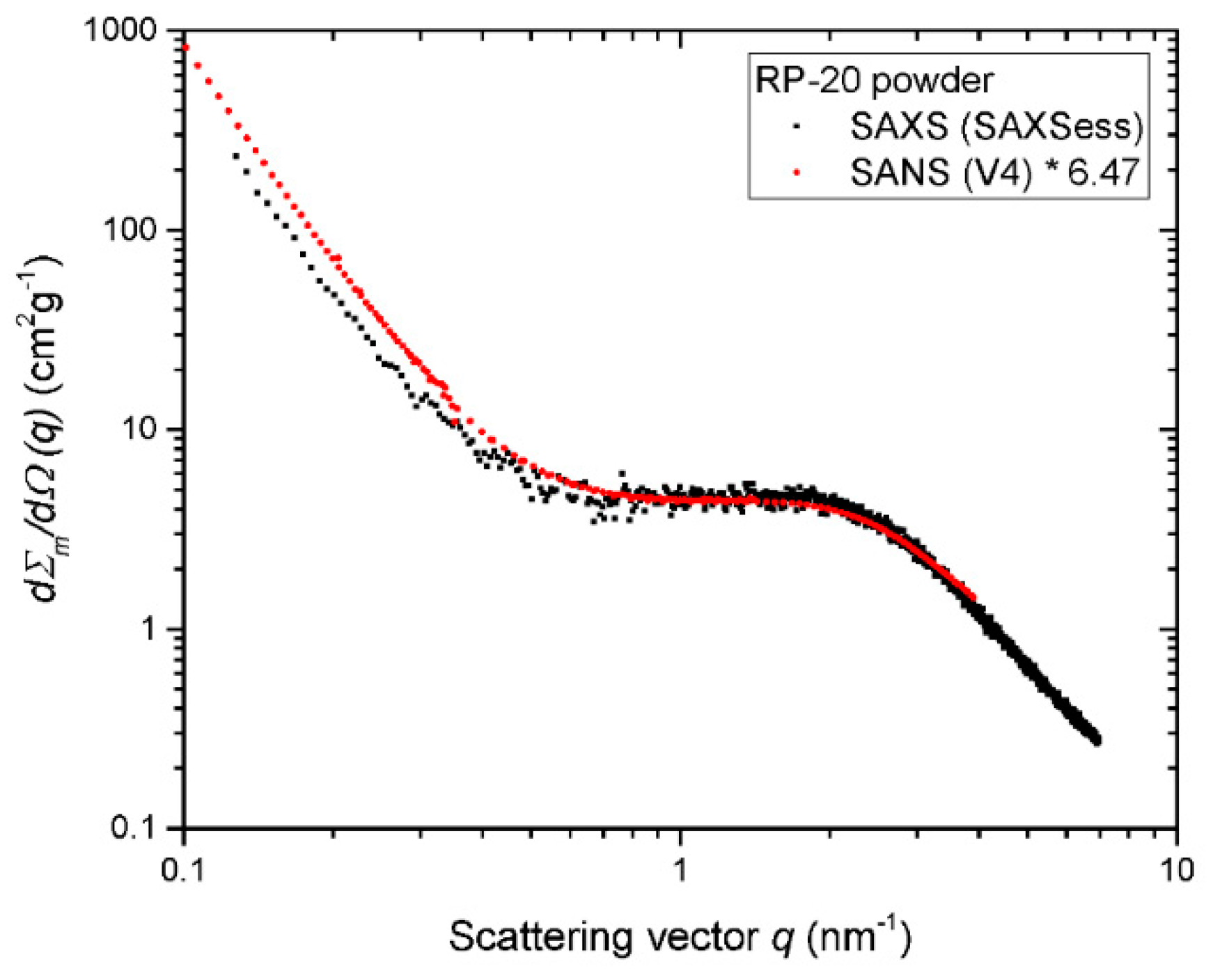
| Property | 600 [75] | 700 [75] | 800 [75] | 900 [75] | 1000 [75] | ACN [73] | RP-20 [74] |
|---|---|---|---|---|---|---|---|
| /cm2 g−1 nm−2 | 10.8 ± 0.2 | 9.7 ± 0.2 | 7.6 ± 0.2 | 7.9 ± 0.1 | 2.23 ± 0.03 | 7.77 ± 0.09 | 10.1 ± 0.1 |
| /cm2 g−1 nm−3 | 3.9 ± 0.2 | 4.0 ± 0.2 | 6.8 ± 0.2 | 9.0 ± 0.2 | 6.8 ± 0.1 | 4.2 ± 0.1 | 3.6 ± 0.2 |
| /cm2 g−1 nm−4 | 0.112 ± 0.004 | 0.110 ± 0. 004 | 0.152 ± 0.005 | 0.158 ± 0.002 | 0.072 ± 0.001 | 0.126 ± 0.002 | 0.098 ± 0.002 |
| /m2 g−1 | 965 ± 102 | 950 ± 100 | 1310 ± 137 | 1363 ± 137 | 621 ± 62 | 1090 ± 110 | 842 ± 86 |
| 0.27 ± 0.02 | 0.28 ± 0.02 | 0.47 ± 0.03 | 0.63 ± 0.03 | 0.47 ± 0.03 | 0.29 ± 0.02 | 0.25 ± 0.02 | |
| /nm | 0.57 ± 0.04 | 0.59 ± 0.04 | 0.72 ± 0.03 | 0.92 ± 0.02 | 1.52 ± 0.02 | 0.54 ± 0.03 | 0.59 ± 0.03 |
| /nm | 0.58 ± 0.1 | 0.63 ± 0.1 | 0.74 ± 0.2 | 0.93 ± 0.2 | 1.71 ± 0.1 | 0.53 ± 0.1 | 0.62 ± 0.06 |
| /nm | 0.78 ± 0.6 | 0.81 ± 0.05 | 1.35 ± 0.1 | 2.5 ± 0.2 | 2.9 ± 0.1 | 0.76 ± 0.05 | 0.79 ± 0.04 |
| /nm | 2.1 ± 0.2 | 2.1 ± 0.2 | 1.5 ± 0.1 | 1.5 ± 0.1 | 3.2 ± 0.2 | 1.9 ± 0.2 | 2.4 ± 0.2 |
| /nm | 4.1 ± 0.3 | 5.2 ± 0.3 | 4.5 ± 0.2 | 4.9 ± 0.1 | 9.7 ± 0.1 | 1.2 ± 0.1 | 0.91 ± 0.1 |
| 7.2 ± 0.02 | 8.81 ± 0.09 | 6.25 ± 0.02 | 5.33 ± 0.01 | 6.38 ± 0.02 | 2.22 ± 0.06 | 1.54 ± 0.09 | |
| /nm | 4.0 ± 0.2 | 9.0 ± 0.5 | >20 | >20 | >20 | 1.0 ± 0.1 | 1.2 ± 0.1 |
| /nm−1 | 1.24 ± 0.04 | 1.16 ± 0.05 | 1.13 ± 0.03 | 0.92 ± 0.02 | 0.25 ± 0.1 | 1.0 ± 0.02 | 0.75 ± 0.08 |
| 0.36 ± 0.03 | 0.32 ± 0.03 | 0.25 ± 0.02 | 0.26 ± 0.02 | 0.074 ± 0.004 | 0.25 ± 0.02 | 0.33 ± 0.03 |
| Carbon/Contrast Matching Agent | Density (g cm−3) at 25 °C | Neutron SLD (10−6 Å2) | X-ray SLD (10−6 Å2) |
|---|---|---|---|
| Carbon | 2 | 6.334 | 16.159 |
| Deuterated Water | 1.107 | 6.375 | 9.429 |
| Deuterated Toluene | 0.943 | 5.664 | 8.008 |
| Sulfur | 2.07 | 1.107 | 17.896 |
| Deuterated p-Xylene | 0.861 | 5.350 | 7.311 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Härk, E.; Ballauff, M. Carbonaceous Materials Investigated by Small-Angle X-ray and Neutron Scattering. C 2020, 6, 82. https://doi.org/10.3390/c6040082
Härk E, Ballauff M. Carbonaceous Materials Investigated by Small-Angle X-ray and Neutron Scattering. C. 2020; 6(4):82. https://doi.org/10.3390/c6040082
Chicago/Turabian StyleHärk, Eneli, and Matthias Ballauff. 2020. "Carbonaceous Materials Investigated by Small-Angle X-ray and Neutron Scattering" C 6, no. 4: 82. https://doi.org/10.3390/c6040082
APA StyleHärk, E., & Ballauff, M. (2020). Carbonaceous Materials Investigated by Small-Angle X-ray and Neutron Scattering. C, 6(4), 82. https://doi.org/10.3390/c6040082