Prediction of the Near-Infrared Absorption Spectrum of Single-Walled Carbon Nanotubes Using a Bayesian Regularized Back Propagation Neural Network Model
Abstract
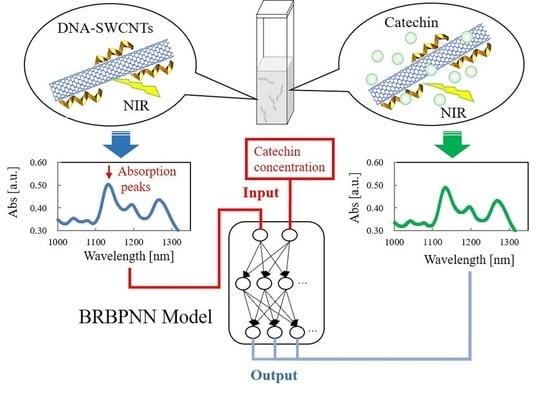
:1. Introduction
2. Materials and Methods
2.1. Sample Data
2.2. Bayesian Regularized Backpropagation Neural Network
2.3. Input/Output Data and the Verification Method
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sni, K.S.; Thomas, B.; Kar, R.V. A Comprehensive Review on CNTs and CNT-Reinforced Composites: Syntheses, Characteristics and Applications. Mater. Today Commun. 2020, 25, 101546. [Google Scholar] [CrossRef]
- Nakamura, G.; Narimatsu, K.; Niidome, Y.; Nakashima, N. Green Tea Solution Individually Solubilizes Single-walled Carbon Nanotubes. Chem. Lett. 2007, 36, 1140–1141. [Google Scholar] [CrossRef]
- Miyashiro, D.; Hamano, R.; Umemura, K. A Review of Applications Using Mixed Materials of Cellulose, Nanocellulose and Carbon Nanotubes. Nanomaterials 2020, 10, 186. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Barone, P.W.; Baik, S.; Heller, D.A.; Strano, M.S. Near-infrared optical sensors based on single-walled carbon nanotubes. Nat. Mater. 2005, 4, 86–92. [Google Scholar] [CrossRef] [PubMed]
- Zheng, M.; Jagota, A.; Semke, E.D.; Diner, R.S.; McLean, R.S.; Lustig, S.R.; Richardson, R.E.; Tassi, N.G. DNA-assisted dispersion and separation of carbon nanotubes. Nat. Mater. 2003, 2, 338–342. [Google Scholar] [CrossRef] [PubMed]
- Nakashima, N.; Okuzono, S.; Murakami, H.; Nakai, T.; Yoshikawa, K. DNA dissolves single-walled carbon nanotubes in water. Chem. Lett. 2003, 32, 456–457. [Google Scholar] [CrossRef]
- Ishibashi, Y.; Ito, M.; Homma, Y.; Umemura, K. Monitoring the antioxidant effects of catechin using single-walled carbon nanotubes: Comparative analysis by near-infrared absorption and near-infrared photoluminescence. Colloids Surf. B Biointerfaces 2018, 161, 139–146. [Google Scholar] [CrossRef] [PubMed]
- Bachilo, S.M.; Strano, M.S.; Kittrell, C.; Hauge, R.H.; Smalley, R.E.; Weisman, R.B. Structure-Assigned Optical Spectra of Single-Walled Carbon Nanotubes. Science 2002, 298, 2361–2366. [Google Scholar] [CrossRef] [Green Version]
- Zhao, E.H.; Ergul, B.; Zhao, W. Caffeine’s Antioxidant Potency Optically Sensed with Double-Stranded DNA-Encased Single-Walled Carbon Nanotubes. J. Phys. Chem. B. 2015, 119, 4068. [Google Scholar] [CrossRef]
- Hamano, R.; Miyashiro, D.; Umemura, K. Study on optical response sensitivity in hybrid of single-walled carbon nanotubes mixed with double-stranded DNA and carboxymethylcellulose. Opt. Mater. 2020, 109, 110386. [Google Scholar] [CrossRef]
- Miyashiro, D.; Taira, H.; Hamano, R.; Reserva, R.L.; Umemura, K. Mechanical vibration of single-walled carbon nanotubes at different lengths and carbon nanobelts by modal analysis method. Compos. Part C 2020, 2, 100028. [Google Scholar] [CrossRef]
- Miyashiro, D.; Taira, H.; Umemura, K. Vibration analysis of single-stranded DNA-wrapped single-walled carbon nanotubes using finite element method. Compos. Part B Eng. 2019, 173, 106896. [Google Scholar] [CrossRef]
- Miyashiro, D.; Hamano, R.; Taira, H.; Umemura, K. Analysis of vibration behavior in single strand DNA-wrapped single-walled carbon nanotubes adhered to lipid membranes. Forces Mech. 2021, 2, 100008. [Google Scholar] [CrossRef]
- Chen, X.; Lin, X. Big Data Deep Learning: Challenges and Perspectives. IEEE Access 2014, 2, 514–525. [Google Scholar] [CrossRef]
- Zhang, Y.; Guo, Q.; Wang, J. Big data analysis using neural networks. Adv. Eng. Sci. 2017, 49, 9–18. [Google Scholar] [CrossRef]
- Al-Saffar, A.A.M.; Tao, H.; Talab, M.A. Review of deep convolution neural network in image classification. In Proceedings of the 2017 International Conference on Radar, Antenna, Microwave, Electronics, and Telecommunications (ICRAMET), Jakarta, Indonesia, 23–24 October 2017. [Google Scholar] [CrossRef]
- Wang, D.; Khosla, A.; Gargeya, R.; Irshad, H.; Beck, A. Deep Learning for Identifying Metastatic Breast Cancer. arXiv 2016, arXiv:1606.05718. [Google Scholar]
- Deng, L.; Hinton, G.; Kingsbury, B. New types of deep neural network learning for speech recognition and related applications: An overview. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013. [Google Scholar] [CrossRef]
- van Hasselt, H.; Guez, A.; Silver, D. Deep Reinforcement Learning with Double Q-Learning. In Proceedings of the AAAI Conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016. [Google Scholar]
- Geng, Z.; Zhang, Y.; Li, C.; Han, Y.; Cui, Y.; Yu, B. Energy optimization and prediction modeling of petrochemical industries: An improved convolutional neural network based on cross-feature. Energy 2020, 194, 116851. [Google Scholar] [CrossRef]
- Pang, Z.; Niu, F.; O’Neill, Z. Solar radiation prediction using recurrent neural network and artificial neural network: A case study with comparisons. Renew. Energy 2020, 156, 279–289. [Google Scholar] [CrossRef]
- Dao, D.V.; Jaafari, A.; Bayat, M.; Mafi-Gholami, D.; Qi, C.; Moayedi, H.; Phong, T.V.; Ly, H.-B.; Le, T.-T.; Trinh, P.T.; et al. A spatially explicit deep learning neural network model for the prediction of landslide susceptibility. CATENA 2020, 188, 104451. [Google Scholar] [CrossRef]
- Kumar, P.; Lai, S.H.; Mohd, N.S.; Kamal, M.R.; Afan, H.A.; Ahmed, A.N.; Sherif, M.; Sefelnasr, A.; El-Shafie, A. Optimised neural network model for river-nitrogen prediction utilizing a new training approach. PLoS ONE 2020, 15, e0239509. [Google Scholar] [CrossRef]
- Ahmed, K.T.; Park, S.; Jiang, Q.; Yeu, Y.; Hwang, T.; Zhang, W. Network-based drug sensitivity prediction. BMC Med. Genom. 2020, 13, 193. [Google Scholar] [CrossRef] [PubMed]
- Nistal-Nuño, B. A neural network for prediction of risk of nosocomial infection at intensive care units: A didactic preliminary model. Einstein 2020, 18, eAO5480. [Google Scholar] [CrossRef]
- Chen, Y.C.; Zhang, Z.; Yoon, E. Early Prediction of Single-Cell Derived Sphere Formation Rate Using Convolutional Neural Network Image Analysis. Anal. Chem. 2020, 92, 7717–7724. [Google Scholar] [CrossRef] [PubMed]
- Le, T.-T. Prediction of tensile strength of polymer carbon nanotube composites using practical machine learning method. J. Compos. Mater. 2020, 55, 787–811. [Google Scholar] [CrossRef]
- Hajilounezhad, T.; Oraibi, Z.A.; Surya, R.; Bunyak, F.; Maschmann, M.R.; Calyam, P.; Palaniappan, K. Exploration of Carbon Nanotube Forest Synthesis-Structure Relationships Using Physics-Based Simulation and Machine Learning. In Proceedings of the 2019 IEEE Applied Imagery Pattern Recognition Workshop (AIPR), Washington, DC, USA, 15–17 October 2019. [Google Scholar] [CrossRef]
- Yang, Y.; Zheng, M.; Jagota, A. Learning to predict single-wall carbon nanotube-recognition DNA sequences. NPJ Comput. Mater. 2019, 5, 3. [Google Scholar] [CrossRef]
- Matsukawa, Y.; Ohura, S.; Umemura, K. Differences in the response of the near-infrared absorbance spectra of single-walled carbon nanotubes; Effects of chirality and wrapping polymers. Colloids Surf. B Biointerfaces 2018, 172, 684–689. [Google Scholar] [CrossRef]
- Xu, Y.; Pehrsson, P.E.; Chen, L.W.; Zhang, R.; Zhao, W. Double-stranded DNA single-walled carbon nanotube hybrids for optical hydrogen peroxide and glucose sensing. J. Phys. Chem. C. 2007, 111, 8638. [Google Scholar] [CrossRef]
- Levenberg, K. A method for the solution of certain non-linear problems in least squares. Quart. Appl. Math. 1944, 2, 164–168. [Google Scholar] [CrossRef] [Green Version]
- Mackay, C.J.D. Bayesian Interpolation. Neural Comput. 1992, 4, 415–447. [Google Scholar] [CrossRef]
- Foresee, D.F.; Hagan, T.M. GAUSS-Newton Approximation to Bayesian Learning. In Proceedings of the International Conference on Neural Networks, Houston, TX, USA, 12 June 1997. [Google Scholar] [CrossRef]
- Yamazaki, Y.; Umemura, K. Sensing of epigallocatechin gallate and tannic acid based on near infrared optical spectroscopy of DNA-wrapped single-walled carbon nanotube hybrids. J. Near Infrared Spectrosc. 2020, 29, 73–83. [Google Scholar] [CrossRef]
- Miyashiro, D.; Ohtsuki, M.; Shimamoto, Y.; Wakayama, J.; Kunioka, Y.; Kobayashi, T.; Ishiwata, S.; Yamada, T. Radial stiffness characteristics of the overlap regions of sarcomeres in isolated skeletal myofibrils in pre-force generating state. Biophys. Physico. 2017, 14, 207–220. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Miyashiro, D.; Akiyama, N.; Wakayama, J.; Kunioka, Y.; Yamada, T. Radial stability of the actomyosin filament latice in isolated skeletal myofibrils studied using atomicforce microscopy. J. Physiol. Sci. 2013, 63, 299–310. [Google Scholar] [CrossRef] [PubMed]





| Input Data | Output Data | |||
|---|---|---|---|---|
| Catechin Concentration [μg/mL] | (8,4)/(9,4) Peak | (8,4)/(9,4) Peak | ||
| Absorption [a.u.] | Data Type | Absorption [a.u.] | Wavelength [nm] | |
| 15 | 0.513 | Verification | 0.502 ± 0.009 | 1135.0 ± 0.1 |
| Prediction | 0.499 ± 0.000 | 1134.8 ± 0.3 | ||
| 1.5 | 0.499 | Verification | 0.491 ± 0.005 | 1133.5 ± 0.2 |
| Prediction | 0.489 ± 0.001 | 1133.4 ± 0.2 | ||
| 0.15 | 0.500 | Verification | 0.461 ± 0.005 | 1133.0 ± 0.2 |
| Prediction | 0.461 ± 0.001 | 1132.9 ± 0.2 | ||
| 0.075 | 0.498 | Verification | 0.457 ± 0.001 | 1133.0 ± 0.0 |
| Prediction | 0.458 ± 0.001 | 1133.0 ± 0.0 | ||
| 0.030 | 0.500 | Verification | 0.457 ± 0.006 | 1133.0 ± 0.0 |
| Prediction | 0.453 ± 0.002 | 1133.0 ± 0.0 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Onishi, T.; Matsukawa, Y.; Yamazaki, Y.; Miyashiro, D. Prediction of the Near-Infrared Absorption Spectrum of Single-Walled Carbon Nanotubes Using a Bayesian Regularized Back Propagation Neural Network Model. C 2021, 7, 80. https://doi.org/10.3390/c7040080
Onishi T, Matsukawa Y, Yamazaki Y, Miyashiro D. Prediction of the Near-Infrared Absorption Spectrum of Single-Walled Carbon Nanotubes Using a Bayesian Regularized Back Propagation Neural Network Model. C. 2021; 7(4):80. https://doi.org/10.3390/c7040080
Chicago/Turabian StyleOnishi, Takao, Yuji Matsukawa, Yuto Yamazaki, and Daisuke Miyashiro. 2021. "Prediction of the Near-Infrared Absorption Spectrum of Single-Walled Carbon Nanotubes Using a Bayesian Regularized Back Propagation Neural Network Model" C 7, no. 4: 80. https://doi.org/10.3390/c7040080
APA StyleOnishi, T., Matsukawa, Y., Yamazaki, Y., & Miyashiro, D. (2021). Prediction of the Near-Infrared Absorption Spectrum of Single-Walled Carbon Nanotubes Using a Bayesian Regularized Back Propagation Neural Network Model. C, 7(4), 80. https://doi.org/10.3390/c7040080