A Grand Canonical Monte Carlo Simulation for the Evaluation of Pore Size Distribution of Nuclear-Grade Graphite from Kr Adsorption Isotherms
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental
2.2. Modelling
3. Results and Discussion
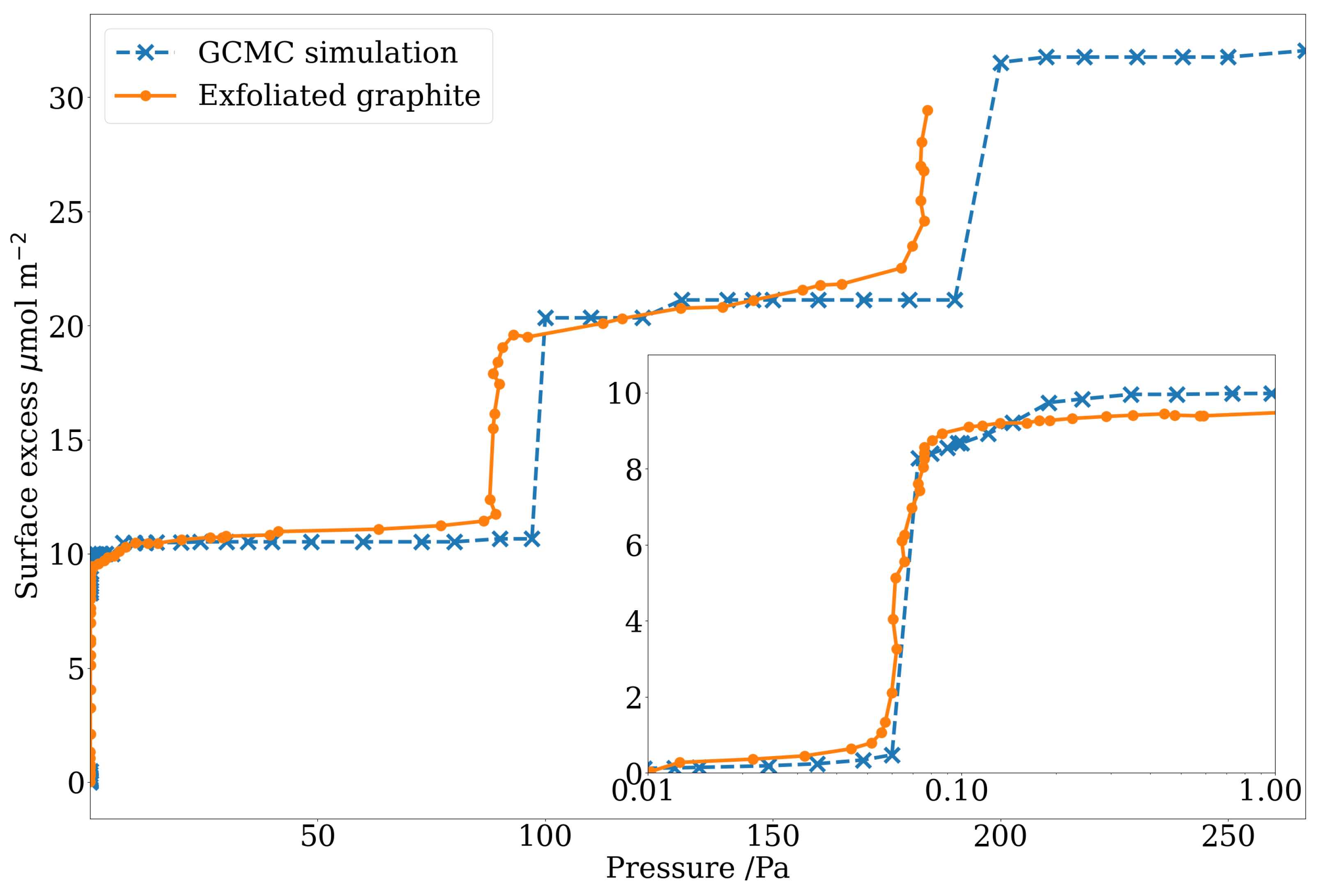
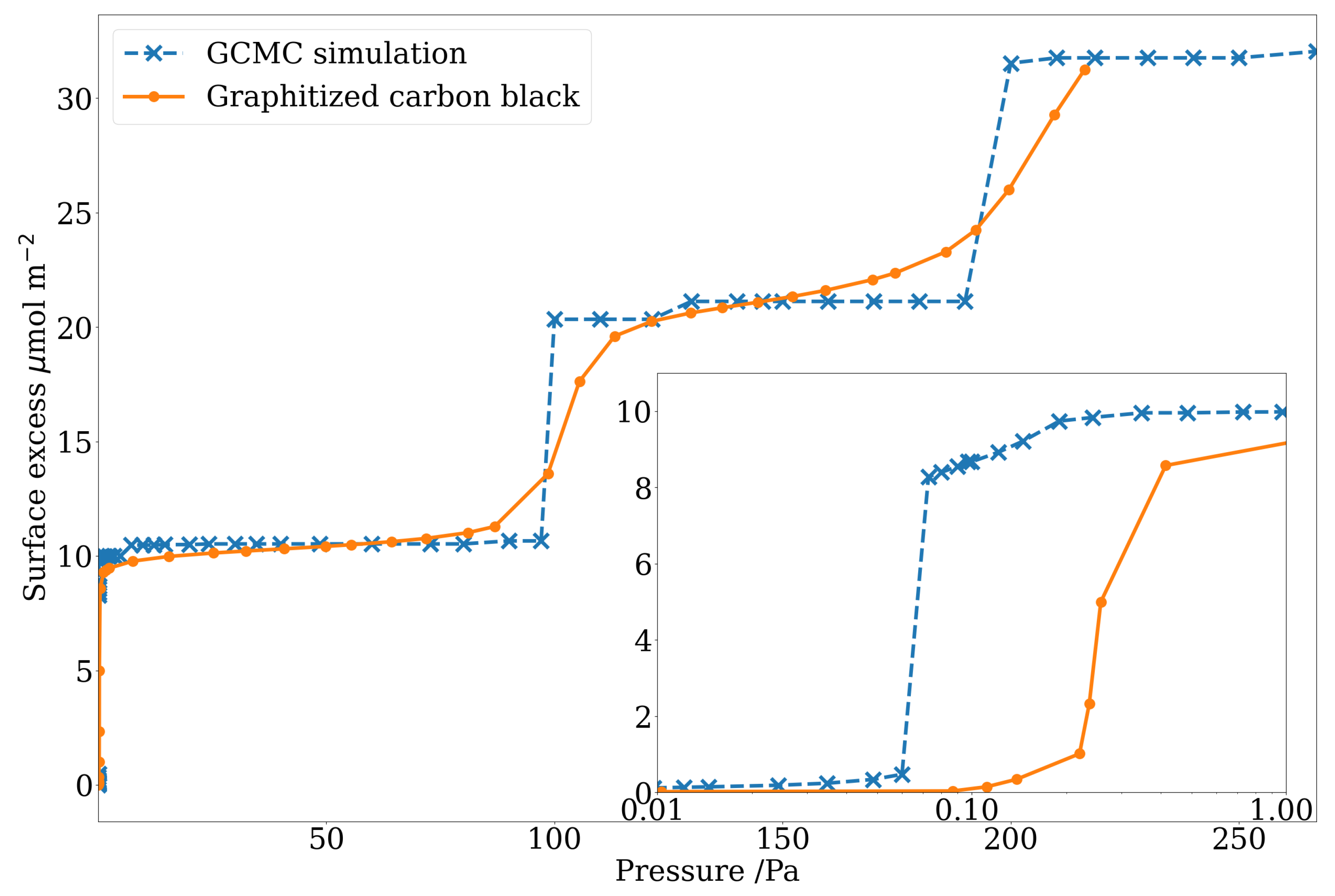
3.1. Interaction between Kr and Graphite
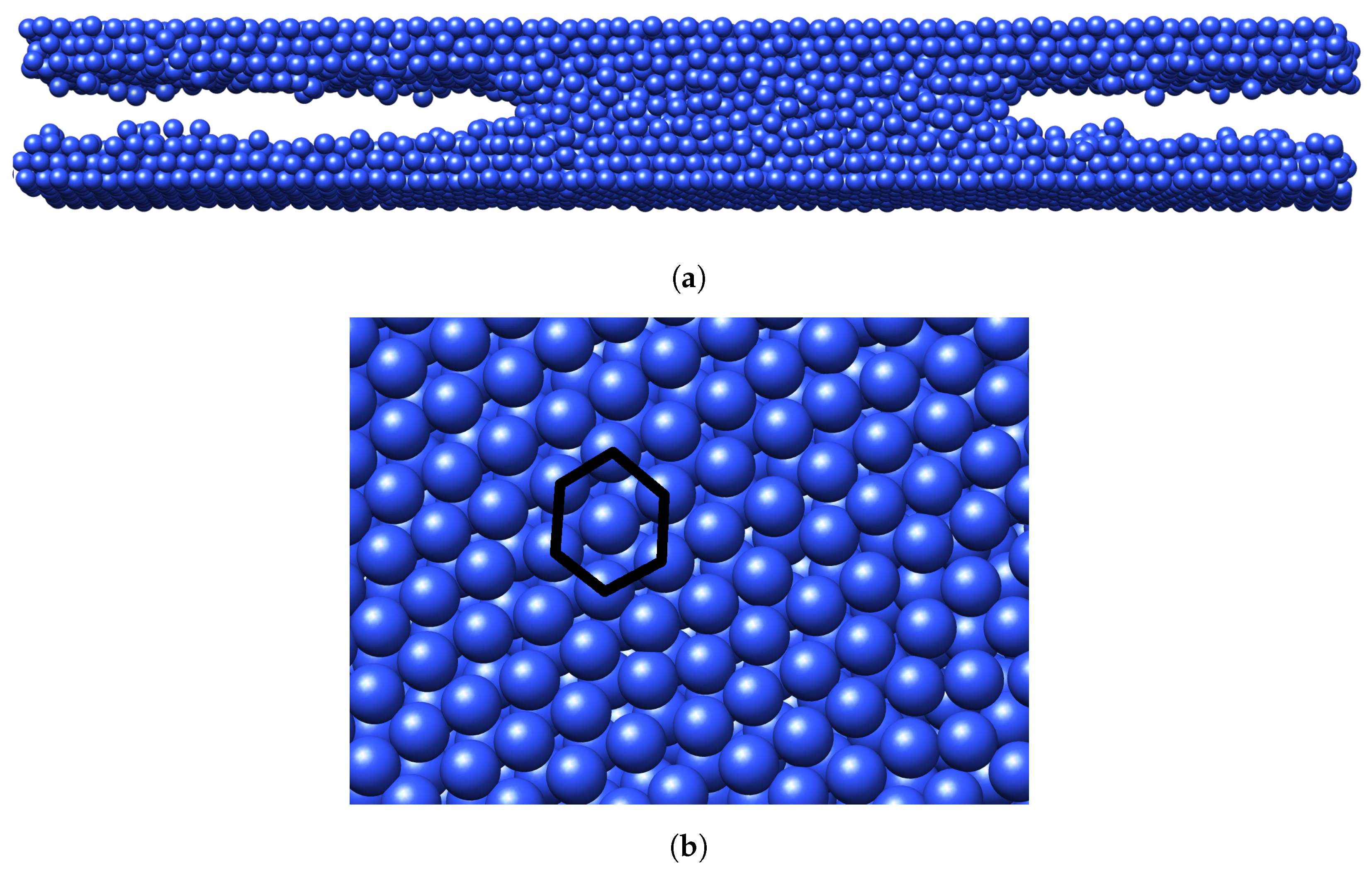
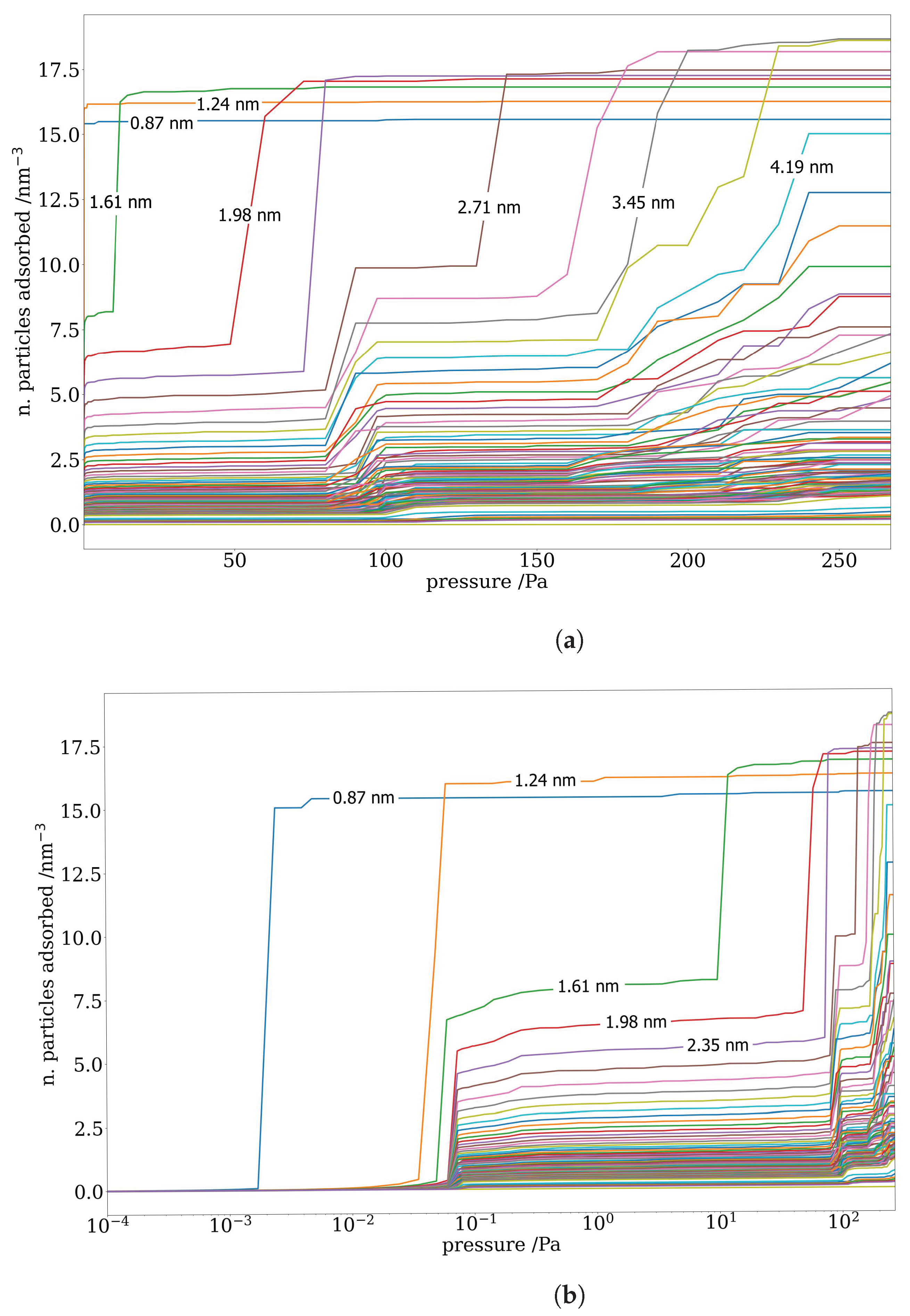
3.2. Slit Pores and GCMC-Generated Kernel
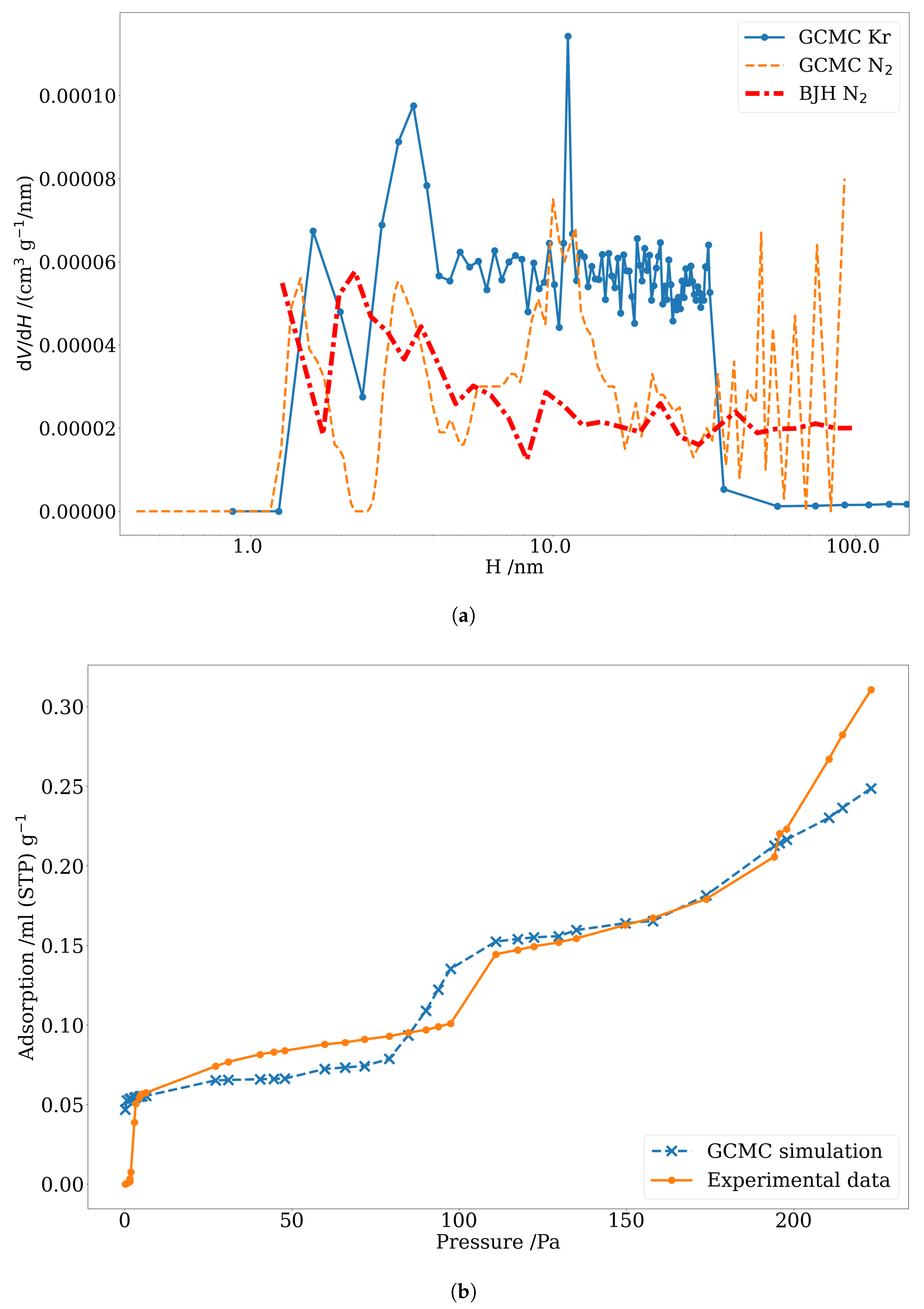
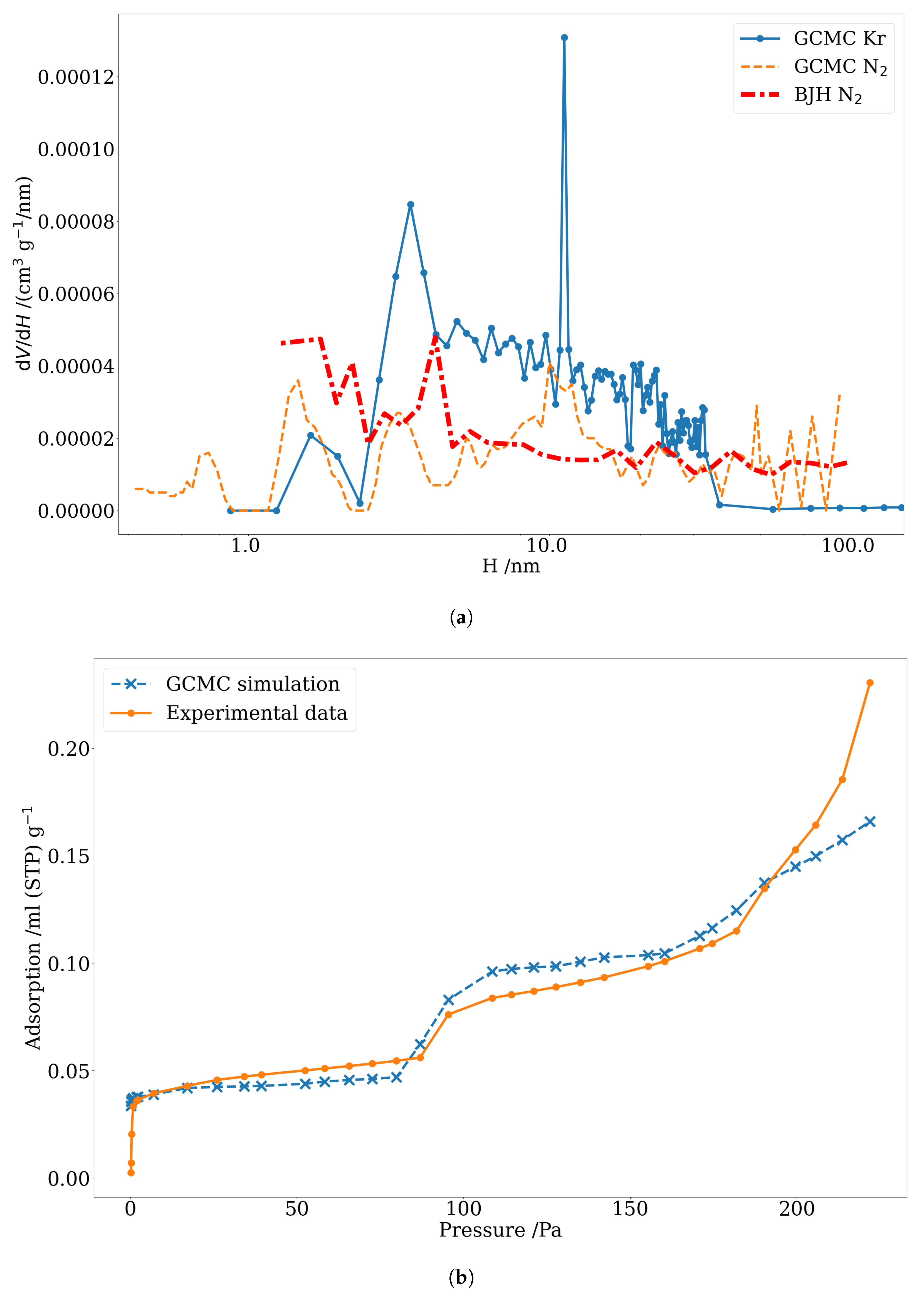
3.3. Pore Size Distribution of Nuclear-Grade Graphite and Activated Carbon
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| BET | Brunauer, Emmet and Teller |
| BJH | Barret, Joyner and Halenda |
| GCB | Graphitized Carbon Black |
| GCMC | Grand Canonical Monte Carlo |
| LJ | Lennard-Jones |
| NLDFT | Non-Localized Density Functional Theory |
| PSD | Pore Size Distribution |
References
- Gregg, S.; Sing, K. Adsorption, Surface Area and Porosity, 2nd ed.; Academic Press: Cambridge, MA, USA, 1982. [Google Scholar]
- Sing, K.S. 7—Assessment of Surface Area by Gas Adsorption. In Adsorption by Powders and Porous Solids, 2nd ed.; Rouquerol, F., Rouquerol, J., Sing, K., Llewellyn, P., Maurin, G., Eds.; Academic Press: Oxford, UK, 2014; pp. 237–268. [Google Scholar]
- Salama, R.S.; El-Bahy, S.M.; Mannaa, M.A. Sulfamic acid supported on mesoporous MCM-41 as a novel, efficient and reusable heterogenous solid acid catalyst for synthesis of xanthene, dihydropyrimidinone and coumarin derivatives. Colloids Surfaces A Physicochem. Eng. Asp. 2021, 628, 127261. [Google Scholar] [CrossRef]
- Contescu, C.I.; Arregui-Mena, J.D.; Campbell, A.A.; Edmondson, P.D.; Gallego, N.C.; Takizawa, K.; Katoh, Y. Development of mesopores in superfine grain graphite neutron-irradiated at high fluence. Carbon 2019, 141, 663–675. [Google Scholar]
- Arregui-Mena, J.D.; Contescu, C.I.; Campbell, A.A.; Edmondson, P.D.; Gallego, N.C.; Smith, Q.B.; Takizawa, K.; Katoh, Y. Nitrogen adsorption data, FIB-SEM tomography and TEM micrographs of neutron-irradiated superfine grain graphite. Data Brief 2018, 21, 2643–2650. [Google Scholar] [CrossRef] [PubMed]
- Thommes, M. Physical Adsorption Characterization of Nanoporous Materials. Chem. Ing. Tech. 2010, 82, 1059–1073. [Google Scholar]
- Gallego, N.C.; Arregui-Mena, J.D.; Contescu, C.I. Probing basal planes and edge sites in polygranular nuclear graphite by gas adsorption: Estimation of active surface area. Carbon 2021, 179, 633–645. [Google Scholar]
- Amberg, C.H.; Spencer, W.B.; Beebe, R.A. Heats of adsorption of Krypton on highly graphitized carbon black. Can. J. Chem. 1955, 33, 305–313. [Google Scholar]
- Thomy, A.; Matecki, M.; Duval, X. Adsorption de krypton sur membranes et fibres de carbone. Carbon 1971, 9, 587–592. [Google Scholar]
- Duval, X.; Thomy, A. The interpretation of Krypton adsorption isotherms on exfoliated graphite. Carbon 1975, 13, 242–243. [Google Scholar] [CrossRef]
- Wang, Y.; Razak, M.A.; Do, D.; Horikawa, T.; Morishige, K.; Nicholson, D. A computer simulation and experimental study of the difference between krypton adsorption on a graphite surface and in a graphitic hexagonal pore. Carbon 2012, 50, 2908–2917. [Google Scholar]
- Morishige, K. Monolayer Solids of Kr on Graphitized Carbon Black Surfaces and in Graphitic Hexagonal Pores. J. Phys. Chem. C 2013, 117, 10360–10365. [Google Scholar]
- Diao, R.; Fan, C.; Do, D.; Nicholson, D. On the 2D-transition, hysteresis and thermodynamic equilibrium of Kr adsorption on a graphite surface. J. Colloid Interface Sci. 2015, 460, 281–289. [Google Scholar] [PubMed]
- Prasetyo, L.; Horikawa, T.; Phadungbut, P.; Tan, S.J.; Do, D.; Nicholson, D. A GCMC simulation and experimental study of krypton adsorption/desorption hysteresis on a graphite surface. J. Colloid Interface Sci. 2016, 478, 402–412. [Google Scholar] [CrossRef] [PubMed]
- Mbaye, M.T.; Maiga, S.M.; Gatica, S.M. Commensurate phases of Kr adsorbed on single-walled carbon nanotubes. J. Low Temp. Phys. 2016, 185, 129–137. [Google Scholar] [CrossRef]
- Barrett, E.P.; Joyner, L.G.; Halenda, P.P. The Determination of Pore Volume and Area Distributions in Porous Substances. I. Computations from Nitrogen Isotherms. J. Am. Chem. Soc. 1951, 73, 373–380. [Google Scholar] [CrossRef]
- Ravikovitch, P.I.; Neimark, A.V. Calculations of pore size distributions in nanoporous materials from adsorption and desorption isotherms. Stud. Surf. Sci. Catal. 2000, 129, 597–606. [Google Scholar]
- Ravikovitch, P.I.; Neimark, A.V. Characterization of Micro- and Mesoporosity in SBA-15 Materials from Adsorption Data by the NLDFT Method. J. Phys. Chem. B 2001, 105, 6817–6823. [Google Scholar] [CrossRef]
- Jagiello, J.; Kenvin, J.; Olivier, J.P.; Lupini, A.R.; Contescu, C.I. Using a New Finite Slit Pore Model for NLDFT Analysis of Carbon Pore Structure. Adsorpt. Sci. Technol. 2011, 29, 769–780. [Google Scholar]
- Norman, G.; Filinov, V. Investigations of phase transitions by a Monte-Carlo method. High Temp. 1969, 7, 216. [Google Scholar]
- Adams, D. Grand canonical ensemble Monte Carlo for a Lennard-Jones fluid. Mol. Phys. 1975, 29, 307–311. [Google Scholar] [CrossRef]
- Konstantakou, M.; Gotzias, A.; Stubos, A.; Kainourgiakis, M.; Steriotis, T. GCMC Simulations of Gas Adsorption in Carbon Pore Structures. In Applications of Monte Carlo Method in Science and Engineering; Mordechai, S., Ed.; INTECH Open Access Publisher: London, UK, 2011; pp. 653–676. [Google Scholar]
- Lee, E.J.; Chang, R.W.; Han, J.H.; Chung, T.D. Effect of Pore Geometry on Gas Adsorption: Grand Canonical Monte Carlo Simulation Studies. Bull. Korean Chem. Soc. 2012, 33, 901–905. [Google Scholar] [CrossRef]
- Miyahara, M.T.; Tanaka, H. Determination of phase equilibria in confined systems by open pore cell Monte Carlo method. J. Chem. Phys. 2013, 138, 084709. [Google Scholar] [CrossRef]
- Herrera, L.F.; Fan, C.; Do, D.D.; Nicholson, D. Monte Carlo Optimization Scheme to Determine the Physical Properties of Porous and Nonporous Solids. Langmuir 2010, 26, 15278–15288. [Google Scholar] [CrossRef]
- Bottani, E.J.; Bakaev, V.A. The Grand Canonical Ensemble Monte Carlo Simulation of Nitrogen on Graphite. Langmuir 1994, 10, 1550–1555. [Google Scholar] [CrossRef]
- Fan, C.; Do, D.D.; Nicholson, D. New Monte Carlo Simulation of Adsorption of Gases on Surfaces and in Pores: A Concept of Multibins. J. Phys. Chem. B 2011, 115, 10509–10517. [Google Scholar] [CrossRef]
- Fan, C.; Do, D.; Nicholson, D.; Jagiello, J.; Kenvin, J.; Puzan, M. Monte Carlo simulation and experimental studies on the low temperature characterization of nitrogen adsorption on graphite. Carbon 2013, 52, 158–170. [Google Scholar] [CrossRef]
- Maiga, S.M.; Gatica, S.M. Monolayer adsorption of noble gases on graphene. Chem. Phys. 2018, 501, 46–52. [Google Scholar] [CrossRef]
- Siderius, D.W.; Shen, V.K. Use of the Grand Canonical Transition-Matrix Monte Carlo Method to Model Gas Adsorption in Porous Materials. J. Phys. Chem. C 2013, 117, 5861–5872. [Google Scholar] [CrossRef]
- Samios, S.; Stubos, A.K.; Kanellopoulos, N.K.; Cracknell, R.F.; Papadopoulos, G.K.; Nicholson, D. Determination of Micropore Size Distribution from Grand Canonical Monte Carlo Simulations and Experimental CO2 Isotherm Data. Langmuir 1997, 13, 2795–2802. [Google Scholar] [CrossRef]
- Steele, W.A.; Bojan, M.J. Simulation studies of sorption in model cylindrical micropores. Adv. Colloid Interface Sci. 1998, 76–77, 153–178. [Google Scholar] [CrossRef]
- Konstantakou, M.; Steriotis, T.; Papadopoulos, G.; Kainourgiakis, M.; Kikkinides, E.; Stubos, A. Characterization of nanoporous carbons by combining CO2 and H2 sorption data with the Monte Carlo simulations. Appl. Surf. Sci. 2007, 253, 5715–5720. [Google Scholar] [CrossRef]
- Paul, R.M.; Arregui-Mena, J.D.; Contescu, C.I.; Gallego, N.C. Effect of microstructure and temperature on nuclear graphite oxidation using the 3D Random Pore Model. Carbon 2022, 191, 132–145. [Google Scholar] [CrossRef]
- Laudone, G.M.; Gribble, C.M.; Matthews, G.P. Characterisation of the porous structure of Gilsocarbon graphite using pycnometry, cyclic porosimetry and void-network modeling. Carbon 2014, 73, 61–70. [Google Scholar] [CrossRef]
- Jones, K.L.; Laudone, G.M.; Matthews, G.P. A multi-technique experimental and modelling study of the porous structure of IG-110 and IG-430 nuclear graphite. Carbon 2018, 128, 1–11. [Google Scholar] [CrossRef]
- Jones, K.L.; Matthews, G.P.; Laudone, G.M. The effect of irradiation and radiolytic oxidation on the porous space of Gilsocarbon nuclear graphite measured with mercury porosimetry and helium pycnometry. Carbon 2020, 158, 256–266. [Google Scholar] [CrossRef]
- Murdie, N.; Edwards, I.A.; Marsh, H. Changes in porosity of graphite caused by radiolytic gasification by carbon dioxide. Carbon 1986, 24, 267–275. [Google Scholar] [CrossRef]
- Nicholson, D.; Parsonage, N.G. Computer Simulation and the Statistical Mechanics of Adsorption; Academic Press: Cambridge, MA, USA, 1982. [Google Scholar]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids; Clarendon Press: New York, NY, USA, 1989. [Google Scholar]
- Shkolin, A.V.; Fomkin, A.A.; Sinitsyn, V.A. Methane adsorption on AUK microporous carbon adsorbent. Colloid J. 2008, 70, 796. [Google Scholar] [CrossRef]
- Saurel, D.; Segalini, J.; Jauregui, M.; Pendashteh, A.; Daffos, B.; Simon, P.; Casas-Cabanas, M. A SAXS outlook on disordered carbonaceous materials for electrochemical energy storage. Energy Storage Mater. 2019, 21, 162–173. [Google Scholar] [CrossRef]
- Dubinin, M.; Plavnik, G. Microporous structures of carbonaceous adsorbents. Carbon 1968, 6, 183–192. [Google Scholar] [CrossRef]
- Coasne, B.; Pellenq, R.J.M. A grand canonical Monte Carlo study of capillary condensation in mesoporous media: Effect of the pore morphology and topology. J. Chem. Phys. 2004, 121, 3767–3774. [Google Scholar] [CrossRef]
- Fan, W.; Chakraborty, A. Investigation of the Interaction of Polar Molecules on Graphite Surface: Prediction of Isosteric Heat of Adsorption at Zero Surface Coverage. J. Phys. Chem. C 2016, 120, 23490–23499. [Google Scholar] [CrossRef]
- Steele, W.A. The physical interaction of gases with crystalline solids. Surf. Sci. 1973, 36, 317–352. [Google Scholar] [CrossRef]
- Kaneko, K.; Cracknell, R.F.; Nicholson, D. Nitrogen Adsorption in Slit Pores at Ambient Temperatures: Comparison of Simulation and Experiment. Langmuir 1994, 10, 4606–4609. [Google Scholar] [CrossRef]
- Miyahara, M.T.; Numaguchi, R.; Hiratsuka, T.; Nakai, K.; Tanaka, H. Fluids in nanospaces: Molecular simulation studies to find out key mechanisms for engineering. Adsorption 2014, 20, 213–223. [Google Scholar] [CrossRef]
- Herdes, C.; Santos, M.A.; Medina, F.; Vega, L.F. Pore Size Distribution Analysis of Selected Hexagonal Mesoporous Silicas by Grand Canonical Monte Carlo Simulations. Langmuir 2005, 21, 8733–8742. [Google Scholar] [CrossRef]
- Diamond, S.; Boyd, S. CVXPY: A Python-Embedded Modeling Language for Convex Optimization. J. Mach. Learn. Res. 2016, 17, 1–5. [Google Scholar]
- Thomy, A.; Duval, X.; Regnier, J. Two-dimensional phase transitions as displayed by adsorption isotherms on graphite and other lamellar solids. Surf. Sci. Rep. 1981, 1, 1–38. [Google Scholar] [CrossRef]
- Bläker, C.; Muthmann, J.; Pasel, C.; Bathen, D. Characterization of Activated Carbon Adsorbents—State of the Art and Novel Approaches. ChemBioEng Rev. 2019, 6, 119–138. [Google Scholar] [CrossRef]


| Pair | /nm | /K |
|---|---|---|
| Kr–Kr | 0.3685 | 164.4 |
| C–C | 0.3400 | 28 |
| Kr–C | 0.3543 | 67.85 |
| IG110 | IG430 | Activated Carbon | ||
|---|---|---|---|---|
| 0.38 | 0.22 | |||
| 0.37 | 0.21 |
| IG110 | IG430 | Activated Carbon | ||
|---|---|---|---|---|
| 1.55 | ||||
| 1.63 | ||||
| 1.26 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Laudone, G.M.; Jones, K.L. A Grand Canonical Monte Carlo Simulation for the Evaluation of Pore Size Distribution of Nuclear-Grade Graphite from Kr Adsorption Isotherms. C 2023, 9, 86. https://doi.org/10.3390/c9030086
Laudone GM, Jones KL. A Grand Canonical Monte Carlo Simulation for the Evaluation of Pore Size Distribution of Nuclear-Grade Graphite from Kr Adsorption Isotherms. C. 2023; 9(3):86. https://doi.org/10.3390/c9030086
Chicago/Turabian StyleLaudone, Giuliano M., and Katie L. Jones. 2023. "A Grand Canonical Monte Carlo Simulation for the Evaluation of Pore Size Distribution of Nuclear-Grade Graphite from Kr Adsorption Isotherms" C 9, no. 3: 86. https://doi.org/10.3390/c9030086
APA StyleLaudone, G. M., & Jones, K. L. (2023). A Grand Canonical Monte Carlo Simulation for the Evaluation of Pore Size Distribution of Nuclear-Grade Graphite from Kr Adsorption Isotherms. C, 9(3), 86. https://doi.org/10.3390/c9030086







