Measurement of the Diffusion Coefficient of Xenon in Self-Sintered Nanopore Graphite for Molten Salt Reactor
Abstract
:1. Introduction
2. Materials and Methods
2.1. Specimen Preparation and Irradiation
2.2. Characterizations
3. Results and Discussion
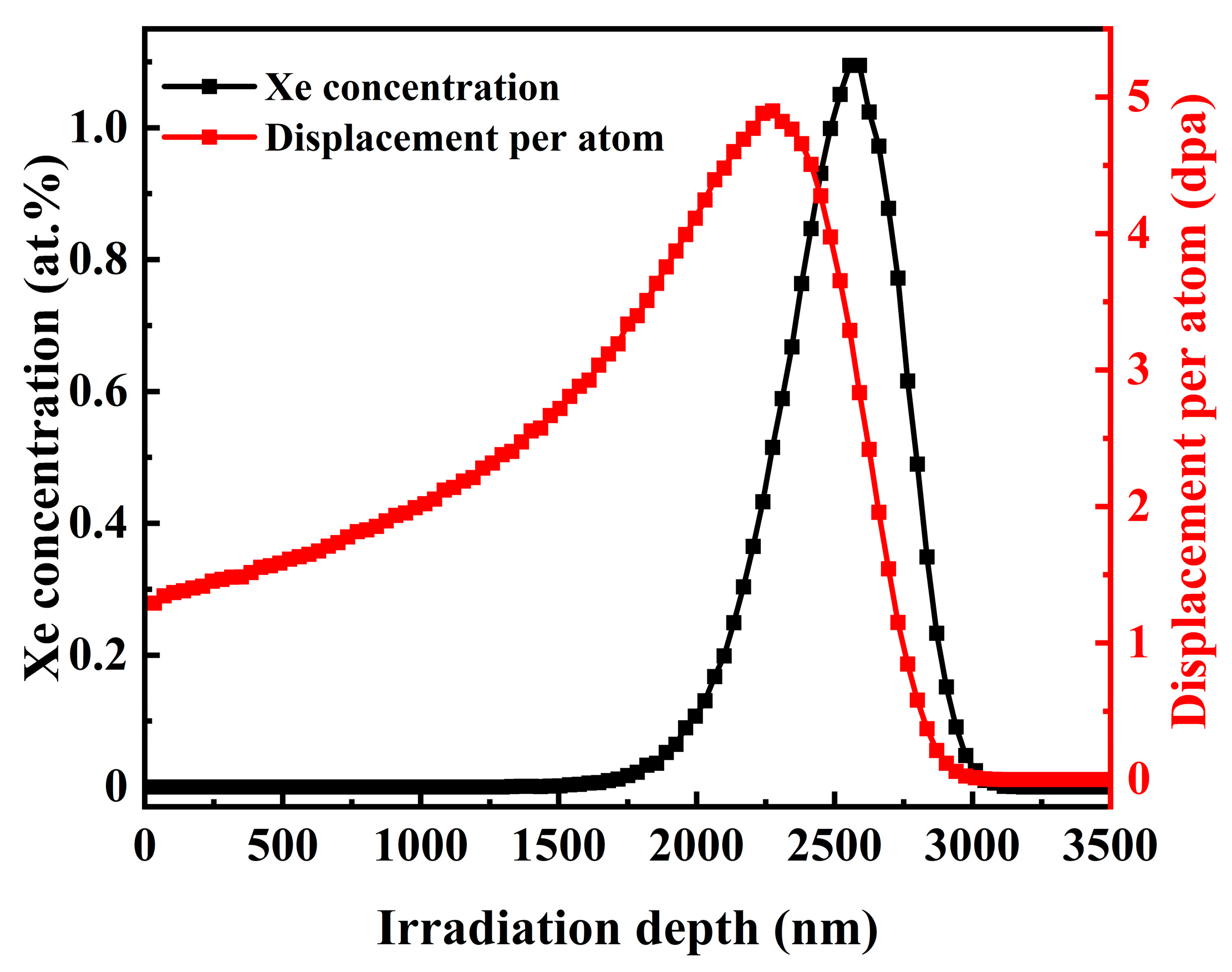
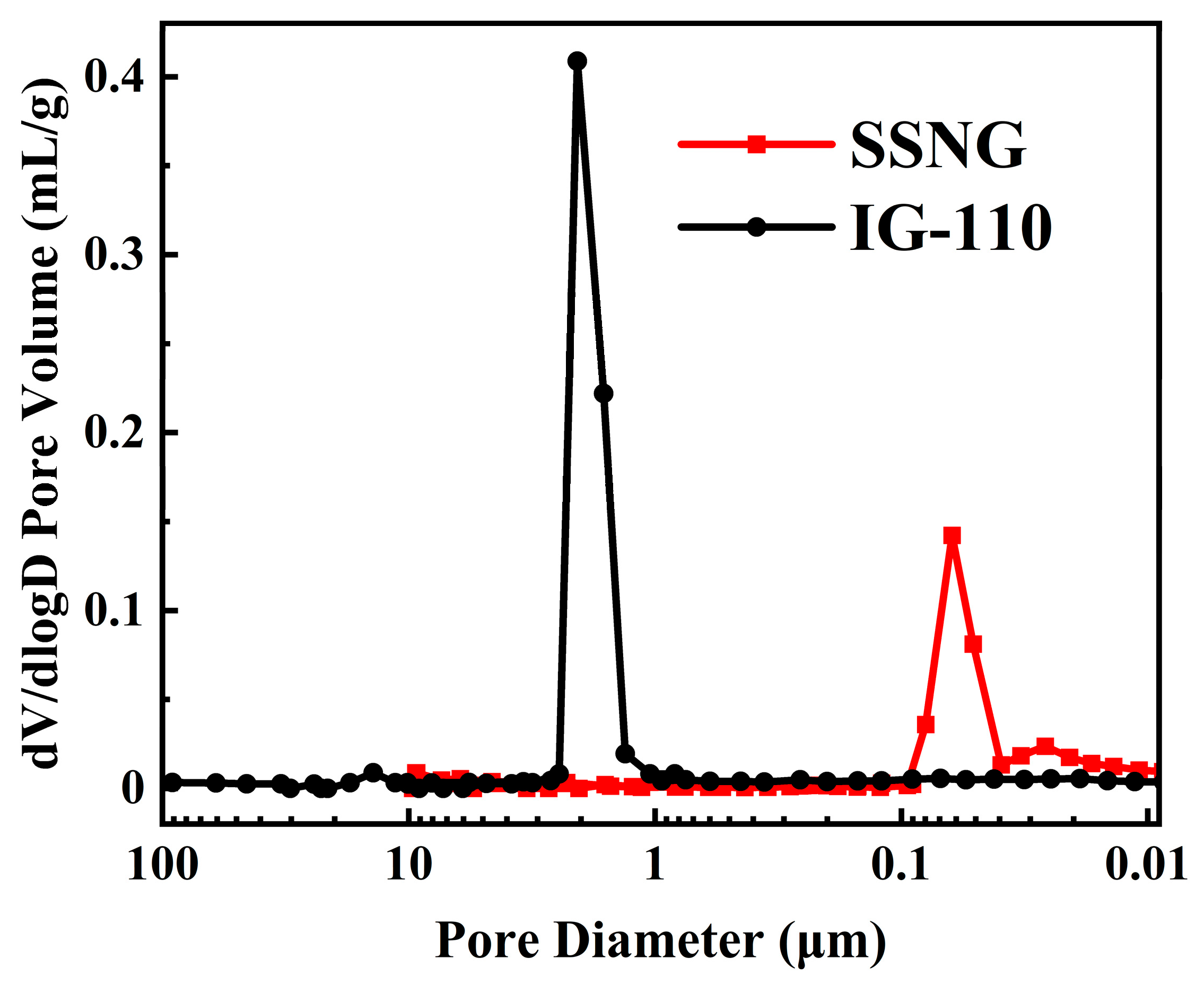
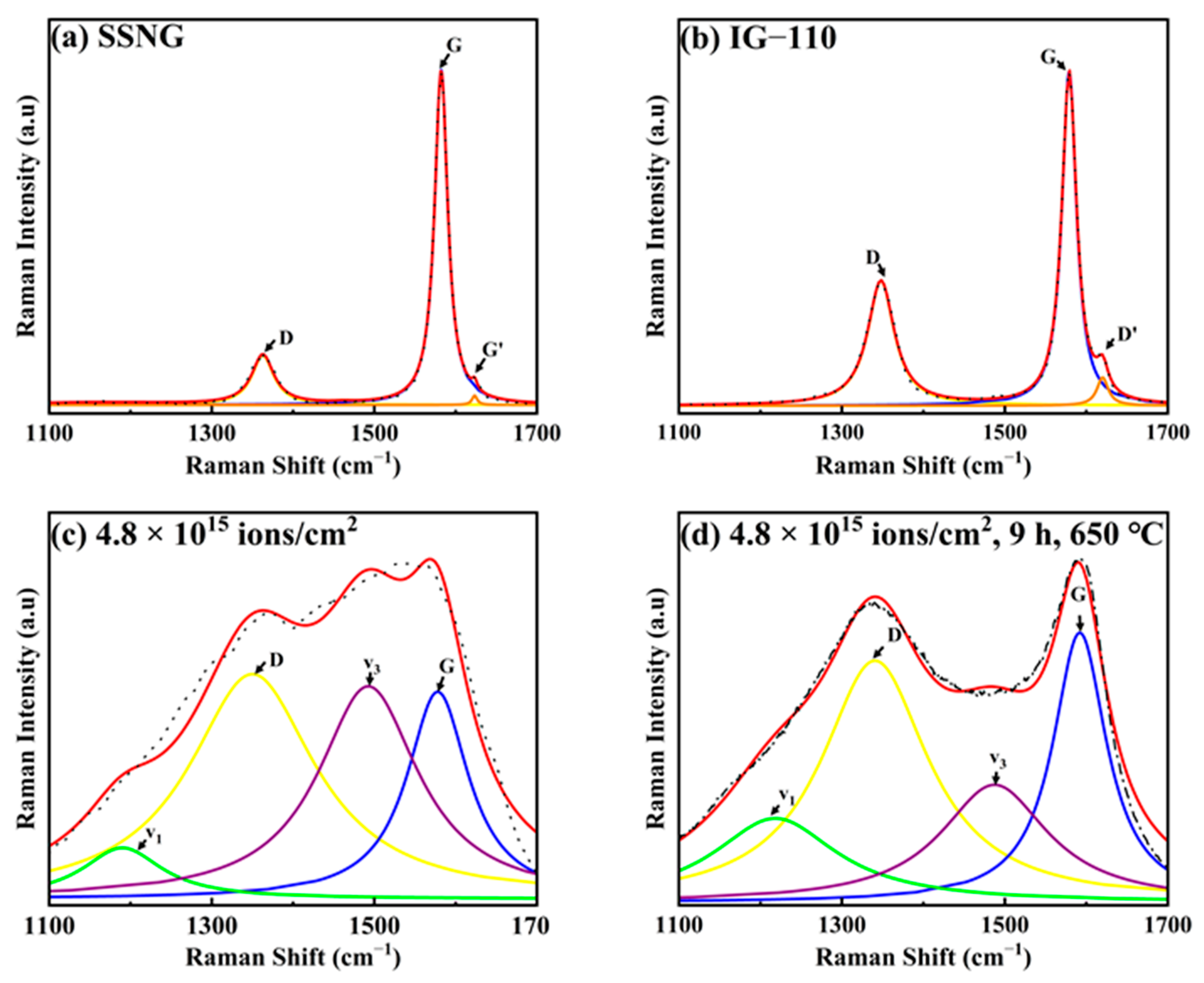
3.1. Pore Diameter Analysis
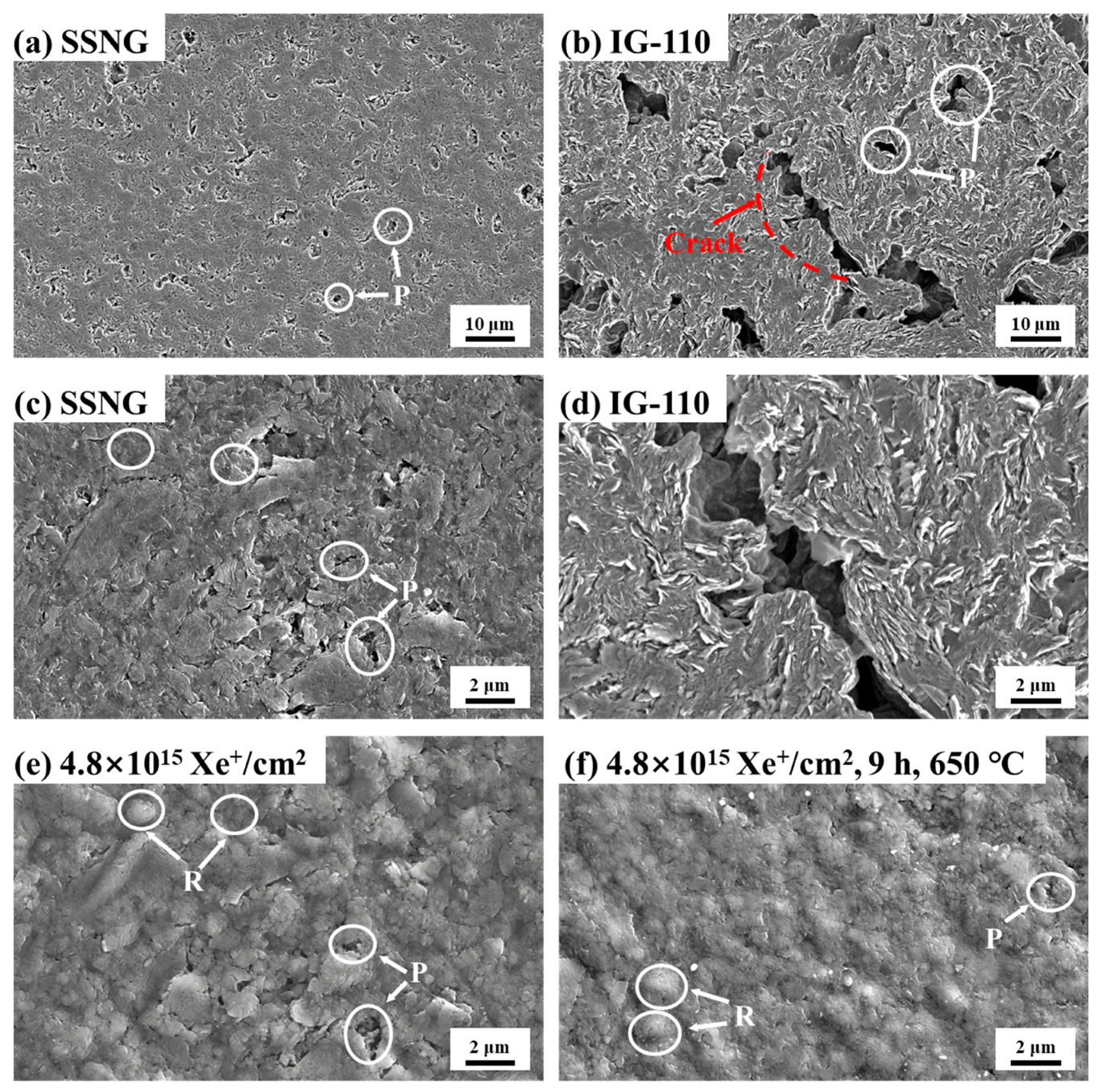
3.2. Microstructure Analysis
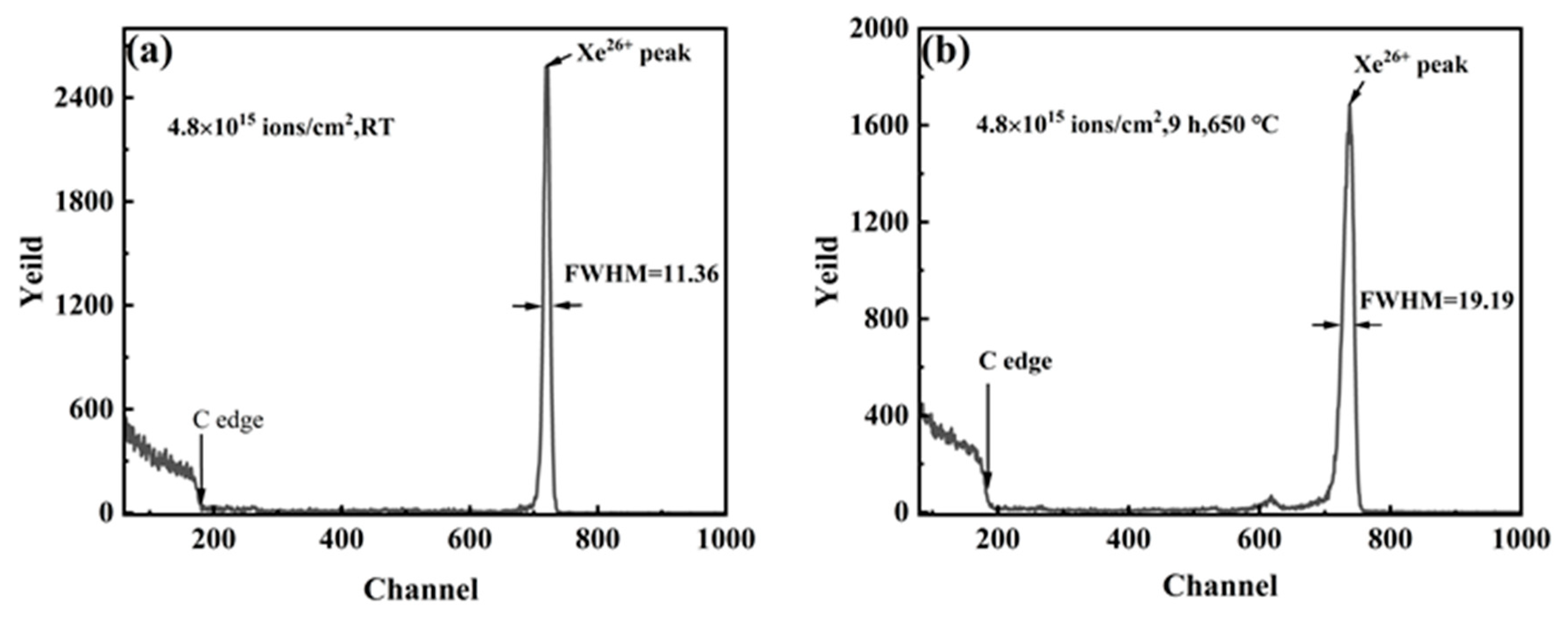
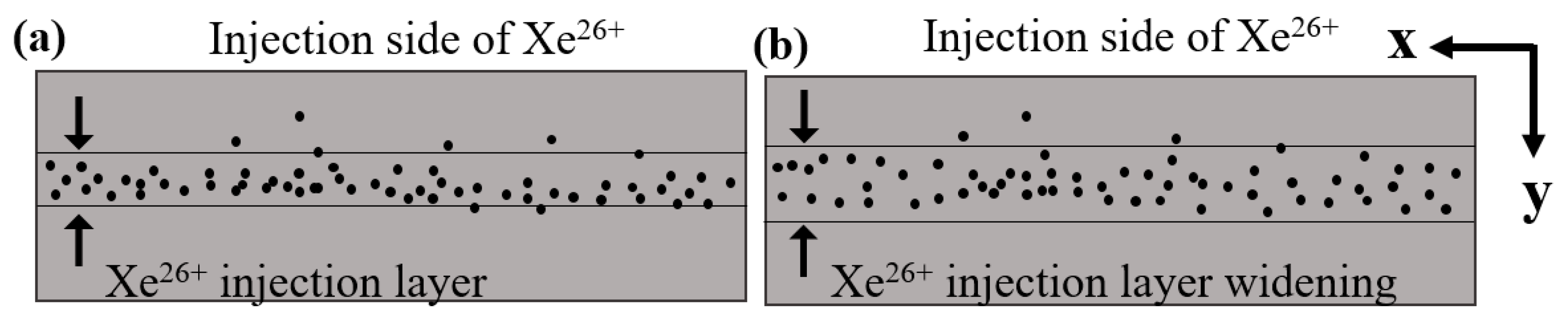
3.3. Rutherford Backscattering Analysis
4. Conclusions
- (1)
- The prepared SSNG (~40 nm) not only met the pore size required for a molten salt reactor but also exhibited better irradiation resistance.
- (2)
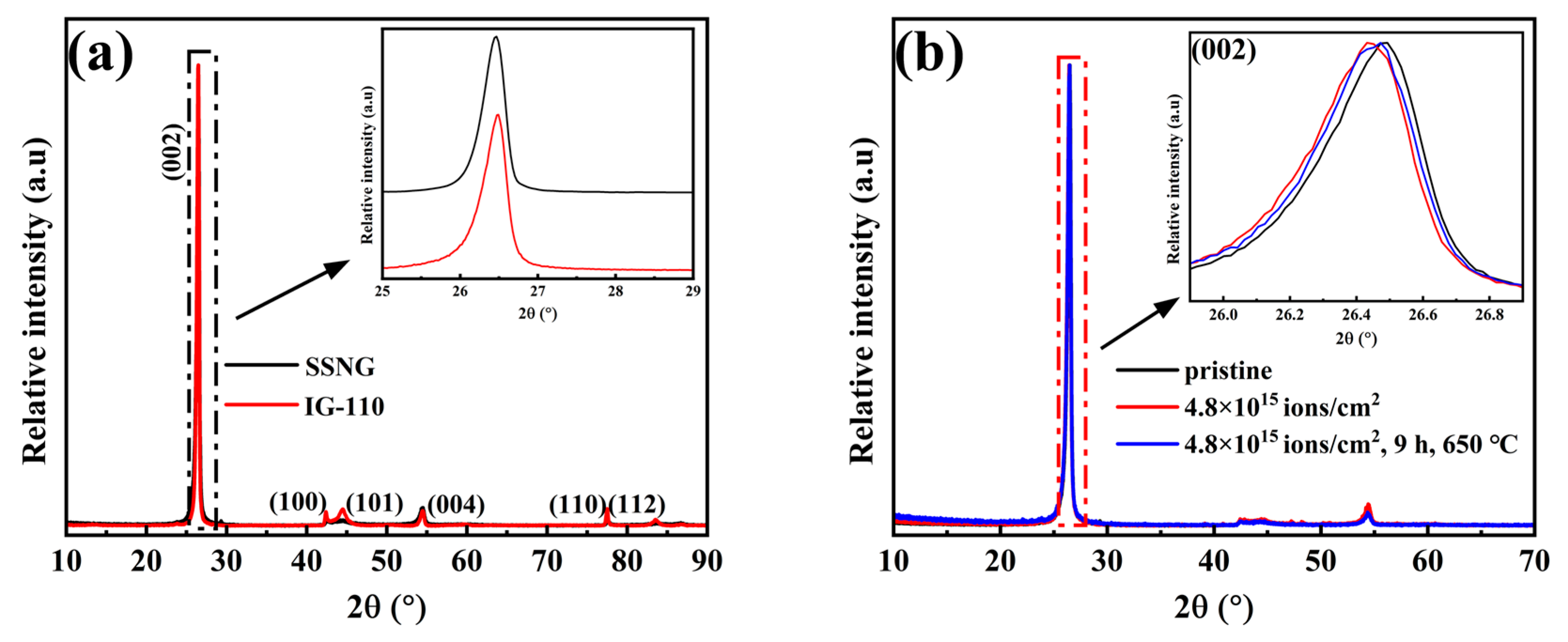
- Annealing had little effect on the morphology of the SSNG but restored the structure of graphite, and this restoration was limited, which may have been related to the amorphization and diffusion of ions in graphite.
- (3)
- The “sandwich” model was shown to be a viable method for calculating ion diffusion coefficients. The RBS energy spectrums before and after the annealing showed that the xenon peak distributions were all close to being Gaussian, which suggests that Fickian diffusion of xenon occurred within the SSNG after annealing.
- (4)
- The diffusion coefficient of Xe26+ in graphite was measured using RBS for the first time. The diffusion coefficient D(Xe, 650 °C) = 6.49 × 10−20 m2/s, which showed that the nanopore graphite SSNG had an excellent ability to inhibit xenon diffusion.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Haubenreich, P.N.; Engel, J.R. Experience with the Molten-Salt Reactor Experiment. Nucl. Appl. Technol. 1970, 8, 118–136. [Google Scholar] [CrossRef]
- Price, T.; Chvala, O.; Bereznai, G. A dynamic model of xenon behavior in the Molten Salt Reactor Experiment. Ann. Nucl. Energy 2020, 144, 107535. [Google Scholar] [CrossRef]
- Scott, D.; Eatherly, W.P. Graphite and Xenon Behavior and their Influence on Molten-Salt Reactor Design. Nucl. Appl. Technol. 1970, 8, 179–189. [Google Scholar] [CrossRef]
- Dunkle, N.; Chvala, O. Effect of xenon removal rate on load following in high power thermal spectrum Molten-Salt Reactors (MSRs). Nucl. Eng. Des. 2023, 409, 112329. [Google Scholar] [CrossRef]
- Zhao, H.C.; He, Z.; Liu, Z.J.; Song, J.L.; Tsang, D.K.L.; Zhang, H.Y. Self-sintered nanopore-isotropic graphite derived from green pitch coke for application in molten salt nuclear reactor. Ann. Nucl. Energy 2019, 131, 412–416. [Google Scholar] [CrossRef]
- Zhang, H.Y.; Song, J.L.; Tang, Z.F.; He, Z.; Liu, X.D. The surface topography and microstructure of self-sintered nanopore graphite by Xe ions irradiation. Appl. Surf. Sci. 2020, 515, 146022. [Google Scholar] [CrossRef]
- Zhao, Y.M.; Lv, S.S.; Gao, J.; Zhou, Z.; Yeli, G.M.; Li, Z.C. Microstructure and defect evolution of nuclear graphite under temperature-dependent ion irradiation. J. Nucl. Mater. 2023, 577, 154308. [Google Scholar] [CrossRef]
- Zhu, Y.Q.; He, Z.T.; Ma, H.L.; Liu, F.G.; Theodosiou, A.; Smith, A.; Jones, A.; Marsden, B.; Zhou, X.T. High dose 30 MeV 58Ni5+ ion irradiation causes microstructure evolution in nuclear graphite at 400 °C. J. Nucl. Mater. 2022, 559, 153460. [Google Scholar] [CrossRef]
- Zhang, H.Y.; Lei, Q.T.; Song, J.L.; Liu, M.; Zhang, C.; Gao, Y.T.; Zhang, W.T.; Xia, H.H.; Liu, X.D. Direct characterization of ion implanted nanopore pyrolytic graphite coatings for molten salt nuclear reactors. RSC Adv. 2018, 8, 33927–33938. [Google Scholar] [CrossRef]
- Zhang, H.Y.; Cheng, J.X.; Song, J.L.; Yin, H.Q.; Tang, Z.F.; Liu, Z.J.; Liu, X.D. Topography changes and microstructural evolution of nuclear graphite (IG-110) induced by Xe26+ irradiation. New Carbon Mater. 2023, 38, 393–402. [Google Scholar] [CrossRef]
- Lv, S.S.; Gao, J.; Jin, Y.H.; Zhou, Z.; Zhao, Y.M.; Yano, T.; Li, Z.C. The structure evolution in neutron-Irradiated nuclear graphite and post-annealing. Radiat. Phys. Chem. 2022, 197, 110156. [Google Scholar] [CrossRef]
- Houska, C.R.; Warren, B.E. X-ray Study of the Graphitization of Carbon Black. J. Appl. Phys. 1954, 25, 1503–1509. [Google Scholar] [CrossRef]
- Burchell, T.D.; Pappano, P.J.; Strizak, J.P. A study of the annealing behavior of neutron irradiated graphite. Carbon 2011, 49, 3–10. [Google Scholar] [CrossRef]
- Mathew, S.; Chan, T.K.; Zhan, D.; Gopinadhan, K.; Barman, A.R.; Breese, M.B.H.; Dhar, S.; Shen, Z.X.; Venkatesan, T.; Thong, J.T.L. The effect of layer number and substrate on the stability of graphene under MeV proton beam irradiation. Carbon 2011, 49, 1720–1726. [Google Scholar] [CrossRef]
- Odutemowo, O.S.; Malherbe, J.B.; Prinsloo, L.; Langa, D.F.; Wendler, E. High temperature annealing studies of strontium ion implanted glassy carbon. Nucl. Instrum. Methods Phys. Res. Sect. B—Beam Interact. Mater. At. 2016, 371, 332–335. [Google Scholar] [CrossRef]
- Lasithiotakis, M.; Marsden, B.J.; Marrow, T.J. Annealing of ion irradiation damage in nuclear graphite. J. Nucl. Mater. 2013, 434, 334–346. [Google Scholar] [CrossRef]
- Niwase, K.; Tanabe, T.; Tanaka, I. Annealing experiment of ion-irradiated graphite by laser Raman spectroscopy. J. Nucl. Mater. 1992, 191, 335–339. [Google Scholar] [CrossRef]
- Adeojo, S.A.; Malherbe, J.B.; Njoroge, E.G.; Mlambo, M.; Odutemowo, O.S.; Thabethe, T.T.; Abdalla, Z.A.Y.; Hlatshwayo, T.T. Effect of sequential isochronal annealing on the structure and migration behaviour of selenium-ion implanted in glassy carbon. Vacuum 2020, 182, 109689. [Google Scholar] [CrossRef]
- Laricchiuta, G.; Vandervorst, W.; Meersschaut, J. High-sensitivity Rutherford backscattering spectrometry employing an analyzing magnet and silicon strip detector. Nucl. Instrum. Methods Phys. Res. Sect. B—Beam Interact. Mater. At. 2019, 439, 59–63. [Google Scholar] [CrossRef]
- Qi, M.B.; Lian, P.F.; Li, P.D.; Zhang, H.Y.; Cheng, J.X.; Wang, Q.B.; Tang, Z.F.; Pan, T.J.; Song, J.L.; Liu, Z.J. Diffusion Behavior of Iodine in the Micro/Nano-Porous Graphite for Nuclear Reactor at High Temperature. C 2023, 9, 81. [Google Scholar] [CrossRef]
- Gao, J.; Huang, H.F.; Liu, J.Z.; Lei, Q.T.; Wang, C.J.; Han, Z.B.; Yang, G.; Li, Y. Helium release and lattice swelling in nickel foil irradiated by multiply-energy helium ions. Nucl. Instrum. Methods Phys. Res. Sect. B—Beam Interact. Mater. At. 2019, 450, 108–113. [Google Scholar] [CrossRef]
- Odutemowo, O.S.; Dhlamini, M.S.; Wendler, E.; Langa, D.F.; Ismail, M.Y.A.; Malherbe, J.B. Effect of heat treatment on the migration behaviour of Sr and Ag CO-implanted in glassy carbon. Vacuum 2020, 171, 109027. [Google Scholar] [CrossRef]
- Christie, H.J.; Robinson, M.; Roach, D.L.; Ross, D.K.; Suarez-Martinez, I.; Marks, N.A. Simulating radiation damage cascades in graphite. Carbon 2015, 81, 105–114. [Google Scholar] [CrossRef]
- Hlatshwayo, T.T.; Sebitla, L.D.; Njoroge, E.G.; Mlambo, M.; Malherbe, J.B. Annealing effects on the migration of ion-implanted cadmium in glassy carbon. Nucl. Instrum. Methods Phys. Res. Sect. B—Beam Interact. Mater. At. 2017, 395, 34–38. [Google Scholar] [CrossRef]
- Odutemowo, O.S.; Malherbe, J.B.; Limbach, R.; Wondraczek, L.; Wendler, E.; Undisz, A.; Njoroge, E.G.; Idisi, D.O.; Dhlamini, M.S. Changes in the mechanical, structural and electrical properties of glassy carbon due to strontium and silver co-implantation and annealing. Appl. Surf. Sci. 2021, 537, 147929. [Google Scholar] [CrossRef]
- Malherbe, J.B.; Selyshchev, P.A.; Odutemowo, O.S.; Theron, C.C.; Njoroge, E.G.; Langa, D.F.; Hlatshwayo, T.T. Diffusion of a mono-energetic implanted species with a Gaussian profile. Nucl. Instrum. Methods Phys. Res. Sect. B—Beam Interact. Mater. At. 2017, 406, 708–713. [Google Scholar] [CrossRef]
- Malherbe, J.B.; Odutemowo, O.S. Diffusion and segregation of Sr in glassy carbon: Model and analysis. Diam. Relat. Mater. 2021, 120, 108709. [Google Scholar] [CrossRef]
- Mukhawana, M.B.; Theron, C.C.; Malherbe, J.B.; van der Berg, N.G.; Botha, A.J.; Grote, W.; Wendler, E.; Wesch, W.; Chakraborty, P. Behavior of iodine implanted in highly oriented pyrolytic graphite (HOPG) after heat treatment. Nucl. Instrum. Methods Phys. Res. Sect. B—Beam Interact. Mater. At. 2012, 273, 65–67. [Google Scholar] [CrossRef]
- Myers, S.M.; Picraux, S.T.; Prevender, T.S. Study of Cu diffusion in Be using ion backscattering. Phys. Rev. B 1974, 9, 3953–3964. [Google Scholar] [CrossRef]
- Friedland, E.; van der Berg, N.G.; Malherbe, J.B.; Hancke, J.J.; Barry, J.; Wendler, E.; Wesch, W. Investigation of silver and iodine transport through silicon carbide layers prepared for nuclear fuel element cladding. J. Nucl. Mater. 2011, 410, 24–31. [Google Scholar] [CrossRef]
- Rocchini, M.; Chiari, M.; Pasquali, E.; Nannini, A.; Hadyńska-Klęk, K.; Sona, P.; Bazzacco, D.; Benzoni, G.; Camera, F.; Czelusniak, C.; et al. Applications of Rutherford backscattering analysis methods to nuclear physics experiments. Nucl. Instrum. Methods Phys. Res. Sect. B—Beam Interact. Mater. At. 2021, 486, 68–72. [Google Scholar] [CrossRef]
- Murarka, S. Diffusion Barriers in Semiconductor Devices/Circuits; William Andrew Publishing: Norwich, NY, USA, 2005; pp. 239–281. [Google Scholar]


| Properties | SSNG | IG-110 |
|---|---|---|
| Bulk density (g/cm3) | 1.92 ± 0.02 | 1.77 ± 0.02 |
| Open porosity (%) | 10.0 ± 0.1 | 18.4 ± 0.1 |
| Median pore diameter (volume, μm) | 0.400 | 1.840 |
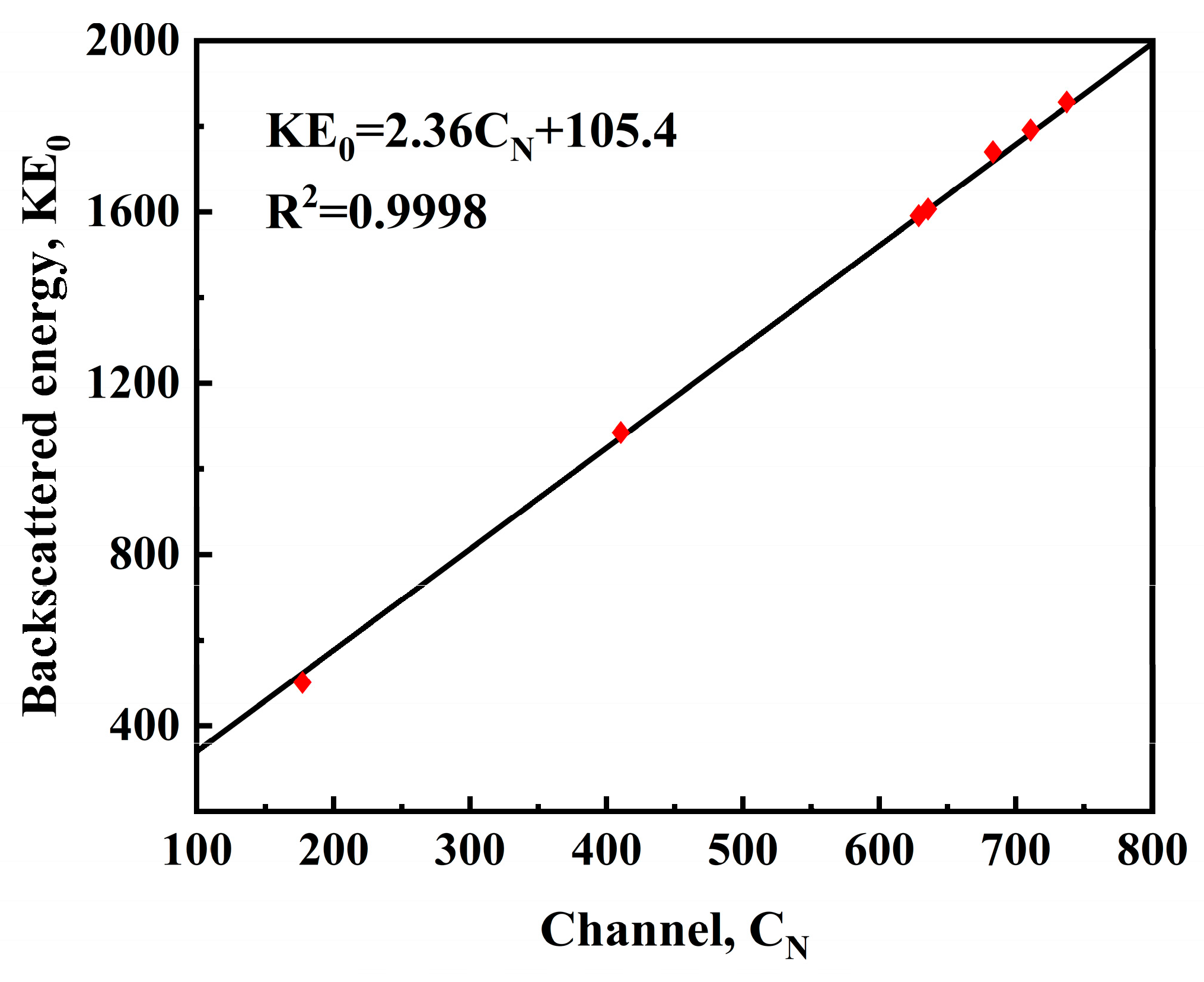
| Element | Kinematic Factor/K | Backscattered/E0K | Channel/CN | Incident Energy E0/MeV |
|---|---|---|---|---|
| Au | 0.92 | 1.840 | 735 | 2.000 |
| Si | 0.54 | 1.080 | 412 | 2.000 |
| C | 0.26 | 0.520 | 176 | 2.000 |
| I | 0.89 | 1.783 | 711 | 2.000 |
| Pd | 0.86 | 1.720 | 684 | 2.000 |
| As | 0.81 | 1.620 | 642 | 2.000 |
| Ga | 0.80 | 1.600 | 633 | 2.000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, P.; Lei, Q.; Zhang, H.; Qi, M.; Song, J.; Lian, P.; Cheng, J.; Wang, Q.; Tang, Z.; Liu, Z. Measurement of the Diffusion Coefficient of Xenon in Self-Sintered Nanopore Graphite for Molten Salt Reactor. C 2023, 9, 113. https://doi.org/10.3390/c9040113
Li P, Lei Q, Zhang H, Qi M, Song J, Lian P, Cheng J, Wang Q, Tang Z, Liu Z. Measurement of the Diffusion Coefficient of Xenon in Self-Sintered Nanopore Graphite for Molten Salt Reactor. C. 2023; 9(4):113. https://doi.org/10.3390/c9040113
Chicago/Turabian StyleLi, Pengda, Qiantao Lei, Heyao Zhang, Mingbo Qi, Jinliang Song, Pengfei Lian, Jinxing Cheng, Qingbo Wang, Zhongfeng Tang, and Zhanjun Liu. 2023. "Measurement of the Diffusion Coefficient of Xenon in Self-Sintered Nanopore Graphite for Molten Salt Reactor" C 9, no. 4: 113. https://doi.org/10.3390/c9040113
APA StyleLi, P., Lei, Q., Zhang, H., Qi, M., Song, J., Lian, P., Cheng, J., Wang, Q., Tang, Z., & Liu, Z. (2023). Measurement of the Diffusion Coefficient of Xenon in Self-Sintered Nanopore Graphite for Molten Salt Reactor. C, 9(4), 113. https://doi.org/10.3390/c9040113








