Continuous Monitoring of Olive Fruit Growth by Automatic Extensimeter in Response to Vapor Pressure Deficit from Pit Hardening to Harvest
Abstract
:1. Introduction
2. Materials and Methods
2.1. Site Description and Phenology
2.2. Fruit Growth
2.3. Time-Lapse Video
2.4. Meteorological Data
2.5. Hysteresis Curves
2.6. Data Analysis and Presentation
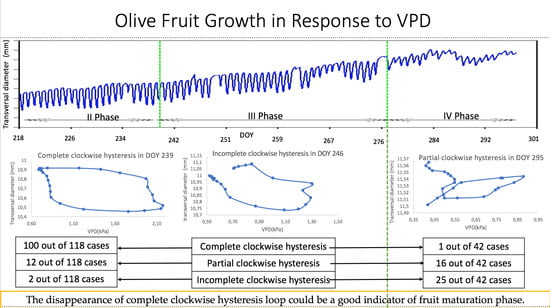
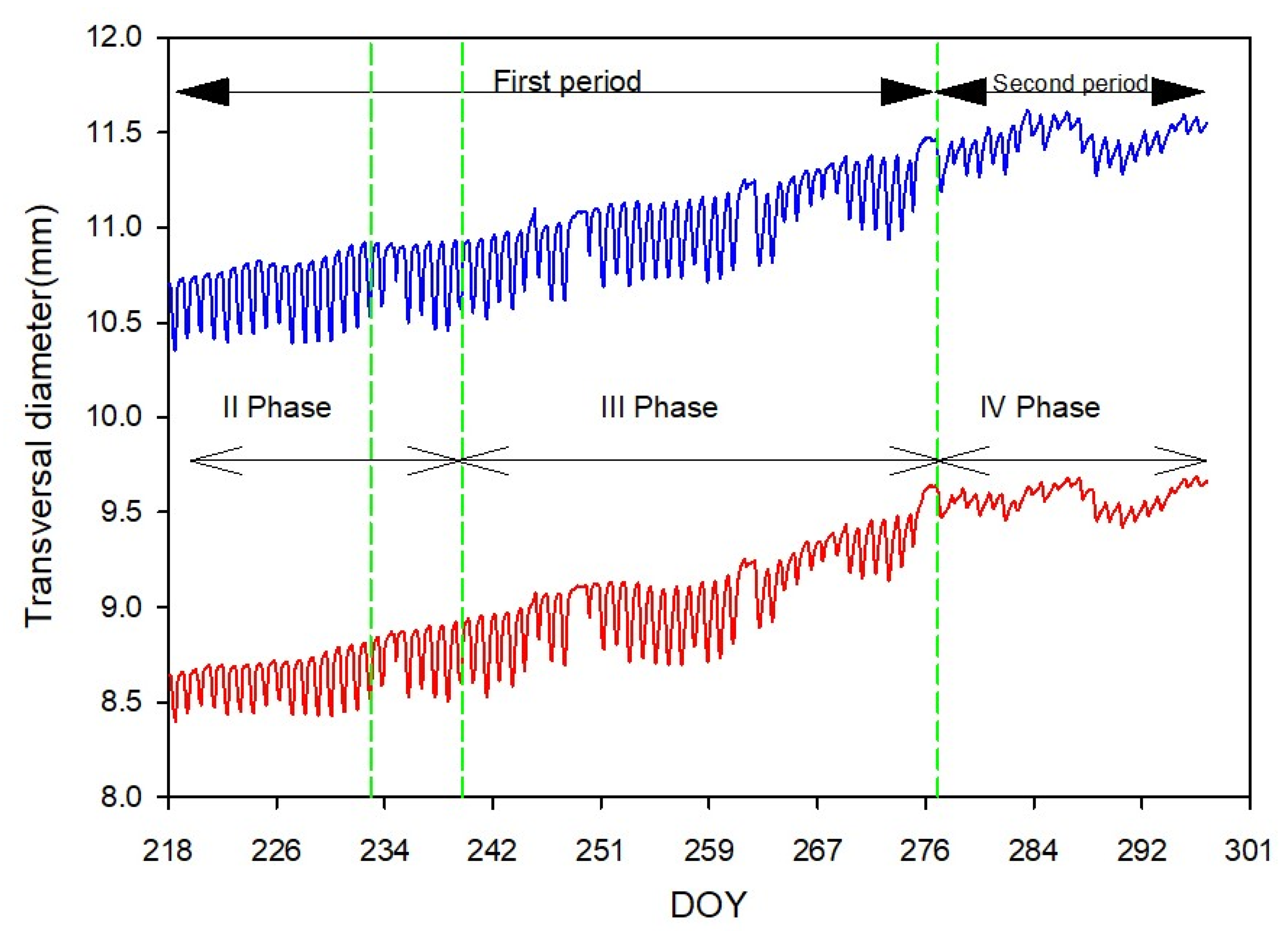
3. Results
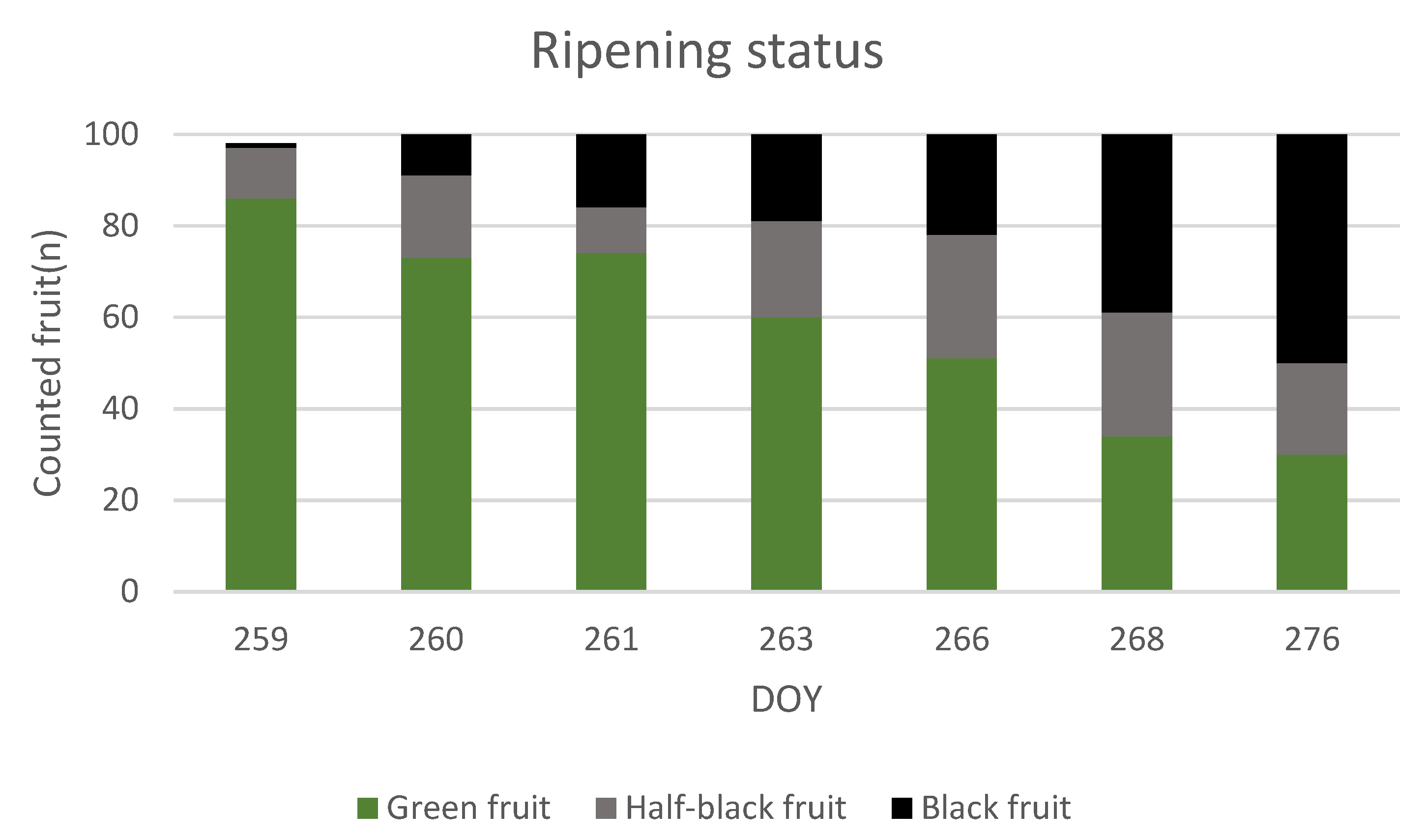
3.1. Fruit Growth
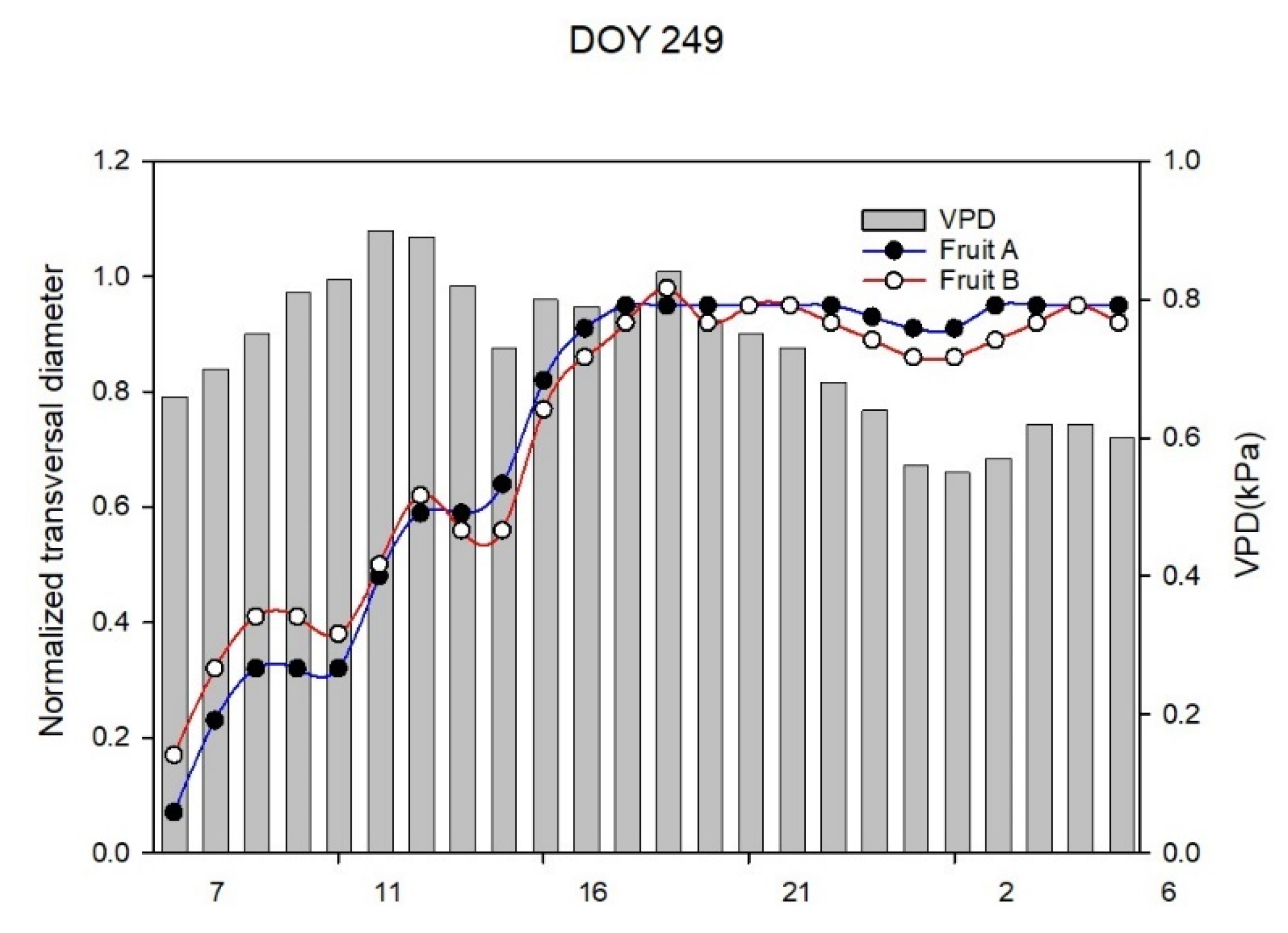
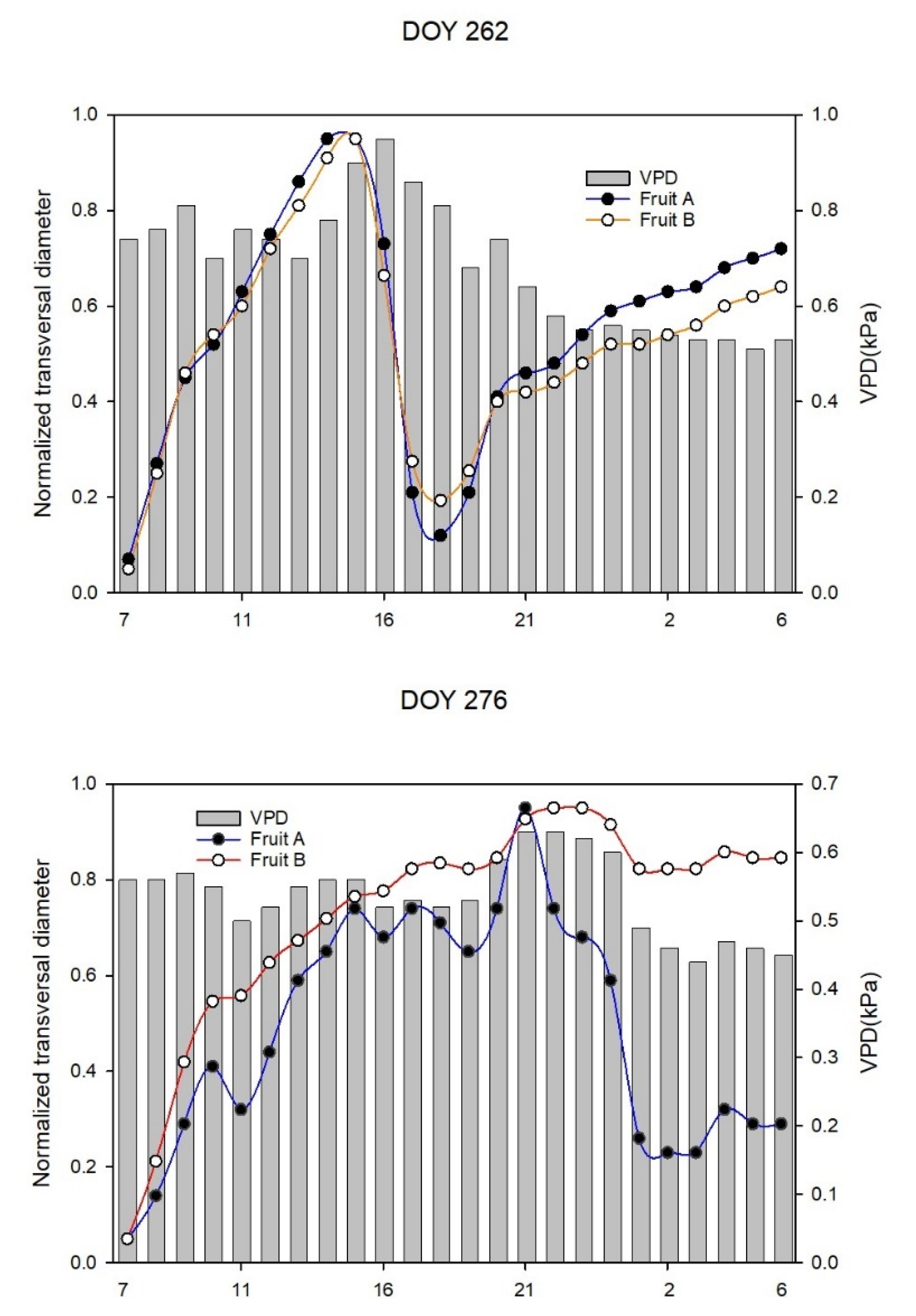
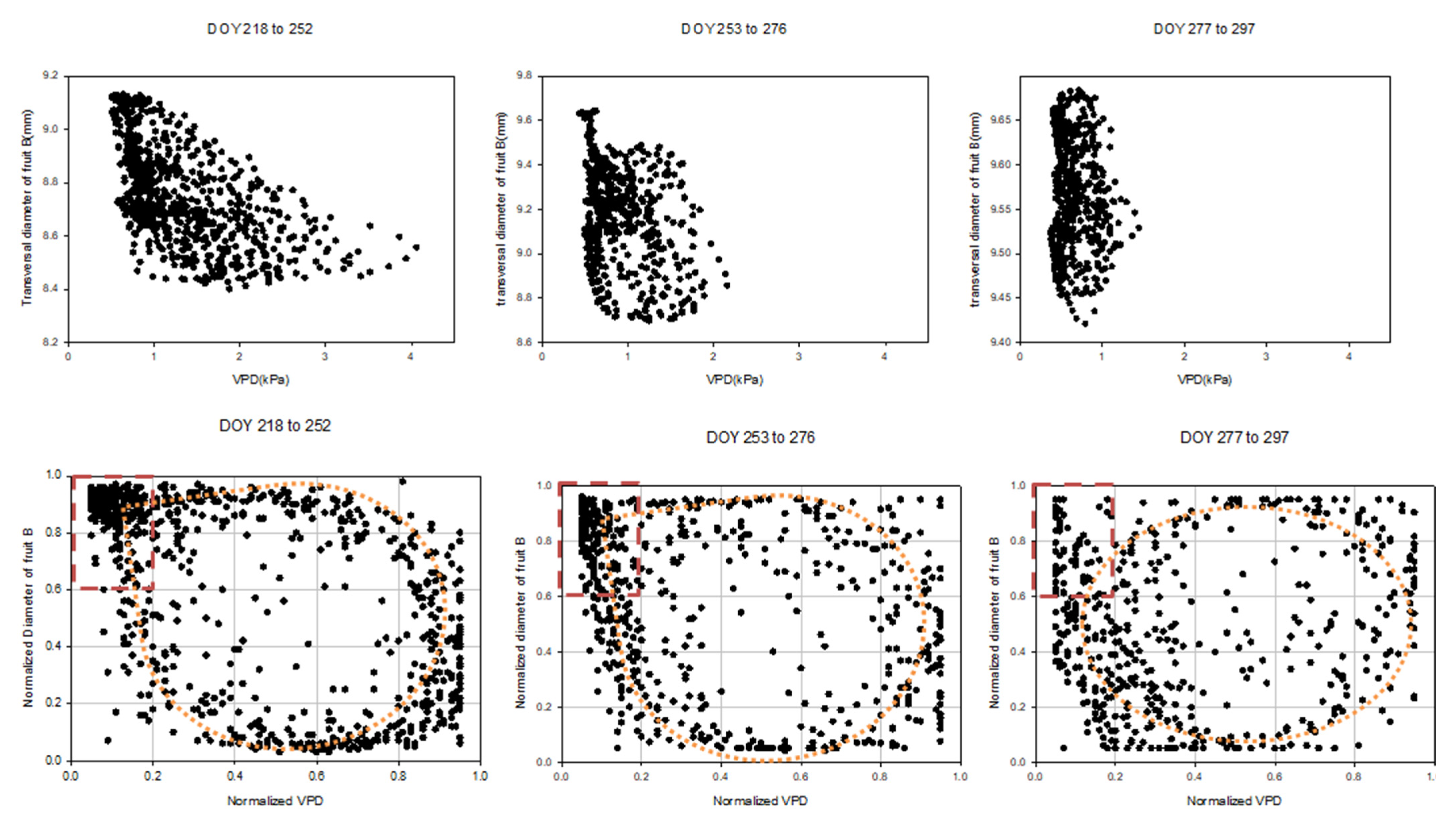
3.2. Analysis of Diameter Growth versus VPD and Hysteresis Curves
3.3. Fruit Monitoring by Time-Lapse Camera
4. Discussion
4.1. Diurnal Transversal Diameter Change and Its Influencing Factor
4.2. Hysteresis Loop, Challenges and Variations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Conde, C.; Delrot, S.; Gerós, H. Physiological, biochemical and molecular changes occurring during olive development and ripening. J. Plant Physiol. 2008, 165, 1545–1562. [Google Scholar] [CrossRef]
- Tombesi, A. Olive fruit growth and metabolism. Acta Hortic. 1994, 356, 225–232. [Google Scholar] [CrossRef]
- Martinelli, F.; Sebastiani, L.; Tonutti, P.; d’Andria, R. Molecular and metabolic analyses in developing olive fruit in relation to different water regimes. Acta Hortic. 2011, 888, 163–168. [Google Scholar] [CrossRef]
- Fernández, F.J.; Ladux, J.L.; Hammami, S.B.; Rapoport, H.F.; Searles, P.S. Fruit, mesocarp, and endocarp responses to crop load and to different estimates of source: Sink ratio in olive (cv. Arauco) at final harvest. Sci. Hortic. 2018, 234, 49–57. [Google Scholar] [CrossRef]
- Gucci, R.; Lodolini, E.M.; Rapoport, H.F. Water deficit-induced changes in mesocarp cellular processes and the relationship between mesocarp and endocarp during olive fruit development. Tree Physiol. 2009, 29, 1575–1585. [Google Scholar] [CrossRef] [PubMed]
- Corelli-Grappadelli, L.; Lakso, A.N. Fruit development in deciduous tree crops as affected by physiological factors and environmental conditions (keynote). In Proceedings of the XXVI International Horticultural Congress: Key Processes in the Growth and Cropping of Deciduous Fruit and Nut Trees 636, Toronto, ON, Canada, 11–17 August 2002; pp. 425–441. [Google Scholar]
- Hammami, S.B.; Manrique, T.; Rapoport, H.F. Cultivar-based fruit size in olive depends on different tissue and cellular processes throughout growth. Sci. Hortic. 2011, 130, 445–451. [Google Scholar] [CrossRef]
- Amitrano, C.; Arena, C.; Rouphael, Y.; De Pascale, S.; De Micco, V. Vapour pressure deficit: The hidden driver behind plant morphofunctional traits in controlled environments. Ann. Appl. Biol. 2019, 175, 313–325. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; Hubbard, N.; Loudjani, P. Precision Agriculture: An Opportunity for EU Farmers—Potential Support with the CAP 2014–2020; Joint Research Centre (JRC) of the European Commission; Monitoring Agriculture ResourseS (MARS) Unit H04: Brussels, Belgium, 2014. [Google Scholar]
- Marino, G.; Scalisi, A.; Guzmán-Delgado, P.; Caruso, T.; Marra, F.P.; Lo Bianco, R. Detecting Mild Water Stress in Olive with Multiple Plant-Based Continuous Sensors. Plants 2021, 10, 131. [Google Scholar] [CrossRef] [PubMed]
- Zucchini, M.; Khosravi, A.; Giorgi, V.; Mancini, A.; Neri, D. Is There Daily Growth Hysteresis versus Vapor Pressure Deficit in Cherry Fruit? Horticulturae 2021, 7, 131. [Google Scholar] [CrossRef]
- Fishman, S.; Génard, M. A biophysical model of fruit growth: Simulation of seasonal and diurnal dynamics of mass. Plant Cell Environ. 1998, 21, 739–752. [Google Scholar] [CrossRef]
- Brüggenwirth, M.; Winkler, A.; Knoche, M. Xylem, phloem, and transpiration flows in developing sweet cherry fruit. Trees 2016, 30, 1821–1830. [Google Scholar] [CrossRef]
- Manfrini, L.; Pierpaoli, E.; Taylor, J.A.; Morandi, B.; Losciale, P.; Zibordi, M.; Grappadelli, L.C.; Bastías, R.M. Precision fruit growing: How to collect and interpret data on seasonal variation in apple orchards. In Proceedings of the XXVIII International Horticultural Congress on Science and Horticulture for People (IHC2010): International Symposium on Plant 932, Lisbon, Portugal, 22–27 August 2010; pp. 461–469. [Google Scholar]
- Fernandes, R.D.M.; Cuevas, M.V.; Diaz-Espejo, A.; Hernandez-Santana, V. Effects of water stress on fruit growth and water relations between fruits and leaves in a hedgerow olive orchard. Agric. Water Manag. 2018, 210, 32–40. [Google Scholar] [CrossRef]
- Morandi, B.; Manfrini, L.; Zibordi, M.; Noferini, M.; Fiori, G.; Grappadelli, L.C. A Low-cost Device for Accurate and Continuous Measurements of Fruit Diameter. HortScience 2007, 42, 1380–1382. [Google Scholar] [CrossRef] [Green Version]
- Goldhamer, D.A. Regulated deficit irrigation for California canning olives. In Proceedings of the III International Symposium on Olive Growing 474, Chania, Greece, 12–26 September 1997; pp. 369–372. [Google Scholar]
- Tovar, M.J.; Romero-Fabregat, M.-P.; Alegre, S.M.; Girona, J.; Motilva, M.J. Composition and organoleptic characteristics of oil fromArbequina olive (Olea europaea L.) trees under deficit irrigation. J. Sci. Food Agric. 2002, 82, 1755–1763. [Google Scholar] [CrossRef]
- Tognetti, R.; d’Andria, R.; Lavini, A.; Morelli, G. The effect of deficit irrigation on crop yield and vegetative development of Olea europaea L.(cvs. Frantoio and Leccino). Eur. J. Agron. 2006, 25, 356–364. [Google Scholar] [CrossRef]
- Alhaoui, N.; Gómez-Caravaca, A.M.; Leon, L.; De la Rosa, R.; Fernandez-Gutierrez, A.; Segura-Carretero, A. Pattern of variation of fruit traits and phenol content in olive fruits from six different cultivars. J. Agric. Food Chem. 2015, 63, 10466–10476. [Google Scholar]
- Fernández, J. Plant-based methods for irrigation scheduling of woody crops. Horticulturae 2017, 3, 35. [Google Scholar] [CrossRef] [Green Version]
- Jones, H.G. Monitoring plant and soil water status: Established and novel methods revisited and their relevance to studies of drought tolerance. J. Exp. Bot. 2006, 58, 119–130. [Google Scholar] [CrossRef] [Green Version]
- Mayergoyz, I.D. Mathematical Models of Hysteresis and Their Applications, 2nd ed.; Electromagnetism; Academic Press: Cambridge, MA, USA, 2003; ISBN 978-0-12-480873-7. [Google Scholar]
- Phillips, J.D. Sources of nonlinearity and complexity in geomorphic systems. Prog. Phys. Geogr. 2003, 27, 1–23. [Google Scholar] [CrossRef]
- O’Kane, J.P. Hysteresis in hydrology. Acta Geophys. Pol. 2005, 53, 373–383. [Google Scholar]
- Zhang, Q.; Manzoni, S.; Katul, G.; Porporato, A.; Yang, D. The hysteretic evapotranspiration—Vapor pressure deficit relation. J. Geophys. Res. Biogeosciences 2014, 119, 125–140. [Google Scholar] [CrossRef]
- Ewers, B.E.; Gower, S.T.; Bond-lamberty, B.; Wang, C.K. Effects of stand age and tree species on canopy transpiration and average stomatal conductance of boreal forests. Plant Cell Environ. 2005, 28, 660–678. [Google Scholar] [CrossRef]
- Meinzer, F.C.; Goldstein, G.; Franco, A.C.; Bustamante, M.; Igler, E.; Jackson, P.; Caldas, L.; Rundel, P.W. Atmospheric and hydraulic limitations on transpiration in Brazilian cerrado woody species. Funct. Ecol. 1999, 13, 273–282. [Google Scholar] [CrossRef]
- O’Brien, J.J.; Oberbauer, S.F.; Clark, D.B. Whole tree xylem sap flow responses to multiple environmental variables in a wet tropical forest. Plant Cell Environ. 2004, 27, 551–567. [Google Scholar] [CrossRef]
- O’Grady, A.P.; Worledge, D.; Battaglia, M. Constraints on transpiration of Eucalyptus globulus in southern Tasmania, Australia. Agric. Meteorol. 2008, 148, 453–465. [Google Scholar] [CrossRef]
- Unsworth, M.H.; Phillips, N.; Link, T.; Bond, B.J.; Falk, M.; Harmon, M.E.; Hinckley, T.M.; Marks, D.; Paw, U.K.T. Components and controls of water flux in an old-growth douglas-fir-western hemlock ecosystem. Ecosystems 2004, 7, 468–481. [Google Scholar] [CrossRef]
- Wullschleger, S.D.; Hanson, P.J.; Tschaplinski, T.J. Whole-plant water flux in understory red maple exposed to altered precipitation regimes. Tree Physiol. 1998, 18, 71–79. [Google Scholar] [CrossRef]
- Zeppel, M.J.B.; Murray, B.R.; Barton, C.; Eamus, D. Seasonal responses of xylem sap velocity to VPD and solar radiation during drought in a stand of native trees in temperate Australia. Funct. Plant Biol. 2004, 31, 461–470. [Google Scholar] [CrossRef] [PubMed]
- Bai, Y.; Li, X.; Liu, S.; Wang, P. Modelling diurnal and seasonal hysteresis phenomena of canopy conductance in an oasis forest ecosystem. Agric. For. Meteorol. 2017, 246, 98–110. [Google Scholar] [CrossRef]
- Scalisi, A.; Marino, G.; Marra, F.P.; Caruso, T.; Lo Bianco, R. A Cultivar-Sensitive Approach for the Continuous Monitoring of Olive (Olea europaea L.) Tree Water Status by Fruit and Leaf Sensing. Front. Plant Sci. 2020, 11, 340. [Google Scholar] [CrossRef]
- Kottek, M.; Grieser, J.; Beck, C.; Rudolf, B.; Rubel, F. World map of the Köppen-Geiger climate classification updated. Meteorol. Z. 2006, 15, 259–263. [Google Scholar] [CrossRef]
- COI (International Olive Council). Guide for the Determination of the Characteristics of Oil Olives, COI/OH/Doc. No 1 November 2011. Available online: http://www.internationaloliveoil.org (accessed on 15 September 2021).
- Monteith, J.; Unsworth, M. Principles of Environmental Physics: Plants, Animals, and the Atmosphere; Academic Press: Cambridge, MA, USA, 2013. [Google Scholar]
- Perez-Martin, A.; Flexas, J.; Ribas-Carbó, M.; Bota, J.; Tomàs, M.; Infante, J.M.; Diaz-Espejo, A. Interactive effects of soil water deficit and air vapour pressure deficit on mesophyll conductance to CO2 in Vitis vinifera and Olea europaea. J. Exp. Bot. 2009, 60, 2391–2405. [Google Scholar] [CrossRef]
- Novick, K.A.; Miniat, C.F.; Vose, J.M. Drought limitations to leaf-level gas exchange: Results from a model linking stomatal optimization and cohesion-tension theory. Plant Cell Environ. 2016, 39, 583–596. [Google Scholar] [CrossRef] [Green Version]
- Morandi, B.; Rieger, M.; Grappadelli, L.C. Vascular flows and transpiration affect peach (Prunus persica Batsch.) fruit daily growth. J. Exp. Bot. 2007, 58, 3941–3947. [Google Scholar] [CrossRef] [Green Version]
- Bianco, R.L.; Scalisi, A. Water relations and carbohydrate partitioning of four greenhouse-grown olive genotypes under long-term drought. Trees 2016, 31, 717–727. [Google Scholar] [CrossRef]
- Kong, W.; Rui, H.; Na, L.; Wanming, B.; Junyi, M.; Xiaoyong, B.; Junyu, L.; Junlong, W.; Ji, Z. Dynamic assessment of the fruit quality of olives cultivated in Longnan (China) during ripening. Sci. Hortic. 2019, 253, 8–16. [Google Scholar] [CrossRef]
- Zhang, R.; Xu, X.; Liu, M.; Zhang, Y.; Xu, C.; Yi, R.; Luo, W.; Soulsby, C. Hysteresis in sap flow and its controlling mechanisms for a deciduous broad-leaved tree species in a humid karst region. Sci. China Earth Sci. 2019, 62, 1744–1755. [Google Scholar] [CrossRef]
- Chen, L.; Zhang, Z.; Li, Z.; Tang, J.; Caldwell, P.; Zhang, W. Biophysical control of whole tree transpiration under an urban environment in Northern China. J. Hydrol. 2011, 402, 388–400. [Google Scholar] [CrossRef]
- Bai, Y.; Zhu, G.; Su, Y.; Zhang, K.; Han, T.; Ma, J.; Wang, W.; Ma, T.; Feng, L. Hysteresis loops between canopy conductance of grapevines and meteorological variables in an oasis ecosystem. Agric. For. Meteorol. 2015, 214-215, 319–327. [Google Scholar] [CrossRef]
- Janssen, R.H.H.; Meinders, M.B.J.; van Nes, E.H.; Scheffer, M. Microscale vegetation-soil feedback boosts hysteresis in a regional vegetation-climate system. Glob. Chang. Biol. 2008, 14, 1104–1112. [Google Scholar] [CrossRef]




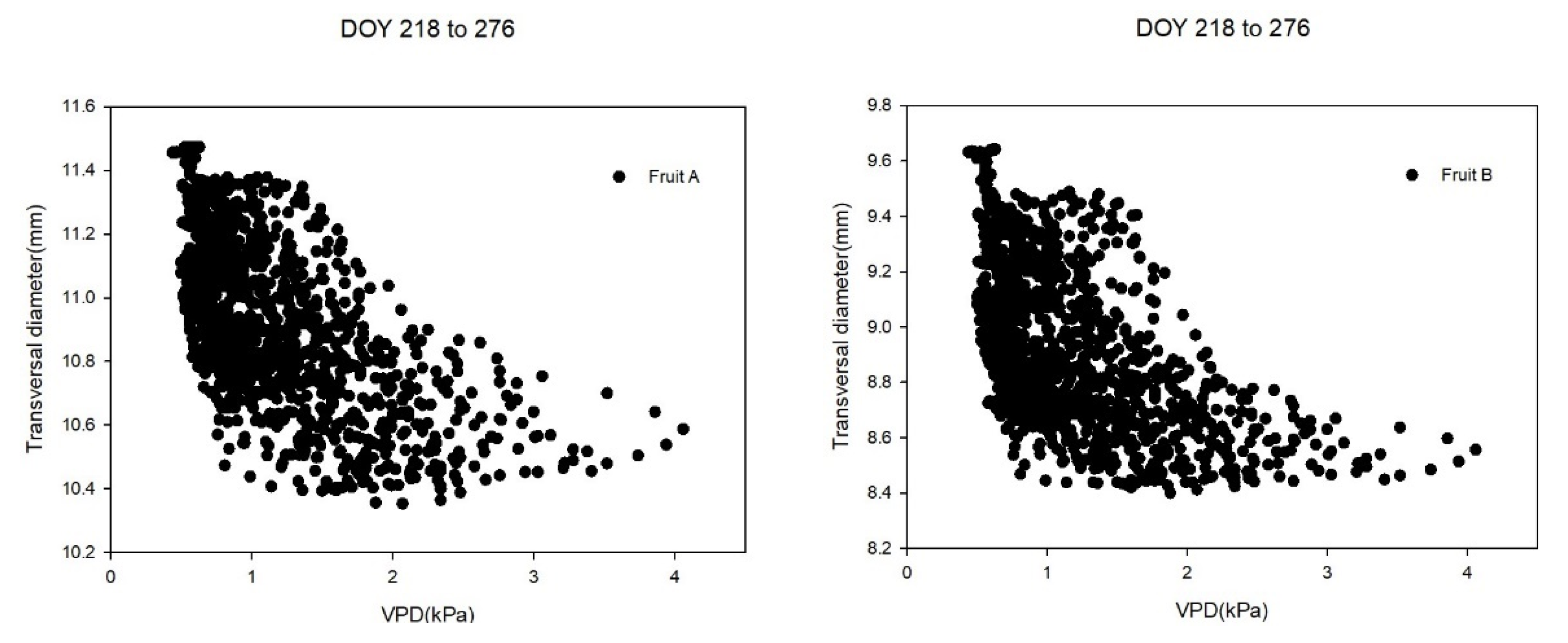
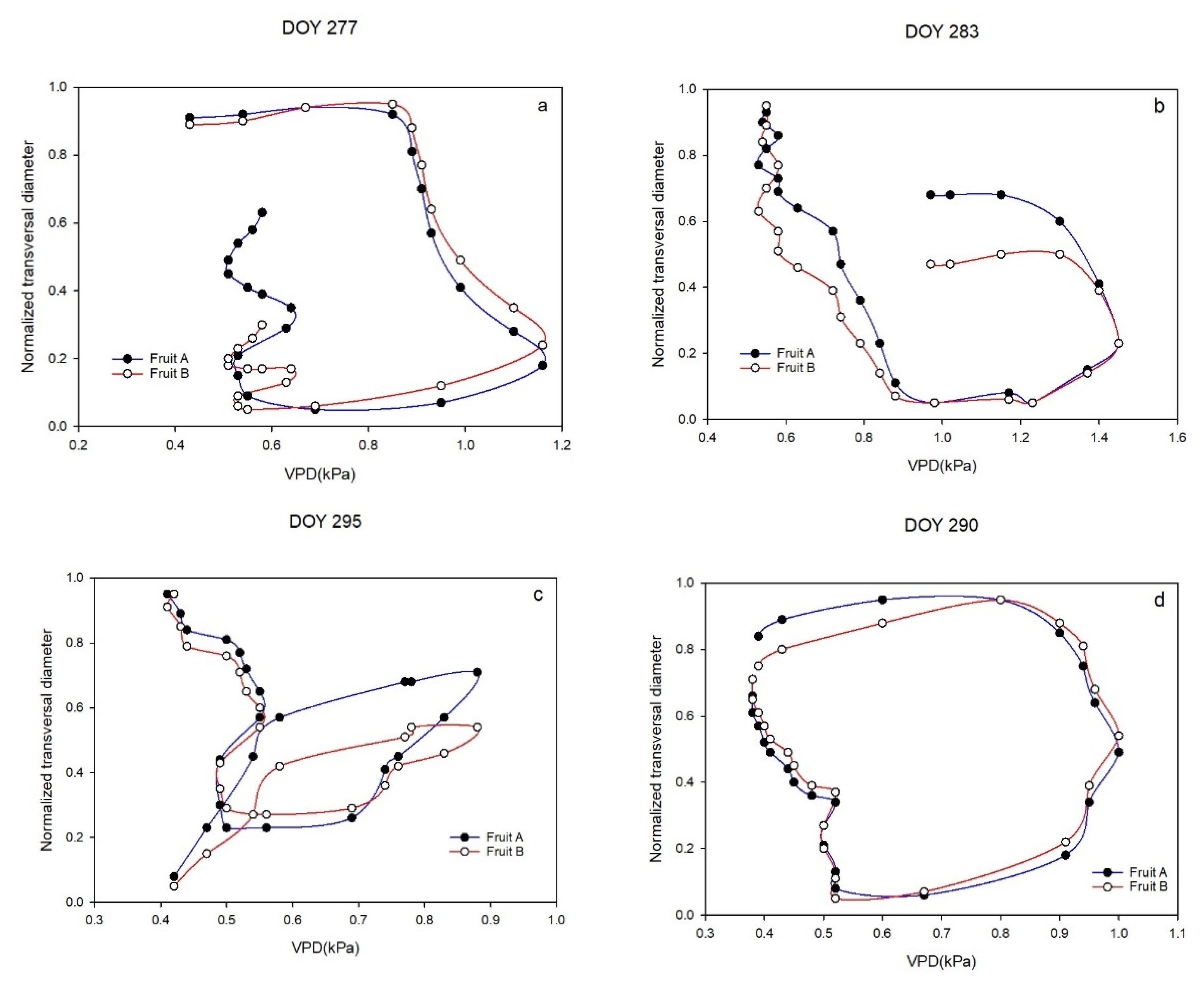
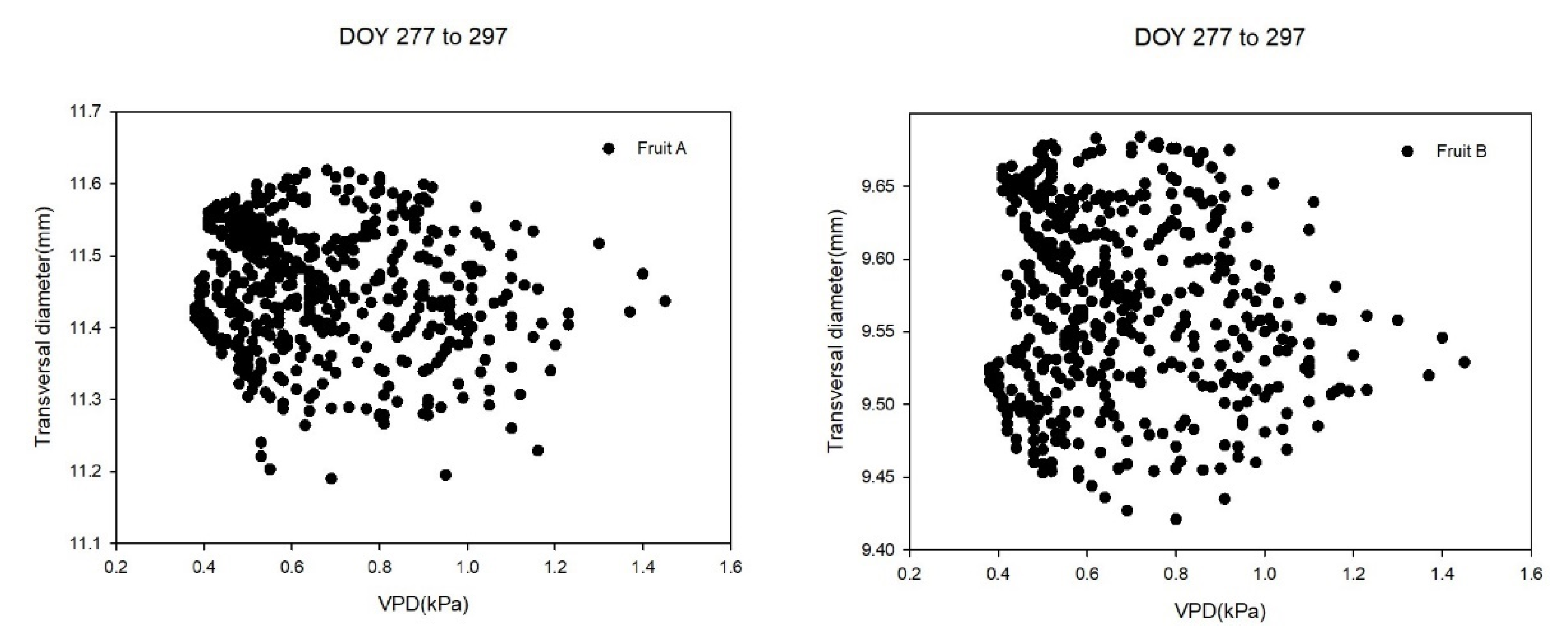
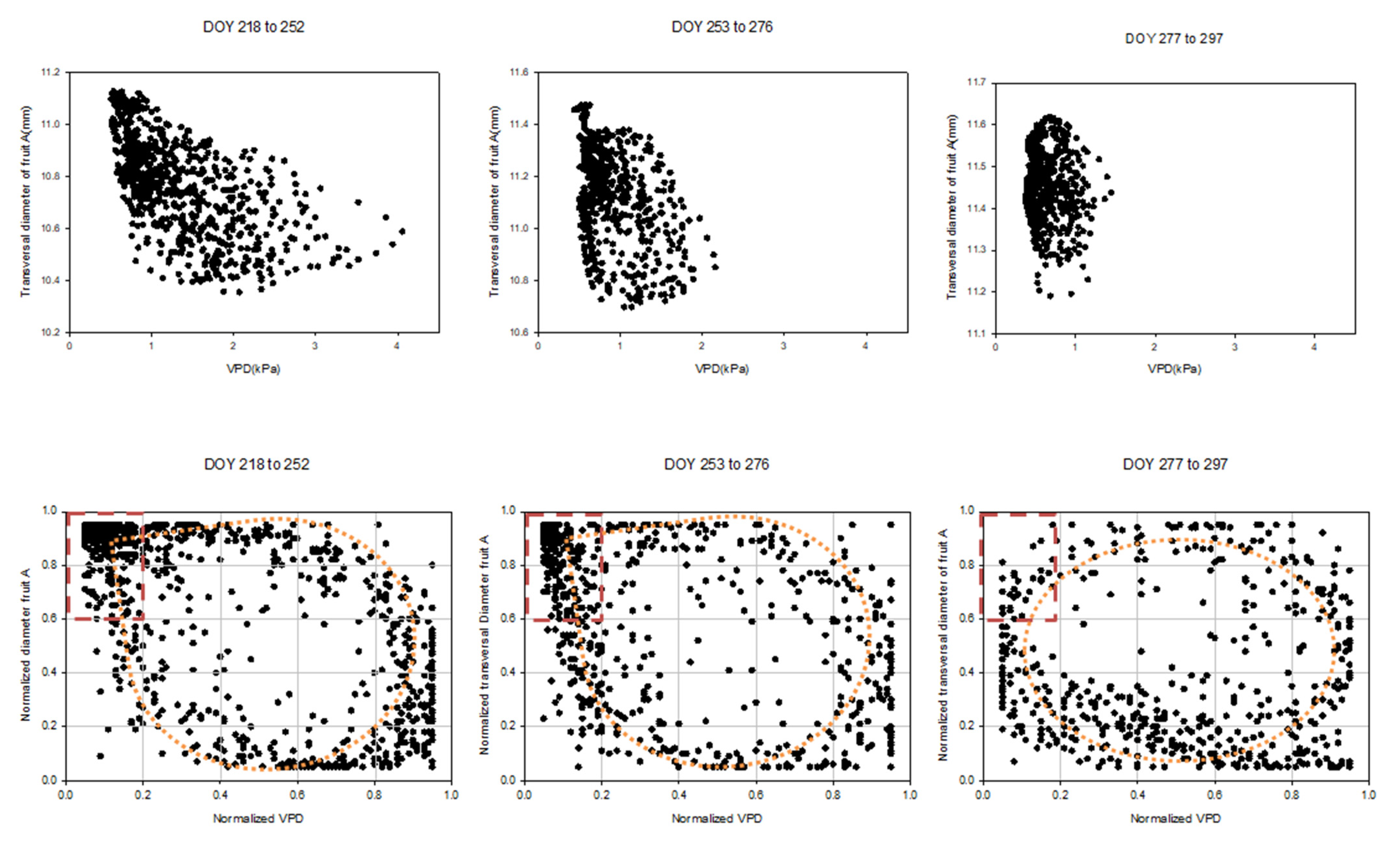

| DOY | VPD (kPa) | VPD Daily Variation (%) | Normalized VPD | DOY | VPD (kPa) | VPD Daily Variation (%) | Normalized VPD | DOY | VPD (kPa) | VPD Daily Variation (%) | Normalized VPD |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 218 | 2.48 | - | 0.78 | 245 | 0.98 | −33.33 | 0.25 | 272 | 1.58 | −13.19 | 0.46 |
| 219 | 1.96 | −21.00 | 0.59 | 246 | 0.90 | −8.16 | 0.22 | 273 | 1.85 | 17.09 | 0.56 |
| 220 | 1.53 | −21.91 | 0.44 | 247 | 1.47 | 63.33 | 0.42 | 274 | 1.28 | −30.81 | 0.36 |
| 221 | 1.54 | 0.75 | 0.45 | 248 | 1.64 | 11.56 | 0.48 | 275 | 0.80 | −37.50 | 0.19 |
| 222 | 2.57 | 66.99 | 0.81 | 249 | 0.41 | −75.00 | 0.05 | 276 | 0.47 | −41.25 | 0.07 |
| 223 | 2.97 | 15.56 | 0.95 | 250 | 0.66 | 60.98 | 0.14 | 277 | 0.93 | 97.87 | 0.37 |
| 224 | 2.72 | −8.42 | 0.86 | 251 | 2.02 | 206.06 | 0.62 | 278 | 0.48 | −48.39 | 0.10 |
| 225 | 1.65 | −39.34 | 0.49 | 252 | 1.45 | −28.22 | 0.42 | 279 | 1.15 | 139.58 | 0.50 |
| 226 | 1.41 | −14.55 | 0.40 | 253 | 1.19 | −17.93 | 0.32 | 280 | 0.94 | −18.26 | 0.37 |
| 227 | 1.88 | 33.33 | 0.57 | 254 | 1.10 | −7.56 | 0.29 | 281 | 0.97 | 3.19 | 0.39 |
| 228 | 1.65 | −12.23 | 0.49 | 255 | 1.18 | 7.27 | 0.32 | 282 | 1.92 | 97.94 | 0.95 |
| 229 | 1.99 | 20.61 | 0.61 | 256 | 1.10 | −6.78 | 0.29 | 283 | 1.08 | −43.75 | 0.46 |
| 230 | 2.66 | 33.67 | 0.84 | 257 | 1.27 | 15.45 | 0.35 | 284 | 0.53 | −50.93 | 0.13 |
| 231 | 2.83 | 6.39 | 0.90 | 258 | 0.99 | −22.05 | 0.25 | 285 | 0.66 | 24.53 | 0.21 |
| 232 | 2.79 | −1.41 | 0.89 | 259 | 1.52 | 53.54 | 0.44 | 286 | 0.46 | −30.30 | 0.09 |
| 233 | 1.76 | −36.92 | 0.52 | 260 | 2.18 | 43.42 | 0.67 | 287 | 0.39 | −15.22 | 0.05 |
| 234 | 1.39 | −21.02 | 0.39 | 261 | 1.58 | −27.52 | 0.46 | 288 | 0.95 | 143.59 | 0.38 |
| 235 | 0.96 | −30.94 | 0.24 | 262 | 0.51 | −67.72 | 0.09 | 289 | 1.34 | 41.05 | 0.61 |
| 236 | 1.25 | 30.21 | 0.35 | 263 | 1.30 | 154.90 | 0.36 | 290 | 0.98 | −26.87 | 0.40 |
| 237 | 1.03 | −17.60 | 0.27 | 264 | 1.19 | −8.46 | 0.32 | 291 | 1.02 | 4.08 | 0.42 |
| 238 | 1.25 | 21.36 | 0.35 | 265 | 0.69 | −42.02 | 0.15 | 292 | 0.88 | −13.73 | 0.34 |
| 239 | 1.58 | 26.40 | 0.46 | 266 | 0.51 | −26.09 | 0.09 | 293 | 0.93 | 5.68 | 0.37 |
| 240 | 1.64 | 3.80 | 0.48 | 267 | 0.72 | 41.18 | 0.16 | 294 | 0.83 | −10.75 | 0.31 |
| 241 | 1.43 | −12.80 | 0.41 | 268 | 0.86 | 19.44 | 0.21 | 295 | 0.40 | −51.81 | 0.06 |
| 242 | 1.70 | 18.88 | 0.50 | 269 | 0.62 | −27.91 | 0.12 | 296 | 0.51 | 27.50 | 0.12 |
| 243 | 1.42 | −16.47 | 0.41 | 270 | 0.88 | 41.94 | 0.22 | 297 | 0.51 | 0.00 | 0.12 |
| 244 | 1.47 | 3.52 | 0.42 | 271 | 1.82 | 106.82 | 0.55 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khosravi, A.; Zucchini, M.; Giorgi, V.; Mancini, A.; Neri, D. Continuous Monitoring of Olive Fruit Growth by Automatic Extensimeter in Response to Vapor Pressure Deficit from Pit Hardening to Harvest. Horticulturae 2021, 7, 349. https://doi.org/10.3390/horticulturae7100349
Khosravi A, Zucchini M, Giorgi V, Mancini A, Neri D. Continuous Monitoring of Olive Fruit Growth by Automatic Extensimeter in Response to Vapor Pressure Deficit from Pit Hardening to Harvest. Horticulturae. 2021; 7(10):349. https://doi.org/10.3390/horticulturae7100349
Chicago/Turabian StyleKhosravi, Arash, Matteo Zucchini, Veronica Giorgi, Adriano Mancini, and Davide Neri. 2021. "Continuous Monitoring of Olive Fruit Growth by Automatic Extensimeter in Response to Vapor Pressure Deficit from Pit Hardening to Harvest" Horticulturae 7, no. 10: 349. https://doi.org/10.3390/horticulturae7100349
APA StyleKhosravi, A., Zucchini, M., Giorgi, V., Mancini, A., & Neri, D. (2021). Continuous Monitoring of Olive Fruit Growth by Automatic Extensimeter in Response to Vapor Pressure Deficit from Pit Hardening to Harvest. Horticulturae, 7(10), 349. https://doi.org/10.3390/horticulturae7100349