Predicting the Chemical Attributes of Fresh Citrus Fruits Using Artificial Neural Network and Linear Regression Models
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Site and Plant Materials
2.2. Measurements
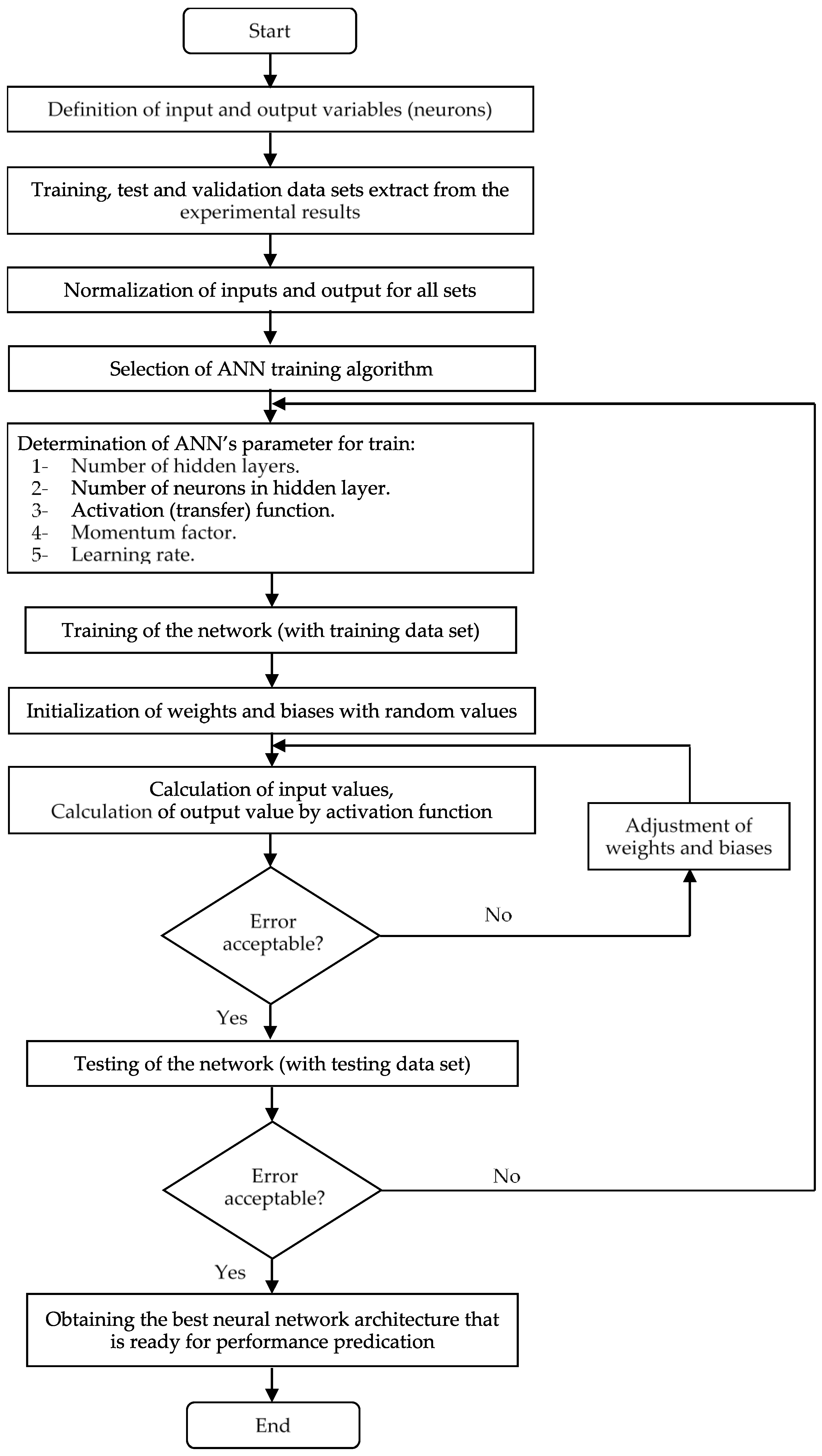
2.3. Artificial Neural Networks (ANNs)
2.4. ANN Development
2.5. Multiple Linear Regression
2.6. Models Evaluation
3. Results
3.1. Exploratory Analysis with Six Cultivars
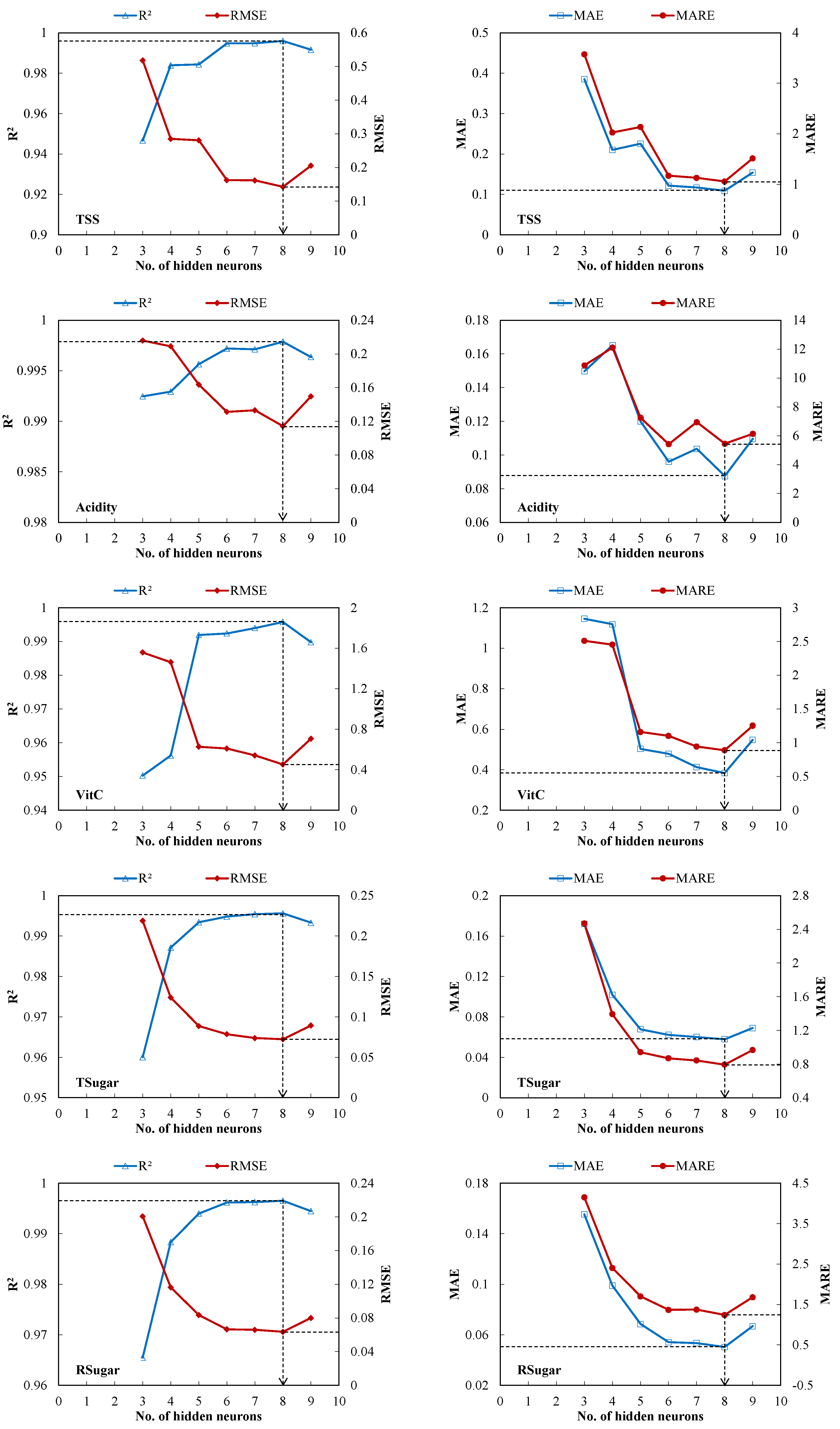
3.2. Optimal ANN Architecture Selection
3.3. ANN Model Performance
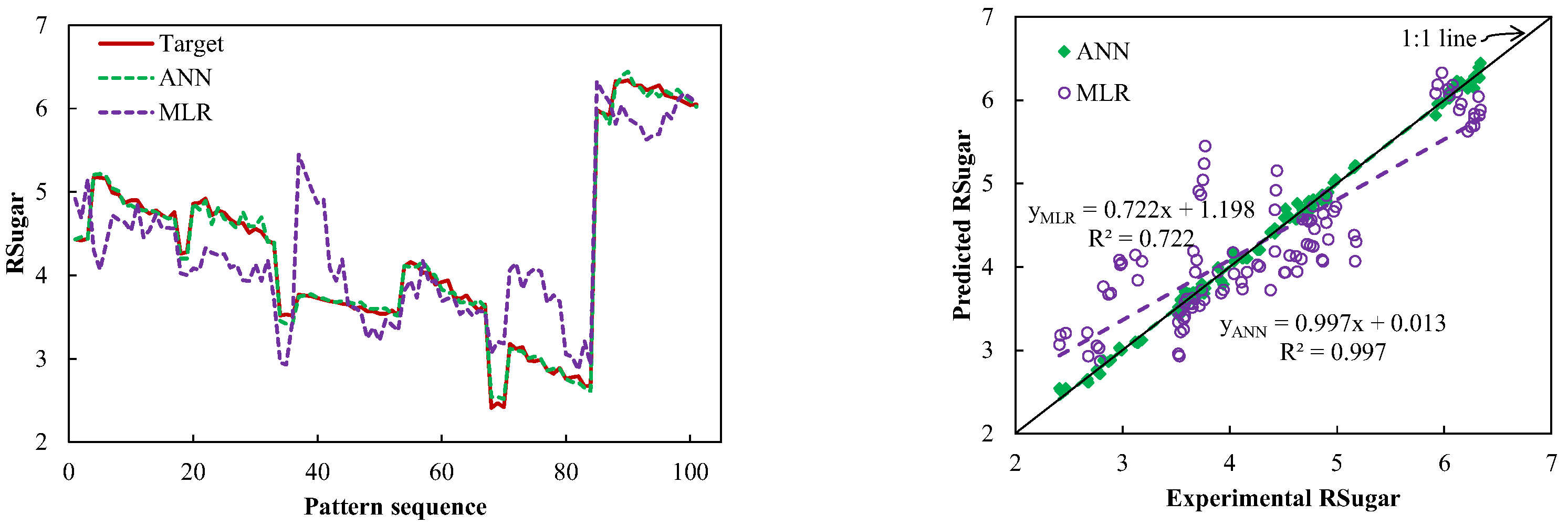
3.4. Comparison between the Selected ANN and MLR Models
3.5. TSS, Acidity, VitC, Tsugar, and Rsugar of the Citrus Fruits Groups with the Selected ANN and MLR Models
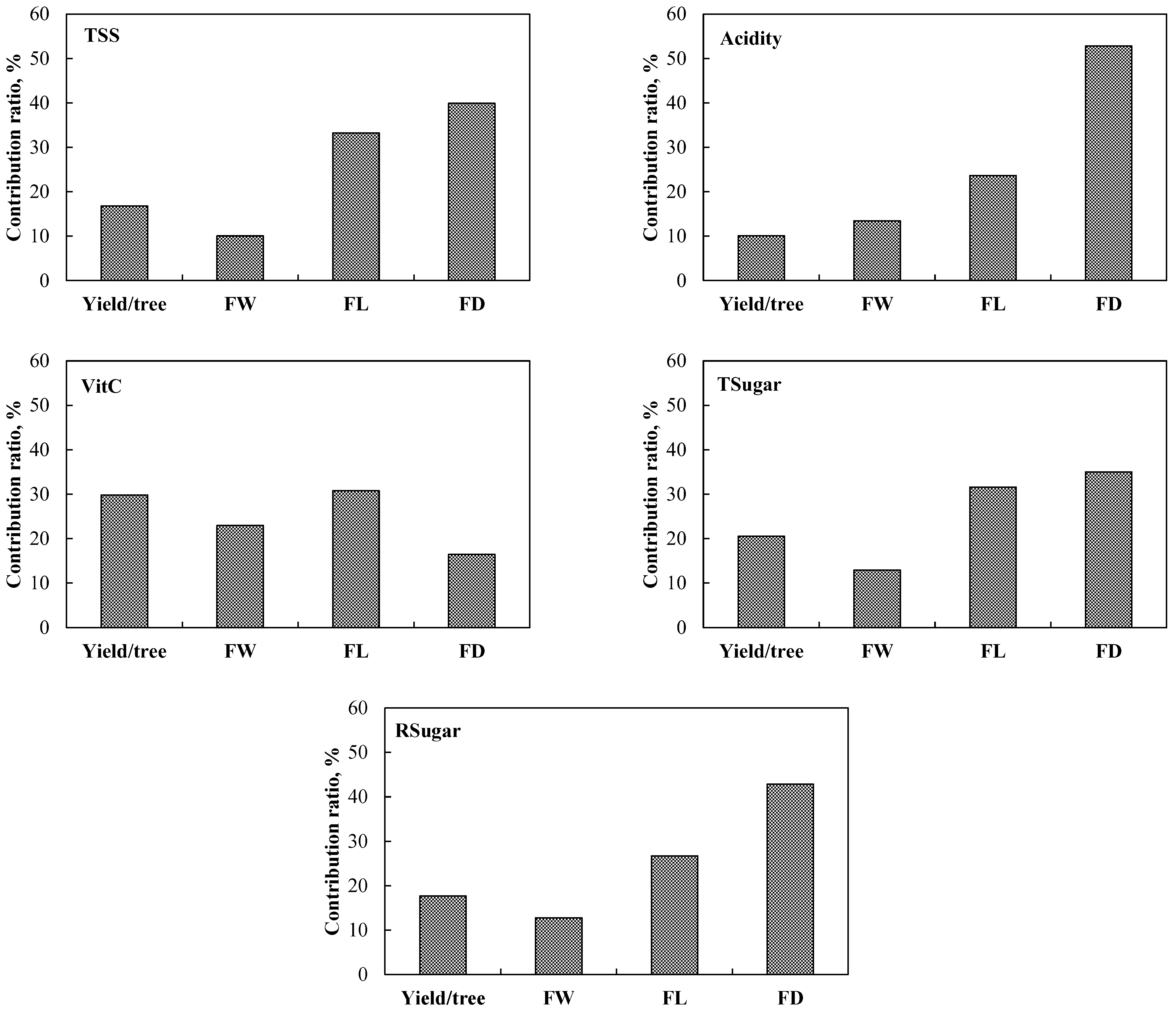
3.6. Importance-Ratio Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Food and Agriculture Organization of the United Nations. FAO Statistical Databases 2020. Available online: https://www.fao.org/faostat/ (accessed on 22 August 2022).
- Agricultural Static; Ministry of Agriculture; Egypt-Economic Affairs Sector. 2022. Available online: https://egypt.opendataforafrica.org/data#topic=Agriculture (accessed on 22 August 2022).
- Qi, L.; Qi, C.J. Status quo and development trend of world’s citrus Industry. Agric. Outlook 2016, 12, 46–52. [Google Scholar]
- Balfagón, D.; Arbona, V.; Gómez-Cadenas, A. El futuro de los cítricos: Impacto del cambio climático en la citricultura. Mètode Rev. Difus. Investig. 2021, 3, 60–67. [Google Scholar] [CrossRef]
- Dhillon, B.S.; Randhawa, J.S. Fruit Growth and Development in Citrus: Advance in Horticulture; Malhotra Publishing House: New Dehli, India, 1993; Volume 3. [Google Scholar]
- Nicolosi, E. Origin and taxonomy. In Citrus Genetics, Breeding and Biotechnology; Khan, I.A., Ed.; CAB International: Wallingford, UK, 2007; pp. 19–44. [Google Scholar]
- Liu, Y.; Heying, E.; Tanumihardjo, S.A. History, Global Distribution, and Nutritional Importance of Citrus Fruits. Compr. Rev. Food Sci. Food Saf. 2012, 11, 530–545. [Google Scholar] [CrossRef]
- Varnam, A.; Sutherland, J.M. Beverages: Technology, Chemistry and Microbiology; Springer Science & Business Media: New York, USA, 2012. [Google Scholar]
- Zhang, Y.; Sun, Y.; Xi, W.; Shen, Y.; Qiao, L.; Zhong, L.; Ye, X.; Zhou, Z. Phenolic compositions and antioxidant capacities of Chinese wild mandarin (Citrus reticulata Blanco) fruits. Food Chem. 2014, 145, 674–680. [Google Scholar] [CrossRef]
- Lado, J.; Gambeeta, G.; Zacarias, L. Key determinants of citrus fruit quality: Metabolites and main changes during maturation. Sci. Hortic. 2018, 233, 238–248. [Google Scholar] [CrossRef]
- Zou, Z.; Xi, W.; Hu, Y.; Nie, C.; Zhou, Z. Antioxidant activity of Citrus fruits. Food Chem. 2016, 196, 885–896. [Google Scholar] [CrossRef]
- Singh, B.; Singh, J.P.; Kaur, A.; Yadav, M.P. Insight into the chemical composition and bioactivities of citrus peel essential oils. Food Res. Int. 2021, 143, 110231. [Google Scholar] [CrossRef]
- Tanaka, T. Fundamental discussion of Citrus classification. Stud. Citrog. 1977, 14, 1–6. [Google Scholar]
- Taia, W.K.; Ibrahim, M.M.; Abdel-Sattar, M. Pollen morphological variations among some cultivated citrus species and its related genera in Egypt. Jordan J. Biol. Sci. 2020, 13, 499–508. [Google Scholar]
- Klimek-Szczykutowicz, M.; Szopa, A.; Ekiert, H. Citrus limon (Lemon) phenomenon—A review of the chemistry, pharmacological properties, applications in the modern pharmaceutical, food, and cosmetics industries, and biotechnological studies. Plants 2020, 9, 119. [Google Scholar] [CrossRef]
- Moore, G.A. Oranges and lemons: Clues to the taxonomy of Citrus from molecular markers. Trends Genet. 2001, 17, 536–540. [Google Scholar] [CrossRef]
- Obenland, D.; Collin, S.; Mackey, B.; Sievert, J.; Arpaia, M.L. Storage temperature and time influences sensory quality of mandarins by altering soluble solids, acidity and aroma volatile composition. Postharvest Biol. Technol. 2011, 59, 187–193. [Google Scholar] [CrossRef]
- Ziena, H.M.S. Quality attributes of Bearss Seedless lime (Citrus latifolia Tan) juice during storage. Food Chem. 2000, 71, 167–172. [Google Scholar] [CrossRef]
- Gupta, A.K.; Pathak, U.; Tongbram, T.; Medhi, M.; Terdwongworakul, A.; Magwaza, L.S.; Mditshwa, A.; Tao Chen, T.; Mishra, P. Emerging approaches to determine maturity of citrus fruit. Crit. Rev. Food Sci. Nutr. 2022, 62, 5245–5266. [Google Scholar] [CrossRef]
- Onwude, D.; Bahrami, F.; Shrivastava, C.; Berry, T.; Cronje, P.; North, J.; Kirsten, N.; Schudel, S.; Crenna, E.; Shoji, K.; et al. Physics-driven digital twins to quantify the impact of pre- and postharvest variability on the end quality evolution of orange fruit. Resour. Conserv. Recycl. 2022, 186, 106585. [Google Scholar] [CrossRef]
- Pedrero, F.; Maestre-Valero, J.F.; Mounzer, O.; Alarcón, J.J.; Nicolás, E. Physiological and agronomic mandarin trees performance under saline reclaimed water combined with regulated deficit irrigation. Agric. Water Manag. 2014, 146, 228–237. [Google Scholar] [CrossRef]
- Pedrero, F.; Maestre-Valero, J.F.; Mounzer, O.; Nortes, P.A.; Alcobendas, R.; Romero-Trigueros, C.; Bayona, J.M.; Alarcón, J.J.; Nicolás, E. Response of young ‘Star Ruby’ grapefruit trees to regulated deficit irrigation with saline reclaimed water. Agric. Water Manag. 2015, 158, 51–60. [Google Scholar] [CrossRef]
- Besset, J.; Génard, M.; Girard, T.; Serra, V.; Bussi, C. Effect of water stress applied during the final stage of rapid growth on peach trees (cv. Big-Top). Sci. Hortic. 2001, 91, 289–303. [Google Scholar] [CrossRef]
- Rahmati, M.; Vercambre, G.; Davarynejad, G.; Bannayan, M.; Azizi, M.; Génard, M. Water scarcity conditions affect peach fruit size and polyphenol contents more severely than other fruit quality traits. J. Sci. Food Agric. 2015, 95, 1055–1065. [Google Scholar] [CrossRef]
- Laribi, A.I.; Palou, L.; Intrigliolo, D.S.; Nortes, P.A.; Rojas-Argudo, C.; Taberner, V.; Bartual, J.; Pérez-Gago, M.B. Effect of sustained and regulated deficit irrigation on fruit quality of pomegranate cv. ‘Mollar de Elche’ at harvest and during cold storage. Agric. Water Manag. 2013, 125, 61–70. [Google Scholar] [CrossRef]
- Romero-Trigueros, C.; Parra, M.; Bayona, J.M.; Nortes, P.A.; Alarcón, J.J.; Nicolás, E. Effect of deficit irrigation and reclaimed water on yield and quality of grapefruits at harvest and postharvest. LWT Food Sci. Technol. 2017, 85, 405–411. [Google Scholar] [CrossRef]
- Pérez-Pérez, J.G.; Robles, J.M.; Botía, P. Effects of deficit irrigation in different fruit growth stages on ‘Star Ruby’ grapefruit trees in semi-arid conditions. Agric. Water Manag. 2014, 133, 44–54. [Google Scholar] [CrossRef]
- Navarro, J.M.; Pérez-Pérez, J.G.; Romero, P.; Botía, P. Analysis of the changes in quality in mandarin fruit, produced by deficit irrigation treatments. Food Chem. 2010, 119, 1591–1596. [Google Scholar] [CrossRef]
- Pérez-Pérez, J.G.; García-Sánchez, F.; Robles, J.M.; Botía, P. ‘Star Ruby’ grapefruit and ‘Clemenules’ mandarin trees show different physiological and agronomic responses to irrigation with saline water. Irrig. Sci. 2015, 33, 191–204. [Google Scholar] [CrossRef]
- Romero, P.; Navarro, J.M.; Pérez-Pérez, J.; García-Sánchez, F.; Gómez-Gómez, A.; Porras, I.; Martinez, V.; Botía, P. Deficit irrigation and rootstock: Their effects on water relations, vegetative development, yield, fruit quality and mineral nutrition of Clemenules mandarin. Tree Physiol. 2006, 26, 1537–1548. [Google Scholar] [CrossRef] [PubMed]
- Mattar, M.A.; Soliman, S.S.; Al-Obeed, R.S. Effects of Various Quantities of Three Irrigation Water Types on Yield and Fruit Quality of ‘Succary’ Date Palm. Agronomy 2021, 11, 796. [Google Scholar] [CrossRef]
- Shahin, M.M.; Alhajhoj, M.R. Effect of different irrigation water qualities on the content of some macro and micronutrients in leaves fruit, as well as yield and fruit quality of some date palm cultivars in Al-Hassa Oasis, Saudi Arabia. Middle East. J. Agric. Res. 2015, 4, 834–847. [Google Scholar]
- Legua, P.; Forner, J.B.; Hernández, F.; Forner-Giner, M.A. Total phenolics, organic acids, sugars and antioxidant activity of mandarin (Citrus clementina Hort. ex Tan.): Variation from rootstock. Sci. Hortic. 2014, 174, 60–64. [Google Scholar] [CrossRef]
- Iqbal, M.; NiamatullahKhan, M.; Zafar, M.; Munir, M. Effect of harvesting date on fruit size, fruit weight and total soluble solids of feutrell’s early and kinnow cultivars of madarin (Citrus reticulata) on the economic conditions of farming community of Faisalabad. Sarhad J. Agric. 2012, 28, 19–22. [Google Scholar]
- Singh, K.K.; Mridula, D.; Barnwal, P.; Rehal, J. Selected engineering and biochemical properties of 11 flaxseed varieties. Food Bioprocess Technol. 2013, 6, 598–605. [Google Scholar] [CrossRef]
- Kumar, M.; Raghuwanshi, N.S.; Singh, R.; Wallender, W.W.; Pruitt, W.O. Estimating evapotranspiration using artificial neural network. J. Irrig. Drain. Eng. 2002, 128, 224–233. [Google Scholar] [CrossRef]
- Mattar, M.A.; Alazba, A.A.; Zin El-Abedin, T.K. Forecasting furrow irrigation infiltration using artificial neural networks. Agric. Water Manag. 2015, 148, 63–71. [Google Scholar] [CrossRef]
- Mattar, M.A. Using gene expression programming in monthly reference evapotranspiration modeling: A case study in Egypt. Agric. Water Manag. 2018, 198, 28–38. [Google Scholar] [CrossRef]
- Shahabi, M.; Jafarzadeh, A.A.; Neyshabouri, M.R.; Ghorbani, M.A.; Kamran, K.V. Spatial modeling of soil salinity using multiple linear regression, ordinary kriging and artificial neural network methods. Arch. Agron. Soil Sci. 2016, 63, 151–160. [Google Scholar] [CrossRef]
- Abdipour, M.; Younessi-Hmazekhanlu, M.; Ramazani, S.H.R.; Omidi, A.H. Artificial neural networks and multiple linear regression as potential methods for modeling seed yield of safflower (Carthamus tinctorius L.). Ind. Crops Prod. 2019, 127, 185–194. [Google Scholar] [CrossRef]
- Rai, P.; Majumdar, G.C.; DasGupta, S.; De, S. Prediction of the viscosity of clarified fruit juice using artificial neural network: A combined effect of concentration and temperature. J. Food Eng. 2005, 68, 527–533. [Google Scholar] [CrossRef]
- Furferi, R.; Carfagni, M.; Daou, M. Artificial neural network software for real time estimation of olive oil qual-itative parameters during continuous extraction. Comput. Electron. Agric. 2007, 55, 115–131. [Google Scholar] [CrossRef]
- Cimpoiu, C.; Cristea, V.; Hosu, A.; Sandru, M.; Seserman, L. Antioxidant activity prediction and classification of some teas using artificial neural networks. Food Chem. 2011, 127, 1323–1328. [Google Scholar] [CrossRef]
- Yalcin, H.; Toker, O.S.; Ozturk, I.; Dogan, M.; Kism, O. Prediction of fatty acid composition of vegetable oils based on rheological measurements using nonlinear models. Eur. J. Lipid Sci. Technol. 2012, 114, 1217–1224. [Google Scholar] [CrossRef]
- Huang, X.; Wang, H.; Luo, W.; Xue, S.; Hayat, F.; Gao, Z. Prediction of loquat soluble solids and titratable acid content using fruit mineral elements by artificial neural network and multiple linear regression. Sci. Hortic. 2021, 278, 109873. [Google Scholar] [CrossRef]
- Abdel-Sattar, M.; Al-Obeed, R.S.; Aboukarima, A.; Eshra, D.H. Development of an artificial neural network as a tool for predicting the chemical attributes of fresh peach fruits. PLoS ONE 2021, 16, e0251185. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.; Chen, T.; Zhou, P.; Huang, X.; Liu, D.; Jin, W.; Zhang, H.; Zhou, J.; Wang, Z.; Gao, Z. Prediction and optimization of fruit quality of peach based on artificial neural network. J. Food Compos. Anal. 2022, 111, 104604. [Google Scholar] [CrossRef]
- Zanetti, S.S.; Sousa, E.F.; Oliveira, V.P.S. Estimating evapotranspiration using artificial neural network and minimum climatological data. J. Irrig. Drain. Eng. 2007, 133, 83–89. [Google Scholar] [CrossRef]
- Landeras, G.; Ortiz-Barredo, A.; López, J.J. Comparison of artificial neural network models and empirical and semi-empirical equations for daily reference evapotranspiration estimation in the Basque Country Northern Spain. Agric. Water Manag. 2008, 95, 553–565. [Google Scholar] [CrossRef]
- Landeras, G.; Ortiz-Barredo, A.; López, J.J. Forecasting weekly evapotranspiration with ARIMA and artificial neural network Models. J. Irrig. Drain. Eng. 2009, 135, 323–334. [Google Scholar] [CrossRef]
- Yassin, M.A.; Alazba, A.A.; Mattar, M.A. Modelling daily evapotranspiration using artificial neural networks under hyper arid conditions. Pak. J. Agric. Sci. 2016, 53, 695–712. [Google Scholar] [CrossRef]
- Roy, D.K.; Sarkar, T.K.; Kamar, S.S.A.; Goswami, T.; Muktadir, M.A.; Al-Ghobari, H.M.; Alataway, A.; Dewidar, A.Z.; El-Shafei, A.A.; Mattar, M.A. Daily Prediction and Multi-Step Forward Forecasting of Reference Evapotranspiration Using LSTM and Bi-LSTM Models. Agronomy 2022, 12, 594. [Google Scholar] [CrossRef]
- Emamgholizadeh, S.; Parsaeian, M.; Baradaran, M. Seed yield prediction of sesame using artificial neural network. Eur. J. Agron. 2015, 68, 89–96. [Google Scholar] [CrossRef]
- Niedbała, G. Application of multiple linear regression for multi-criteria yield prediction of winter wheat. J. Res. Appl. Agric. Eng. 2018, 63, 125–131. [Google Scholar]
- Torkashvand, A.M.; Ahmadi, A.; Nikravesh, N.L. Prediction of kiwifruit firmness using fruit mineral nutrient concentration by artificial neural network (ANN) and multiple linear regressions (MLR). J. Integr. Agric. 2017, 16, 1634–1644. [Google Scholar] [CrossRef]
- Niazian, M.; Sadat-Noori, S.A.; Abdipour, M. Artificial neural network and multiple regression analysis models to predict essential oil content of ajowan (Carum copticum L.). J. Appl. Res. Med. Aromat. Plants 2018, 9, 124–131. [Google Scholar] [CrossRef]
- Ivanovski, T.; Zhang, G.; Jemrić, T.; Gulić, M.; Matetić, M. Fruit firmness prediction using multiple linear regression. In Proceedings of the 2020 43rd International Convention on Information, Communication and Electronic Technology (MIPRO), Opatija, Croatia, 28 September–2 October 2020; pp. 1306–1311. [Google Scholar] [CrossRef]
- Shezi, S.; Magwaza, L.S.; Tesfay, S.Z.; Mditshwa, A. Simple and multiple linear regression models for predicting maturity of ‘Mendez#1’ and ‘Hass’ avocado fruit harvested from inside and outside tree canopy positions. Int. J. Fruit Sci. 2020, 20, 1969–1983. [Google Scholar] [CrossRef]
- Abdel-Sattar, M.; Al-Saif, A.M.; Aboukarima, A.M.; Eshra, D.H.; Sas-Paszt, L. Quality Attributes Prediction of Flame Seedless Grape Clusters Based on Nutritional Status Employing Multiple Linear Regression Technique. Agriculture 2022, 12, 1303. [Google Scholar] [CrossRef]
- Khalifa, S.; Komarizadeh, M.H.; Tousi, B. Usage of fruit response to both force and forced vibration applied to assess fruit firmness- a review. Aust. J. Crop Sci. 2011, 5, 516–522. [Google Scholar]
- Page, A.; Miller, R.; Keeney, D. Chemical and microbiological properties. In Methods of Soil Analysis, Part 2, 2nd ed.; Agronomy Monogram 9; Agronomy Society of America and Soil Science Society of America: Madison, WI, USA, 1982. [Google Scholar]
- Klute, A. Methods of Soil Analysis; Part 1 Book Series No. 9; American Society of Agronomy and Soil Science America: Madison, WI, USA, 1986. [Google Scholar]
- Abdel-Sattar, M.; EL-Tanany, M.; EL-Kouny, H.M. Reducing mineral fertilizers by using organic manure to improve Washington navel orange productivity and sandy soil characteristics. Alex. Sci. Exch. J. 2011, 32, 372–380. [Google Scholar]
- AOAC. Association of official analytical chemists. In Official Method of Analysis, 18th ed.; AOAC: Gaithersburg, MD, USA, 2005. [Google Scholar]
- Malik, C.P.; Singh, M.B. Plant enzymology and histoenzymology. In A Text Manual; Kalyani Publishers: New Delhi, India, 1980. [Google Scholar]
- Egan, H.; Kirk, R.S.; Sawyer, R. Pearson’s Chemical Analysis of Food: Churchill Livingstone; Churchill Livingstone: Minneapolis, MN, USA, 1981; p. 591. [Google Scholar]
- Thirumalaiah, K.; Deo, M.C. River stage forecasting using artificial neural networks. J. Hydrol. Eng. 1998, 3, 26–32. [Google Scholar] [CrossRef]
- Cigizoglu, H.K. Estimation, forecasting and extrapolation of river flows by artificial neural networks. Hydrol. Sci. J. 2003, 48, 349–361. [Google Scholar] [CrossRef]
- Jain, A.; Srinivasulu, S. Development of effective and efficient rainfall-runoff models using integration of deterministic, real-coded genetic algorithms, and artificial neural network techniques. Water Resour. Res. 2004, 40, W04302. [Google Scholar] [CrossRef]
- Fernando, D.A.K.; Shamseldin, A.Y. Investigation of internal functioning of the radial-basis-function neural network river flow forecasting models. J. Hydrol. Eng. 2009, 14, 286–292. [Google Scholar] [CrossRef]
- Maier, H.R.; Dandy, G.C. Neural networks for the prediction and forecasting of water resources variables: A review of modeling issues and application. Environ. Model. Softw. 2000, 15, 101–124. [Google Scholar] [CrossRef]
- Haykin, S. Neural networks. In A Comprehensive Foundation; Prentice Hall International Inc.: Hoboken, NJ, USA, 1999. [Google Scholar]
- Swingler, K. Applying Neural Networks, A Practical Guide, 3rd ed.; Academic Press: Cambridge, MA, USA; Morgan Kaufmann: San Francisco, CA, USA, 2001. [Google Scholar]
- Garson, G.D. Interpreting neuralnetwork connection weights. Artif. Intell. Expert. 1991, 6, 47–51. [Google Scholar]
- Jain, S.K.; Nayak, P.C.; Sudhir, K.P. Models for estimating evapotranspiration using artificial neural networks, and their physical interpretation. Hydrol. Process. 2008, 22, 2225–2234. [Google Scholar] [CrossRef]
- Legates, D.R.; McCabe, G.J., Jr. Evaluating the use of ‘‘goodness-of fit’’ measures in hydrologic and hydroclimatic model validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Pagano, M.; Gauvreau, K. Princípios de Bioestatística; Cengage Learning: São Paulo, Brazil, 2012; p. 506. [Google Scholar]
- Cun, D.; Pu, J.; Gao, J.; Li, J.; Yue, J.; Du, Y.; Li, D.; Li, X.; Chen, L.; Zhou, X.; et al. The relationship between mineral element content in the peel and pulp of Yunnan Bingtang orange and fruit quality. Jiangsu Agric. Sci. 2020, 48, 207–214. [Google Scholar]
- Lowe, A.; Stephen, H.; Ashton, P. Ecological Genetics: Design, Analysis and Application; Blackwell Publishing: Hoboken, NJ, USA, 2004; p. 6-100.15. [Google Scholar]
- Kaveh, M.; Chayan, R.A. Prediction of some physical and drying properties of terebinth fruit (Pistacia atlantica L.) using artificial neural networks. Acta Sci. Pol. Technol. Aliment. 2014, 13, 65–78. [Google Scholar] [CrossRef]
- Gholipoor, M.; Nadali, F. Fruit yield prediction of pepper using artificial neural network. Sci. Hortic. 2019, 250, 249–253. [Google Scholar] [CrossRef]
- Jamshidi, S.; Yadollahi, A.; Ahmadi, H.; Arab, M.M.; Eftekhari, M. Predicting in vitro culture medium macro-nutrients composition for pear rootstocks using regression analysis and neural network models. Front. Plant Sci. 2016, 7, 274. [Google Scholar] [CrossRef]
- Eftekhari, M.; Yadollahi, A.; Ahmadi, H.; Shojaeiyan, A.; Ayyari, M. Development of an artificial neural networkas a tool for predicting the targeted phenolic profile of grapevine (Vitis vinifera) foliar wastes. Front. Inplant Sci. 2018, 9, 837. [Google Scholar] [CrossRef]
- Davoudi Kakhki, F.; Freeman, S.A.; Mosher, G.A. Evaluating Machine Learning Performance in Predicting Injury Severity in Agribusiness Industries. Saf. Sci. 2019, 117, 257–262. [Google Scholar] [CrossRef]
- Pianosi, F.; Wagener, T. A Simple and Efficient Method for Global Sensitivity Analysis Based Oncumulative Distribution Functions. Environ. Model. Softw. 2015, 67, 1–11. [Google Scholar] [CrossRef]
- Baykal, H.; Yildirim, H.K. Application of artificial neural networks (ANNs) in wine technology. Crit. Rev. Food Sci. Nutr. 2013, 53, 415–421. [Google Scholar] [CrossRef] [PubMed]
- Mazen, F.M.; Nashat, A.A. Ripeness classification of bananas using an artificial neural network. Arab. J. Sci. Eng. 2019, 44, 6901–6910. [Google Scholar] [CrossRef]
- Kaur, M.; Sharma, R. Quality detection of fruits by using ANN technique. IOSR J. Electron. Commun. Eng. (IOSR-JECE) 2015, 10, 35–41. [Google Scholar]
- Zhang, G.; Fu, Q.; Fu, Z.; Li, X.; Matetić, M.; Brkić, B.M.; Jemrić, T. A comprehensive peach fruit quality evaluation method for grading and consumption. Appl. Sci. 2020, 10, 1348. [Google Scholar] [CrossRef]
- Torkashvand, A.M.; Ahmadipour, A.; Khaneghah, A.M. Estimation of kiwifruit yield by leaf nutrients concentration and artificial neural network. J. Agric. Sci. 2019, 158, 185–193. [Google Scholar] [CrossRef]
- Huang, X.; Wang, H.; Qu, S.; Luo, W.; Gao, Z. Using artificial neural network in predicting the key fruit quality of loquat. Food Sci. Nutr. 2021, 9, 1780–1791. [Google Scholar] [CrossRef]
- Ahmadi, H.; Rodehutscord, M. Application of artificial neural network and support vector machines in predicting metabolizable energy in compound feeds for pigs. Front Nutr. 2017, 4, 27. [Google Scholar] [CrossRef]
- Abdel-Sattar, M.; Aboukarima, A.M.; Alnahdi, B.M. Application of artificial neural network and support vector regression in predicting massof ber fruits (Ziziphus mauritiana Lamk.) based on fruit axial dimensions. PLoS ONE 2021, 16, e0245228. [Google Scholar] [CrossRef]
- Rad, M.R.N.; Koohkan, S.; Fanaei, H.R.; Rad, M.R.P. Application of artificial neural networks to predict the final fruit weight and random forest to select important variables in native population of Melon (Cucumis melo L.). Sci Hortic. 2015, 181, 108–112. [Google Scholar] [CrossRef]
- Rad, M.R.N.N.; Ghalandarzehi, A.; Koohpaygani, J.A. Predicting eggplant individual fruit weight using an artificial neural network. Int. J. Veg. Sci. 2017, 23, 331–339. [Google Scholar] [CrossRef]




| Depth (cm) | Particle Size (%) | Texture | Soil’s Physical Properties | Soil’s Chemical Properties | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sand | Silt | Clay | ρb (g cm−3) | FC (%) | WP (%) | TAW m3 m−3 | EC (dS m−1) | pH | OM (%) | CaCO3 (%) | ||
| 0–30 | 73.1 | 12.9 | 14.0 | Sandy loam | 1.39 | 11.0 | 4.5 | 0.11 | 1.48 | 7.63 | 0.46 | 2.33 |
| 30–60 | 70.4 | 12.0 | 17.6 | Sandy loam | 1.25 | 12.1 | 5.2 | 0.12 | 1.44 | 7.67 | 0.52 | 2.28 |
| 60–90 | 71.2 | 11.8 | 17.0 | Sandy loam | 1.46 | 11.2 | 4.6 | 0.10 | 1.57 | 7.82 | 0.36 | 2.45 |
| Statistics | EC | Yield/Tree | FW | FL | FD | TSS | Acidity | VitC | Tsugar | Rsugar |
|---|---|---|---|---|---|---|---|---|---|---|
| Training set | ||||||||||
| xmean | 1.50 | 103.37 | 134.82 | 6.43 | 6.39 | 11.06 | 2.80 | 43.63 | 7.39 | 4.31 |
| xmax | 1.68 | 162.12 | 246.69 | 8.55 | 7.82 | 14.60 | 7.22 | 58.98 | 8.98 | 6.34 |
| xmin | 1.28 | 64.45 | 34.56 | 4.30 | 4.20 | 7.08 | 0.90 | 33.46 | 5.18 | 2.41 |
| Sx | 0.12 | 24.44 | 61.34 | 1.44 | 1.14 | 2.26 | 2.49 | 7.02 | 1.10 | 1.08 |
| Csx | −0.27 | 0.66 | 0.04 | −0.10 | −0.45 | −0.41 | 0.75 | 0.38 | −0.31 | 0.37 |
| kx | −0.98 | −0.35 | −1.09 | −1.68 | −1.25 | −1.32 | −1.38 | −0.95 | −1.24 | −0.68 |
| Testing set | ||||||||||
| xmean | 1.50 | 103.94 | 136.21 | 6.48 | 6.43 | 11.08 | 2.75 | 43.86 | 7.42 | 4.31 |
| xmax | 1.68 | 161.48 | 246.78 | 8.59 | 7.84 | 14.58 | 7.14 | 57.89 | 8.95 | 6.38 |
| xmin | 1.28 | 66.08 | 34.98 | 4.31 | 4.29 | 7.05 | 0.90 | 33.59 | 5.15 | 2.48 |
| Sx | 0.12 | 22.20 | 60.72 | 1.42 | 1.13 | 2.28 | 2.48 | 6.99 | 1.10 | 1.09 |
| Csx | −0.14 | 0.62 | 0.06 | −0.16 | −0.45 | −0.42 | 0.81 | 0.38 | −0.41 | 0.41 |
| kx | −1.16 | 0.14 | −0.99 | −1.66 | −1.22 | −1.28 | −1.33 | −0.91 | −1.08 | −0.50 |
| Cultivars | Yield/tree | FW | FL | FD | TSS | Acidity | VitC | Tsugar | Rsugar |
|---|---|---|---|---|---|---|---|---|---|
| (Kg) | (gm) | (cm) | (cm) | (%) | (%) | (mg/100mL Juice) | (%) | (%) | |
| Washington Navel orange | 95.01 c | 226.20 a | 7.84 a | 7.49 a | 11.93 c | 0.99 d | 53.00 a | 8.44 a | 4.79 b |
| Valencia orange | 136.11 a | 171.05 b | 7.82 a | 7.21 b | 11.52 d | 1.14 c | 49.51 b | 8.14 b | 4.55 c |
| Murcott mandarin | 92.67 c | 146.86 c | 5.71 c | 7.44 a | 13.05 b | 0.99 d | 38.15 e | 6.55 d | 3.63 e |
| Clementine tangerine | 80.42 d | 49.88 f | 4.49 e | 5.43 d | 13.57 a | 1.04 cd | 43.70 c | 6.93 c | 3.81 d |
| Eureka lemon | 116.65 b | 136.24 d | 7.65 b | 6.17 c | 7.86 f | 5.77 b | 40.85 d | 5.67 e | 2.78 f |
| Bearss Seedless lime | 91.78 c | 72.92 e | 5.03 d | 4.53 e | 8.26 e | 6.67 a | 34.99 f | 8.45 a | 6.15 a |
| LSD (5%) | 4.28 | 5.21 | 0.15 | 0.08 | 0.29 | 0.1335 | 1.1415 | 0.1134 | 0.0836 |
| EC | Yield/Tree | FW | FL | FD | TSS | Acidity | VitC | Tsugar | Rsugar | |
|---|---|---|---|---|---|---|---|---|---|---|
| Washington Navel orange | ||||||||||
| EC | 1 | −0.983 | −0.962 | −0.974 | −0.924 | −0.960 | 0.964 | −0.959 | −0.967 | −0.957 |
| Yield/tree | 1 | 0.965 | 0.988 | 0.919 | 0.957 | −0.961 | 0.967 | 0.968 | 0.955 | |
| FW | 1 | 0.952 | 0.970 | 0.985 | −0.977 | 0.988 | 0.977 | 0.962 | ||
| FL | 1 | 0.910 | 0.954 | −0.949 | 0.949 | 0.974 | 0.967 | |||
| FD | 1 | 0.980 | −0.940 | 0.966 | 0.965 | 0.957 | ||||
| TSS | 1 | −0.965 | 0.976 | 0.985 | 0.979 | |||||
| Acidity | 1 | −0.972 | −0.963 | −0.956 | ||||||
| VitC | 1 | 0.973 | 0.960 | |||||||
| Tsugar | 1 | 0.988 | ||||||||
| Rsugar | 1 | |||||||||
| Valencia orange | ||||||||||
| EC | 1.000 | −0.966 | −0.955 | −0.894 | −0.956 | −0.965 | 0.939 | −0.982 | −0.990 | −0.974 |
| Yield/tree | 1 | 0.988 | 0.962 | 0.991 | 0.991 | −0.980 | 0.976 | 0.974 | 0.978 | |
| FW | 1 | 0.968 | 0.992 | 0.986 | −0.975 | 0.969 | 0.966 | 0.972 | ||
| FL | 1 | 0.969 | 0.958 | −0.966 | 0.909 | 0.903 | 0.908 | |||
| FD | 1 | 0.992 | −0.985 | 0.967 | 0.971 | 0.974 | ||||
| TSS | 1 | −0.985 | 0.974 | 0.977 | 0.976 | |||||
| Acidity | 1 | −0.950 | −0.953 | −0.959 | ||||||
| VitC | 1 | 0.987 | 0.986 | |||||||
| Tsugar | 1 | 0.987 | ||||||||
| Rsugar | 1 | |||||||||
| Murcott mandarin | ||||||||||
| EC | 1 | −0.988 | −0.978 | −0.911 | −0.958 | −0.957 | 0.959 | −0.975 | −0.972 | −0.962 |
| Yield/tree | 1 | 0.992 | 0.941 | 0.977 | 0.978 | −0.968 | 0.989 | 0.985 | 0.981 | |
| FW | 1 | 0.923 | 0.964 | 0.974 | −0.961 | 0.984 | 0.974 | 0.979 | ||
| FL | 1 | 0.978 | 0.947 | −0.942 | 0.927 | 0.956 | 0.932 | |||
| FD | 1 | 0.984 | −0.972 | 0.976 | 0.989 | 0.971 | ||||
| TSS | 1 | −0.965 | 0.982 | 0.982 | 0.989 | |||||
| Acidity | 1 | −0.966 | −0.967 | −0.960 | ||||||
| VitC | 1 | 0.978 | 0.985 | |||||||
| Tsugar | 1 | 0.977 | ||||||||
| Rsugar | 1 | |||||||||
| Clementine tangerine | ||||||||||
| EC | 1 | −0.971 | −0.971 | −0.987 | −0.953 | −0.987 | 0.954 | −0.986 | −0.964 | −0.972 |
| Yield/tree | 1 | 0.985 | 0.983 | 0.973 | 0.988 | −0.978 | 0.984 | 0.978 | 0.974 | |
| FW | 1 | 0.984 | 0.980 | 0.992 | −0.979 | 0.988 | 0.987 | 0.982 | ||
| FL | 1 | 0.970 | 0.992 | −0.976 | 0.989 | 0.975 | 0.978 | |||
| FD | 1 | 0.981 | −0.988 | 0.968 | 0.984 | 0.957 | ||||
| TSS | 1 | −0.983 | 0.994 | 0.989 | 0.985 | |||||
| Acidity | 1 | −0.969 | −0.982 | −0.963 | ||||||
| VitC | 1 | 0.981 | 0.991 | |||||||
| Tsugar | 1 | 0.978 | ||||||||
| Rsugar | 1 | |||||||||
| Eureka lemon | ||||||||||
| EC | 1 | −0.982 | −0.966 | −0.866 | −0.980 | −0.989 | 0.956 | −0.976 | −0.981 | −0.971 |
| Yield/tree | 1 | 0.986 | 0.891 | 0.986 | 0.989 | −0.965 | 0.987 | 0.983 | 0.978 | |
| FW | 1 | 0.918 | 0.976 | 0.982 | −0.975 | 0.978 | 0.974 | 0.968 | ||
| FL | 1 | 0.901 | 0.877 | −0.970 | 0.908 | 0.922 | 0.926 | |||
| FD | 1 | 0.983 | −0.973 | 0.984 | 0.994 | 0.986 | ||||
| TSS | 1 | −0.959 | 0.978 | 0.982 | 0.974 | |||||
| Acidity | 1 | −0.975 | −0.981 | −0.981 | ||||||
| VitC | 1 | 0.984 | 0.980 | |||||||
| Tsugar | 1 | 0.991 | ||||||||
| Rsugar | 1 | |||||||||
| Bearss Seedless lime | ||||||||||
| EC | 1 | −0.972 | −0.985 | −0.933 | −0.958 | −0.975 | 0.960 | −0.982 | −0.979 | −0.957 |
| Yield/tree | 1 | 0.968 | 0.967 | 0.978 | 0.967 | −0.984 | 0.971 | 0.984 | 0.977 | |
| FW | 1 | 0.933 | 0.963 | 0.975 | −0.957 | 0.974 | 0.981 | 0.953 | ||
| FL | 1 | 0.965 | 0.940 | −0.972 | 0.937 | 0.955 | 0.988 | |||
| FD | 1 | 0.953 | −0.979 | 0.965 | 0.971 | 0.971 | ||||
| TSS | 1 | −0.967 | 0.964 | 0.969 | 0.956 | |||||
| Acidity | 1 | −0.977 | −0.979 | −0.975 | ||||||
| VitC | 1 | 0.981 | 0.959 | |||||||
| Tsugar | 1 | 0.972 | ||||||||
| Rsugar | 1 | |||||||||
| Inputs | Inputs Neurons (i) | Hidden Neurons (j) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| (W1)ji | ||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |||
| Yield/tree | 1 | −2.84 | 1.90 | −3.90 | −1.09 | −3.42 | 3.61 | 0.35 | 4.27 | |
| FW | 2 | 1.04 | −5.01 | 1.31 | 4.20 | −1.93 | −2.53 | 1.43 | 3.36 | |
| FL | 3 | 3.22 | −3.53 | −8.77 | 3.57 | 0.45 | 0.72 | −5.33 | −3.10 | |
| FD | 4 | −6.13 | −0.76 | 16.53 | 0.10 | −7.76 | −5.50 | 2.33 | −15.45 | |
| (B1)j | −0.04 | 6.90 | −3.00 | −1.48 | 4.75 | 2.67 | 0.79 | 3.54 | ||
| Outputs | Outputs Neurons (k) | (W2)kj | (B2)k | |||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |||
| TSS | 1 | 0.23 | −1.66 | 2.69 | −3.50 | −3.24 | 2.49 | 1.13 | 0.69 | 1.46 |
| Acidity | 2 | 2.49 | −0.94 | −5.08 | 1.76 | 0.87 | −1.61 | 3.04 | −0.78 | 0.61 |
| VitC | 3 | 1.75 | −7.01 | 2.85 | 0.72 | −2.40 | 5.98 | 0.83 | 0.11 | 0.45 |
| TSugar | 4 | −2.69 | −1.42 | 4.92 | 0.40 | −2.08 | 2.47 | −4.60 | 6.75 | −0.93 |
| RSugar | 5 | −3.22 | −0.07 | 3.30 | 1.08 | −0.98 | 1.00 | −3.22 | 6.42 | −2.20 |
| Statistical Parameters | TSS | Acidity | VitC | Tsugar | Rsugar |
|---|---|---|---|---|---|
| Training process | |||||
| RMSE | 0.143 | 0.119 | 0.453 | 0.072 | 0.064 |
| MAE | 0.109 | 0.090 | 0.384 | 0.058 | 0.050 |
| MARE | 1.057 | 5.007 | 0.891 | 0.793 | 1.241 |
| Testing process | |||||
| RMSE | 0.137 | 0.106 | 0.634 | 0.080 | 0.068 |
| MAE | 0.098 | 0.085 | 0.506 | 0.061 | 0.052 |
| MARE | 0.973 | 4.819 | 1.153 | 0.834 | 1.231 |
| Model Equation | R2 | |
|---|---|---|
| TSS | TSS = 5.05 + 6.58 × 10−3YT − 6.51 × 10−3FW − 1.46FL + 2.44FD | 0.741 |
| Acidity | Acidity = 13.82 + 8.24 × 10−3YT + 15.34 × 10−3FW + 0.71FL − 2.90FD | 0.911 |
| VitC | VitC = 23.83 + 36.81 × 10−3YT + 48.27 × 10−3FW + 0.55FL + 0.93FD | 0.534 |
| Tsugar | Tsugar = 14.12 + 25.47 × 10−3YT + 42.26 × 10−3FW − 1.13FL − 1.22FD | 0.542 |
| Rsugar | Rsugar = 13.45 + 26.49 × 10−3YT + 44.33 × 10−3FW − 1.26FL − 1.52FD | 0.722 |
| Intercept | Independent Variables | ||||
|---|---|---|---|---|---|
| Yield/Tree | FW | FL | FD | ||
| TSS | |||||
| SE | 1.29 | 7.44 × 10−3 | 6.37 × 10−3 | 22.89 × 10−2 | 22.14 × 10−2 |
| t-stat | 3.92 | 0.89 | –1.02 | –6.36 | 11.00 |
| p-value | 1.68 × 10−4 | 37.84 × 10−2 | 30.88 × 10−2 | 6.8 × 10−9 | 1.06 × 10−18 |
| Acidity | |||||
| SE | 1.45 | 8.37 × 10−3 | 7.17 × 10−3 | 25.76 × 10−2 | 24.91 × 10−2 |
| t-stat | 9.52 | 0.98 | 2.14 | 2.77 | –11.63 |
| p-value | 1.58 × 10−15 | 32.75 × 10−2 | 34.82 × 10−3 | 6.77 × 10−3 | 4.93 × 10−20 |
| VitC | |||||
| SE | 5.38 | 3.10 × 10−2 | 2.66 × 10−2 | 95.52 × 10−2 | 92.38 × 10−2 |
| t-stat | 4.43 | 1.19 | 1.82 | 0.58 | 1.01 |
| p-value | 2.53 × 10−5 | 23.86 × 10−2 | 7.23 × 10−2 | 56.51 × 10−2 | 31.64 × 10−2 |
| Tsugar | |||||
| SE | 85.05 × 10−2 | 4.91 × 10−3 | 4.20 × 10−3 | 15.09 × 10−2 | 14.60 × 10−2 |
| t-stat | 16.60 | 5.19 | 10.07 | –7.50 | –8.33 |
| p-value | 5.72 × 10−30 | 1.16 × 10−6 | 1.08 × 10−16 | 3.17 × 10−11 | 5.58 × 10−13 |
| Rsugar | |||||
| SE | 68.65 × 10−2 | 3.96 × 10−3 | 3.39 × 10−3 | 12.19 × 10−2 | 11.78 × 10−2 |
| t-stat | 19.59 | 6.69 | 13.08 | –10.34 | –12.94 |
| p-value | 2.65 × 10−35 | 1.49 × 10−9 | 4.73 × 10−23 | 2.80 × 10−17 | 9.17 × 10−23 |
| Statistical Parameters | TSS | Acidity | VitC | Tsugar | Rsugar |
|---|---|---|---|---|---|
| Training process | |||||
| RMSE | 1.143 | 1.200 | 4.768 | 0.740 | 0.568 |
| MAE | 1.023 | 1.126 | 4.211 | 0.619 | 0.446 |
| MARE | 9.263 | 75.397 | 9.925 | 8.880 | 11.523 |
| Testing process | |||||
| RMSE | 1.140 | 1.187 | 4.830 | 0.724 | 0.550 |
| MAE | 1.013 | 1.115 | 4.206 | 0.619 | 0.440 |
| MARE | 9.167 | 73.393 | 9.845 | 8.734 | 10.905 |
| Statistical Parameters | Orange Group | Mandarin Group | Acid Group | |||
|---|---|---|---|---|---|---|
| ANN | MLR | ANN | MLR | ANN | MLR | |
| TSS | ||||||
| RMSE | 0.131 | 0.762 | 0.088 | 1.610 | 0.177 | 0.882 |
| MAE | 0.093 | 0.681 | 0.072 | 1.569 | 0.129 | 0.814 |
| MARE | 0.811 | 5.728 | 0.534 | 11.645 | 1.586 | 10.373 |
| Acidity | ||||||
| RMSE | 0.084 | 0.977 | 0.118 | 1.664 | 0.121 | 1.104 |
| MAE | 0.066 | 0.952 | 0.098 | 1.663 | 0.098 | 1.016 |
| MARE | 5.677 | 8.525 | 9.345 | 16.131 | 1.638 | 16.734 |
| VitC | ||||||
| RMSE | 0.799 | 3.428 | 0.478 | 6.906 | 0.567 | 3.368 |
| MAE | 0.649 | 2.745 | 0.382 | 6.743 | 0.477 | 3.234 |
| MARE | 1.252 | 5.060 | 0.945 | 16.235 | 1.253 | 8.580 |
| Tsugar | ||||||
| RMSE | 0.072 | 0.695 | 0.108 | 0.821 | 0.046 | 0.647 |
| MAE | 0.064 | 0.659 | 0.078 | 0.642 | 0.042 | 0.554 |
| MARE | 0.775 | 7.955 | 1.124 | 9.428 | 0.608 | 8.876 |
| Rsugar | ||||||
| RMSE | 0.075 | 0.492 | 0.074 | 0.627 | 0.053 | 0.528 |
| MAE | 0.062 | 0.451 | 0.048 | 0.413 | 0.047 | 0.455 |
| MARE | 1.328 | 9.683 | 1.244 | 11.112 | 1.115 | 12.007 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Saif, A.M.; Abdel-Sattar, M.; Eshra, D.H.; Sas-Paszt, L.; Mattar, M.A. Predicting the Chemical Attributes of Fresh Citrus Fruits Using Artificial Neural Network and Linear Regression Models. Horticulturae 2022, 8, 1016. https://doi.org/10.3390/horticulturae8111016
Al-Saif AM, Abdel-Sattar M, Eshra DH, Sas-Paszt L, Mattar MA. Predicting the Chemical Attributes of Fresh Citrus Fruits Using Artificial Neural Network and Linear Regression Models. Horticulturae. 2022; 8(11):1016. https://doi.org/10.3390/horticulturae8111016
Chicago/Turabian StyleAl-Saif, Adel M., Mahmoud Abdel-Sattar, Dalia H. Eshra, Lidia Sas-Paszt, and Mohamed A. Mattar. 2022. "Predicting the Chemical Attributes of Fresh Citrus Fruits Using Artificial Neural Network and Linear Regression Models" Horticulturae 8, no. 11: 1016. https://doi.org/10.3390/horticulturae8111016
APA StyleAl-Saif, A. M., Abdel-Sattar, M., Eshra, D. H., Sas-Paszt, L., & Mattar, M. A. (2022). Predicting the Chemical Attributes of Fresh Citrus Fruits Using Artificial Neural Network and Linear Regression Models. Horticulturae, 8(11), 1016. https://doi.org/10.3390/horticulturae8111016







