Site-Specific Nutrient Diagnosis of Orange Groves
Abstract
:1. Introduction
2. Material and Methods
2.1. Experimental Setup
2.2. Crop Management
2.3. Meteorological Data
2.4. Tissue Analysis
2.5. Soil Analysis
2.6. Centered Log-Ratio Transformation
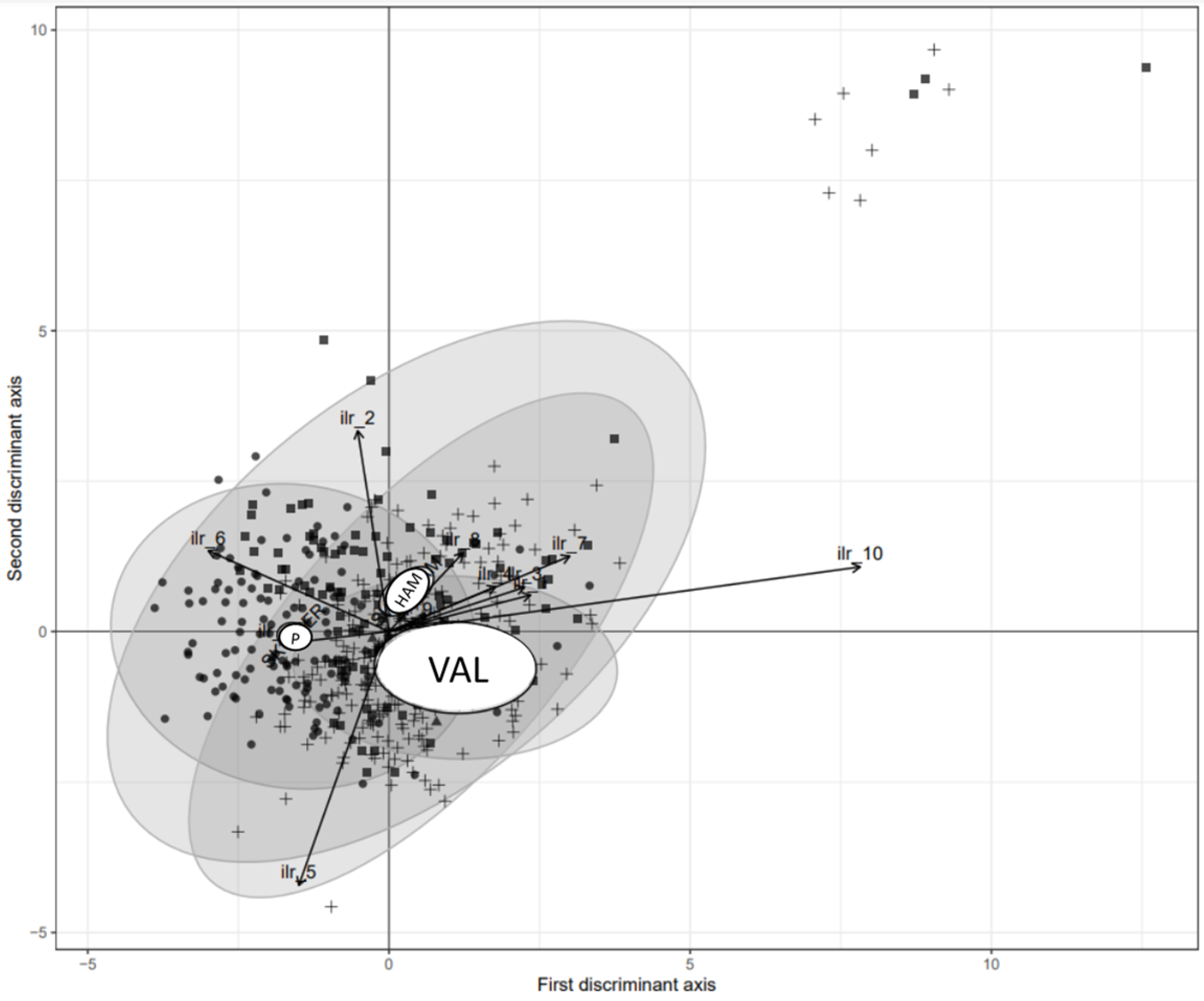
2.7. Statistical Analysis
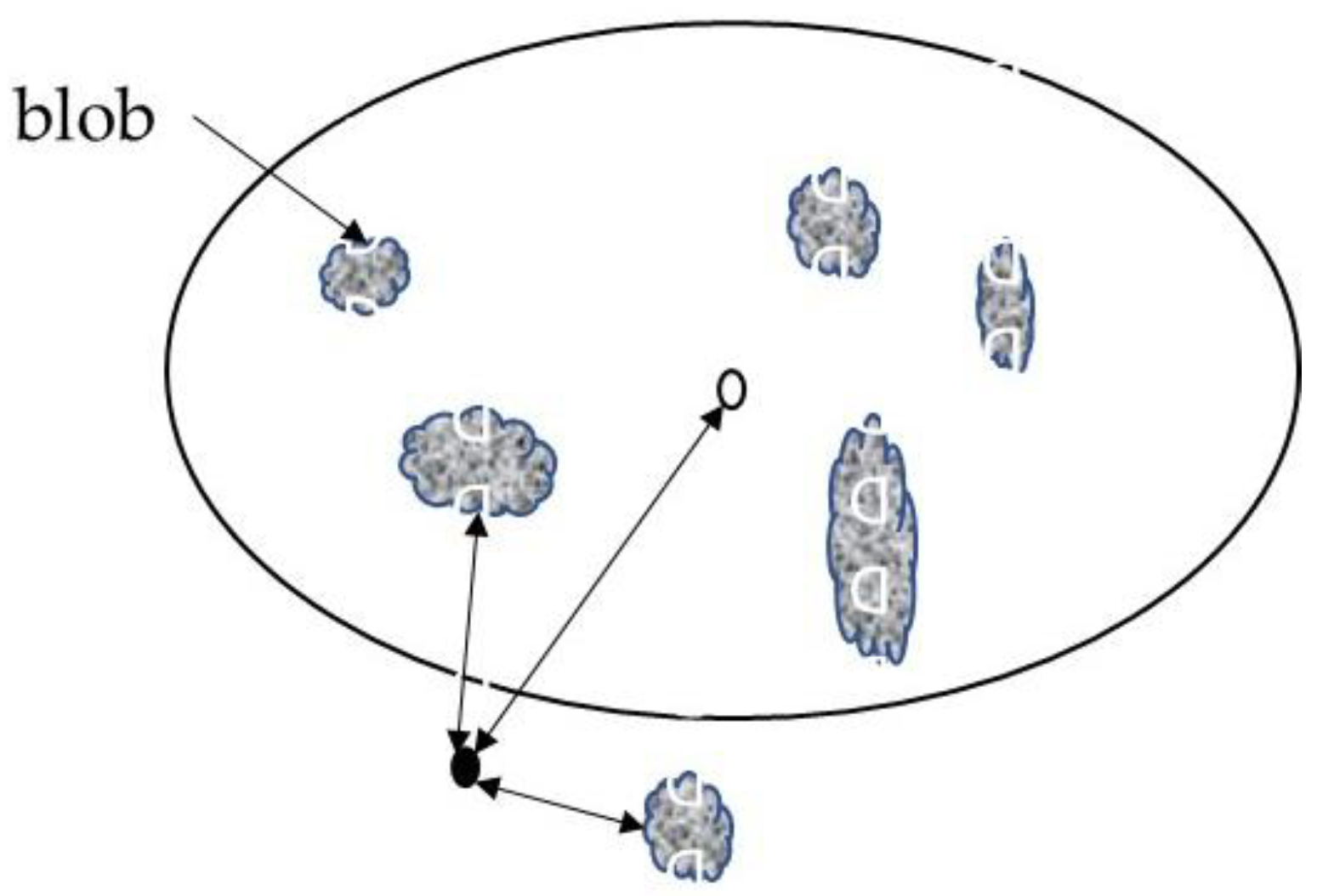
2.8. Delineation of the Regional and Blob Spaces
2.9. Regional and ‘Blob’-Scale Nutrient Standards
3. Results
3.1. Results of Tissue and Soil Tests
3.2. Random Forest Regression Models
3.3. Random Forest Classification Models
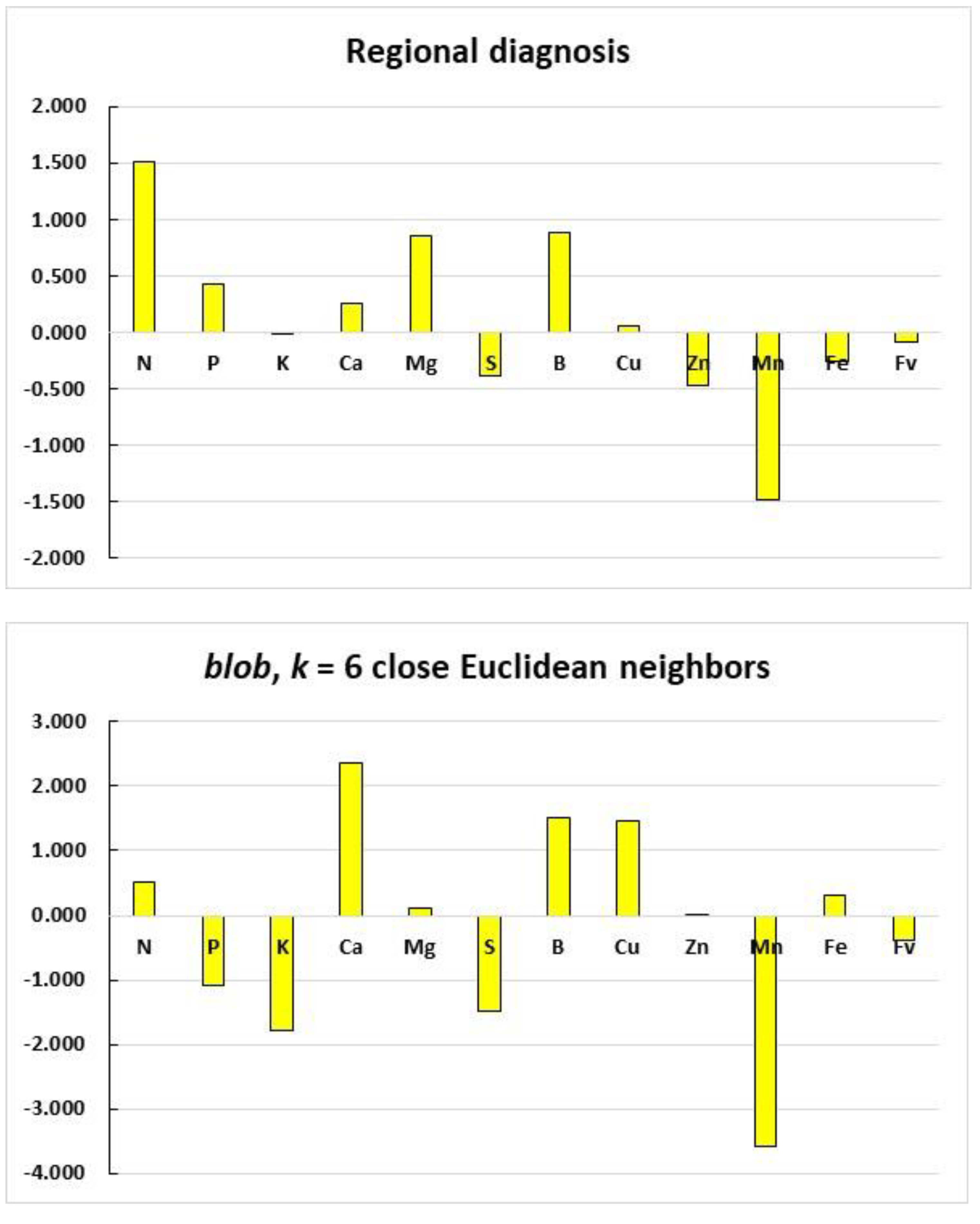
3.4. Nutrient Standards at Regional Scale
3.5. Order of Nutrient Limitations at the Regional and Blob Scales: Example
4. Discussion
4.1. Contribution of Documented Features to ML Models
4.2. Nutrient Diagnosis
4.3. Boron Limitations
4.4. Nutrient Excess and Shortage
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- AGRIANUAL. Anuário Da Agricultura Brasileira; Agribusiness Intelligence/Informa IEG/FNP: São Paulo, Brazil, 2022. [Google Scholar]
- Neves, C.S.V.J.; Murata, I.M.; Stenzel, N.M.C.; Medina, C.d.C.; Borges, A.V.; Okumoto, S.H.; Lee, R.H.C.; Kanai, H.T. Root Distribution of Rootstocks for “Tahiti” Lime. Sci. Agric. 2004, 61, 94–99. [Google Scholar] [CrossRef] [Green Version]
- Quaggio, J.A.; Cantarella, H.; Van Raij, B. Phosphorus and Potassium Soil Test and Nitrogen Leaf Analysis as a Base for Citrus Fertilization. Nutr. Cycl. Agroecosyst. 1998, 52, 67–74. [Google Scholar] [CrossRef]
- Quaggio, J.A.; Mattos, D., Jr.; Boaretto, R.M. Citros. Boas Práticas para Uso Eficiente de Fertilizantes; Prochnow, L.I., Casarin, V., Stipp, S.R., Eds.; International Plant Names Index: Piracicaba, Brazil, 2010; pp. 371–409. [Google Scholar]
- Rozane, D.E.; Mattos, D.; Parent, S.-É.; Natale, W.; Parent, L.E. Meta-Analysis in the Selection of Groups in Varieties of Citrus. Commun. Soil Sci. Plant Anal. 2015, 46, 1948–1959. [Google Scholar] [CrossRef]
- Mendonça, L.; Zambolim, L.; Badel, J. Bacterial Citrus Diseases: Major Threats and Recent Progress. J. Bacteriol. Mycol. Open Access 2017, 5, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Behlau, F. An Overview of Citrus Canker in Brazil. Trop. Plant Pathol. 2021, 46, 1–12. [Google Scholar] [CrossRef]
- Machado, F.J.; Lanza, F.E.; Ferretti, M.O.; Fialho, R.O.; Behlau, F.; Silva-Junior, G.J. Citrus Black Spot Severity Related to Premature Fruit Drop in Sweet Orange Orchards. Plant Pathol. 2022, 71, 400–410. [Google Scholar] [CrossRef]
- Martinez, D.A.; Loening, U.E.; Graham, M.C.; Gathorne-Hardy, A. When the Medicine Feeds the Problem; Do Nitrogen Fertilisers and Pesticides Enhance the Nutritional Quality of Crops for Their Pests and Pathogens? Front. Sustain. Food Syst. 2021, 5, 701310. [Google Scholar] [CrossRef]
- Smith, G.; Asher, G.J.; Clark, C. Kiwifruit Nutrition Diagnosis of Nutritional Disorders, 3rd ed.; Agpress Communications Ltd.: Washignton, DC, USA, 1997; ISBN 0-9597693-0-7. [Google Scholar]
- Munson, R.D.; Nelson, W.L. Principles and Practices in Plant Analysis. In Soil Testing and Plant Analysis; Westerman, R.L., Ed.; Soil Science Society of America: Madison, WI, USA, 1990; pp. 359–387. [Google Scholar]
- Mourão Filho, F.d.A.A.; Azevedo, J.C. DRIS Norms for “Valencia” Sweet Orange on Three Rootstocks. Pesqui. Agropecuária Bras. 2003, 38, 85–93. [Google Scholar] [CrossRef]
- Filho, F.d.A.A.M. DRIS and Sufficient Range Approaches in Nutritional Diagnosis of “Valencia” Sweet Orange on Three Rootstocks. J. Plant Nutr. 2005, 28, 691–705. [Google Scholar] [CrossRef]
- Betemps, D.L.; Paula, B.V.d.; Parent, S.-É.; Galarça, S.P.; Mayer, N.A.; Marodin, G.A.B.; Rozane, D.E.; Natale, W.; Melo, G.W.B.; Parent, L.E.; et al. Humboldtian Diagnosis of Peach Tree (Prunus persica) Nutrition Using Machine-Learning and Compositional Methods. Agronomy 2020, 10, 900. [Google Scholar] [CrossRef]
- Lima Neto, A.J.d.; Deus, J.A.L.d.; Rodrigues Filho, V.A.; Natale, W.; Parent, L.E. Nutrient Diagnosis of Fertigated “Prata” and “Cavendish” Banana (Musa spp.) at Plot-Scale. Plants 2020, 9, 1467. [Google Scholar] [CrossRef]
- Bates, T.E. Factors Affecting Critical Nutrient Concentrations in Plants and Their Evaluation: A Review. Soil Sci. 1971, 112, 116–130. [Google Scholar] [CrossRef]
- Baxter, I. Should We Treat the Ionome as a Combination of Individual Elements, or Should We Be Deriving Novel Combined Traits? J. Exp. Bot. 2015, 66, 2127–2131. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wilkinson, S.R.; Grunes, D.L.; Sumner, M.E. Nutrient Interactions in Soil and Plant Nutrition. In Handbook of Soil Fertility and Plant Nutrition; Sumner, M.E., Ed.; CRC Press: London, UK, 2000; p. 91. [Google Scholar]
- Courbet, G.; Gallardo, K.; Vigani, G.; Brunel-Muguet, S.; Trouverie, J.; Salon, C.; Ourry, A. Disentangling the Complexity and Diversity of Crosstalk between Sulfur and Other Mineral Nutrients in Cultivated Plants. J. Exp. Bot. 2019, 70, 4183–4196. [Google Scholar] [CrossRef] [PubMed]
- Parent, L.E.; Dafir, M. A Theoretical Concept of Compositional Nutrient Diagnosis. J. Am. Soc. Hortic. Sci. 1992, 117, 239–242. [Google Scholar] [CrossRef] [Green Version]
- Hernandes, A.; Parent, S.-É.; Natale, W.; Parent, L.É. Balancing Guava Nutrition with Liming and Fertilization. Rev. Bras. Frutic. 2012, 34, 1224–1234. [Google Scholar] [CrossRef]
- Parent, S.-É.; Parent, L.E.; Egozcue, J.J.; Rozane, D.E.; Hernandes, A.; Lapointe, L.; Hébert-Gentile, V.; Naess, K.; Marchand, S.; Lafond, J.; et al. The Plant Ionome Revisited by the Nutrient Balance Concept. Front. Plant Sci. 2013, 4, 39. [Google Scholar] [CrossRef] [Green Version]
- Parent, S.-É.; Parent, L.E.; Rozane, D.E.; Natale, W. Plant Ionome Diagnosis Using Sound Balances: Case Study with Mango (Mangifera indica). Front. Plant Sci. 2013, 4, 449. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Khairiddine, N.; Khiari, L.; Leblanc, M.; Cambouris, A.; Parent, L.E. Dependence of SPAD Readings on Nutrient Balance in Potato (Solanum tuberosum L.). In Proceedings of the 13th International Symposium for Soil and Plant Analysis, Queenstown, New Zealand, 8–12 April 2013. [Google Scholar]
- Liu, S.; Yang, X.; Guan, Q.; Lu, Z.; Lu, J. An Ensemble Modeling Framework for Distinguishing Nitrogen, Phosphorous and Potassium Deficiencies in Winter Oilseed Rape (Brassica napus L.) Using Hyperspectral Data. Remote Sens. 2020, 12, 4060. [Google Scholar] [CrossRef]
- D’Oria, A.; Courbet, G.; Lornac, A.; Pluchon, S.; Arkoun, M.; Maillard, A.; Etienne, P.; Diquélou, S.; Ourry, A. Specificity and Plasticity of the Functional Ionome of Brassica Napus and Triticum Aestivum Exposed to Micronutrient or Beneficial Nutrient Deprivation and Predictive Sensitivity of the Ionomic Signatures. Front. Plant Sci. 2021, 12, 641678. [Google Scholar] [CrossRef]
- Beaufils, E. Diagnosis and Recommendation Integrated System (DRIS), 1st ed.; University of Natal: Pietermaritzburg, South Africa, 1973. [Google Scholar]
- Beverly, R.B. Modified Dris Method for Simplified Nutrient Diagnosis of ‘Valencia’ Oranges. J. Plant Nutr. 1987, 10, 1401–1408. [Google Scholar] [CrossRef]
- Rodríguez, O.; Rojas, E.; Sumner, M. Valencia Orange DRIS Norms for Venezuela. Commun. Soil Sci. Plant Anal. 1997, 28, 1461–1468. [Google Scholar] [CrossRef]
- Hernandes, A.; de Souza, H.A.; de Amorim, D.A.; Natale, W.; Lavres, J., Jr.; Boaretto, A.E.; Camacho, M.A. DRIS Norms for Pêra Orange. Commun. Soil Sci. Plant Anal. 2014, 45, 2853–2867. [Google Scholar] [CrossRef] [Green Version]
- Beverly, R.B. Comparison of DRIS and Alternative Nutrient Diagnostic Methods for Soybean. J. Plant Nutr. 1987, 10, 901–920. [Google Scholar] [CrossRef]
- Walworth, J.L.; Sumner, M.E. The Diagnosis and Recommendation Integrated System (DRIS). Adv. Soil Sci. 1987, 6, 149–188. [Google Scholar] [CrossRef]
- Souza, H.A.; Parent, S.É.; Rozane, D.E.; Amorim, D.A.; Modesto, V.C.; Natale, W.; Parent, L.E. Guava Waste to Sustain Guava (Psidium Guajava) Agroecosystem: Nutrient “Balance” Concepts. Front. Plant Sci. 2016, 7, 1252. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Paula, B.V.; Squizani Arruda, W.; Etienne Parent, L.; Frank de Araujo, E.; Brunetto, G. Nutrient Diagnosis of Eucalyptus at the Factor-Specific Level Using Machine Learning and Compositional Methods. Plants 2020, 9, 1049. [Google Scholar] [CrossRef] [PubMed]
- Rodrigues Filho, V.A.; Neves, J.C.L.; Donato, S.L.R.; Guimarães, B.V.C. Universality of Kenworthy and DRIS Norms for Prata and Cavendish Bananas Grown in Two Environments. Rev. Bras. Ciência Do Solo 2021, 45, e0200120. [Google Scholar] [CrossRef]
- Aitchison, J. The Statistical Analysis of Compositional Data. J. R. Stat. Soc. Ser. B 1982, 44, 139–160. [Google Scholar] [CrossRef]
- Parent, S.-É.; Lafond, J.; Paré, M.C.; Parent, L.E.; Ziadi, N. Conditioning Machine Learning Models to Adjust Lowbush Blueberry Crop Management to the Local Agroecosystem. Plants 2020, 9, 1401. [Google Scholar] [CrossRef]
- Parent, S.-É. Why We Should Use Balances and Machine Learning to Diagnose Ionomes. Authorea 2020, 1–13. [Google Scholar] [CrossRef]
- Witten, I.H.; Frank, E.; Hall, M.A. Data Mining: Practical Machine Learning Tools and Techniques (Google EBook), 2nd ed.; Morgan Kaufmann: Burlington, MA, USA, 2011. [Google Scholar]
- McQueen, R.J.; Garner, S.R.; Nevill-Manning, C.G.; Witten, I.H. Applying Machine Learning to Agricultural Data. Comput. Electron. Agric. 1995, 12, 275–293. [Google Scholar] [CrossRef] [Green Version]
- Behmann, J.; Mahlein, A.-K.; Rumpf, T.; Römer, C.; Plümer, L. A Review of Advanced Machine Learning Methods for the Detection of Biotic Stress in Precision Crop Protection. Precis. Agric. 2015, 16, 239–260. [Google Scholar] [CrossRef]
- Pietersma, D.; Lacroix, R.; Lefebvre, D.; Wade, K.M. Performance Analysis for Machine-Learning Experiments Using Small Data Sets. Comput. Electron. Agric. 2003, 38, 1–17. [Google Scholar] [CrossRef]
- Demšar, J.; Zupan, B. Hands-on Training about Overfitting. PLoS Comput. Biol. 2021, 17, e1008671. [Google Scholar] [CrossRef]
- Kampichler, C.; Wieland, R.; Calmé, S.; Weissenberger, H.; Arriaga-Weiss, S. Classification in Conservation Biology: A Comparison of Five Machine-Learning Methods. Ecol. Inform. 2010, 5, 441–450. [Google Scholar] [CrossRef]
- Scott, I.M.; Lin, W.; Liakata, M.; Wood, J.E.; Vermeer, C.P.; Allaway, D.; Ward, J.L.; Draper, J.; Beale, M.H.; Corol, D.I.; et al. Merits of Random Forests Emerge in Evaluation of Chemometric Classifiers by External Validation. Anal. Chim. Acta 2013, 801, 22–33. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shekoofa, A.; Emam, Y.; Shekoufa, N.; Ebrahimi, M.; Ebrahimie, E. Determining the Most Important Physiological and Agronomic Traits Contributing to Maize Grain Yield through Machine Learning Algorithms: A New Avenue in Intelligent Agriculture. PLoS ONE 2014, 9, e97288. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Brungard, C.W.; Boettinger, J.L.; Duniway, M.C.; Wills, S.A.; Edwards, T.C. Machine Learning for Predicting Soil Classes in Three Semi-Arid Landscapes. Geoderma 2015, 239–240, 68–83. [Google Scholar] [CrossRef] [Green Version]
- Kirkwood, C.; Cave, M.; Beamish, D.; Grebby, S.; Ferreira, A. A Machine Learning Approach to Geochemical Mapping. J. Geochem. Explor. 2016, 167, 49–61. [Google Scholar] [CrossRef]
- Grunwald, S. Artificial Intelligence and Soil Carbon Modeling Demystified: Power, Potentials, and Perils. Carbon Footpr. 2022, 1, 6. [Google Scholar] [CrossRef]
- Li, H.; Lee, W.S.; Wang, K. Identifying Blueberry Fruit of Different Growth Stages Using Natural Outdoor Color Images. Comput. Electron. Agric. 2014, 106, 91–101. [Google Scholar] [CrossRef]
- Li, H.; Li, M.; Luo, J.; Cao, X.; Qu, L.; Gai, Y.; Jiang, X.; Liu, T.; Bai, H.; Janz, D.; et al. N-Fertilization Has Different Effects on the Growth, Carbon and Nitrogen Physiology, and Wood Properties of Slow- and Fast-Growing Populus Species. J. Exp. Bot. 2012, 63, 6173–6185. [Google Scholar] [CrossRef] [PubMed]
- Chaudhary, A.; Kolhe, S.; Kamal, R. A Hybrid Ensemble for Classification in Multiclass Datasets: An Application to Oilseed Disease Dataset. Comput. Electron. Agric. 2016, 124, 65–72. [Google Scholar] [CrossRef]
- Romero, J.R.; Roncallo, P.F.; Akkiraju, P.C.; Ponzoni, I.; Echenique, V.C.; Carballido, J.A. Using Classification Algorithms for Predicting Durum Wheat Yield in the Province of Buenos Aires. Comput. Electron. Agric. 2013, 96, 173–179. [Google Scholar] [CrossRef]
- Natarajan, R.; Subramanian, J.; Papageorgiou, E.I. Hybrid Learning of Fuzzy Cognitive Maps for Sugarcane Yield Classification. Comput. Electron. Agric. 2016, 127, 147–157. [Google Scholar] [CrossRef]
- Pantazi, X.E.; Moshou, D.; Alexandridis, T.; Whetton, R.L.; Mouazen, A.M. Wheat Yield Prediction Using Machine Learning and Advanced Sensing Techniques. Comput. Electron. Agric. 2016, 121, 57–65. [Google Scholar] [CrossRef]
- Aregay, N.; Belew, D.; Zenebe, A.; Grima, A.; Haile, M.; Gebresamuel, G. Influences of Rootstock and Agro-Climatic Condition on Physico-Chemical and Bioactive Compounds of Gunda Gundo Orange (Citrus sinensis L. Osbeck) in the Northern Ethiopia. Hortic. Plant J. 2021, 7, 509–519. [Google Scholar] [CrossRef]
- Edition, T. Soil Survey Staff-Keys to Soil Taxonomy, 12th ed.; USDA-Natural Resources Conservation Service: Washington, DC, USA, 2014.
- Lepsch, I.F.; Buol, S.W.; Daniels, R.B. Soil-landscape Relationships in the Occidental Plateau of São Paulo State, Brazil: II. Soil Morphology, Genesis, and Classification. Soil Sci. Soc. Am. J. 1977, 41, 109–115. [Google Scholar] [CrossRef]
- Ribeiro, L.d.O.; Costa, D.P.; Ledo, C.A.d.S.; Carvalho, L.M.d.; Carvalho, H.W.L.d.; Soares Filho, W.d.S.; Girardi, E.A. ‘Tropical Sunki’ Mandarin and Hybrid Citrus Rootstocks under ‘Pera’ Sweet Orange in Cohesive Soil and As Climate without Irrigation. Bragantia 2021, 80, e1321. [Google Scholar] [CrossRef]
- Natale, W.; Rozane, D.E.; Parent, S.-E.; Etienne, L. Soil Acidity and Liming in Tropical Fruit Orchards. In Soil Fertility; InTech: London, UK, 2012. [Google Scholar] [CrossRef] [Green Version]
- Mattos, D., Jr.; Quaggio, J.A.; Cantarella, H.; Alva, A.K. Nutrient Content of Biomass Components of Hamlin Sweet Orange Trees. Sci. Agric. 2003, 60, 155–160. [Google Scholar] [CrossRef]
- Hardy, S.; Khurshgid, T. Calculating Heat Units for Citrus. Primefact 2021, 749, 1–4. [Google Scholar]
- Bataglia, O.C.; Furlani, A.M.C.; Teixeira, J.P.F.; Furlani, P.R.; Gallo, J.R. Métodos de Análise Química de Plantas, 1st ed.; Instituto Agronômico: Campinas, Brazil, 1983.
- van Raij, B.; Andrade, J.C.; Cantarella, H.; Quaggio, J.A. Análise Química Para a Avaliação Da Fertilidade de Solos Tropicais, 1st ed.; Instituto Agronômico: Campinas, Brazil, 2001.
- Quaggio, J.A.; van Raij, B.; Malavolta, E. Alternative Use of the SMP-buffer Solution to Determine Lime Requirement of Soils. Commun. Soil Sci. Plant Anal. 1985, 16, 245–260. [Google Scholar] [CrossRef]
- Soares, M.R.; Alleoni, L.R.F. Contribution of Soil Organic Carbon to the Ion Exchange Capacity of Tropical Soils. J. Sustain. Agric. 2008, 32, 439–462. [Google Scholar] [CrossRef]
- Kuhn, M. Building Predictive Models in R Using the Caret Package. J. Stat. Softw. 2008, 28. [Google Scholar] [CrossRef] [Green Version]
- Hastie, T.; Tibshirani, R.; Friedman, J. Springer Series in Statistics the Elements of Statistical Learning-Data Mining, Inference, and Prediction; Springer: Berkeley, CA, USA, 2009; Volume 2. [Google Scholar]
- Weiss, S.M.; Kulikowski, C.A. Computer Systems That Learn: Classification and Prediction Methods from Statistics Nets, Machine Learning, and Expert Systems; Morgan Kaufmann Publishing: San Mateo, CA, USA, 1991. [Google Scholar]
- R Foundation for Statistical Computing R Core Team. R: A Language and Environment for Statistical Computing. 2017. Available online: https://www.R-project.org/ (accessed on 6 October 2022).
- Van Den Boogaart, D.G.; Tolosana-Delgado, R.; Bren, M. Compositions: Compositional Data Analysis in R Package. 2013. Available online: https://cran.r-project.org/web/packages/compositions/compositions.pdf (accessed on 6 October 2022).
- Amrhein, V.; Greenland, S.; McShane, B. Scientists Rise up against Statistical Significance. Nature 2019, 567, 305–307. [Google Scholar] [CrossRef] [Green Version]
- Delacour, H.; Servonnet, A.; Perrot, A.; Vigezzi, J.F.; Ramirez, J.M. ROC (Receiver Operating Characteristics) Curve: Principles and Application in Biology. Ann. Biol. Clin. 2005, 63, 145–154. [Google Scholar]
- Coulibali, Z.; Cambouris, A.N.; Parent, S.-É. Cultivar-Specific Nutritional Status of Potato (Solanum tuberosum L.) Crops. PLoS ONE 2020, 15, e0230458. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hahn, L.; Parent, L.-É.; Feltrim, A.L.; Rozane, D.E.; Ender, M.M.; Tassinari, A.; Krug, A.V.; Berghetti, Á.L.P.; Brunetto, G. Local Factors Impact Accuracy of Garlic Tissue Test Diagnosis. Agronomy 2022, 12, 2714. [Google Scholar] [CrossRef]
- Montañés, L.; Heras, L.; Abadía, J.; Sanz, M. Plant Analysis Interpretation Based on a New Index: Deviation from Optimum Percentage (DOP). J. Plant Nutr. 1993, 16, 1289–1308. [Google Scholar] [CrossRef] [Green Version]
- Quaggio, J.; Mattos, D., Jr.; Boaretto, R.M.; Zambrosi, F.C.; Cantarella, H. Citros. In Recomendações de Adubação e Calagem para o Estado de São Paulo; Cantarella, H., Quaggio, J.A., Mattos, D., Jr., Boaretto, R., van Raij, B., Eds.; Campinas, Brazil, 2022; pp. 187–198. ISBN 9786588414095. Available online: https://d1wqtxts1xzle7.cloudfront.net/56601012/boletim_tecnico_100_pdf-with-cover-page-v2.pdf?Expires=1670230027&Signature=DD5V28udQ6-suRcCw6VRjrt57xzWwTeulenQR~q77yurrFCYXLKIK8rG0aOjan082AQM1DihplrUbKIVVW9q2OyA9i7Fs9R78xUw0RvlQNA9STjML2kC-CG3K4014D1NGpCGmPArfjVv3-Sytk7QM0KpFrdBVYU3ME0ecST4iJMa-hLbbe~5Qd89i4QrCQhKe-0spanNoXDFmQe3SmCyaLjAI9NCbqeB4H~cxSMIwQ2PoTc8aTPEI4d5B~smP8o2aWE7VjrKUbpIkj0SYgLjTsIpnRbHaS63ukhNBPUC3DmjFyj9tz6y7UaMHlbwZeb6nb~T7F7EJLMlsmoMuq0MNg__&Key-Pair-Id=APKAJLOHF5GGSLRBV4ZApdf (accessed on 6 October 2022).
- Brunetto, G.; Ernani, P.R.; Melo, G.W.B.d.; Nava, G. Frutíferas. In Manual de Calagem e Adubação para os Estados do Rio Grande do Sul e de Santa Catarina; Comissão de Química e Fertilidade Do Solo RS/SC; Santa Maria, Brazil, 2016; pp. 189–232. ISBN 978-85-66301-80-9. Available online: https://www.sbcs-nrs.org.br/docs/Manual_de_Calagem_e_Adubacao_para_os_Estados_do_RS_e_de_SC-2016.pdf (accessed on 6 October 2022).
- Bevington, K.B.; Castle, W.S. Annual Root Growth Pattern of Young Citrus Trees in Relation to Shoot Growth, Soil Temperature, and Soil Water Content. J. Am. Soc. Hortic. Sci. 1985, 110, 840–845. [Google Scholar] [CrossRef]
- Zambrosi, F.C.B.; Mattos, D.; Quaggio, J.A.; Cantarella, H.; Boaretto, R.M. Phosphorus Uptake by Young Citrus Trees in Low-P Soil Depends on Rootstock Varieties and Nutrient Management. Commun. Soil Sci. Plant Anal. 2013, 44, 2107–2117. [Google Scholar] [CrossRef]
- Quaggio, J.; Mattos, D.; Cantarella, H.; Almeida, E.L.; Cardoso, S.A. Lemon Yield and Fruit Quality Affected by NPK Fertilization. Sci. Hortic. 2002, 96, 151–162. [Google Scholar] [CrossRef]
- Quaggio, J.A.; Mattos, D.; Cantarella, H. Fruit Yield and Quality of Sweet Oranges Affected by Nitrogen, Phosphorus and Potassium Fertilization in Tropical Soils. Fruits 2006, 61, 293–302. [Google Scholar] [CrossRef] [Green Version]
- Quaggio, J.A.; Mattos Junior, D.; Boaretto, R.M. Sources and Rates of Potassium for Sweet Orange Production. Sci. Agric. 2011, 68, 369–375. [Google Scholar] [CrossRef]
- Alva, A.K.; Mattos, D.; Paramasivam, S.; Patil, B.; Dou, H.; Sajwan, K.S. Potassium Management for Optimizing Citrus Production and Quality. Int. J. Fruit Sci. 2006, 6, 3–43. [Google Scholar] [CrossRef]
- Parent, L.E.; Jamaly, R.; Atucha, A.; Jeanne Parent, E.; Workmaster, B.A.; Ziadi, N.; Parent, S.-É. Current and Next-Year Cranberry Yields Predicted from Local Features and Carryover Effects. PLoS ONE 2021, 16, e0250575. [Google Scholar] [CrossRef]
- Nava, G.; Reisser Júnior, C.; Parent, L.-É.; Brunetto, G.; Moura-Bueno, J.M.; Navroski, R.; Benati, J.A.; Barreto, C.F. Esmeralda Peach (Prunus persica) Fruit Yield and Quality Response to Nitrogen Fertilization. Plants 2022, 11, 352. [Google Scholar] [CrossRef] [PubMed]
- Badra, A.; Parent, L.E. Early Nutrient Diagnosis of Kentucky Bluegrass Combining Machine Learning and Compositional Methods. Am. J. Plant Sci. 2022, 13, 1247–1260. [Google Scholar] [CrossRef]
- Brunetto, G.; Stefanello, L.O.; Kulmann, M.S.d.S.; Tassinari, A.; Souza, R.O.S.d.; Rozane, D.E.; Tiecher, T.L.; Ceretta, C.A.; Ferreira, P.A.A.; Siqueira, G.N.d.; et al. Prediction of Nitrogen Dosage in ‘Alicante Bouschet’ Vineyards with Machine Learning Models. Plants 2022, 11, 2419. [Google Scholar] [CrossRef] [PubMed]
- Nowaki, R.H.D.; Parent, S.-É.; Cecílio Filho, A.B.; Rozane, D.E.; Meneses, N.B.; Silva, J.A.d.S.d.; Natale, W.; Parent, L.E. Phosphorus Over-Fertilization and Nutrient Misbalance of Irrigated Tomato Crops in Brazil. Front. Plant Sci. 2017, 8, 825. [Google Scholar] [CrossRef]
- Mattos, D.; Hippler, F.W.R.; Boaretto, R.M.; Stuchi, E.S.; Quaggio, J.A. Soil Boron Fertilization: The Role of Nutrient Sources and Rootstocks in Citrus Production. J. Integr. Agric. 2017, 16, 1609–1616. [Google Scholar] [CrossRef] [Green Version]
- Liu, G.; Dong, X.; Liu, L.; Wu, L.; Peng, S.; Jiang, C. Boron Deficiency Is Correlated with Changes in Cell Wall Structure That Lead to Growth Defects in the Leaves of Navel Orange Plants. Sci. Hortic. 2014, 176, 54–62. [Google Scholar] [CrossRef]
- Goldberg, S.; Suarez, D.L. Influence of Soil Solution Cation Composition on Boron Adsorption by Soils. Soil Sci. 2011, 176, 80–83. [Google Scholar] [CrossRef] [Green Version]
- Mesquita, G.L.; Zambrosi, F.C.B.; Tanaka, F.A.O.; Boaretto, R.M.; Quaggio, J.A.; Ribeiro, R.V.; Mattos, D. Anatomical and Physiological Responses of Citrus Trees to Varying Boron Availability Are Dependent on Rootstock. Front. Plant Sci. 2016, 7, 224. [Google Scholar] [CrossRef] [Green Version]
- Matoh, T. Boron in Plant Cell Walls. Plant Soil 1997, 193, 59–70. [Google Scholar] [CrossRef]
- Brown, P.H.; Shelp, B.J. Boron Mobility in Plants. Plant Soil 1997, 193, 85–101. [Google Scholar] [CrossRef]
- Boaretto, R.M.; Quaggio, J.A.; de Assis Alves Mourão Filho, F.; Giné, M.F.; Boaretto, A.E. Absorption and Mobility of Boron in Young Citrus Plants. Commun. Soil Sci. Plant Anal. 2008, 39, 2501–2514. [Google Scholar] [CrossRef]
- Boaretto, R.M.; Quaggio, J.A.; Mattos, D.; Muraoka, T.; Boaretto, A.E. Boron Uptake and Distribution in Field Grown Citrus Trees. J. Plant Nutr. 2011, 34, 839–849. [Google Scholar] [CrossRef]
- Tagliavini, M.; Zavalloni, C.; Rombolà, A.D.; Quartieri, M.; Malaguti, D.; Mazzanti, F.; Millard, P.; Marangoni, B. Mineral Nutrient Partitioning to Fruits of Deciduous Trees. Acta Hortic. 2000, 512, 131–140. [Google Scholar] [CrossRef]
- Roy, E.D.; Richards, P.D.; Martinelli, L.A.; Coletta, L.D.; Lins, S.R.M.; Vazquez, F.F.; Willig, E.; Spera, S.A.; VanWey, L.K.; Porder, S. The Phosphorus Cost of Agricultural Intensification in the Tropics. Nat. Plants 2016, 2, 16043. [Google Scholar] [CrossRef] [PubMed]
- Novais, R.; Kamprath, E.J. Phosphorus Supplying Capacities of Previously Heavily Fertilized Soils. Soil Sci. Soc. Am. J. 1978, 42, 931–935. [Google Scholar] [CrossRef]
- Baligar, V.C.; Bennett, O.L. Outlook on Fertilizer Use Efficiency in the Tropics. Fertil. Res. 1986, 10, 83–96. [Google Scholar] [CrossRef]
- Baligar, V.C.; Bennett, O.L. NPK-Fertilizer Efficiency—A Situation Analysis for the Tropics. Fertil. Res. 1986, 10, 147–164. [Google Scholar] [CrossRef]
- Sumner, M.E.; Farina, M.P.W. Phosphorus Interactions with Other Nutrients and Lime in Field Cropping Systems. Adv. Soil Sci. 1986, 5, 201–236. [Google Scholar] [CrossRef]
- Mattos Junior, D.; Quaggio, J.A.; Cantarella, H.; Carvalho, S.A. De Superfícies de Resposta Do Tangor “Murcott” à Fertilização Com N, P e K. Rev. Bras. Frutic. 2004, 26, 164–167. [Google Scholar] [CrossRef] [Green Version]
- Boaretto, A.E.; Muraoka, T.; Boaretto, R.M. Absorção E Translocação De Micronutrientes, Aplicados Via Foliar, Pelos Citros. Laranja 2003, 24, 177–197. [Google Scholar]
- Boaretto, A.E.; Boaretto, R.M.; Muraoka, T.; Nascimento Filho, V.F.; Tiritan, C.S.; Mourão Filho, F.A.A. Foliar Micronutrient Application Effects on Citrus Fruit Yield, Soil and Leaf Zn Concentrations and 65Zn Mobilization within the Plant. Acta Hortic. 2002, 594, 203–209. [Google Scholar] [CrossRef]
- Quaggio, J.A.; Souza, T.R.; Bachiega Zambrosi, F.C.; Marcelli Boaretto, R.; Mattos, D. Nitrogen-Fertilizer Forms Affect the Nitrogen-Use Efficiency in Fertigated Citrus Groves. J. Plant Nutr. Soil Sci. 2014, 177, 404–411. [Google Scholar] [CrossRef]
- Parent, S.-É.; Parent, L.E. Balance Designs Revisit Indices Commonly Used in Agricultural Science and Eco-Engineering. In Proceedings of the 7th International Workshop on Compositional Data Analysis, Abbadia San Salvatore, Italy, 5–9 June 2017; pp. 95–227. [Google Scholar]
- Brunetto, G.; Bastos de Melo, G.W.; Terzano, R.; Del Buono, D.; Astolfi, S.; Tomasi, N.; Pii, Y.; Mimmo, T.; Cesco, S. Copper Accumulation in Vineyard Soils: Rhizosphere Processes and Agronomic Practices to Limit Its Toxicity. Chemosphere 2016, 162, 293–307. [Google Scholar] [CrossRef] [Green Version]
- Brunetto, G.; Ferreira, P.A.A.; Melo, G.W.; Ceretta, C.A.; Toselli, M. Heavy Metals in Vineyards and Orchard Soils1. Rev. Bras. Frutic. 2017, 39, e-263. [Google Scholar] [CrossRef] [Green Version]
- Hippler, F.W.R.; Boaretto, R.M.; Quaggio, J.A.; Azevedo, R.A.; Mattos, D. Towards Soil Management with Zn and Mn: Estimates of Fertilisation Efficacy of Citrus Trees. Ann. Appl. Biol. 2015, 166, 484–495. [Google Scholar] [CrossRef]
- Keppel, G.; Kreft, H. Integration and Synthesis of Quantitative Data: Alexander von Humboldt’s Renewed Relevance in Modern Biogeography and Ecology. Front. Biogeogr. 2019, 11, e43187. [Google Scholar] [CrossRef]


| ‘Hamlin’ | ‘Pêra’ | ‘Valência’ | |
|---|---|---|---|
| No. of observations | 121 | 126 | 300 |
| tons ha−1 | |||
| Minimum yield | 18.8 | 6.4 | 1.1 |
| Median yield | 62.8 | 39.4 | 52.1 |
| Maximum yield | 136.4 | 102.4 | 141.4 |
| 2012 season | |||
| Flowering period | September–October 2012 | September–October 2012 | September–October 2012 |
| Harvest period | May–June 2013 | July–October 2013 | October–December 2013 |
| 2013 season | |||
| Flowering period | September–October 2013 | September–October 2013 | September–October 2013 |
| Harvest period | May–June 2014 | July–October 2014 | October–December 2014 |
| ‘Hamlin’ X ‘Citrumelo Swingle’ | ‘Valência’ X ‘Citrumelo Swingle’ | |||||
| Minimum | Median | Maximum | Minimum | Median | Maximum | |
| g kg−1 | g kg−1 | |||||
| N | 21.6 | 25.6 | 33.0 | 18.2 | 25.7 | 36.1 |
| P | 0.9 | 1.2 | 2.7 | 0.8 | 1.2 | 3.0 |
| K | 8.0 | 13.9 | 70.7 | 6.50 | 13.6 | 87.1 |
| Ca | 13.8 | 34.6 | 49.7 | 17.5 | 35.7 | 56.0 |
| Mg | 1.8 | 3.3 | 7.9 | 2.0 | 3.7 | 8.4 |
| S | 1.8 | 2.6 | 21.3 | 1.7 | 2.6 | 23.4 |
| B | 0.038 | 0.099 | 0.211 | 0.028 | 0.097 | 0.251 |
| Cu | 0.005 | 0.052 | 0.333 | 0.005 | 0.064 | 0.545 |
| Zn | 0.014 | 0.037 | 0.147 | 0.012 | 0.041 | 0.154 |
| Mn | 0.018 | 0.052 | 0.200 | 0.011 | 0.049 | 0.176 |
| Fe | 0.040 | 0.129 | 3.974 | 0.048 | 0.116 | 3.746 |
| ‘Pêra’ X ‘Tangerina Sunki’ | Current Brazilian standards | |||||
| Minimum | Median | Maximum | Lower Bound | Centroid | Upper Bound | |
| g kg−1 | g kg−1 | |||||
| N | 20.1 | 24.1 | 35.0 | 25 | 27.5 | 30 |
| P | 0.8 | 1.2 | 1.7 | 1.2 | 1.4 | 1.6 |
| K | 8.8 | 13.7 | 27.1 | 10 | 12.5 | 15 |
| Ca | 12.5 | 32.8 | 56.0 | 35 | 42.5 | 50 |
| Mg | 1.6 | 3.1 | 5.3 | 3.5 | 4.2 | 5.0 |
| S | 1.6 | 2.5 | 3.2 | 2.0 | 2.5 | 3.0 |
| B | 0.036 | 0.065 | 0.201 | 0.050 | 0.100 | 0.150 |
| Cu | 0.007 | 0.063 | 0.486 | 0.010 | 0.015 | 0.020 |
| Zn | 0.015 | 0.043 | 0.218 | 0.035 | 0.053 | 0.070 |
| Mn | 0.019 | 0.045 | 0.165 | 0.030 | 0.045 | 0.060 |
| Fe | 0.041 | 0.107 | 0.292 | 0.050 | 0.010 | 0.150 |
| Scion | pH (CaCl2) | SOM | P | K | Ca | Mg | (H+Al) † | CEC | Base Saturation |
|---|---|---|---|---|---|---|---|---|---|
| g dm−3 | mg dm−3 | mmolc dm−3 | % | ||||||
| 0–20 cm layer | |||||||||
| ‘Hamlin’ | 5.19 ± 0.55 | 25 ± 12 | 34 ± 25 | 3 ± 2 | 30 ± 26 | 14 ± 10 | 29 ± 14 | 75 ± 38 | 57 ± 16 |
| ‘Valência’ | 5.30 ± 0.54 | 22 ± 13 | 32 ± 20 | 2 ± 1 | 26 ± 17 | 12 ± 8 | 24 ± 12 | 63 ± 29 | 60 ± 15 |
| ‘Pêra’ | 5.06 ± 0.56 | 15 ± 6 | 28 ± 21 | 2 ± 1 | 19 ± 10 | 9 ± 5 | 21 ± 8 | 50 ± 17 | 56 ± 14 |
| 20–40 cm layer | |||||||||
| ‘Hamlin’ | 5.06 ± 0.73 | 25 ± 15 | 32 ± 49 | 2 ± 1 | 28 ± 24 | 12 ± 9 | 26 ± 11 | 69 ± 35 | 57 ± 15 |
| ‘Valência’ | 5.05 ± 0.50 | 21 ± 13 | 24 ± 24 | 2 ± 1 | 24 ± 18 | 11 ± 8 | 23 ± 8 | 60 ± 29 | 57 ± 14 |
| ‘Pêra’ | 4.73 ± 0.46 | 14 ± 6 | 18 ± 16 | 2 ± 1 | 16 ± 11 | 8 ± 6 | 22 ± 7 | 47 ± 18 | 50 ± 15 |
| Features | Yield as tons ha−1 § | Yield as kg Tree−1 † | ||
|---|---|---|---|---|
| R2 | RMSE | R2 | RMSE | |
| Training data set | ||||
| Temperature, rainfall, scion, age, tissue nutrients, soil classification, S1, S2 | 0.905 | 7.295 | 0.913 | 14.544 |
| Scion, age, tissue nutrients, soil classification, S1, S2 | 0.898 | 7.571 | 0.907 | 15.061 |
| Scion, age, tissue nutrients, soil classification, S1 | 0.897 | 7.593 | 0.905 | 15.196 |
| Scion, age, tissue nutrients, soil classification | 0.898 | 7.575 | 0.908 | 14.970 |
| Scion, age, nutrient balances | 0.897 | 7.586 | 0.899 | 15.647 |
| Nutrient balances | 0.860 | 8.852 | 0.885 | 16.674 |
| Testing data set | ||||
| Temperature, rainfall, scion, age, tissue nutrients, soil classification, S1, S2 | 0.285 | 17.874 | 0.506 | 36.804 |
| Scion, age, tissue nutrients, soil classification, S1, S2 | 0.321 | 17.415 | 0.515 | 35.691 |
| Scion, age, tissue nutrients, soil classification, S1 | 0.257 | 18.217 | 0.520 | 36.274 |
| Scion, age, tissue nutrients, soil classification | 0.109 | 19.951 | 0.489 | 37.438 |
| Scion, age, nutrient balances | 0.144 | 19.562 | 0.494 | 37.248 |
| Nutrient balances | 0.086 | 20.210 | 0.423 | 39.759 |
| Features | 50 tons ha−1 | 60 tons ha−1 | ||
|---|---|---|---|---|
| AUC | Accuracy | AUC | Accuracy | |
| Temperature, rainfall, scion, age, tissue nutrients, soil classification, S1, S2 | 0.796 | 0.748 | 0.806 | 0.740 |
| Scion, age, tissue nutrients, soil classification, S1, S2 | 0.797 | 0.730 | 0.813 | 0.750 |
| Scion, age, tissue nutrients, soil classification, S1 | 0.811 | 0.742 | 0.801 | 0.755 |
| Scion, age, tissue nutrients, soil classification | 0.799 | 0.748 | 0.799 | 0.731 |
| Scion, age, nutrient balances | 0.783 | 0.735 | 0.783 | 0.728 |
| Nutrient balances | 0.683 | 0.662 | 0.658 | 0.633 |
| Scion X Rootstock | TN | FN | FP | TP | Total | NPV | PPV | Specificity | Sensitivity | Accuracy |
|---|---|---|---|---|---|---|---|---|---|---|
| 60 tons ha−1 | ||||||||||
| ‘Hamlin’ X ‘Citrumelo Swingle’ | 67 | 12 | 19 | 23 | 121 | 0.85 | 0.55 | 0.78 | 0.66 | 0.74 |
| ‘Pêra’ X ‘Tangerina Sunki’ | 0 | 4 | 21 | 101 | 126 | 0.00 | 0.83 | 0.00 | 0.96 | 0.80 |
| ‘Valência’ X ‘Citrumelo Swingle’ | 83 | 43 | 45 | 133 | 304 | 0.66 | 0.75 | 0.65 | 0.76 | 0.71 |
| 150 | 59 | 85 | 257 | 551 | 0.72 | 0.75 | 0.64 | 0.81 | 0.74 | |
| 50 tons ha−1 | ||||||||||
| ‘Hamlin’ X ‘Citrumelo Swingle’ | 87 | 10 | 12 | 12 | 121 | 0.90 | 0.50 | 0.88 | 0.55 | 0.82 |
| ‘Pêra’ X ‘Tangerina Sunki’. | 21 | 17 | 21 | 67 | 126 | 0.55 | 0.76 | 0.50 | 0.80 | 0.70 |
| ‘Valência’ X ‘Citrumelo Swingle’ | 153 | 49 | 29 | 73 | 304 | 0.76 | 0.72 | 0.84 | 0.60 | 0.74 |
| 261 | 76 | 62 | 152 | 551 | 0.77 | 0.71 | 0.81 | 0.67 | 0.75 | |
| Nutrients | ‘Hamlin’ X ‘Citrumelo Swingle’ | ‘Pêra’ X ‘Tangerina Sunki’ | ‘Valência’ X ‘Citrumelo Swingle’ | |||
|---|---|---|---|---|---|---|
| Lower Quartile | Upper Quartile | Lower Quartile | Upper Quartile | Lower Quartile | Upper Quartile | |
| N | 24.3 | 27.4 | 22.6 | 25.9 | 24.3 | 26.8 |
| P | 1.1 | 1.4 | 1.0 | 1.3 | 1.1 | 1.3 |
| K | 11.8 | 16.9 | 12.3 | 15.5 | 11.7 | 15.4 |
| Ca | 30.8 | 40.4 | 25.8 | 39.2 | 31.9 | 40.9 |
| Mg | 2.8 | 3.8 | 2.6 | 3.5 | 3.2 | 4.0 |
| S | 2.4 | 2.9 | 2.3 | 2.8 | 2.4 | 2.8 |
| B | 0.081 | 0.118 | 0.054 | 0.080 | 0.076 | 0.127 |
| Cu | 0.025 | 0.080 | 0.027 | 0.062 | 0.032 | 0.087 |
| Zn | 0.025 | 0.056 | 0.028 | 0.048 | 0.029 | 0.056 |
| Mn | 0.037 | 0.074 | 0.030 | 0.062 | 0.037 | 0.068 |
| Fe | 0.093 | 0.144 | 0.075 | 0.121 | 0.096 | 0.140 |
| Nutrients | ‘Hamlin’ X ‘Citrumelo Swingle’ | ‘Pêra’ X ‘Tangerina Sunki’ | ‘Valência’ X ‘Citrumelo Swingle’ | |||
|---|---|---|---|---|---|---|
| clr Mean | clr SD | clr Mean | clr SD | clr Mean | clr SD | |
| 50 tons ha−1 | ||||||
| N | 2.866 | 0.209 | 2.923 | 0.220 | 2.789 | 0.155 |
| P | −0.142 | 0.239 | −0.116 | 0.236 | −0.272 | 0.198 |
| K | 2.261 | 0.326 | 2.354 | 0.211 | 2.157 | 0.323 |
| Ca | 3.153 | 0.247 | 3.040 | 0.278 | 3.141 | 0.171 |
| Mg | 0.812 | 0.241 | 0.863 | 0.255 | 0.833 | 0.216 |
| S | 0.607 | 0.281 | 0.591 | 0.163 | 0.558 | 0.320 |
| B | −2.538 | 0.370 | −2.728 | 0.262 | −2.540 | 0.314 |
| Cu | −3.355 | 0.430 | −3.544 | 0.309 | −3.404 | 0.370 |
| Zn | −3.674 | 0.875 | −3.330 | 0.765 | −3.328 | 0.668 |
| Mn | −3.732 | 0.414 | −3.660 | 0.255 | −3.554 | 0.438 |
| Fe | −2.678 | 0.335 | −2.924 | 0.408 | −2.744 | 0.366 |
| Fv | 6.365 | 0.134 | 6.532 | 0.211 | 6.421 | 0.199 |
| 60 tons ha−1 | ||||||
| N | 2.889 | 0.213 | - | - | 2.780 | 0.140 |
| P | −0.116 | 0.226 | - | - | −0.322 | 0.161 |
| K | 2.261 | 0.332 | - | - | 2.093 | 0.247 |
| Ca | 3.166 | 0.261 | - | - | 3.160 | 0.143 |
| Mg | 0.827 | 0.245 | - | - | 0.827 | 0.191 |
| S | 0.636 | 0.299 | - | - | 0.490 | 0.114 |
| B | −2.524 | 0.388 | - | - | −2.595 | 0.212 |
| Cu | −3.321 | 0.434 | - | - | −3.385 | 0.436 |
| Zn | −3.787 | 0.846 | - | - | −3.233 | 0.481 |
| Mn | −3.764 | 0.416 | - | - | −3.456 | 0.467 |
| Fe | −2.697 | 0.364 | - | - | −2.732 | 0.396 |
| Fv | 6.431 | 0.212 | - | - | 6.372 | 0.112 |
| Component | Concentration | Brazilian Nutrient Ranges § | Specimen | Regional † | ||
|---|---|---|---|---|---|---|
| g kg−1 | clr | |||||
| N | 31.0 | 25 | 30 | 3.024 | 2.789 | 0.155 |
| P | 1.3 | 1.2 | 1.6 | −0.188 | −0.272 | 0.198 |
| K | 13.0 | 10 | 15 | 2.156 | 2.157 | 0.323 |
| Ca | 36.5 | 35 | 50 | 3.186 | 3.141 | 0.171 |
| Mg | 4.2 | 3.5 | 5.0 | 1.019 | 0.833 | 0.216 |
| S | 2.3 | 2.0 | 3.0 | 0.435 | 0.558 | 0.320 |
| B | 0.134 | 0.050 | 0.150 | −2.619 | −2.540 | 0.314 |
| Cu | 0.056 | 0.010 | 0.020 | −3.950 | −3.404 | 0.370 |
| Zn | 0.035 | 0.035 | 0.070 | −3.287 | −3.328 | 0.668 |
| Mn | 0.029 | 0.030 | 0.060 | −3.760 | −3.554 | 0.438 |
| Fe | 0.110 | 0.050 | 0.150 | −2.421 | −2.744 | 0.366 |
| Filling value | - | - | - | 6.404 | 6.421 | 0.199 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yamane, D.R.; Parent, S.-É.; Natale, W.; Cecílio Filho, A.B.; Rozane, D.E.; Nowaki, R.H.D.; Mattos Junior, D.d.; Parent, L.E. Site-Specific Nutrient Diagnosis of Orange Groves. Horticulturae 2022, 8, 1126. https://doi.org/10.3390/horticulturae8121126
Yamane DR, Parent S-É, Natale W, Cecílio Filho AB, Rozane DE, Nowaki RHD, Mattos Junior Dd, Parent LE. Site-Specific Nutrient Diagnosis of Orange Groves. Horticulturae. 2022; 8(12):1126. https://doi.org/10.3390/horticulturae8121126
Chicago/Turabian StyleYamane, Danilo Ricardo, Serge-Étienne Parent, William Natale, Arthur Bernardes Cecílio Filho, Danilo Eduardo Rozane, Rodrigo Hiyoshi Dalmazzo Nowaki, Dirceu de Mattos Junior, and Léon Etienne Parent. 2022. "Site-Specific Nutrient Diagnosis of Orange Groves" Horticulturae 8, no. 12: 1126. https://doi.org/10.3390/horticulturae8121126
APA StyleYamane, D. R., Parent, S.-É., Natale, W., Cecílio Filho, A. B., Rozane, D. E., Nowaki, R. H. D., Mattos Junior, D. d., & Parent, L. E. (2022). Site-Specific Nutrient Diagnosis of Orange Groves. Horticulturae, 8(12), 1126. https://doi.org/10.3390/horticulturae8121126







