Characteristics of Rotary Sprinkler Water Distribution under Dynamic Water Pressure

Abstract

In order to explore water distribution in sprinkler irrigation systems under dynamic water pressure, an irrigation test was conducted in a sprinkler irrigation system equipped with the Hunter MP2000 full circular rotator ray sprinkler under “trapezoidal” waveform pressure to explore the influencing factors such as basic water pressure, dynamic pressure period, and the sprinkler combination spacing. The result shows that the basic pressure, sprinkler combination spacing, and their interaction significantly affected the coefficient of variation, average intensity, and coefficient of uniformity. The normalized comprehensive evaluation indexes were selected as the measurement standards. The optimal factor combination was found to be the basic pressure of 250 kPa, the dynamic pressure period of 200 s, and the sprinkler combination spacing of 6 m, and the corresponding evaluation index values were 0.08, 10.54 mm/h, and 93.20%, respectively. The uniformity coefficient was increased by 6.54% compared with the constant pressure of the same flow rate. Compared with the constant pressure of the same flow rate, the sprinkler area and the average intensity increased by 39.67% and decreased by 8.62% when the basic pressure was 250 kPa and the dynamic pressure period was 200 s. The average uniformity coefficient increased by 11.76% at the combined spacing of 6.0, 6.5, 7.0, 7.5, and 8.0 m. The results provide a theoretical basis for sprinkler irrigation decisions under dynamic pressure.

1. Introduction

Sprinkler irrigation is an important agricultural irrigation method in the field. It has the advantage of strong terrain adaptability, is time saving and labor saving, and has high water use efficiency [1,2,3]. As important parameters for evaluating sprinkler irrigation performance, the water uniformity of the sprinkler irrigation surface and radial water distribution are affected by many factors such as sprinkler installation height, working pressure, and sprinkler spacing [4,5]. Therefore, improving the water use efficiency and water distribution of sprinkler irrigation technology has important application value and research significance.

In recently years, many new irrigation methods and equipment at home and abroad have been developed, which can be divided into constant pressure and dynamic pressure according to the classification of pressure conditions. Silva (2006) studied the influence of different baffles on the surface runoff and water distribution of the impact sprinkler [6]. Zhu et al. (2015) and Zhu et al. (2012) concluded that the complete fluidic sprinkler was better than the impact sprinkler by comparing the hydraulic performance of the sprinkler under different working pressures [7,8]. In addition, the secondary nozzle flow channel was adjusted to an “S” shape, which could increase the flow resistance and near-end water distribution [9]. Tarjuelo et al. (1999) explored the influencing factors of water distribution and provided theoretical support for obtaining a high coefficient of uniformity [10]. The study found that water distribution of sprinklers was related to sprinkler height and rain gauge height, and the difference in heights produced different uniformity coefficients [11]. In addition, the interaction of sprinkler diameter and installation spacing on a uniform sprinkler irrigation system under constant pressure showed that sprinkler installation spacing > working pressure > sprinkler diameter [12]. Dynamic pressure irrigation improves the transport capacity of water flow to particles, thereby slowing down the clogging resistance of a drip irrigation system [13,14,15,16]. The study found that when the combination mode with dynamic pressure waveform as a trigonometric function and period of 18 s was applied to a slope sprinkler irrigation, the coefficient of uniformity at 1.0R square combined spacing was 75.7% [17]. Ge et al. (2015) through the comparative study of a constant pressure and dynamic pressure water supply of a Nelson D3000 sprinkler, found that the dynamic pressure effectively improved the water and energy distribution, expanded the wetting range, and reduced the intensity of sprinkler irrigation [18]. King and Wall (2000) compared the energy consumption of variable-rate spraying of a variable displacement pump and showed that the use of frequency control can reduce energy consumption by 20.2% [19].

At present, many scholars have studied the changes in hydraulic performance of sprinklers under a constant pressure or dynamic pressure water supply. However, most of them focus on changing the structure of sprinklers by adding auxiliary mechanisms, a non-circular spray field, and other aspects. The influence of dynamic hydraulic pressure parameters on the hydraulic performance of sprinkler irrigation has not been systematically studied. Although a few scholars have carried out radial water distribution experiments of sprinklers under single factor dynamic pressure [18] and the coefficient of uniformity improvement test of slope sprinkler sunder dynamic pressure [17], the influence of dynamic basic pressure, dynamic pressure period, combination spacing, and their interactions on the water distribution of sprinkler irrigation are still unclear, and how to optimize decision-making in dynamic pressure sprinkler irrigation has not been reported.

In this research, the dynamic pressure sprinkler irrigation of a Hunter MP2000 circular rotating sprinkler was studied based on Programmable Logic Controller (PLC) control technology. The unique feature of the Hunter MP sprinkler head is that it can control the amount of water through the nozzle at various spray angle and range settings, resulting in matching irrigation intensity regardless of the nozzle setting. The radial water distribution of sprinklers was measured under the conditions of the basic pressures under different dynamic pressures and at different periods. The contour map of water distribution of multi-sprinkler combination was simulated and calculated. Finally, the CV (coefficient of variation), $\overline{p}$ (average intensity), and CU (coefficient of uniformity) were used as evaluation indexes to optimize the parameters of the influencing factors of the overall experiment. A dynamic pressure sprinkler irrigation model was established in order to provide reliable theoretical support for dynamic pressure sprinkler irrigation decision-making and theoretical data for application of dynamic pressure on rotator sprinklers.

2. Materials and Methods

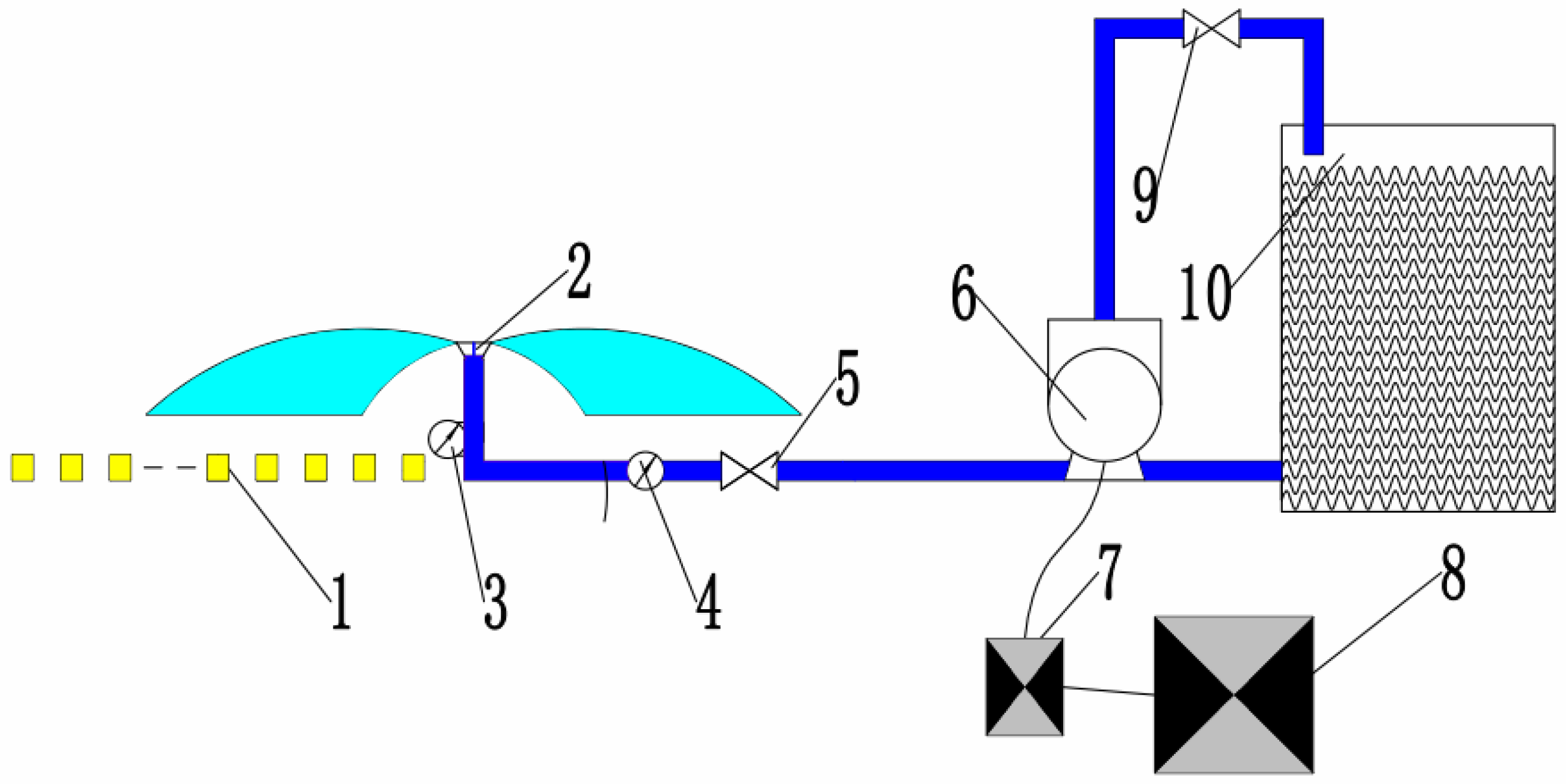
2.1. Experiment Design

The experiment was conducted in a rain shelter plastic shed at the agricultural water conservancy project test site (24°50′57″ N, 102°51′49″ E) of the College of Agriculture and Food, Kunming University of Science and Technology (Kunming, Yunnan Province). The test site belongs to the northern subtropical low latitude plateau mountain monsoon climate. The average temperature in the greenhouse was 28.5 °C, the average relative humidity was 58%, and the annual average sunshine duration was about 2200 h. The experimental conditions and methods referred to the Procedure for Sprinkler Distribution Testing for Research Purposes, American Society of Agricultural Engineers [20], and Agricultural Irrigation Equipment—Sprinklers—Part 3: Characterization of distribution and test methods (GB/T 27612.3) [21]. Test equipment is mainly composed of PLC (Shenzhen Jinghuichuan Electric Appliance Co., Ltd., Type EC10-1410-BRA), frequency converter (Type EV510 of Nanjing Oulu Electric Appliance Co., Ltd., Nanjing, China), water pump, water storage tank, long-distance transmission pressure gauge (accuracy ± 0.5%), flowmeter (accuracy ± 0.5%), and sprinkler (Figure 1). The sprinkler was installed on a vertical pipe 413.6 mm away from the ground. The inner diameter of the measuring cylinder is 108.3 mm, and the height is 141.7 mm, and the sprinkler is the Hunter MP2000 circular rotator sprinkler (Figure 2). The sprinkler is in a round spraying state when working, so the distribution of radial water volume under dynamic water pressure is not affected by different pressure periods, the basic water pressure, and other different factors. Therefore, it can be assumed that the distribution of each jet water quantity emitted by the sprinkler is consistent. Therefore, the measuring cylinder arrangement adopts a single radial distribution to measure the change law of irrigation intensity [22,23]. The distance between measuring cylinders with radial distribution was 0.5 m, with a total of 14 measuring points. Each group of tests was repeated 3 times, and each test time was 30 min; this test time includes the delay of the sprinkler reaching steady state.

In order to explore the influence of basic dynamic pressure and dynamic pressure period on the hydraulic performance of the sprinkler and the optimal combination under different combined spacing, the coefficient of variation, average intensity, and coefficient of uniformity were used as test indexes, the basic dynamic pressure, dynamic pressure period, and sprinkler combined spacing were used as test factors, and L27 (3 × 3 × 3) was adopted to conduct a comprehensive test. The test adopted three factors and three levels of comprehensive design. The basic pressure levels for dynamic pressures were 100~300, 150~350, and 200~400 kPa and for constant pressure were 200 kPa (CI), 250 kPa (CII), and 300 kPa (CIII), respectively. The three dynamic pressure period levels were 120 s (T120), 160 s (T160), and 200 s (T200), and the combined spacing levels of the three sprinklers were 6 m (S6), 7 m (S7), and 8 m (S8), respectively. Factors and levels are shown in

Table 1. Factors and levels of comprehensive test.

Levels	Factors
	A (kPa)	B (s)	C (m)
1	200	120	6
2	250	160	7
3	300	200	8

Note: A-Basic pressure; B-Dynamic period; C-Combined sprinkler spacing.

.

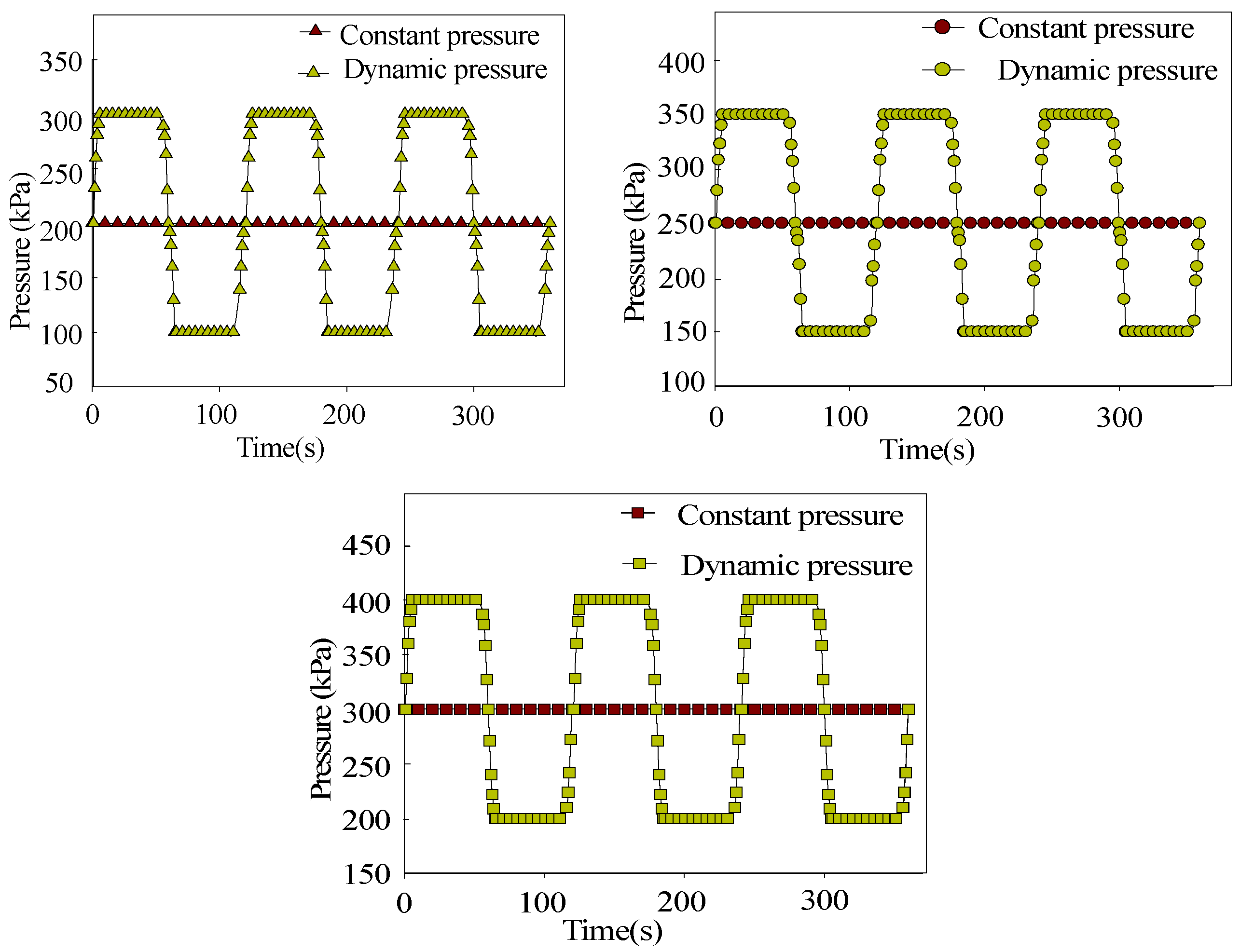
2.2. Dynamic and Constant Pressure Changes

Working pressure is the key factor affecting the water distribution of a sprinkler [24]. The effect of dynamic pressure on improving the hydraulic performance of sprinkler irrigation is especially significant [17]. Dynamic water pressure was obtained by operating the PLC program to control the output of the frequency converter and then regulating the rotating speed of the water pump regularly. In this paper, the “trapezoidal” waveform dynamic pressure model was adopted with the basic water pressure at 200 kPa, 250 kPa, and 300 kPa, respectively, the dynamic pressure period at 120 s, 160 s, and 200 s respectively, and the dynamic pressure amplitude at 100 kPa. The pressure variation curves under dynamic water pressure (100~300, 150~350, 200~400 kPa) and constant pressure (200 kPa, 250 kPa, 300 kPa) are shown in Figure 3.

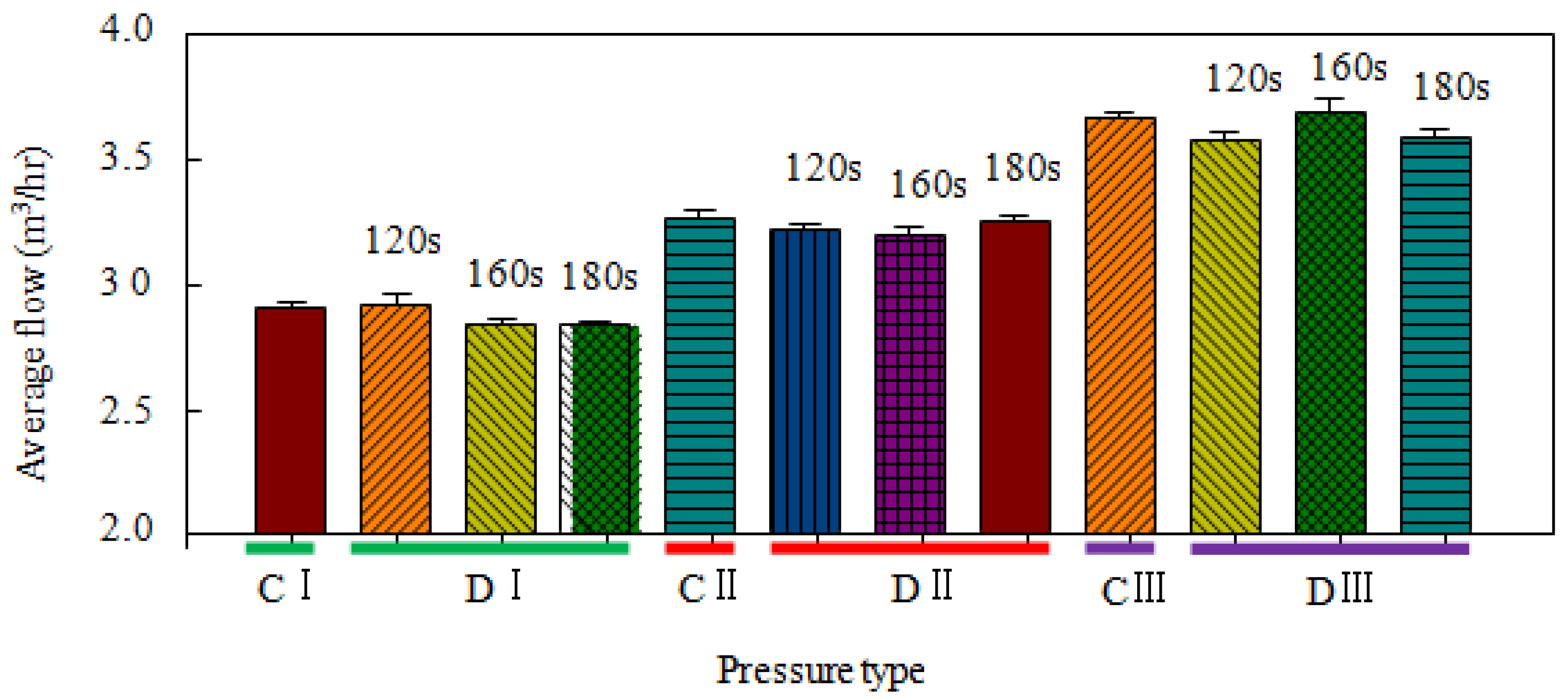
2.3. Comparison of the Sprinkler Flow Rates

The constant pressure 200, 250, and 300 kPa were marked as CI, CII, and CIII respectively. The dynamic pressure 100~300, 150~350, and 200~400 kPa were marked as DI, DII, and DIII respectively. Corresponding cycle time was marked according to the dynamic pressure period. For example, the cycle time of DI is 120 s, which is marked as DIT120. When exploring the application performance of dynamic pressure with different basic pressures and different periods in the circular rotator fluidics sprinkler, the flow deviation of water supply type under dynamic and constant pressures should be avoided. In the preliminary test, the average flow rates of the sprinkler CI, CII, and CIII in 30 min were 2.911, 3.263, and 3.668 m³/h, respectively. The flow rate errors corresponding to DI, DII, and DIII were 1.574%, 1.400%, and 1.50% respectively. The error range was within 2%, indicating that the dynamic pressure sprinkler irrigation and constant pressure sprinkler irrigation with the same basic pressure had the same flow rates. When sprinkler irrigation of DI, DII, and DIII were in the periods of 120, 160, and 200 s, respectively, the average flow rates were 2.87, 3.22, and 3.61 m³/h, respectively, and the maximum margins of error were 2.71%, 1.715%, and 3.061%, respectively. The error range was less than 3.1%, which indicated that the dynamic pressure sprinkler irrigation flow rate under the same basic pressure was not affected by the dynamic pressure period (Figure 4).

2.4. Calculation Model of Combined Water Volume

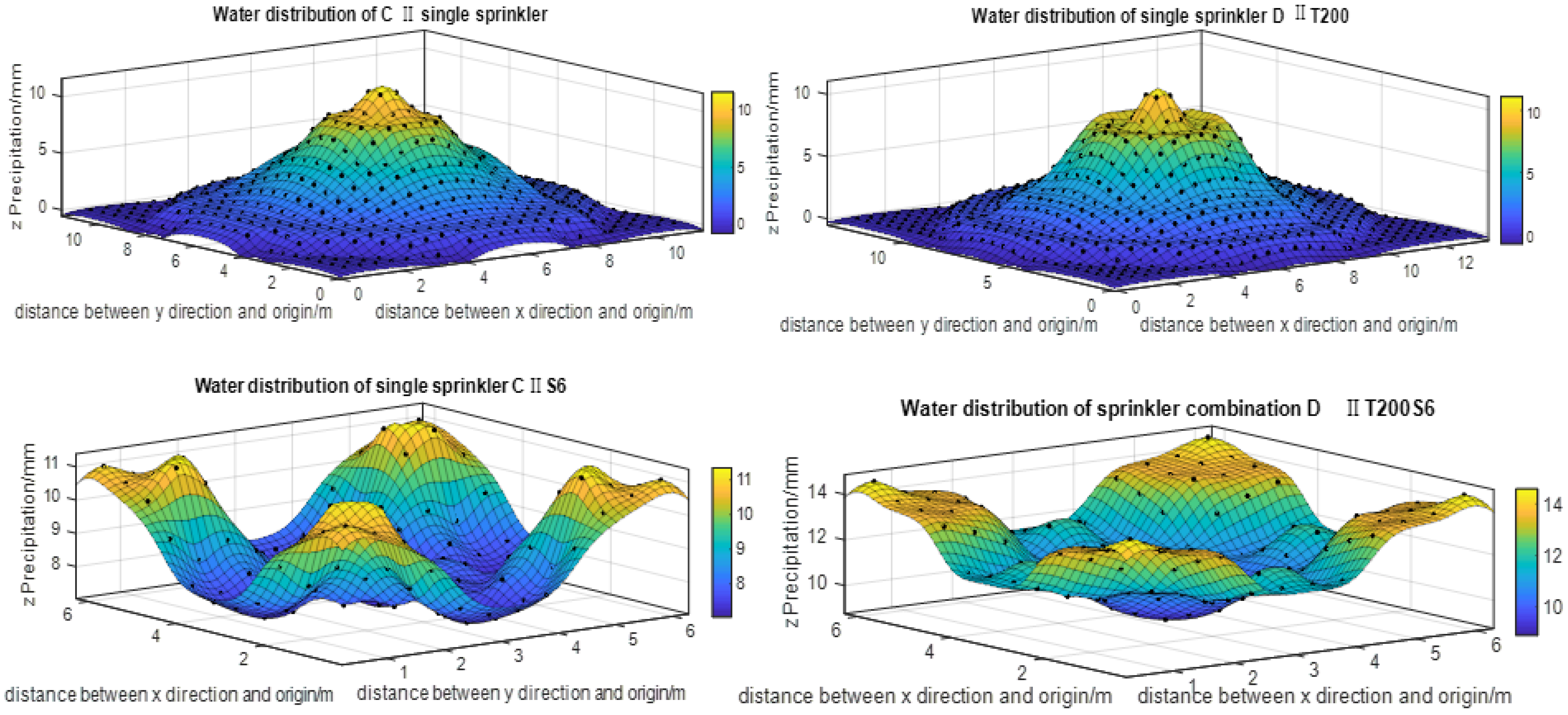
2.4.1. Water Distribution Calculation Theory of Single Sprinkler

The relationship between the precipitation depth of the sprinkler and the distance from the point to the sprinkler was obtained by calculating the water distribution of a single jet measuring cylinder to a single sprinkler. The calculation process adopts cubic spline interpolation calculation, and the method is as follows: given that the function S(x) ϵ [a,b] and its second derivative is continuous, the function is a polynomial or zero polynomial of no higher than third degree in each interval [x_j, x_j + 1], and a = x₀ < x₁ < … < x_n = b is the given node, set the function

$$S\left(x\right)=\{\begin{array}{l}{S}_1\left(x\right)\\ S_i\left(x\right)\\ S_n\left(x\right)\end{array}\begin{array}{l}x\in \left[x_1,x_2\right]\\ x\in \left[x_i,x_{i+1}\right]\\ x\in \left[x_n,x_{n+1}\right]\end{array}$$

(1)

where S(x) is the cubic spline function on nodes x₀, x₁, … x_n. If the function value y = f (x_j) (j = 0, 1, …, n) is given on the node x_j, and S(x_j) = y_j, j = 1, 2, …, n is established, then S(x) is the cubic spline function of the function f(x). Set m_i = S’’(x), f(x) = f_i, because S(x) is a cubic polynomial on the interval [x_j, x_j + 1], thus S’’(x) is

$$S_j^{″}(x)=m_i\frac{x_{i+1}-x}{h_i}+m_{i+1}\frac{x-x_i}{h_i}(x\in \left[x_j,x_{j+1}\right]$$

(2)

Integrating S’’(x) twice in a row can obtain:

$$S_i=h_i+\left[\frac{m_i}{6}{(x_{i+1}+x)}^3+\frac{m_{i+1}}{6}{(x-x_i)}^3\right]+f_i+f\left[x_i+x_{i+1}\right](x-x_i)-\frac{h_i^2}{6}\left[(m_{i+1}-m_i)\frac{x-x_i}{h_i}+m_i\right]$$

(3)

Given the values of m_i and m_i+1, the expression of S_i(x) can be obtained, and then the amount of water at any point on the radial water distribution of the sprinkler can be obtained.

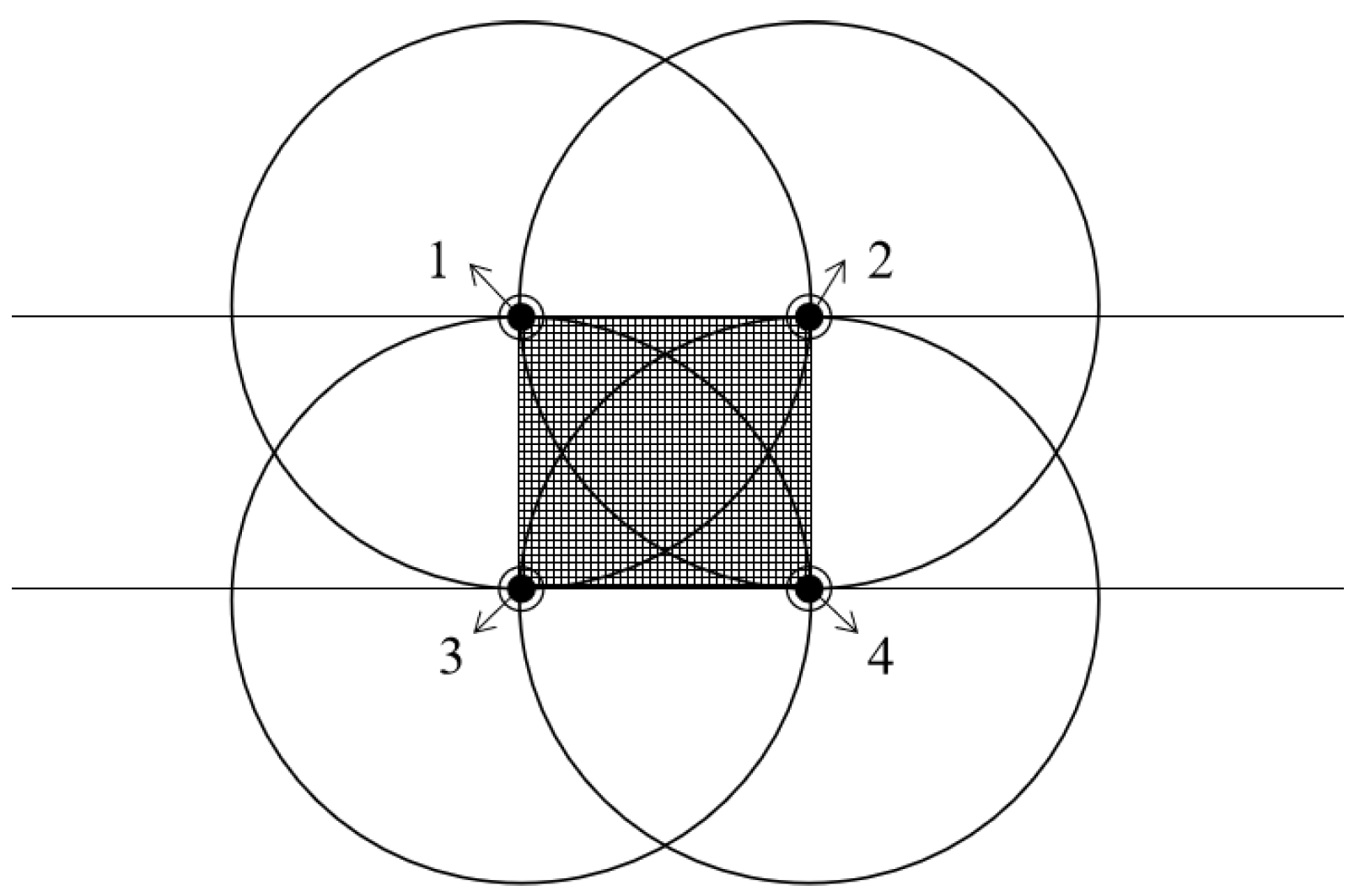
2.4.2. Multi-Sprinkler Combination Mode

The quadratic interpolation method [25] is based on the continuous water distribution of sprinkler irrigation. The water precipitation depths of radial and circumferential sprinklers (radial measuring cylinder placement mode) were calculated by the quadratic interpolation method to obtain the coefficient of uniformity of multi-sprinkler combinations. The water volume superposition calculation was arranged by square combination in the multi-sprinkler combination method. The square area is called a typical calculation area [26], and the distribution locations of multi-sprinklers are shown in Figure 5.

2.5. Evaluation Indicators

(1)

Coefficient of variation (CV) is used to measure the discrete degree of water distribution in the spraying area [27]. The calculation formula is shown in Formula (4);

(2)

Average intensity ($\overline{p}$) refers to the average precipitation in a typical calculated area [27]. Since the permeable speed should be higher than the sprinkler irrigation intensity in actual engineering experience, the smaller the intensity is, the better it is within a certain range. The calculation formula is shown in Formula (5);

(3)

Coefficient of uniformity (CU) is calculated using the J. E. Christiansen coefficient [15,28,29], as shown in Formula (6).

$$CV=\sqrt{\frac{{\displaystyle \sum \left(\frac{p_i-\overline{p}}{\overline{p}}\right)}}{n-1}}$$

(4)

$$\overline{p}=\frac{{\displaystyle \sum _{i=1}^n{p}^i}}{n}$$

(5)

$$CU=\left(1-\frac{{\displaystyle \sum _{i=1}^n|x_i-\stackrel{\_}{x}|}}{{\displaystyle \sum _{i=1}^n{x}_i}}\right)\times 100\%$$

(6)

where CV is the coefficient of variation; $\overline{p}$ is the average intensity in the area, mm; CU is the J. E. Christiansen coefficient, %; pⁱ is the intensity of the measuring point of the measuring cylinder, mm; n is the number of valid measuring points; x_i is the height of the water volume at the calculation point I, mm; and $\overline{x}$is the average spraying water depth of all measuring points on the valid calculation area, mm.

Coefficient of variation and average intensity belong to low-priority indexes, while coefficient of uniformity belong to the high-priority index. In order to make the evaluation indexes in the same trend, X^′_ij = −X_ij was used to reverse the coefficient of variation and the average intensity. Then, the coefficient of variation, the average intensity, and the coefficient of variation of the sprinkler irrigation are normalized to their extreme values [30] (e.g., Formula (6)) and then normalized according to the weights of 0.3, 0.3, and 0.4, respectively. The comprehensive evaluation index is a single evaluation index.

$$Z=\frac{x_j-min(x_j)}{max(x_j)-min(x_j)}$$

(7)

where Z is the dimensionless index; x_j refers to the index values of the same trending; min(x_j) is the minimum index value of the same trending; and max(x_j) is the maximum index value of the same trending.

2.6. Establishment of Dynamic Pressure Evaluation Index Prediction Model

The influence of dynamic pressure on the hydraulic performance index of the Hunter MP2000 rotator sprinkler was predicted by establishing a multivariate nonlinear regression model [31,32].

The set of binary function points is:

$$\left\{\left(x,y,z\right)|z=f\left(x,y\right),\left(x,y\right)\in D\right\},f\left(x,y\right)={\beta }_0+{\beta }_{1}x+{\beta }_{2}y+{\beta }_3{x}^2+{\beta }_4{y}^2+{\beta }_{5}xy$$

(8)

where β_i is an unknown constant, x and y are independent variables, and f (x, y) is the dependent variable. The factors such as function type and the amplitude of dynamic pressure are ignored in the function model, and x and y are dynamic pressure period and sprinkler combined spacing, respectively. The evaluation indicators such as coefficient of variation, average intensity, and coefficient of uniformity are all set as dependent variables f (x, y).

3. Test results and Analysis

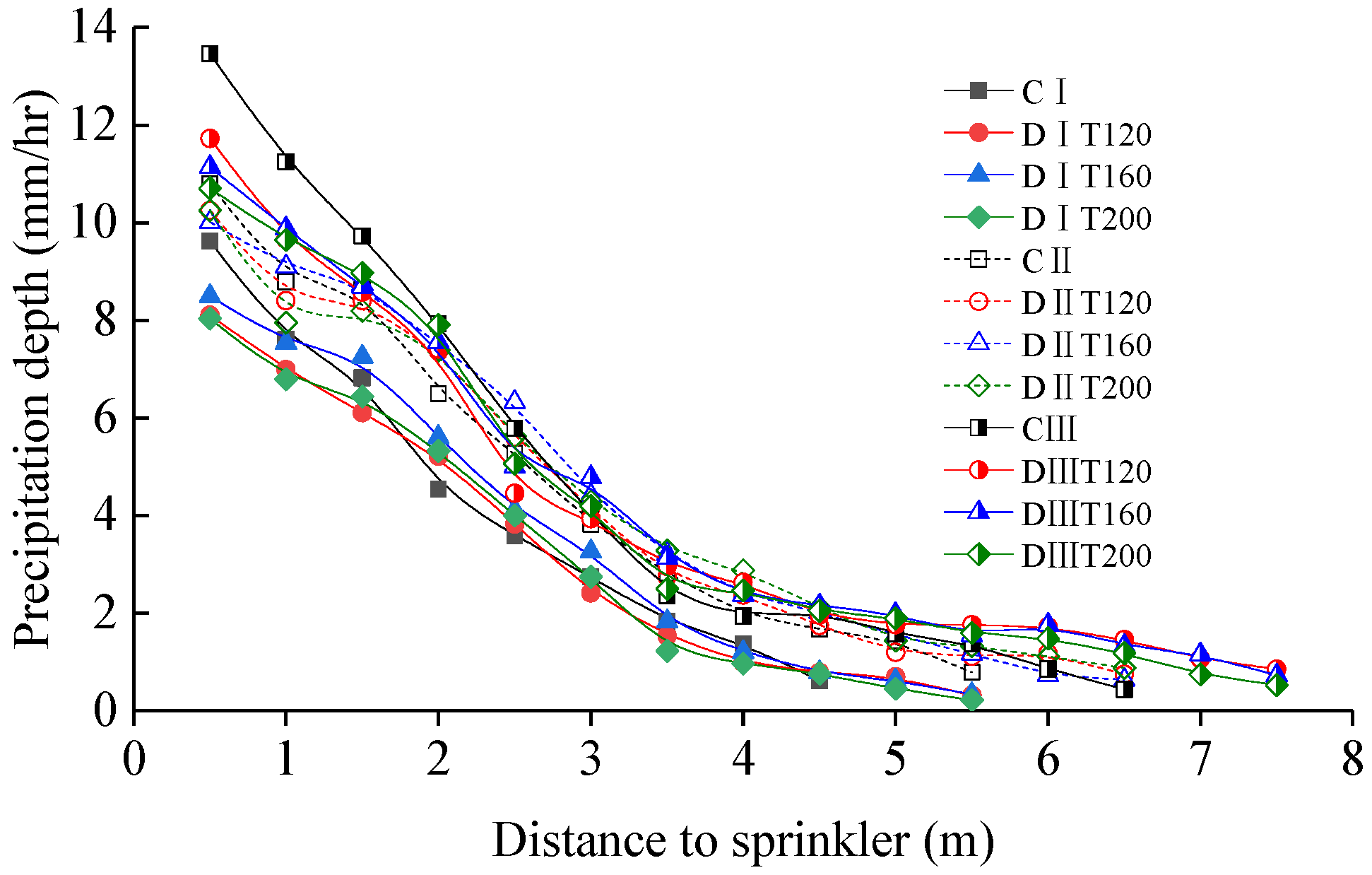
3.1. Radial Water Distribution Curve of Single Sprinkler

The water distribution of the relationship between precipitation depth and the distance to the sprinkler measured by a rain gauge under the constant pressure and dynamic pressure is shown in Figure 6. As shown in the figure, overall water distribution was “triangular”. The water volume was more in the area close to the sprinkler, concentrated in 0~3 m, and the coverage range was 4.5~7.5 m. Compared with DI, DII, and DIII with the same average flow rate, CI, CII, and CIII drop spraying sprinkler irrigation had shorter ranges and slightly higher peak intensities. The variation in the overall water volume was the highest, with a maximum precipitation depth of CIII of 13.46 mm/h at a distance of 0.5 m. The water distribution of DIII sprinklers was similar at 120, 160, and 200 s, and the range was about 7.5 m. The range of CI was the shortest and the average intensity was relatively small. DI had a large difference in sprinkler water distribution between 0~3 m under 120, 160, and 200 s periods. Water distribution of DII was 18% more uniform than that of CII.

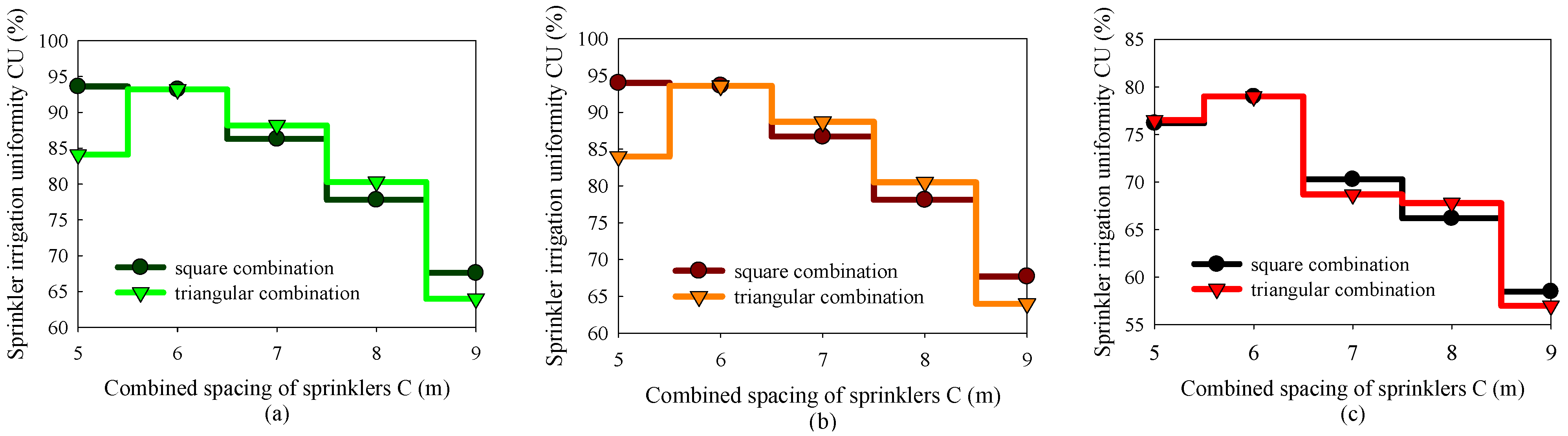
3.2. Water Distribution of Combined Sprinkler

CIII and DIII had the longest range in constant pressure and dynamic pressure sprinkler irrigation, which were 6.5 m and 7.5 m, respectively. When the square combined sprinkler spacing was 7 m, the water distribution under the three constant pressure modes and nine different basic pressure and periodic dynamic pressure modes is shown in Figure 7.

The intensity of the precipitation contour reflects the difference in water potential gradient. The intensity of sprinkler irrigation was higher in the corner area of the square, and the contour of water distribution was mostly an open curve, while the water volume in the central area was less, and the water distribution was a mostly closed curve. When the differences in water volume between the central area and the corner area was more obvious, the sprinkler irrigation uniformity was lower. The water distribution of different periods under dynamic pressure was similar under the same basic pressure, that is, the water distribution of the combination was less affected by the dynamic pressure period. When the combined spacing was 7 m, the average intensities in the square spray field using CI, CII, and CIII were 4.04, 6.43, and 7.88 mm/h, respectively. If the average intensity of the same dynamic basic pressure in different periods was taken, the corresponding values of DI, DII, and DIII were 4.32, 7.72, and 9.18 mm/h, respectively. The uniformity coefficient of CI, CII, and CIII in the spraying area were 62.32%, 77.33%, and 72.94%, respectively. The average uniformity coefficient of DI, DII, and DIII under the same flow rate were 64.17%, 83.03%, and 81.43%, respectively. The results show that the dynamic pressure water supply is helpful to improve the uniformity of combined sprinkler irrigation and reduce the water distribution difference in the combination under a certain combined spacing.

3.3. Comprehensive Test under Dynamic Pressure

3.3.1. Comprehensive Test Design

Compared with the constant pressure, the dynamic pressure increased the water volume range of the single sprinkler and reduced the peak value of radial water volume at the same flow rate. When the sprinkler combined spacing was 7 m, the difference in water distribution in the former area was small. According to range analysis, the influence degree of various factors on the coefficient of variation, average intensity, and coefficient of uniformity of the sprinkler irrigation was sprinkler combined spacing C > basic pressure A > dynamic pressure period B, basic pressure A > sprinkler combined spacing C > dynamic pressure period B, sprinkler combined spacing C > basic pressure A > dynamic pressure period B, respectively (

Table 2. Performance of evaluation indexes corresponding to experiment design scheme.

Treatment	Test Factors			Coefficient of Variation CV	Average Irrigation Intensity $\overline{\mathit{p}}$/(mm)	Coefficient of Uniformity CU/(%)
	A	B	C
T1	200	120	6	0.2390	5.682	79.20
T2	250	120	6	0.1156	10.01	88.90
T3	300	120	6	0.1469	11.51	82.80
T4	200	160	6	0.2100	6.378	82.20
T5	250	160	6	0.08819	10.53	91.00
T6	300	160	6	0.1460	11.32	83.40
T7	200	200	6	0.2499	5.590	78.80
T8	250	200	6	0.07936	10.54	93.20
T9	300	200	6	0.1412	13.01	84.70
T10	200	120	7	0.4147	4.174	63.70
T11	250	120	7	0.2248	7.497	80.60
T12	300	120	7	0.2078	9.195	80.70
T13	200	160	7	0.3919	4.686	67.40
T14	250	160	7	0.1948	7.845	82.20
T15	300	160	7	0.2165	8.870	80.40
T16	200	200	7	0.4478	4.107	61.40
T17	250	200	7	0.1576	7.806	86.30
T18	300	200	7	0.1835	9.479	83.20
T19	200	120	8	0.6055	3.196	40.20
T20	250	120	8	0.3343	5.740	71.00
T21	300	120	8	0.2802	7.153	77.90
T22	200	160	8	0.5944	3.588	51.00
T23	250	160	8	0.3130	6.006	72.20
T24	300	160	8	0.2952	6.863	75.50
T25	200	200	8	0.6543	3.145	44.00
T26	250	200	8	0.2657	5.976	77.80
T27	300	200	8	0.2638	7.368	78.80
k1	0.4231	0.2854	0.1574	Coefficient of variation CV
k2	0.1970	0.2722	0.2710
k3	0.2090	0.2715	0.4007
R	0.2260	0.0140	0.2434
k1	4.505	7.129	9.273	Average irrigation intensity $\overline{p}$/(mm)
k2	7.994	7.343	7.073
k3	9.295	7.323	5.448
R	4.790	0.2143	3.825
k1	63.10	73.89	84.91	Coefficient of uniformity CU/(%)
k2	82.58	76.14	76.21
k3	80.82	76.47	65.38
R	19.48	2.578	19.53

). The results showed that the sprinkler combined spacing C had the greatest influence on the coefficient of variation, followed by the basic pressure A. The dynamic pressure period B had little influence on the coefficient of variation. The coefficient of variation increased with the increase in the combined spacing C. The influence of the basic pressure A on the coefficient of variation first decreased and then increased, while the influence of dynamic pressure period B gradually decreased. The coefficient of variation reflects the difference in each measuring point in the spray area. Water distribution uniformity was larger when the coefficient of variation was small. The results showed that coefficient of variation of the C1A2B3 combination (the sprinkler combined spacing is 6 m, the base pressure is 250 kPa, and the dynamic pressure period is 200 s) was the smallest. For engineering applications, the higher intensity of sprinkler irrigation is more likely to cause runoff in the spraying area. The higher intensity of drop sprinkler irrigation will disturb the soil, which easily changes the physical and chemical properties of the soil. The coefficient of uniformity reflects the uniformity of water distribution: the greater the value, the better the uniformity. The results showed that the combination of A1C3B1 (the basic pressure was 200 kPa, the sprinkler spacing was 8 m, and the dynamic pressure period was 120 s) and C1A3B3 (the sprinkler spacing was 6 m, the basic pressure was 300 kPa, and the dynamic pressure period was 200 s) had the smallest average intensity and the largest coefficient of uniformity.

3.3.2. Variance Analysis

The results of the variance analysis [33] using Design-Expert software are shown in

Table 3. Variance analysis of influence of three factors on hydraulic performance of sprinkler.

Factors	CV	$\overline{\mathit{p}}$	CU
Basic Pressure A	181.60 **	559.5 **	112.8 **
Dynamic Pressure Period B	0.69	1.28	1.92
Combined Spacing of Sprinkler C	166.5 **	336.0 **	93.05 **
Basic pressure A × Combined sprinkler spacing C	15.40 **	9.080 **	17.06 **
Dynamic pressure period × Combined sprinkler spacing C	0.086	0.1	0.11

Note: ** p < 0.01.

. Basic pressure A, sprinkler combined spacing C, and their interaction significantly affected the coefficient of variation, average intensity, and coefficient of uniformity (p < 0.01). Dynamic pressure period B and the interaction between dynamic pressure period B and sprinkler combined spacing C had no significant effect on the three evaluation indexes (p > 0.05). The basic pressure had the greatest influence on the coefficient of variation, average intensity, and coefficient of uniformity, followed by the combined spacing of sprinklers, and the influence of dynamic pressure period was small. The spray range was the largest and the range was the farthest when the pressure was at the maximum value during the dynamic pressure period; the spray range was the smallest and the range was the shortest when the pressure was at the minimum value. Different basic pressures produced different water distribution, and the dynamic pressure period changed the switching frequency of the two spray states, indicating that the water distribution in the spray area of the sprinkler was less affected by the dynamic pressure period.

3.3.3. Positive and Normalized Analysis of Indicators

The above studies analyzed the influence of three factors on a single index. Here, we use the comprehensive evaluation index to comprehensively analyze the application of the evaluation index in the actual irrigation situation [30].

The results showed that the comprehensive evaluation index was the highest in T8 (A2C1B3 combination), indicating that the optimal scheme under this combination of factors was DIIT200S6 (the basic pressure of dynamic pressure is 250 kPa, the sprinkler combined spacing is 6 m, and the dynamic pressure period is 200 s). The corresponding variation coefficient of sprinkler irrigation was 0.08, the average intensity of sprinkler irrigation was 10.54 mm/h, and the uniformity coefficient was 93.20% (

Table 4. Positive and normalized calculation of indicators.

Number of Test	Positive Values			Normalized Values			Comprehensive Evaluation Index
	CV	$\overline{\mathit{p}}$	CU	CV1	$\overline{\mathit{p}}$1	CU1
T1	−0.2309	−5.682	79.20	0.7364	0.7428	0.7358	0.7381
T2	−0.1156	−10.01	88.90	0.9370	0.3041	0.9189	0.7399
T3	−0.1469	−11.51	82.80	0.8825	0.1521	0.8038	0.6319
T4	−0.2100	−6.378	82.20	0.7728	0.6723	0.7925	0.7505
T5	−0.08819	−10.53	91.00	0.9846	0.2514	0.9585	0.7542
T6	−0.1460	−11.32	83.40	0.8841	0.1713	0.8151	0.6427
T7	−0.2499	−5.590	78.80	0.7034	0.7522	0.7283	0.7280
T8	−0.07936	−10.54	93.20	1.0000	0.2504	1.000	0.7751
T9	−0.1412	−13.01	84.70	0.8924	0	0.8396	0.6036
T10	−0.4147	−4.174	63.70	0.4167	0.8957	0.4434	0.5711
T11	−0.2248	−7.497	80.60	0.7470	0.5588	0.7623	0.6967
T12	−0.2078	−9.195	80.70	0.7766	0.3867	0.7642	0.6547
T13	−0.3919	−4.686	67.40	0.4564	0.8438	0.5132	0.5953
T14	−0.1948	−7.845	82.20	0.7992	0.5236	0.7925	0.7138
T15	−0.2165	−8.870	80.40	0.7615	0.4197	0.7585	0.6577
T16	−0.4478	−4.107	61.40	0.3592	0.9025	0.4000	0.5385
T17	−0.1576	−7.806	86.30	0.8639	0.5275	0.8698	0.7654
T18	−0.1835	−9.479	83.20	0.8189	0.3579	0.8113	0.6776
T19	−0.6055	−3.196	40.20	0.08488	0.9948	0	0.3239
T20	−0.3343	−5.740	71.00	0.5566	0.7369	0.5811	0.6205
T21	−0.2802	−7.153	77.90	0.6507	0.5937	0.7113	0.6578
T22	−0.5944	−3.588	51.00	0.1042	0.9551	0.2038	0.3993
T23	−0.3130	−6.006	72.20	0.5936	0.7100	0.6038	0.6326
T24	−0.2952	−6.863	75.50	0.6246	0.6231	0.6660	0.6407
T25	−0.6543	−3.145	44.00	0	1.000	0.07170	0.3287
T26	−0.2657	−5.976	77.80	0.6759	0.7130	0.7094	0.7005
T27	−0.2638	−7.368	78.80	0.6792	0.5719	0.7283	0.6667

).

3.4. Verification Test

In order to verify the feasibility of the optimal combination scheme to improve the sprinkler irrigation performance, this study compared the sprinkler irrigation hydraulic performance of CII and DIIT200 under constant pressure and dynamic pressure water supply with the same flow rate.

The spray areas of DIIT200 and CII at the same flow rate were 132.72 m² and 95.03 m², respectively, and DIIT200 had a wider spray area than CII in the single sprinkler spray area. The average radial sprinkler irrigation intensity of DIIT200 and CII were low, which were 4.358 mm/h and 4.77 mm/h, respectively, and the increase in DIIT200 was −8.62% compared with that of CII. The irrigation uniformity coefficients of CIIS6 and DIIT200S6 were 93.20% and 87.40% respectively, and the increase in DIIT200S6 was 6.64% compared with CIIS6 (Figure 8).

The average sprinkling uniformity coefficients of DIIT200 and CII at other spacings (the combined spacing of 6.0, 6.5, 7.0, 7.5, and 8.0 m) were 85.92% and 76.88%, respectively, and the increase in DIIT200 compared with CII was 11.76% (Figure 8). The results showed that the dynamic pressure water supply with the same flow rate had better hydraulic performance than the constant pressure water supply. The specific performance was due to that the irrigation area was larger, the average irrigation intensity was smaller, and the uniformity coefficient of the combination of multiple sprinklers was higher, resulting in higher water use efficiency and more uniform water distribution. In actual irrigation, this can effectively avoid excessive disturbance of water runoff and soil caused by excessive local sprinkler irrigation intensity.

3.5. Establishment of Dynamic Pressure Evaluation Index Prediction Model

The multivariate nonlinear function of MATLAB was used to perform polynomial fitting of CV and CU with respect to x and y (with 95% confidence bounds), respectively. The model fitting effect is good, and the determination coefficient R² is greater than 0.96, indicating that the model can be used to predict the overall trend of test data (

Table 5. Table of fitting function coefficients.

A (kPa)	x(s)	y(m)	f(x,y)		Binary Function Constant					R2
				β0	β1	β2	β3	β4	β5
200	120	6	CV	0.1910	0.1441	−0.1492	0.007383	0.03643	0.009475	0.9999
	160	7
	200	8
250	120	6		0.02715	0.09332	−0.002747	0.006958	−0.002437	−0.00809	0.9967
	160	7
	200	8
300	120	6		0.05969	0.03440	0.05895	0.009617	−0.002675	−0.01533	0.9916
	160	7
	200	8
200	120	6	$\overline{p}$	6.209	−2.404	2.218	0.2742	−0.5683	0.01025	0.9967
	160	7
	200	8
250	120	6		12.22	−3.557	1.315	0.3861	−0.2306	−0.1210	0.9999
	160	7
	200	8
300	120	6		15.23	−2.821	−1.430	0.1710	0.4165	−0.04370	0.9999
	160	7
	200	8
200	120	6	CU	77.77	−13.20	20.68	−1.600	−5.650	1.050	0.9913
	160	7
	200	8
250	120	6		98.46	−7.200	−3.117	−0.6833	1.167	0.6250	0.9969
	160	7
300	200	8
	120	6		86.51	1.050	−4.950	−0.9167	−0.2500	1.583	0.9656
	160	7
	200	8

). The model can be used to predict the performance indexes of sprinkler irrigation under different factor combinations, which has certain credibility for the application decision of dynamic pressure sprinkler irrigation projects.

4. Discussion

4.1. Feasibility of Sprinkler Irrigation and Analysis of Factors Affecting Water Distribution under Dynamic Pressure

Many domestic and foreign scholars have studied the effects of structure, elevation angle, the internal flow channel model, and pressure on the variable spray of sprinklers. The rotator sprinkler developed abroad has a certain amount of water distribution and energy distribution [34,35,36,37,38]. In this study, in order to explore how to improve the hydraulic performance of the sprinkler without increasing the flow rate, the Hunter MP2000 was used as the material and the dynamic pressure water supply method was used for the sprinkler irrigation test. In this study, the Hunter MP2000 round rotator sprinkler is used to avoid the influence of function types, amplitudes, dynamic pressure periods, and other factors on the spray water flow during rotation. The sprinkler produces a contraction or expansion of the circular sprinkler irrigation surface under a dynamic pressure water supply, which ensures the water distribution in all (360°) directions is basically the same, so as to ensure the accuracy of the radial water distribution measurement method. In this study, the cubic spline interpolation method in Catch 3D software was used to simulate the multi-sprinkler combined spray in the transformation from radial water distribution to round water distribution by setting relevant parameters [39]. The optimal scheme obtained through normalization analysis was DIIT200S6. Considering that the interpolation method and multi-sprinkler combined mode have a certain impact on the sprinkler irrigation uniformity coefficient, this paper explores this, and the results are shown in Figure 9. The results showed that the variation trend of the sprinkler coefficient of uniformity was similar under different interpolation methods, and the overall CU decreases with the increase in combined spacing. The CU values under cubic spline interpolation and linear interpolation were both higher, and the changes were basically the same. However, the Lagrange interpolation method had a great impact on the calculation results, and the overall CU values were low. In the selection of sprinkler combination mode, the characteristics of economy and easy management should be considered. This study compares the effects of triangular square combination on the sprinkler coefficient of uniformity. The data distributions under Lagrange interpolation were basically the same, while the data under cubic spline interpolation and linear interpolation showed that the square combination mode was better when the combination spacing was 5.0 and 9.0 m, which increased by 8.85% and 9.26%, respectively, compared with the triangular combination. The triangular combination was slightly higher than the square combination under the other combination spacing, which was 1.71% and 1.70% higher, respectively.

4.2. Influence of Dynamic Pressure Water Supply on Sprinkler Irrigation and Optimization Ideas

It was found that the basic pressure A and sprinkler combined spacing C had significant effects on the test results through a comprehensive test of sprinkler evaluation indexes [38,40,41] by three factors (CV, $\overline{p}$, CU), which provides a theoretical basis for exploring dynamic pressure sprinkler irrigation. Meanwhile, it was found that dynamic pressure sprinkler irrigation has certain advantages, by comparing the optimal dynamic pressure and constant pressure test under the same flow rates. If only considering the influence of dynamic pressure on coefficient of uniformity under different combined spacing alone, DI was less influenced compared with CI, and the two coefficients of uniformity were basically the same in a certain period. The coefficients of uniformity of DII and CII were significantly different. The coefficient of uniformity decreased rapidly with the increase in combination spacing, but the uniformity was high at low combined spacing. There were obvious differences between DIII and CIII under the high spacing combination, and the variation range of the coefficient of uniformity was very small with the increase in combined sprinkler spacing (Figure 10). Due to the limitations in test conditions and space, the influence of dynamic pressure waveform, dynamic pressure amplitude, duty ratio, and other factors have not been thoroughly discussed in this paper. Increasing the dynamic pressure amplitude can expand the moving range of the sprinkler’s farthest range point, and different amplitudes will produce different water distribution. Dynamic pressure waveforms include triangle type, trigonometric function type, trapezoidal type, etc. Different waveforms can make the sprinkler generate different instantaneous flow rates at different times, thus affecting the water distribution of the sprinkler irrigation surface. A 50% duty ratio was used in the study, which refers to the ratio of the time when the pressure is higher than the average value of dynamic pressure in a dynamic pressure period to the whole period. The change in duty ratio with time also affects the water volume in the sprinkler irrigation process. The above three assumptions are the influences of dynamic pressure parameters on sprinkler irrigation, which will be the focus of future research.

The research results show that the dynamic pressure water supply is beneficial in improving the hydraulic performance of sprinklers, as well as the distribution uniformity of water volume of the single sprinklers and the combined sprinklers. In addition, the sprinkler flow channel model can be established by Solid Works, and the CFD method can be used to explore the fluid movement laws of the sprinkler under dynamic pressure [42], so as to optimize the structural parameters of the sprinkler and design a sprinkler more suitable for dynamic pressure sprinkler irrigation. Low uniformity is not conducive to crop water use, and high uniformity will increase equipment costs. Therefore, in setting dynamic pressure factors affecting sprinkler irrigation uniformity, the factors such as saving energy, cost input, and water use efficiency should be considered, and the high uniformity of water distribution should be unilaterally pursued when setting the dynamic pressure factor affecting the uniformity of sprinkler irrigation.

5. Conclusions

This study explored the effects of basic water pressure, dynamic pressure period, and sprinkler combination spacing on the water distribution of sprinkler irrigation under dynamic water pressure by using the Hunter MP2000 full circular rotary ray sprinkler to conduct a “trapezoidal” waveform dynamic pressure sprinkler irrigation experiment. The results show that the intensity of sprinkler irrigation at the corner of the dynamic pressure multi-sprinkler irrigation area was relatively large, while that in the central area was relatively small. The water distribution of sprinklers with dynamic pressure is more uniform than that with a constant pressure water supply. Compared with CII, the spraying area of DIIT200 increased by 39.67%, the average radial sprinkling intensity decreased by 8.62%, and the average coefficients of uniformity were 85.92% and 11.76% at combined spacing of 6.0, 6.5, 7.0, 7.5, and 8.0 m. Compared with CIIS6, the coefficient of uniformity of DIIT200S6 sprinkler irrigation was as high as 93.20%, which was 6.54% higher than that of CIIS6. The optimal scheme for the influence of each factor on the comprehensive evaluation index (CV, P, and CU were normalized with weights of 0.3, 0.3 and 0.4) was A2C1B3, and the factor–level combination is the optimal scheme DIIT200S6. This paper provides new ideas and methods for optimizing the hydraulic performance of sprinklers and provides a theoretical basis and technical references for the application of the dynamic pressure sprinkler irrigation system.