Utilization of the Fusion of Ground-Space Remote Sensing Data for Canopy Nitrogen Content Inversion in Apple Orchards
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data Collection and Pre-Processing
2.2.1. Leaf Collection and CNC Measurement
2.2.2. Ground-Based Hyper-Spectral Data Acquisition and Pre-Processing
2.2.3. UAV Multi-Spectral Data Acquisition and Pre-Processing
2.3. Construction of CNC Inversion Model Based on Ground-Space Remote Sensing Data
2.3.1. Extraction of Spectral Information of Apple Canopy
2.3.2. Fusion of Ground-Space Remote Sensing Data
2.3.3. Construction and Screening of Spectral Feature Parameters
2.3.4. Construction of Canopy Abundance Parameter Based on Data Fusion
2.3.5. Establishment and Verification of CNC Inversion Model
2.3.6. Spatial Inversion Mapping of CNC
3. Results
3.1. Analysis of Spectral Features of Apple Canopy
3.2. Results of Spectral Information Extraction from Apple Canopy
3.3. Results of Ground-Space Remote Sensing Data Fusion
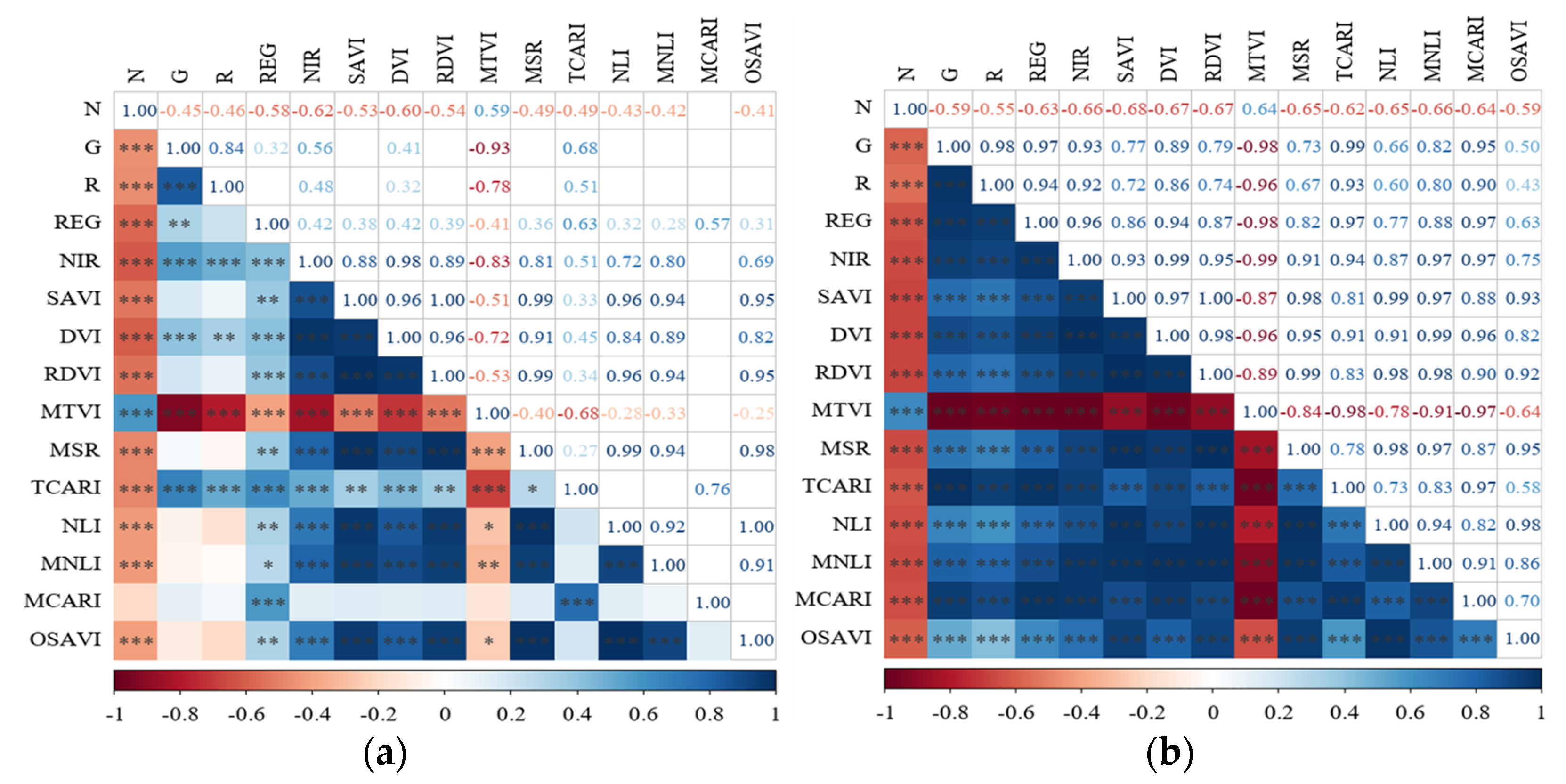
3.4. Results of Spectral Feature Parameters Screening
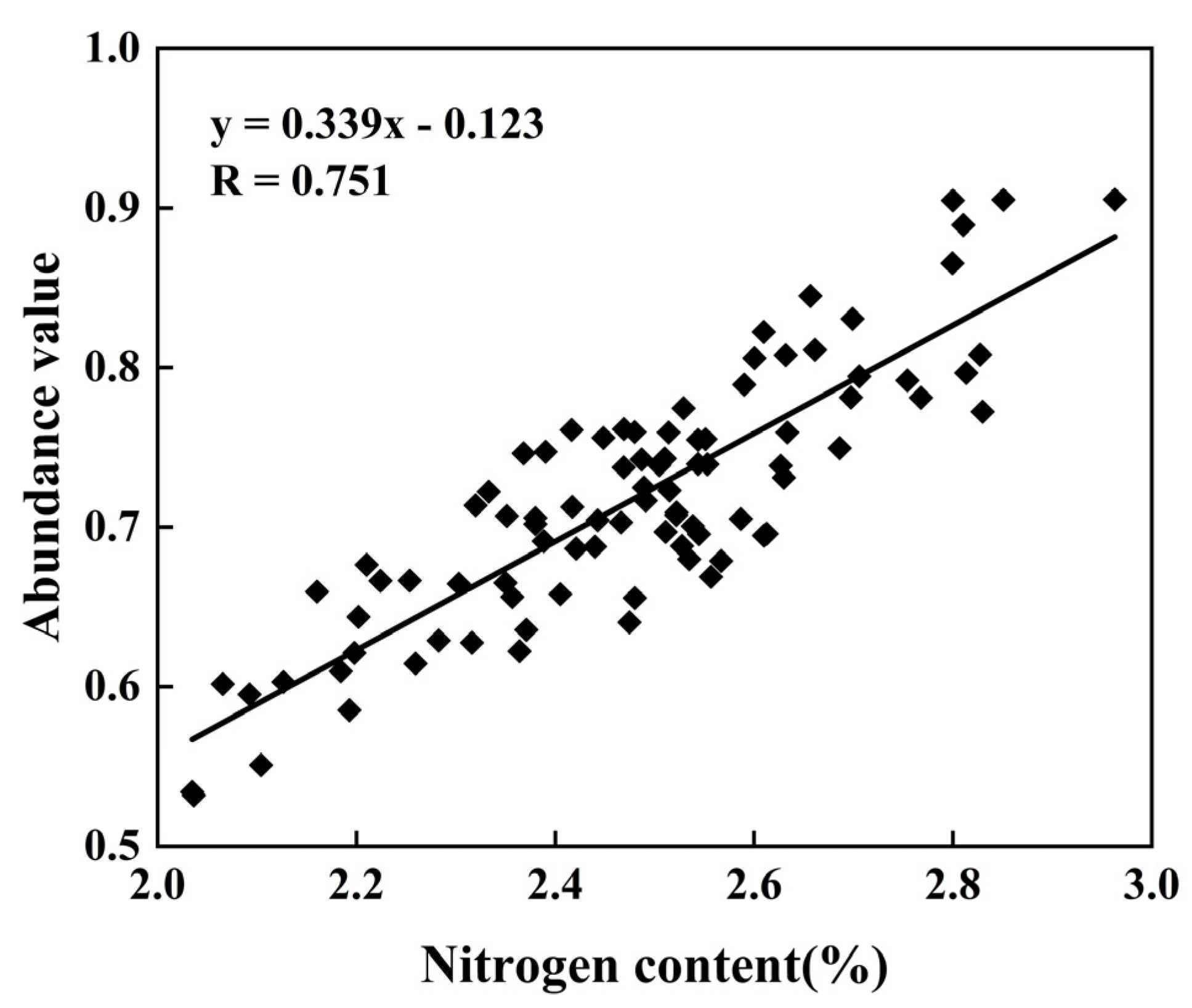
3.5. Construction of Apple Canopy Abundance Parameters Based on Data Fusion
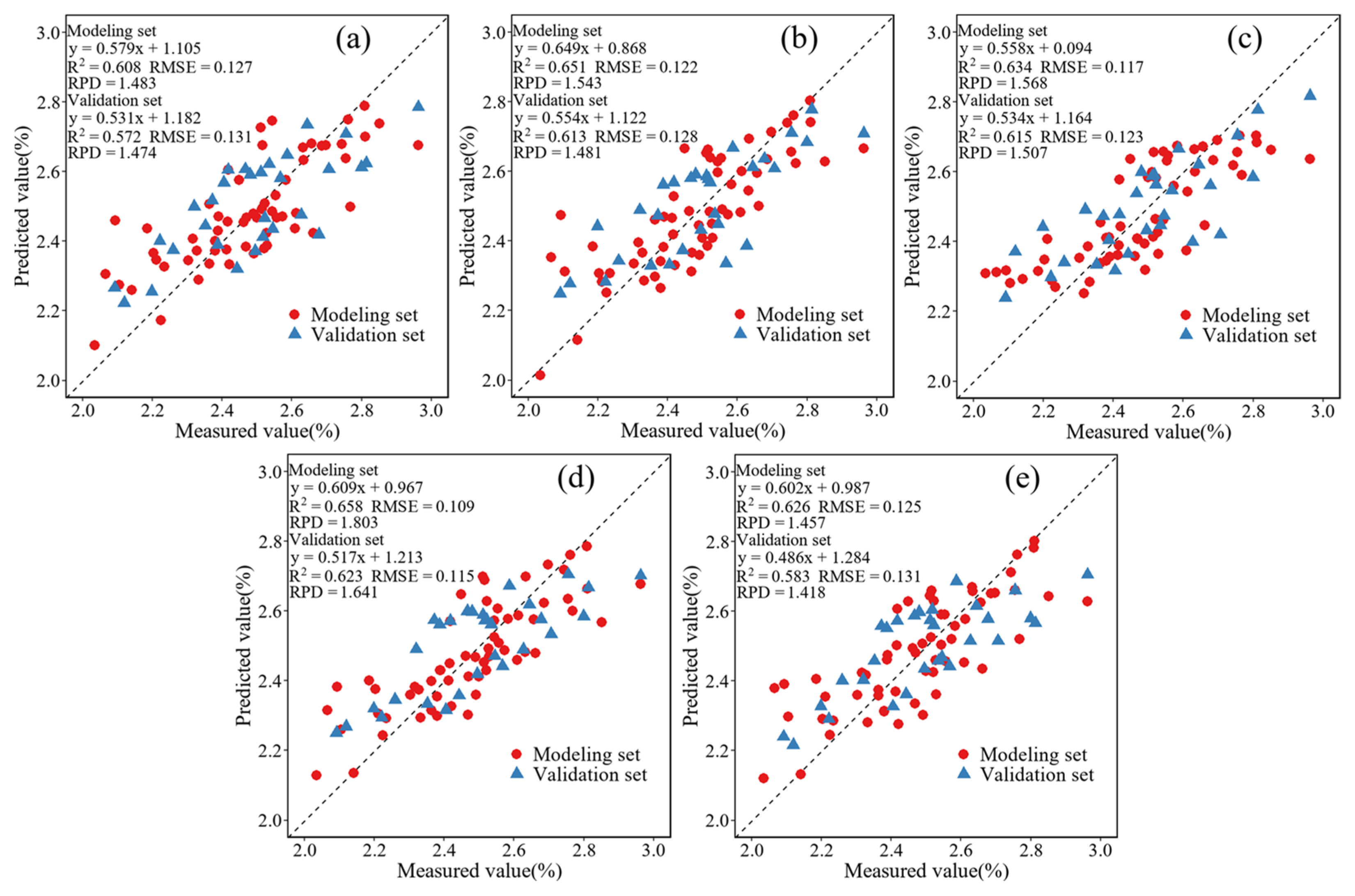
3.6. Selection of the CNC Optimal Inversion Model
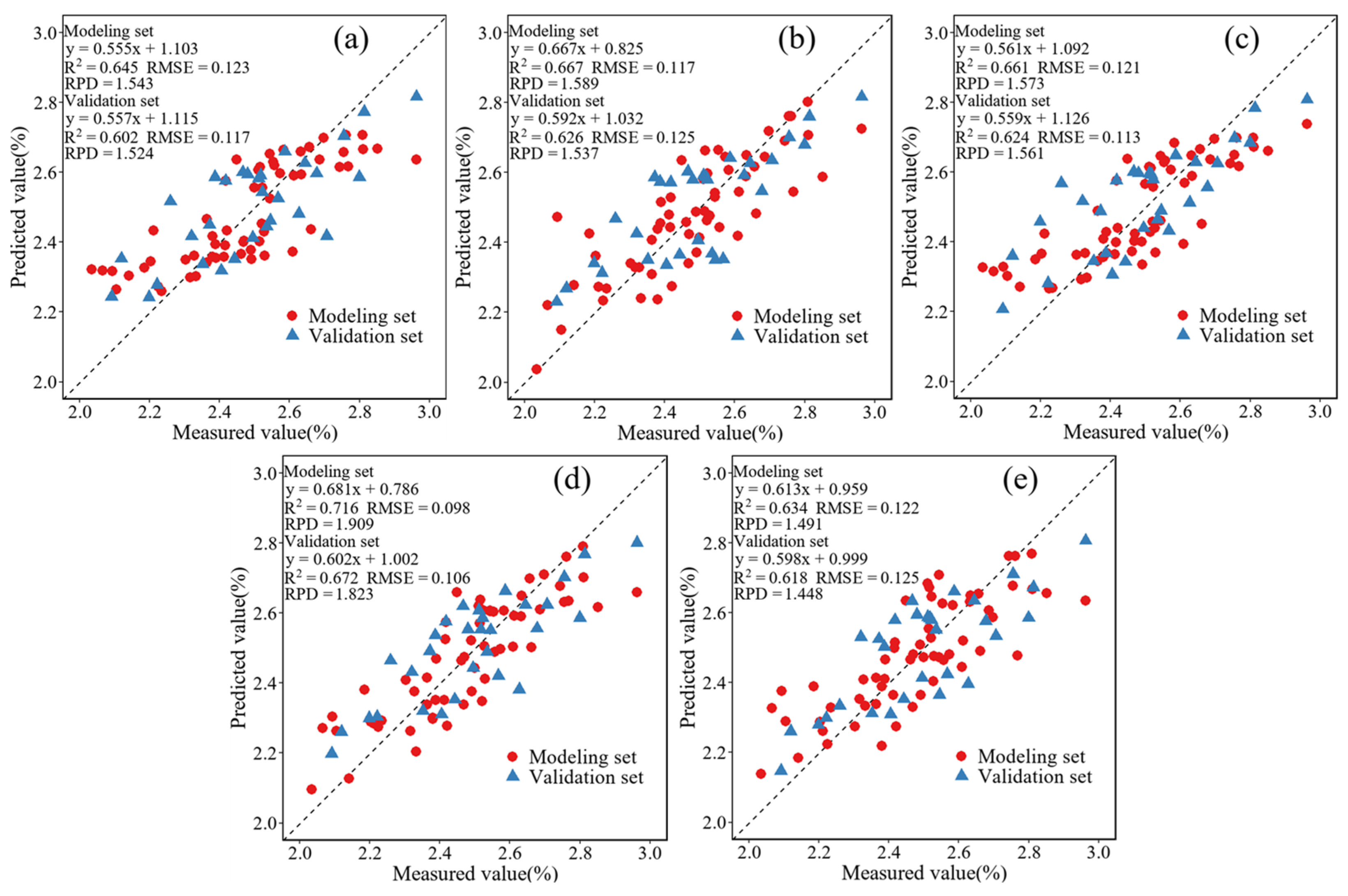
3.6.1. Inversion Model of CNC Based on Raw Multi-Spectral Data
3.6.2. Inversion Model of CNC Based on Simulated Multi-Spectral Data
3.6.3. Inversion Model of CNC Based on Simulated Multi-Spectral Data and Canopy Abundance Parameters
3.7. Spatial Inversion Mapping of CNC Based on Optimal Model
4. Discussion
4.1. Extraction of Spectral Information from Canopy Based on NN-SC
4.2. Ground-Space Remote Sensing Data Fusion Based on SRF-CC
4.3. Construction of Canopy Abundance Parameters Based on Mixed Pixel Decomposition
4.4. Selection of the CNC Optimal Inversion Model
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, S.B.; Yang, G.J.; Jing, H.T.; Feng, H.K.; Li, H.L.; Chen, P.; Yang, W.P. Inversion of winter wheat nitrogen content based on UAV digital image. Trans. Chin. Soc. Agric. Eng. 2019, 35, 75–85. [Google Scholar]
- Meng, X.T.; Bao, Y.L.; Wang, Y.A.; Zhang, X.L.; Liu, H.J. An advanced soil organic carbon content prediction model via fused temporal-spatial-spectral (TSS) information based on machine learning and deep learning algorithms. Remote Sens. Environ. 2022, 280, 113–166. [Google Scholar] [CrossRef]
- Peng, Y.; Zhu, X.; Xiong, J.; Yu, R.; Liu, T.; Jiang, Y.; Yang, G. Estimation of Nitrogen Content on Apple Tree Canopy through Red-Edge Parameters from Fractional-Order Differential Operators using Hyperspectral Reflectance. J. Indian Soc. Remote Sens. 2020, 49, 377–392. [Google Scholar] [CrossRef]
- Chen, S.M.; Hu, T.T.; Luo, L.H.; He, Q.; Zhang, S.W.; Li, M.Y.; Cui, X.L.; Li, H.X. Rapid estimation of leaf nitrogen content in apple-trees based on canopy hyperspectral reflectance using multivariate methods. Infrared Phys. Technol. 2020, 111, 103542. [Google Scholar] [CrossRef]
- Ye, X.J.; Abe, S.; Zhang, S.H. Estimation and mapping of nitrogen content in apple trees at leaf and canopy levels using hyperspectral imaging. Precis Agric. 2020, 21, 198–225. [Google Scholar] [CrossRef]
- Chen, S.M.; Hu, T.T.; Luo, L.H.; He, Q.; Zhang, S.W.; Lu, J.S. Prediction of Nitrogen, Phosphorus, and Potassium Contents in Apple Tree Leaves Based on In-Situ Canopy Hyperspectral Reflectance Using Stacked Ensemble Extreme Learning Machine Model. J. Soil Sci. Plant Nutr. 2022, 22, 10–24. [Google Scholar] [CrossRef]
- Li, W.; Zhu, X.C.; Yu, X.Y.; Li, M.X.; Tang, X.Y.; Zhang, J.; Xue, Y.L.; Zhang, C.T.; Jiang, Y.M. Inversion of Nitrogen Concentration in Apple Canopy Based on UAV Hyperspectral Images. Sensors 2022, 22, 3503. [Google Scholar] [CrossRef]
- Sun, G.Z.; Hu, T.T.; Chen, S.H.; Sun, J.X.; Zhang, J.; Ye, R.R.; Zhang, S.W.; Liu, J. Using UAV-based multispectral remote sensing imagery combined with DRIS method to diagnose leaf nitrogen nutrition status in a fertigated apple orchard. Precis Agric. 2023. [Google Scholar] [CrossRef]
- Wang, L.; Zhao, G.X.; Zhu, X.C.; Wang, R.Y.; Chang, C.Y. Satellite remote sensing inversion of crown nitrogen nutrition of apple at flowering stage. Chin. J. Appl. Ecol. 2013, 24, 2863–2870. [Google Scholar]
- Sankey, J.B.; Sankey, T.T.; Li, J.; Ravi, S.; Wang, G.; Caster, J.; Kasprak, A. Quantifying plant-soil-nutrient dynamics in rangelands: Fusion of UAV hyperspectral-LiDAR, UAV multispectral-photogrammetry, and ground-based LiDAR-digital photography in a shrub-encroached desert grassland. Remote Sens. Environ. 2021, 253, 112–223. [Google Scholar] [CrossRef]
- Qi, G.H.; Chang, C.Y.; Yang, W.; Gao, P.; Zhao, G.X. Soil salinity inversion in coastal corn planting areas by the satellite-uav-ground integration approach. Remote Sens. 2021, 13, 3100. [Google Scholar] [CrossRef]
- Zhou, Y.J.; Liu, T.X.; Batelaan, O.; Duan, L.M.; Wang, Y.X.; Li, X.; Li, M.Y. Spatiotemporal fusion of multi-source remote sensing data for estimating aboveground biomass of grassland. Ecol. Indic. 2023, 146, 109892. [Google Scholar] [CrossRef]
- Sun, M.Y.; Li, Q.; Jiang, X.Z.; Ye, T.T.; Li, X.J.; Niu, B.B. Estimation of Soil Salt Content and Organic Matter on Arable Land in the Yellow River Delta by Combining UAV Hyperspectral and Landsat-8 Multispectral Imagery. Sensors 2022, 22, 3990. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Zhao, G. A Harmonious Satellite-Unmanned Aerial Vehicle-Ground Measurement Inversion Method for Monitoring Salinity in Coastal Saline Soil. Remote Sens. 2019, 11, 1700. [Google Scholar] [CrossRef]
- Wang, D.; Chen, H.; Wang, Z.; Ma, Y. Inversion of soil salinity according to different salinization grades using multi-source remote sensing. Geocarto Int. 2022, 37, 1274–1293. [Google Scholar] [CrossRef]
- Yang, C.; Lv, D.; Jiang, S.; Lin, H.; Sun, J.; Li, K.; Sun, J. Soil salinity regulation of soil microbial carbon metabolic function in the Yellow River Delta, China. Sci. Total Environ. 2021, 790, 148258. [Google Scholar] [CrossRef]
- Yang, L.; Cai, Y.Y.; Zhang, L.; Guo, M.; Li, A.Q.; Zhou, C.H. A deep learning method to predict soil organic carbon content at a regional scale using satellite-based phenology variables. Int. J. Appl. Earth Obs. 2021, 102, 102428. [Google Scholar] [CrossRef]
- Chen, H.Y.; Ma, Y.; Zhu, A.X.; Wang, Z.R.; Zhao, G.X.; Wei, Y.A. Soil salinity inversion based on differentiated fusion of satellite image and ground spectra. Int. J. Appl. Earth Obs. 2021, 101, 102360. [Google Scholar] [CrossRef]
- Chatterjee, S.; Hartemink, A.E.; Triantafilis, J.; Desai, A.R.; Soldat, D.; Zhu, J.; Townsend, P.A.; Zhang, Y.K.; Huang, J.Y. Characterization of field-scale soil variation using a stepwise multi-sensor fusion approach and a cost-benefit analysis. Catena 2021, 201, 105190. [Google Scholar] [CrossRef]
- Fernandez-Guisuraga, J.M.; Verrelst, J.; Calvo, L.; Suarez-Seoane, S. Hybrid inversion of radiative transfer models based on high spatial resolution satellite reflectance data improves fractional vegetation cover retrieval in heterogeneous ecological systems after fire. Remote Sens. Environ. 2021, 255, 112304. [Google Scholar] [CrossRef]
- Al-Ali, Z.M.; Bannari, A.; Rhinane, H.; El-Battay, A.; Shahid, S.A.; Hameid, N. Validation and Comparison of Physical Models for Soil Salinity Mapping over an Arid Landscape Using Spectral Reflectance Measurements and Landsat-OLI Data. Remote Sens. 2021, 13, 494. [Google Scholar] [CrossRef]
- Qi, G.H.; Chang, C.Y.; Yang, W.; Zhao, G.X. Soil salinity inversion in coastal cotton growing areas: An integration method using satellite-ground spectral fusion and satellite-UAV collaboration. Land Degrad Dev. 2022, 33, 2289–2302. [Google Scholar] [CrossRef]
- Shi, J.; Shen, Q.; Yao, Y.; Li, J.; Chen, F.; Wang, R.; Xu, W.; Gao, Z.; Wang, L.; Zhou, Y. Estimation of Chlorophyll-a Concentrations in Small Water Bodies: Comparison of Fused Gaofen-6 and Sentinel-2 Sensors. Remote Sens. 2022, 14, 229. [Google Scholar] [CrossRef]
- Li, M.X.; Zhu, X.C.; Li, W.; Tang, X.Y.; Yu, X.Y.; Jiang, Y.M. Retrieval of Nitrogen Content in Apple Canopy Based on Unmanned Aerial Vehicle Hyperspectral Images Using a Modified Correlation Coefficient Method. Sustainability 2022, 14, 1992. [Google Scholar] [CrossRef]
- Azadnia, R.; Rajabipour, A.; Jamshidi, B.; Omid, M. New approach for rapid estimation of leaf nitrogen, phosphorus, and potassium contents in apple-trees using Vis/NIR spectroscopy based on wavelength selection coupled with machine learning. Comput. Electron. Agric. 2023, 207, 107746. [Google Scholar] [CrossRef]
- Omia, E.; Bae, H.; Park, E.; Kim, M.S.; Baek, I.; Kabenge, I.; Cho, B.K. Remote Sensing in Field Crop Monitoring: A Comprehensive Review of Sensor Systems, Data Analyses and Recent Advances. Remote Sens. 2023, 15, 354. [Google Scholar] [CrossRef]
- Saez-Plaza, P.; Navas, M.J.; Wybraniec, S.; Michalowski, T.; Asuero, A.G. An Overview of the Kjeldahl Method of Nitrogen Determination. Part II. Sample Preparation, Working Scale, Instrumental Finish, and Quality Control. Crit. Rev. Anal. Chem. 2013, 43, 224–272. [Google Scholar] [CrossRef]
- Zhao, H.S.; Zhu, X.C.; Li, C.; Wei, Y.; Zhao, G.X.; Jiang, Y.M. Improving the Accuracy of the Hyperspectral Model for Apple Canopy Water Content Prediction using the Equidistant Sampling Method. Sci. Rep. 2017, 7, 11192. [Google Scholar] [CrossRef]
- Bai, X.Y.; Song, Y.Q.; Yu, R.Y.; Xiong, J.L.; Peng, Y.F.; Jiang, Y.M.; Yang, G.J.; Li, Z.H.; Zhu, X.C. Hyperspectral estimation of apple canopy chlorophyll content using an ensemble learning approach. Appl. Eng. Agric. 2021, 37, 505–511. [Google Scholar] [CrossRef]
- Yang, G.J.; Wan, P.; Yu, H.Y.; Xu, B.; Feng, H.K. Automatic radiation consistency correction for UAV multispectral images. Trans. Chin. Soc. Agric. Eng. 2015, 31, 147–153. [Google Scholar]
- Paliwal, M.; Kumar, U.A. Neural networks and statistical techniques: A review of applications. Expert Syst. Appl. 2009, 36, 2–17. [Google Scholar] [CrossRef]
- Gupta, R.; Nanda, S.J. Cloud detection in satellite images with classical and deep neural network approach: A review. Multimed Tools Appl. 2022, 81, 31847–31880. [Google Scholar] [CrossRef]
- Mann, D.; Joshi, P.K. Evaluation of Image Classification Algorithms on Hyperion and ASTER Data for Land Cover Classification. Proc. Natl. Acad. Sci. India Sect. A Phys. Sci. 2017, 87, 855–865. [Google Scholar] [CrossRef]
- Xu, H.Y.; Huang, W.X.; Si, X.L.; Li, X.; Xu, W.W.; Zhang, L.M.; Song, Q.J.; Gao, H.T. Onboard spectral calibration and validation of the satellite calibration spectrometer on HY-1C. Opt. Express 2022, 30, 27645–27661. [Google Scholar] [CrossRef]
- He, J.; Li, J.; Yuan, Q.; Li, H.; Shen, H. Spatial–Spectral Fusion in Different Swath Widths by a Recurrent Expanding Residual Convolutional Neural Network. Remote Sens. 2019, 11, 2203. [Google Scholar] [CrossRef]
- Shao, Z.F.; Cai, J.J. Remote Sensing Image Fusion With Deep Convolutional Neural Network. IEEE Trans. Geosci. Remote Sens. 2018, 11, 1656–1669. [Google Scholar] [CrossRef]
- Inoue, Y.; Sakaiya, E.; Zhu, Y.; Takahashi, W. Diagnostic mapping of canopy nitrogen content in rice based on hyperspectral measurements. Remote Sens. Environ. 2012, 126, 210–221. [Google Scholar] [CrossRef]
- Wang, L.; Peng, G.; Gregory, S. Individual tree-crown delineation and treetop detection in high-spatial-resolution aerial imagery. Photogramm. Eng. Remote Sens. 2004, 70, 351–357. [Google Scholar] [CrossRef]
- Haboudane, D.; Miller, J.R.; Pattey, E.; Zarco-Tejada, P.J.; Strachan, I.B. Hyperspectral vegetation indices and novel algorithms for predicting green LAI of crop canopies: Modeling and validation in the context of precision agriculture. Remote Sens. Environ. 2004, 90, 337–352. [Google Scholar] [CrossRef]
- Gong, P.; Pu, R.L.; Biging, G.S.; Larrieu, M.R. Estimation of forest leaf area index using vegetation indices derived from Hyperion hyperspectral data. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1355–1362. [Google Scholar] [CrossRef]
- Li, X.C.; Xu, X.G.; Bao, Y.S.; Huang, W.J.; Luo, J.H.; Dong, Y.Y.; Song, X.Y.; Wang, J.H. Remote sensing inversion of leaf area index of winter wheat by selecting sensitive vegetation index based on subsection method. Sci. Agric. Sin. 2012, 45, 3486–3496. [Google Scholar]
- Bian, L.L.; Wang, J.L.; Guo, B.; Cheng, K.; Wei, H.S. Remote sensing extraction of soil salt in Kenli County of Yellow River Delta based on feature space. Remote Sens. Technol. Appl. 2020, 35, 211–218. [Google Scholar]
- Du, M.M.; Li, M.Z.; Noguchi, N.; Ji, J.T.; Ye, M.C. Retrieval of Fractional Vegetation Cover from Remote Sensing Image of Unmanned Aerial Vehicle Based on Mixed Pixel Decomposition Method. Drones 2023, 7, 43. [Google Scholar] [CrossRef]
- Pu, H.Y.; Chen, Z.; Wang, B.; Xia, W. Constrained Least Squares Algorithms for Nonlinear Unmixing of Hyperspectral Imagery. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1287–1303. [Google Scholar] [CrossRef]
- Yang, J.; Du, L.; Cheng, Y.J.; Shi, S.; Xiang, C.Z.; Sun, J.; Chen, B.W. Assessing different regression algorithms for paddy rice leaf nitrogen concentration estimations from the first-derivative fluorescence spectrum. Opt. Express 2020, 28, 18728–18741. [Google Scholar] [CrossRef]
- Chen, X.; Li, F.; Shi, B.; Chang, Q. Estimation of Winter Wheat Plant Nitrogen Concentration from UAV Hyperspectral Remote Sensing Combined with Machine Learning Methods. Remote Sens. 2023, 15, 2831. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, M.; Zhang, Y.; Mao, D.; Li, F.; Wu, F.; Song, J.; Li, X.; Kou, C.; Li, C.; et al. Comparison of Machine Learning Methods for Predicting Soil Total Nitrogen Content Using Landsat-8, Sentinel-1, and Sentinel-2 Images. Remote Sens. 2023, 15, 2907. [Google Scholar] [CrossRef]
- Zhang, J.; Fu, Z.; Zhang, K.; Li, J.; Cao, Q.; Tian, Y.; Zhu, Y.; Cao, W.; Liu, X. Optimizing rice in-season nitrogen topdressing by coupling experimental and modeling data with machine learning algorithms. Comput. Electron. Agr. 2023, 209, 107858. [Google Scholar] [CrossRef]
- Gaston, E.; Frias, J.M.; Cullen, P.J.; O’Donnell, C.P.; Gowen, A.A. Prediction of Polyphenol Oxidase Activity Using Visible Near-Infrared Hyperspectral Imaging on Mushroom (Agaricus bisporus) Caps. J. Agric. Food Chem. 2010, 58, 6226–6233. [Google Scholar] [CrossRef]
- Jiang, H.; Wang, S.; Cao, X.J.; Yang, C.H.; Zhang, Z.M.; Wang, X.Q. A shadow-eliminated vegetation index (SEVI) for removal of self and cast shadow effects on vegetation in rugged terrains. Int. J. Digit. Earth 2019, 12, 1013–1029. [Google Scholar] [CrossRef]
- Liu, X.N.; Jiang, H.; Wang, X.Q. Extraction of mountain vegetation information based on vegetation distinguished and shadow eliminated vegetation index. Trans. Chin. Soc. Agric. Eng. 2019, 35, 135–144. [Google Scholar]
- Kuras, A.; Brell, M.; Rizzi, J.; Burud, I. Hyperspectral and Lidar Data Applied to the Urban Land Cover Machine Learning and Neural-Network-Based Classification: A Review. Remote Sens. 2021, 13, 3393. [Google Scholar] [CrossRef]
- Chang, L.Y.; Li, D.R.; Hameed, M.K.; Yin, Y.L.; Huang, D.F.; Niu, Q.L. Using a Hybrid Neural Network Model DCNN-LSTM for Image-Based Nitrogen Nutrition Diagnosis in Muskmelon. Horticulturae 2021, 7, 489. [Google Scholar] [CrossRef]
- Li, H.J.; Li, J.Z.; Lei, Y.P.; Zhang, Y.M. Diagnosis of nitrogen nutrition in wheat and maize by aerial photography with digital camera. Chin. J. Eco-Agric. 2017, 25, 1832–1841. [Google Scholar]
- Li, C.C.; Chen, P.; Lu, G.Z.; Ma, C.Y.; Ma, X.X.; Wang, S.T. Inversion of nitrogen balance index of typical growth period of soybean based on UAV high-definition digital images and hyperspectral remote sensing data. Chin. J. Appl. Ecol. 2018, 29, 1225–1232. [Google Scholar]
- Youme, O.; Bayet, T.; Dembele, J.; Cambier, C. Deep Learning and Remote Sensing: Detection of Dumping Waste Using UAV. Procedia Comput. Sci. 2021, 185, 361–369. [Google Scholar] [CrossRef]
- Azarang, A.; Kehtarnavaz, N. Image fusion in remote sensing by multi-objective deep learning. Int. J. Remote Sen. 2020, 41, 9507–9524. [Google Scholar] [CrossRef]
- Deng, L.; Mao, Z.H.; Li, X.J.; Hu, Z.W.; Duan, F.Z.; Yan, Y.N. UAV-based multispectral remote sensing for precision agriculture: A comparison between different cameras. Isprs. J. Photogramm. 2018, 146, 124–136. [Google Scholar] [CrossRef]
- Li, M.X.; Zhu, X.C.; Bai, X.Y.; Peng, Y.F.; Tian, Z.Y.; Jiang, Y.M. Remote sensing inversion of nitrogen content in apple canopy based on shadow removal from unmanned aerial vehicle images. Sci. Agric. Sin. 2021, 54, 2084–2094. [Google Scholar]
- Yu, R.; Zhu, X.; Bai, X.; Tian, Z.; Jiang, Y.; Yang, G. Inversion reflectance by apple tree canopy ground and unmanned aerial vehicle integrated remote sensing data. J. Plant Res. 2021, 134, 729–736. [Google Scholar] [CrossRef]
- Guo, L.; Zhang, H.T.; Shi, T.Z.; Chen, Y.Y.; Jiang, Q.H.; Linderman, M. Prediction of soil organic carbon stock by laboratory spectral data and airborne hyperspectral images. Geoderma 2019, 337, 32–41. [Google Scholar] [CrossRef]
- Bao, Y.L.; Ustin, S.; Meng, X.T.; Zhang, X.L.; Guan, H.X.; Qi, B.S.; Liu, H.J. A regional-scale hyperspectral prediction model of soil organic carbon considering geomorphic features. Geoderma 2021, 403, 115263. [Google Scholar] [CrossRef]
- Hao, D.L.; Xiao, Q.; Wen, J.G.; You, D.Q.; Wu, X.D.; Lin, X.W.; Wu, S.B. Research progress of upscaling conversion methods for quantitative remote sensing. Remote Sens. 2018, 22, 408–423. [Google Scholar]
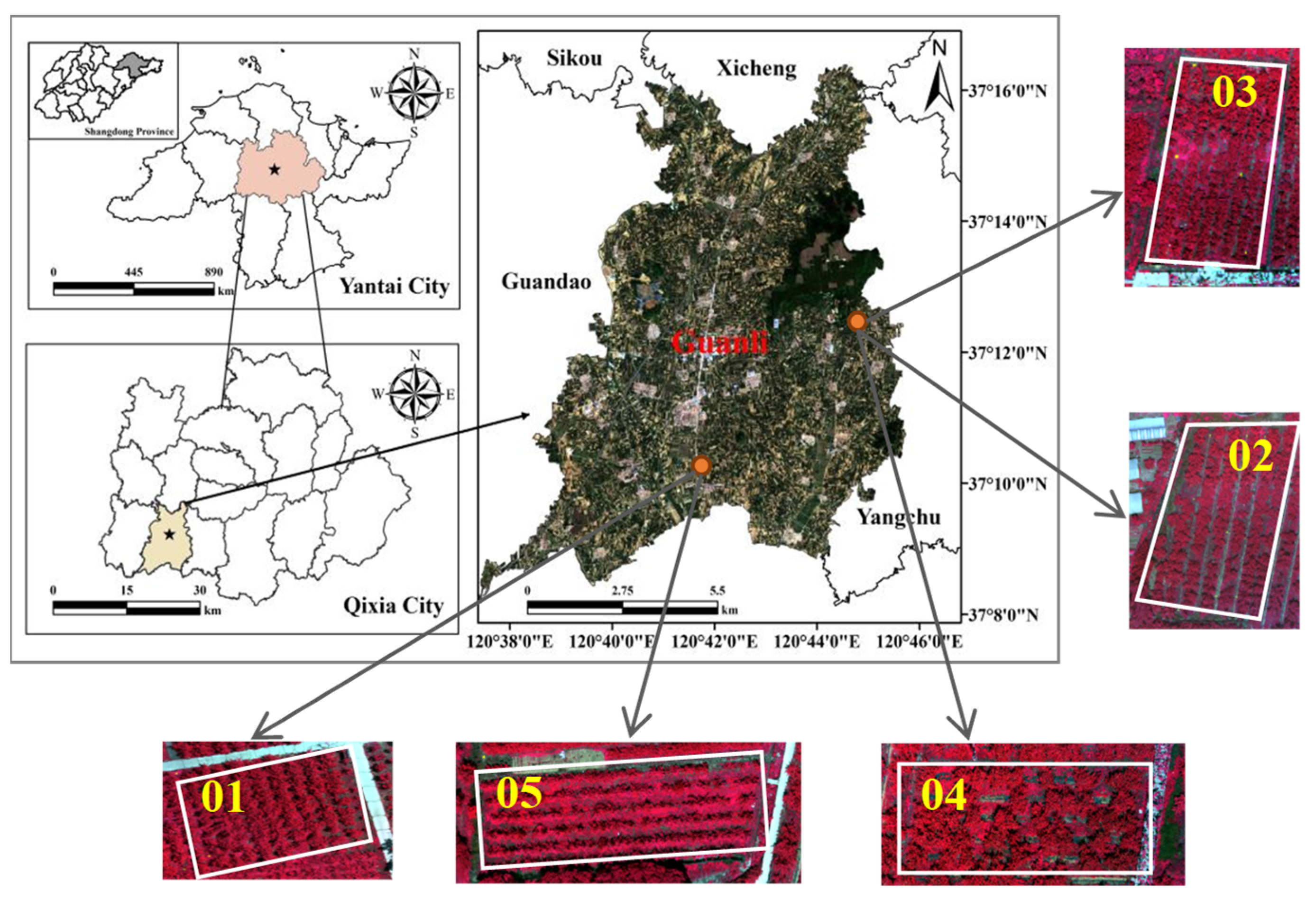









| Dataset | Samples | Max (%) | Min (%) | Avg (%) | SD | CV (%) |
|---|---|---|---|---|---|---|
| Total | 90 | 2.963 | 2.035 | 2.483 | 0.205 | 8.256 |
| Modeling Set | 60 | 2.963 | 2.035 | 2.478 | 0.206 | 8.313 |
| Validation Set | 30 | 2.963 | 2.091 | 2.493 | 0.207 | 8.303 |
| Variable Group | Spectral Feature Parameters | Formula |
|---|---|---|
| Remote sensing bands | G | / |
| R | ||
| REG | ||
| NIR | ||
| Vegetation indices | Difference Vegetation Index (DVI) | |
| Renormalized Difference Vegetation Index (RDVI) | ||
| Soil-Adjusted Vegetation Index (SAVI) | ||
| Transformed Chlorophyll Absorption in Reflectance Index (TCARI) | 3[()0.2()()] | |
| Modified Chlorophyll Absorption in Reflectance Index (MCARI) | [()0.2()]() | |
| Modified Triangular Vegetation Index (MTVI) | 1.2[1.2()2.5()] | |
| Modified Non-Linear Index (MNLI) | (1.51.5)( 0.5) | |
| Optimized Soil Adjusted Vegetation Index (OSAVI) | 1.16()( 0.16) | |
| Improved Simple Ratio Vegetation Index (MSR) | () 1) | |
| Nonlinear Vegetation index (NLI) | ()() |
| Orchard ID | Overlay Accuracy (%) | Kappa Coefficient |
| 01 | 93.410 | 0.888 |
| 02 | 95.132 | 0.905 |
| 03 | 96.371 | 0.923 |
| 04 | 92.968 | 0.861 |
| 05 | 95.763 | 0.897 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, C.; Zhu, X.; Li, M.; Xue, Y.; Qin, A.; Gao, G.; Wang, M.; Jiang, Y. Utilization of the Fusion of Ground-Space Remote Sensing Data for Canopy Nitrogen Content Inversion in Apple Orchards. Horticulturae 2023, 9, 1085. https://doi.org/10.3390/horticulturae9101085
Zhang C, Zhu X, Li M, Xue Y, Qin A, Gao G, Wang M, Jiang Y. Utilization of the Fusion of Ground-Space Remote Sensing Data for Canopy Nitrogen Content Inversion in Apple Orchards. Horticulturae. 2023; 9(10):1085. https://doi.org/10.3390/horticulturae9101085
Chicago/Turabian StyleZhang, Canting, Xicun Zhu, Meixuan Li, Yuliang Xue, Anran Qin, Guining Gao, Mengxia Wang, and Yuanmao Jiang. 2023. "Utilization of the Fusion of Ground-Space Remote Sensing Data for Canopy Nitrogen Content Inversion in Apple Orchards" Horticulturae 9, no. 10: 1085. https://doi.org/10.3390/horticulturae9101085
APA StyleZhang, C., Zhu, X., Li, M., Xue, Y., Qin, A., Gao, G., Wang, M., & Jiang, Y. (2023). Utilization of the Fusion of Ground-Space Remote Sensing Data for Canopy Nitrogen Content Inversion in Apple Orchards. Horticulturae, 9(10), 1085. https://doi.org/10.3390/horticulturae9101085





