Towards a Physiological Modeling of Sweet Cherry Blossom

Abstract

For several years, there has been a need in phenological modeling to better account for physiological processes during the winter dormancy of woody plants, which is here addressed to the sweet cherry cultivar ‘Summit’ (Prunus avium L.). This study compares three sequential phenology models (M1–M3) for the beginning of ‘Summit’ blossom in the experimental sweet cherry orchard in Berlin-Dahlem (Germany) between 2011/12–2019/20 (model development) and 2020/21–2022/23 (model validation). M1 represents an inverse modeling approach where the chilling and forcing requirements of ‘Summit’ were optimized solely from observed flowering data. In contrast, M2 and M3 are more physiologically based as they already incorporate biological knowledge, so that the model parameters were calculated directly within the specified developmental phases. Here, M2 is a two-phase model that considers experimental data for the date of endodormancy release (t₁) of nine years (2011/12–2019/20) to calculate the chilling and forcing requirements. Finally, M3 is a newly developed three-phase model that additionally includes the onset of ontogenetic development (t₁*) and the abscisic acid (ABA) content of ‘Summit’ flower buds during the ecodormancy phase (t₁ − t₁*). The results indicate that the inclusion of ABA-related heat weighting during ecodormancy significantly improves the performance of M3 compared to M1 and M2. While M1 gives satisfactory results in terms of fit and validation, it is considered physiologically unacceptable as it greatly overestimates the chilling requirement of ‘Summit’ by ignoring the ecodormancy phase. M2 accumulates too much heat during ecodormancy as it does not include control by the bud ABA content. The results highlight the need for parameters such as t₁, t₁*, and the bud ABA content for the physiological modeling of ‘Summit’ blossom. To the best of our knowledge, this is the first study to provide a pathway towards a physiologically based modeling approach.

1. Introduction

In process-based phenology models, some relevant model parameters, such as the timing of endodormancy release (t₁) and the onset of ontogenetic development (t₁*), still need to be optimized, as direct observations of these stages are not possible. Experimental studies are required to derive these relevant parameters. The models follow the concept of Lang et al. [1], who divided winter dormancy into the endo- (LF–t₁) and ecodormancy (t₁ − t₁*) phase, although ecodormancy is usually not sufficiently considered in these approaches. In mid- and high latitudes, the establishment of the endodormancy phase (true dormancy) can be related to the date of leaf fall (LF) [2], when the tree has stopped measurable effects of bud growth [3]. When endodormancy is released, i.e., the chilling requirement (C*) of the bud is met, the ecodormancy phase (climatic dormancy) begins. No visible bud development is observed during this phase, as winter temperatures in temperate climates are not sufficient to force bud development. However, in forcing experiments, buds are able to develop until bud burst or flowering. Such experiments have shown that the time taken for buds to develop and start flowering under controlled conditions decreases as ecodormancy progresses [4,5,6]. For the sweet cherry cultivar ‘Summit’, the time to flowering was reduced from 32 days at the beginning of ecodormancy to 13 days at the end of this phase under forcing conditions (~24 °C air temperature, 12 h light, and 70% relative humidity). To our knowledge, this was associated with a decrease in the endogenous abscisic acid (ABA) content of ‘Summit’ flower buds, and is not related to an additional chilling demand [7]. Finally, the resumption of bud growth and bud development at the end of winter is associated with favorable temperatures in the orchard, which are then fully effective to force the development of ‘Summit’ flower buds. However, it should be noted that the ontogenetic development starts some weeks earlier before the bud development of ‘Summit’ becomes visible [7]. Therefore, the timing of t₁* cannot be directly observed in the orchard. The first visible phenological stage is ‘bud swelling’, which is related to an increasing water content in the flower buds of ‘Summit’ [8].

Chuine et al. [9] have provided a comprehensive overview of the different approaches to phenological modeling, which can be broadly divided into pure forcing models (one-phase models) and chilling/forcing models (two-phase models). One-phase models consider only the heat required to force bud development to bud burst or flowering in spring, expressed as the forcing requirement (F*). The onset of heat accumulation is an additional optimized model parameter—here called t₁*. Two-phase models also take the accumulation of chill units into account (chilling requirement, C*), required to release buds from endodormancy at time t₁. The reason why these semi-mechanistic models are widely used is that no experimental work is required apart from the initial data (temperature and phenological observations). All model parameters are optimized on phenological time series. These models are able to calculate plant development for current climatic conditions, often with sufficient accuracy [10]. However, this is no guarantee that the models will continue to make reliable predictions under warmer climatic conditions due to climate change, as the derived model parameters may be physiologically incorrect. Some of the shortcomings of process-based phenology models have been pointed out several times [11,12]. One of the main problems was to find a reliable marker for the date of endodormancy release [11,13], which leads to several problems. For example, in sequential two-phase models, where the termination of the endodormancy phase is an optimized parameter, the timing of t₁ is often assumed to be late, i.e., close to the onset of ontogenetic development [14]. As a result, the chilling requirement of trees is overestimated, so that with rising temperatures due to climate change, the timing of phenological events is estimated too late or, in the worst case, it is assumed that the tree will not sprout or bloom due to an insufficient accumulation of chill units during the endodormancy phase.

For this reason, scientists have suggested for several years that physiological processes should be better considered in phenology models [11,15,16,17,18,19,20]. This requires extensive physiological studies, which are time-consuming, expensive, and probably not feasible for all woody plants. However, in recent years, more and more scientific papers have been published focusing on experimental studies [19,21,22,23,24,25,26], metabolomic pathways [27,28,29], or transcriptomic processes [29,30,31,32,33,34,35,36] in selected plants to gain a deeper understanding of bud dormancy. A prerequisite for all these studies is an accurate knowledge of the timing and duration of the bud development cycle, including the two winter dormancy phases [37], as the ignorance of these phases can also lead to the misinterpretation of experimental results.

The authors of this study have been studying the physiology of ‘Summit’ buds for nine years, identifying the timing and duration of dormancy phases [3,37], analyzing metabolites in ‘Summit’ buds during winter dormancy and at the beginning of ontogenetic development [37], and highlighting the important role of the phytohormone abscisic acid as a biological indicator for the termination of the endodormancy phase [3,7,38,39].

The aim of this study was to compare the performance and physiological accuracy of three sequential phenology models (M1–M3) for the beginning of sweet cherry blossom (cv. ‘Summit’). M1 is a classical two-phase model in which two model parameters—the chilling (C*) and the forcing requirement (F*) of the buds—were optimized using observed flowering data (inverse modeling approach [40]). However, the next two models (M2, M3) already include biological insights, so that the model parameters were calculated directly within the specified development phases. M2 is a physiologically based two-phase model in which the timing of endodormancy release (t₁) was already derived from climate chamber experiments, so that the forcing requirement between t₁ and the beginning of blossom (BB) could be easily calculated without the optimization of this parameter. M3 is a newly developed physiological three-phase model in which the ecodormancy phase (t₁ − t₁*) was considered as a separate phase during which the heat accumulation was suppressed by the ABA content in the flower buds. In M3, the model parameters for the forcing requirement during ecodormancy and during ontogenetic development could also be derived from the observations without model optimization. We hypothesized that model M3 would outperform models M1 and M2 due to the additional physiological insights. To our knowledge, this is the first study that incorporates ABA as a key physiological marker of bud dormancy into a phenological modeling approach.

2. Materials and Methods

2.1. Study Area

The experimental work was carried out in the sweet cherry orchard at Berlin-Dahlem, NE-Germany (52.47° N, 13.30° E, h = 51 m a.s.l.). The orchard (980 m²) was established in autumn 1999 and consisted of 80 cherry trees of the cultivars ‘Regina’, ‘Karina’, and ‘Summit’ (all grafted on Gisela-5 rootstocks and oriented N-S). The average air temperature for the reference period 1991–2020 was 10.4 °C, with an annual precipitation of 562 mm. The main soil type is parabrown with weak traces of light soil (Albic Luvisol).

2.2. Phenological and Meteorological Data

During the 9-year study period, 2011/12–2019/20, detailed phenological observations were made for the sweet cherry cultivar ‘Summit’, starting with ‘total leaf fall’ in autumn (LF) and continuing with the development stages between ‘swollen bud’ and ‘beginning of flowering’ in spring. The focus of this study is the beginning of sweet cherry blossom (‘BBCH-code 60′ [41]). Hourly air temperature data from the agrometeorological station near the orchard were used to calculate the chilling (C*) and forcing (F*) requirements of ‘Summit’ over 9 years in chill portions (CP) and growing degree hours (GDH), respectively. The chill portions were calculated according to Fishman et al. [42,43] (Dynamic Model) without any parameter modifications for sweet cherries [20], and the growing degree hours according to the approach of Anderson et al. [44], which was originally developed for sour cherries (cultivar ‘Montmorency’).

2.3. Physiological Data

For both physiologically based models (M2, M3), the date of endodormancy release (t₁) had to be known (

Table 1. Observed date of endodormancy release (t₁), calculated chilling requirement (C*) in chill portions (CP) between 1 September (244 DOY) and t₁, and beginning of ontogenetic development (t₁*). BB: observed start of ‘Summit’ blossom in the orchard (BBCH 60) in the 2011/12–2019/20 period, x: mean, s: standard deviation, DOY: day of year; all data from [37].

Season	2011/12	2012/13	2013/14	2014/15	2015/16	2016/17	2017/18	2018/19	2019/20	x	s
t1 in DOY	335	332	323	343	328	341	340	333	339	334.9	6.6
C* in CP	42	43	40	40	41	46	49	40	41	42.4	3.1
t1* in DOY	45	85	35	41	61	45	59	45	51	51.9	14.9
BB in DOY	105	116	95	111	111	97	108	99	105	105.2	8.5

). This important date, which cannot be observed in the orchard, was derived from climate chamber experiments [7,37]. Each year between November and December, 2 multi-branched twigs from selected ‘Summit’ trees were cut off weekly and placed in 500 mL plastic flasks filled with water to observe the onset of flowering in a climate chamber at 12 h of light, temperatures of ~20/~15 °C (day/night), and 70% relative humidity. When the twigs began to flower (BBCH 60) under controlled conditions, we had an indication that the chilling requirement had been met at the time of sampling in the orchard. The chilling requirement (C*) for ‘Summit’ was calculated for each season from 1 September (244 DOY) until t₁ (Table 1). On average, 42 ± 3.1 CP were required to release ‘Summit’ flower buds from endodormancy (range 40–49 CP). This was observed on average on 1 December (t₁, 335 DOY ± 6.6 d) with a low annual variability (Table 1). After t₁, all twig samples taken from the orchard were able to flower under forcing conditions in the climate chamber, while the buds in the orchard entered the ecodormancy phase due to the unfavorable winter temperatures outside (mean air temperature T(t₁ − t₁*) = 2.4 °C, range 0.5–5.3 °C, 2011/12–2019/20) and, to our knowledge, due to high ABA levels in the buds [7].

For model M3, it was necessary to know additionally the start of ontogenetic development (t₁*), which occurs 2–4 weeks before the ‘swollen bud’ stage is observed in the orchard. This stage cannot therefore be observed outside, and starts on average on 21 February (52 DOY, Table 1) with a high annual variability (s = 14.9 d). In order to determine t₁*, the water content of the ‘Summit’ flower buds was measured each season between September (previous year) and April (flowering year). During ecodormancy, this value was almost constant at 54%, and only started to increase continuously with rising air temperatures at the end of winter, indicating the beginning of ontogenetic development [3]. The beginning of ‘Summit’ blossom was observed on average on 15 April (105 ± 8.5 DOY, Table 1).

In addition to the data for t₁ and t₁*, the ABA content of the ‘Summit’ flower buds was required for M3. Bud ABA levels were analyzed (Agilent 1290/AB Sciex QTrap 5500 LC-MS/MS) in a targeted assay by Metabolon Inc, 617 Davis Drive, Morrisville, NC 27560 (www.metabolon.com, accessed 6 November 2023), details published in [39]. Flower buds for this assay were weekly collected from ‘Summit’ trees between ‘total leaf fall’ (LF) and ‘open cluster’ stage (OC) in each season, frozen in liquid nitrogen, and stored at −80 °C until lyophilized just prior to analysis [7,39].

2.4. Model Development

2.4.1. Optimized Classical Two-Phase Model M1

Model M1 required the fitting of two parameters. It optimizes the chilling (C*) and forcing (F*) requirement from observed flowering dates (2012–2020), using a simulated annealing algorithm [45,46]. This is an iterative method to find, in an n-dimensional parameter space (n = number of parameters to optimize), the tuple that best fits the observed flowering data. This means that for this combination of parameters, the root mean square error (RMSE) has a minimum. This procedure is described in detail for the ‘PhenoFlex’ model [10], which can be used for an inverse model optimization. However, in the case of only n = 2 parameters (C*, F*), all parameter combinations can be computed in a reasonable time on a personal computer, so that the use of simulated annealing is not mandatory in this case.

The chilling requirement (C*) to release sweet cherry flower buds from endodormancy was optimized from 1 September (244 DOY), as no effective chilling temperatures occurred in August or earlier at the experimental site. The forcing requirement (F*) was then adjusted until the beginning of flowering (Figure 1).

No physiological parameters were considered in this modeling approach. The dashed vertical line in Figure 1 indicates the transition from chilling to forcing, but is not physiologically justified. M1 assumes that the sweet cherry flower buds are released from endodormancy at the end of chilling phase.

2.4.2. Physiologically Based Two-Phase Model M2

For model M2 (Figure 2), only one parameter (F*) had to be calculated, because the timing of t₁ and C* were experimentally derived for each year (Table 1). Therefore, only the annual heat accumulation F(t₁ − BB) was calculated for each season (2011/12–2019/20). The average over 9 years represents the forcing requirement of ‘Summit’ flower buds between endodormancy release and beginning of blossom F*(t₁ − BB).

2.4.3. Physiologically Based Three-Phase Model M3

Beside the timing of t₁ and t₁*, for model M3, two parameters (F*_W, F*) must be known. F*_W(t₁ − t₁*) is the weighted forcing requirement during ecodormancy, and F*(t₁* − BB) the succeeding forcing requirement during ontogenetic development. Both parameters were calculated in model M3 by the mean of the annual forcing accumulation F_W(t₁ − t₁*), F(t₁* − BB) over 9 years (Figure 3).

The heat which is annually accumulated during the ecodormancy phase (t₁ − t₁*) was weighted by the bud ABA content, as ABA is known to regulate bud dormancy [29].

$${\mathrm{F}}_{\mathrm{w}}={\displaystyle \sum _{\mathrm{i}={\mathrm{t}}_1}^{{\mathrm{t}}_1*}{\displaystyle \sum _{\mathrm{j}=1}^{24}{\mathrm{F}}_{\mathrm{j}}}·\left[1-{\mathrm{ABA}}_{{\mathrm{rel}}_{\mathrm{i}}}\right]} \mathrm{in} {\mathrm{GDH}}_{\mathrm{W}}; \mathrm{with} {\mathrm{ABA}}_{{\mathrm{rel}}_{\mathrm{i}}}=\frac{{\mathrm{ABA}}_{\mathrm{i}}}{{\mathrm{ABA}(\mathrm{t}}_1)} , {\mathrm{t}}_1\le \mathrm{i} <{\mathrm{t}}_1^{*}$$

(1)

Instead of conventional growing degree hours (GDH), weighted growing degree hours (GDH_W) were used (Equation (1)). Here, F_j is the accumulated heat in the hour j in GDH, and ${\mathrm{ABA}}_{{\mathrm{rel}}_{\mathrm{i}}}$ the relative ABA content on the day i during ecodormancy. Thus, F_W(t₁ − t₁*) is the annual heat accumulation during ecodormancy in GDH_W, calculated for each individual season.

The use of weighted GDH was supported by the results of a climate chamber experiment in the 2018/19 season [7], in which ‘Summit’ twigs were cut weekly after t₁ in the orchard and placed in a climate chamber under forcing conditions (~24 °C air temperature, 12 h light, and 70% relative humidity) until blossom (BBCH 60). Immediately after t₁, twigs took 32 days (corresponding to ~16,000 GDH) to flower. This time was reduced to 13 days (~7000 GDH) at t₁* as the ABA content in the buds decreased to ~50% of its content at t₁ (Figure 4). The further reduction of ABA between t₁* and the ‘open cluster’ (OC) stage is related to the onset of bud development. From here, ABA is catabolized to abscisic acid glucose ester (ABA-GE), an inactive storage form of free ABA [39,47], as the growth inhibitory function of ABA, manifested during ecodormancy, is no longer required.

The decrease in the bud ABA content between t₁ and OC varied slightly between years (Figure S1), and was approximated in M3 by a linear regression function (

Table 2. Linear regression coefficients (a, b) for the declining relative ABA content (ABA_rel) in ‘Summit’ buds between endodormancy release (t₁) and ‘open cluster’ (OC) stage in each individual season (see Figure S1) and averaged over 9 years (2011/12–2019/20, see Figure 4). a: constant, b: regression coefficient (slope), R²: coefficient of determination, p: significance level for the regression coefficients (t-test).

Season	a	b	R2	p
2011/12	2.9410	−0.0062	0.91	<0.001
2012/13	2.4044	−0.0047	0.89	<0.001
2013/14	2.8191	−0.0053	0.80	<0.001
2014/15	2.9890	−0.0058	0.97	<0.001
2015/16	2.8390	−0.0057	0.95	<0.001
2016/17	3.6243	−0.0076	0.95	<0.001
2017/18	2.2479	−0.0040	0.84	<0.001
2018/19	3.2097	−0.0065	0.96	<0.001
2019/20	1.9284	−0.0029	0.56	<0.001
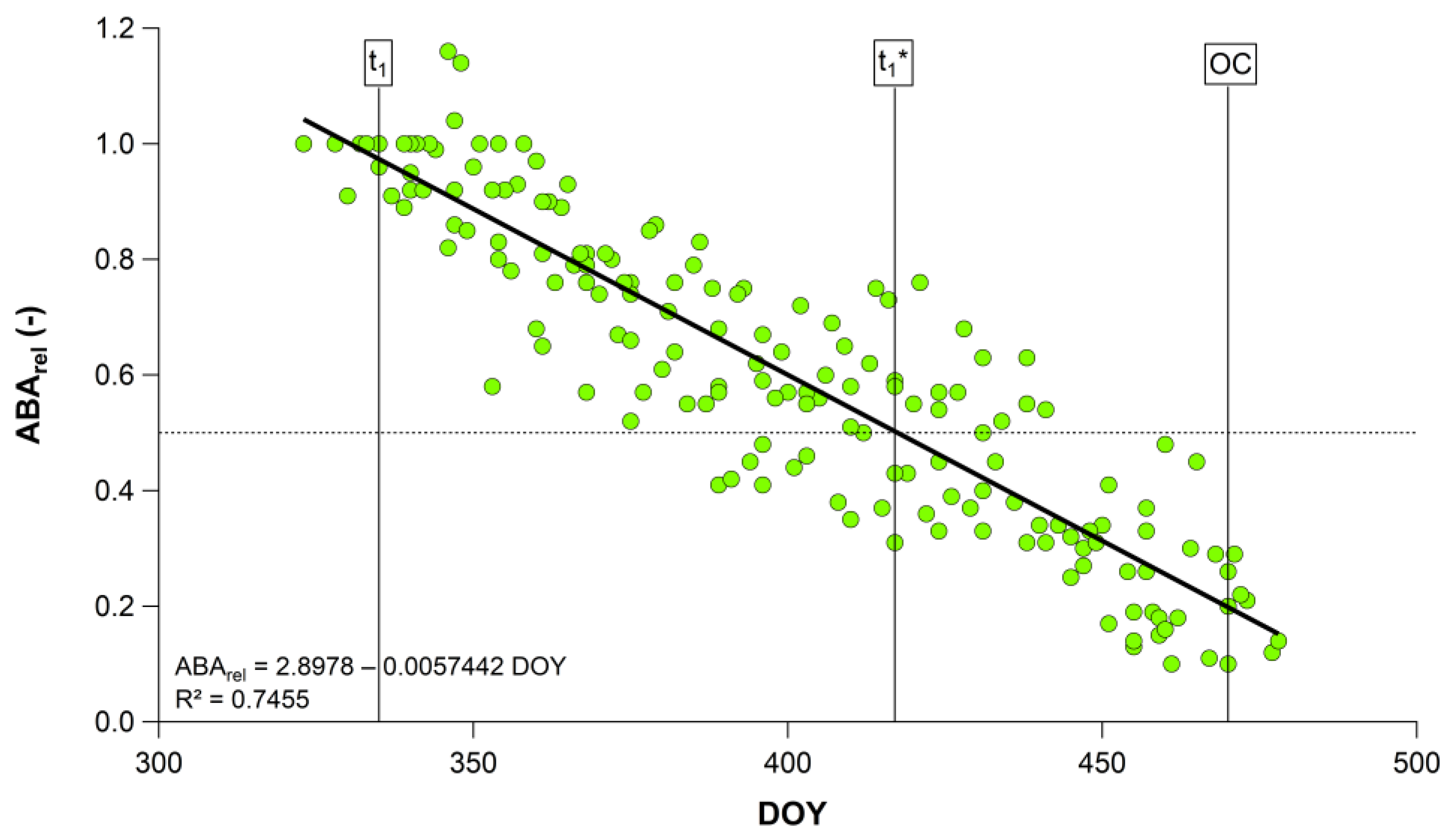
2011/12–2019/20	2.8978	−0.0057	0.75	<0.001

) to obtain daily data of ABA_rel. The regression coefficients were significant (p < 0.001) in all years, but slightly lower in the 2019/20 season (Table 2), which is discussed in Section 4.1. From the beginning of ontogenetic development (t₁*), ABA_rel was set to 0 (Equation (1)), so that from this time on, the heat was accumulated in the conventional GDH (Figure 3).

The annual heat accumulation during ecodormancy in M3 was therefore calculated for each season according to Equation (2).

$${\mathrm{F}}_{\mathrm{W}}={\displaystyle \sum _{\mathrm{i} = {\mathrm{t}}_1}^{{\mathrm{t}}_1*}{\displaystyle \sum _{\mathrm{j}=1}^{24}{\mathrm{F}}_{\mathrm{j}}}·\left[1-\left(\mathrm{a}+\mathrm{b}· {\mathrm{DOY}}_{\mathrm{i}}\right)\right]} \mathrm{in} {\mathrm{GDH}}_{\mathrm{W}}$$

(2)

The forcing requirement in this phase F*_W(t₁ − t₁*) was the mean accumulated heat in n = 9 seasons (Equation (3)).

$${\mathrm{F}*}_{\mathrm{W}}=\frac{1}{\mathrm{n}} {\displaystyle \sum _{\mathrm{k}=1}^{\mathrm{n}}{\mathrm{F}}_{{\mathrm{W}}_{ \mathrm{k}}}} \mathrm{in} {\mathrm{GDH}}_{\mathrm{W}}, \mathrm{n}=9$$

(3)

2.5. Model Validation

Following of our physiological studies between 2011/12 and 2019/20, three additional years were available for model validation (2020/21–2022/23). To validate M1, the optimized parameters for C* and F* were used to calculate the onset of ‘Summit’ blossom for these years. The chilling requirement (C*) had to be met before heat (F*) was accumulated.

Model M2 works in the same way as model M1, with the only exception that the chilling requirement of ‘Summit’ is known in this model. When the buds received C* = 42 CP in all three seasons, we assumed that the buds were released from endodormancy (t₁), and heat accumulation began. For M2, the beginning of ‘Summit’ blossom was the day when the mean forcing requirement F*(t₁ − BB), derived from the 2011/12–2019/20 seasons, was reached for the first time.

For the validation of model M3, the annual reduction in ABA content of the bud must be known for each season. As we had no further ABA measurements for the 3 validation years, we used the average reduction in the ABA_rel content, measured in the 9 seasons (2011/12–2019/20) as an approximation (Figure 4, Table 2). Thus, the annual heat accumulation during the ecodormancy phase was calculated as given in Equation (4).

$${\mathrm{F}}_{\mathrm{W}}={\displaystyle \sum _{\mathrm{i} = {\mathrm{t}}_1}^{{\mathrm{t}}_1*}{\displaystyle \sum _{\mathrm{j}=1}^{24}{\mathrm{F}}_{\mathrm{j}}}·\left[1-\left(2.8978 - 0.0057442· {\mathrm{DOY}}_{\mathrm{i}}\right)\right]} \mathrm{in} {\mathrm{GDH}}_{\mathrm{W}}$$

(4)

The date of endodormancy release (t₁) was the same as in model M2 (C* = 42 CP), and the onset of ontogenetic development (t₁*) was taken as the day when ABA_rel < 0.50, for the first time. From t₁*, the available heat was then calculated in GDH (ABA_rel = 0, Equation (1)). Beginning of blossom (BB) was the first day when the total forcing requirement F*(t₁ − BB) was met (Equation (5)), which is the average forcing requirement over 9 seasons (2011/12–2019/20). GDH* indicates that F*_W(t₁ − t₁*) was calculated in GDH_W and F*(t₁* − BB) in conventional GDH.

$$\mathrm{F}*\left({\mathrm{t}}_1-\mathrm{BB}\right)={\mathrm{F}*}_{\mathrm{W}}\left({\mathrm{t}}_1-{\mathrm{t}}_1*\right)+\mathrm{F}*\left({\mathrm{t}}_1*-\mathrm{BB}\right) \mathrm{in} \mathrm{GDH}*$$

(5)

2.6. Statistical Analysis

The statistical analysis was performed with the IBM SPSS V29 software. The model parameters of M1 were calculated using the simulated annealing algorithm, implemented in a Fortran program [14]. The modeling approach of M2 and M3 was implemented in MS EXCEL (V1808), including the calculation of chill and heat units, to be able to transparently trace the accumulation of these two model parameters in each season. All figures were plotted with IGOR Pro V6.3.7.2.

The model performance was evaluated by the mean absolute error (MAE) and the root mean square error (RMSE) between observed (BB) and calculated (BB_cal) flowering dates (Equations (6) and (7)).

$$\mathrm{MAE}=\frac{1}{\mathrm{n}}{\displaystyle \sum _{\mathrm{k}=1}^{\mathrm{n}}\left|{\mathrm{BB}}_{{\mathrm{cal}}_{\mathrm{k}}}-{\mathrm{BB}}_{\mathrm{k}}\right| } \mathrm{in} \mathrm{d}; \mathrm{n}: \mathrm{number} \mathrm{of} \mathrm{years}$$

(6)

$$\mathrm{RMSE}=\sqrt{\frac{1}{\mathrm{n}} {\displaystyle \sum _{\mathrm{k}=1}^{\mathrm{n}}{\left({\mathrm{BB}}_{{\mathrm{cal}}_{\mathrm{k}}}-{\mathrm{BB}}_{\mathrm{k}}\right)}^2}} \mathrm{in} \mathrm{d}; \mathrm{n}: \mathrm{number} \mathrm{of} \mathrm{years}$$

(7)

3. Results

3.1. Parameter Estimation and Performance of Model M1

The parameter optimization of M1 in the 9-year fitting period (2011/12–2019/20) resulted in a low model error (MAE = 2.4 d, RMSE = 2.6 d) for a combination of C* = 92 CP and F* = 3541 GDH (

Table 3. Parameters of model M1. t₁(92CP): calculated date of endodormancy release t₁ at 92 CP in the flowering year (DOY), annual heat accumulation F(t₁ − BB) in growing degree hours (GDH). Observed (BB) and calculated (BB_cal) start of ‘Summit’ blossom at a forcing requirement of F*(t₁ − BB) = 3541 GDH; Diff = BB_cal − BB in days (d). MAE: mean absolute error, RMSE: root mean square error in d, x: mean, s: standard deviation, cv: coefficient of variation %, DOY: day of year.

Season	t1(92 CP) in DOY	F(t1 − BB) in GDH	BB in DOY	BBcal in DOY	Diff in d
(a) Calculation of model parameters
2011/12	53	3012	105	111	6
2012/13	62	3444	116	116	0
2013/14	38	3645	95	94	−1
2014/15	56	3217	111	113	2
2015/16	38	3278	111	114	3
2016/17	53	3226	97	99	2
2017/18	40	4003	108	106	−2
2018/19	42	3879	99	97	−2
2019/20	40	4165	105	101	−4
x	47	3541	105.2	105.7
s	9.1	401.6	7.1	8.2	MAE = 2.44 d
cv	19.4	11.3	6.7	7.7	RMSE = 2.62 d
(b) Model Validation with C* = 96 CP, F* = 3541 GDH
2020/21	56	3546	110	117	7
2021/22	41	3541	109	107	−2
2022/23	47	3541	112	111	−1
					MAE = 3.33 d
					RMSE = 4.24 d

a). For the 3 validation years (2020/21–2022/23), the MAE and RMSE increased slightly to 3.3 and 4.2 days, respectively (Table 3b).

In order to gain a deeper insight into the optimized model, the timing of endodormancy release (for M1, the date when 92 CP were accumulated from 1 September) and the accumulated heat in each season between t₁ and BB were calculated, retrospectively (Table 3a,b). This additional information allowed a better comparison of the optimized model M1 with models M2 and M3. In M1, the timing of endodormancy release ranged from 38 DOY (7 February 2014, 2016) to 62 DOY (3 March 2013), with a mean date for t₁(92 CP) on 16 February (47 ± 9.1 DOY). The annual accumulated heat (F) between t₁ and BB, which was subsequently also calculated for M2, showed a variability of cv = 11.3%, which should be almost constant for a good model.

3.2. Parameter Estimation and Performance of Model M2

In M2, the annual heat accumulation started from t₁ until BB (Table 1). On average, a forcing requirement of F*(t₁ − BB) = 4471 ± 717 GDH (cv = 16.0%) was necessary to force ‘Summit’ blossom after t₁ (

Table 4. Parameters of model M2. Annual accumulated heat during ecodormancy F(t₁ − t₁*) and ontogenetic development F(t₁* − BB) in growing degree hours (GDH) as well as total heat accumulation between endodormancy release (t₁) and ‘Summit’ blossom F(t₁ − BB), t₁*: beginning of ontogenetic development. Observed (BB) and calculated (BB_cal) start of ‘Summit’ blossom at a forcing requirement of F*(t₁ − BB) = 4471 GDH; Diff = BB_cal − BB in days (d). MAE: mean absolute error, RMSE: root mean square error in d, x: mean, s: standard deviation, cv: coefficient of variation %, DOY: day of year.

Season	F(t1 − t1*) in GDH	F(t1* − BB) in GDH	F(t1 − BB) in GDH	BB in DOY	BBcal in DOY	Diff in d
(a) Calculation of model parameters
2011/12	642	3029	3671	105	112	7
2012/13	645	3315	3960	116	120	4
2013/14	802	3664	4466	95	95	0
2014/15	744	3290	4034	111	114	3
2015/16	2460	3050	5510	111	100	−11
2016/17	312	3378	3690	97	104	7
2017/18	763	3998	4761	108	107	−1
2018/19	711	3848	4559	99	98	−1
2019/20	1900	3685	5585	105	98	−7
x	998	3473	4471	105.2	105.3
s	699.4	343.0	717.2	7.1	8.5	MAE = 4.56 d
cv	70.1	9.9	16.0	6.7	8.1	RMSE = 5.23 d
(b) Model Validation with F*(t1 − BB) = 4471 GDH
2020/21	756	3714	4479	110	111	1
2021/22	1488	3459	4947	109	104	−5
2022/23	1845	3191	5036	112	104	−8
						MAE = 4.67 d
						RMSE = 5.48 d

a). This amount was used to calculate the beginning of blossom (BB_cal) for all nine seasons and subsequently for the model validation (Table 4b).

For a better comparison of the M2 and M3 models, the accumulated heat for the ecodormancy and ontogenetic phase is additionally shown in Table 4, although t₁* was not a model parameter in M2. The results show that large negative deviations between calculated and observed blooming dates were obtained in years when a high amount of heat was available during ecodormancy, and positive deviations in years when a low amount of heat was available during this phase.

Table 4b shows that in 2021/22 and 2022/23 a relatively high amount of heat was also available during the ecodormancy phase (1488, 1845 GDH), which forced ‘Summit’ blossom in M2 to start earlier than observed, by −5 and −8 days, respectively. The MAE and RMSE were in the same range as shown in Table 4a.

3.3. Parameter Estimation and Performance of Model M3

Model M3 used the same data for t₁, t₁*, and BB as in M2. Heat accumulation also started from t₁, when the chilling requirement of the bud was met (Table 1). However, weighted heat units were now calculated during the ecodormancy phase (t₁ − t₁*) according to Equation (2). The relative ABA content in this phase was calculated for each season using the regression functions given in Table 2. At the beginning of ontogenetic development (t₁*), heat accumulation was continued in the conventional GDH until the start of ‘Summit’ blossom (

Table 5. Parameters of model M3. Annual accumulated heat during ecodormancy F_W(t₁ − t₁*) in weighted growing degree hours (GDH_W) and during ontogenetic development F(t₁*-BB) in growing degree hours (GDH). Total heat accumulation F(t₁ − BB) in GDH* (during ecodormancy in GDH_W and during ontogenetic development in GDH). t₁: endodormancy release, t₁*: beginning of ontogenetic development. Observed (BB) and calculated (BB_cal) start of ‘Summit’ blossom at F*(t₁ − BB) = 3679 GDH*; Diff = BB_cal − BB in days (d). MAE: mean absolute error, RMSE: root mean square error in d, x: mean, s: standard deviation, cv: coefficient of variation %, DOY: day of year.

Season	FW(t1 − t1*) in GDHW	F(t1* − BB) in GDH	F(t1 − BB) in GDH*	BB in DOY	BBcal in DOY	Diff in d
(a) Calculation of model parameters
2011/12	183	3029	3212	105	110	5
2012/13	254	3315	3569	116	116	0
2013/14	71	3664	3735	95	94	−1
2014/15	90	3290	3380	111	113	2
2015/16	606	3050	3656	111	111	0
2016/17	17	3378	3395	97	99	2
2017/18	188	3998	4186	108	105	−3
2018/19	93	3850	3943	99	97	−2
2019/20	347	3685	4032	105	102	−3
x	205	3473	3679	105.2	105.2
s	181.4	343.3	327.0	7.1	7.7	MAE = 2.00 d
cv	88.3	9.9	8.9	6.7	7.3	RMSE = 2.29 d
(b) Model Validation with F*(t1 − BB) = 3679 GDH*
2020/21	192	3492	3684	110	110	0
2021/22	422	3459	3881	107	106	−1
2022/23	496	3191	3687	112	111	−1
						MAE = 0.76 d
						RMSE = 0.82 d

).

The calculation of weighted growing degree hours (GDH_W) during ecodormancy significantly reduced the forcing requirement in this phase. Instead of F*(t₁ − t₁*) = 998 GDH in M2 (Table 4a), now only F*_W(t₁ − t₁*) = 205 GDH_W were calculated in M3 (Table 5a). However, the coefficient of variation of the accumulated heat during ecodormancy was even higher in M3 (cv = 88.3%) compared to M2 (cv = 70.1%). The strong heat accumulation of M2 in the 2015/16 and 2019/20 seasons (F = 2460 GDH and F = 1900 GDH, respectively) during ecodormancy (Table 4a) was significantly reduced in M3 by 75% and 82%, respectively. According to this approach a total forcing requirement of F*(t₁ − BB) = 3679 ± 327 GDH* is required until ‘Summit’ blossom. Interestingly, the annual variability of the total accumulated heat between endodormancy release and beginning of blossom (t₁ − BB) was reduced from cv = 16.0% in M2 (Table 4a) to only cv = 8.9% in M3 (Table 5a). MAE and RMSE were also reduced by more than 50% in M3, compared to M2, and were also lower than in M1. This improved model performance was achieved by considering the annual ABA content in the buds during ecodormancy. The high deviations between observed and calculated flowering dates in M2, especially in 2015/16 and 2019/20, were greatly reduced from −11 to 0 days and from −7 to −3 days, respectively. The difference between the BB_cal and BB of 5 days in 2011/12 could probably be the result of a slightly inaccurate observation of BB in the first year of our experimental work, as even the optimized model M1 was not able to match the observed flowering date sufficiently.

The approximations used in M3 for t₁ (C* = 42 CP) and t₁* (ABA_rel < 0.50), and the application of Equation (4) to calculate the ABA reduction during ecodormancy in the three validation years also gave acceptable results with absolute errors between observed and calculated flowering dates of maximum 1 day (Table 5b).

4. Discussion

4.1. Physiological Parameters Used for Modeling

To the best of our knowledge, this is the first study to provide a route to a physiologically based modeling approach for sweet cherry blossom based on physiological and molecular data. The relevant parameters for t₁ and t₁*, which cannot be observed in the orchard, were derived from the experiments, so that it was possible to calculate the chilling and forcing requirements of the buds within the relevant phases. In order to determine the dates for t₁ and t₁*, a careful experimental design is required. Endodormancy is released when the flower buds regain the ability to grow and develop. A shortcoming of these experiments is that the time to bud break or flowering was sometimes limited to a short period, e.g., 8–10 d (references in [7]). This assumption is still based on classical dormancy release experiments where no distinction was made between endo- and ecodormancy ([48,49] and references therein). On the other hand, in a recently published study [50], a period of three weeks was used to determine the time of endodormancy release in Prunus mume, which was probably sufficient for this cultivar.

An alternative method of estimating the date of endodormancy release (t₁) in a relatively short period of forcing conditions was presented by Fadón et al. [51]. The time of t₁ was considered as the date when the weight of the flower buds in the climate chamber increased by at least 30% within 7 days. The chilling requirements of the four sweet cherry cultivars studied ranged from 32 ± 4 to 49 ± 2 CP, in agreement with our value for ‘Summit’ (42 CP). In order to find the onset of ontogenetic development, the timing of male meiosis was studied, which starts up to 2 weeks before the flower bud weight increases in the field. This allowed the dormancy phase to be divided into ecodormancy (chilling–male meiosis) and ontogenetic development (male meiosis–full bloom), during which the buds show active growth until full bloom (FB). However, it is questionable whether t₁* could be determined more easily by changes in bud water content than by microscopic methods [8].

Meanwhile, it is known from several studies that twigs, taken from trees in the field and then brought to bud break or flowering under controlled conditions, required a long time, which can be equated to a high heat requirement, before a clear bud response was observed. This time gradually decreased during ecodormancy [4,5,6], which can now be explained for ‘Summit’ by the decreasing bud ABA content. Since the ABA content in the buds during ecodormancy was not considered in the classical chilling/forcing experiments, it was assumed that endodormancy had not yet been broken. Accordingly, it was assumed that a further accumulation of chill units would be required before visible bud development resumed after optimal forcing conditions of 8–10 days. Recently, it has been shown for ‘Summit’ cherry trees that this occurs in the orchard almost at the beginning of ontogenetic development, when bud ABA levels are reduced by 50% during ecodormancy [7]. The agreement of the results of these probably incorrectly conducted chilling/forcing experiments with the results of purely optimized chilling/forcing models, such as M1, led to the fact that ecodormancy could not be detected in either experiments or phenology models. Unfortunately, this stage cannot be observed as there are no visible morphological or developmental changes in the bud [23]. This study has confirmed that the consideration of the bud ABA content during ecodormancy significantly improves the modeling results, which provides further evidence that ABA controls the bud development during this phase.

Our experimental findings were additionally confirmed by the course of relevant metabolites, which were detected in the ‘Summit’ flower buds. The timing of t₁ was mainly confirmed by the beginning of a continuous decrease in the ABA content of the buds [39], which can also be seen in Figure 4. Figure S1 shows that in almost all years, ABA_rel decreased after t₁ to 0.1–0.3 at OC. The only exception was the season 2019/20, where ABA_rel was 0.73 at t₁* and still 0.59 at OC. Interestingly, this was the mildest winter of all nine seasons, without a single day with a mean daily air temperature below 0 °C. The mean air temperature during ecodormancy was 2.9 °C above average. It is therefore possible that the higher ABA content in this season was necessary to protect the buds against early budbreak. Further research, especially in warmer (subtropical) regions, is needed to prove this hypothesis, as these regions already have much higher winter temperatures today. Therefore, it would be interesting to study bud ABA levels of subtropical tree species in chilling/forcing experiments [52].

During the ecodormancy phase, the energy metabolism in the form of glycolysis and the tricarboxylic acid cycle was significantly reduced in ‘Summit’ [37]. Accordingly, the onset of ontogenetic development (t₁*) was closely related to the up-regulation of the carbohydrate metabolism, as confirmed by a decrease in chrysin content in ‘Summit’ flower buds and an increase in arabonic and pentose acids. This shows that the experimentally derived parameters for t₁ and t₁* are supported by other physiological processes within the sweet cherry bud.

4.2. Model Comparison

Model M1 represents a common sequential modeling approach in phenology, which is based on the optimization of two model parameters (C*, F*) using phenological observations [10,53,54,55,56,57,58]. This inverse modeling approach can, however, lead to unrealistic parameter estimations, as discussed in [14,59]. Model M1 only considers the physiological background that fruit tree buds have a cultivar-specific chilling and forcing requirement until the beginning of flowering, which is optimized within the model. The aim of the optimization process is to find a model that best fits the observations, not a model that is physiologically sound.

The results of model M1 were to be expected. As the model has no information on the timing of the eco- and endodormancy phase, chilling was accumulated in the model until the end of winter, before temperatures became increasingly effective for bud development. This explains why the optimized chilling requirement in M1 (C* = 92 CP) was 119% higher than the experimentally derived chilling requirement for ‘Summit’ (C* = 42 CP). An average of 92 CP was reached on 16 February (47 ± 9.1 DOY, Table 3a), which corresponds to the beginning of ontogenetic development on 21 February (52 ± 14.9 DOY) in Berlin-Dahlem (Table 1). The reason for this is that the ecodormancy phase was not captured by M1, because the favorable temperatures for bud development, that actually occurred during ecodormancy, were not effective due to the high ABA levels in the buds, as shown in model M3. This would not be the main shortcoming of this model, as only a small part of the heat that occurs during ecodormancy is actually relevant to bud development. A good example was the 2015/16 season, where only 606 GDH_W (M3, Table 5a) out of 2460 GDH (M2, Table 4a) were effective to force bud development. However, the total overestimation of the bud chilling requirement in M1 is fatal. This demonstrates the limitations of purely statistical methods for determining the chilling and forcing periods of tree species [60,61], as these methods are unable to detect the ecodormancy phase. As a result, either the estimated chilling requirement, especially in temperate continental climates [62], or the forcing requirement in Mediterranean climates [63] may be too high.

In summary, model M1 fitted the phenological data very well, with an acceptable RMSE of 2.6 days for the optimization period and 4.2 days for the validation period. However, from a physiological point of view, M1 is rather a one-phase model than a two-phase model, because the optimized value for C* is physiologically incorrect, and represents approximately the start of heat accumulation from t₁* rather than the time of endodormancy release. Consequently, this model cannot be used to estimate shifts in the timing of cherry blossoming due to climate change.

Model M2 is similar to M1 in that it also starts heat accumulation when the chilling requirement of the bud is met. However, for M2, the chilling requirement (on average C* = 42 CP) and thus the end of endodormancy (t₁ = 335 DOY) was physiologically confirmed. This allowed to calculate the heat, required to force ‘Summit’ blossom from t₁ to BB, directly, which for ‘Summit’ was F*(t₁ − BB) = 4471 GDH. Assuming that in an accurate phenology model, the forcing requirement between t₁ and BB should be nearly constant in each year, the coefficient of variation (cv) should be minimal. However, the coefficient of variation for the annually accumulated heat between t₁ and BB was cv = 16.0%, even higher than in M1 (11.3%). This indicates that something must be wrong with modeling approach M2. The weakness of the model became apparent when the accumulated heat between t₁ and BB was split into the two relevant phases, ecodormancy and ontogenetic development. The annual heat required to force ‘Summit’ blossom from t₁* was relatively constant: F*(t₁* − BB) = 3473 GDH, cv = 9.9%. However, the heat accumulated during ecodormancy F*(t₁ − t₁*) = 998 GDH was highly variable (cv = 70.1%, Table 4a), ranging from 312 GDH in 2016/17 to 2460 GDH in 2015/16. Especially during the mild winters of 2015/16 and 2019/20, a lot of heat was accumulated in this phase (2460 GDH and 1900 GDH, respectively), which was probably not relevant for bud development. As a result, the beginning of ‘Summit’ blossom in 2016 and 2020 was calculated too early by −11 and −7 days, respectively. However, a later onset of ‘Summit’ blossom than observed (+7d) was calculated by M2 when a relatively small amount of heat was accumulated between t₁ and t₁* (312 GDH in 2016/17 and 642 GDH in 2011/12). This indicates a systematic bias of M2, which is related to the heat accumulation during ecodormancy.

In a previously cited study [51], forcing temperatures were assumed to be fully effective between t₁ and full bloom (FB), in agreement with the assumption in M2. As a result, very high forcing requirements were calculated for sweet cherry cultivars up to FB, ranging from 6969 ± 728 to 9528 ± 894 GDH, which are probably too high. Under the warmer climatic conditions of Zaragoza (Spain), compared to Berlin (Germany), especially in the cold years, a higher variability of accumulated heat between t₁ and FB was found, with an annual variability between cv = 7% (only one cultivar) and cv = 14–16% (three cultivars), which is similar to the variability found in M2 (cv = 16%).

In summary, M2 showed a high annual variability of the accumulated heat between t₁ and BB, although the timing of t₁ was known. This is reflected in the high RMSE of 5.2 days for the years of model development and the RMSE of 5.5 days for model validation. Since the accumulated heat between t₁* and BB was already relatively constant (cv = 9.9%, Table 4a), it is obvious that the accumulation of heat during ecodormancy needs to be better represented in M2. This means that knowing t₁ alone is not sufficient for a physiological modelling approach.

Model M3 was most physiologically based, as it included the ABA content in the buds during ecodormancy in addition to t₁ and t₁*. As a result, the annual variability of the total forcing requirement between t₁ and BB decreased from 16.0% in M2 (Table 4a) to 8.9% in M3 (Table 5a). This occurred even though the variability of heat available during ecodormancy had increased from cv = 70.1% in M2 to cv = 88.3% in M3. This indicates that the accumulated heat during ecodormancy, which was weighted by the ABA content in the buds in M3, was effective in fine-tuning the total forcing amount until ‘Summit’ blossom of F*(t₁ − BB) = 3679 GDH*, cv = 8.9%. On average, only ~20% of the heat available during ecodormancy actually forced bud development (998 GDH in M2, 205 GDH_W in M3). This result was finally confirmed by the model validation, and shows that the sequential modeling approach leads to plausible results when biological reality is included in the model. The modeling approach confirms that during ecodormancy, the buds gradually recover their growth capacity [2], which is fully present towards the end of this phase, i.e., with the beginning of ontogenetic development.

In summary, it can be stated that M3 solved the problem of too high forcing accumulation during ecodormancy which still occurred in M2. It shows that the ABA content in the ‘Summit’ buds depresses the bud development time-dependedly during the course of the ecodormancy phase. The model showed the lowest RMSE of all three approaches (RMSE = 2.3 d for model development, RMSE < 1 d for model validation). This result confirmed our hypothesis that the physiological modeling approach M3 is superior to the classical approach M1 and even to model M2, due to the additional physiological insights.

5. Conclusions

This study highlights the need for phenological models to include physiological aspects of bud development. Ignoring or misinterpreting the ecodormancy phase may have significant implications for estimating the chilling requirements of fruit trees and the timing of sweet cherry blossom under changed climate conditions. The results show that the timing of t₁ and t₁*, and the bud ABA level during ecodormancy are essential parameters for a physiological modeling approach.

It is likely that ecodormancy in other perennials is also controlled by bud ABA levels. We therefore suggest that the bud ABA levels of a range of trees species should be investigated to see if processes similar to those in ‘Summit’ trees occur. The modeling of bud ABA levels and their dynamics is necessary in order to include bud ABA levels in phenological models in the future. First investigations in this direction have been proposed [25,35,64].

In addition, we would like to emphasize the need for multi-year data in physiological studies related to phenology modeling, although this is challenging and rather exceptional when considering metabolites. In this study, this was the only way to identify the influence of weather variability on bud metabolism in sweet cherry.

This study also highlights the limitations of purely optimized phenology models in terms of the derived model parameters and the conclusions that can be drawn from them. As the ecodormancy phase at the study site lasts on average 82 days [37], there is a large scope for misinterpretation of the biological processes during this phase, which was clearly demonstrated with model M1. This is also possible when phenological modeling approaches are applied to large-scale phenological datasets, without consideration of any physiological processes [58]. The optimization of parallel models [9], not considered in this study, also has a wide range of parameter adjustments during ecodormancy, although the biological reality is not guaranteed. This study shows that phenological modeling cannot progress without incorporating deeper physiological knowledge.

It should also be noted that the investigations in this study could only be carried out on the sweet cherry cultivar ‘Summit’, grown in Berlin-Dahlem. However, the limitation only to ‘Summit’ has allowed a deeper understanding of the dormancy phases of this ‘model plant’. Although this study does not present a universally applicable model for the onset of sweet cherry blossom, it points the way forward for the development of reliable and physiologically based phenology models, away from the simple statistical methods which are still in use.