Prediction Models for the Plant Coverage Percentage of a Vertical Green Wall System: Regression Models and Artificial Neural Network Models
Abstract
:1. Introduction
2. Materials and Methods
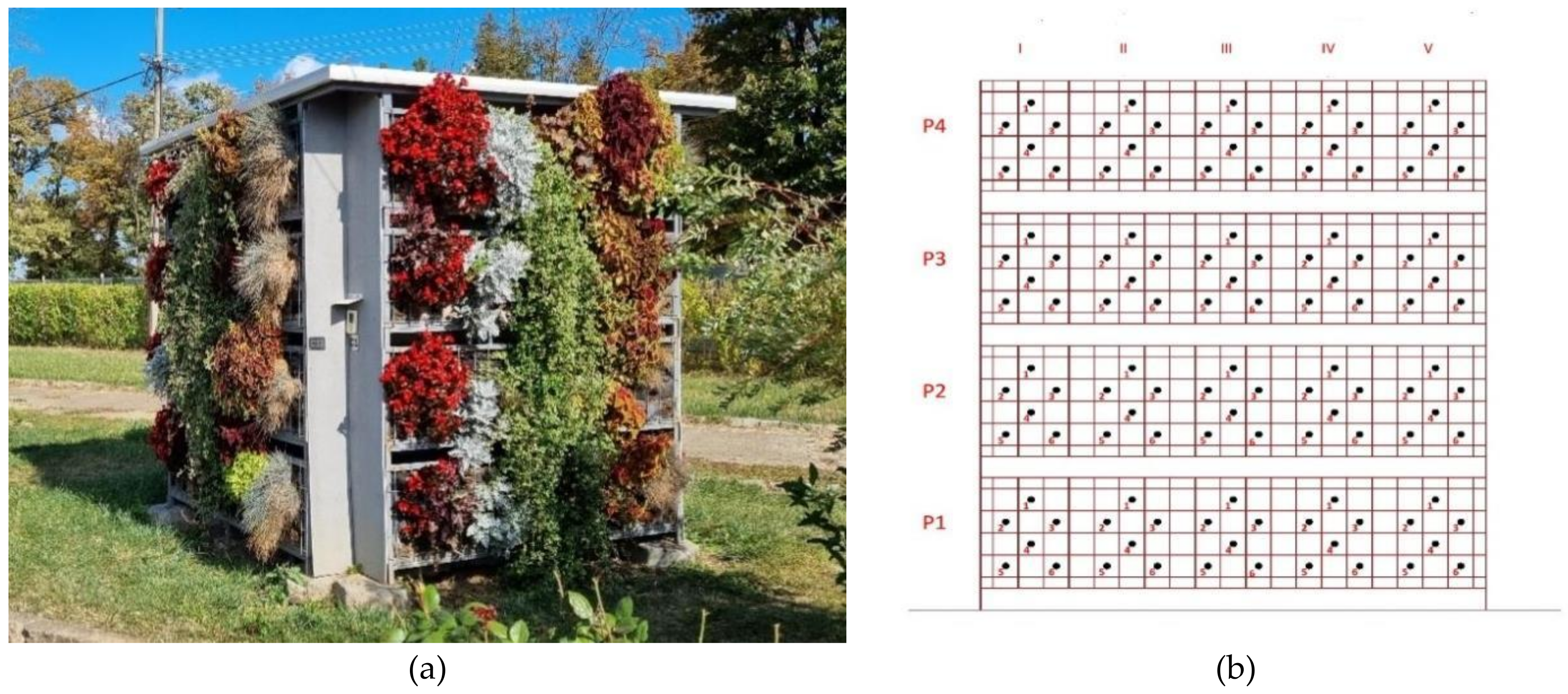
2.1. Experimental Site and Plant Materials
2.2. Measurements
2.3. Model Development
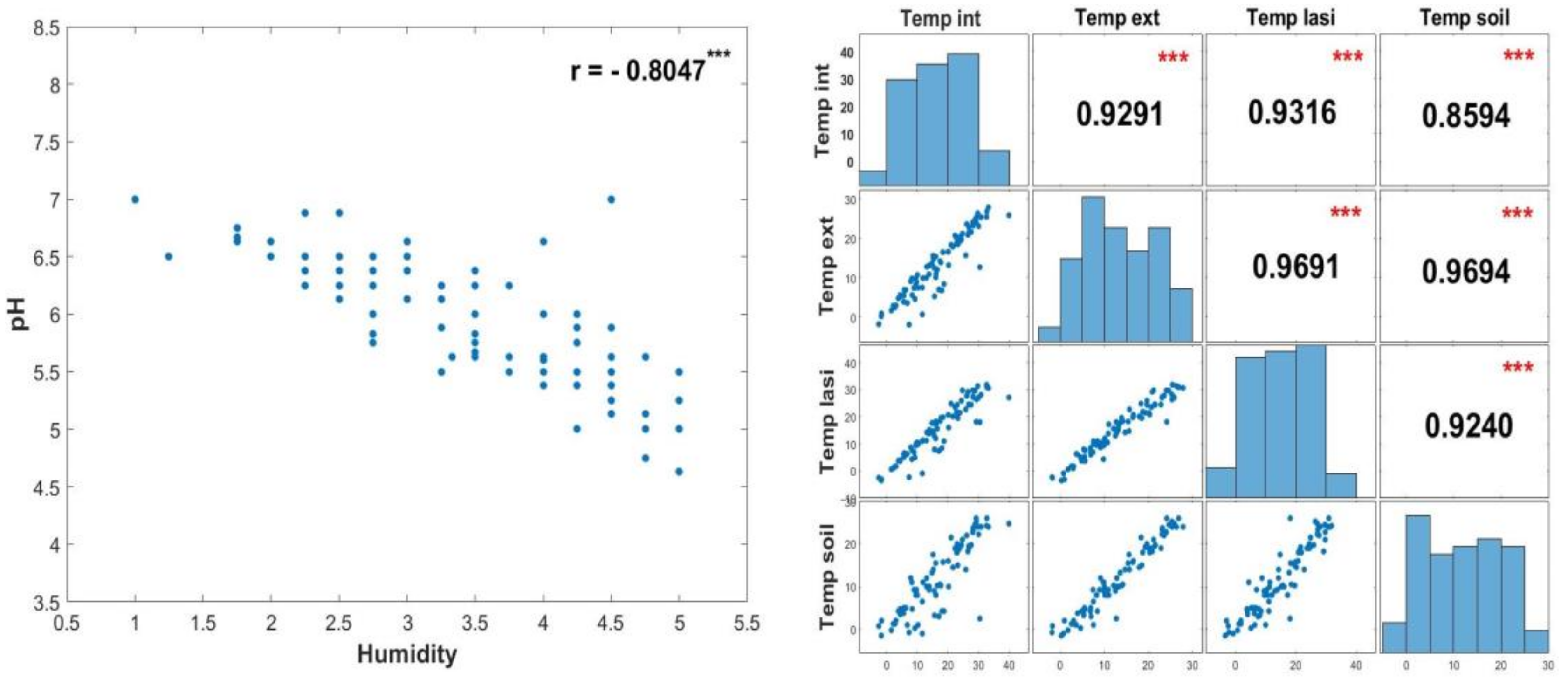
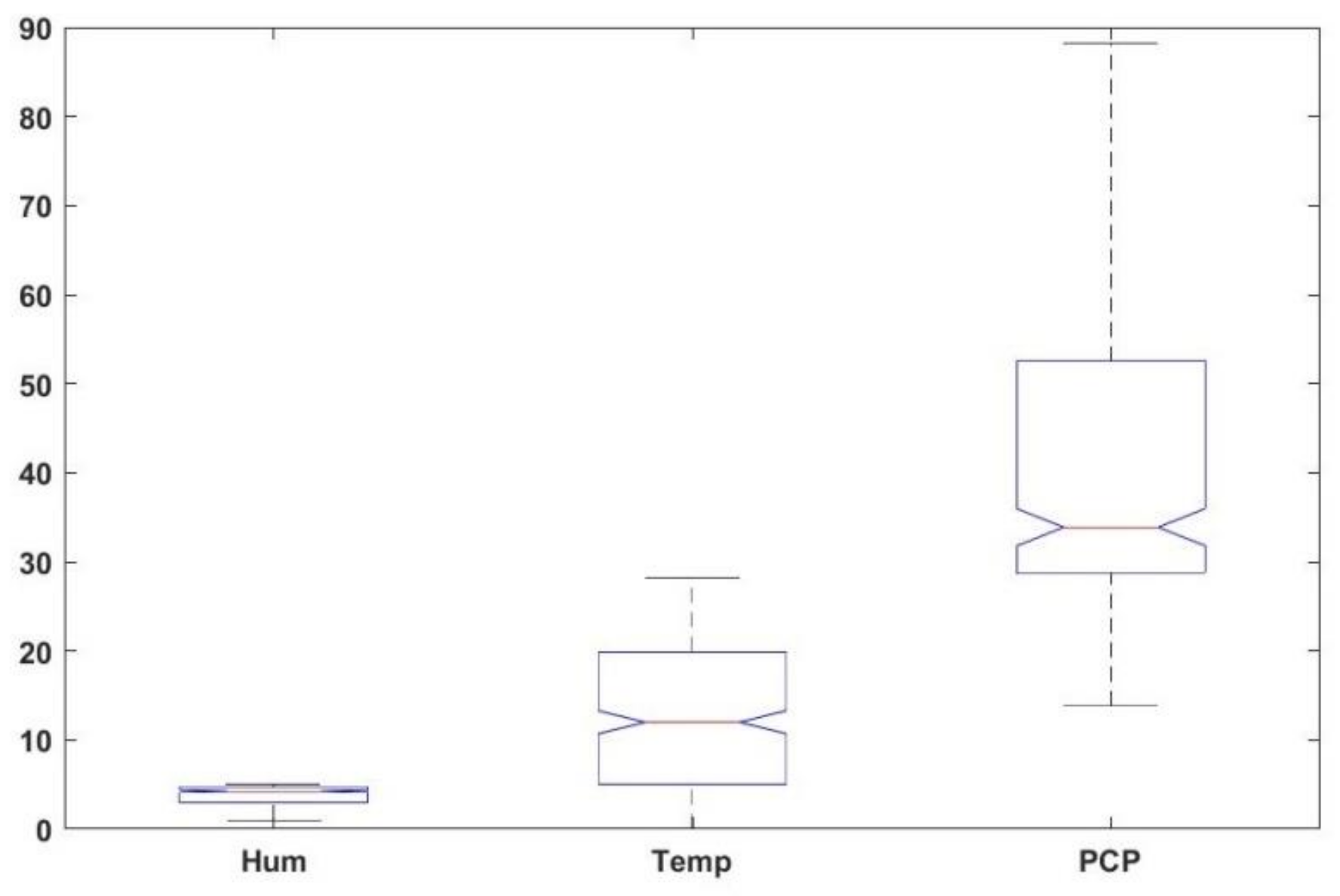
2.3.1. Data Preprocessing
- The variable Hum, representing the soil humidity on a façade of the experimental module;
- The variable Temp, representing the soil temperature on a façade of the experimental module;
- The variable WkNo (week number), which keeps track of the time of the year when the data were recorded. It was coded to take values from 1 (the first week of January) to 52 (the last week of December).
- The variable Side represents the façade of the experimental module where the plants are grown. It could be N, E, S, or W, which are codified here as 1, 2, 3, and 4, respectively.
2.3.2. Multiple Linear Regression (MLR)
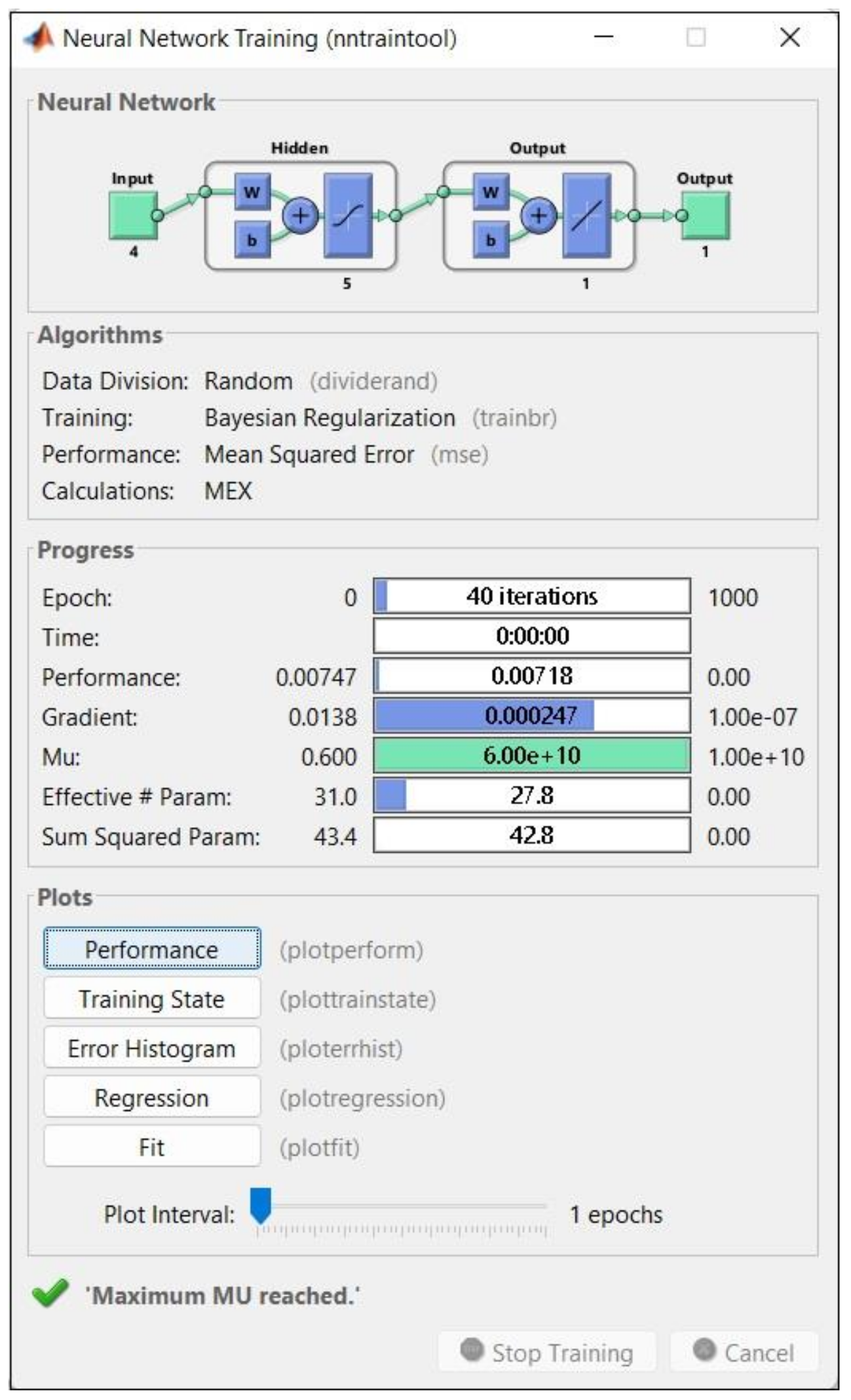
2.3.3. Artificial Neural Networks (ANNs)
2.3.4. The Bootstrap Method for Confidence Intervals
- choose the number of Bootstrap samples of size to perform;
- resample with replacement of the given dataset, obtaining B Bootstrap samples of volume
- for each bootstrap sample, calculate the statistic of interest, say , .
- calculate the mean and the standard deviation of the calculated sample statistic;
- write a 100(1 − α)% confidence interval for θ as follows:
3. Results
3.1. A Multiple Linear Regression Model (MLR)
- From the displayed p-values, we see that all the model coefficients are significant at any significance level less than 0.005.
- An increase of one unit in humidity will determine an increase of almost 5.1% in plant coverage percentage;
- An increase of 1 °C in temperature will determine a decrease of almost 1.21% in plant coverage percentage;
- The variable represented by the week of the year when the data were collected had a significant influence on the plant coverage percentage.
- The choice of the experimental module façade had a significant influence (of magnitude 1.9073) on the plant coverage percentage.
- The coefficient 0.03804 suggests that, for each fixed week number, an increase of 1 °C in soil temperature will determine an increase of almost 4% in plant coverage percentage. The interaction between these two parameters, the soil temperature and the week of the year, is important for the model. It is possible that the soil registers the same temperature in different seasons, but the effect produced on the degree of plant coverage of the wall is totally different (for example, the soil can have temperatures of 10 °C both on a summer week and a winter week, and the influence on the PCP can be totally different).
3.2. Confidence Interval for the PCP Based on the Multiple Linear Regression
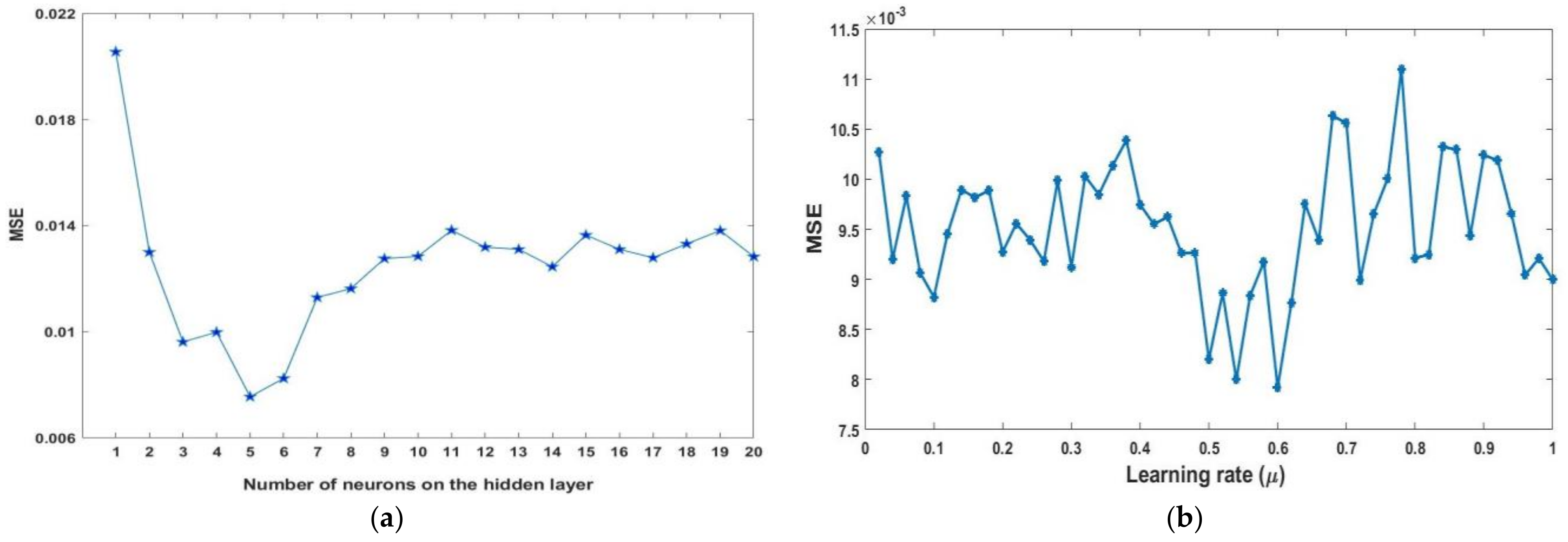
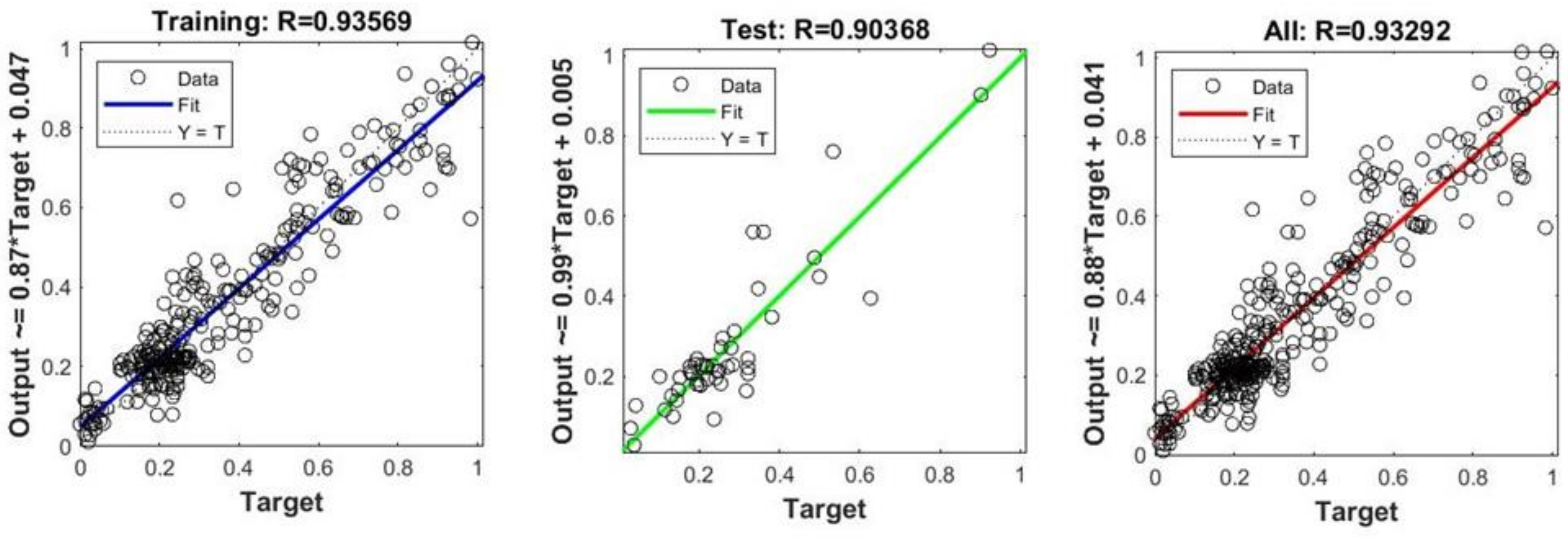
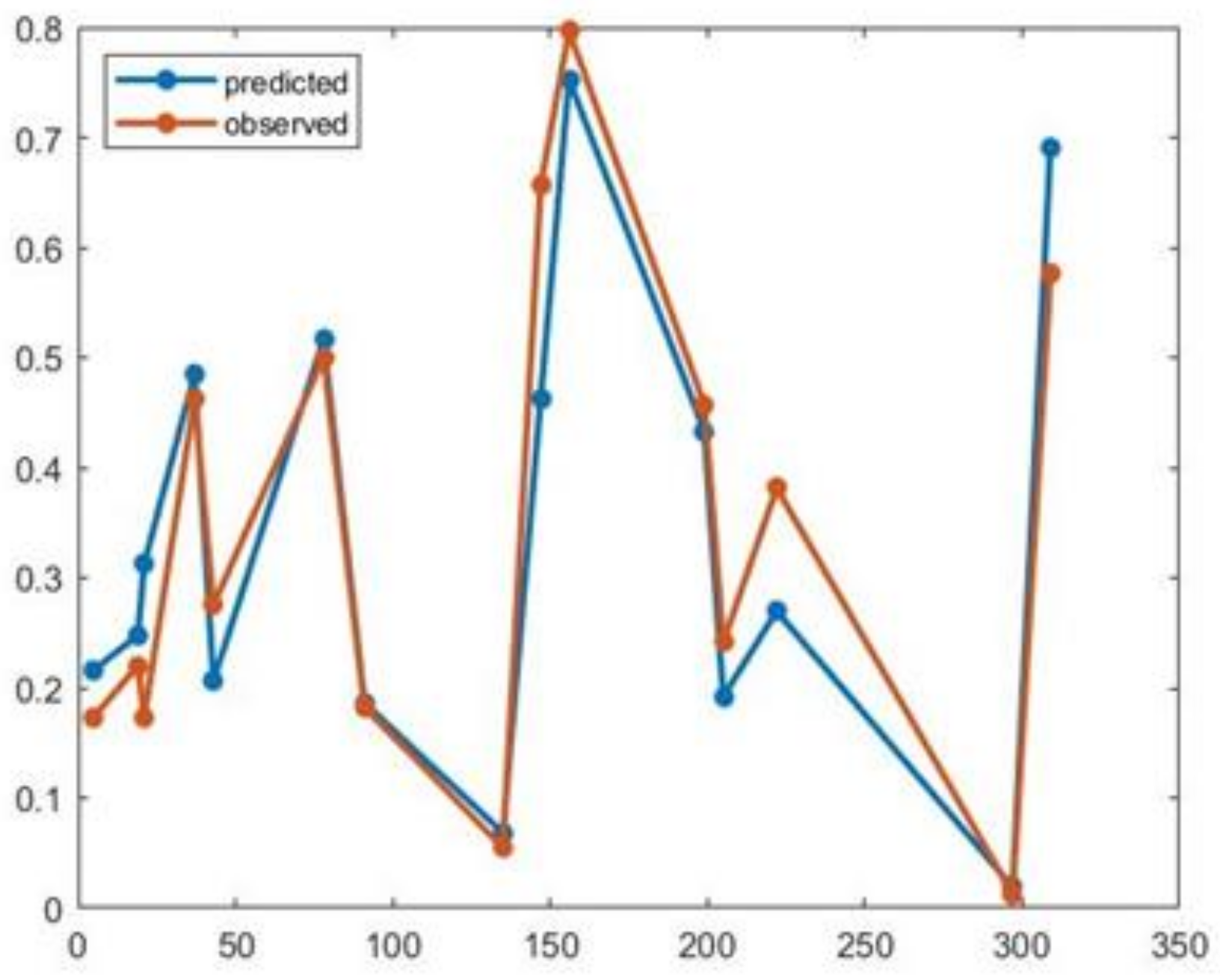
3.3. An Artificial Neural Network Model (ANN)
3.4. Confidence Interval for the PCP Based on Artificial Neural Networks
- -
- the bootstrap mean is
- -
- the bootstrap standard deviation is
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Peschardt, K.K.; Schipperijn, J.; Stigsdotter, U.K. Use of Small Public Urban Green Spaces (SPUGS). Urban For. Urban Green. 2012, 11, 235–244. [Google Scholar] [CrossRef]
- Akbari, H.; Pomerantz, M.; Taha, H. Cool Surfaces and Shade Trees to Reduce Energy Use and Improve Air Quality in Urban Areas. Sol. Energy 2001, 70, 295–310. [Google Scholar] [CrossRef]
- Yang, J.; Yu, Q.; Gong, P. Quantifying Air Pollution Removal by Green Roofs in Chicago. Atmos. Environ. 2008, 42, 7266–7273. [Google Scholar] [CrossRef]
- Strohbach, M.W.; Arnold, E.; Haase, D. The Carbon Footprint of Urban Green Space—A Life Cycle Approach. Landsc. Urban Plan. 2012, 104, 220–229. [Google Scholar] [CrossRef]
- Peschardt, K.K.; Stigsdotter, U.K. Associations between Park Characteristics and Perceived Restorativeness of Small Public Urban Green Spaces. Landsc. Urban Plan. 2013, 112, 26–39. [Google Scholar] [CrossRef]
- Price, A.; Jones, E.C.; Jefferson, F. Vertical Greenery Systems as a Strategy in Urban Heat Island Mitigation. Water Air Soil Pollut. 2015, 226, 247. [Google Scholar] [CrossRef]
- Ghazalli, A.J.; Brack, C.; Bai, X.; Said, I. Physical and Non-Physical Benefits of Vertical Greenery Systems: A Review. J. Urban Technol. 2019, 26, 53–78. [Google Scholar] [CrossRef]
- Chiesura, A. The Role of Urban Parks for the Sustainable City. Landsc. Urban Plan. 2004, 68, 129–138. [Google Scholar] [CrossRef]
- Wolch, J.R.; Byrne, J.; Newell, J.P. Urban Green Space, Public Health, and Environmental Justice: The Challenge of Making Cities “Just Green Enough”. Landsc. Urban Plan. 2014, 125, 234–244. [Google Scholar] [CrossRef] [Green Version]
- Currie, B.A.; Bass, B. Estimates of Air Pollution Mitigation with Green Plants and Green Roofs Using the UFORE Model. Urban Ecosyst. 2008, 11, 409–422. [Google Scholar] [CrossRef]
- Perez-Urrestarazu, L.; Fernandez-Canero, R.; Franco-Salas, A.; Egea, G. Vertical Greening Systems and Sustainable Cities. J. Urban Technol. 2015, 22, 65–85. [Google Scholar] [CrossRef]
- Frumkin, P. Beyond Toxicity—Human Health and the Natural Environment. Am. J. Prev. Med. 2001, 20, 234–240. [Google Scholar] [CrossRef] [PubMed]
- Sheweka, S.M.; Mohamed, N.M. Green Facades as a New Sustainable Approach Towards Climate Change. In Proceedings of the Terragreen 2012: Clean Energy Solutions for Sustainable Environment (Cesse), Beirut, Lebanon, 16–18 February 2012; Salame, C., Aillerie, M., Khoury, G., Eds.; Elsevier Science Bv: Amsterdam, The Netherlands, 2012; Volume 18, pp. 507–520. [Google Scholar]
- Eumorfopoulo, E.A.; Kontoleon, K.J. Experimental Approach to the Contribution of Plant-Covered Walls to the Thermal Behaviour of Building Envelopes. Build. Environ. 2009, 44, 1024–1038. [Google Scholar] [CrossRef]
- Synnefa, A.; Dandou, A.; Santamouris, M.; Tombrou, M.; Soulakellis, N. On the Use of Cool Materials as a Heat Island Mitigation Strategy. J. Appl. Meteorol. Climatol. 2008, 47, 2846–2856. [Google Scholar] [CrossRef]
- Zinzi, M.; Agnoli, S. Cool and Green Roofs. An Energy and Comfort Comparison between Passive Cooling and Mitigation Urban Heat Island Techniques for Residential Buildings in the Mediterranean Region. Energy Build. 2012, 55, 66–76. [Google Scholar] [CrossRef]
- Djedjig, R.; Bozonnet, E.; Belarbi, R. Experimental Study of the Urban Microclimate Mitigation Potential of Green Roofs and Green Walls in Street Canyons. Int. J. Low-Carbon Technol. 2015, 10, 34–44. [Google Scholar] [CrossRef] [Green Version]
- Wong, N.H.; Chen, Y.; Ong, C.L.; Sia, A. Investigation of Thermal Benefits of Rooftop Garden in the Tropical Environment. Build. Environ. 2003, 38, 261–270. [Google Scholar] [CrossRef]
- Takebayashi, H.; Moriyama, M. Surface Heat Budget on Green Roof and High Reflection Roof for Mitigation of Urban Heat Island. Build. Environ. 2007, 42, 2971–2979. [Google Scholar] [CrossRef] [Green Version]
- Teemusk, A.; Mander, U. Greenroof Potential to Reduce Temperature Fluctuations of a Roof Membrane: A Case Study from Estonia. Build. Environ. 2009, 44, 643–650. [Google Scholar] [CrossRef]
- Cheng, C.Y.; Cheung, K.K.S.; Chu, L.M. Thermal Performance of a Vegetated Cladding System on Facade Walls. Build. Environ. 2010, 45, 1779–1787. [Google Scholar] [CrossRef]
- Kozamernik, J.; Rakuša, M.; Nikšič, M. How Green Facades Affect the Perception of Urban Ambiences: Comparing Slovenia and the Netherlands. Urbani Izziv 2020, 31, 88–100. [Google Scholar] [CrossRef]
- Tsantopoulos, G.; Varras, G.; Chiotelli, E.; Fotia, K.; Batou, M. Public Perceptions and Attitudes toward Green Infrastructure on Buildings: The Case of the Metropolitan Area of Athens, Greece. Urban For. Urban Green. 2018, 34, 181–195. [Google Scholar] [CrossRef]
- Gantar, D.; Kozamernik, J.; Erjavec, I.S.; Koblar, S. From Intention to Implementation of Vertical Green: The Case of Ljubljana. Sustainability 2022, 14, 3198. [Google Scholar] [CrossRef]
- Sari, A.A. Thermal Performance of Vertical Greening System on the Building Facade: A Review. AIP Conf. Proc. 2017, 1887, 020054. [Google Scholar] [CrossRef] [Green Version]
- Feng, L.-H.; Lu, J. The Practical Research on Flood Forecasting Based on Artificial Neural Networks. Expert Syst. Appl. 2010, 37, 2974–2977. [Google Scholar] [CrossRef]
- Wu, X.D.; Cao, H.X.; Flitman, A.; Wei, F.Y.; Feng, G.L. Forecasting Monsoon Precipitation Using Artificial Neural Networks. Adv. Atmos. Sci. 2001, 18, 950–958. [Google Scholar] [CrossRef]
- Sohn, S.H.; Oh, S.C.; Yeo, Y.K. Prediction of Air Pollutants by Using an Artificial Neural Network. Korean J. Chem. Eng. 1999, 16, 382–387. [Google Scholar] [CrossRef]
- Erdil, A.; Arcaklioglu, E. The Prediction of Meteorological Variables Using Artificial Neural Network. Neural Comput. Appl. 2013, 22, 1677–1683. [Google Scholar] [CrossRef]
- Runge, J.; Zmeureanu, R. Forecasting Energy Use in Buildings Using Artificial Neural Networks: A Review. Energies 2019, 12, 3254. [Google Scholar] [CrossRef] [Green Version]
- Lehnert, L.W.; Meyer, H.; Wang, Y.; Miehe, G.; Thies, B.; Reudenbach, C.; Bendix, J. Retrieval of Grassland Plant Coverage on the Tibetan Plateau Based on a Multi-Scale, Multi-Sensor and Multi-Method Approach. Remote Sens. Environ. 2015, 164, 197–207. [Google Scholar] [CrossRef]
- Al-Saif, A.M.; Abdel-Sattar, M.; Eshra, D.H.; Sas-Paszt, L.; Mattar, M.A. Predicting the Chemical Attributes of Fresh Citrus Fruits Using Artificial Neural Network and Linear Regression Models. Horticulturae 2022, 8, 1016. [Google Scholar] [CrossRef]
- Abdipour, M.; Younessi-Hmazekhanlu, M.; Ramazani, S.H.R.; Omidi, A.H. Artificial Neural Networks and Multiple Linear Regression as Potential Methods for Modeling Seed Yield of Safflower (Carthamus Tinctorius L.). Ind. Crops Prod. 2019, 127, 185–194. [Google Scholar] [CrossRef]
- Abdel-Sattar, M.; Al-Obeed, R.S.; Aboukarima, A.M.; Eshra, D.H. Development of an Artificial Neural Network as a Tool for Predicting the Chemical Attributes of Fresh Peach Fruits. PLoS ONE 2021, 16, e0251185. [Google Scholar] [CrossRef] [PubMed]
- Huang, X.; Chen, T.; Zhou, P.; Huang, X.; Liu, D.; Jin, W.; Zhang, H.; Zhou, J.; Wang, Z.; Gao, Z. Prediction and Optimization of Fruit Quality of Peach Based on Artificial Neural Network. J. Food Compos. Anal. 2022, 111, 104604. [Google Scholar] [CrossRef]
- Abdel-Sattar, M.; Al-Saif, A.M.; Aboukarima, A.M.; Eshra, D.H.; Sas-Paszt, L. Quality Attributes Prediction of Flame Seedless Grape Clusters Based on Nutritional Status Employing Multiple Linear Regression Technique. Agriculture 2022, 12, 1303. [Google Scholar] [CrossRef]
- Brion, G.M.; Lingireddly, S. Artificial Neural Network Modelling: A Summary of Successful Applications Relative to Microbial Water Quality. Water Sci. Technol. 2003, 47, 235–240. [Google Scholar] [CrossRef]
- Li, Y.; Wang, J. Water Quality Forecast Based on Artificial Neural Network. In Proceedings of the Progress in Intelligence Computation and Applications, Wuhan, China, 21–23 September 2007; Zeng, S., Liu, Y., Zhang, Q., Kang, L., Eds.; China Univiversity Geosciences Press: Wuhan, China, 2007; pp. 266–268. [Google Scholar]
- Madhiarasan, M.; Tipaldi, M.; Siano, P. Analysis of Artificial Neural Network Performance Based on Influencing Factors for Temperature Forecasting Applications. J. High Speed Netw. 2020, 26, 209–223. [Google Scholar] [CrossRef]
- Hinkley, D. Bootstrap Methods. J. R. Stat. Soc. Ser. B-Methodol. 1988, 50, 321–337. [Google Scholar] [CrossRef]
- Chernick, M.R. Bootstrap Methods: A Guide for Practitioners and Researchers, 2nd ed.; Wiley: Hoboken, NJ, USA, 2007. [Google Scholar]
- Cojocariu, M.; Chelariu, E.L.; Chiruta, C. Study on Behavior of Some Perennial Flowering Species Used in Vertical Systems for Green Facades in Eastern European Climate. Appl. Sci. 2022, 12, 474. [Google Scholar] [CrossRef]
- Devore, J.L.; Berk, K.N. Modern Mathematical Statistics with Applications; Springer Texts in Statistics; Springer: New York, NY, USA, 2012; ISBN 978-1-4614-0390-6. [Google Scholar]
- Graupe, D. Principles of Artificial Neural Networks, 3rd ed.; Advanced Series in Circuits and Systems; World Scientific: Singapore, 2013; Volume 7, ISBN 978-981-4522-73-1. [Google Scholar]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer Feedforward Networks Are Universal Approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- MacKay, D.J.C. Bayesian Interpolation. Neural Comput. 1992, 4, 415–447. [Google Scholar] [CrossRef]
- Negoita, G.A.; Luecke, G.R.; Vary, J.P.; Maris, P.; Shirokov, A.M.; Shin, I.J.; Kim, Y.; Ng, E.G.; Yang, C. Deep Learning: A Tool for Computational Nuclear Physics. arXiv 2018, arXiv:1803.03215. [Google Scholar]

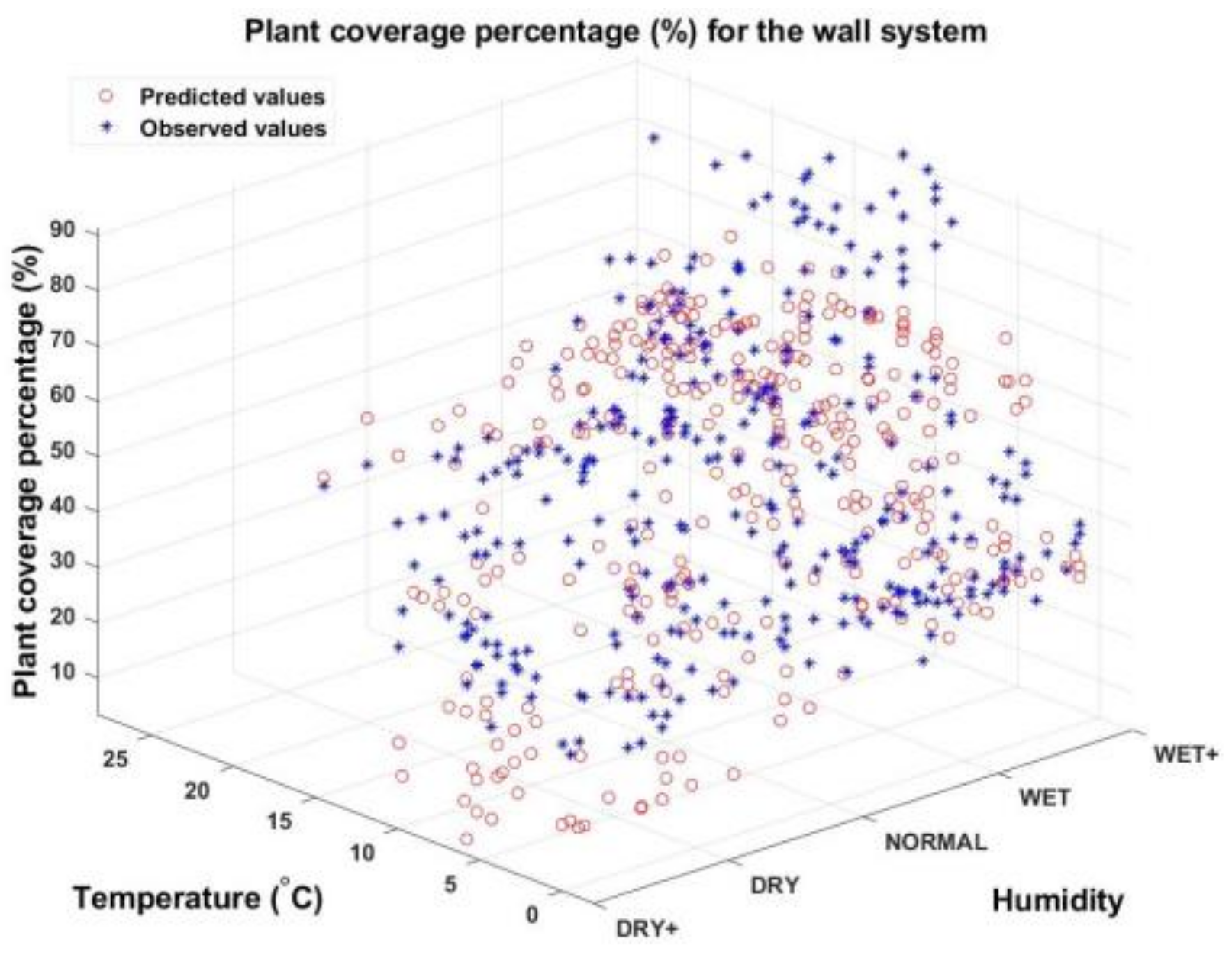

| Temp Int 2020 (°C) | Temp Ext 2020 (°C) | Temp Iasi 2020 (°C) | Humidity Soil 2020 | Temp Soil 2020 (°C) | Plant Cover Green Wall (%) 2020 | |
|---|---|---|---|---|---|---|
| Mean | 17.37 | 14.38 | 16.33 | 3.42 | 14.35 | 36.63 |
| Minimum | −1.70 | 0.90 | −3.10 | 1.00 | −0.25 | 21.71 |
| Maximum | 39.90 | 26.90 | 31.80 | 5.00 | 28.25 | 71.05 |
| CI mean | 17.37 ± 1.59 | 14.38 ± 1.22 | 16.33 ± 1.53 | 3.42 ± 0.18 | 14.35 ± 1.29 | 36.63 ± 1.76 |
| Temp Int 2021 (°C) | Temp Ext 2021 (°C) | Temp Iasi 2021 (°C) | Humidity Soil 2021 | Temp Soil 2021 (°C) | Plant Cover Green Wall (%) 2021 | |
|---|---|---|---|---|---|---|
| Mean | 16.35 | 12.38 | 14.18 | 4.21 | 10.93 | 45.61 |
| Minimum | −2.60 | −1.90 | −3.50 | 1.25 | −2.00 | 13.82 |
| Maximum | 33.20 | 27.90 | 31.30 | 5.00 | 25.50 | 91.45 |
| CI mean | 16.35 ± 1.44 | 12.38 ± 1.25 | 14.18 ± 1.51 | 4.21 ± 0.14 | 10.93 ± 1.25 | 45.61 ± 3.57 |
| Estimated Parameter | Standard Error | Test Statistic | p-Value | |
|---|---|---|---|---|
| Hum | 5.0908 | 0.63696 | 7.9942 | 2.4462 × 10−14 |
| Temp | −1.2014 | 0.25157 | −4.7755 | 2.7369 × 10−6 |
| WkNo | 0.62273 | 0.06814 | 9.1319 | 7.5291 × 10−18 |
| Side | 1.90730 | 0.66521 | 2.8673 | 0.0044126 |
| Temp·WkNo | 0.03804 | 0.00813 | 4.6797 | 4.2531 × 10−6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chiruţă, C.; Stoleriu, I.; Cojocariu, M. Prediction Models for the Plant Coverage Percentage of a Vertical Green Wall System: Regression Models and Artificial Neural Network Models. Horticulturae 2023, 9, 419. https://doi.org/10.3390/horticulturae9040419
Chiruţă C, Stoleriu I, Cojocariu M. Prediction Models for the Plant Coverage Percentage of a Vertical Green Wall System: Regression Models and Artificial Neural Network Models. Horticulturae. 2023; 9(4):419. https://doi.org/10.3390/horticulturae9040419
Chicago/Turabian StyleChiruţă, Ciprian, Iulian Stoleriu, and Mirela Cojocariu. 2023. "Prediction Models for the Plant Coverage Percentage of a Vertical Green Wall System: Regression Models and Artificial Neural Network Models" Horticulturae 9, no. 4: 419. https://doi.org/10.3390/horticulturae9040419
APA StyleChiruţă, C., Stoleriu, I., & Cojocariu, M. (2023). Prediction Models for the Plant Coverage Percentage of a Vertical Green Wall System: Regression Models and Artificial Neural Network Models. Horticulturae, 9(4), 419. https://doi.org/10.3390/horticulturae9040419






