Determination of Fast Battery-Charging Profiles Using an Electrochemical Model and a Direct Optimal Control Approach
Abstract
:1. Introduction
2. Literature Review
3. Battery Fast-Charging Problem
4. Optimal Control Problem Formulation
- : state 1 (mol/m)
- : state 2 (mol/m)
- : bulk concentration (mol/m)
4.1. Case 1: Baseline
4.2. Case 2: Balanced
4.3. Case 3: Parameterisation of the Objective Functional
5. Results and Discussion
5.1. Case 1: Baseline Scenario
5.2. Case 2: Balanced Scenario
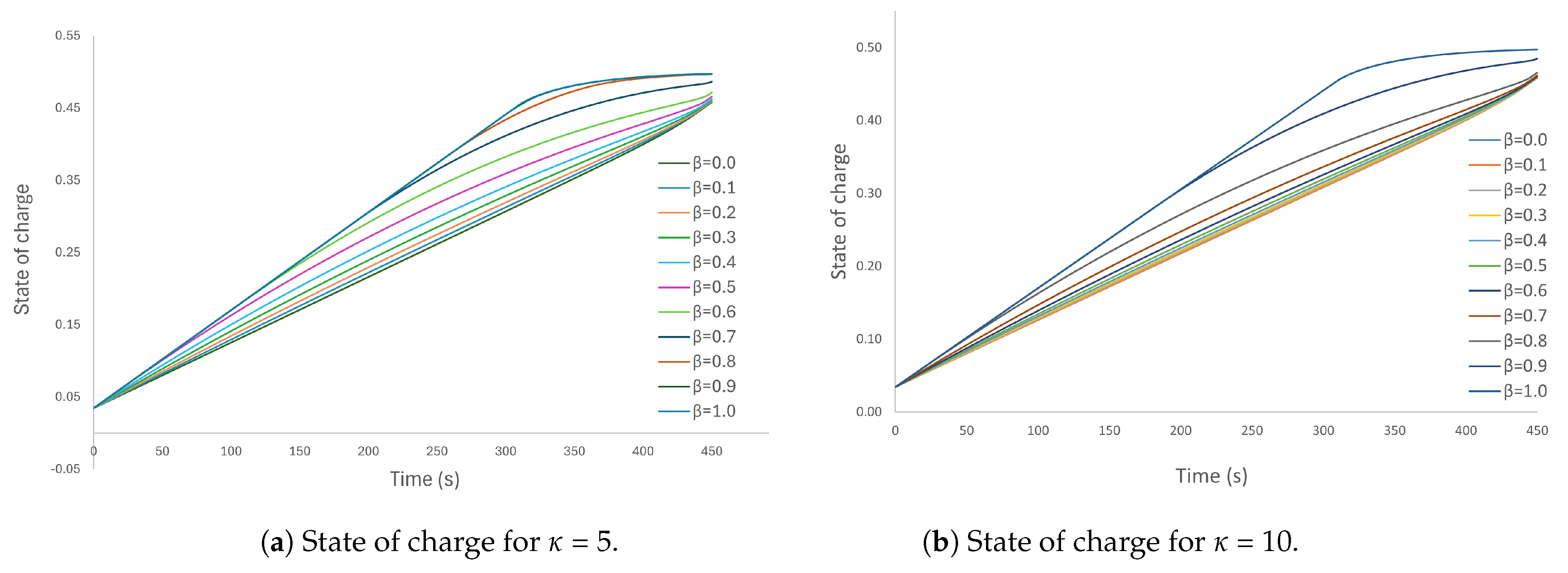
5.3. Case 3: Parameterisation of the Objective Functional
5.3.1. Case 3.1:
5.3.2. Case 3.2: , and
5.3.3. Case 3.3: = 0.8, , = 5
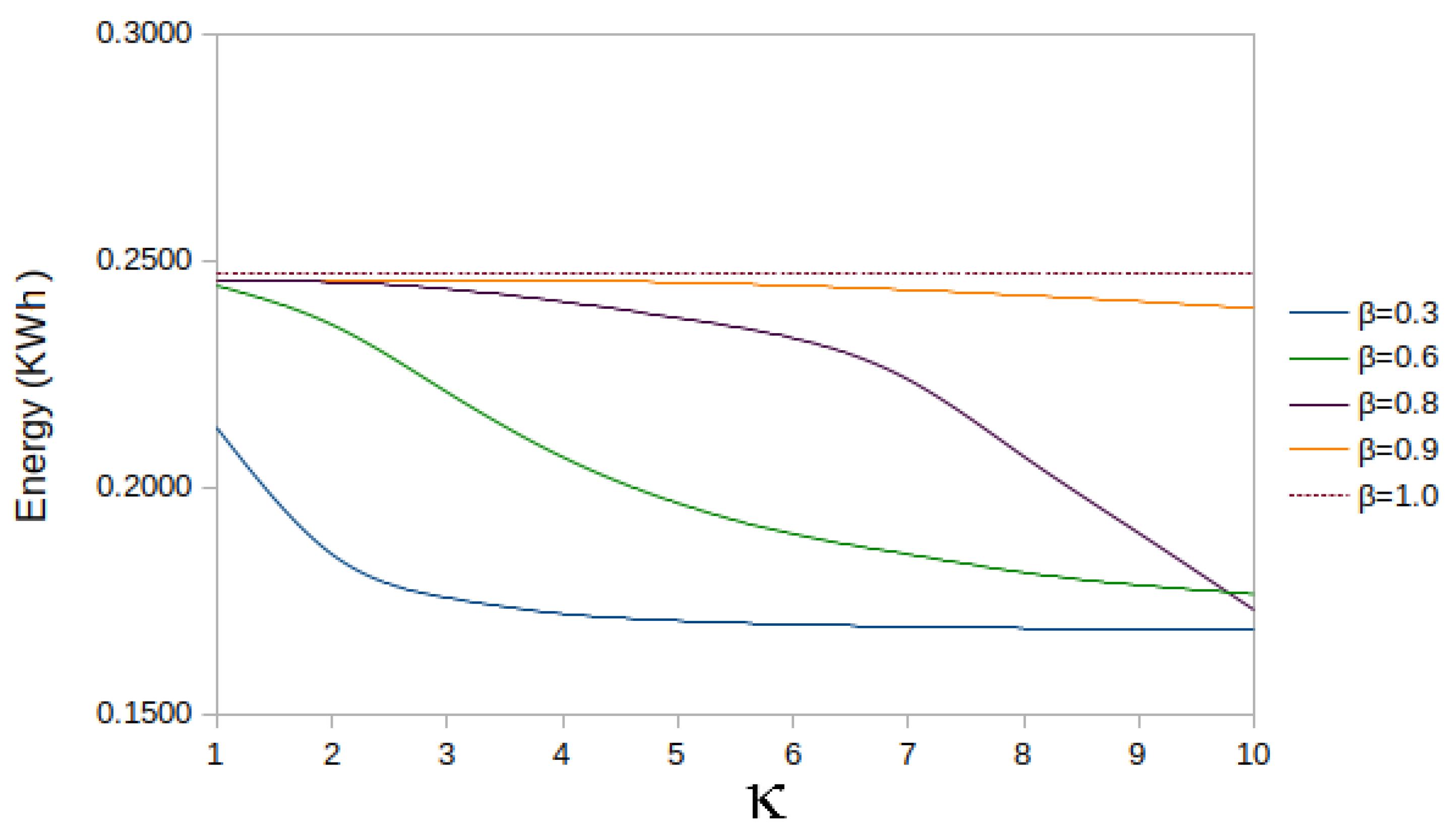
5.4. Analysis of Energy Dissipation in the Parameterised Case
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tan, H.; Li, J.; He, M.; Li, J.; Zhi, D.; Qin, F.; Zhang, C. Global evolution of research on green energy and environmental technologies: A bibliometric study. J. Environ. Manag. 2021, 297, 113382. [Google Scholar] [CrossRef] [PubMed]
- Fan, X.; Liu, B.; Liu, J. Battery Technologies for Grid-Level Large-Scale Electrical Energy Storage. Trans. Tianjin Univ. 2020, 26, 92–103. [Google Scholar] [CrossRef]
- Park, S.; Lee, D.; Ahn, H.J.; Tomlin, C.; Moura, S. Optimal Control of Battery Fast Charging Based-on Pontryagin’s Minimum Principle. In Proceedings of the 59th IEEE Conference on Decision and Control, Jeju, Republic of Korea, 14–18 December 2020. [Google Scholar]
- Liu, H.; Naqvi, I.H.; Li, F.; Liu, C.; Shafiei, N.; Li, Y.; Pecht, M. An analytical model for the CC-CV charge of Li-ion batteries with application to degradation analysis. J. Energy Storage 2020, 29, 101342. [Google Scholar] [CrossRef]
- TrueBluepower. A123-Systems, Nanophosphate High Power Lithium Ion Cell Datasheet. 2022. Available online: https://www.truebluepowerusa.com/pdfs/ANR26650M1-B_ProductFlier.pdf (accessed on 27 February 2023).
- Mohtat, P.; Pannala, S.; Sulzer, V.; Siegel, J.B.; Stefanopoulou, A.G. An Algorithmic Safety VEST for Li-ion Batteries During Fast Charging. IFAC-PapersOnLine 2021, 54, 522–527. [Google Scholar] [CrossRef]
- Carter, R.; Kingston, T.A.; Atkinson, R.W.; Parmananda, M.; Dubarry, M.; Fear, C.; Mukherjee, P.P.; Love, C.T. Directionality of thermal gradients in lithium-ion batteries dictates diverging degradation modes. Cell Rep. Phys. Sci. 2021, 2, 100351. [Google Scholar] [CrossRef]
- Ren, B.; Xie, C.; Sun, X.; Zhang, Q.; Yan, D. Parameter identification of a lithium-ion battery based on the improved recursive least square algorithm. IET Power Electron. 2020, 13, 2531–2537. [Google Scholar] [CrossRef]
- Jacobsen, T.; West, K. Diffusion impedance in planar, cylindrical and spherical symmetry. Electrochim. Acta 1995, 40, 255–262. [Google Scholar] [CrossRef]
- Han, W.; Kalateh Bojdi, Z.; Ahmadi-Asl, S.; Aminataei, A. A New Extended Padé Approximation and Its Application. Adv. Numer. Anal. 2013, 2013, A93–A101. [Google Scholar]
- Shamash, Y. Model reduction using the Routh stability criterion and the Padé approximation technique. Int. J. Control 1975, 21, 475–484. [Google Scholar] [CrossRef]
- Mellodge, P. A Practical Approach to Dynamical Systems for Engineers; Woodhead Publishing: Sawston, UK, 2016. [Google Scholar]
- Chen, T.C. Linear Systems Theory and Design, 3rd ed.; Oxford University Press: Oxford, UK, 1998. [Google Scholar]
- Dorf, R.C.; Bishop, R.H. Modern Control Systems, 14th ed.; Pearson Publishing: London, UK, 2022. [Google Scholar]
- Bernstein, D.S. Matrix Mathematics Theory, Facts, and Formulas with Application to Linear Systems Theory; Oxford Press: Oxford, UK, 2003. [Google Scholar]
- Moon, J. Optimization-Based Reduction and Padeé Approximants for Lithium-Ion Battery Cell Models with Degradation. Master’s Thesis, Texas Tech University, Lubbock, TX, USA, 2022. [Google Scholar]
- Forman, J.C.; Bashash, S.; Stein, J.L.; Fathy, H.K. Reduction of an Electrochemistry-Based Li-Ion Battery Model via Quasi-Linearization and Padé Approximation. J. Electrochem. Soc. 2011, 158, A93–A101. [Google Scholar] [CrossRef]
- Appleton, S.; Fotouhi, A. A Model-Based Battery Charging Optimization Framework for Proper Trade-offs Between Time and Degradation. Automot. Innov. 2023, 6, 204–221. [Google Scholar] [CrossRef]
- Chen, G.J.; Liu, Y.H.; Cheng, S.; Pai, H.Y. A Novel Optimal Charging Algorithm for Lithium-Ion Batteries Based on Model Predictive Control. Energies 2021, 14, 2238. [Google Scholar] [CrossRef]
- Lan, T.; Hu, J.; Kang, Q.; Si, C.; Wang, L.; Wu, Q. Optimal control of an electric vehicle’s charging schedule under electricity markets. Neural Comput. Appl. 2013, 23, 1865–1872. [Google Scholar] [CrossRef]
- Klein, R.; Chaturvedi, N.; Christensen, J.; Ahmed, J.; Findeisen, R.; Kojic, A. Optimal Charging Strategies in Lithium-Ion Battery. In Proceedings of the 2011 American Control Conference, San Francisco, CA, USA, 29 June–1 July 2011; pp. 382–387. [Google Scholar]
- Zou, C.; Kallapur, A.G.; Manzie, C.; Nesic, D. PDE battery model simplification for SOC and SOH estimator design. In Proceedings of the 2015 54th IEEE Conference on Decision and Control (CDC), Osaka, Japan, 15–18 December 2015; pp. 1328–1333. [Google Scholar]
- Stoer, J.; Bulirsch, R. Introduction to Numerical Analysis; Springer: Berlin/Heidelberg, Germany, 1980. [Google Scholar]
- Alt, W.; Schneider, C.; Seydenschwanz, M. Regularization and implicit Euler discretization of linear-quadratic optimal control problems with bang-bang solutions. Appl. Math. Comput. 2016, 287–288, 104–124. [Google Scholar] [CrossRef]
- Plett, G. Battery Management Systems, Volume I: Battery Modeling; Artech House Publishers: Boston, MA, USA, 2015. [Google Scholar]
- Xiong, R.; Li, L.; Li, Z.; Yu, Q.; Mu, H.U. An electrochemical model based degradation state identification method of Lithium-ion battery for all-climate electric vehicles application. Appl. Energy 2018, 219, 264–275. [Google Scholar] [CrossRef]
- Li, X.; Huang, Z.; Tian, J.; Tian, Y. State-of-charge estimation tolerant of battery aging based on a physics-based model and an adaptive cubature Kalman filter. Energies 2021, 2020, 119767. [Google Scholar] [CrossRef]
- Liu, B.; Tang, X.; Gao, F. Joint estimation of battery state-of-charge and state-of-health based on a simplified pseudo-two-dimensional model. Electrochim. Acta 2020, 344, 136098. [Google Scholar] [CrossRef]
- Doyle, C. Design and Simulation of Lithium Rechargeable Batteries. Ph.D. Thesis, University of California, Berkley, CA, USA, 1995. [Google Scholar]
- Thakkar, R.R. Electrical Equivalent Circuit Models of Lithium-ion Battery. In Management and Applications of Energy Storage Devices; Okedu, K.E., Ed.; IntechOpen: Rijeka, India, 2021; Chapter 1. [Google Scholar]
- Cheng, X.; Yao, L.; Xing, Y.; Pecht, M. Novel Parametric Circuit Modeling for Li-Ion Batteries. Energies 2016, 9, 539. [Google Scholar] [CrossRef]
- Zhang, C.; Li, K.; Mcloone, S.; Yang, Z. Battery modelling methods for electric vehicles—A review. In Proceedings of the 2014 European Control Conference (ECC), Strasbourg, France, 24–27 June 2014; pp. 2673–2678. [Google Scholar]
- Zhang, C.; Zhu, Y.; Dong, G.; Wei, J. Data-driven lithium-ion battery states estimation using neural networks and particle filtering. Int. J. Energy Res. 2019, 43, 8230–8241. [Google Scholar] [CrossRef]
- Gomadam, P.M.; Weidner, J.W.; Dougal, R.A.; White, R.E. Mathematical modeling of lithium-ion and nickel battery systems. J. Power Sources 2002, 110, 267–284. [Google Scholar] [CrossRef]
- Planella, F.B.; Ai, W.; Boyce, A.M.; Ghosh, A.; Korotkin, I.; Sahu, S.; Sulzer, V.; Timms, R.; Tranter, T.G.; Zyskin, M.; et al. A continuum of physics-based lithium-ion battery models reviewed. Prog. Energy 2022, 4, 042003. [Google Scholar] [CrossRef]
- Doyle, C.; Fuller, T.F.; Newman, J. Modeling of galvanostatic charge and discharge of the lithium/polymer/insertion cell. J. Electrochem. Soc. 1993, 140, 1526–1533. [Google Scholar] [CrossRef]
- Doyle, C.; Newman, J. The use of mathematical modeling in the design of lithium/polymer battery systems. Electrochim. Acta 1995, 40, 2191–2196. [Google Scholar] [CrossRef]
- Sarkar, S.; Halim, Z.; El-Halwagi, M.; Khan, F. Electrochemical Models: Methods and Applications for Safer Lithium-Ion Battery Operation. J. Electrochem. Soc. 2022, 169. [Google Scholar] [CrossRef]
- Korotkin, I.; Sahu, S.; O’Kane, S.E.J.; Richardson, G.; Foster, J.M. DandeLiion v1: An Extremely Fast Solver for the Newman Model of Lithium-Ion Battery (Dis)charge. J. Electrochem. Soc. 2021, 168, 060544. [Google Scholar] [CrossRef]
- Liu, J.; Pang, H.; Geng, Y.; Chen, K.; Wu, L. Thermal-Coupled Single Particle Modeling and Multi-Objective Stepwise Parameter Identification of Lithium-Ion Batteries Over Different Temperatures. J. Electrochem. Soc. 2023, 170, 060542. [Google Scholar] [CrossRef]
- Schimpe, M.; von Kuepach, M.E.; Naumann, M.; Hesse, H.C.; Smith, K.; Jossen, A. Comprehensive Modeling of Temperature-Dependent Degradation Mechanisms in Lithium Iron Phosphate Batteries. J. Electrochem. Soc. 2018, 165, A181–A193. [Google Scholar] [CrossRef]
- Ramadass, P.; Haran, B.; White, R.; Popov, B.N. Capacity fade of Sony 18,650 cells cycled at elevated temperatures: Part II. Capacity fade analysis. J. Power Sources 2002, 112, 614–620. [Google Scholar] [CrossRef]
- van Beers, J.J. Exploration of the Identifiability and Distinguishability of Battery Degradation Mechanisms in a DFN Model Framework. Master’s Thesis, Eindhoven University of Technology, Eindhoven, The Netherlands, 2023. [Google Scholar]
- Hariharan, K.S.; Tagade, P.; Ramachandran, S. Mathematical Modeling of Lithium Batteries: From Electrochemical Models to State Estimator Algorithms; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Kirkwood, J. Chapter 10—Solving Partial Differential Equations in Spherical Coordinates Using Separation of Variables. In Mathematical Physics with Partial Differential Equations, 2nd ed.; Kirkwood, J., Ed.; Academic Press: Cambridge, MA, USA, 2018; pp. 337–373. [Google Scholar]
- Liu, H.; Yan, J. The Direct Discontinuous Galerkin (DDG) Methods for Diffusion Problems. SIAM J. Numer. Anal. 2009, 47, 675–698. [Google Scholar] [CrossRef]
- de Groen, P.P.N.; van Veldhuizen, M. A Stabilized Galerkin Method for Convection-Diffusion Problems. SIAM J. Sci. Stat. Comput. 1989, 10, 274–297. [Google Scholar] [CrossRef]
- Zhong, L.; Xuan, Y.; Cui, J. Two-grid discontinuous Galerkin method for convection–diffusion–reaction equations. J. Comput. Appl. Math. 2022, 404, 113903. [Google Scholar] [CrossRef]
- Skinner, L.A. Singular Perturbation Theory; Springer: New York, NY, USA, 2011. [Google Scholar]
- Fan, G.; Canova, M. Model Order Reduction of Electrochemical Batteries Using Galerkin Method. In Proceedings of the ASME 2015 5th Annual Dynamic Systems and Control Conference, Columbus, OH, USA, 28–30 October 2015; pp. 1–7. [Google Scholar]
- Dao, T.S.; Vyasarayani, C.P.; McPhee, J. Simplification and order reduction of lithium-ion battery model based on porous-electrode theory. J. Power Sources 2012, 198, 329–337. [Google Scholar] [CrossRef]
- Gu, Y.; Wang, J.; Chen, Y.; Xiao, W.; Deng, Z.; Chen, Q. A simplified electro-chemical lithium-ion battery model applicable for in situ monitoring and online control. Energy 2023, 264, 126192. [Google Scholar] [CrossRef]
- Planden, B.; Lukow, K.; Henshall, P.; Collier, G.; Morrey, D. A computationally informed realisation algorithm for lithium-ion batteries implemented with LiiBRA.jl. J. Energy Storage 2022, 55, 105637. [Google Scholar] [CrossRef]
- Couto, L.D.; Romagnoli, R.; Park, S.; Zhang, D.; Moura, S.J.; Kinnaert, M.; Garone, E. Faster and Healthier Charging of Lithium-Ion Batteries via Constrained Feedback Control. IEEE Trans. Control Syst. Technol. 2022, 30, 1990–2001. [Google Scholar] [CrossRef]
- Biju, N.; Fang, H. BattX: An equivalent circuit model for lithium-ion batteries over broad current ranges. Appl. Energy 2023, 339, 120905. [Google Scholar] [CrossRef]
- Delacourt, C.; Safari, M. Analysis of lithium deinsertion/insertion in LiyFePO4 with a simple mathematical model. Electrochim. Acta 2011, 56, 5222–5229. [Google Scholar] [CrossRef]
- Barbir, F. Chapter Three—Fuel Cell Electrochemistry. In PEM Fuel Cells, 2nd ed.; Barbir, F., Ed.; Academic Press: Boston, MA, USA, 2013; pp. 33–72. [Google Scholar]
- Santhanagopalan, S.; Guo, Q.; Ramadass, P.; White, R.E. Review of models for predicting the cycling performance of lithium ion batteries. J. Power Sources 2006, 156, 620–628. [Google Scholar] [CrossRef]
- Guo, M.; Sikha, G.; Whitea, R.E. Single-Particle Model for a Lithium-Ion Cell: Thermal Behavior. J. Electrochem. Soc. 2010, 158, A122–A132. [Google Scholar] [CrossRef]
- Zhang, D.; Popov, B.; White, R.E. Modelling Lithium Intercalation of a Single Spinel Particle under Potentiodynamic Control. J. Electrochem. Soc. 2000, 147, 831–838. [Google Scholar] [CrossRef]
- Gao, T.; Lu, W. Reduced-order electrochemical models with shape functions for fast, accurate prediction of lithium-ion batteries under high C-rates. Appl. Energy 2024, 353, 121954. [Google Scholar] [CrossRef]
- Di Domenico, D.; Stefanopoulou, A.; Fiengo, G. Lithium-Ion Battery State of Charge and Critical Surface Charge Estimation Using an Electrochemical Model-Based Extended Kalman Filter. J. Dyn. Syst. Meas. Control 2010, 132, 061302. [Google Scholar] [CrossRef]
- Wang, Y.; Fang, H.; Sahinoglu, Z.; Wada, T.; Hara, S. Adaptive Estimation of the State of Charge for Lithium-Ion Batteries: Nonlinear Geometric Observer Approach. IEEE Trans. Control Syst. Technol. 2015, 23, 948–962. [Google Scholar] [CrossRef]
- Rahimian, S.K.; Rayman, S.C.; White, R.E. Maximizing the life of a lithium-Ion cell by optimization of charging rates. J. Electrochem. Soc. 2010, 157, A1302. [Google Scholar] [CrossRef]
- Klein, R.; Chaturvedi, N.A.; Christensen, J.; Ahmed, J.; Findeisen, R.; Kojic, A. Model Order Reduction of Electrochemical Batteries Using Galerkin Method. In Proceedings of the 2011 American Control Conference, San Francisco, CA, USA, 29 June–1 July 2011; pp. 382–387. [Google Scholar]
- Lee, S.; Kim, Y.; Siegel, J.B.; Stefanopoulou, A.G. Optimal control for fast acquisition of equilibrium voltage for Li-ion batteries. J. Energy Storage 2021, 40, 102814. [Google Scholar] [CrossRef]
- Anthony, P. Solving 1-Dimensional diffusion process by Padé approximation. Sci. World J. 2019, 14, 44–47. [Google Scholar]
- Basdebant, J. The Padé approximant and its physical applications. Protein Sci. 1972, 20, 283–331. [Google Scholar]
- Backer, G. Essential of Pade Approximants; Academic Press: London, UK, 1975. [Google Scholar]
- Tran, N.T.; Vilathgamuwa, M.; Farrell, T.; Choi, S.S.; Li, Y.; Teague, J. A Padé Approximate Model of Lithium Ion Batteries. J. Electrochem. Soc. 2018, 165, A1409–A1421. [Google Scholar] [CrossRef]
- Yuan, S.; Jiang, L.; Yin, C.; Wu, H.; Zhang, X. A transfer function type of simplified electrochemical model withmodified boundary conditions and Pade approximation for Li-ion battery. Part 1. lithium concentration estimation. J. Power Sources 2017, 352, 245–257. [Google Scholar] [CrossRef]
- Wu, L.; Liu, K.; Pang, H. Evaluation and observability analysis of an improved reduced-order electrochemical model for lithium-ion battery. Electrochim. Acta 2021, 368, 137604. [Google Scholar] [CrossRef]
- Zhao, Y.; Choe, S. A highly efficient reduced order electrochemical model for a large format LiMn2O4/Carbon polymer battery for real time applications. Electrochim. Acta 2015, 164, 97–107. [Google Scholar] [CrossRef]
- Wu, L.; Pang, H.; Geng, Y.; Liu, X.; Liu, J.; Liu, K. Low-complexity state of charge and anode potential prediction for lithium-ion batteries using a simplified electrochemical model-based observer under variable load condition. Int. J. Energy Res. 2022, 46, 11834–11848. [Google Scholar] [CrossRef]
- Liberzon, D. Calculus of Variations and Optimal Control Theory: A Concise Introduction; Princeton University Press: Princeton, NJ, USA, 2012. [Google Scholar]
- Vinter, R. Optimal Control; Springer Science & Business Media: New York, NY, USA, 2010. [Google Scholar]
- Kirk, D. Optimal Control Theory: An Introduction; Prentice-Hall: Hoboken, NJ, USA, 1970. [Google Scholar]
- Bryson, A.; Ho, Y. Applied Optimal Control-Optimization. Estimation and Control; Taylor & Francis Inc.: Oxon, UK, 1975. [Google Scholar]
- Lao, D.; Zhao, S. Fundamental Theories and Their Applications of the Calculus of Variations; Springer: Beijing, China, 2022. [Google Scholar]
- Lindfield, G.; Penny, J. Numerical Methods Using MATLAB; Oxford Press: Oxford, UK, 2019. [Google Scholar]
- Betts, J. Chapter 1—Issues in the Direct Transcription of Optimal Control Problems to Sparse Nonlinear Programs. In Computational Optimal Control; Bulirsch, R., Kraft, D., Eds.; Birkhauser Verlag: Basel, Switzerland, 1994; Volume 115, pp. 3–17. [Google Scholar]
- Betts, J. Survey of Numerical Methods for Trajectory Optimization. Adv. Astronaut. Sci. 1998, 21, 193–207. [Google Scholar] [CrossRef]
- Betts, J.T. Practical Methods for Optimal Control Using Nonlinear Programming; SIAM: Philadelphia, PA, USA, 2001. [Google Scholar]
- Perez, H.E.; Hu, X.; Dey, S.; Moura, S.J. Optimal Charging of Li-Ion Batteries with Coupled Electro-Thermal-Aging Dynamics. IEEE Trans. Veh. Technol. 2017, 66, 7761–7770. [Google Scholar] [CrossRef]
- Abdollahi, A.; Han, X.; Avvari, G.; Raghunathan, N.; Balasingam, B.; Pattipati, K.; Bar-Shalom, Y. Optimal battery charging, Part I: Minimizing time-to-charge, energy loss, and temperature rise for OCV-resistance battery model. J. Power Sources 2016, 303, 388–398. [Google Scholar] [CrossRef]
- Srinivasan, B.; Bonvin, D.; Palanki, S. Dynamic optimization of batch processes: I. Characterization of the nominal solution. Comput. Chem. Eng. 2003, 27, 185–202. [Google Scholar] [CrossRef]
- Riemann, B.J.C.; Li, J.; Adewuyi, K.; Landers, R.G.; Park, J. Control-Oriented Modeling of Lithium-Ion Batteries. J Dyn. Syst-T ASME 2020, 143, 021002. [Google Scholar] [CrossRef]
- Moura, S. Fast DFN/. 2016. Available online: https://github.com/scott-moura/dfn/blob/master/param/params.m (accessed on 23 November 2023).
- Becerra, V.M. PSOPT Optimal Control Software. 2020. Available online: https://www.psopt.net/ (accessed on 28 November 2022).
- Wang, Z.; Chen, S.; He, X.; Wang, C.; Zhao, D. A multi-factor evaluation method for the thermal runaway risk of lithium-ion batteries. J. Energy Storage 2022, 45, 103767. [Google Scholar] [CrossRef]
- Park, C.; Jaura, A.K. Dynamic Thermal Model of Li-Ion Battery for Predictive Behavior in Hybrid and Fuel Cell Vehicles. SAE Trans. 2003, 112, 1835–1842. [Google Scholar]
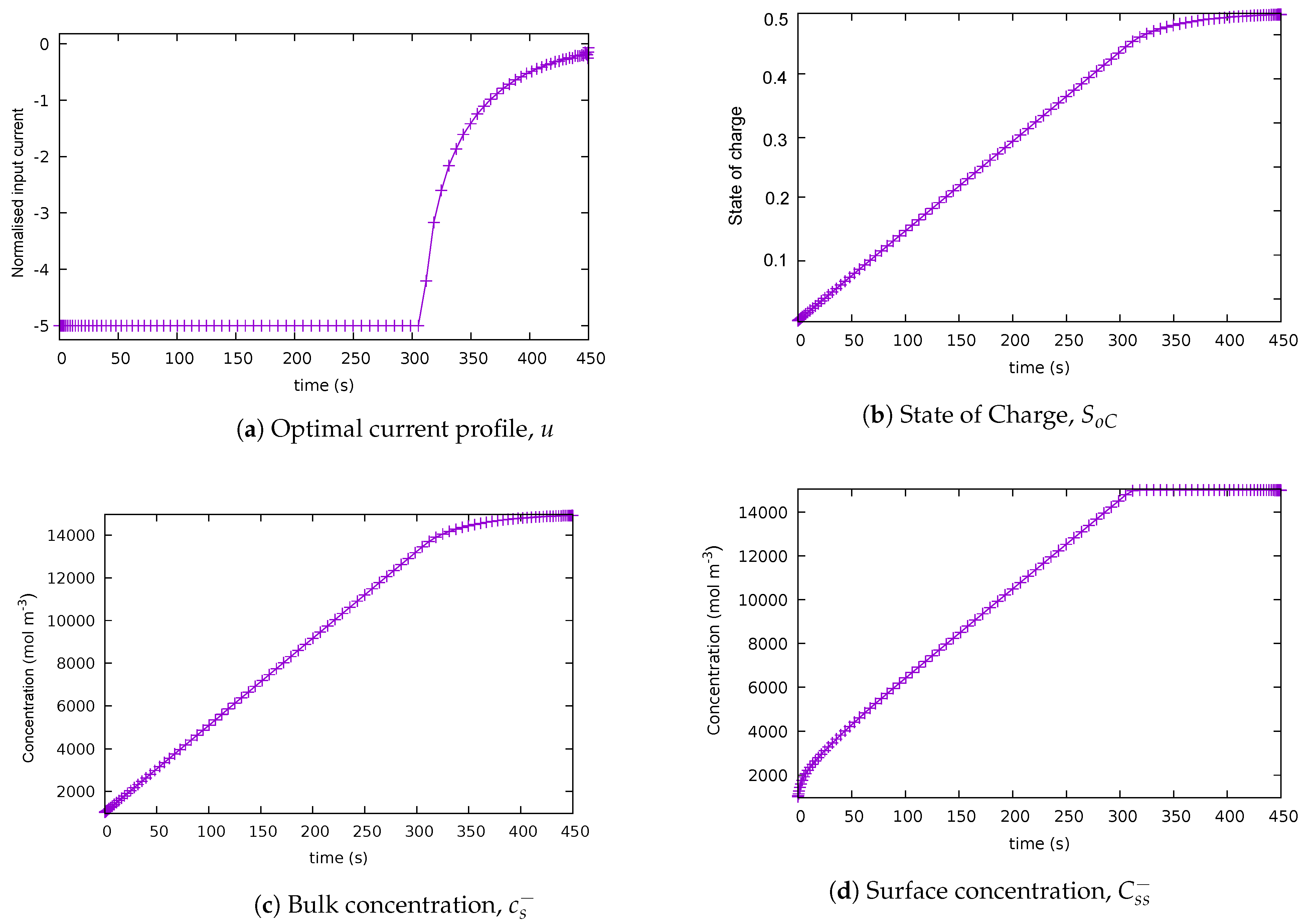

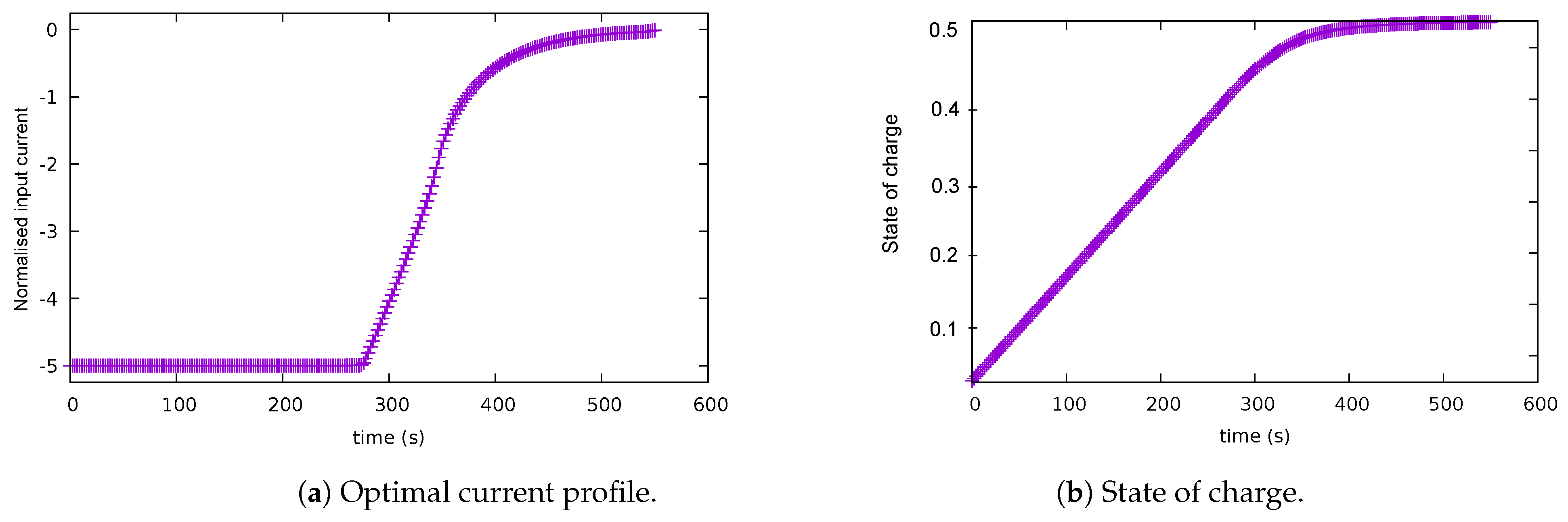
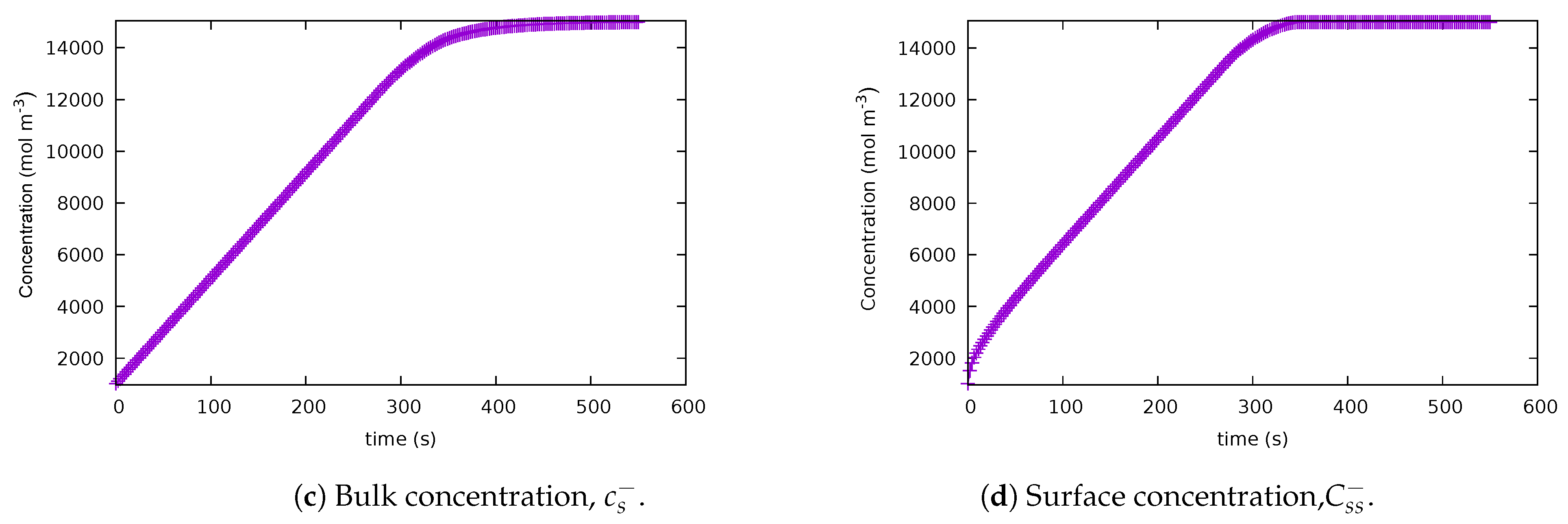
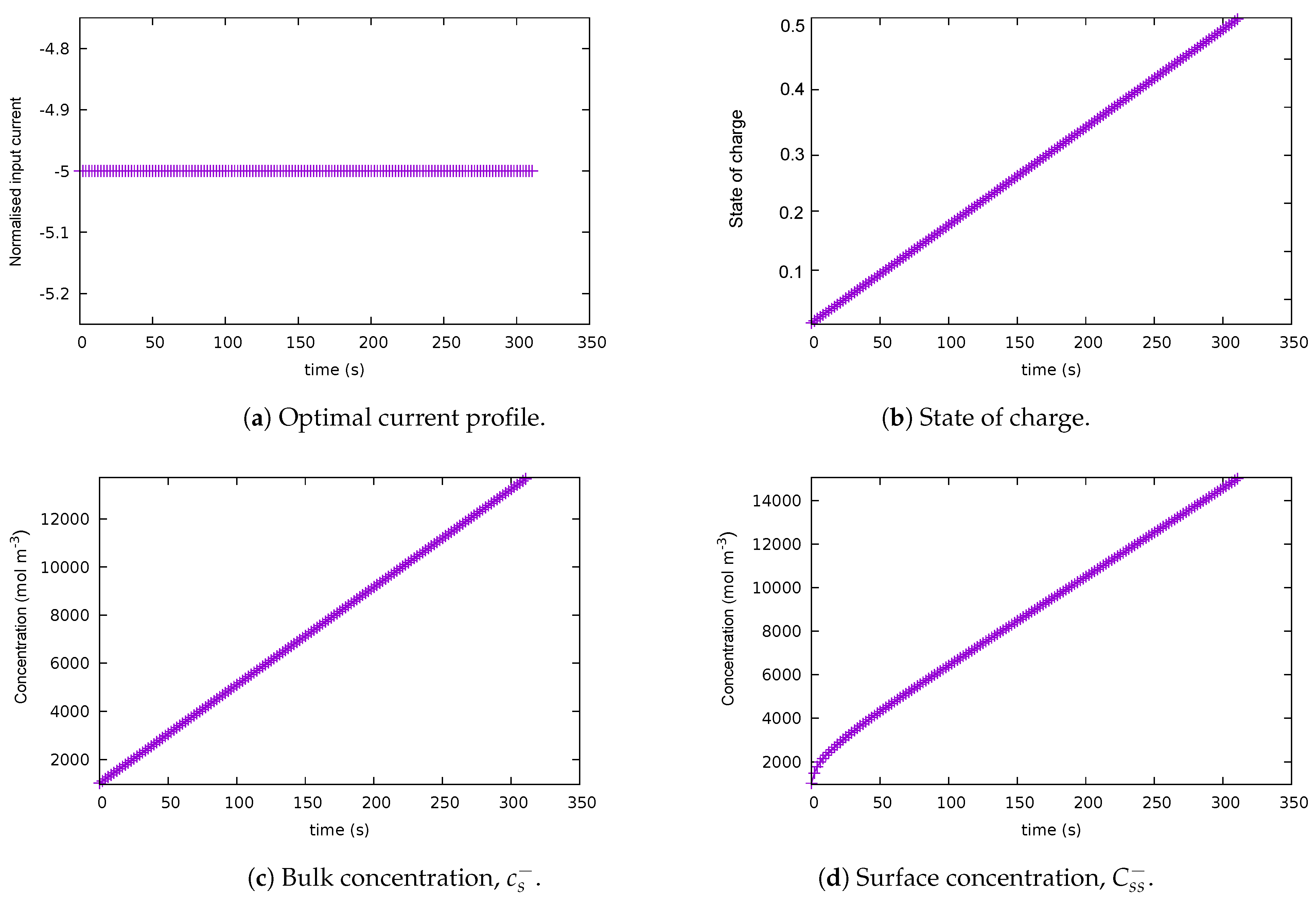


| Case | Description | Path Constraints | End Cost | Integrand | Final Time |
|---|---|---|---|---|---|
| 1 | Baseline | 0 | free | ||
| 2 | Balanced | 0 | free | ||
| 3 | Parameterised | free |
| Case | End Cost | Integrand | |||
|---|---|---|---|---|---|
| 3.1 | 1 | n/a | n/a | 0 | |
| 3.2 | 0 | 0 | |||
| 3.3 |
| Parameter | Results from [3] | This Work | |
|---|---|---|---|
| Final Time, (s) | 450 (fixed) | 450 | 0% |
| Switching Time (s) | 317 | 311 | 1.89% |
| 0.5 | 0.5 | 0% | |
| (mol/m) | 15,000 | 15,000 | 0% |
| 0C | −0.012C | 1.2% 1 |
| Final Time, (s) | Cost | Max Relative Local Error |
|---|---|---|
| 450 | 3.44 × | 8.38 × |
| 550 | 6.43 × | 1.73 × |
| = 0.3 | = 0.6 | = 0.8 | = 0.9 | = 1.0 | |
|---|---|---|---|---|---|
| 1 | 0.2131 | 0.2444 | 0.2451 | 0.2456 | 0.2473 |
| 2 | 0.1852 | 0.2358 | 0.2451 | 0.2455 | 0.2473 |
| 3 | 0.1756 | 0.2209 | 0.2436 | 0.2456 | 0.2473 |
| 4 | 0.1721 | 0.2066 | 0.2409 | 0.2455 | 0.2473 |
| 5 | 0.1705 | 0.1964 | 0.2373 | 0.2451 | 0.2473 |
| 6 | 0.1697 | 0.1896 | 0.2328 | 0.2444 | 0.2473 |
| 7 | 0.1692 | 0.1852 | 0.2237 | 0.2434 | 0.2473 |
| 8 | 0.1689 | 0.1812 | 0.2067 | 0.2423 | 0.2473 |
| 9 | 0.1686 | 0.1784 | 0.1898 | 0.2409 | 0.2473 |
| 10 | 0.1684 | 0.1764 | 0.1729 | 0.2394 | 0.2473 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gonzalez-Saenz, J.; Becerra, V. Determination of Fast Battery-Charging Profiles Using an Electrochemical Model and a Direct Optimal Control Approach. Batteries 2024, 10, 2. https://doi.org/10.3390/batteries10010002
Gonzalez-Saenz J, Becerra V. Determination of Fast Battery-Charging Profiles Using an Electrochemical Model and a Direct Optimal Control Approach. Batteries. 2024; 10(1):2. https://doi.org/10.3390/batteries10010002
Chicago/Turabian StyleGonzalez-Saenz, Julio, and Victor Becerra. 2024. "Determination of Fast Battery-Charging Profiles Using an Electrochemical Model and a Direct Optimal Control Approach" Batteries 10, no. 1: 2. https://doi.org/10.3390/batteries10010002
APA StyleGonzalez-Saenz, J., & Becerra, V. (2024). Determination of Fast Battery-Charging Profiles Using an Electrochemical Model and a Direct Optimal Control Approach. Batteries, 10(1), 2. https://doi.org/10.3390/batteries10010002







