Thermal Modeling of Lithium-Ion Battery Under High-Frequency Current Excitation and Comparative Study of Self-Heating Scheme
Abstract
:1. Introduction
1.1. Study on the Thermal Model of LIBs Under High-Frequency Current
1.2. Study on Low-Temperature Self-Heating Schemes of Different Types of Batteries
1.3. The Structure of This Article
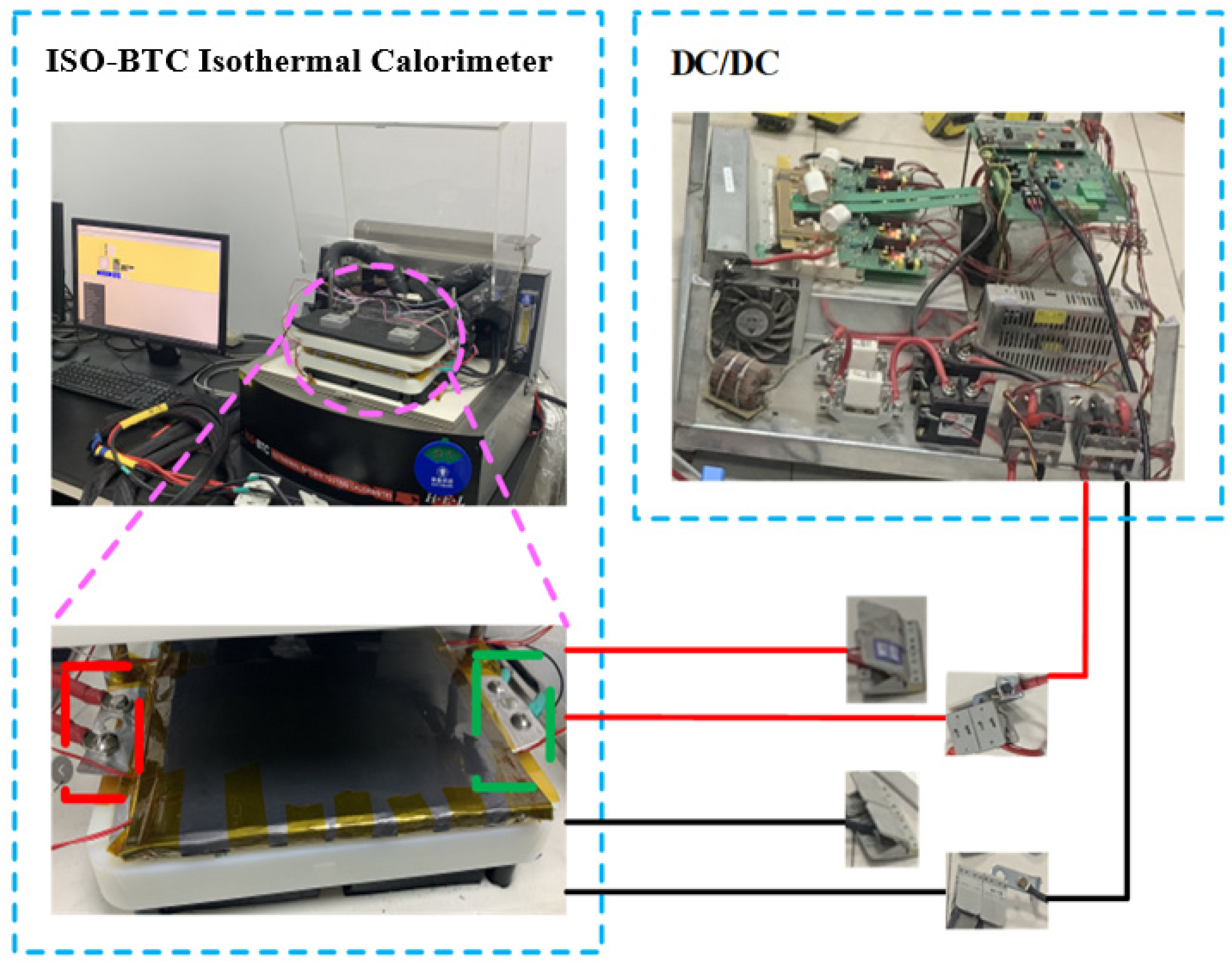
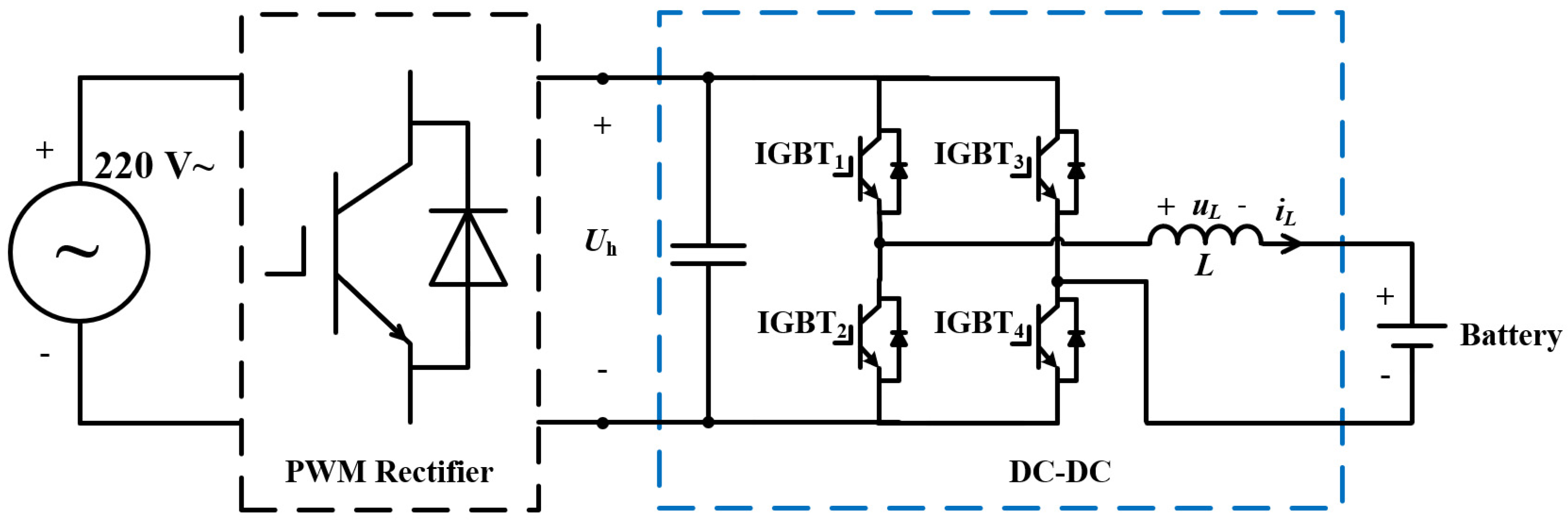
2. Experimental Setup
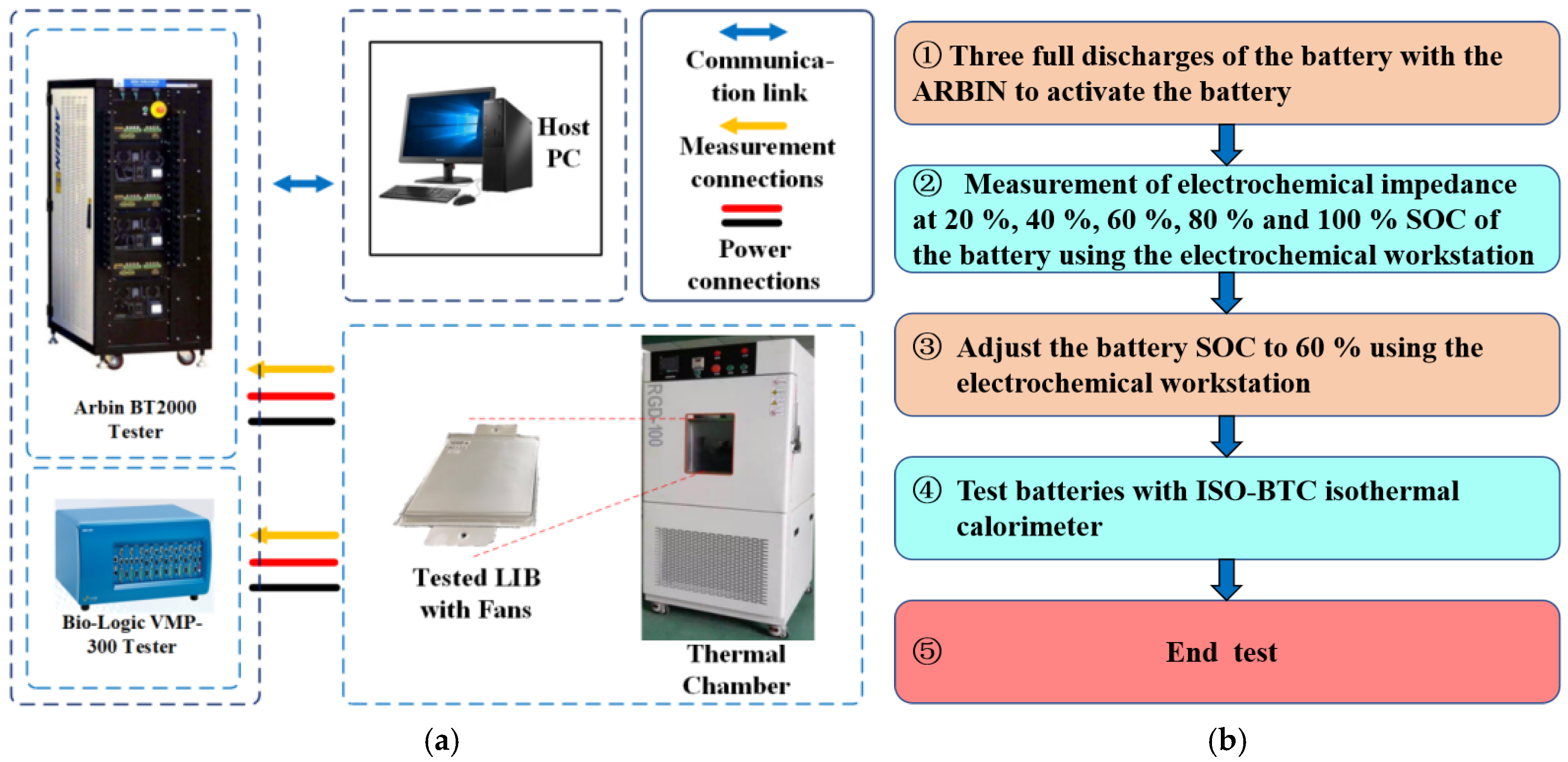
2.1. Battery Testing Systems
2.2. Battery Test Schedule
3. Related Work on Modeling
3.1. Heat Generation and Heat Transfer Mechanism of Lithium-Ion Batteries
3.2. Heat Transfer Modeling for LIBs
4. Experimental Results and Data Analysis
4.1. Calculation of Heat-Producing Power of LIBs Under High-Frequency Ripple Current Excitation
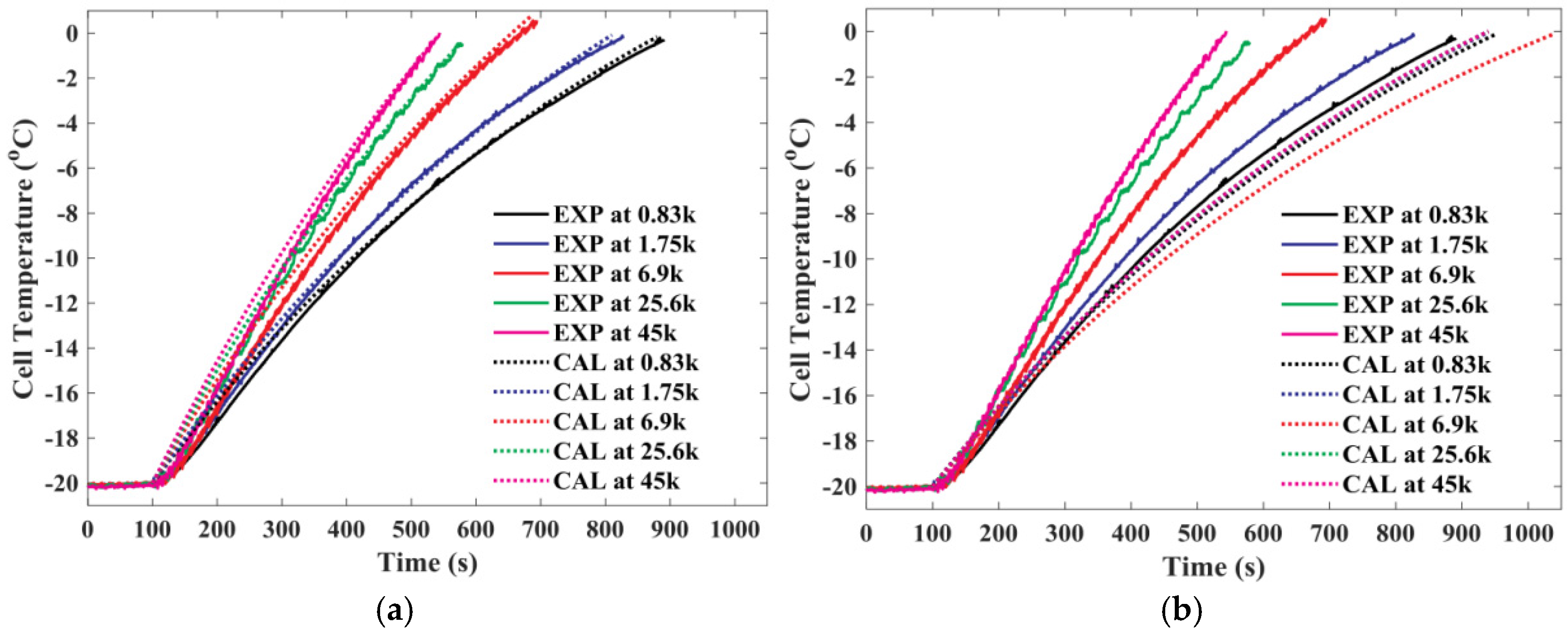
4.2. Heat Production Test of Lithium-Ion Battery Under High-Frequency Ripple Current Excitation
5. Comparative Study of Low-Temperature Self-Heating Methods
5.1. Calculation of the Minimum Self-Heating Power Required for LIBs at Low Temperatures
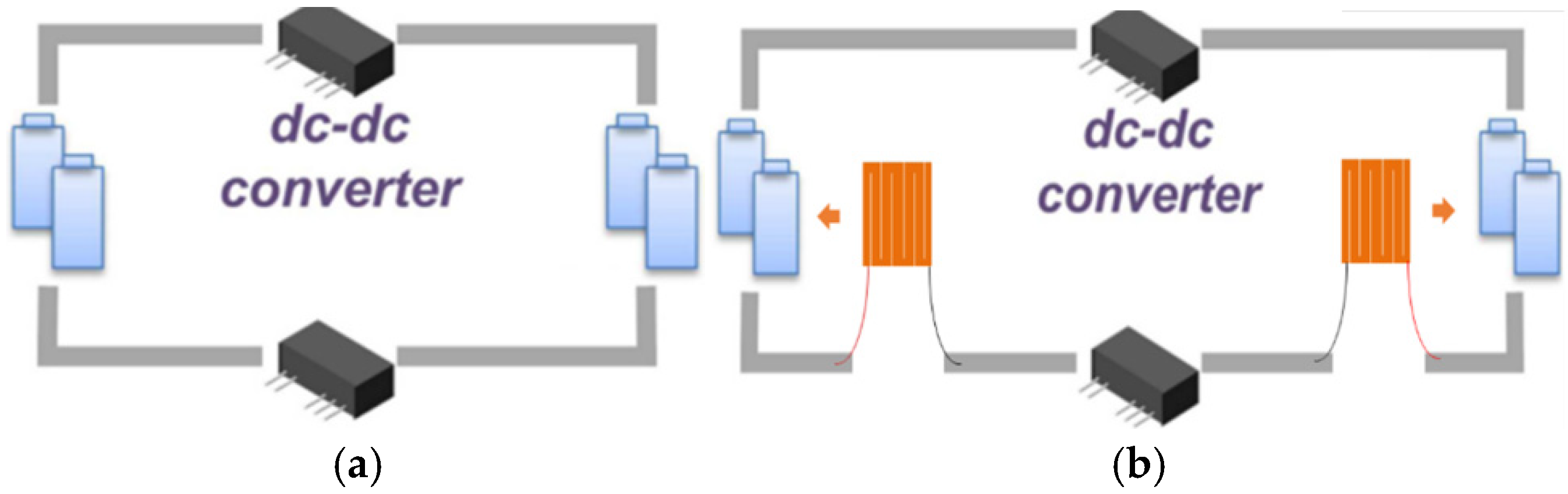
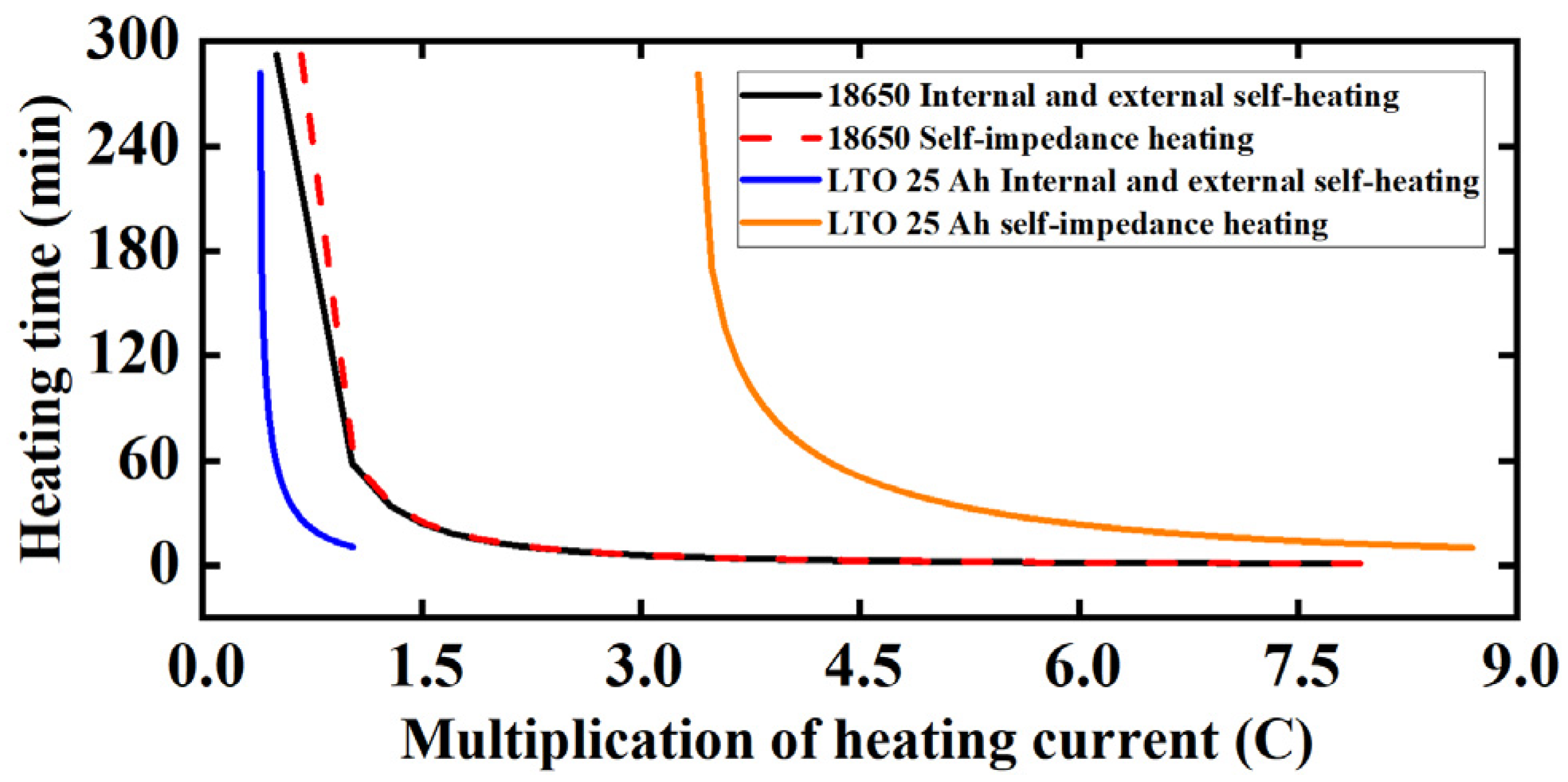
5.2. Preferred Low-Temperature Self-Heating Methods for Different Types of LIBs
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Nomenclature | DGPC | Double group power cable | |
| Z | Impedance value | DC | Direct Current |
| Zreal | Real impedance value | LTO | Lithium-titanate Battery |
| Zimag | Imaginary impedance value | SOC | State of Charge |
| P | Total power of the battery | Subscript | |
| Q | Heat produced | ave | the average voltage |
| I | Charge/discharge current | amb | ambient temperature |
| Uocv | Open circuit voltage | re | reversible reaction |
| U | Output voltage | he | heat exchange |
| η | Efficiency | hc | change of the heat capacity |
| Acronyms | me | mixing effect | |
| DC-DC | Direct Current to Direct Current converter | ha | heat build-up accumulated |
| PC | Personal computers | ht | heat exchange |
| RL | Resistance-Inductance | ocv | Open circuit voltage |
| LIB | Lithium-ion battery | om | Ohmic internal resistance |
| LIBs | Lithium-ion batteries | p | terminal voltage |
| EIS | Electrochemical impedance spectrum | bat | Battery |
| RMS | Root Mean Square | amb | Ambient |
| EXP | Experience model | hf | high-frequency |
| CAL | Theoretical calculation | real | Real part of impedance |
| EIS | Electrochemical impedance spectrum | imag | Imaginary part of impedance |
| AC | Alternating Current | imag | Imaginary part of impedance |
| SGPC | Single group power cable | pe | phase change |
| CHTC | Convective heat transfer coefficient |
References
- Tomaszewska, A.; Chu, Z.; Feng, X.; O’Kane, S.; Liu, X.; Chen, J.; Ji, C.; Endler, E.; Li, R.; Liu, L.; et al. Lithium-ion battery fast charging: A review. ETransportation 2019, 1, 100011. [Google Scholar] [CrossRef]
- Ruan, H.; Barreras, J.V.; Steinhardt, M.; Jossen, A.; Offer, G.J.; Wu, B. The heating triangle: A quantitative review of self-heating methods for lithium-ion batteries at low temperatures. J. Power Sources 2023, 581, 233484. [Google Scholar] [CrossRef]
- Yang, X.-G.; Zhang, G.; Ge, S.; Wang, C.-Y. Fast charging of lithium-ion batteries at all temperatures. Proc. Natl. Acad. Sci. USA 2018, 115, 7266–7271. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Ge, H.; Li, Z.; Ding, Z. Internal heating of lithium-ion batteries using alternating current based on the heat generation model in frequency domain. J. Power Sources 2015, 273, 1030–1037. [Google Scholar] [CrossRef]
- Zhu, J.; Sun, Z.; Wei, X.; Dai, H.; Gu, W. Experimental investigations of an AC pulse heating method for vehicular high power lithium-ion batteries at subzero temperatures. J. Power Sources 2017, 367, 145–157. [Google Scholar] [CrossRef]
- Qu, Z.G.; Jiang, Z.Y.; Wang, Q. Experimental study on pulse self–heating of lithium–ion battery at low temperature. Int. J. Heat Mass Transf. 2019, 135, 696–705. [Google Scholar] [CrossRef]
- Ji, Y.; Wang, C.Y. Heating strategies for Li-ion batteries operated from subzero temperatures. Electrochim. Acta 2013, 107, 664–674. [Google Scholar] [CrossRef]
- Ruan, H.; Sun, B.; Jiang, J.; Su, X.; He, X.; Ma, S.; Gao, W. Optimal switching temperature for multi-objective heated-charging of lithium-ion batteries at subzero temperatures. J. Power Sources 2023, 562, 232775. [Google Scholar] [CrossRef]
- Hu, X.; Li, S.; Peng, H. A comparative study of equivalent circuit models for Li-ion batteries. J. Power Sources 2012, 198, 359–367. [Google Scholar] [CrossRef]
- Juang, L.W.; Kollmeyer, P.J.; Jahns, T.M.; Lorenz, R.D. Improved nonlinear model for electrode voltage–current relationship for more consistent online battery system identification. IEEE Trans. Ind. Appl. 2013, 49, 1480–1488. [Google Scholar] [CrossRef]
- Liu, S.; Jiang, J.; Shi, W.; Ma, Z.; Wang, L.Y.; Guo, H. Butler–volmer-equation-based electrical model for high-power lithium titanate batteries used in electric vehicles. IEEE Trans. Ind. Electron. 2015, 62, 7557–7568. [Google Scholar] [CrossRef]
- Chen, A.; Zhang, W.; Zhang, C.; Huang, W.; Liu, S. A temperature and current rate adaptive model for high-power lithium-titanate batteries used in electric vehicles. IEEE Trans. Ind. Electron. 2019, 67, 9492–9502. [Google Scholar] [CrossRef]
- Li, H.; Jiang, J.; Zhang, W.; Zhang, L.; Yang, Y.; Chen, A.; Fan, X. High-accuracy parameters identification of non-linear electrical model for high-energy lithium-ion capacitor. IEEE Trans. Intell. Transp. Syst. 2020, 22, 651–660. [Google Scholar] [CrossRef]
- Sun, B.; He, X.; Zhang, W.; Ruan, H.; Su, X.; Jiang, J. Study of parameters identification method of Li-ion battery model for EV power profile based on transient characteristics data. IEEE Trans. Intell. Transp. Syst. 2020, 22, 661–672. [Google Scholar] [CrossRef]
- Ruan, H.; Sun, B.; Cruden, A.; Zhu, T.; Jiang, J.; He, X.; Su, X.; Ghoniem, E. Optimal external heating resistance enabling rapid compound self-heating for lithium-ion batteries at low temperatures. Appl. Therm. Eng. 2022, 200, 117536. [Google Scholar] [CrossRef]
- Shang, Y.; Xia, B.; Cui, N.; Zhang, C.; Mi, C.C. An automotive onboard AC heater without external power supplies for lithium-ion batteries at low temperatures. IEEE Trans. Power Electron. 2017, 33, 7759–7769. [Google Scholar] [CrossRef]
- Shang, Y.; Zhu, C.; Lu, G.; Zhang, Q.; Cui, N.; Zhang, C. Modeling and analysis of high-frequency alternating-current heating for lithium-ion batteries under low-temperature operations. J. Power Sources 2020, 450, 227435. [Google Scholar] [CrossRef]
- Hu, Z.; Liu, F.; Chen, P.; Xie, C.; Huang, M.; Hu, S.; Lu, S. Experimental study on the mechanism of frequency-dependent heat in AC preheating of lithium-ion battery at low temperature. Appl. Therm. Eng. 2022, 214, 118860. [Google Scholar] [CrossRef]
- Li, J.-Q.; Sun, D. Lithium-ion batteries modeling and optimization strategies for sinusoidal alternating current heating at low temperature. Energy Procedia 2018, 152, 562–567. [Google Scholar] [CrossRef]
- Li, J.; Sun, D.; Chai, Z.; Jiang, H.; Sun, C. Sinusoidal alternating current heating strategy and optimization of lithium-ion batteries with a thermo-electric coupled model. Energy 2019, 186, 115798. [Google Scholar] [CrossRef]
- Fan, X.; Zhang, W.; Wang, Z.; An, F.; Li, H.; Jiang, J. Simplified battery pack modeling considering inconsistency and evolution of current distribution. IEEE Trans. Intell. Transp. Syst. 2020, 22, 630–639. [Google Scholar] [CrossRef]
- Zhang, J.; Ci, S.; Sharif, H.; Alahmad, M. Modeling discharge behavior of multicell battery. IEEE Trans. Energy Convers. 2010, 25, 1133–1141. [Google Scholar] [CrossRef]
- Shi, W.; Hu, X.; Jin, C.; Jiang, J.; Zhang, Y.; Yip, T. Effects of imbalanced currents on large-format LiFePO4/graphite batteries systems connected in parallel. J. Power Sources 2016, 313, 198–204. [Google Scholar] [CrossRef]
- Sung, W.; Hwang, D.S.; Jeong, B.-J.; Lee, J.; Kwon, T. Electrochemical battery model and its parameter estimator for use in a battery management system of plug-in hybrid electric vehicles. Int. J. Automot. Technol. 2016, 17, 493–508. [Google Scholar] [CrossRef]
- Ruan, H.; Jiang, J.; Sun, B.; Zhang, W.; Gao, W.; Wang, L.Y.; Ma, Z. A rapid low-temperature internal heating strategy with optimal frequency based on constant polarization voltage for lithium-ion batteries. Appl. Energy 2016, 177, 771–782. [Google Scholar] [CrossRef]
- Ruan, H.; Jiang, J.; Ju, Q.; Sun, B.; Cheng, G. A reduced wide-temperature-range electro-thermal model and thermal parameters determination for lithium-ion batteries. Energy Procedia 2017, 105, 805–810. [Google Scholar] [CrossRef]
- Waldmann, T.; Wilka, M.; Kasper, M.; Fleischhammer, M.; Wohlfahrt-Mehrens, M. Temperature dependent ageing mechanisms in Lithium-ion batteries–A Post-Mortem study. J. Power Sources 2014, 262, 129–135. [Google Scholar] [CrossRef]
- Jiang, J.; Ruan, H.; Sun, B.; Wang, L.; Gao, W.; Zhang, W. A low-temperature internal heating strategy without lifetime reduction for large-size automotive lithium-ion battery pack. Appl. Energy 2018, 230, 257–266. [Google Scholar] [CrossRef]
- Kizilel, R.; Lateef, A.; Sabbah, R.; Farid, M.; Selman, J.; Al-Hallaj, S. Passive control of temperature excursion and uniformity in high-energy Li-ion battery packs at high current and ambient temperature. J. Power Sources 2008, 183, 370–375. [Google Scholar] [CrossRef]
- Ruan, H.; Sun, B.; Zhang, W.; Su, X.; He, X. Quantitative analysis of performance decrease and fast-charging limitation for lithium-ion batteries at low temperature based on the electrochemical model. IEEE Trans. Intell. Transp. Syst. 2020, 22, 640–650. [Google Scholar] [CrossRef]
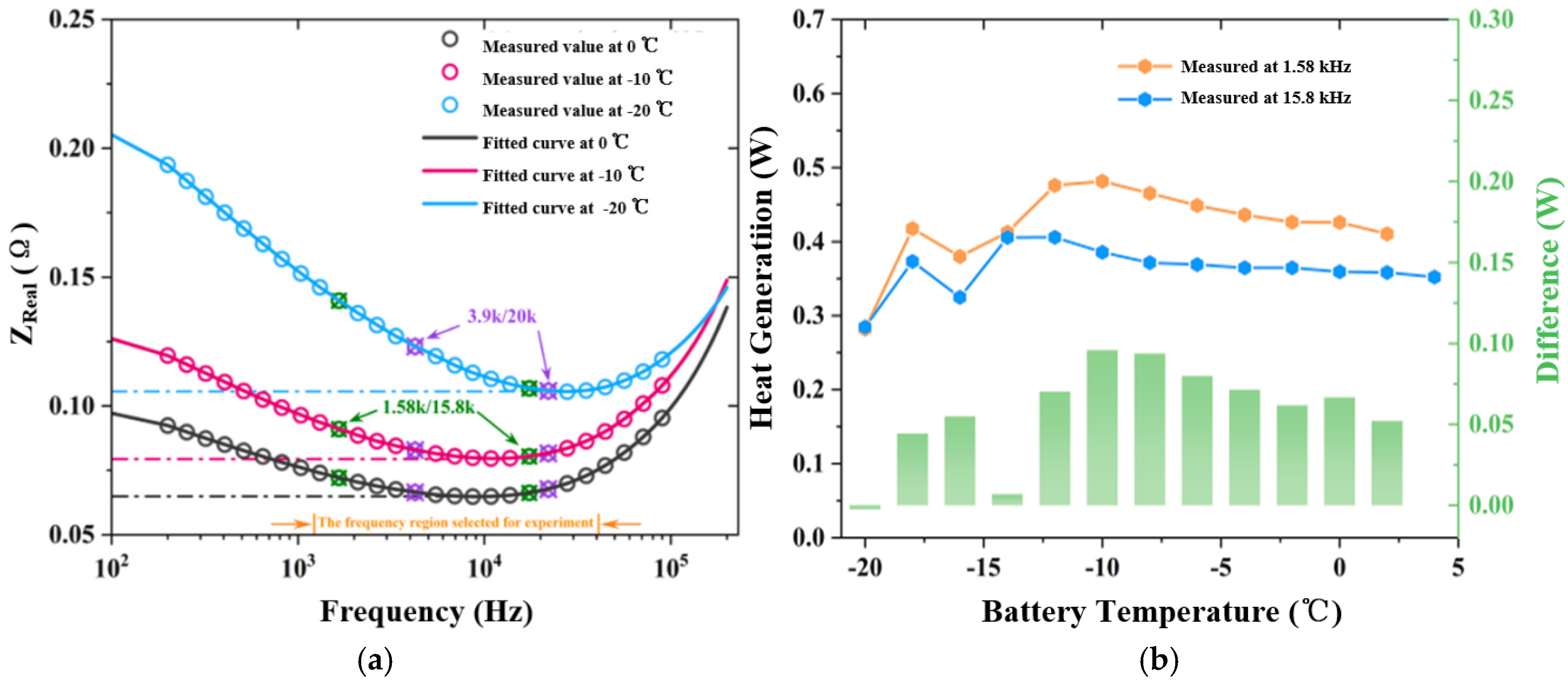

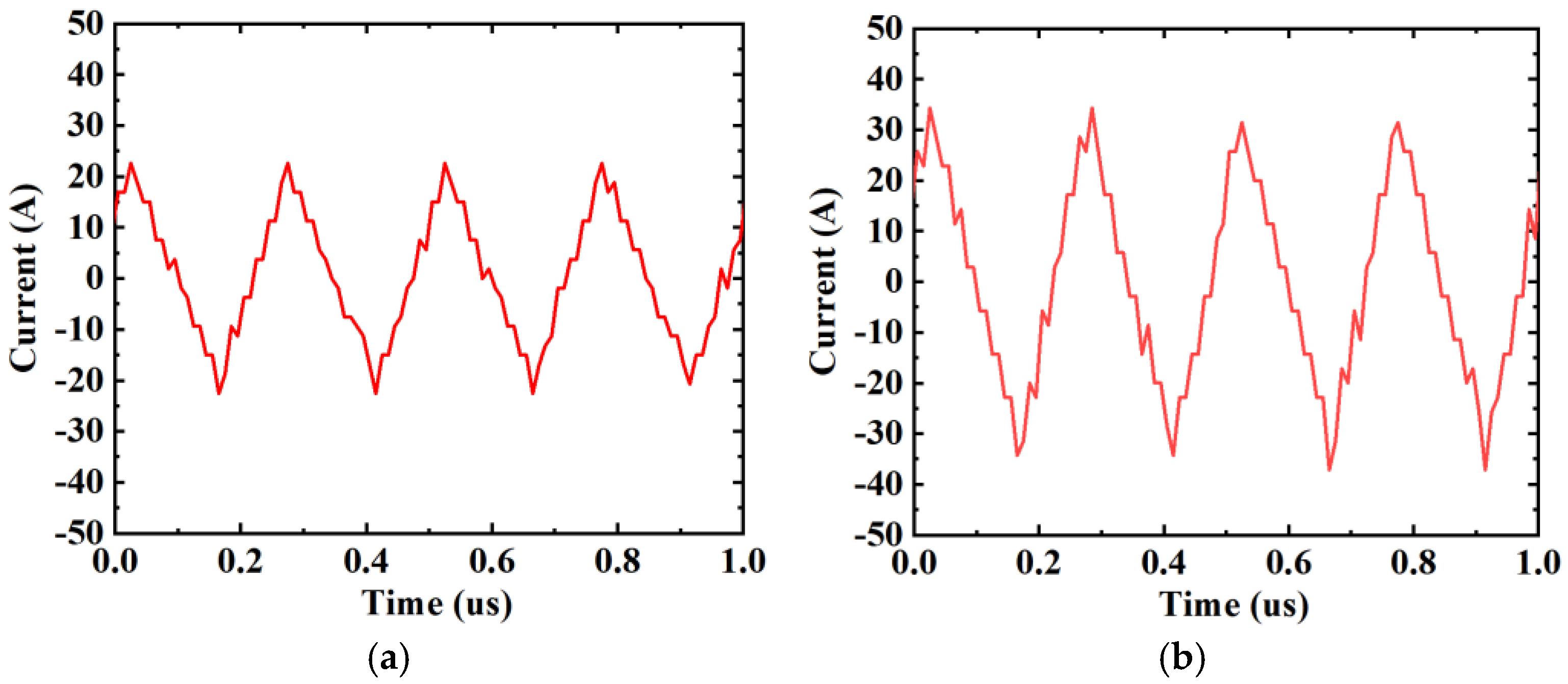
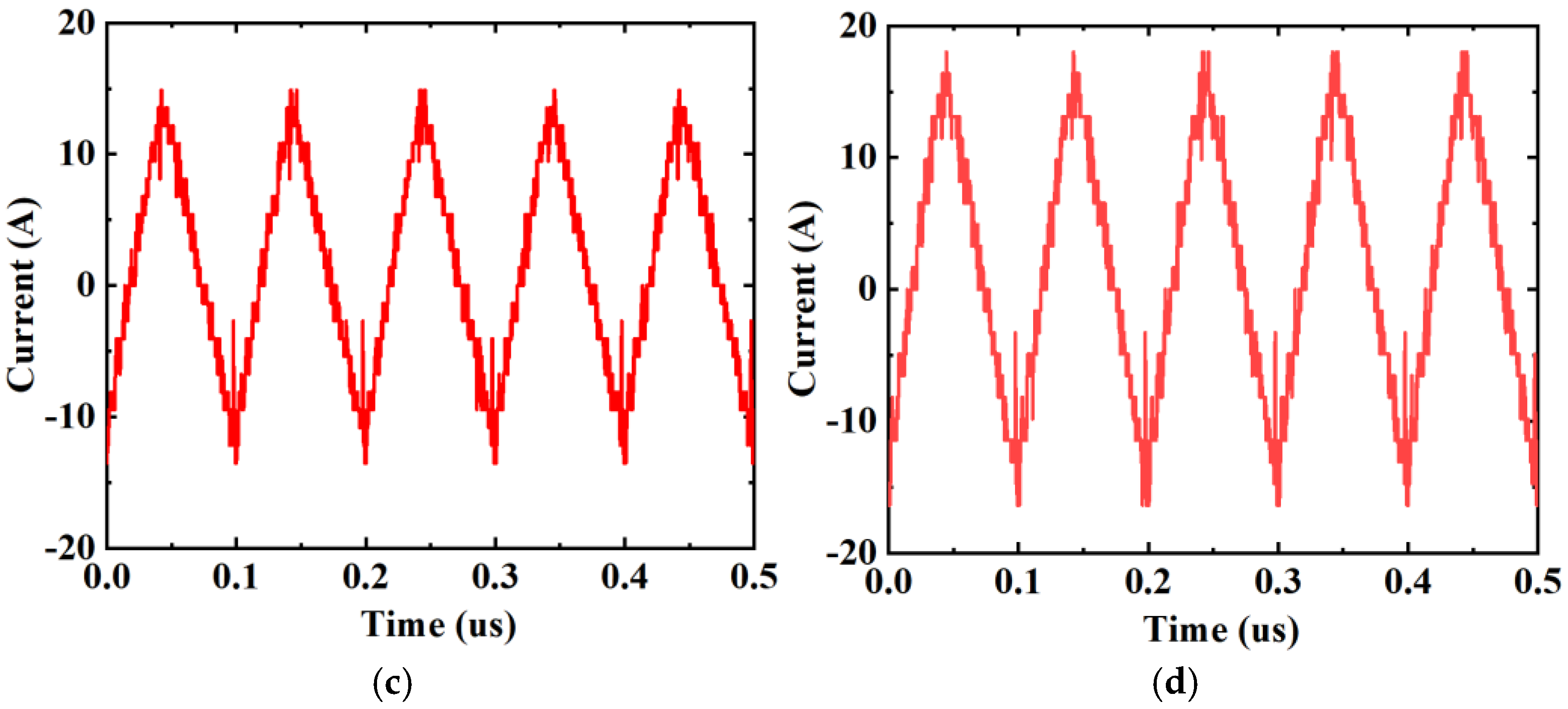

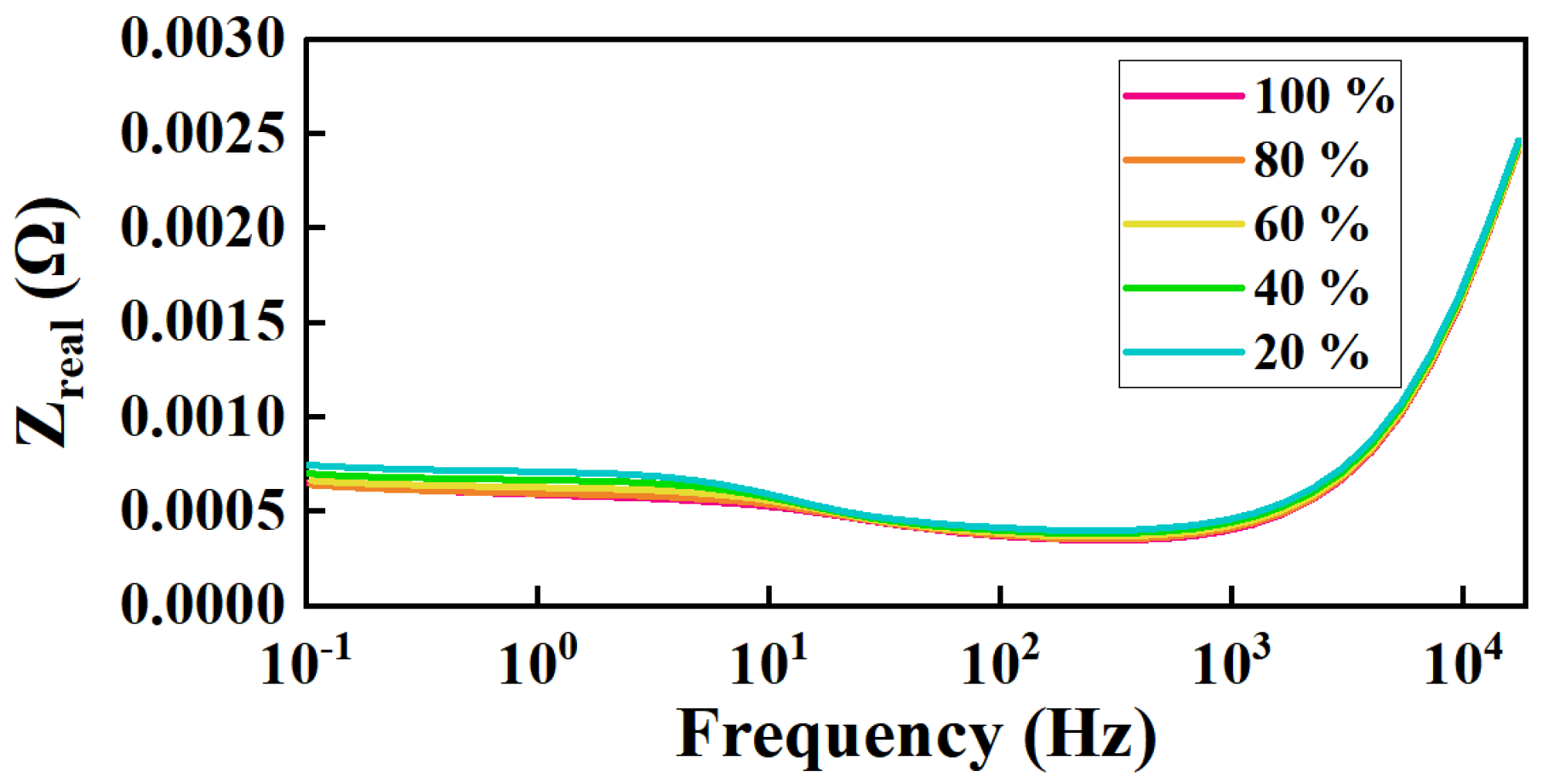


| Frequency (kHz) | Impedance (Ω) | RMS Value (A) | Heating Power of (W) | Theoretical Calculation (W) | Measured Value (W) | Gap (W) | Real Impedance Difference (Ω) |
|---|---|---|---|---|---|---|---|
| 1.58 kHz | 0.130 | 1.4 | 0.01412 | 0.14152 | 0.28 | 0.13847 | 0.1413 |
| 2 | 0.0288 | 0.26 | 0.55 | 0.29 | 0.145 | ||
| 15.8 kHz | 0.105 | 1.625 | 0.0475 | 0.1861 | 0.28 | 0.0939 | 0.0711 |
| 2.2 | 0.087 | 0.297 | 0.525 | 0.0228 | 0.0942 |
| Battery Parameters | Characteristics |
|---|---|
| Anode material | LTO |
| Cathode material | NMC + LiCoO2 |
| Nominal capacity | 25.0 Ah |
| Nominal voltage | 2.35 V |
| Charge condition | CC 25 A, 2.8 V cutoff |
| Discharge condition | CC 25 A, 1.5 V cutoff |
| Serial Number | Type of High-Frequency Current | Frequency of High-Frequency Current (kHz) | Peak—Peak Value of High-Frequency Current (A) | RMS Value of High-Frequency Current (A) | Wire Connection Methods | The Measured Impedance of the DC Contact (mΩ) |
|---|---|---|---|---|---|---|
| 1 | Triangular Wave | 4 | 45.2 | 13.15 | SGPC | 0.448 |
| 2 | Triangular Wave | 4 | 68.6 | 19.97 | SGPC | |
| 3 | Triangular Wave | 10 | 28.4 | 7.89 | SGPC | |
| 4 | Triangular Wave | 10 | 34.4 | 9.61 | SGPC | |
| 5 | Triangular Wave | 10 | 28.4 | 7.89 | DGPC | 0.196 |
| 6 | Triangular Wave | 10 | 34.4 | 9.61 | DGPC |
| Serial Number | Measured Value (W) | Theoretical Calculation (W) | RMS Value (A) | The Calculated Impedance (W) | Wire Connection Methods | Contact Impedance (mΩ) |
|---|---|---|---|---|---|---|
| 1 | 0.257 | 0.119 | 13.15 | 0.138 | SGPC | 0.844 |
| 3 | 0.228 | 0.079 | 7.89 | 0.149 | SGPCe | 2.392 |
| 5 | 0.147 | 0.072 | 7.89 | 0.075 | SGPC | 1.157 |
| Serial Number | Measured Value | Theoretical Calculation (W) | Contact Impedance (mΩ) | Contact Impedance Thermal Power (W) | Production Power After Removal of Contact Impedance (W) | Relative Error (%) | Relative Error Between After Considering Contact Impedance (%) |
|---|---|---|---|---|---|---|---|
| 2 | 0.579 | 0.276 | 0.844 | 0.302 | 0.242 | 109.8 | −12.3 |
| 4 | 0.318 | 0.113 | 2.392 | 0.205 | 0.097 | 181.4 | −14.2 |
| 6 | 0.241 | 0.116 | 1.157 | 0.125 | 0.134 | 107.7 | 15.8 |
| Battery Number | Battery Types | Rated Capacity (Ah) | Mass (kg) | Specific Heat Capacity (J·kg−1·K−1) | CHTC (m2) | Ambition Temperature (℃) | Battery Temperature (℃) | Minimum Power Required (W) | Average Real Part Impedance (mΩ) | Minimum Required Pulse Current Values |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 18650 NCM [20] | 2.15 | 0.045 | 994.65 | 4.18 × 10−3 | −15 | 0 | 1.28 | 35 | 6.04 A (2.81 C) |
| 2 | 18650 NCM [17] | 2.5 | 0.046 | 1720 | 4.18 × 10−3 | −15 | 0 | 2.20 | 43 | 7.16 A (2.86 C) |
| 3 | 18650 NCM (Figure 11 in this paper) | 2.6 | 0.048 | 1048 | 4.18 × 10−3 | −15 | 0 | 1.43 | 30 | 6.90 A (2.65 C) |
| 4 | 18650 NCM [25] | 2.75 | 0.045 | 1147 | 4.18 × 10−3 | −15 | 0 | 1.46 | 30 | 6.98 A (2.54 C) |
| 5 | 18650 NCM [5] | 2.8 | 0.046 | 1720 | 4.18 × 10−3 | −15 | 0 | 2.20 | 45 | 7.00 A (2.50 C) |
| 6 | 18650 NCM [18] | 2.9 | 0.047 | 1618 | 4.18 × 10−3 | −15 | 0 | 2.12 | 108 | 4.43 A (1.53 C) |
| 7 | Pouch battery LTO [26] | 8 | 0.300 | 927.57 | 0.037 | −15 | 0 | 8.16 | 1.1 | 86.11 A (10.76 C) |
| 8 | Pouch battery LTO (Table 2 in this paper) | 25 | 0.695 | 1253 | 0.108 | −15 | 0 | 25.36 | 0.5 | 225.22 A (9.01 C) |
| 9 | Pouch battery LiFePO4 [5] | 30 | 0.675 | 1000~1500 (hypothetical) | 0.05679 | −15 | 0 | 19.17~28.24 | 2 | 97.91–118.82 A (3.26~3.96 C) |
| Battery Number | Battery Types | Rated Capacity (Ah) | Mass (kg) | Energy Density (Wh/L) | Energy Density (Wh/kg) | Average real part Impedance of the Battery (mΩ) | Minimum Required Current Values |
|---|---|---|---|---|---|---|---|
| 1 | 18650 NCM [20] | 2.15 | 0.045 | 467.94 | 164.68 | 35 | 6.04 A (2.81 C) |
| 2 | 18650 NCM [17] | 2.5 | 0.046 | 559.23 | 201.09 | 43 | 7.16 A (2.86 C) |
| 3 | 18650 NCM (Figure 11 in this paper) | 2.6 | 0.048 | 581.60 | 200.42 | 30 | 6.90 A (2.65 C) |
| 4 | 18650 NCM [25] | 2.75 | 0.045 | 598.53 | 220.00 | 30 | 6.98 A (2.54 C) |
| 5 | 18650 NCM [5] | 2.8 | 0.046 | 609.41 | 219.13 | 45 | 7.00 A (2.50 C) |
| 6 | 18650 NCM [18] | 2.9 | 0.047 | 631.18 | 222.13 | 108 | 4.43 A (1.53 C) |
| 7 | Pouch battery LTO [26] | 8 | 0.300 | 207.49 | 96.00 | 1.1 | 86.11 A (10.76 C) |
| 8 | Pouch battery LTO (Table 2 in this paper) | 25 | 0.695 | 196.52 | 82.79 | 0.5 | 225.22 A (9.01 C) |
| 9 | Pouch battery LiFePO4 [5] | 30 | 0.675 | 307.84 | 142.22 | 2 | 97.91–118.82 A (3.26~3.96 C) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Chen, J.; Ma, Y.; Liu, W.; Tang, L.; Liu, B. Thermal Modeling of Lithium-Ion Battery Under High-Frequency Current Excitation and Comparative Study of Self-Heating Scheme. Batteries 2024, 10, 419. https://doi.org/10.3390/batteries10120419
Li H, Chen J, Ma Y, Liu W, Tang L, Liu B. Thermal Modeling of Lithium-Ion Battery Under High-Frequency Current Excitation and Comparative Study of Self-Heating Scheme. Batteries. 2024; 10(12):419. https://doi.org/10.3390/batteries10120419
Chicago/Turabian StyleLi, Hao, Jianan Chen, Yingtao Ma, Weizhi Liu, Lei Tang, and Bing Liu. 2024. "Thermal Modeling of Lithium-Ion Battery Under High-Frequency Current Excitation and Comparative Study of Self-Heating Scheme" Batteries 10, no. 12: 419. https://doi.org/10.3390/batteries10120419
APA StyleLi, H., Chen, J., Ma, Y., Liu, W., Tang, L., & Liu, B. (2024). Thermal Modeling of Lithium-Ion Battery Under High-Frequency Current Excitation and Comparative Study of Self-Heating Scheme. Batteries, 10(12), 419. https://doi.org/10.3390/batteries10120419






