Flexible Deep Learning-Based State of Health Estimation of Lithium-Ion Batteries with Features Extracted from Partial Charging Curves
Abstract
:1. Introduction
1.1. Literature Review
1.2. Motivation and Contribution
- (1)
- The proposed method employs a straightforward multi-perceptron layer (MLP) for accomplishing SOH estimation via randomly sampled short-term charging voltage curves. This approach extracts several features from a statistical standpoint and does not require a designated voltage range for feature extraction. As a result, it offers exceptional flexibility concerning input ranges and a consistent number of features for the MLP model.
- (2)
- The introduced approach extracts features both locally and globally from randomly sampled charging voltage curves. This is achieved by identifying specific points of curves and employing curve fitting parameters. The method employs multiple parameters to characterize the curves, which offer diverse insights compared to other proposed feature extraction techniques. Experimental findings indicate that incorporating these local and global features enhances estimation results when compared to utilizing raw datasets alone. The paper also underscores the significance of the introduced features.
- (3)
- The validity of the proposed method is demonstrated across three distinct battery datasets, encompassing varying operational conditions and sampling frequencies. Despite the extended curve lengths due to feature extraction, the number of inputs for the MLP remains constant. Notably, results indicate enhanced accuracy as curve lengths increase. Furthermore, the MLP exhibits superior generalization capabilities in comparison to other machine learning techniques.
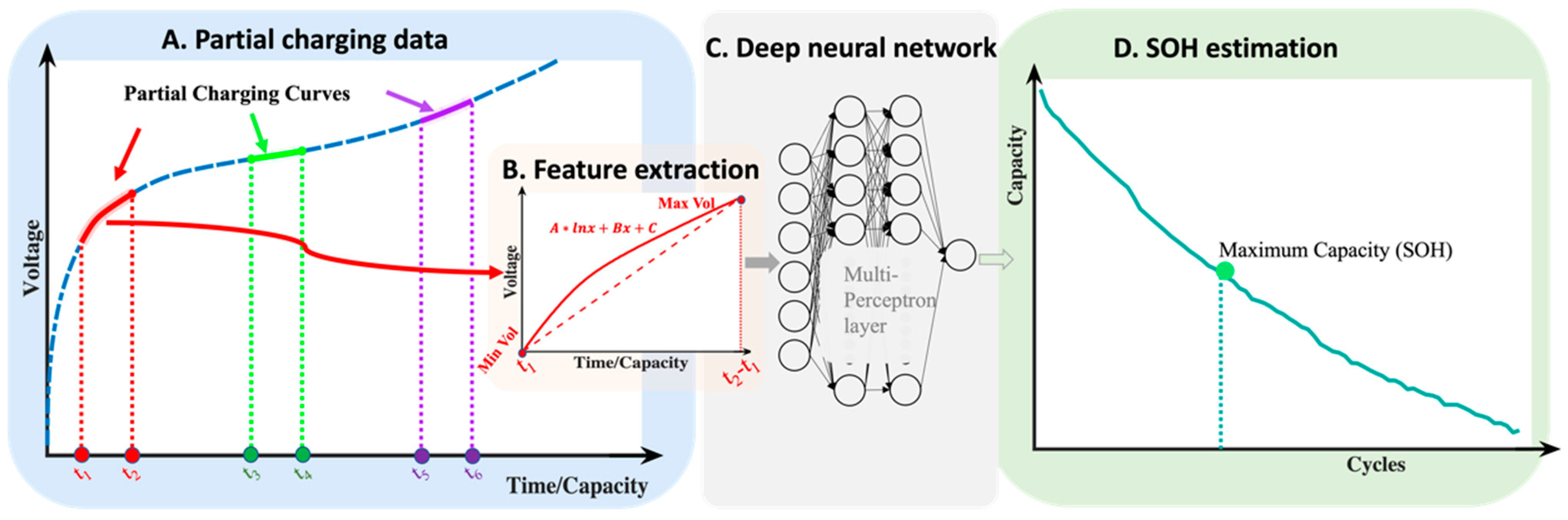
2. Method
2.1. Problem Definition
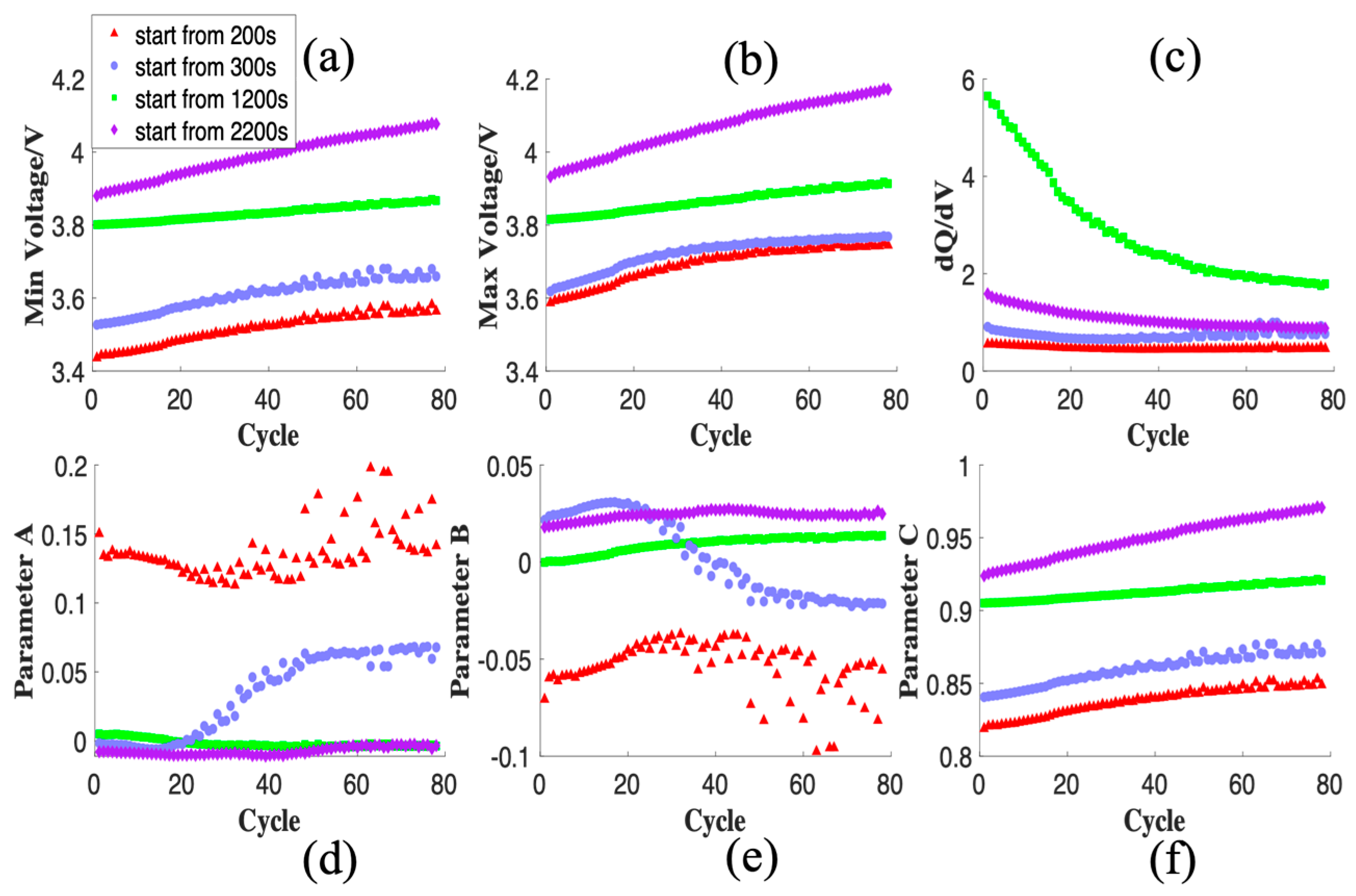
2.2. Feature Extraction and Analysis
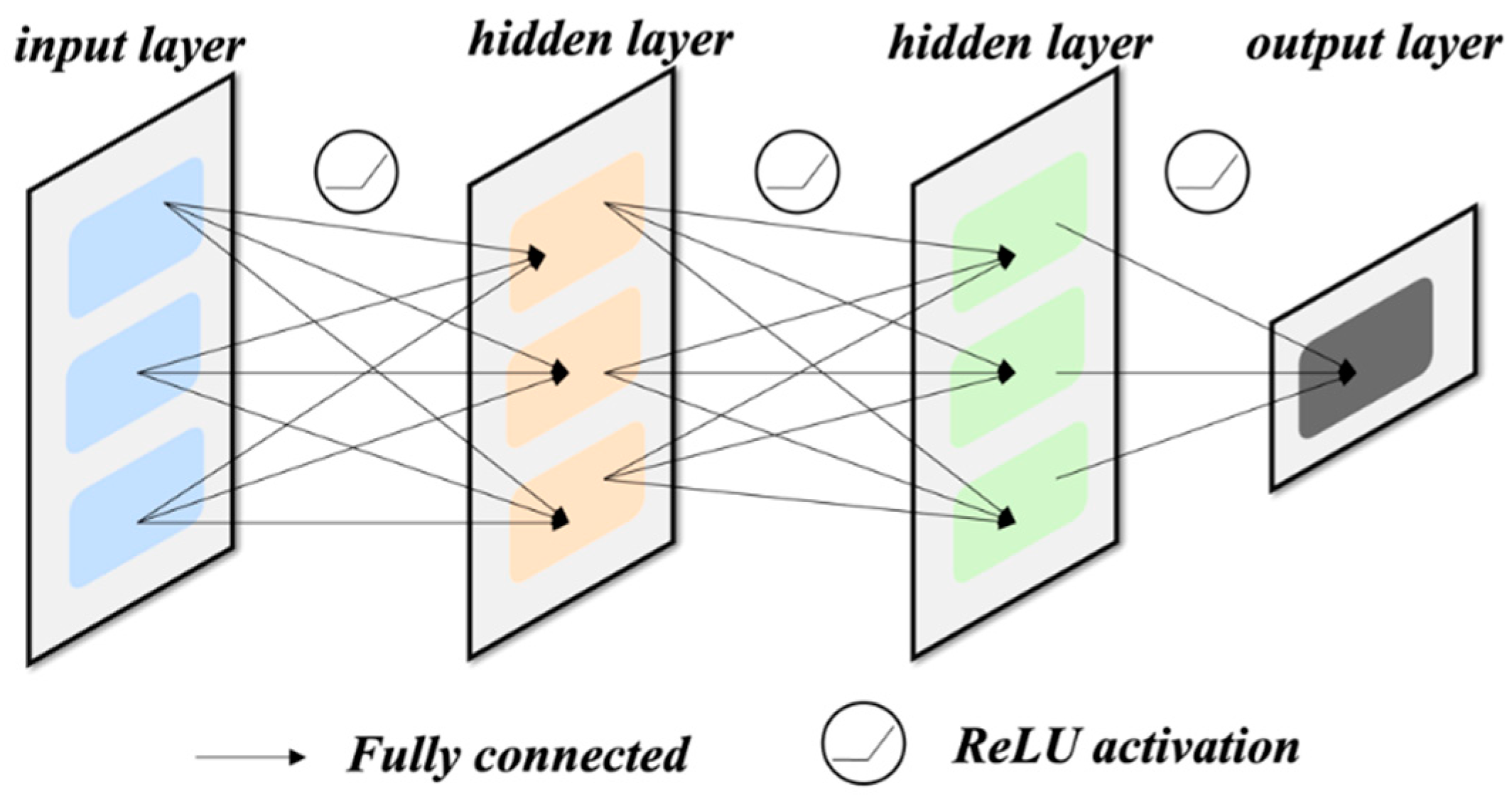
2.3. Muti-Layer Perceptron
2.4. Training Details
3. Results and Discussion
3.1. Ablation Study
3.2. Simultaneous Estimation of SOH
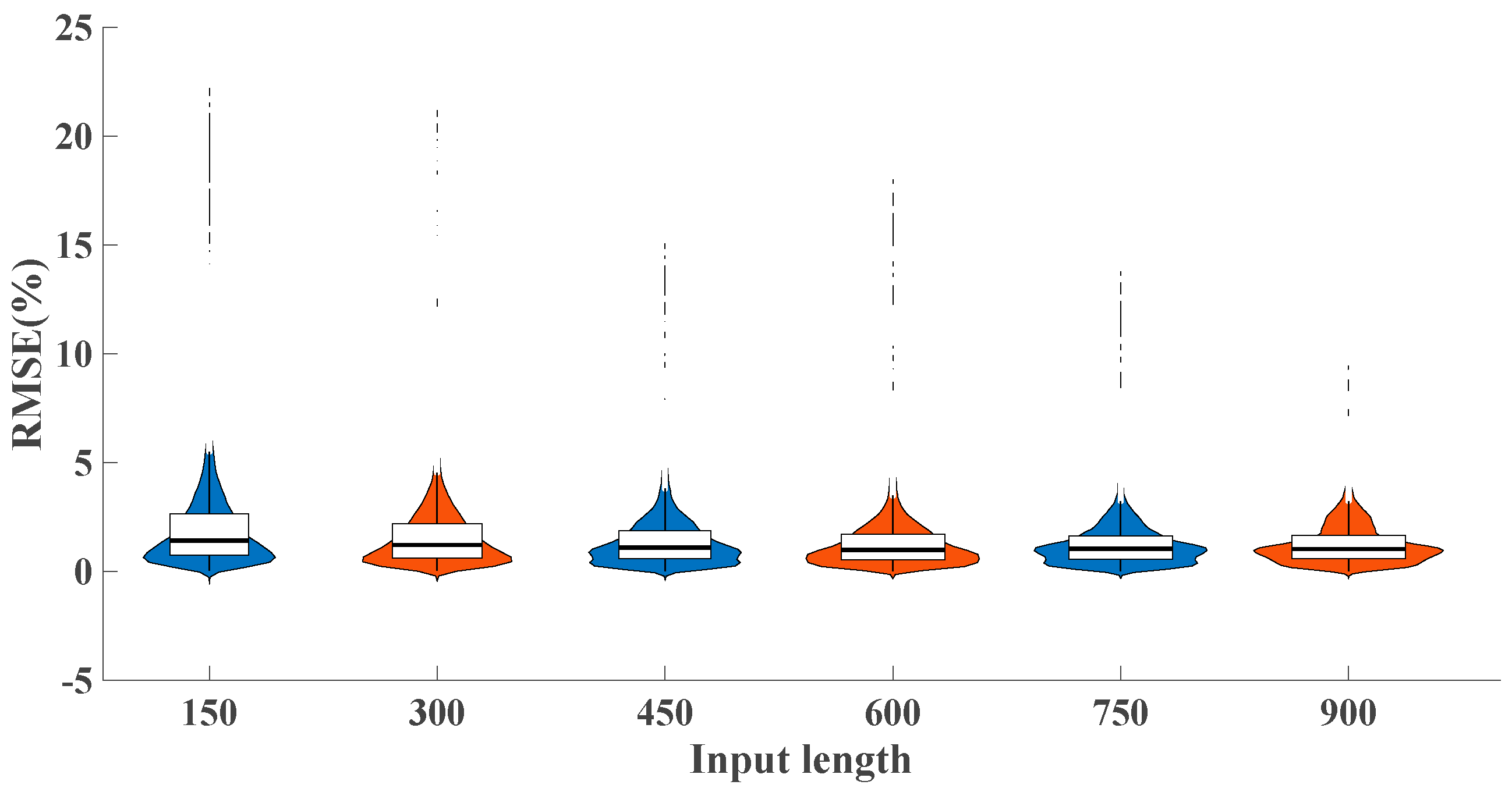
3.3. Influence of Length of Input Series
3.4. A Comparison with Classic Machine Learning Methods
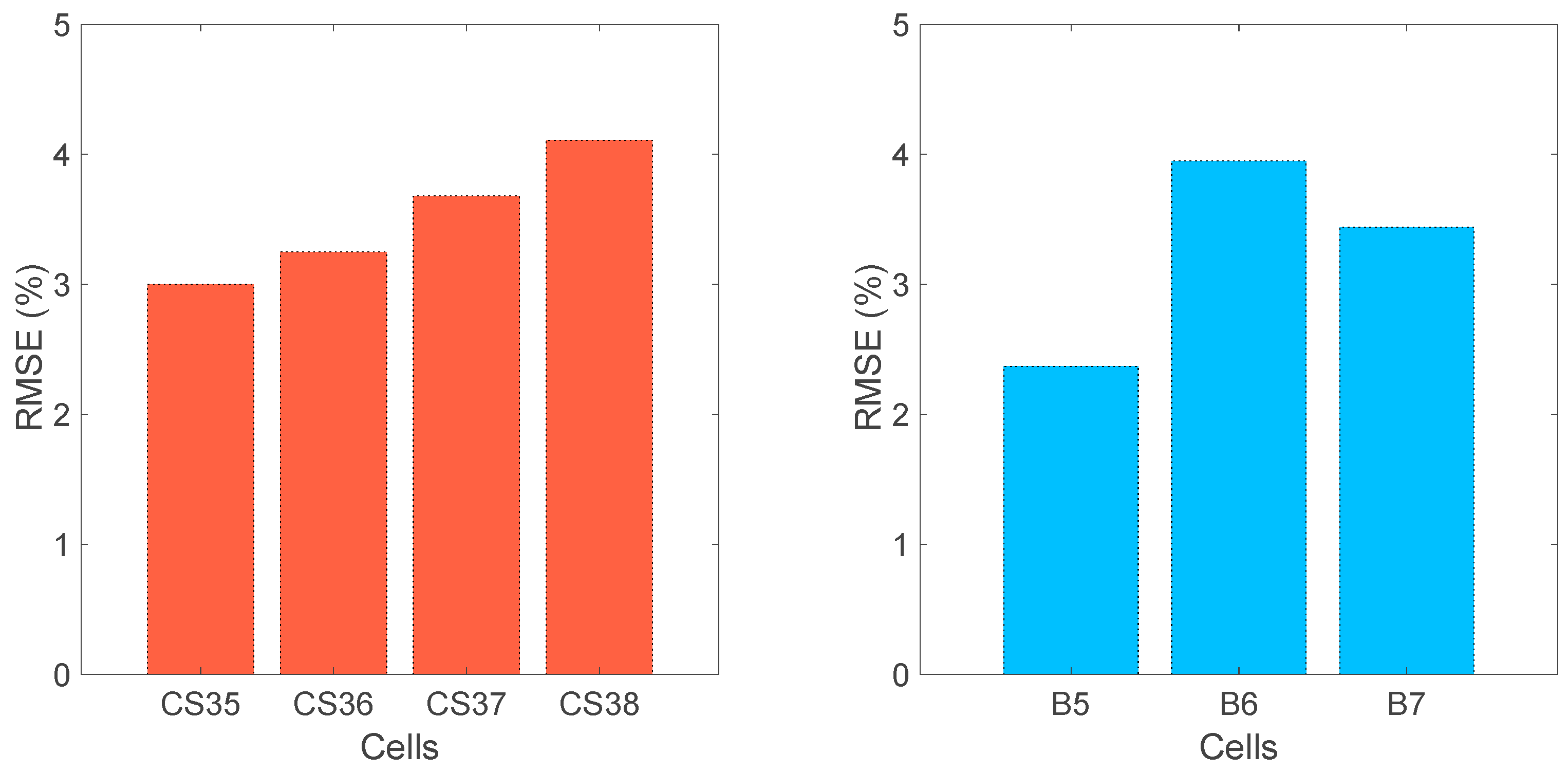
3.5. Validation of Different Batteries and Working Conditions
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xie, J.; Lu, Y.-C. A retrospective on lithium-ion batteries. Nat. Commun. 2020, 11, 2499. [Google Scholar] [CrossRef] [PubMed]
- Han, X.; Lu, L.; Zheng, Y.; Feng, X.; Li, Z.; Li, J.; Ouyang, M. A review on the key issues of the lithium ion battery degradation among the whole life cycle. eTransportation 2019, 1, 100005. [Google Scholar] [CrossRef]
- Vennam, G. A survey on lithium-ion battery internal and external degradation modeling and state of health estimation. J. Energy Storage 2022, 52, 104720. [Google Scholar] [CrossRef]
- Zhang, L.; Hu, X.; Wang, Z.; Sun, F.; Dorrell, D.G. A review of supercapacitor modeling, estimation, and applications: A control/management perspective. Renew. Sustain. Energy Rev. 2018, 81, 1868–1878. [Google Scholar] [CrossRef]
- Messing, M.; Shoa, T.; Habibi, S. Estimating battery state of health using electrochemical impedance spectroscopy and the relaxation effect. J. Energy Storage 2021, 43, 103210. [Google Scholar] [CrossRef]
- Jiang, B.; Zhu, J.; Wang, X.; Wei, X.; Shang, W.; Dai, H. A comparative study of different features extracted from electrochemical impedance spectroscopy in state of health estimation for lithium-ion batteries. Appl. Energy 2022, 322, 119502. [Google Scholar] [CrossRef]
- Xu, L.; Lin, X.; Xie, Y.; Hu, X. Enabling high-fidelity electrochemical P2D modeling of lithium-ion batteries via fast and non-destructive parameter identification. Energy Storage Mater. 2022, 45, 952–968. [Google Scholar] [CrossRef]
- Chen, C.; Xiong, R.; Shen, W. A lithium-ion battery-in-the-loop approach to test and validate multiscale dual h infinity filters for state-of-charge and capacity estimation. IEEE Trans. Power Electron. 2018, 33, 332–342. [Google Scholar] [CrossRef]
- Zheng, L.; Zhang, L.; Zhu, J.; Wang, G.; Jiang, J. Co-estimation of state-of-charge, capacity and resistance for lithium-ion batteries based on a high-fidelity electrochemical model. Appl. Energy 2016, 180, 424–434. [Google Scholar] [CrossRef]
- Topan, P.A.; Ramadan, M.N.; Fathoni, G.; Cahyadi, A.I.; Wahyunggoro, O. State of Charge (SOC) and State of Health (SOH) estimation on lithium polymer battery via Kalman filter. In Proceedings of the 2016 2nd International Conference on Science and Technology-Computer (ICST), Yogyakarta, Indonesia, 27–28 October 2016; pp. 93–96. [Google Scholar] [CrossRef]
- Cheng, Z.; Yang, L.; Sun, X. Estimation of SOC and SOH of lithium-ion batteries based on adaptive square-root traceless kalman filtering algorithm. Chin. J. Electr. Eng. 2008, 38, 2384–2393. [Google Scholar]
- Liu, F.; Shao, C.; Su, W.; Liu, Y. Online joint estimator of key states for battery based on a new equivalent circuit model. J. Energy Storage 2022, 52, 104780. [Google Scholar] [CrossRef]
- Tran, M.-K.; Mathew, M.; Janhunen, S.; Panchal, S.; Raahemifar, K.; Fraser, R.; Fowler, M. A comprehensive equivalent circuit model for lithium-ion batteries, incorporating the effects of state of health, state of charge, and temperature on model parameters. J. Energy Storage 2021, 43, 103252. [Google Scholar] [CrossRef]
- Li, Y.; Vilathgamuwa, M.; Farrell, T.; Choi, S.; Tran, N.; Teague, J. A Physics-Based Distributed-Parameter Equivalent Circuit Model for Lithium-Ion Batteries. Electrochim. Acta 2019, 299, 451–469. [Google Scholar] [CrossRef]
- Li, X.; Yuan, C.; Li, X.; Wang, Z. State of health estimation for Li-Ion battery using incremental capacity analysis and Gaussian process regression. Energy 2020, 190, 116467. [Google Scholar] [CrossRef]
- Wang, L.; Zhao, X.; Liu, L.; Pan, C. State of health estimation of battery modules via differential voltage analysis with local data symmetry method. Electrochim. Acta 2017, 256, 81–89. [Google Scholar] [CrossRef]
- Wang, L.; Pan, C.; Liu, L.; Cheng, Y.; Zhao, X. On-board state of health estimation of LiFePO4 battery pack through differential voltage analysis. Appl. Energy 2016, 168, 465–472. [Google Scholar] [CrossRef]
- Weng, C.; Cui, Y.; Sun, J.; Peng, H. On-board state of health monitoring of lithiumion batteries using incremental capacity analysis with support vector regression. J. Power Sources 2013, 235, 36–44. [Google Scholar] [CrossRef]
- Li, Y.; Abdel-Monem, M.; Gopalakrishnan, R.; Berecibar, M.; Nanini-Maury, E.; Omar, N.; van den Bossche, P.; Van Mierlo, J. A quick on-line state of health estimation method for Li-ion battery with incremental capacity curves processed by Gaussian filter. J. Power Sources 2018, 373, 40–53. [Google Scholar] [CrossRef]
- Tang, X.; Zou, C.; Yao, K.; Chen, G.; Liu, B.; He, Z.; Gao, F. A fast estimation algorithm for lithium-ion battery state of health. J. Power Sources 2018, 396, 453–458. [Google Scholar] [CrossRef]
- Zhu, J.; Wang, Y.; Huang, Y.; Bhushan Gopaluni, R.; Cao, Y.; Heere, M.; Mühlbauer, M.J.; Mereacre, L.; Dai, H.; Liu, X.; et al. Data-driven capacity estimation of commercial lithium-ion batteries from voltage relaxation. Nat. Commun. 2022, 13, 2261. [Google Scholar] [CrossRef]
- Xiong, R.; Li, L.; Tian, J. Towards a smarter battery management system: A critical review on battery state of health monitoring methods. J. Power Sources 2018, 405, 18–29. [Google Scholar] [CrossRef]
- Richardson, R.R.; Birkl, C.R.; Osborne, M.A.; Howey, D.A. Gaussian Process Regression for In Situ Capacity Estimation of Lithium-Ion Batteries. IEEE Trans. Ind. Inform. 2019, 15, 127–138. [Google Scholar] [CrossRef]
- Tian, J.; Xiong, R.; Shen, W.; Lu, J.; Yang, X.-G. Deep neural network battery charging curve prediction using 30 points collected in 10 min. Joule 2021, 5, 1521–1534. [Google Scholar] [CrossRef]
- Tian, J.; Xiong, R.; Shen, W.; Lu, J.; Sun, F. Flexible battery state of health and state of charge estimation using partial charging data and deep learning. Energy Storage Mater. 2022, 51, 372–381. [Google Scholar] [CrossRef]
- Zhao, Y.; Wang, Z.; Shen, Z.; Sun, F. Assessment of battery utilization and energy consumption in the large-scale development of urban electric vehicles. Proc. Natl. Acad. Sci. USA 2021, 118, e2017318118. [Google Scholar] [CrossRef]
- Birkl, C. Oxford Battery Degradation Dataset 1. 2017. Available online: https://ora.ox.ac.uk/objects/uuid:03ba4b01-cfed-46d3-9b1a-7d4a7bdf6fac (accessed on 10 May 2023).
- Li, Y.; Zou, C.; Berecibar, M.; Nanini-Maury, E.; Chan, J.C.-W.; van den Bossche, P.; Van Mierlo, J.; Omar, N. Random forest regression for online capacity estimation of lithium-ion batteries. Appl. Energy 2018, 232, 197–210. [Google Scholar] [CrossRef]
- Xing, Y.; Ma, E.W.M.; Tsui, K.L.; Pecht, M. An ensemble model for predicting the remaining useful performance of lithium-ion batteries. Microelectron. Reliab. 2013, 53, 811–820. [Google Scholar] [CrossRef]
- He, W.; Williard, N.; Osterman, M.; Pecht, M. Prognostics of lithium-ion batteries based on Dempster-Shafer theory and the Bayesian Monte Carlo method. J. Power Sources 2011, 196, 10314–10321. [Google Scholar] [CrossRef]
- Bole, B.; Kulkarni, C.; Daigle, M. Randomized Battery Usage Data Set. NASA AMES Progn. Data Repos, 70. 2014. Available online: https://ti.arc.nasa.gov/tech/dash/groups/pcoe/prognosticdata-repository/#batteryrnddischarge (accessed on 10 May 2023).
- Roman, D.; Saxena, S.; Robu, V.; Pecht, M.; Flynn, D. Machine learning pipeline for battery state-of-health estimation. Nat. Mach. Intell. 2021, 3, 447–456. [Google Scholar] [CrossRef]
- Li, W.; Sengupta, N.; Dechent, P.; Howey, D.; Annaswamy, A.; Sauer, D.U. Online capacity estimation of lithium-ion batteries with deep long short-term memory networks. J. Power Sources 2021, 482, 228863. [Google Scholar] [CrossRef]
- Chang, C.; Wang, Q.; Jiang, J.; Wu, T. Lithium-ion battery state of health estimation using the incremental capacity and wavelet neural networks with genetic algorithm. J. Energy Storage 2021, 38, 102570. [Google Scholar] [CrossRef]
- Hossain Lipu, M.S.; Ansari, S.; Miah, M.d.S.; Meraj, S.T.; Hasan, K.; Shihavuddin, A.S.M.; Hannan, M.A.; Muttaqi, K.M.; Hussain, A. Deep learning enabled state of charge, state of health and remaining useful life estimation for smart battery management system: Methods, implementations, issues and prospects. J. Energy Storage 2022, 55, 105752. [Google Scholar] [CrossRef]
- Tolstikhin, I.O.; Houlsby, N.; Kolesnikov, A.; Beyer, L.; Zhai, X.; Unterthiner, T.; Yung, J.; Steiner, A.; Keysers, D.; Uszkoreit, J.; et al. MLP-Mixer: An all-MLP Architecture for Vision. In Proceedings of the Advances in Neural Information Processing Systems 34 (NeurIPS 2021), Online, 6–14 December 2021; pp. 24261–24272. [Google Scholar]
- Agarap, A.F. Deep Learning Using Rectified Linear Units (ReLU). arXiv 2018, arXiv:1803.08375. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Lu, J.; Xiong, R.; Tian, J.; Wang, C.; Sun, F. Deep learning to estimate lithium-ion battery state of health without additional degradation experiments. Nat. Commun. 2023, 14, 2760. [Google Scholar] [CrossRef] [PubMed]
- Chen, T.; He, T.; Benesty, M.; Khotilovich, V.; Tang, Y.; Cho, H.; Zhou, T.; Xgboost: Extreme Gradient Boosting. R Package Version 0.6-4. 2017. Available online: https://CRAN.R-project.org/package=xgboost (accessed on 10 May 2023).
- Zheng, Y.; Ouyang, M.; Han, X.; Lu, L.; Li, J. Investigating the error sources of the online state of charge estimation methods for lithium-ion batteries in electric vehicles. J. Power Sources 2018, 377, 161–188. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]

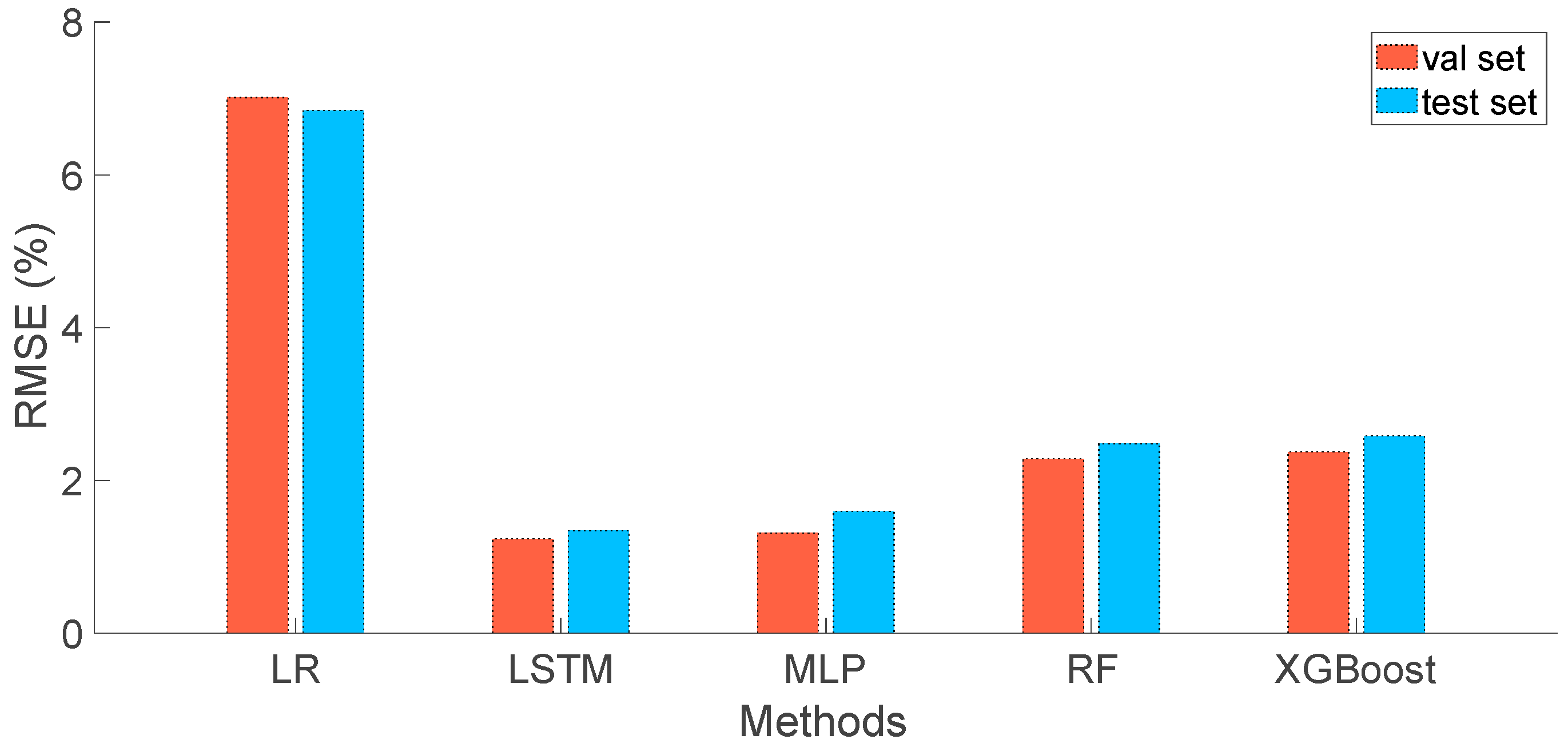
| Component/RMSE (%) | Validation | Test |
|---|---|---|
| XGBoost (raw data) | 1.87 | 4.26 |
| XGBoost (local features) | 3.72 | 5.74 |
| XGBoost (local and global feature) | 0.84 | 3.38 |
| MLP (local and global feature) | 1.32 | 1.87 |
| Features | min vol | max vol | dQ/dV | A | B | C |
|---|---|---|---|---|---|---|
| Importance (%) | 8.24 | 16.75 | 12.03 | 19.63 | 11.27 | 13.06 |
| Cell Index | Cell 5 | Cell 6 | Cell 7 | Cell 8 |
|---|---|---|---|---|
| RMSE (%) | 0.99 | 1.17 | 1.65 | 1.46 |
| Input Length | 150 | 300 | 450 | 600 | 750 | 900 |
|---|---|---|---|---|---|---|
| RMSE (%) | 1.91 | 1.59 | 1.37 | 1.27 | 1.24 | 1.24 |
| Dataset | Cathode Materials | Nominal Capacity (Ah) | Current (A) | Sample Period (s) |
|---|---|---|---|---|
| CALCE | LiCoO2 | 1.1 | 0.55 | 30 |
| NASA | Not reported | 2.0 | 1.50 | 3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lai, R.; Li, X.; Wang, J. Flexible Deep Learning-Based State of Health Estimation of Lithium-Ion Batteries with Features Extracted from Partial Charging Curves. Batteries 2024, 10, 164. https://doi.org/10.3390/batteries10050164
Lai R, Li X, Wang J. Flexible Deep Learning-Based State of Health Estimation of Lithium-Ion Batteries with Features Extracted from Partial Charging Curves. Batteries. 2024; 10(5):164. https://doi.org/10.3390/batteries10050164
Chicago/Turabian StyleLai, Rucong, Xiaoyu Li, and Jie Wang. 2024. "Flexible Deep Learning-Based State of Health Estimation of Lithium-Ion Batteries with Features Extracted from Partial Charging Curves" Batteries 10, no. 5: 164. https://doi.org/10.3390/batteries10050164
APA StyleLai, R., Li, X., & Wang, J. (2024). Flexible Deep Learning-Based State of Health Estimation of Lithium-Ion Batteries with Features Extracted from Partial Charging Curves. Batteries, 10(5), 164. https://doi.org/10.3390/batteries10050164






