Investigations into the Charge Times of Lead–Acid Cells under Different Partial-State-of-Charge Regimes
Abstract
:1. Introduction
2. Materials and Methods
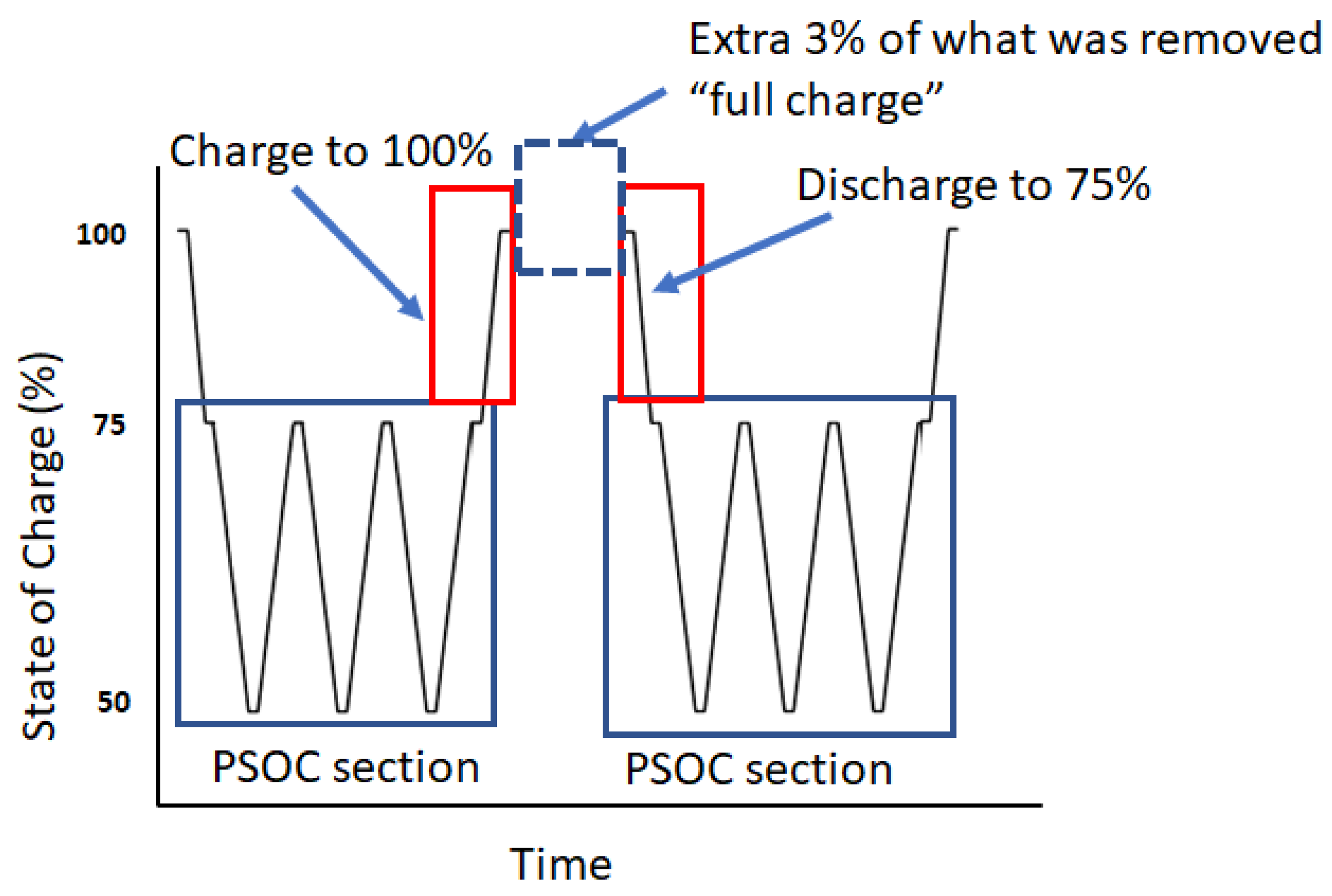
Cyclic Regime
3. Results
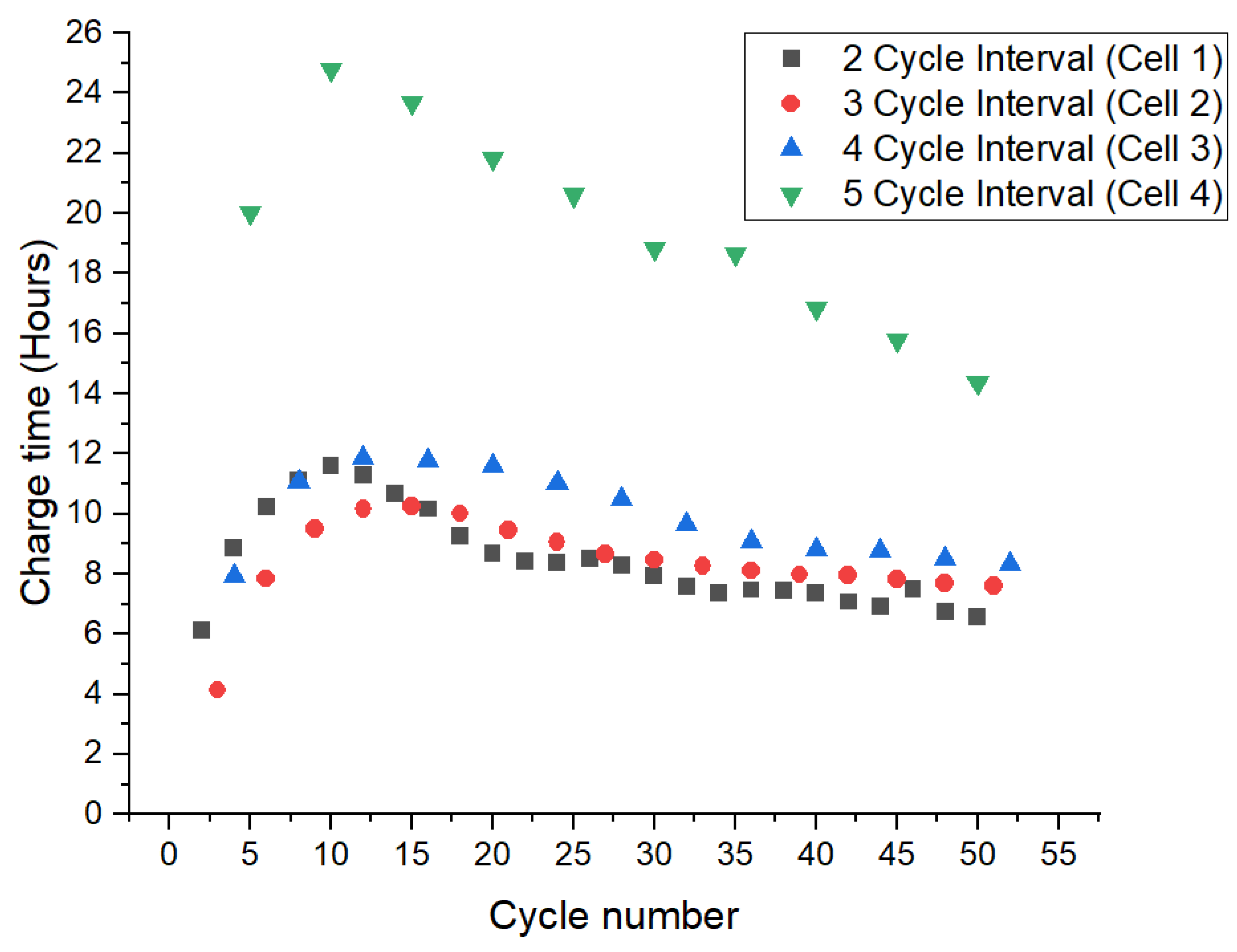
3.1. First 50 Cycles
3.2. Second 50 Cycles
3.3. Capacity Testing
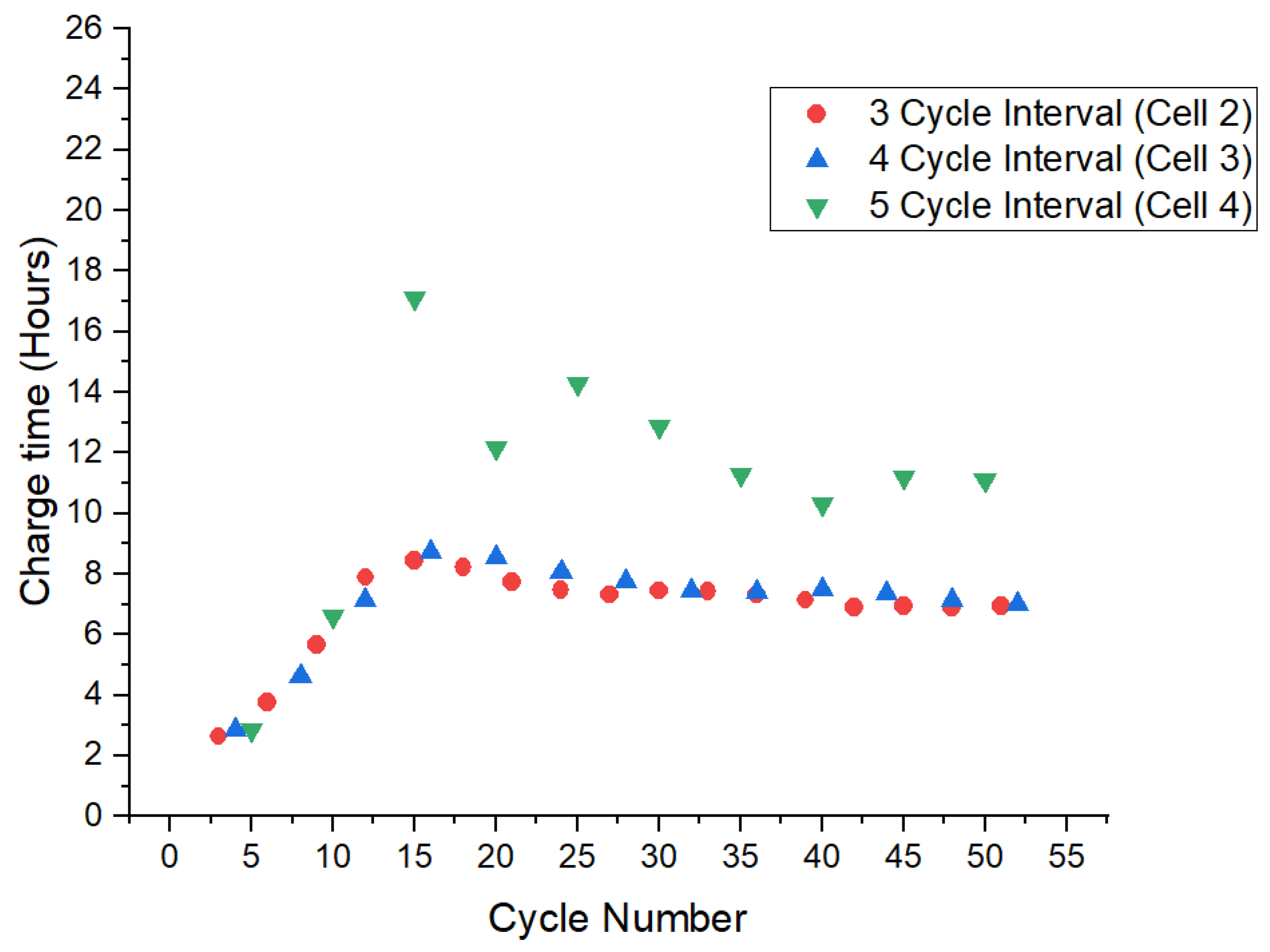
4. Variable-Interval Testing on the Same Cell
4.1. Increasing Interval Test
4.2. Reverse Order Test with Reducing Full-Charge Cycling Interval
4.3. Charge Times
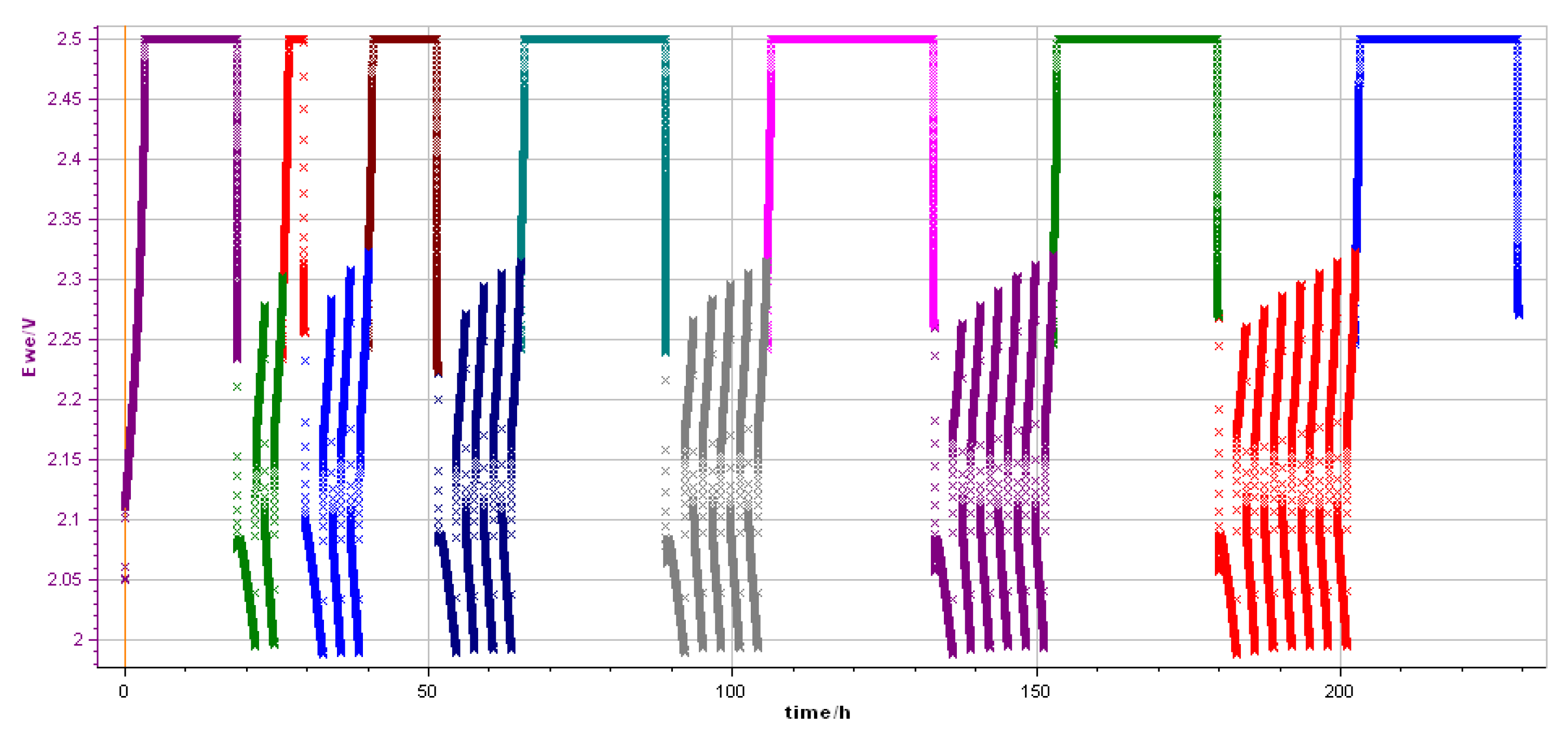
4.4. Internal Resistance
5. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Ah | Ampere-hour |
| AGM | Absorbed glass mat |
| BESS | Battery energy storage system |
| PSOC | Partial state of charge |
| SOC | State of charge |
| UPS | Uninterruptible power supply |
| VRLA | Valve-regulated lead–acid |
References
- Berndt, D.; Teutsch, U. Float Charging of Valve-Regulated Lead-Acid Balteries: A Balancing Act Between Secondary Reactions. J. Electrochem. Soc 1996, 143, 790. [Google Scholar] [CrossRef]
- Jones, W.E.; Feder, D.O. Behavior of VRLA cells on long term float: Part 2. The effects of temperature, voltage and catalysis on gas evolution and consequent water loss. In Proceedings of the Intelec’96—International Telecommunications Energy Conference, Boston, MA, USA, 6–10 October 1996; pp. 358–366. [CrossRef]
- Badeda, J.; Kwiecien, M.; Schulte, D.; Sauer, D.U. Battery state estimation for lead-acid batteries under float charge conditions by impedance: Benchmark of common detection methods. Appl. Sci. 2018, 8, 1308. [Google Scholar] [CrossRef]
- Stewart, I.A. Automotive type batteries in long term float and ups applications. In Proceedings of the INTELEC ’86—International Telecommunications Energy Conference, Toronto, ON, Canada, 19–22 October 1986; pp. 361–364. [Google Scholar] [CrossRef]
- Szymborski, J.; Hunt, G.; Tsagalis, A.; Jungst, R. Examination of VRLA cells sampled from a battery energy storage system (BESS) after 30-months of operation. In Proceedings of the INTELEC, International Telecommunications Energy Conference (Proceedings), Phoenix, AZ, USA, 10–14 September 2000; pp. 484–492. [Google Scholar] [CrossRef]
- Barner, T.; Missouri S&T. Consortium Launches Study of Lead Battery Solar Microgrids in Homes. Available online: https://batteryinnovation.org/wp-content/uploads/2019/04/CBI-Case-Study_EcoVillage_Online_2.5.19-1.pdf (accessed on 28 May 2024).
- Chae, S.Y.; Park, J.H. Efficient Energy Management System of Smart Homes with Distributed Energy Resources. In Proceedings of the 2015 8th International Conference on Grid and Distributed Computing (GDC), Jeju, Republic of Korea, 25–28 November 2015; pp. 9–12. [Google Scholar] [CrossRef]
- Sharma, V.; Haque, M.H.; Aziz, S.M. Energy cost minimization for net zero energy homes through optimal sizing of battery storage system. Renew. Energy 2019, 141, 278–286. [Google Scholar] [CrossRef]
- Quoilin, S.; Kavvadias, K.; Mercier, A.; Pappone, I.; Zucker, A. Quantifying self-consumption linked to solar home battery systems: Statistical analysis and economic assessment. Appl. Energy 2016, 182, 58–67. [Google Scholar] [CrossRef]
- McMahon, R.; Logan, T.; Miles, J.; McMahon, N.; Ridge, A. Operational study of domestic battery energy storage system. J. Eng. 2019, 2019, 3479–3483. [Google Scholar] [CrossRef]
- Wagner, R.; Sauer, D.U. Charge strategies for valve-regulated lead/acid batteries in solar power applications. J. Power Sources 2001, 95, 141–152. [Google Scholar] [CrossRef]
- Sanz-Gorrachategui, I.; Ruiz, C.B.; Usabiaga, E.O.; Nuez, A.B.; Jesús, S.; Sevil, A.; Pérez, E.G.; Larrañaga, I.A.; María, J.; Segade, C. Partial State-of-Charge Mitigation in Standalone Photovoltaic Hybrid Storage Systems. Energies 2019, 12, 4393. [Google Scholar] [CrossRef]
- Uddin, K.; Gough, R.; Radcliffe, J.; Marco, J.; Jennings, P. Techno-economic analysis of the viability of residential photovoltaic systems using lithium-ion batteries for energy storage in the United Kingdom. Appl. Energy 2017, 206, 12–21. [Google Scholar] [CrossRef]
- McKenna, E.; McManus, M.; Cooper, S.; Thomson, M. Economic and environmental impact of lead-acid batteries in grid-connected domestic PV systems. Appl. Energy 2013, 104, 239–249. [Google Scholar] [CrossRef]
- Schaeck, S.; Stoermer, A.O.; Hockgeiger, E. Micro-hybrid electric vehicle application of valve-regulated lead-acid batteries in absorbent glass mat technology: Testing a partial-state-of-charge operation strategy. J. Power Sources 2009, 190, 173–183. [Google Scholar] [CrossRef]
- Wong, Y.; Hurley, W.; Wölfle, W. Charge regimes for valve-regulated lead-acid batteries: Performance overview inclusive of temperature compensation. J. Power Sources 2008, 183, 783–791. [Google Scholar] [CrossRef]
- Franke, M.; Kowal, J. Empirical sulfation model for valve-regulated lead-acid batteries under cycling operation. J. Power Sources 2018, 380, 76–82. [Google Scholar] [CrossRef]
- Lambert, D.W.; Greenwood, P.H.; Reed, M.C. Advances in gelled-electrolyte technology for valve-regulated lead-acid batteries. J. Power Sources 2002, 107, 173–179. [Google Scholar] [CrossRef]
- May, G.J.; Davidson, A.; Monahov, B. Lead batteries for utility energy storage: A review. J. Energy Storage 2018, 15, 145–157. [Google Scholar] [CrossRef]
- Lum, M.G.; Logan, M.W.; Annese, A.D.; Uribe-Romo, F.J. Effect of Inventory Storage on Automotive Flooded Lead-Acid Batteries. SAE International USA SAE Technical Papers 2019. 2019. Available online: https://saemobilus.sae.org/papers/effect-inventory-storage-automotive-flooded-lead-acid-batteries-2019-01-5081 (accessed on 28 May 2024).
- Cárdenas, B.; Swinfen-styles, L.; Rouse, J.; Garvey, S.D. Short-, medium-, and long-duration energy storage in a 100% renewable electricity grid: A UK case study. Energies 2021, 14, 8524. [Google Scholar] [CrossRef]
- Sauer, D.U.; Karden, E.; Fricke, B.; Blanke, H.; Thele, M.; Bohlen, O.; Schiffer, J.; Gerschler, J.B.; Kaiser, R. Charging performance of automotive batteries—An underestimated factor influencing lifetime and reliable battery operation. J. Power Sources 2007, 168, 22–30. [Google Scholar] [CrossRef]
- Iliev, V.; Pavlov, D. Self-Discharge and Passivation Phenomena in Lead-Acid Batteries during Storage. J. Electrochem. Soc 1982, 129, 458–464. [Google Scholar] [CrossRef]
- Berndt, D.; Meissner, E.; Rusch, W. Aging effects in valve-regulated lead-acid batteries. In Proceedings of the Intelec 93: 15th International Telecommunications Energy Conference, Paris, France, 27–30 September 1993; Volume 2, pp. 139–145. [Google Scholar] [CrossRef]

| Cell Number | 1 kHz Impedance (M) | Delivery Voltage (V) | Initial Capacity (Ah) |
|---|---|---|---|
| Cell 1 | 10.14 | 1.979 | 3.81 |
| Cell 2 | 8.01 | 1.985 | 3.90 |
| Cell 3 | 9.27 | 1.977 | 3.89 |
| Cell 4 | 11.82 | 1.949 | 3.78 |
| Cell Number | Cycles before Full Charge | Repeats | Full Charge Ah from 75% (Ah) |
|---|---|---|---|
| Cell 1 | 2 | 25 | 1.035 |
| Cell 2 | 3 | 17 | 1.064 |
| Cell 3 | 4 | 13 | 1.093 |
| Cell 4 | 5 | 10 | 1.121 |
| Cell Number (Full-Charge Interval) | Initial Capacity (Ah) | Capacity after 50 Cycles (Ah) | Capacity after 100 Cycles (Ah) |
|---|---|---|---|
| Cell 1 (2 cycles) | 3.81 | 4.27 | 4.14 1 |
| Cell 2 (3 cycles) | 3.90 | 4.20 | 4.29 |
| Cell 3 (4 cycles) | 3.89 | 4.27 | 4.37 |
| Cell 4 (5 cycles) | 3.78 | 4.22 | 4.35 |
| Interval | 2 Cycles | 3 Cycles | 4 Cycles | 5 Cycles | 6 Cycles | 7 Cycles |
|---|---|---|---|---|---|---|
| Increasing | 3.52 | 11.43 | 23.98 | 27.58 | 27.14 | 26.83 |
| Decreasing | 6.62 | 6.74 | 7.44 | 17.52 | 23.09 | 9.55 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Parker, M.; McMahon, R. Investigations into the Charge Times of Lead–Acid Cells under Different Partial-State-of-Charge Regimes. Batteries 2024, 10, 201. https://doi.org/10.3390/batteries10060201
Parker M, McMahon R. Investigations into the Charge Times of Lead–Acid Cells under Different Partial-State-of-Charge Regimes. Batteries. 2024; 10(6):201. https://doi.org/10.3390/batteries10060201
Chicago/Turabian StyleParker, Max, and Richard McMahon. 2024. "Investigations into the Charge Times of Lead–Acid Cells under Different Partial-State-of-Charge Regimes" Batteries 10, no. 6: 201. https://doi.org/10.3390/batteries10060201
APA StyleParker, M., & McMahon, R. (2024). Investigations into the Charge Times of Lead–Acid Cells under Different Partial-State-of-Charge Regimes. Batteries, 10(6), 201. https://doi.org/10.3390/batteries10060201








