Experimental and Reduced-Order Modeling Research of Thermal Runaway Propagation in 100 Ah Lithium Iron Phosphate Battery Module

Abstract

The thermal runaway propagation (TRP) model of energy storage batteries can provide solutions for the safety protection of energy storage systems. Traditional TRP models are solved using the finite element method, which can significantly consume computational resources and time due to the large number of elements and nodes involved. To ensure solution accuracy and improve computational efficiency, this paper transforms the heat transfer problem in finite element calculations into a state-space equation form based on the reduced-order theory of linear time-invariant (LTI) systems; a simplified method is proposed to solve the heat flow changes in the battery TRP process, which is simple, stable, and computationally efficient. This study focuses on a four-cell 100 Ah lithium iron phosphate battery module, and module experiments are conducted to analyze the TRP characteristics of the battery. A reduced-order model (ROM) of module TRP is established based on the Arnoldi method for Krylov subspace, and a comparison of simulation efficiency is conducted with the finite element model (FEM). Finally, energy flow calculations are performed based on experimental and simulation data to obtain the energy flow rule during TRP process. The results show that the ROM achieves good accuracy with critical feature errors within 10%. Compared to the FEM, the simulation duration is reduced by 40%. The model can greatly improve the calculation efficiency while predicting the three-dimensional temperature distribution of the battery. This work facilitates the efficient computation of TRP simulations for energy storage batteries and the design of safety protection for energy storage battery systems.

1. Introduction

As the demand for frequency regulation in energy storage power stations has increased significantly, energy storage batteries are trending towards higher power and a larger capacity [1]. LFP batteries are widely used in electrochemical energy storage power stations due to their high safety and long cycle life [2]. However, TR is a common safety challenge faced by lithium-ion batteries [3]. TR can occur when batteries are subjected to extreme conditions such as electrical abuse [4,5,6,7], thermal abuse [8,9], and mechanical abuse [10,11,12,13]. Energy storage power stations are composed of thousands of battery cells, and the large amount of heat released by intense chain reactions within the batteries can trigger TRP to adjacent batteries, posing a serious threat to public and property safety and challenging the application of large-scale energy storage.

In recent years, numerous scholars have conducted a series of research works focusing on the TRP characteristics of energy storage batteries and power batteries. Zhu et al. [14] investigated the TRP behavior of lithium iron phosphate (LFP) batteries at three different states of charge (SOC). They found that the time interval for TRP in batteries at 100% SOC was 71.4% shorter compared to that in batteries at 50% SOC. This indicates that batteries with a higher SOC are more prone to rapid thermal runaway propagation under abusive conditions. Jan et al. [15] compared and analyzed the TRP behavior of Li(Ni_0.8Co_0.1Mn_0.1)O₂ and LFP batteries, discovering that Li(Ni_0.8Co_0.1Mn_0.1)O₂ batteries are more hazardous, with a TR reaction speed nine times faster and a TRP speed five times faster than LFP batteries. Huang [16] et al. also studied the TRP characteristics of Li(Ni_xCo_yMn_z)O₂ (NCM) and LFP batteries, finding that LFP battery modules are less likely to be affected by TRP, and that the duration and maximum temperature of NCM batteries during the propagation process are significantly higher than those of LFP batteries. Chen et al. [17] investigated the TRP behavior in a battery pack composed of 24 LFP batteries, each with a capacity of 60 Ah. They found that the total heat release rate of the battery pack reached 314 kW, which was more than eight times that of a single battery cell. Zhai et al. [18] examined the TRP behavior of large-sized LFP batteries at different tilt angles, discovering that a larger ceiling angle provides better heat dissipation conditions for TRP, and that the threshold ceiling angle for TRP cessation ranges between 10 and 30°.

By calculating the energy flow distribution during the TRP process of batteries, we can obtain the TR energy flow conditions of batteries under different paths, providing guidance for the suppression and regulation of battery TR energy as well as system safety protection. Zhu et al. [19] conducted research on the TRP of NCM pouch lithium-ion batteries under different states of charge and spacing, and found that as the SOC increases, the time interval of battery TRP decreases significantly. Through heat transfer calculations, they reported that the energy transfer from the previous cell to the next cell accounts for approximately 35.3–72%. Song et al. [20] experimentally studied the TRP behavior of 280 Ah LFP batteries with different SOC levels and found that TRP only occurs in modules with 100% SOC. Through energy flow calculations, they determined that more than 75% of the energy is used to heat the battery itself, while less than 10% triggers TR in adjacent batteries.

The modeling approaches for battery TRP both domestically and internationally primarily encompass Lumped Parameter Methods (LPMs) [21], two-dimensional modeling [22], and three-dimensional modeling [23]. LPMs offer high computational efficiency but lack the capability to capture the three-dimensional temperature distribution within batteries. Spotnitz et al. [24] utilized accelerated calorimetry data to develop an LPM for eight 18650 batteries, leveraging the model to explore the effects of battery positioning, reaction heat, and heat transfer coefficients. Wang et al. [25] developed an LPM based on the OpenFOAM framework to study the TRP behavior in CTC (Cell-to-Chassis) battery packs. The model successfully captured the evolution process of thermal runaway propagation in the CTC system and identified five typical TRP modes between TR cells and normal cells. He et al. [26] created a high-precision Lumped TR Network model for predicting lithium-ion battery TRP in large-scale power systems. Two-dimensional models, while faster than three-dimensional ones, can only provide two-dimensional temperature distribution information. Coman et al. [27] developed a two-dimensional TRP model for 18650 batteries, finding that the error compared to a three-dimensional model was within 6%, with computation time reduced from 11 h to 25 min. Three-dimensional models, on the other hand, can capture the overall battery temperature distribution but require significant computational resources and are inefficient. Liu et al. [28] established a three-dimensional model of a 16 Ah prismatic battery to study its TR characteristics under conditions such as high temperature, overcharging, and nail penetration. They found that nail penetration was the most likely to trigger TR in the battery, followed by heating and overcharging. Developing a model that can both capture spatial temperature distribution and achieve high computational efficiency would significantly reduce the computational time for simulating TRP in large battery systems. Traditional three-dimensional TRP models are primarily built using finite element software such as Ansys Fluent 2024R1 and COMSOL Multiphysics 6.3. Finite element methods solve partial differential equations between grid cell nodes, which can lead to substantial computational time and resource costs for system-level TRP modeling. Conventional TRP model development typically involves two components: a TR heat generation model and a heat transfer model. The heat generation model can be established based on chemical reaction kinetics using the Arrhenius equation [29] or directly using experimental data from Accelerating Rate Calorimetry (ARC) tests [30]. The heat transfer model can be transformed into a state-space equation form of a linear time-invariant system, which can be simplified through order reduction based on system theory [31]. Evgenii et al. [32] developed a thermal–electric coupling model for traction battery systems using order reduction methods based on Krylov subspaces. Xu et al. [33] first proposed and established a reduced-order TRP model at the vehicle battery pack level using the Arnoldi method from Krylov subspaces, significantly enhancing computational efficiency. Applying reduced-order theory to TRP models for energy storage battery systems has the potential to substantially shorten computational time while maintaining accuracy.

Currently, most research on battery TRP characteristics focuses on NCM batteries and small-capacity LFP batteries, and no work has yet established a TRP model for energy storage batteries based on reduced-order theory. Based on this, the following research work has been conducted and the technology roadmap of this paper is shown in Figure 1.

(1)

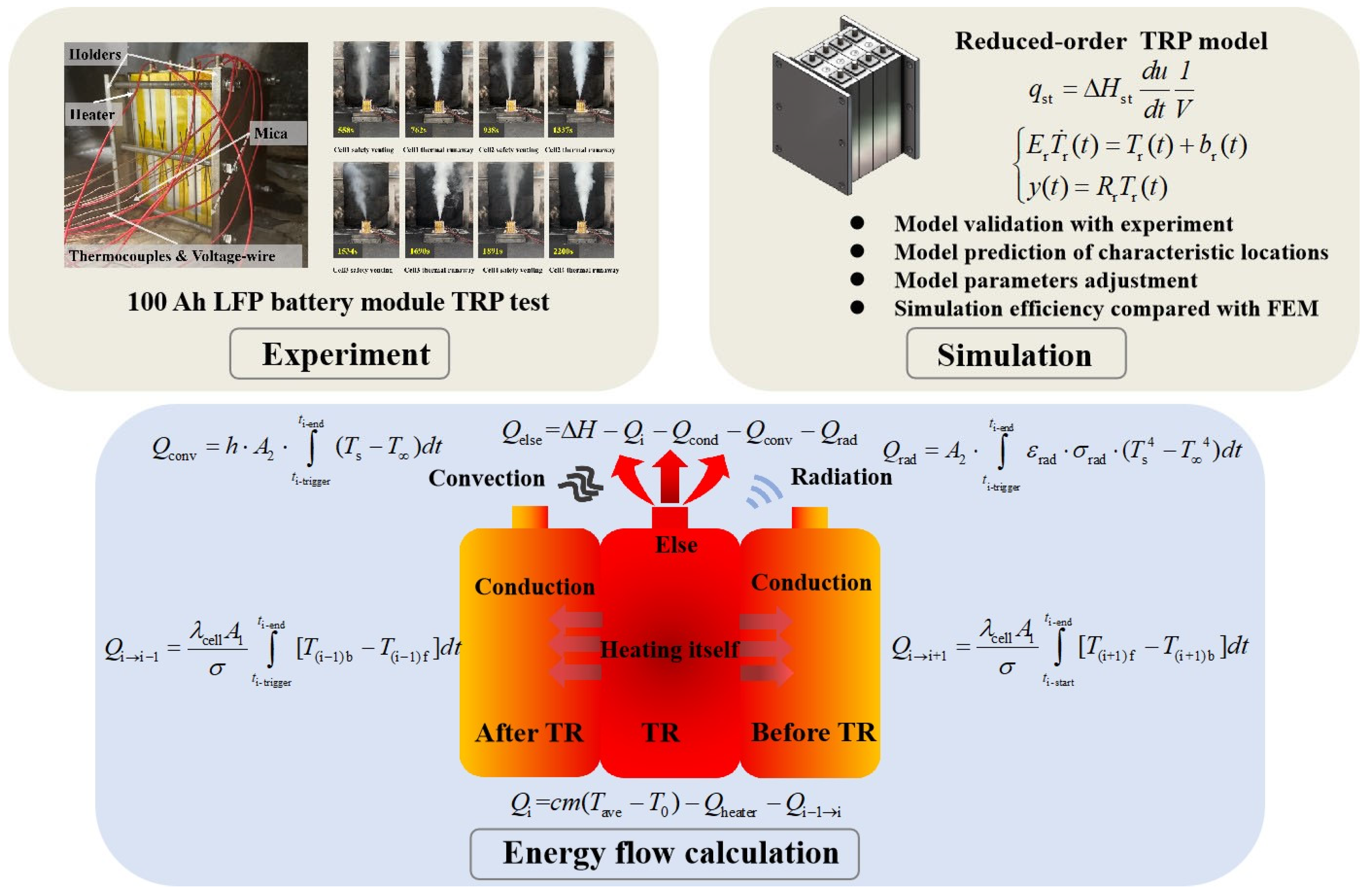
A TRP experiment was conducted on a four-cell 100 Ah LFP battery module. The experimental phenomena, temperature characteristics of each battery cell, and characteristic time were analyzed.

(2)

A reduced-order TRP model that is highly consistent with experimental data was established using the Arnoldi method based on Krylov subspaces. The temperature change at characteristic locations of the battery was predicted through the model. In addition, by adjusting the key parameters of the model, the parameter values for inhibiting TRP in the battery module were obtained. Finally, a finite element TRP model of the same specification was constructed for a comparison of simulation efficiency.

(3)

Energy flow calculations were performed based on experimental and simulation data. By calculating the heat conduction between batteries during the TRP of the module, the thermal convection and radiation heat dissipation of each battery cell, as well as the heat lost through ejection and other behaviors, the flow patterns of energy released during battery TRP through different paths were obtained.

2. Methodology

2.1. Battery Sample

The research object of this paper is a 100 Ah high-power LFP battery produced by a company (Chunlan, Taizhou, China) specifically designed for energy storage applications. This battery features a maximum charging rate of 2 C and a maximum discharge rate capability of up to 4 C. The battery’s nominal voltage stands at 3.2 V, with a cutoff voltage range spanning from 2.5 V to 3.65 V. Physically, the battery weighs 2245 ± 5 g and measures 130 × 36 × 211.8 mm in dimensions. Notably, all batteries utilized in this study were maintained at a 100% SOC.

Table 1. Battery sample parameters.

Parameters	Value
Cathode	Lithium iron phosphate
Anode	Graphite
Nominal voltage	3.2 V
Nominal capacity	100 Ah
Upper voltage limit	3.65 V
Lower voltage limit	2.5 V
Maximum charging rate	2 C
Maximum discharge rate	4 C
Mass	2245 ± 5 g
Size (length × width × height)	130 × 36 × 211.8 mm
State of charge	100%

summarizes the key parameters of the battery samples.

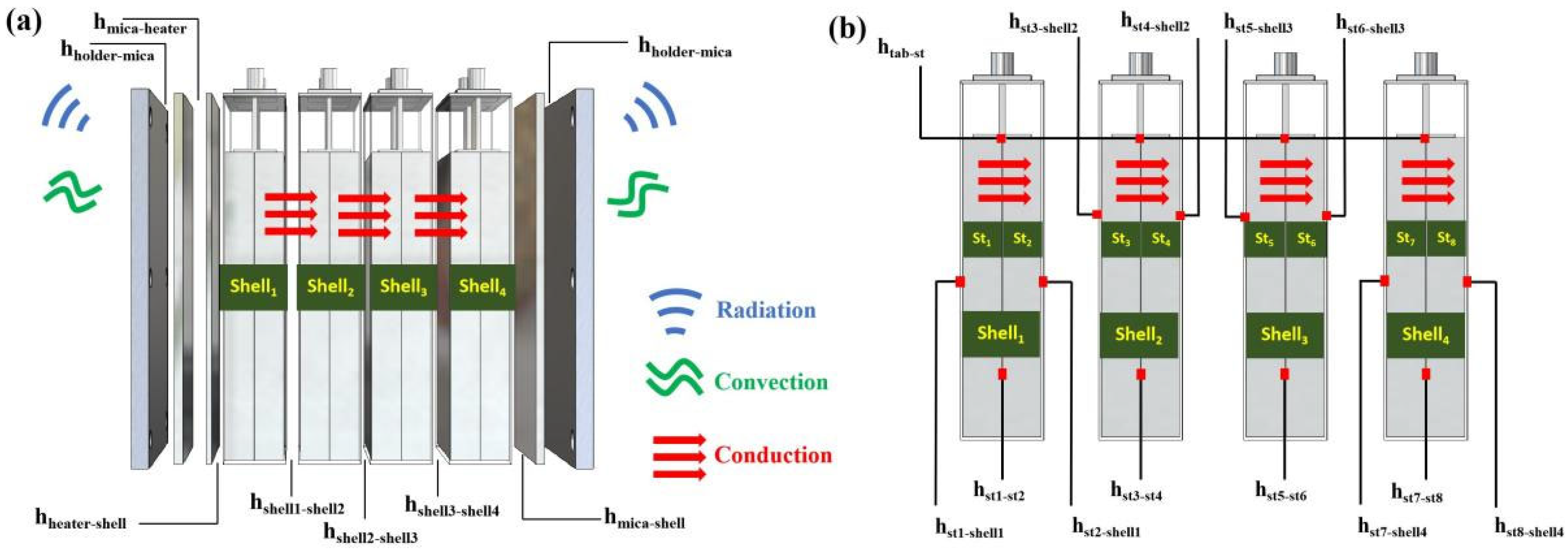
2.2. Geometry

Figure 2 demonstrates the three-dimensional geometric composition of the module TRP model. The battery cell geometry comprises a header, an anode, a cathode, two stacks, and a shell. The dimensions of one stack are 128 × 17 × 177.6 mm. The dimensions of the battery shell are 130 × 36 × 211.8 mm. The geometric model of the battery module includes a heating plate (130 × 3 × 211.8 mm), mica (130 × 5 × 211.8 mm), holders (190.0 × 10 × 211.8 mm), and 4 battery cells. The 4 battery cells are labeled as Cell 1, Cell 2, Cell 3, and Cell 4. The preprocessing of the model was performed in ANSYS Space Claim 2024R1.

Table 2. Material properties.

Component	Material	ρ (kg·m−3)	Cp (J·kg−1·K−1)	λ (W·m−1·K−1)
Shell	Aluminum alloy	2770	875	170
Stack	Stack composite material	2407.7	985.3	λx = λy = 24.93; λz = 0.98
Cathode	Aluminum	2689	951	237.5
Anode	Copper	8933	385	400
Heater	Stainless steel	7750	480	15.1
Mica plate	Mica	2500	500	0.34
Holder	Aluminum alloy	2770	875	170

outlines the material properties of the battery geometric model. The battery holder is made of aluminum alloy; the cathode is aluminum; the anode is copper; the stacks are made of stack composite material, with specific heat capacity C_p and thermal conductivity λ derived from experimental measurements. Notably, the thermal conductivity is anisotropic, with λ_x = λ_y = 24.93 W·m⁻¹·K⁻¹ along the major plane of the stack and λ_z = 0.98 W·m⁻¹·K⁻¹ along the thickness direction. In the battery module, the heating plate is made of stainless steel, the mica plate is made of mica, and the holders are aluminum alloy.

2.3. Reduced-Order TRP Model

2.3.1. Reduced-Order Thermal Model

In finite element analysis, the three-dimensional heat transfer equation can be represented by the following Equation (1), where λ_x, λ_y, and λ_z represent the thermal conductivities in the x, y, and z directions, respectively; T denotes the temperature variation; ρ is the density; and C_p represents the specific heat capacity.

$${\displaystyle \frac{\partial }{\partial x}}({\lambda }_{\mathrm{x}}{\displaystyle \frac{\partial T}{\partial x}})+{\displaystyle \frac{\partial }{\partial y}}({\lambda }_{\mathrm{y}}{\displaystyle \frac{\partial T}{\partial y}})+{\displaystyle \frac{\partial }{\partial z}}({\lambda }_{\mathrm{z}}{\displaystyle \frac{\partial T}{\partial z}})+q=\rho C_{\mathrm{p}}{\displaystyle \frac{\partial T}{\partial t}}$$

(1)

In finite element analysis, the temperature between two nodes can be obtained through interpolation, as shown in the following Equation (2). Here, H_i represents the interpolation function, n denotes the number of elements, and T_i is the node temperature on each element.

$$T(x,y,z,t)={\displaystyle \sum _{i=1}^n{H}_i(x,y,z)T_{\mathrm{i}}(t)}$$

(2)

By incorporating Equations (4)–(7) from

Table 3. State-space matrix and influence factors.

Matrix	Formula	Influence Factors
[A]	$[A]={\displaystyle {\int }_V}\rho C_{\mathrm{p}}{[H]}^T[H]dV$	ρ; Cp
[C]	$\begin{array}{l}[C]={\displaystyle {\int }_V}[{\lambda }_{\mathrm{x}}{\displaystyle \frac{\partial {[H]}^T}{\partial x}}{\displaystyle \frac{\partial [H]}{\partial x}}+{\lambda }_{\mathrm{y}}{\displaystyle \frac{\partial {[H]}^T}{\partial y}}{\displaystyle \frac{\partial [H]}{\partial y}}+{\lambda }_{\mathrm{z}}{\displaystyle \frac{\partial {[H]}^T}{\partial z}}{\displaystyle \frac{\partial [H]}{\partial z}}]dV\\ +{\displaystyle {\int }_S}h{[H]}^T[H]dS\end{array}$	λ; h
[L]	$[L]=\left[{\displaystyle {\int }_V}{[H]}^{T}dV \right. \left.{\displaystyle {\int }_{S}h}{[H]}^{T}dS\right]$	h
[u]	$[u]=\left[\begin{array}{l}q\\ \infty \end{array}\right]$	q; T∞

, the heat transfer problem can be transformed into a state-space equation of the form shown in Equation (3). This step is typically implemented in ANSYS Transient Thermal 2024R1 through programming with ANSYS Parametric Design Language (APDL). In the FEM, the number of nodes is denoted as n_f, which typically ranges in the order of 10⁴ to 10⁶.

The following is a breakdown of the terms involved in the state-space equation: [A] ∈ R_{n_f×n_f} is a diagonal matrix, influenced by the material properties of ρ and C_p, and this matrix captures the thermal inertia of the system; [C] ∈ R_{n_f×n_f} is a positive definite symmetric matrix, influenced by λ and convective heat transfer coefficient h, and this matrix represents the diffusion of heat through the system; [u] ∈ R_{n_i} is the model input vector, where n_i is a user-defined quantity, and it includes inputs such as heat sources q and ambient temperatures T_∞; [L] ∈ R_{n_i×n_f} is the input distribution array, which governs how the inputs [u] are distributed across the finite element nodes, and its influence is primarily determined by h; [y] ∈ R_{n_o} is the model output vector, where n_o is a user-defined quantity, and this vector represents the desired outputs from the simulation, such as temperatures at specific locations; [R_f] ∈ R_{n_o×n_f} is the output distribution array, which defines how the outputs [y] are extracted from the finite element nodes, and the order n_o is user-specified based on the simulation requirements.

The state-space equation in Equation (3) represents the dynamic thermal behavior of the system being analyzed. By solving this equation using numerical methods within ANSYS Transient Thermal, engineers can simulate the transient temperature response of complex systems under various conditions. The high order of the matrices and vectors (especially [A] and [C], which scale with the number of nodes n_f) underscores the importance of efficient computational algorithms and high-performance computing resources for tackling large-scale heat transfer problems.

$$\left\{\begin{array}{l}A\dot{T}(t)+CT(t)=Lu\\ \mathit{y}=R_{\mathrm{f}}T(t)\end{array}\right.$$

(3)

Formula (3) is converted to the form of Formula (4), where E = −C⁻¹A, b = −C⁻¹L. Equation (4) is formally a state-space equation of a linear LTI system, which can be orderly reduced using model reduction theory in control systems. Model reduction involves performing a Laplace transform on the system described by Equation (4) to obtain Equation (5). By eliminating T(s), Equation (6) is derived. The H(s) in Equation (7) is referred to as the transfer function of y_i(s). If there exists a reduced-order system as shown in Equation (8), whose transfer function H_r(s) in Equation (9) matches the first r moments of H(s) after Taylor expansion at s = 0, then the reduced-order system can accurately replace the original system.

$$\left\{\begin{array}{l}E\dot{T}(t)=T(t)+bu(t)\\ y(t)=R_{\mathrm{f}}T(t)\end{array}\right.$$

(4)

$$\left\{\begin{array}{l}sET(s)=T(s)+bu(s)\\ y_{\mathrm{i}}(s)=R_{\mathrm{f}}T(s)\end{array}\right.$$

(5)

$$y_{\mathrm{i}}(s)=R_{\mathrm{f}}{(sE-I)}^{-1}bu(s)$$

(6)

$$H(s)=R_{\mathrm{f}}{(sE-I)}^{-1}b$$

(7)

$$\left\{\begin{array}{l}{E}_{\mathrm{r}}{\dot{T}}_{\mathrm{r}}(t)=T_{\mathrm{r}}(t)+b_{\mathrm{r}}(t)\\ y(t)=R_{\mathrm{r}}{T}_{\mathrm{r}}(t)\end{array}\right.$$

(8)

$$H_{\mathrm{r}}(s)=R_{\mathrm{r}}{(s{E}_{\mathrm{r}}-I)}^{-1}{b}_{\mathrm{r}}$$

(9)

The reduced-order method based on Krylov subspace can achieve an order reduction in Equation (3) with stable calculations. An R-dimensional Krylov subspace K_r(E; b) is the vector space generated by matrix E and vector b, as shown in Equation (10). The transformation matrix V obtained after standard Gram–Schmidt orthogonalization of the K_r(E; b) using the Arnoldi algorithm can be used to reduce the order of the original model, as shown in Equation (11). The moments of the transfer function of the reduced-order system are the same as the first r moments of the transfer function of the original system, indicating the effectiveness of the ROM. Dr. Rudny integrated the Arnoldi method of Krylov subspace into ANSYS and developed it into the Model order reduction (MOR) in ANSYS plugin, enabling a stable order reduction in heat transfer state-space equations within ANSYS [32].

$$K_r(E;b)=span\left\{b,Eb,\dots E^{r}b\right\}$$

(10)

$$\left\{\begin{array}{l}{V}^{\mathrm{T}}EV\dot{T}(t)=T(t)+V^{T}bu(t)\\ y(t)=R_{\mathrm{f}}V{T}_{\mathrm{r}}(t)\end{array}\right.\stackrel{\begin{array}{l}Order\\ Reduction\end{array}}{\to }\left\{\begin{array}{l}{E}_{\mathrm{r}}{\dot{T}}_{\mathrm{r}}(t)=T_{\mathrm{r}}(t)+b_{\mathrm{r}}(t)\\ y(t)=C_{\mathrm{r}}{T}_{\mathrm{r}}(t)\end{array}\right.$$

(11)

2.3.2. TR Model

The TR model can be built based on ARC test data, and the heating power q_st of TR is calculated by Equation (12) below, where u is the normalized reaction concentration; ∆H is the total heat released by the TR of the stacks, which is calculated by Equation (13); V_bat is the volume of battery; C_{p_bat} is the specific heat capacity of the battery; and M indicates the battery quality. Formula (14) is the concentration change rate of the battery TR normalized reaction. By coupling the heat transfer model with the TR model, we can obtain the reduced-order TRP model.

$$q_{\mathrm{s}\mathrm{t}}=\Delta H_{\mathrm{s}\mathrm{t}}{\displaystyle \frac{du}{dt}}{\displaystyle \frac{1}{V}}$$

(12)

$$\Delta H=C_{\mathrm{p}\mathrm{\_}\mathrm{b}\mathrm{a}\mathrm{t}}M\Delta T$$

(13)

$${\displaystyle \frac{du}{dt}}=\left\{\begin{array}{l}{\displaystyle \frac{M{C}_{\mathrm{p}\mathrm{\_}\mathrm{b}\mathrm{a}\mathrm{t}}}{\Delta H_{\mathrm{s}\mathrm{t}}}}{({\displaystyle \frac{dT}{dt}})}_{\mathrm{A}\mathrm{R}\mathrm{C}} 0\le u\le 1,T_1\le T<T_2;\\ \\ C_{\mathrm{r}\mathrm{e}}\hspace{1em}\hspace{1em}\hspace{1em}0\le u\le 1,T_2<T;\\ 0\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\mathrm{else}.\end{array}\right.$$

(14)

2.3.3. Boundary Condition

The model boundary conditions in this study, as depicted in Figure 3, encompass thermal conduction between various solid components of the battery, as well as thermal convection and radiation between the battery surface and the surrounding air.

Thermal Conduction

The thermal conduction between components can be calculated using Equation (15), where λ_i represents the thermal conductivity between the two components; ${\displaystyle \frac{\partial T}{\partial n}}$ is the temperature gradient; h_R is the equivalent heat transfer coefficient between the components, which is the reciprocal of thermal resistance; T_i and T_j are the temperatures of the respective components.

$$-{\lambda }_{\mathrm{i}}{\displaystyle \frac{\partial T}{\partial n}}=h_{\mathrm{R}}(T_{\mathrm{i}}-T_{\mathrm{j}})$$

(15)

Thermal Convection

The boundary condition for thermal convection can be represented by Equation (16). In this study, h represents the convective heat transfer coefficient, defined as 15 W·m⁻²·K⁻¹, and it is a standard value provided by the experimental testing vendor, which takes into account the effect of the top fan’s ventilation; T_bat represents the surface temperature of the battery; and T_∞ is the ambient temperature, which is 17.5 °C.

$$-\lambda {\displaystyle \frac{\partial T}{\partial n}}{|}_{0,\infty }=h(T_{\mathrm{b}\mathrm{a}\mathrm{t}}-T_{\infty })$$

(16)

Thermal Radiation

During the TR process, the internal temperature of the battery rises sharply, potentially reaching several hundred degrees Celsius or even higher. According to the Stefan–Boltzmann law, the energy of thermal radiation is proportional to the fourth power of the temperature [34]. Therefore, at high temperatures, the energy transfer through thermal radiation increases significantly, making it a non-negligible mode of heat transfer.

The boundary condition for thermal radiation is given by Equation (17). In this equation, σ represents the Stefan–Boltzmann constant, which has a value of approximately 5.67 × 10⁻⁸ W·m⁻²·K⁻⁴. The symbol ε denotes the emissivity of the battery surface, which is often assumed to be 0.95.

$$-\lambda {\displaystyle \frac{\partial T}{\partial n}}{|}_{0,\infty }=\epsilon \sigma ({T_{\mathrm{b}\mathrm{a}\mathrm{t}}}^4-{{\mathrm{T}}_{\infty }}^4)$$

(17)

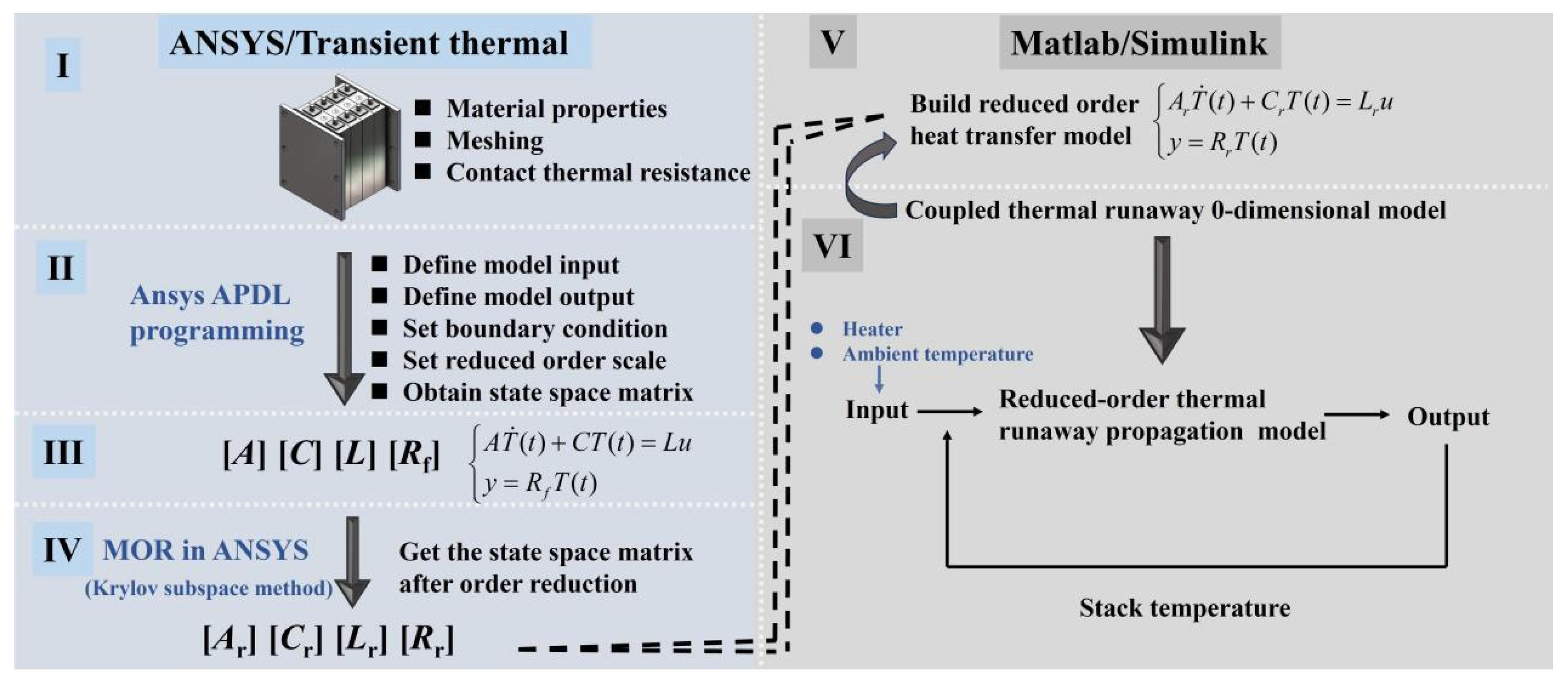
2.3.4. Modeling Procedures

Figure 4 illustrates the modeling process for the reduced-order TRP model. This model requires joint simulation using MATLAB 2024b and ANSYS 2024R1. The main modeling procedures are as follows:

(I)

First, import the established geometric model into ANSYS/Transient Thermal to define the material properties, perform mesh generation, and set the contact thermal resistance of the model.

(II)

Program using ANSYS Parametric Design Language (APDL) to define model inputs and outputs, set boundary conditions, and specify the reduced-order scale.

(III)

Obtain the matrices [A], [C], [L], and [R_f] from the heat transfer state-space equations by APDL.

(IV)

Launch the “MOR for ANSYS” plugin to perform order reduction, resulting in reduced-order matrices [A_r], [C_r], [L_r], and [R_r].

(V)

Use the “Discrete State Space” block in MATLAB/Simulink 2024b to build the reduced-order heat transfer model.

(VI)

Couple the pre-built 0-dimensional TR model with the reduced-order heat transfer model to obtain the reduced-order TRP model. In this model, the heater and ambient temperature serve as the initial inputs, and the resulting stack temperature from the model output are fed back as inputs to the reduced-order TRP model, forming a closed-loop system.

2.4. Experimental Design

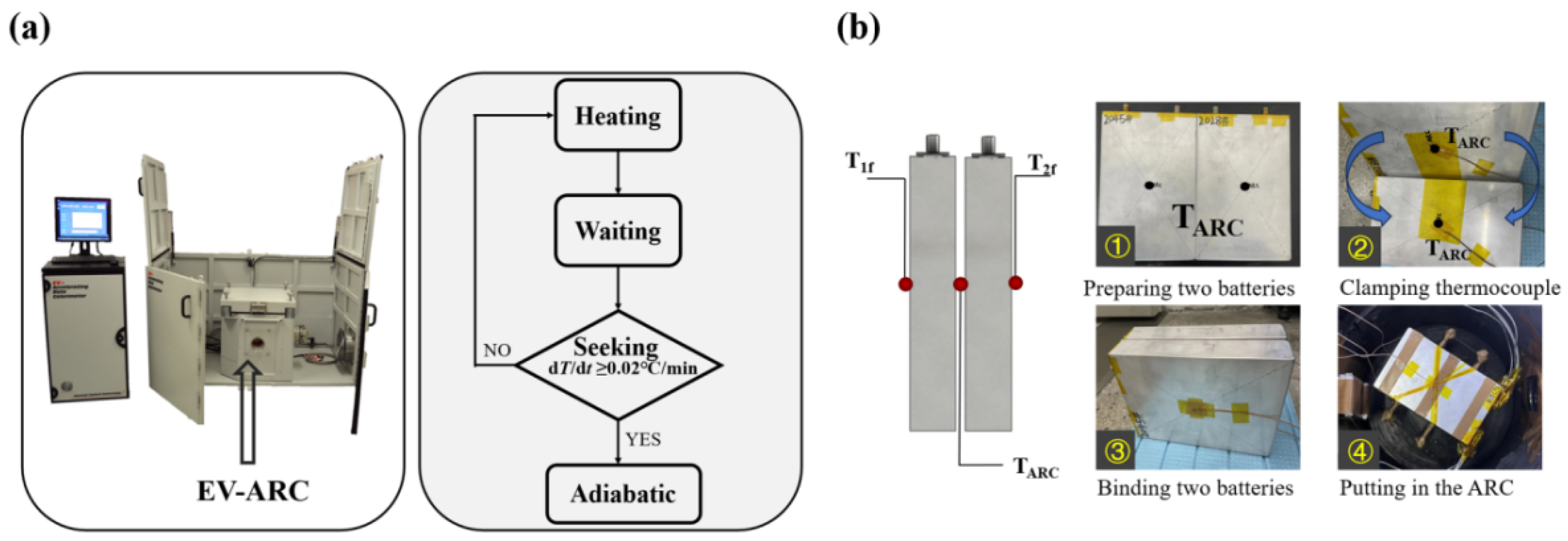
2.4.1. EV-ARC Test

The three characteristic temperatures required for battery TR modeling of the 100 Ah LFP battery, self-heating temperature (T₁), TR triggering temperature (T₂), and maximum TR temperature (T₃), can be acquired through EV-ARC testing. Figure 5a illustrates the typical operating mode of EV-ARC: heating–waiting–seeking. Initially, a temperature rise step is set. After each step of the heating process, the system enters the waiting stage. Once the battery and chamber reach thermal equilibrium, it moves to the seeking stage. EV-ARC determines whether the battery has reached T₁ based on whether the battery’s temperature rise rate reaches 0.02 °C/min. If T₁ is reached, the system enters an adiabatic state, with the ARC chamber temperature following the battery’s temperature changes. Otherwise, it proceeds to the next temperature rise step.

Based on previous disassembly work of battery cells, it is known that this battery has an internal stacked structure, making it impossible to obtain internal temperatures using built-in thermocouples. Therefore, this paper adopts a method of clamping thermocouples on the large surfaces of two batteries to simulate internal temperature measurements, as shown in Figure 5b. The workflow of the large surface clamping method is as follows: (1) prepare two 100% SOC batteries; (2) clamp the main thermocouple at the center of the large surfaces of the two batteries; (3) secure the two batteries and use Teflon tape for binding and fixation; (4) place the two batteries inside the EV-ARC chamber.

2.4.2. Module TRP Test

Figure 6 shows the experimental setup for module TRP testing. During the experiment, four batteries are first charged to 100% SOC. Thermocouples are placed on the front, back, and side of each battery, and voltage lines are connected to the positive and negative tabs of each battery. These wires are then connected to a data acquisition system with a sampling frequency set at 10 Hz. An 800 W heating plate is placed on the front surface of the Cell, and mica shells and holders are used to secure the module at both ends. A torque wrench is used to adjust the pre-tightening force of the module to 2 N·m. The TR of Cell 1 is triggered, and the data acquisition system is monitored. The TR of the battery is determined when the temperature on the back of Cell 1 exceeds 1 °C/s for three consecutive measurements, at which point the heating plate is manually turned off. The entire experimental process is recorded using a high-speed camera; the camera model is WP-CMS1M1000 (WORK POWER, Shenzhen, China), with 1.3 million pixels and 1000 frame rate.

3. Results and Discussion

3.1. Experimental Result

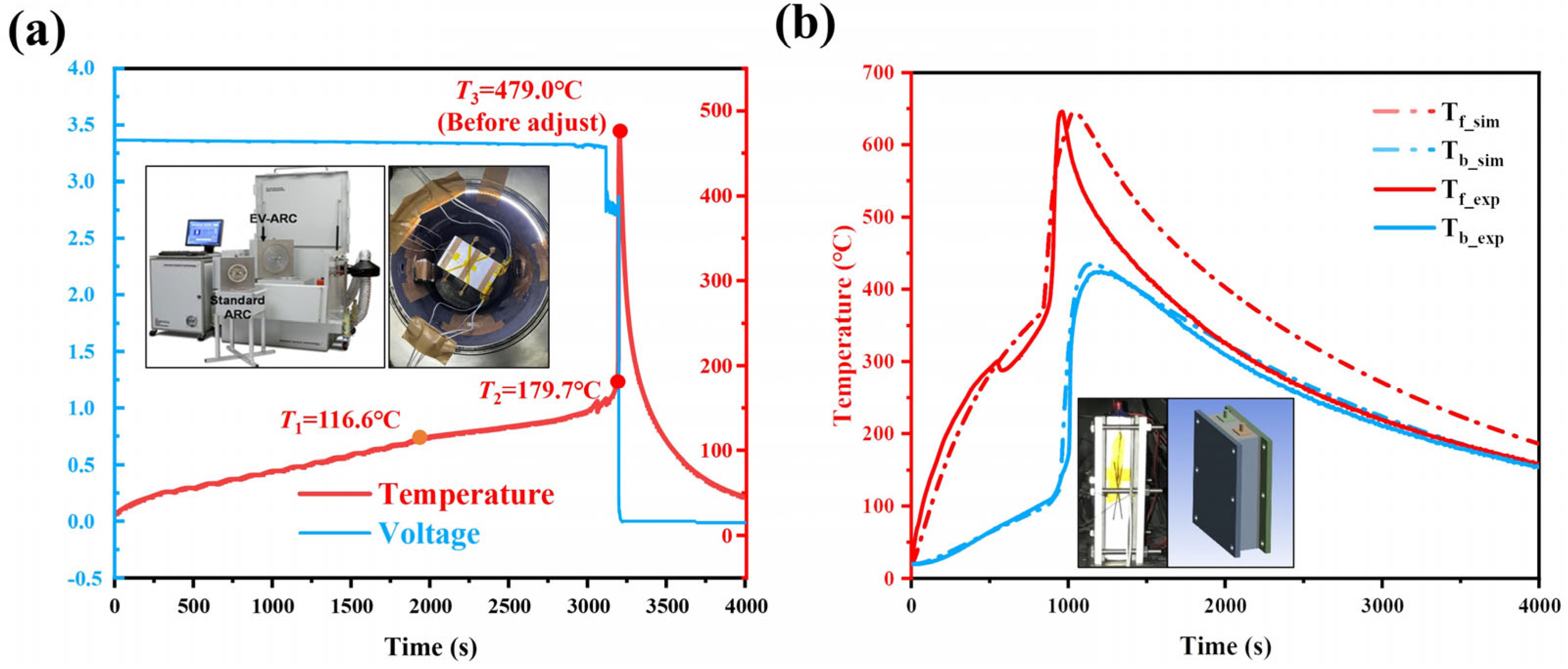
3.1.1. EV-ARC Test Result

To obtain the heat generation characteristics of a single battery cell and provide the input parameters for the TR model, an adiabatic TR test was conducted on the battery cell using an EV-ARC. Figure 7a shows the temperature variation and temperature rise rate during the EV-ARC test, with the test results summarized in

Table 4. TR characteristic temperature.

Characteristic Temperature	T1	T2	T3adj
Values (°C)	116.6	179.7	672.4
Time (min)	2069.40	3187.85	3204.09

. The temperatures T₁, T₂, and T₃ are 116.6 °C, 179.7 °C, and 479.0 °C, respectively. It is known from reference [35] that the T₂ of all kinds of system batteries is mainly distributed between 200 °C and 300 °C, and even the 23 Ah small-capacity LFP battery in the reference [36] has a T₂ of 254 °C. The relatively low T₂ indicates that the 100 Ah LFP battery in this paper requires less energy to reach TR and is prone to TR.

During the test, the large surface clamping method was used. However, due to the thermal barrier effect of the battery’s shell and stack, the heat received by the thermocouple during TR is reduced, resulting in a lower measured temperature T₃ at the clamping point between the two battery centers compared to the actual temperature. According to Xu et al.’s research [37], the measurements of T₁ and T₂ obtained using the large surface clamping method are relatively accurate, but there is a significant temperature gradient between the battery casing and the internal temperature during TR, and the T₃ is more than 150 °C lower than the actual battery temperature.

In this paper, by calibrating T₃, the experimental data and simulation data of thermal runaway of single battery are well matched and, as shown in Figure 7b, the front and back surface temperatures of the single battery thermal runaway test data are matched. After calibration, the battery’s T_3adj is about 672.4 °C and the total heat release ∆H is 1226.3 kJ. The use of this method to calibrate T₃ may cause some errors due to the change in the thermal physical parameters of the battery material, but because the internal material eruption will not occur during the TRP of the LFP battery, the change in the thermal physical parameters of the material in this process is within the acceptable range.

3.1.2. TRP Test Result

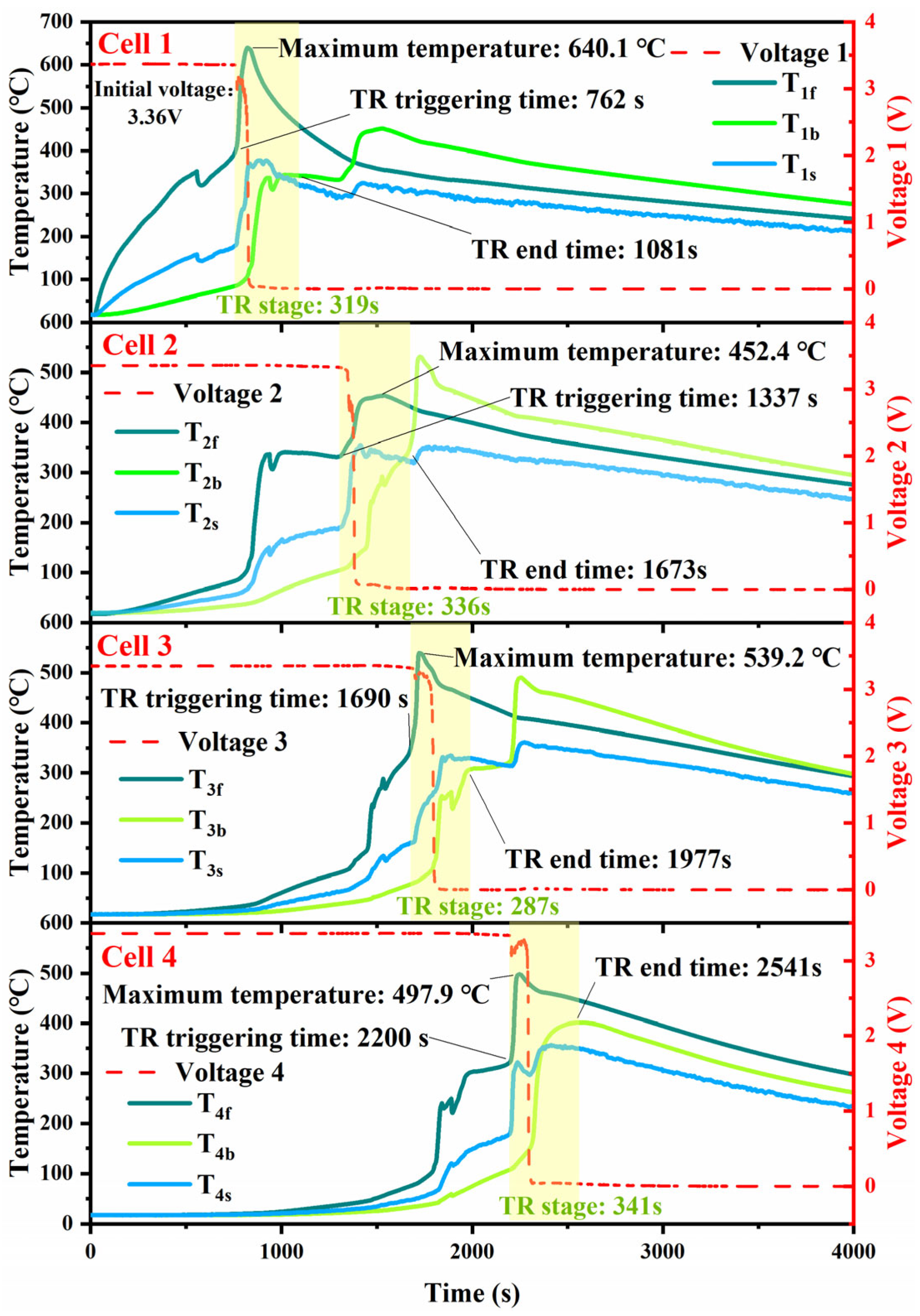
TRP Phenomenon

The experimental phenomena of the module TRP test are illustrated in Figure 8. When the heating process reached 558 s, Cell 1 underwent valve opening, and smoke began to slowly emerge from the vent valve. During this stage, the primary gas composition emitted was electrolyte vapor. The venting process lasted approximately 204 s. At 762 s, Cell 1 experienced TR, as shown in the second image of Figure 8. At this point, a significant amount of flammable gases and electrolyte vapor was ejected at high speed from the vent valve, forming a white mist-like high-speed jet at the nozzle, accompanied by a distinct ejection sound. Unlike TR in NCM battery systems, this LFP battery did not exhibit combustion or explosion. Each of the four cells sequentially underwent TR, with each battery progressing through the stages of valve opening, venting, and TR. The mass loss of the batteries is summarized in

Table 5. Mass loss of each cell.

Cell i	Cell 1	Cell 2	Cell 3	Cell 4
Before test (g)	2243.3	2247.4	2242.4	2240.7
After test (g)	1800.5	1796	1818.5	1804.5
Mass loss (g)	442.8	451.4	423.9	436.2
Mass loss rate	19.74%	20.09%	18.90%	19.47%

, with each battery experiencing a mass loss rate of approximately 20%.

The duration of venting for each battery depended on the time interval between valve opening and TR. The venting times for Cell 1 to Cell 4 were 204 s, 399 s, 156 s, and 309 s, respectively. As can be seen, the venting times of Cell 1 and Cell 3 are relatively short, while those of Cell 2 and Cell 4 are longer. In reference [16], we also observed the phenomenon of inconsistent venting times among batteries. The venting process refers to the period from when the battery begins to vent until TR is triggered. During this process, the internal temperature of the venting battery continuously rises under the heat transfer from the preceding battery until TR occurs. The heat transfer efficiency between batteries determines the duration of venting, and this efficiency is closely related to the contact thermal resistance between batteries. During TR, the intense internal reactions of the battery can cause the shell to expand, which increases the contact thermal resistance between batteries, reduces heat transfer efficiency, and consequently affects the venting time. Due to the complexity and uncertainty of the internal reactions during TR, the impact on the shell’s expansion force varies, which is the reason for the inconsistency in venting duration.

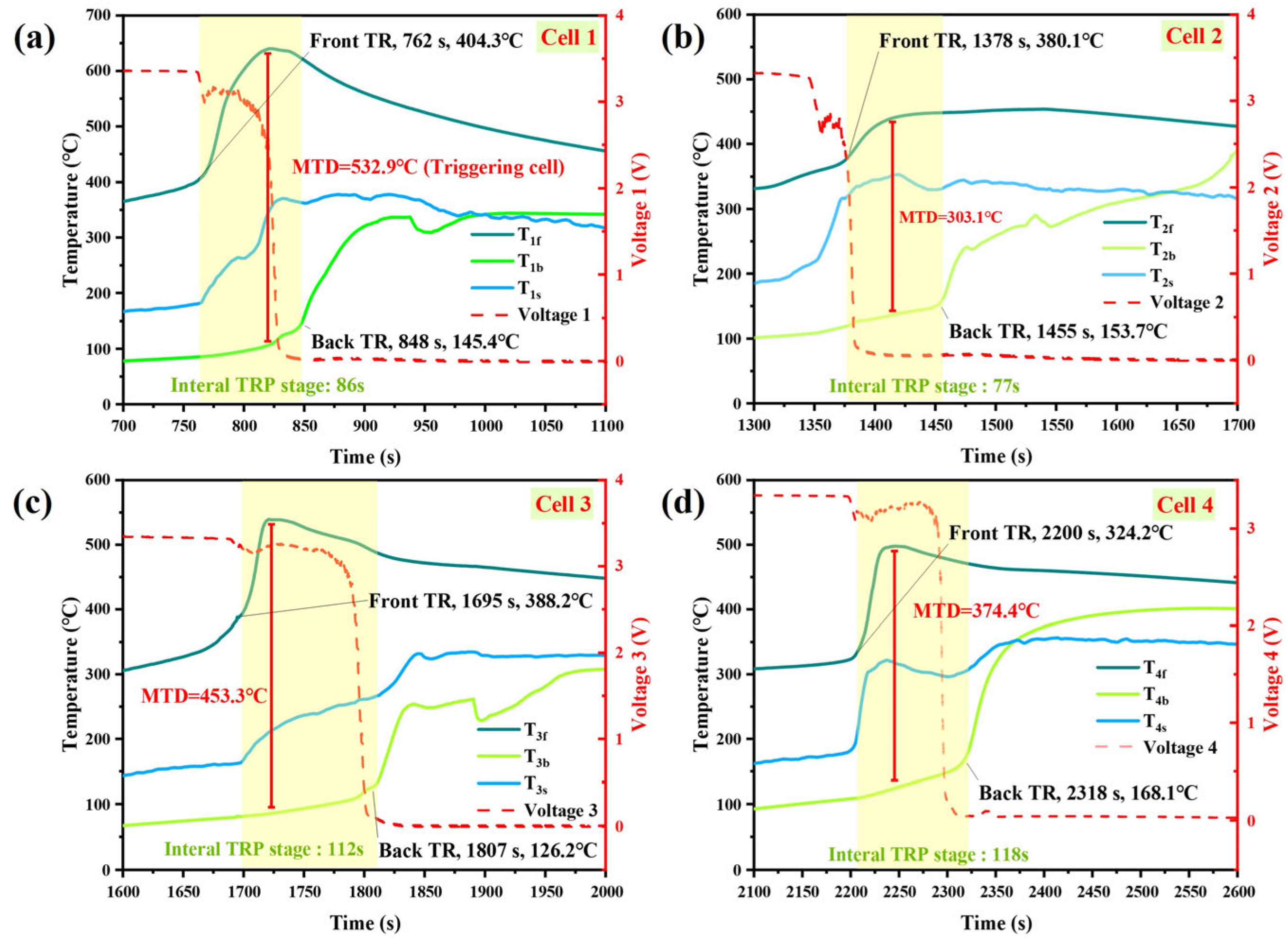
Temperature Characteristics During TRP

Figure 9 shows the surface temperature variations in each cell during the TRP process within the battery module. As can be observed in the figure, when the battery vents, the temperature curve exhibits a slight drop. This is because, at the moment the battery vents due to heating, the phase change of the electrolyte absorbs heat, leading to an overall temperature decrease in the battery.

The non-triggered surface maximum temperatures of the battery range from 452.4 °C to 539.2 °C. In the previous section, it was explained that during the TRP in batteries, an increase in contact thermal resistance slows down the heat transfer from the TR battery to adjacent batteries. The inconsistency in the maximum temperature also stems from this reason: shell expansion leads to an increase in contact thermal resistance, which, in turn, prolongs the venting time of the battery. The extended heat transfer time results in increased heat dissipation, thereby reducing the maximum temperature of the battery during TR. Additionally, there is a positive correlation between the venting duration and the maximum temperature of the battery.

The TR stage of each cell is defined as the period from the onset of TR on the front surface to the completion of TR on the back surface. These stages of TR for each cell were extracted and are annotated in Figure 8. The durations of TR for the respective cells are 319 s, 336 s, 287 s, and 341 s. Equation (18) is introduced below to provide a rough estimate of the internal TRP speed within the cells, where δ represents the thickness of the battery and Δt_i represents the duration of TR. Using this formula, the calculated internal heat propagation speeds within the cells are 0.113 mm/s, 0.107 mm/s, 0.125 mm/s, and 0.106 mm/s, respectively.

$$v_{\mathrm{i}}={\displaystyle \frac{\delta }{\Delta t_{\mathrm{i}}}}$$

(18)

Figure 10 illustrates the internal TRP characteristics inside each cell. There is a significant time interval between the front and back of the battery TR, which is due to the internal propagation of the two stacks of the battery. The temperature gradient between the front and back surfaces drives the heat transfer from the front surface to the back surface. The triggering temperatures of TR on the front surfaces of Cell 1 to Cell 4 are 404.3 °C, 380.1 °C, 388.2 °C, and 324.2 °C, respectively; the triggering temperatures of TR on the back surfaces are 145.4 °C, 153.7 °C, 126.2 °C, and 168.1 °C, respectively; the internal TRP times within each cell are 86 s, 77 s, 112 s, and 118 s, respectively. The maximum temperature differences (MTDs) for non-triggered batteries are 303.1 °C, 453.3 °C, and 374.4 °C.

Additionally, in Cell 1, Cell 3, and Cell 4, the voltage drops to zero almost simultaneously with the onset of TR on the back surface. However, in Cell 2, the front surface experiences TR at the moment the voltage drops to zero. The voltage drop in the battery is caused by the occurrence of a large-area internal short circuit. The venting time of Cell 2 is as long as 399 s. During this process, the heat transfer efficiency from Cell 1 to Cell 2 is relatively low. Prolonged low heat transfer efficiency allows the internal stacks of the battery to heat up uniformly. When TR occurs, the temperature across the stacks remains relatively consistent, accelerating the internal TRP, with the internal TRP time being as short as 77 s. Therefore, when TR occurs on the front surface of Cell 2, a large-area internal short circuit occurs, leading to the immediate voltage drop in Cell 2 after the front surface TR.

3.2. Simulation Result

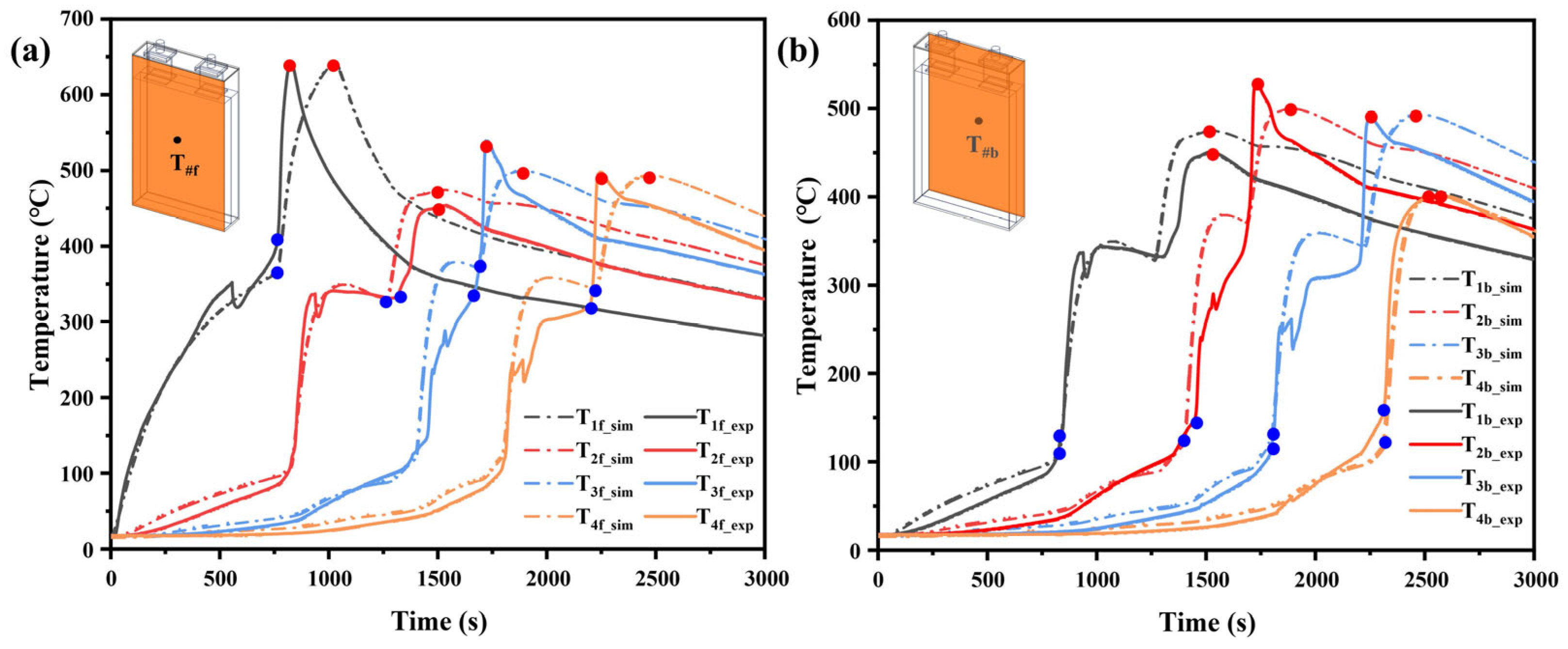
3.2.1. Model Validation

The simulation results of the model were validated against the experimental results in the preceding text to examine its accuracy in simulating the energy flow changes during battery TRP. By giving the constant contact thermal resistance value of the aluminum shell in contact with other components, the heat transfer time is controlled and indexed with the experimental data. Figure 11a presents the validation of the triggering and maximum temperatures for TR on the front surface of Cells 1–4, while Figure 11b shows the alignment of the triggering time and maximum temperatures for TR on the back surface of each cell. The curves from the simulation results closely match those from the experimental results.

The errors in key features between the simulation and the experiment for each cell were calculated using Equation (19), and the details are presented in

Table 6. Error analysis of simulation.

Position	Symbol	Triggering Time (s)			Maximum Temperature (°C)
		Sim	Exp	Error	Sim	Exp	Error
Front	T1f	763	762	0.13%	644.7	640.1	0.72%
	T2f	1263	1337	5.53%	475.0	452.4	5.00%
	T3f	1684	1690	0.36%	500.0	539.2	7.27%
	T4f	2221	2200	0.95%	493.8	497.9	0.82%
Back	T1b	848	827	2.54%	475.1	451.4	5.25%
	T2b	1455	1398	4.08%	500.3	529.8	5.57%
	T3b	1807	1797	0.56%	493.7	490.8	0.59%
	T4b	2318	2308	0.43%	402.1	401.5	0.15%

. Here, a_sim represents the simulation result, a_exp represents the experimental result, and Error denotes the calculation error between the two. The maximum errors for the triggering time and maximum temperature of TR on the front side T_#f of the batteries are 5.53% and 7.27%, respectively. Similarly, the maximum errors for the triggering time and maximum temperature on the back side T_#b are 4.08% and 5.57%, respectively. The accuracy of the TR triggering time for the large surfaces of the batteries can reach a value within 5%, and the maximum temperature error can be kept within 10%. This demonstrates that the model can effectively simulate the main characteristics of the TRP process within the battery module, enabling energy flow calculations and analysis of the heat conduction patterns during TRP.

$$Error={\displaystyle \frac{a_{\exp }-a_{\mathrm{s}\mathrm{i}\mathrm{m}}}{a_{\mathrm{e}\mathrm{x}\mathrm{p}}}}\times 100\%$$

(19)

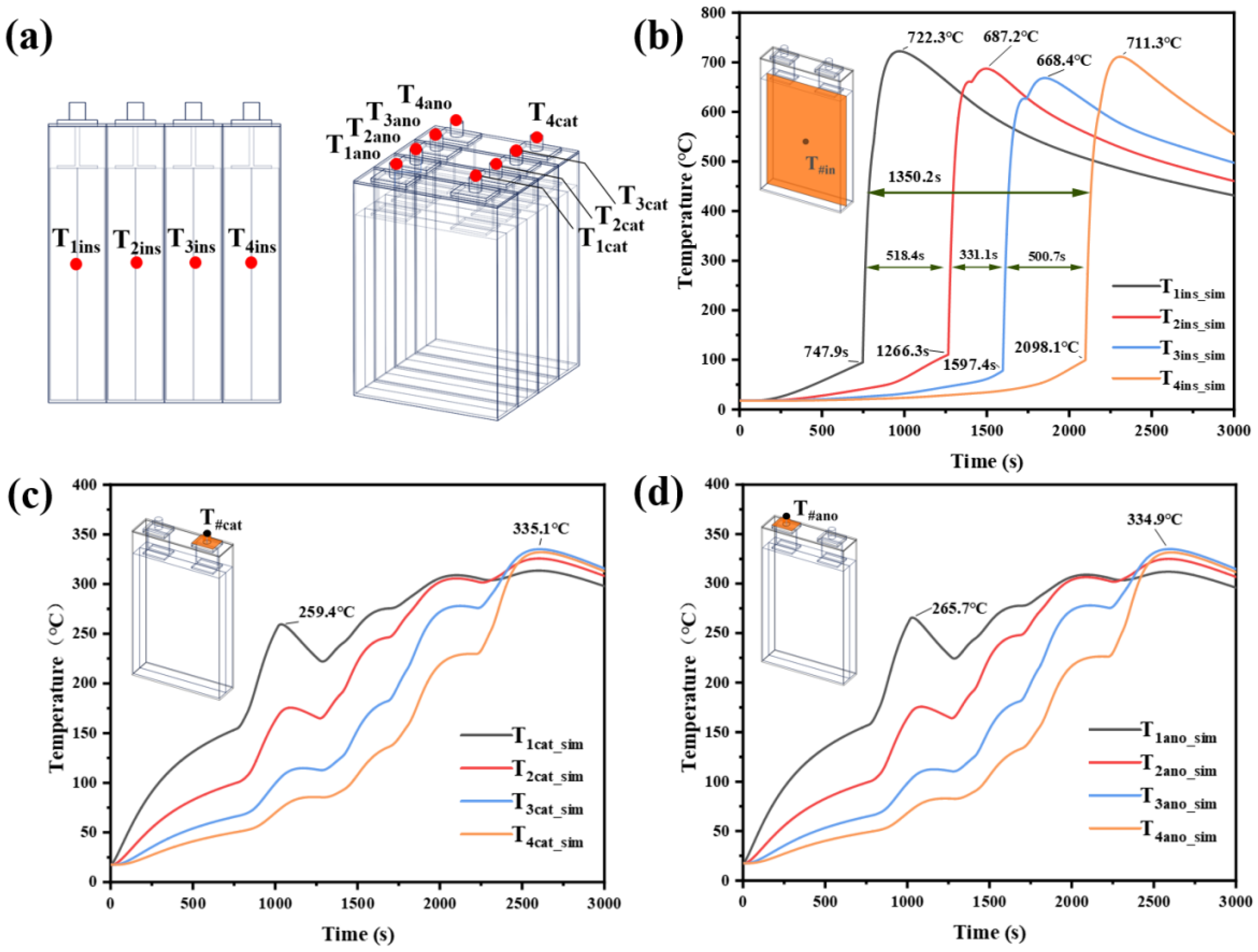
3.2.2. Model Prediction of Characteristic Location

The reduced-order TRP model developed is capable of predicting temperature changes at characteristic locations within the three-dimensional model. In this study, predictions were made for the internal temperatures and tab temperatures of each TR battery, aiming to leverage the engineering application value of the ROM while reducing the experimental costs. Figure 12a shows the layout of the monitoring points of each battery, and Figure 12b–d presents the predicted results for the internal center temperatures and cathode/anode tab temperatures:

(1)

Internal temperature predictions: As depicted in Figure 12b, the model predicts that the internal TR triggering times for Cells 1–4 are 747.9 s, 1266.3 s, 1597.4 s, and 2098.1 s, respectively. Due to the time required for heat transfer, the internal TR triggering times slightly precede those observed on the front surfaces of the cells. The maximum internal temperatures for each battery are 722.3 °C, 687.2 °C, 668.4 °C, and 711.3 °C, respectively. The energy for this temperature rise primarily originates from the energy input of the heating plate and the energy generated by the TR of the stacks. The total TRP time for the module is 1350.2 s, with inter-cell TRP times of 518.4 s, 331.1 s, and 500.7 s. The difference between the internal temperature and the surface temperature of the square-shell battery is more than 150 °C [37], and the difference between the simulated internal temperature and the surface temperature is 150–200 °C, which proves that the predicted temperature is within a reasonable range.

(2)

Tab temperature predictions: Figure 12c,d illustrates that as the TRP process progresses within the battery module, the temperatures of both cathode and anode tabs exhibit a wavelike increasing trend. This temperature rise is primarily attributed to heat conduction from the TR of the stacks to the current collectors and heat transfer from adjacent battery casings. The maximum temperatures of each tab ultimately reach approximately 355 °C. The slight differences between the tabs are primarily due to the higher thermal conductivity of the anode material copper compared to the cathode material aluminum.

3.2.3. Model Parameters’ Adjustment Analysis

Increasing the TR Triggering Temperature T₂

T₂ represents the temperature at which a battery triggers thermal runaway. Therefore, increasing T₂ can reduce the likelihood of thermal runaway in batteries. In practical scenarios, T₂ corresponds to the temperature at which the separator in the battery material undergoes large-scale melting and decomposition. Studying the impact of T₂ can assist in the rational selection of separators during the battery design process.

By adjusting the battery TR triggering temperature T₂ in the model, its impact on battery module TRP was studied. As shown in Figure 13a, the original T₂ of the battery was 180 °C. The onset of TR in Cell 1 occurred at 747.9 s, with a total duration of TRP of 1350.2 s; the average triggering TR temperature at the battery’s internal center was 96 °C, and the mean maximum temperature (MMT) of the four cells was 697.3 °C. When T₂ was increased to 190 °C, the triggering time of TR in Cell 1 was extended by 1.1%, the total duration of TRP was extended by 16.8%, the TR triggering temperature increased to 110.1 °C (an increase of 12.8%), and the MMT was 712.7 °C, a relative increase of 2.2%. When T₂ was raised to 199 °C, the TR triggering time in Cell 1 was extended by 16.2%, the total duration of TRP was extended by 41%, the TR triggering temperature increased to 124.5 °C (an increase of 29.7%), and the MMT was 726.2 °C, a relative increase of 4.1%. When T₂ was increased to 200 °C, no TRP occurred in the battery module. In summary, increasing T₂ can delay the onset of battery TR. When T₂ is increased to 200 °C, TRP in the battery module can be suppressed. Therefore, the selection of separator materials should ensure a melting point above 200 °C.

Reducing the Total Heat Release ΔH

The total heat release ΔH during the thermal runaway process of a battery is a critical parameter for assessing the severity of thermal runaway hazards. It primarily includes the electrical energy released during internal short circuits and the energy generated by chemical reactions between materials. ΔH can be accurately measured through adiabatic calorimetry tests, and its value is closely related to the maximum temperature T₃ reached during thermal runaway. The magnitude of T₃, in turn, depends on the battery’s material system and its SOC. In the actual battery manufacturing process, the magnitude of T₃ can be assessed through ARC testing by improving the battery’s material system. Additionally, T₃ can be reduced by appropriately discharging to lower the SOC, thereby decreasing ΔH. This is of significant practical importance for suppressing thermal propagation in battery modules.

By adjusting ΔH to control the total heat release of the battery, its impact on TRP was studied. As shown in Figure 13b, the original condition was 100% ΔH. When ΔH was adjusted to 95%, the total TRP time of the battery was extended by 17.1%, and the MMT was 676.4 °C, a decrease of 3.0%. When ΔH was reduced to 93%, the total TRP time of the battery was extended by 29.6%, and the MMT was 668.1 °C, a relative decrease of 4.2%. When ΔH was reduced to 90%, no TRP occurred in the battery module, and the maximum temperature of the first cell was 659.5 °C, a relative decrease of 5.4%. The TR triggering time of the battery remained basically unchanged in all four scenarios because it is related to the energy absorbed by the battery when it reaches the T₂. In summary, reducing the total heat release ΔH of the battery can extend the TRP time, and ultimately, at 90% ΔH, TRP can be suppressed. Moreover, due to the reduction in total heat release, the maximum temperature also decreases somewhat, but it has little impact on the TR triggering time. In the battery design process, the use of safe battery materials to reduce TR chemical reaction energy release, and reasonable control of SOC during battery storage can achieve this effect.

Increasing Convective Heat Transfer Coefficient h

The impact of the convective heat transfer coefficient h on the module’s TRP was studied, as shown in Figure 13c. The original condition was h = 15 W·m⁻²·K⁻¹. When the convective heat transfer coefficient was increased to h = 25 W·m⁻²·K⁻¹, the total duration of TRP increased from 1350.2 s to 1748.9 s, an increase of 29.5%. The TR triggering time increased from 747.9 s to 772.5 s, a relative increase of 3.3%. When h was increased to 35 W·m⁻²·K⁻¹, no TRP occurred in the battery module, and the TR triggering time was extended by 3.7%. In practical scenarios, the incorporation of air cooling or liquid cooling can be considered to achieve suppression effects.

Adding an Additional Insulation Layer

h_R represents the equivalent heat transfer coefficient between batteries. Adjusting h_R can be equated to adding an insulation layer in reality. The calculation formula is shown in Equation (20), where λ represents the thermal conductivity of the insulation layer, and d is the thickness of the insulation layer. A smaller h_R indicates weaker heat transfer capability between batteries.

$$h_{\mathrm{R}}={\displaystyle \frac{1}{R}}={\displaystyle \frac{\lambda }{d}}$$

(20)

As shown in Figure 13d, the original condition was without an additional thermal resistance. When h_R = 120 W·m⁻²·K⁻¹, the total duration of TRP increased from 1350.2 s to 1692.4 s, an increase of 25.3%. When h_R = 100 W·m⁻²·K⁻¹, no TRP occurred in the battery pack. At this point, if calculated based on 1 mm of insulation material, the thermal conductivity λ of the required insulation material needs to be lower than 0.1 W·m⁻¹·K⁻¹. In addition, adding a thermal resistance layer has little impact on the maximum temperature of the battery and the onset time of TR.

3.2.4. Simulation Efficiency Compared with FEM

To validate the efficiency improvement brought by the reduced-order TRP model, this study established a finite element TRP model using ANSYS Fluent for comparative analysis of simulation efficiency. To control the variables, the mesh file used is the same as that employed before the order reduction for the ROM, as shown in Figure 14a. Both models are simulated on a computer equipped with a Core i9-9900k processor, 128 GB of random-access memory (RAM), 8 cores, and 16 threads. Both models are set to calculate 3000 s operating conditions. To avoid chance effects, no other computing software is opened during the simulation process.

Figure 14b presents the simulation results of the FEM and ROM, demonstrating that the FEM can effectively simulate the internal temperature of the battery module and it fits well with ROM.

Table 7. Simulation duration.

Category	Duration
ROM (Order reduction and Calculation)	8 min 45 s
FEM	328 min 49 s

records the simulation duration for both the ROM and the FEM. The simulation duration for the ROM consists of two parts: the order reduction time in ANSYS, which is 2 min 12 s, and the calculation time in Simulink, which is 6 min 33 s. The total duration for the ROM is 8 min 54 s, while the FEM requires 328 min 49 s. It is evident that the ROM can significantly reduce calculation time, improving computational efficiency by approximately 40 times compared to the FEM. In the future, we will further expand the model to a greater extent, thereby amplifying the significance of ROM.

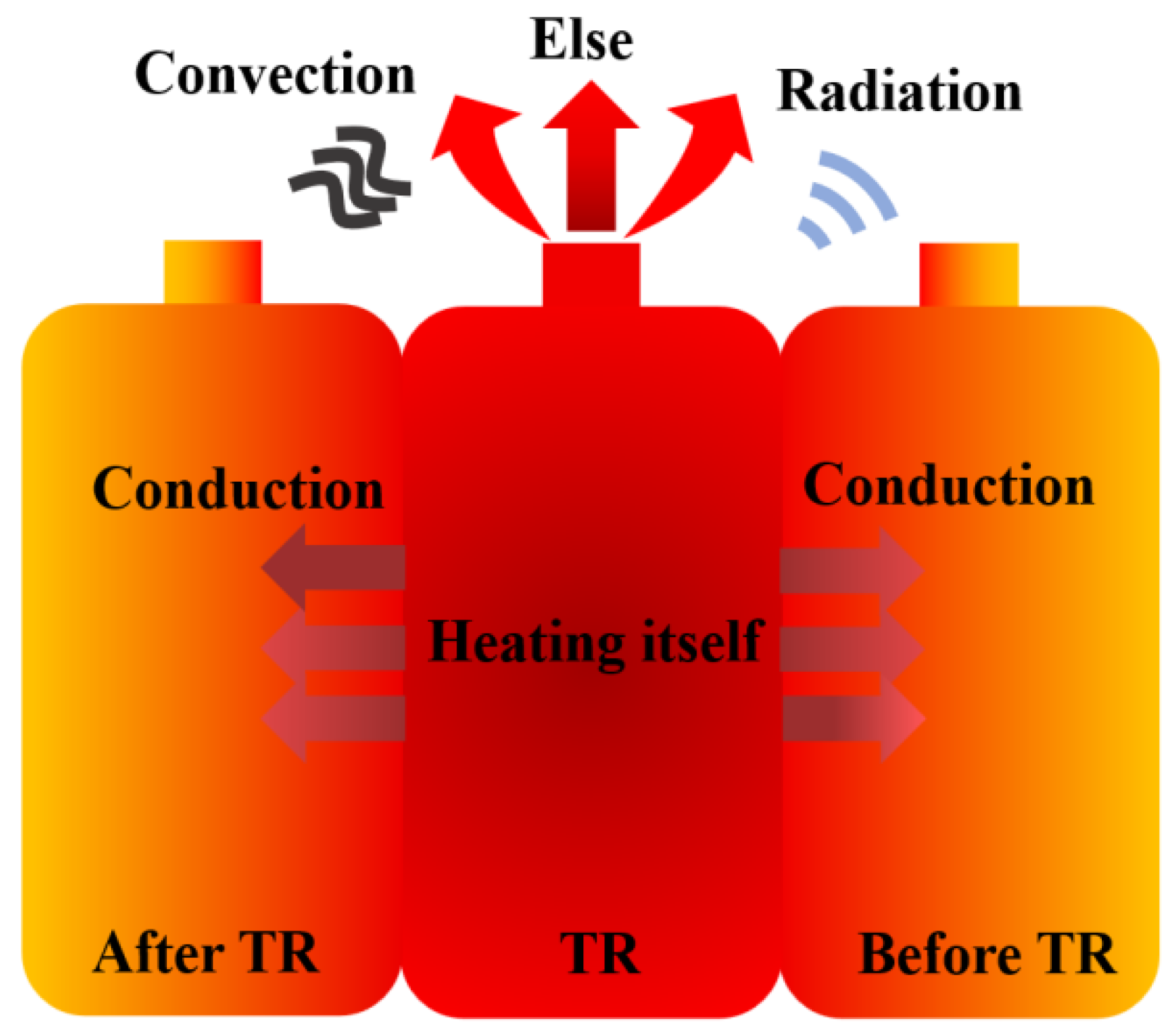
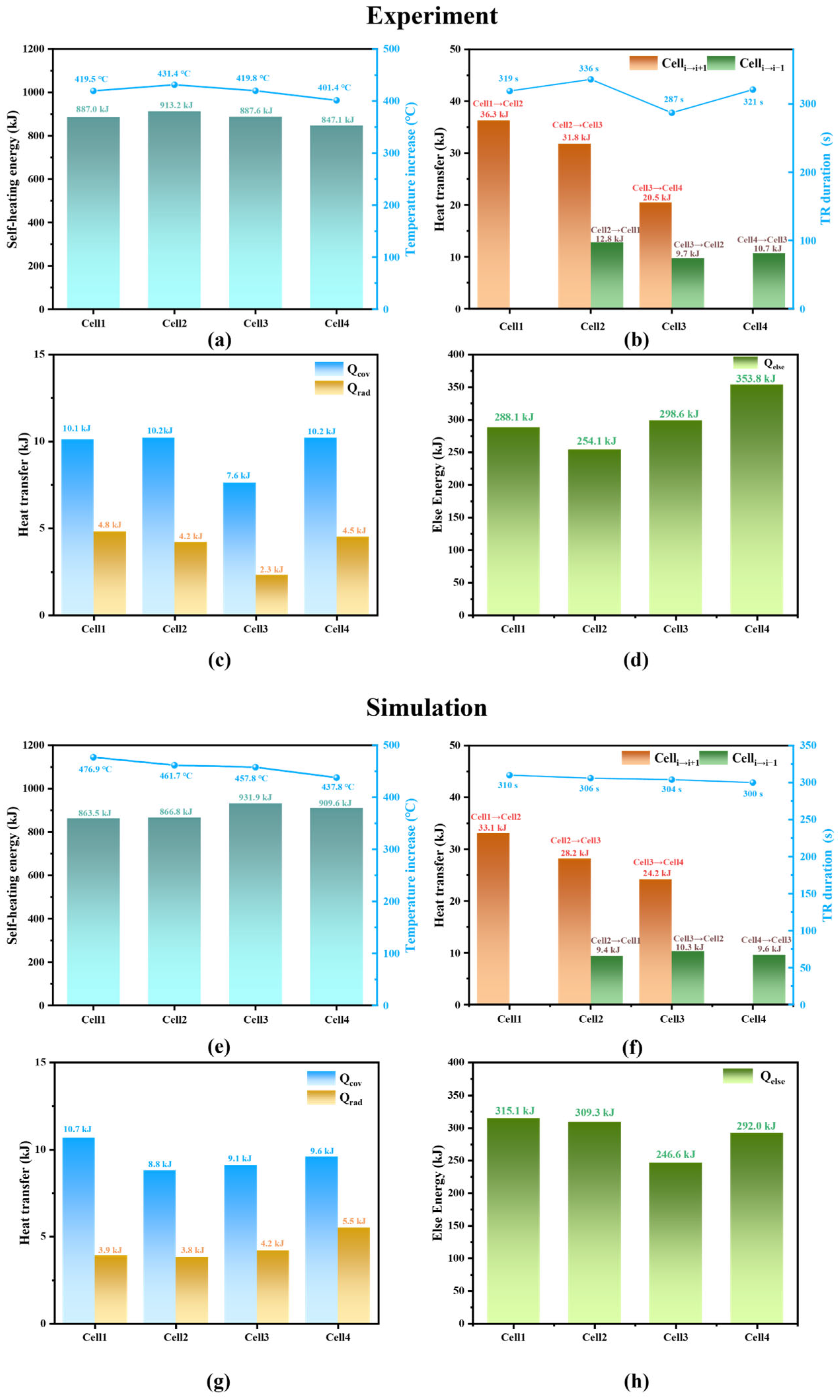
3.3. Energy Flow Analysis

3.3.1. Energy Flow Composition

During TRP in a battery module, there is a process of energy flow when a cell experiences TR. According to reference [20], the energy flow distribution resulting from TR in a single cell includes six components: the energy Q_i that heats the cell itself, the energy Q_i→i+1 that flows to the next non-runaway cell, the energy Q_i→i−1 that flows to the previous runaway cell, the energy Q_rad lost through thermal radiation, the energy Q_cov lost through thermal convection, and other energy Q_else lost through behaviors such as venting.

Figure 15 illustrates the composition of energy flow during TR of a single cell in the process of TRP in a battery module. Q_i→i+1 and Q_i→i−1 can be calculated using Fourier’s law of heat conduction [38], with the calculation formulas given by Equations (21) and (22). In these formulas, A₁ represents the large surface area of the battery, which is 0.028 m²; t_i-trigger and t_i-end, respectively, represent the triggering and end times of TR for Cell i; T_if and T_ib, respectively, represent the temperatures of the front and back surfaces of Cell i. The axial thermal conductivity λ_cell of the battery can be calculated using Equation (23), where L_cell is the axial thickness of the battery, which is 0.036 m; λ_shell is the thermal conductivity of the battery shell; λ_stack is the axial thermal conductivity of the stacks; L_shell is the thickness of the battery shell, which is 0.002 m; and L_stack is the thickness of the stacks, which is 0.034 m. The energy Q_i used by the battery to heat itself can be calculated using Equation (24), where T_ave represents the average temperature rise of the battery; T₀ represents the initial temperature of the battery, which is 17.5 °C; Q_heater represents the energy input by the heater; Q_i−1→i represents the energy from the previous battery.

$$Q_{\mathrm{i}\mathrm{\to }\mathrm{i}\mathrm{+}\mathrm{1}}={\displaystyle \frac{{\lambda }_{\mathrm{c}\mathrm{e}\mathrm{l}\mathrm{l}}{A}_1}{\sigma }}{\displaystyle \underset{t_{\mathrm{i}-\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{r}\mathrm{t}}}{\overset{t_{\mathrm{i}-\mathrm{e}\mathrm{n}\mathrm{d}}}{\int }}[T_{(\mathrm{i}\mathrm{+}\mathrm{1})\mathrm{f}}-T_{(\mathrm{i}\mathrm{+}\mathrm{1})\mathrm{b}}]d}t$$

(21)

$$Q_{\mathrm{i}\mathrm{\to }\mathrm{i}\mathrm{-}\mathrm{1}}={\displaystyle \frac{{\lambda }_{\mathrm{cell}}{A}_1}{\sigma }}{\displaystyle \underset{t_{\mathrm{i}-\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{g}\mathrm{g}\mathrm{e}\mathrm{r}}}{\overset{{\mathrm{t}}_{\mathrm{i}-\mathrm{e}\mathrm{n}\mathrm{d}}}{\int }}[T_{(\mathrm{i}-\mathrm{1})\mathrm{b}}-T_{(\mathrm{i}-\mathrm{1})\mathrm{f}}]d}t$$

(22)

$${\lambda }_{\mathrm{c}\mathrm{e}\mathrm{l}\mathrm{l}}={\displaystyle \frac{L_{\mathrm{c}\mathrm{e}\mathrm{l}\mathrm{l}}{\lambda }_{\mathrm{shell}}{\lambda }_{\mathrm{s}\mathrm{t}\mathrm{a}c\mathrm{k}}}{L_{\mathrm{s}\mathrm{h}\mathrm{e}\mathrm{l}\mathrm{l}}{\lambda }_{\mathrm{stack}}+L_{\mathrm{stack}}{\lambda }_{\mathrm{shell}}}}$$

(23)

$$Q_{\mathrm{i}}=cm(T_{\mathrm{ave}}-T_0)-Q_{\mathrm{h}\mathrm{e}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{r}}-Q_{\mathrm{i}-\mathrm{1}\to \mathrm{i}}$$

(24)

The heat dissipation through thermal convection Q_cov and thermal radiation Q_rad during the TR process of a battery can be calculated using Formulas (25) and (26). In these formulas, A₂ represents the surface area of the battery exposed to the air, which is 0.02 m². The heat loss Q_else through venting and other behaviors is calculated by subtracting the sum of the above energies from the total heat generated during TR ΔH, as shown in Formula (27). The TR process involves numerous uncertainties, and there is currently no relevant research or theory that can quantitatively analyze Q_else during this process. This represents a significant breakthrough point for our future studies.

$$Q_{\mathrm{conv}}=h\cdot A_2\cdot {\displaystyle \underset{t_{\mathrm{i}-\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{g}\mathrm{g}\mathrm{e}\mathrm{r}}}{\overset{t_{\mathrm{i}-\mathrm{e}\mathrm{n}\mathrm{d}}}{\int }}(T_{\mathrm{s}}\mathrm{-}{T}_{\mathrm{\infty }})dt}$$

(25)

$$Q_{\mathrm{r}\mathrm{a}\mathrm{d}}=A_2\cdot {\displaystyle \underset{t_{\mathrm{i}-\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{g}\mathrm{g}\mathrm{e}\mathrm{r}}}{\overset{t_{\mathrm{i}-\mathrm{e}\mathrm{n}\mathrm{d}}}{\int }}{\epsilon }_{\mathrm{r}\mathrm{a}\mathrm{d}}\cdot {\sigma }_{\mathrm{rad}}\cdot ({T_{\mathrm{s}}}^4-{T_{\mathrm{\infty }}}^4)dt}$$

(26)

$$Q_{\mathrm{e}\mathrm{l}\mathrm{s}\mathrm{e}}=\Delta H-Q_{\mathrm{i}}-Q_{\mathrm{cond}}-Q_{\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{v}}-Q_{\mathrm{r}\mathrm{a}\mathrm{d}}$$

(27)

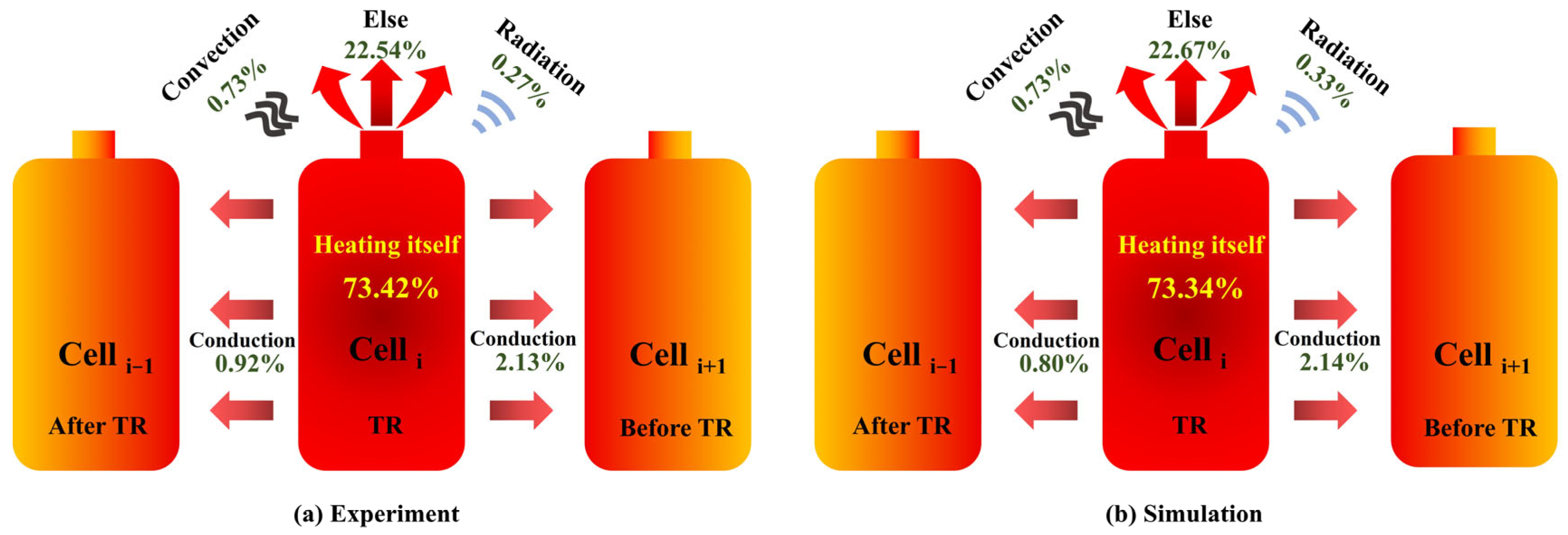
3.3.2. Energy Flow Distribution Characteristic

Using the above formulas, energy flow calculations were performed on both the simulation results and the experimental results. Figure 16a–d shows the energy flow calculation results obtained from experimental data for each cell.

As shown in Figure 16a, the energy used by each cell to heat itself is mainly calculated based on the average temperature rise of the cell. The temperature rises of each cell are 419.5 °C, 431.4 °C, 419.8 °C, and 401.4 °C, respectively; the energies used for heating itself are 887.0 kJ, 913.2 kJ, 887.6 kJ, and 847.1 kJ, respectively.

As shown in Figure 16b, the calculation of energy transferred between batteries through thermal conduction is related to the TR duration of each cell. The TR durations of each cell are 319 s, 336 s, 287 s, and 321 s, respectively. Among them, the energy transferred from Cell 1 to Cell 2 (before TR) during the TR is 36.3 kJ; the energy transferred from Cell 2 to Cell 3 (before TR) is 31.8 kJ, and the energy transferred to Cell 1 (after TR) is 12.8 kJ; the energy transferred from Cell 3 to Cell 4 (before TR) is 20.5 kJ, and the energy transferred to Cell 2 (after TR) is 9.7 kJ; the energy transferred from Cell 4 to Cell 3 (after TR) is 10.7 kJ. It can be seen that there is a decreasing trend in the energy transferred to the next cell, which is because the battery deformation occurs during the TRP process, resulting in increased contact thermal resistance between batteries; the energy transferred to the next non-runaway cell is about 2–3 times that transferred to the previous cell, which is mainly due to the destruction of the internal stacks’ structure of the already TR battery compared to a fresh battery, leading to reduced internal heat transfer capability.

Figure 16c shows the energy lost through thermal radiation and thermal convection during the TRP process. The energy lost through thermal convection is approximately around 10 kJ, while the heat lost through thermal radiation is only below 5 kJ. Figure 16d shows the energy lost through behaviors such as venting and ejection, which ranges from 254.1 kJ to 353.8 kJ, representing a significant portion of the energy that cannot be ignored.

Figure 16e–h shows the energy distribution calculated from the simulation results. The simulation results are similar to the experimental calculation results, indicating that the model can effectively predict the energy flow during the TRP process.

In the battery module, most cells are located inside the module and exhibit complete energy flow path characteristics. To more intuitively illustrate the energy flow during the TR process of the cells within the module, the average values of Cell 2 and Cell 3 were taken to represent the energy flow characteristics of the internal cells, as shown in Figure 17a. From this, we can derive the energy flow distribution pattern during the TRP process of the 100 Ah LFP battery studied.

For the cells inside the module, out of the total energy generated by each TR cell, approximately 73.42% is used to heat the battery itself, 2.13% is transferred to the next cell, 0.92% is transferred to the previous cell, 0.73% is lost through convective heat transfer, 0.27% is lost through radiative heat transfer, and 22.54% of the energy is dissipated through exhaust and other means, which is similar to the battery TR mass loss rate recorded in Table 6. As shown in Figure 17b, the results obtained by simulation are similar to the experimental results, which also verifies the accuracy of ROM. This result is significant for research on quantitative and targeted suppression methods based on energy distribution during battery TRP processes.

4. Conclusions

In this paper, a TRP experiment was conducted on a four-cell 100 Ah LFP battery module, and the TRP characteristics of the battery were analyzed. Based on the Arnoldi method in Krylov subspace, a reduced-order TRP model for the energy storage battery module was established. The model can significantly save computation time while obtaining the temperature of specified monitoring points in three-dimensional space. Finally, energy flow analysis and calculations were performed based on the experimental and simulation results to obtain the energy flow patterns of each cell within the module during TRP. The following conclusions were drawn from the research results:

(1)

The experimental results of the battery module’s TRP indicate that the 100 Ah LFP battery module experienced TRP. The maximum surface temperatures of each cell range between 452.4 °C and 539.2 °C, and there is a time interval of 77 s to 118 s between the triggering of TR on the front and back surfaces of the battery. The MTD inside the battery is between 303.1 °C and 453.3 °C, and the internal TRP speed of the battery is approximately 0.12 mm/s.

(2)

The simulation results show that the ROM achieves good accuracy with critical feature errors within 10%. The model predicts that the internal maximum temperature of the four cells is approximately 700 °C, and the temperatures of the cathode and anode tabs show a wave-like increasing trend with a maximum temperature of about 355 °C. The total duration for the ROM is 8 min 54 s, while the FEM requires 328 min 49 s. The ROM can improve computational efficiency by approximately 40 times compared to the FEM.

(3)

The adjustment results of key model parameters indicate that increasing the TR triggering temperature T₂ from 190 °C to 200 °C, reducing the total heat release ΔH from 100% to 90%, increasing the convective heat transfer coefficient h from 15 W·m⁻²·K⁻¹ to 35 W·m⁻²·K⁻¹, and adding a thermal resistance of h_R = 100 W·m⁻²·K⁻¹ can all suppress TRP in the battery module.

(4)

Energy flow calculations were performed based on the simulation and experimental results of the four cells, revealing the energy flow patterns during the TRP process of the cells within the module. Of the total energy released during TR of an individual cell within the module, more than 70% of the energy is used to heat itself, over 20% is lost through venting and other behaviors, about 2% is transferred to the next cell, 1% is transferred to the previous cell, and approximately 1% is dissipated through convection and radiation.

This work provides a solution for achieving efficient computation of system-level TRP simulations and reveals the energy flow patterns during the TRP process of 100 Ah LFP energy storage batteries. It is beneficial for guiding the safe design and protection of electrochemical energy storage power stations.