Investigation of Reactant Conversion in the Vanadium Redox Flow Battery Using Spatially Resolved State of Charge Mapping
Abstract
:1. Introduction
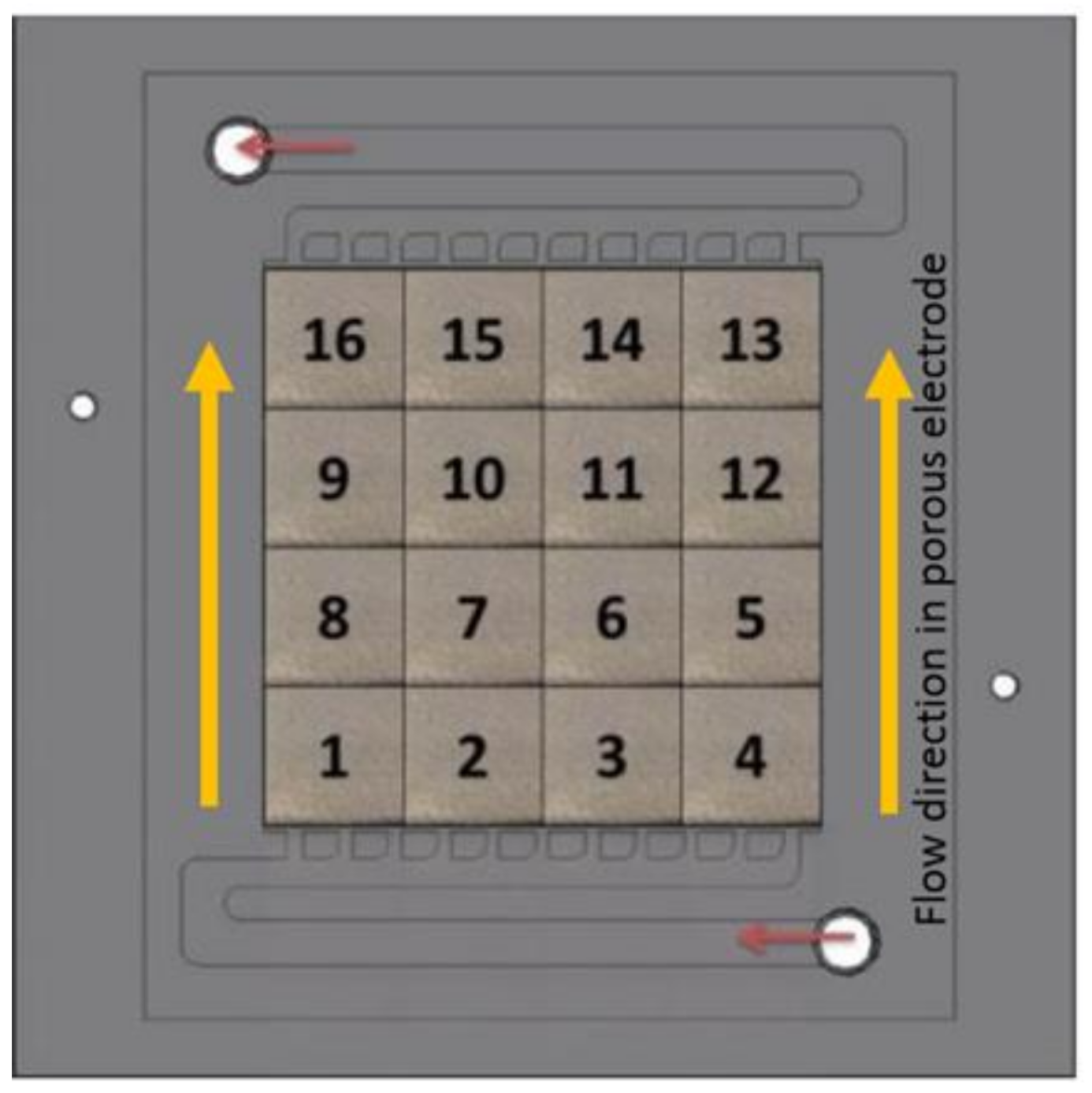
2. Materials and Methods
3. Results and Discussions
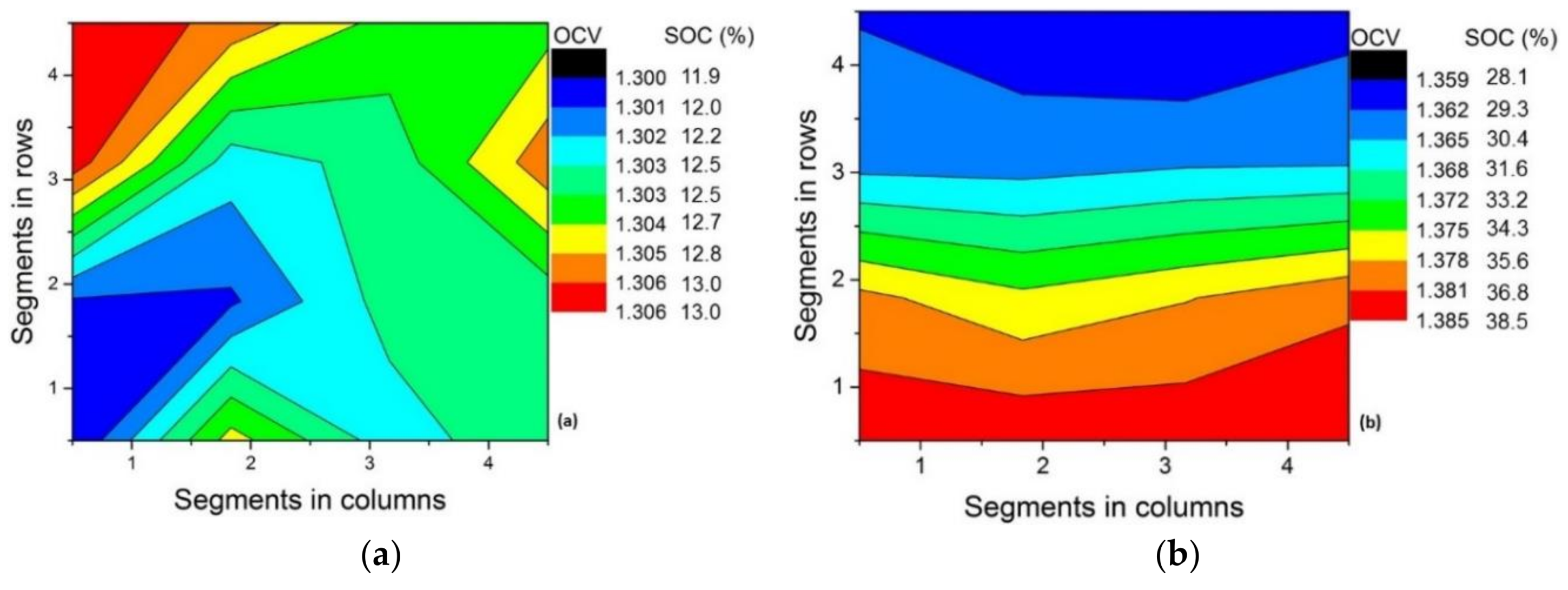
3.1. Effect of Electrode Modification
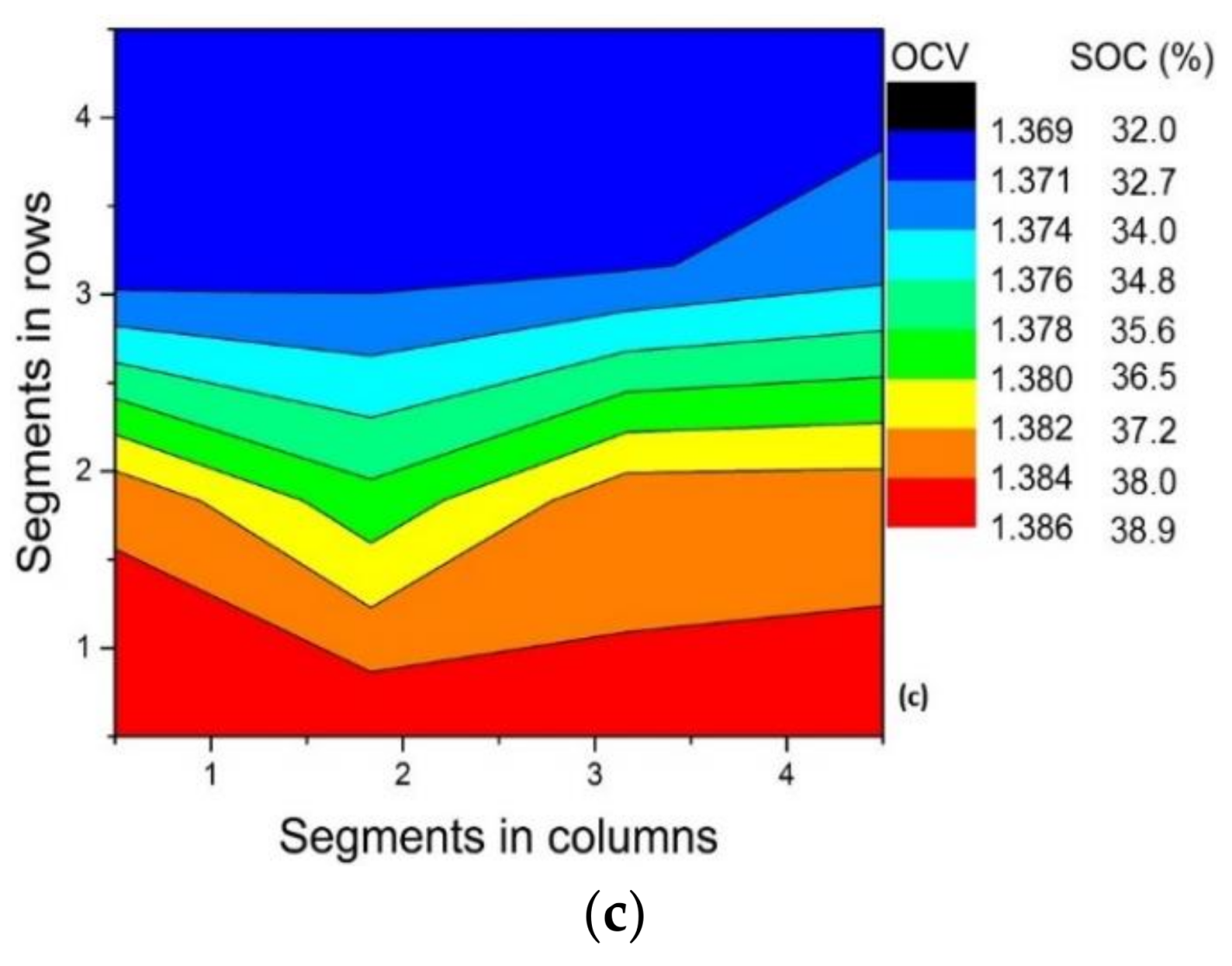
3.2. Effect of Flow Rate
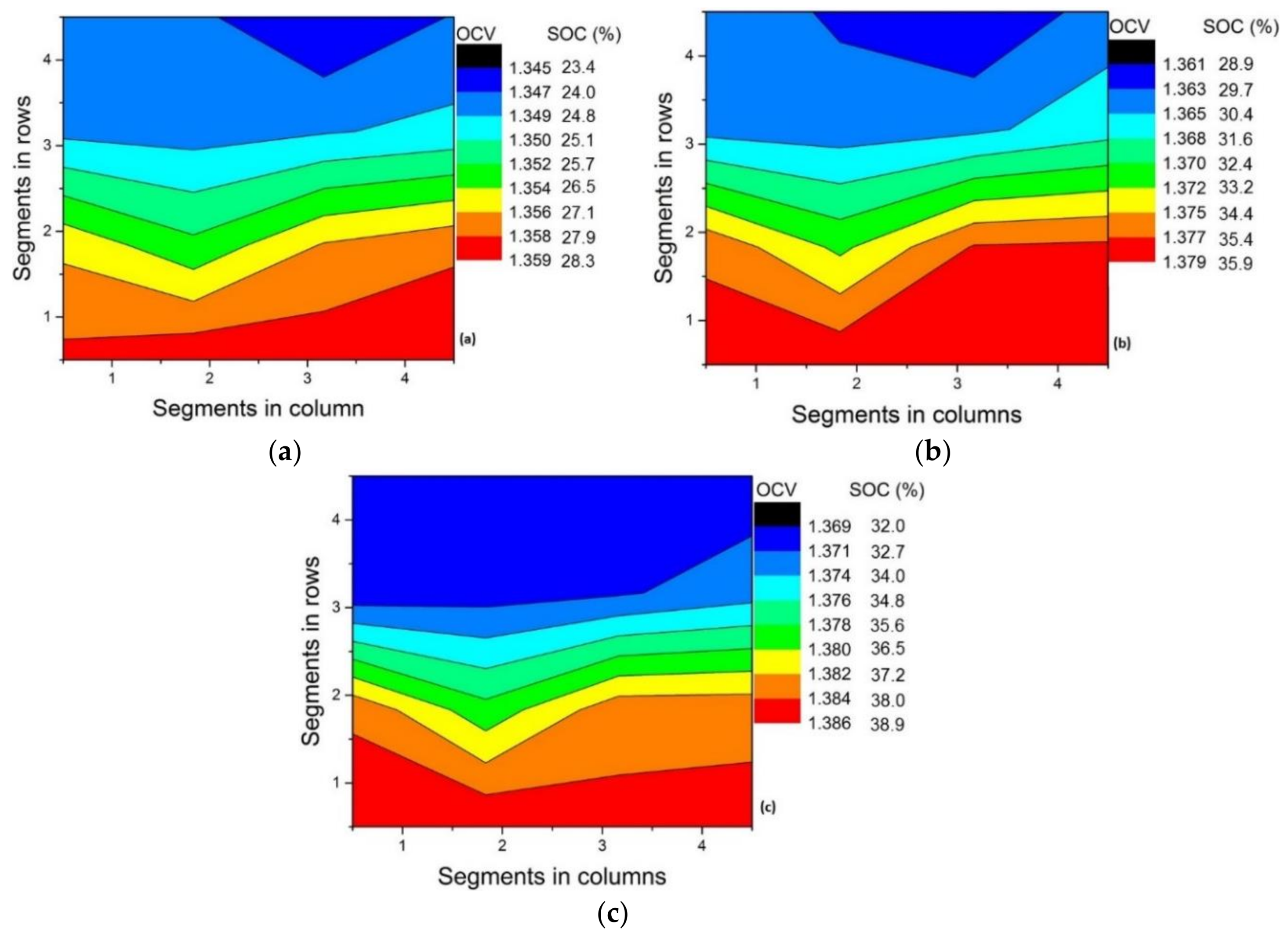
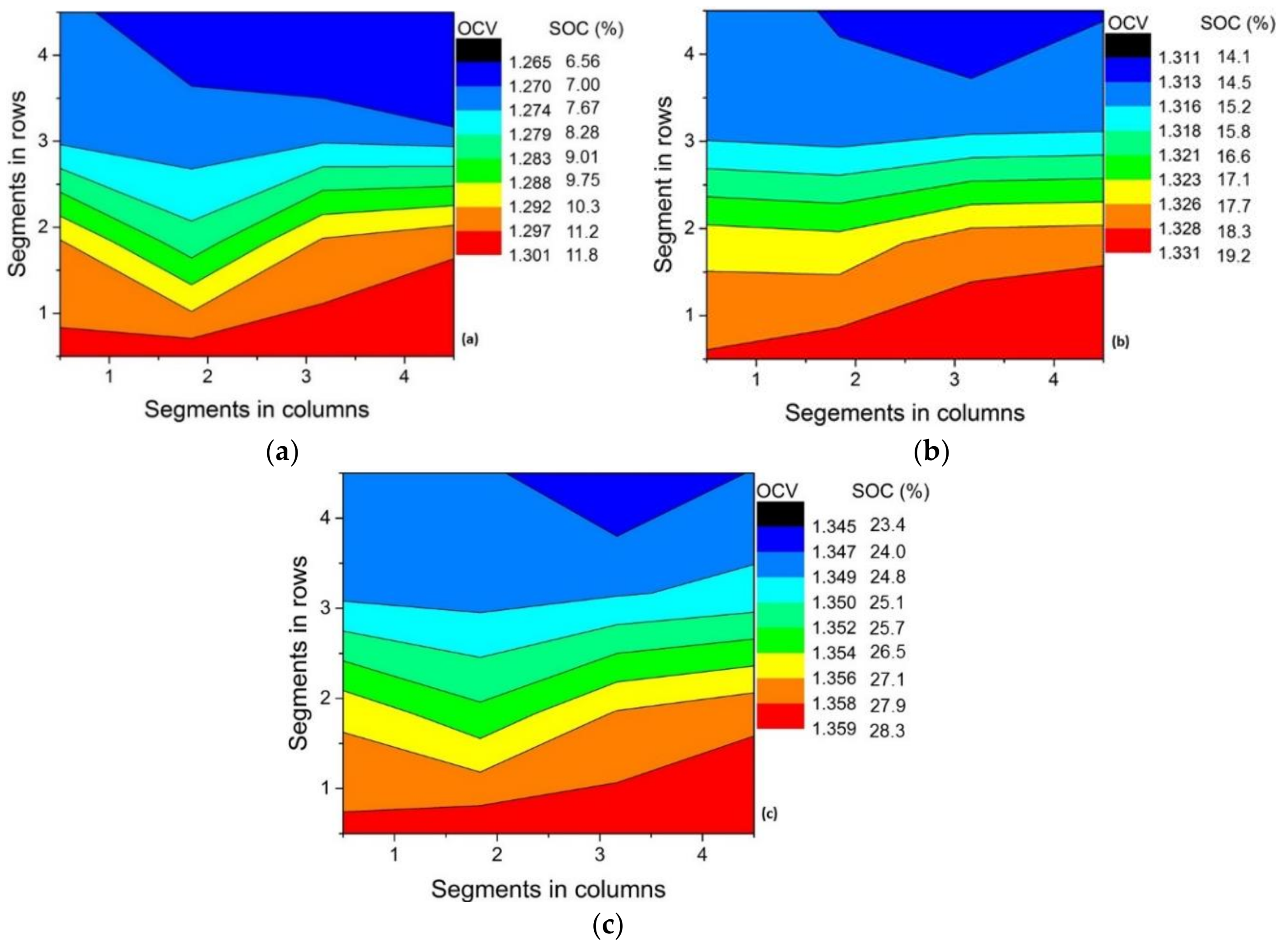
3.3. Effect of Variation in Current Density
3.4. Upward vs. Downward Flow
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Weber, A.Z.; Mench, M.M.; Meyers, J.P.; Ross, P.N.; Gostick, J.T.; Liu, Q. Redox flow batteries: A review. J. Appl. Electrochem. 2011, 41, 1137. [Google Scholar] [CrossRef]
- De Leon, C.P.; Frías-Ferrer, A.; González-García, J.; Szánto, D.; Walsh, F.C. Redox flow cells for energy conversion. J. Power Sources 2006, 160, 716–732. [Google Scholar] [CrossRef] [Green Version]
- Ulaganathan, M.; Aravindan, V.; Yan, Q.; Madhavi, S.; Skyllas-Kazacos, M.; Lim, T.M. Recent advancements in all-vanadium redox flow batteries. Adv. Mater. Interfaces 2016, 3. [Google Scholar] [CrossRef]
- Sun, B.; Skyllas-Kazacos, M. Modification of graphite electrode materials for vanadium redox flow battery application—I. Thermal treatment. Electrochim. Acta 1992, 37, 1253–1260. [Google Scholar] [CrossRef]
- Sun, B.; Skyllas-Kazacos, M. Chemical modification of graphite electrode materials for vanadium redox flow battery application—Part II. Acid treatments. Electrochim. Acta 1992, 37, 2459–2465. [Google Scholar] [CrossRef]
- Kim, K.J.; Kim, Y.J.; Kim, J.H.; Park, M.S. The effects of surface modification on carbon felt electrodes for use in vanadium redox flow batteries. Mater. Chem. Phys. 2011, 131, 547–553. [Google Scholar] [CrossRef]
- Schweiss, R. Influence of bulk fibre properties of PAN-based carbon felts on their performance in vanadium redox flow batteries. J. Power Sources 2015, 278, 308–313. [Google Scholar] [CrossRef]
- Ghimire, P.C.; Schweiss, R.; Scherer, G.G.; Wai, N.; Lim, T.M.; Bhattarai, A.; Nguyen, T.D.; Yan, Q. Titanium carbide-decorated graphite felt as high performance negative electrode in vanadium redox flow batteries. J. Mater. Chem. A 2018, 6, 6625–6632. [Google Scholar] [CrossRef]
- Lei, Y.; Liu, S.Q.; Gao, C.; Liang, X.X.; He, Z.X.; Deng, Y.H.; He, Z. Effect of amino acid additives on the positive electrolyte of vanadium redox flow batteries. J. Electrochem. Soc. 2013, 160, A722–A727. [Google Scholar] [CrossRef]
- Wu, X.; Liu, S.; Wang, N.; Peng, S.; He, Z. Influence of organic additives on electrochemical properties of the positive electrolyte for all-vanadium redox flow battery. Electrochim. Acta 2012, 78, 475–482. [Google Scholar] [CrossRef]
- Wang, G.; Chen, J.; Wang, X.; Tian, J.; Kang, H.; Zhu, X.; Zhang, Y.; Liu, X.; Wang, R. Study on stabilities and electrochemical behavior of V (V) electrolyte with acid additives for vanadium redox flow battery. J. Energy Chem. 2014, 23, 73–81. [Google Scholar] [CrossRef]
- Nguyen, T.D.; Whitehead, A.; Scherer, G.G.; Wai, N.; Oo, M.O.; Bhattarai, A.; Chandra, G.P.; Xu, Z.J. The oxidation of organic additives in the positive vanadium electrolyte and its effect on the performance of vanadium redox flow battery. J Power Sources 2016, 334, 94–103. [Google Scholar] [CrossRef]
- Li, X.; Zhang, H.; Mai, Z.; Zhang, H.; Vankelecom, I. Ion exchange membranes for vanadium redox flow battery (VRB) applications. Energy Environ. Sci. 2011, 4, 1147–1160. [Google Scholar] [CrossRef] [Green Version]
- Chen, D.; Hickner, M.A.; Agar, E.; Kumbur, E.C. Selective anion exchange membranes for high coulombic efficiency vanadium redox flow batteries. Electrochem. Commun. 2013, 26, 37–40. [Google Scholar] [CrossRef]
- Latha, T.J.; Jayanti, S. Hydrodynamic analysis of flow fields for redox flow battery applications. J. Appl. Electrochem. 2014, 44, 995–1006. [Google Scholar] [CrossRef]
- Aaron, D.; Liu, Q.; Tang, Z.; Grim, G.; Papandrew, A.; Turhan, A.; Zawodzinski, T.; Mench, M. Dramatic performance gains in vanadium redox flow batteries through modified cell architecture. J. Power Sources 2012, 206, 450–453. [Google Scholar] [CrossRef]
- Bhattarai, A.; Wai, N.; Schweiss, R.; Whitehead, A.; Lim, T.M.; Hng, H.H. Advanced porous electrodes with flow channels for vanadium redox flow battery. J. Power Sources 2017, 341, 83–90. [Google Scholar] [CrossRef]
- Hartnig, C.; Manke, I.; Kardjilov, N.; Hilger, A.; Grünerbel, M.; Kaczerowski, J.; Banhart, J.; Lehnert, W. Combined neutron radiography and locally resolved current density measurements of operating PEM fuel cells. J. Power Sources 2008, 176, 452–459. [Google Scholar] [CrossRef]
- Zamel, N.; Hanke Rauschenbach, R.; Kirsch, S.; Bhattarai, A.; Gerteisen, D. Relating the N-shaped polarization curve of a PEM fuel cell to local oxygen starvation and hydrogen evolution. Int. J. Hydrogen Energy 2013, 38, 15318–15327. [Google Scholar] [CrossRef]
- Cleghorn, S.; Derouin, C.; Wilson, M.; Gottesfeld, S. A printed circuit board approach to measuring current distribution in a fuel cell. J. Appl. Electrochem. 1998, 28, 663–672. [Google Scholar] [CrossRef]
- Schneider, I.; Von Dahlen, S.; Wokaun, A.; Scherer, G. A segmented microstructured flow field approach for submillimeter resolved local current measurement in channel and land areas of a PEFC. J. Electrochem. Soc. 2010, 157, B338–B341. [Google Scholar] [CrossRef]
- Kalyvas, C.; Kucernak, A.; Brett, D.; Hinds, G.; Atkins, S.; Brandon, N. Spatially resolved diagnostic methods for polymer electrolyte fuel cells: A review. Wiley Interdiscip. Rev. Energy Environ. 2014, 3, 254–275. [Google Scholar] [CrossRef]
- Pérez, L.C.; Brandão, L.; Sousa, J.M.; Mendes, A. Segmented polymer electrolyte membrane fuel cells—A review. Renew. Sustain. Energy Rev. 2011, 15, 169–185. [Google Scholar] [CrossRef]
- Hsieh, W.Y.; Leu, C.H.; Wu, C.H.; Chen, Y.S. Measurement of local current density of all-vanadium redox flow batteries. J. Power Sources 2014, 271, 245–251. [Google Scholar] [CrossRef]
- Clement, J.T.; Aaron, D.S.; Mench, M.M. In situ localized current distribution measurements in all-vanadium redox flow batteries. J. Electrochem. Soc. 2016, 163, A5220–A5228. [Google Scholar] [CrossRef]
- Bhattarai, A.; Wai, N.; Schweiss, R.; Whitehead, A.; Scherer, G.G.; Ghimire, P.C.; Nguyen, T.D.; Hng, H.H. Study of flow behavior in all-vanadium redox flow battery using spatially resolved voltage distribution. J. Power Sources 2017, 360, 443–452. [Google Scholar] [CrossRef]
- Ghimire, P.C.; Bhattarai, A.; Schweiss, R.; Scherer, G.G.; Wai, N.; Yan, Q. A comprehensive study of electrode compression effects in all vanadium redox flow batteries including locally resolved measurements. Appl. Energy 2018, 230, 974–982. [Google Scholar] [CrossRef]
- Pezeshki, A.M.; Clement, J.T.; Veith, G.M.; Zawodzinski, T.A.; Mench, M.M. High performance electrodes in vanadium redox flow batteries through oxygen-enriched thermal activation. J. Power Sources 2015, 294, 333–338. [Google Scholar] [CrossRef] [Green Version]


| Case | Relation | Interpretation |
|---|---|---|
| (i) | ΔSOCexp ≈ ΔSOCth | Optimum utilization of electrolyte and excellent flow distribution |
| (ii) | ΔSOCexp >> ΔSOCth | Poor utilization (higher overpotential either due to over-discharge at the retarded/stagnant zone or higher contact resistance) |
| (iii) | ΔSOCexp << ΔSOCth | Insufficient availability of redox species to sustain the applied current |
| Electrode Type | ΔSOC (42 mL min−1, λ = 3.4) | |
|---|---|---|
| Theoretical | 14.8% | |
| Experimental | Pristine | 33.8% |
| Thermally treated | 13.5% | |
| Chemically treated | 15.2% | |
| Flow Rate | ΔSOCth | ΔSOCexp |
|---|---|---|
| 16 mL min−1 (λ = 1.3) | 38.8% | 20.3% |
| 32 mL min−1 (λ = 2.6) | 19.4% | 17.4% |
| 42 mL min−1 (λ = 3.4) | 14.8% | 13.5% |
| Current Density | ΔSOCth | ΔSOCexp |
|---|---|---|
| 150 mA cm−2 | 72.8% | 36.3% |
| 120 mA cm−2 | 58.2% | 29.3% |
| 80 mA cm−2 | 38.8% | 20.3% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghimire, P.C.; Bhattarai, A.; Schweiss, R.; Scherer, G.G.; Wai, N.; Lim, T.M.; Yan, Q. Investigation of Reactant Conversion in the Vanadium Redox Flow Battery Using Spatially Resolved State of Charge Mapping. Batteries 2019, 5, 2. https://doi.org/10.3390/batteries5010002
Ghimire PC, Bhattarai A, Schweiss R, Scherer GG, Wai N, Lim TM, Yan Q. Investigation of Reactant Conversion in the Vanadium Redox Flow Battery Using Spatially Resolved State of Charge Mapping. Batteries. 2019; 5(1):2. https://doi.org/10.3390/batteries5010002
Chicago/Turabian StyleGhimire, Purna C., Arjun Bhattarai, Rüdiger Schweiss, Günther G. Scherer, Nyunt Wai, Tuti M. Lim, and Qingyu Yan. 2019. "Investigation of Reactant Conversion in the Vanadium Redox Flow Battery Using Spatially Resolved State of Charge Mapping" Batteries 5, no. 1: 2. https://doi.org/10.3390/batteries5010002
APA StyleGhimire, P. C., Bhattarai, A., Schweiss, R., Scherer, G. G., Wai, N., Lim, T. M., & Yan, Q. (2019). Investigation of Reactant Conversion in the Vanadium Redox Flow Battery Using Spatially Resolved State of Charge Mapping. Batteries, 5(1), 2. https://doi.org/10.3390/batteries5010002








