1. Introduction
Lithium ion cells suffer from power and capacity loss during their lifetime; the so-called ageing. The performance loss in mobile devices, such as cell phones, is merely an inconvenience, since the usual lifetime of the whole device and especially the cost of replacing degraded batteries in those cases is pretty low. In electric vehicles, however, where the storage system amounts to a significant part of the total costs, ageing is of bigger concern. The knowledge about those ageing effects is of great importance for both, the cell manufacturers, to possibly minimize certain ageing mechanisms through a modified cell design, and the battery pack producers and integrators, to consider those effects in their battery management system (BMS) [
1]. An additional group of interest are service providers for stationary storage systems with second-life batteries.
Different ageing effects result in power and/or capacity fade. This degradation is caused by the loss of active material, loss of cyclable lithium or the reduction in conductivity [
2,
3]. Two of the main degradation processes are unwanted side reactions, the continuous formation of a solid electrolyte interface (SEI) layer and the plating of metallic lithium (LiP) at the negative graphite electrode [
4]. The formation of a passivating, but ion conducting, surface film on the graphite anode, called the SEI, is required for the operation of a lithium ion cell [
5]. The SEI layer is made up of different reaction products, containing decomposed electrolyte components [
6]. An ideal SEI forms during the first cycles and hinders further unwanted side reactions completely. Yet, the reaction rate gradually decreases but never stops completely. This continuous unwanted layer growth during cycling uses up lithium, solvent and salt [
7]. Fractures in the SEI, due to the graphite’s volume change during cycling, which will be repaired, are one reason for the continuing SEI formation [
8]. The electro-deposition of metallic lithium on the electrode surface, the so called lithium plating, is an unwanted process in li-ion batteries. After being plated on the electrode, there are four “paths” for the metallic lithium: (1) an electro-neutral chemical intercalation into the electrode; (2) a stripping process during a subsequent cycle; (3) a reaction with the electrolyte forming additional SEI; and (4) becoming inactive [
9,
10,
11,
12]. Although not causing severe damage, the plating/stripping process exhibits a lower Coulombic efficiency compared to de/intercalation into the graphite anode [
13]. Cases (3) and (4) pose major implications for cell operation: a loss of cyclable lithium, an increase in cell resistance and a potentially fatal failure mode due to growth of dendrites [
14,
15]. The electro-deposition of metals can result in the formation of dendrites in different shapes, which might grow through the separator and cause an internal short circuit of the cell [
16]. A common assumption is, that during charging with nominal parameters no metallic lithium will be deposited and that plating will only occur at extreme conditions, like high C-rates and low temperatures [
17]. Recently, the occurrence of lithium plating has been shown during normal operating conditions. Cannarella et al. [
18] demonstrated the appearance of lithium plating by mechanically introducing local defects which lead to an inhomogeneous utilization of active material.
The sudden-death effect describes a strong increase in capacity fade per cycle, which has been almost linear before. A sudden-death is shown in
Figure 1 for the solid line shortly after point A. This frequently happens when the cell’s resistance has risen to 1.5 times of the initial value and at around 80% of initial capacity
[
19]. Often, the sudden-death effect is linked with a change in the predominant ageing mechanism, from SEI formation to local ageing-induced lithium plating in the anode. Broussely et al. [
4] ascribed the sudden-death to significant self enhancing lithium plating due to the clogging of pores caused by the growth of the surface film. Burns et al. [
20] also named the clogging of pores, which obstructs the ion transport into the negative electrode and therefore creating a kinetic hindrance, as a cause for the fast degradation. As summarized by Schuster et al. [
21], the appearance of ageing-induced lithium plating was responsible for the sudden-death. This even happens at moderate operating conditions and in turn may be caused by the negative influence on the ionic kinetics of a growing SEI or the active material loss of graphite. The ageing-induced lithium plating can also be caused mechanically by heterogeneous compression [
22].
Reusing batteries in a different application is called second-life. An increasing electrification of the transport sector will increase the amount of replaced batteries from electric vehicles. Since requirements in the automotive sector are high, batteries will be replaced early and still offer some usefulness in a less demanding and more flexible second-life application under favorable operating conditions. This makes traction batteries an excellent candidate for second-life application, e.g., stationary storage systems for buffering photovoltaics. An important aspect is the time of transition between the primary and secondary application. Commonly, this is realised by an end-of-life (EoL) criterion for the first application based on remaining capacity, e.g., 80% of initial capacity. Around the same State-of-Health a change in ageing behaviour, the sudden-death, has been observed [
19]. Therefore, this ageing effect might conflict with the second-life application. In a simplified way,
Figure 1 shows this interaction. For both ageing curves, idealised linear (dashed line) and non-linear (solid line), the transition between first and secondary application (1st/2nd) is based on the remaining capacity and shown in red. The EoL is again based on the capacity is shown in blue. Compared to the linear degradation (A to C), the cycle count for the second-life is much smaller in case of non-linear ageing behaviour (A to B) because of the increased capacity fade associated with the sudden-death effect.
Electrodes in lithium ion batteries consist of active material, binder and conductive agent. During electrode preparation, these components are mixed in a solvent and then coated on the current collector. Afterwards, the solvent needs to be removed and the layer is compressed. The composition, form and size distribution of the different particles and the calendering process will determine the porosity and tortuosity. Traditionally, batteries have a constant porosity across the thickness of each electrode and the separator. When assembling the cell, pores are filled with liquid electrolyte and, therefore, the pores influence the cell performance by providing a path for ion transport in the liquid phase.
In 1995, Newman [
23] mentioned an optimal porosity while striking a balance between the amount of active material and ionic conductivity in the cathode’s pores. Sikha et al. [
24] presented a model which includes the change of porosity due to an irreversible parasitic reaction and shows a decreasing performance for a cell with constant initial porosity. Focusing on the minimization of the ohmic resistance of a porous electrode, Ramadesigan et al. [
25] optimized a spatially varying porosity profile. Qi et al. [
26] applied a multi-objective optimization to a layered porosity profile for optimally balancing the ohmic resistance, the average overpotential and the standard deviation of the overpotential.
In this model-based ageing analysis, we investigate the effect of different initial porosity profiles in graphite anodes with regard to cycle life, second-life application and the sudden-death effect. Ageing is considered by a growing surface layer consisting of formed SEI and plated lithium. To compensate for the increased layer growth, at the separator side of the anode, we introduce electrodes with higher porosity at the separator side. We investigate a two-stage porosity, in other words, an anode consisting out of two layers with different porosities, and a linearly increasing porosity. Both modified porosity profiles show an enhanced cycling stability.
2. Model Description
We use COMSOL Multiphysics
® 5.4 software (COMSOL AB, Stockholm, Sweden) for simulation. The model is based on the pseudo two-dimensional (P2D) approach following Doyle, Fuller and Newman. An elaborate description of the underlaying partial differential equations is available in literatures [
27,
28,
29,
30,
31,
32]. A set of four coupled non-linear partial differential equations describe the charge and species conservation in the solid and liquid phases of the porous electrodes. Solid active material particles in the electrode and the liquid electrolyte phase are coupled with the Butler-Volmer equation for current density.
The implementation of ageing mechanism and their implications is similar to the model presented by Yang et al. [
33]. Lithium plating and SEI formation, at the negative electrode and during the charge process, are incorporated as competing reactions in addition to the desired reaction of intercalation. This results in the total local current density:
consisting of the intercalation current density
, the current density of the SEI formation
and of lithium plating
. The intercalation current density:
is based on the Butler-Volmer equation with the exchange current density for the intercalation reaction
, the anodic and cathodic transfer coefficients
and
. The surface overpotential for intercalation:
includes the potential of solid
and electrolyte phase
, the potential drop across the surface film
and the equilibrium potential for lithium intercalation
.
Besides the eligible intercalation, SEI formation and lithium plating side reactions can occur. For SEI formation, we assume a reaction of the solvent, ethylene carbonate (EC), lithium ions and electrons. Both side reactions are assumed to be irreversible to simplify the simulation. In case of Li plating the stripping of plated lithium in later discharge phases is not considered. Furthermore the oxidation of plated lithium, the formation of additional SEI, as well as the intercalation of plated lithium is neglected. Following the work of Safari et al. [
34] and also Darling et al. [
35], the current density for each side reaction:
is computed with a cathodic Tafel equation for either SEI or LiP. The exchange current density for SEI formation:
includes the kinetic rate constant of SEI formation
and the surface concentration of EC
. The surface overpotential
is calculated analogue to Equation (
3) except
being replaced with equilibrium potential for SEI reaction
or Li plating
. Rearranging the mass conservation of EC from Yang et al. [
33] yields:
with an over the cell averaged EC concentration in the electrolyte
, the thickness of the surface film
and the diffusion coefficient of EC in the film layer
. With the initial EC concentration
, the concentration of SEI
, the area of the cell
and the volume of the liquid phase
we calculate the mean EC concentration:
This concentration considers loss of EC through SEI formation.
Both side reactions deposit products which form a surface film, lining the active material of the negative electrode as a homogeneous layer. The film thickness change:
includes the active specific surface area
. Respectively for SEI and plated Li, the concentration
c, the molar weight
M and the density
are included. Finally, the total film thickness
can be calculated with the initial film thickness
and thickness change
.
There are several implications of the increasing film thickness: (1) the resistance rises; (2) the volume fraction of electrolyte decreases; and (3) the cycleable lithium is lost. The film resistance:
is calculated with the conductivity of the SEI layer
. Only the SEI part of the layer is considered for ionic conductivity, therefore
denotes the volumetric SEI fraction in the film. The second effect, the reduction of electrolyte volume in the anode, is considered by the electrolyte volume fraction in the negative electrode:
with the initial electrolyte fraction
. The expressions electrolyte volume fraction and porosity are synonymous in this work. Reducing the electrolyte volume fraction does impair the effective transport parameters, like conductivity and diffusion coefficient of the electrolyte. The effective transport parameters are calculated with the Bruggeman correlation. For the effective diffusion coefficient in the liquid phase:
the correlation includes the materials diffusion coefficient
, the electrolyte volume fraction
and the Bruggeman exponent
.
Cell parameters stem from an experimental high-energy cell. Key cell and ageing parameters are listed in
Table A1,
Appendix A. The cycling is simulated using a constant current/constant voltage (CC/CV) charging strategy. Discharge is simulated using CC only, C/2 current rates are applied for the whole simulation. Between the single phases, 10 min relaxation periods are included.
Figure 2 shows the three different porosity profiles considered in this work. Each sub-figure shows the porosity throughout the anode, from the current collector on the left side
to the separator on the right side
. Besides the conventional constant initial porosity shown in
Figure 2A from the previously mentioned parameter set, a two-stage profile
Figure 2B and a linearly increasing porosity
Figure 2C are included.
Averaged over the thickness of the anode, all porosity profiles result in the same volume fraction of active material and therefore the same initial capacity and anode dimensions. Preliminary simulations showed an increased reduction of porosity, electrolyte volume fraction, at the separator side of the anode. Therefore, the increased porosity at that side is aimed at compensating the heterogeneous ageing, the increased layer growth at the separator side. By combining two electrode layers with different porosity, the two-stage or graded porosity profile can be achieved. The two-stage profile could provide a reasonable compromise between additional effort during electrode production on one hand and longer lifetime on the other hand. A linearly increasing porosity, basically an large number of stages, was introduced for comparison, since this profile fits the simulated layer growth better than the graded porosity.
3. Results
Figure 3 shows the development of discharge capacity in relation to the first cycle’s discharge capacity
over the cycle number
n for the cell with constant initial porosity. A stronger decrease during the initial cycles, when the SEI is initially formed, is followed by a phase of almost linear decline, when SEI formation is settled. After around 250 cycles and at approximately 75% of initial capacity, there is a sudden-death event and the capacity fade per cycle starts to increase dramatically.
Assuming a capacity criteria of 80% initial capacity for transitioning from primary to secondary application, this cell configuration can be cycled 165 times during the first-life and 110 times during second-life before reaching an EoL at 60% . If we shift the transition between applications towards lower capacities and therefore closer to the sudden-death, the usefulness for second-life will be lower.
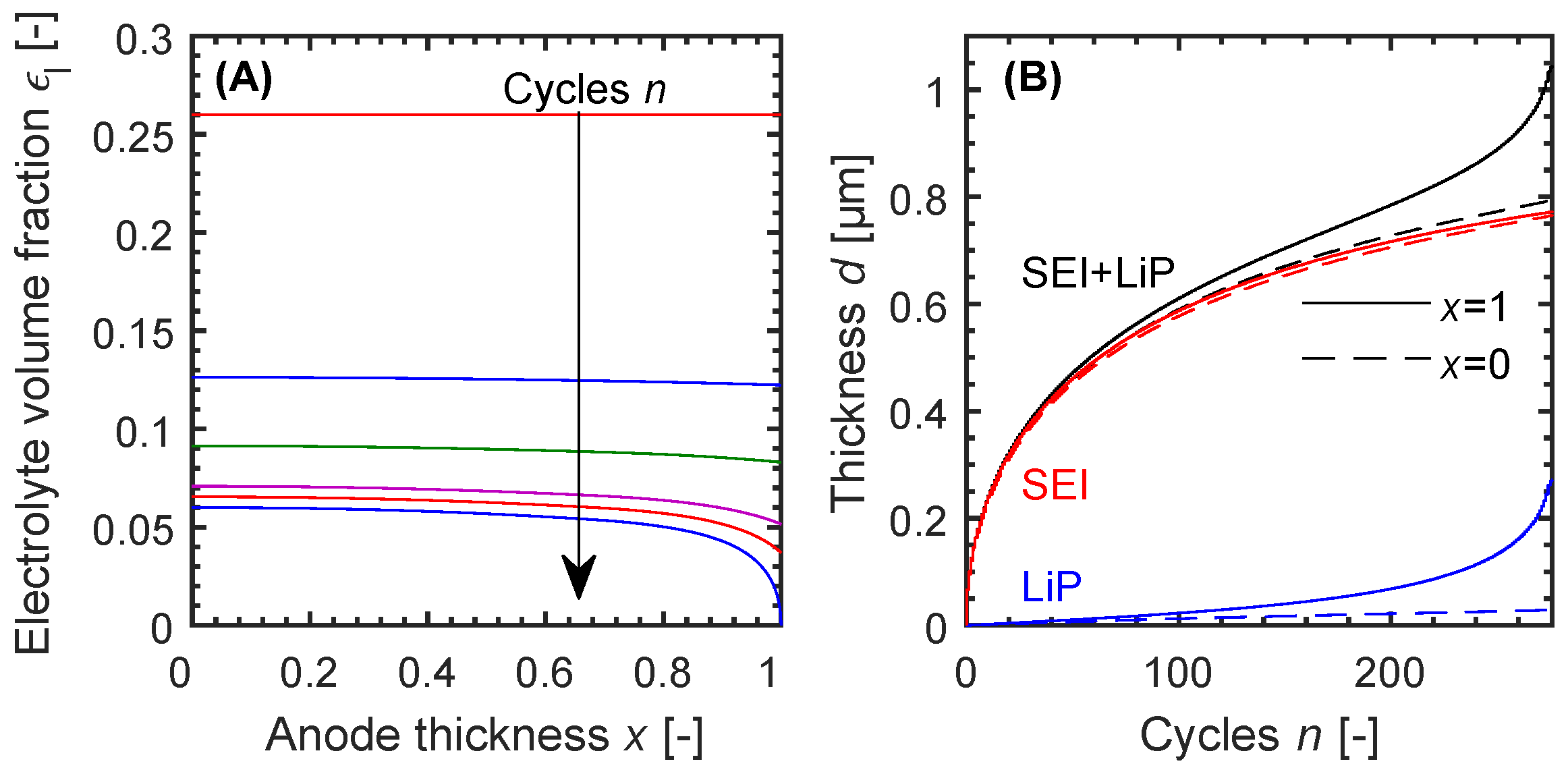
Looking at the trend of electrolyte volume fraction across the anode thickness in
Figure 4A, we can see an increasing gradient between the current collector at
and the separator at
with increasing cycle number. Especially in the later stages of the life-time starting from cycle 225, the inhomogeneity of porosity reduction is distinct. Ultimately, this leads to pore clogging at the separator and therefore no ion transport into the electrode. Based on the deposit concentration, it is possible to calculate an equivalent thickness of a layer consisting of one product only (see Equation (
8)). This equivalent thickness, in addition to the actual thickness, is shown in
Figure 4B. Each pair consists of the thickness at the current collector and separator side of the anode. The SEI formation starts with a high reaction rate, which decreases because of limitations due to the EC diffusion through the growing layer as well as the lower EC concentration in the electrolyte. Furthermore, the SEI growth is almost uniform across the thickness of the anode. Lithium plating however shows an opposite behaviour. The reaction rate at the current collector side is basically constant and negligible during the whole simulation, whereas at the separator side the growth is linear until cycle
and thereafter it appears to be exponential. At around 230 cycles, the curvature of the discharge capacity graph changes, there is an inflection point and the degradation per cycle increases again. A change in curvature can also be seen in the total film thickness, with a strong change at the separator side. It can be concluded, that continuous formation of SEI reduces the porosity. As soon as the reduction of porosity advances beyond a certain stage, if it falls below 4% in this case, lithium plating at the separator side increases significantly until ion transport is completely prevented. Because of the inhomogeneity between the two sides of the anode, both modified porosity profiles will counteract the increased layer growth with an increased initial porosity at the separator side of the anode.
As the first alternative to the conventional anode, we will look at a graded two-stage porosity profile from
Figure 2B. The resulting discharge capacity, as well as for comparison the result of the conventional electrode in grey, is shown in
Figure 5. For the first 100 cycles, the behaviour of discharge capacity are basically identical. For the following 100 cycles, the degradation is slightly lower for the cell with graded porosity. The first distinct difference is a small kink after 240 cycles, shortly before the reference cell shows the sudden-death, which separates the capacity curve into halves. The second half shows an increased ageing rate followed by the sudden-death.
By introducing a graded porosity the cycle count until the terminal sudden-death almost doubles from 250 to around 500 cycles at less than 50% of initial capacity. Until an EoL criteria of 60% remaining capacity, the cell can be cycled an additional 90 cycles. These can also be added to 110 second-life cycles of the reference cell, resulting in around 200 cycles during the second-life application.
Figure 6A shows the porosity profile across the anode for cycles
0, 100, 230, 300, 400 and 520. The results are similar to the cell with conventional porosity. During the first phase, for around 300 cycles, an almost homogeneous reduction in electrolyte volume fraction due to SEI formation occurs. Afterwards, the reduction proceeds locally, at the separator boundary
and to a lesser degree in front of the porosity step
, at an increased rate until the pores are clogged. Looking at the profile for cycle
, during the occurrence of the first capacity kink, the electrolyte volume fraction has been reduced to
at the beginning of the low porosity layer
. This indicates a hindrance of lithium ion transport across the porosity step, in the electrolyte, into the rear part of the electrode. As a result, the utilization of active material in the rear part of the electrode is limited. Therefore, this first kink represents an incomplete loss of parts of the electrode due to less effective ionic conductivity in the electrolyte. After 520 cycles, all pores are filled with products of the side reactions at the anode/separator boundary
as well as just next to the step at
. The equivalent thickness of pure layers in
Figure 6B show the same behavior like before. The SEI growth is uniform across the anode while the lithium plating strongly depends on the location
x.
To avoid the kinetic limitation for half of the electrode caused by the step in porosity, we investigate a linearly increasing porosity profile as shown in
Figure 2C. The cycling results for this anode configuration are shown in
Figure 7. Like before, the grey lines represent the previous results. There are basically no differences in discharge capacity for the first 200 cycles, however between cycle 200 and 380 the linearly increasing porosity profile shows the highest discharge capacity. Similar to the graded profile, there is a slight bend visible, but it appears 40 cycles later. Unlike the two other cells, there is no distinct sudden-death ending the battery life. Instead, starting from the bend at cycle
, the capacity fade gradually increases.
When the same transition and EoL criteria are applied, the cycle count for the primary application is identical to the two other designs. The linearly increasing porosity profile trumps the two-stage approach in second-life cycles by a small margin, the difference is below 20 cycles. However, during this period, it offers a higher discharge capacity. If we extend the EoL criteria to i.e., 50% of initial capacity, the two-stage profile will perform better.
The development of electrolyte volume fraction, in
Figure 8A, shows a homogeneous reduction during the first 200 cycles. Staring with the 300th cycle, an increased reduction at the anode/separator boundary can be seen, which indicates the onset of increased lithium plating. The kink in the capacity curve happens after
cycles, around the same time the electrolyte volume fraction at the current collector side
falls below
. From that moment, the access to active material in the rear part of the electrode diminishes. While this inaccessibility of active material happens in the two-stage profile cell for half of the anode at the same time when the porosity in the middle
falls below a certain value. For the linearly increasing profile, this starts with the kink after
cycles and happens continuously from the far side of the anode. It seems that a porosity value below
is the lower limit for the combination of parameters in this study.
When transferring these results to real cells, the properties of this P2D model approach need to be considered. One beeing the areal homogenization of the electrode structure. In an electrode stack with the dimensions
X,
Y and
Z, where
X represents the dimension form negative to positive current collector, differences in the electrode structure in the
Y and
Z dimension are not considered. Therefore, the reduction of porosity accompanied by the layer growth are homogenized values. As stated earlier, in this simulation with this set of parameters a local porosity of
seems to be the lower limit. Because of differences in electrode structure, due to manufacturing, windings or external pressure, we don’t expect these 4% to be uniform across the electrode area but rather an area averaged value. The same is valid for the thickness of the layer. The SEI grows to around
≈ 800 nm for all three investigated cases. In literature, there are some mentions of simulated and measured layer thicknesses in a similar range. Kindermann et al. [
36] more elaborate SEI modelling approach led to an simulated layer thickness of up to around
≈ 600 nm. Yoshida et al. [
37] report a thickness of
nm after storage for 392 day at 40
C. Cycling tests conducted by Zier et al. [
38] found local layer thickness below
µm and Klett et al. [
39] observed a SEI layer on the electrode/separator interface of several µm thickness, both also mention almost or complete clogging of pores by said layer.