Energy Management of a DC Microgrid Composed of Photovoltaic/Fuel Cell/Battery/Supercapacitor Systems

Abstract

In this paper, a classic proportional–integral (PI) control strategy as an energy management strategy (EMS) and a microgrid stand-alone power system configuration are proposed to work independently out of grid. The proposed system combines photovoltaics (PVs), fuel cells (FCs), batteries, and supercapacitors (SCs). The system supplies a dump load with its demand power. The system includes DC/DC and DC/AC converters, as well as a maximum power point tracking (MPPT) to maximize the harvested energy from PV array. The system advantages are represented to overcome the problem of each source when used individually and to optimize the hydrogen consumption. The classic PI control strategy is used to control the main system parameters like FC current and the state-of-charge (SOC) for the battery and SC. In order to analyze and monitor the system, it was implemented in the MATLAB/Simulink. The simulation done for fuzzy logic and high frequency decoupling and state machine control strategies to validate the PI classic control strategy. The obtained results confirmed that the system works efficiently as a microgrid system. The results show that the SOC for the battery is kept between 56 and 65.4%, which is considered a proper value for such types of batteries. The DC bus voltage (VDC) is kept within the acceptable level. Moreover, the H₂ fuel consumption is 12.1 gm, as the FCs are used as supported sources working with the PV. A big area for improvement is available for cost saving, which suggests the need for further research through system optimization and employing different control strategies.

1. Introduction

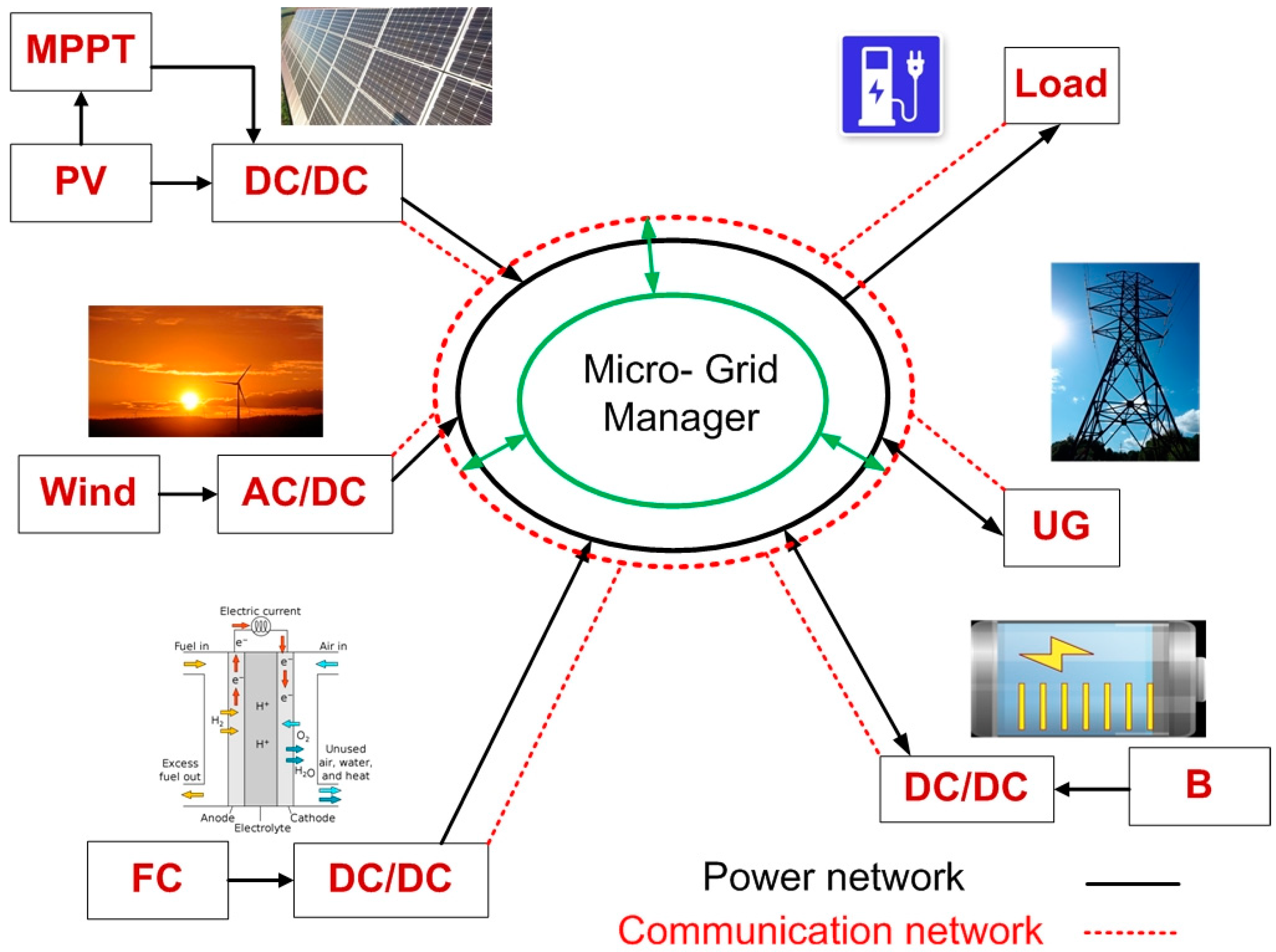
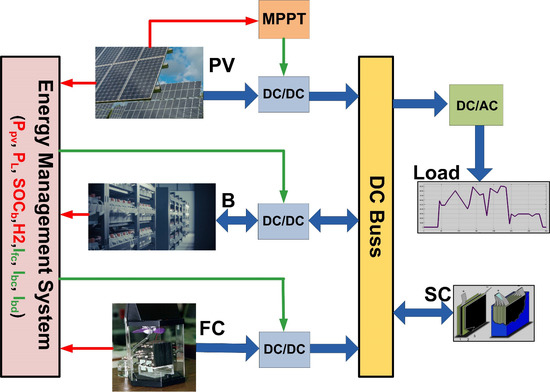
In power system grids, the microgrid is identified as a distributed energy system (DES), including generators, energy storage elements like batteries (B) and supercapacitors to balance the generated power and the consumed power [1,2,3], an energy management system to control the entire operation of the microgrid sources [4,5], and load. All of these items are combined together and work in parallel with the utility grid, or out of grid as a stand-alone system used for a small area and few consumers [6,7]. Generally, the microgrid is considered a cluster of the utility grid [8], as shown in Figure 1. Using a utility grid for power distribution has some disadvantages, such as transmission losses, especially when the generating plants are far away from the consumers, bad environmental impact because of emission, and climate change due to the use of conventional resources in the generation phase. Microgrids represent an alternative option that has the potential to overcome these problems. Microgrids can minimize power losses through transmission, reduce CO₂ emissions, and limit climate change, especially when using renewable energy resources in electricity generation. It also saves money in several ways, such as preventing outage, selling electricity to national grids through feed, and tariff or net metering systems. Using power systems that combine renewable sources with zero emission besides energy storage elements makes the system able to achieve maximum efficiency compared to systems containing conventional sources [9,10,11]. An energy management system is a system that controls the operation of the microgrid (MG) system. It uses many approaches and control strategies to get maximum system performance. These control strategies may include a state machine, a classic proportional–integral (PI) control, a fuzzy logic control, an external energy maximization, an equivalent minimization, and a frequency decoupling control strategy [12].

Manoj et al. [13] discussed the two main types of MG: Alternative current microgrid (ACMG) and direct current microgrid (DCMG). The DCMG has some advantages over the ACMG, such as high efficiency, easy connection on the DC bus, and system reliabilities. They confirmed that in DCMGs, there are three factors influencing power disturbance: Fluctuation of power exchange, power variation between the storage system and the power sources, and the fast change in the DC bus load. Ravichandrudu et al. [14] designed an MG system using renewable sources, which has the benefits of utilizing renewable energy sources and reducing transmission losses when using wind and hydro. The proposed microgrid system has three operation modes. Phurailatpam et al. [15] proposed a DCMG system that includes a photovoltaic (PV) power system and uses the battery as an energy storage system. The DC/DC converters were discussed, as well as the maximum power point tracking (MPPT) for the PV. The system performance at constant and variable values for irradiance, wind speed, and load was monitored and analyzed. The simulation results showed that the system maintained the DC bus voltage at constant value, which confirmed the advantages of the DCMG compared with the ACMG. Elsied et al. [16] proposed a novel energy management strategy based on binary particle swarm optimization (BPSO) to optimize the performance of the MG, maximize the micro grid power, and decrease the system CO₂ emissions. The system was supported by an experimental lab test. The obtained results proved that the BPSO is efficient when used with the MG. For a DCMG hybrid system, Garita et al. [17] examined the efficiency of an energy management strategy (EMS) used in a DCMG configuration containing a PV and a battery integrated together in one unit. An energy management system was used with three main system configurations. It works through seven operation modes as power flow direction under two different case studies (OFF—grid and peak shaving) to achieve maximum system performance. In their study of DCMG, Eghtedarpour et al. [18] propose three levels of control to improve the performance of the DCMG. The first level is where no communication is required and the control is done based on the local measurements. The second level is based on a DC microgrid energy management system. The third level is the top level of control, which controls multi-microgrids. Shehata et al. [19] proposed an energy management strategy for DCMG based on a multi-agent system applied using the JADE framework, where PI controllers are used as an EMS. The interface between the multi-agent system and the MATLAB/Simulink software was done through the MACSimJX interface. An analytical solution used as a reference model supported by a numerical method was proposed by Hadj-Said et al. [20] to confirm the suitability of the proposed EMS used in parallel hybrid electric vehicles (HEV) to achieve maximum system performance. The proposed EMS was applied successfully on continuous and discrete optimization cases. Sedaghati et al. [21] discussed a PV–FC–B–SC hybrid system based on grid-connected microgrids. A control strategy called adaptive fractional fuzzy sliding mode control (AFFSMC) was used for the inverter. The fuzzy rules are designed to accurately estimate the uncertain parameters. The results showed that the proposed strategy works efficiently. When the analytical solution was applied for a certain model, such as the optimal auxiliary functions method (OAFM) proposed by Herisanu et al. [22], it was found to be a reliable and efficient tool for mechanical and electrical performance of the system. For the PV/wind hybrid system in a microgrid, the wind turbine generator is characterized by its slow response, while the PV array enjoys a fast response. If both generators are combined in one system, the voltage of the DC bus takes a long time to reach a stable condition that affects the overall system response, especially when the load is variably switching [23]. For the battery/supercapacitor hybrid system, as proposed by Vasily et al. [24], a number of the internal problems of the battery negatively affects the system’s overall performance, such as its short life cycle and its low efficiency due to the number of charging/discharging times, causing fast breakdown of the battery. For the PV/FC hybrid power system, the main problem is the efficiency of both the PV and the FC, and the low density and high initial cost of the PV arrays. Despite the concerns raised for the mentioned hybrid systems, sometimes the configuration itself cannot achieve its target, as [25], when all the system components are connected in a series and, as a result, if there is a problem in any component (PV, Electrolyzer, storage, and FC), the power production could be affected, thus impacting the system’s financial return and cost. Using the PV as a preliminary source decreases the unwanted side effects of using the FC, such as low efficiency during the operation period, high cost, unstable low generated voltage, and finally, the high ripple current linked to the output voltage which reduces the FC lifetime [26,27].

Along the same lines, a number of studies explored the same application with the same configuration; however, compared with the present paper, it was found that all the previous works that have the same components connected the SC to the DC bus through a DC/DC converter to control the charging/discharging of the SC [28,29,30]. By contrast, in the present paper, the SC has been directly connected to the DC, which has two advantages over other connection methods. The first one is reducing the cost of the system through removing one DC/DC converter, and the second advantage is the fast response of the SC to load changing. One of the important parameters for the proton exchange membrane fuel cell (PEMFC) used in this paper is that it works at low temperatures, which gives the chance to enhance its size to achieve maximum power production. The solid oxide fuel cell (SOFC) used for the hybrid system [21], by contrast, needs long start-up times and requires insulation and heat dispersion due to temperature concerns. In addition, the PEMFC has higher efficiency, more fuel flexibility, smaller size as it does not require cooling or thermal dissipation, and is less expensive compared to SOFC. The main contribution of this paper is to propose an MG configuration containing PV/FC/B/SC to supply a dump AC variable load with its needed power. It also proposes a classic PI control strategy as an EMS to control the FC current and calculate the hydrogen consumed by the fuel cell. For the proposed system, the PV system decreases the FC hydrogen consumption during day light when it is available, especially in areas of high irradiance values, for a long time. It also gives a chance to increase the size of the clean power generated to decrease greenhouse gasses and global warming, which is good for the environment and climate change. Also, using a battery and a supercapacitor as storage elements gives the system an advantage over individual systems, as the specific power is low, while the specific energy is high—but the supercapacitor has a high specific power and low specific energy [31,32]. In this paper, the performance of the system is simulated using two different energy management strategies (fuzzy logic control strategy and high frequency decoupling and state machine control strategies) to validate the proposed PI control strategy. The simulation results show that the PI control strategy is better than the high frequency decoupling and state machine control strategy in terms of hydrogen consumption. Although the hydrogen consumed by the fuzzy logic control strategy is close to the consumed value by PI, the PI control strategy is easy and simple for implementation. The overall system performance proves that the system works efficiently when applied for a three-phase AC variable load. The cost optimization issue was not calculated in this study, and could be considered in future papers. The next sections of this paper present the overall system description of the proposed system structure, system components, the control strategy, results and discussion, and finally, the conclusion.

2. Overall System Description

A hybrid power system containing a PV, FC, battery, and SC is designed to examine the optimal configuration for the power system shown in Figure 2. It is implemented and simulated in MATLAB/Simulink (version 2018a) software to monitor, control, and analyze the system. The PV panel is connected to a DC/DC boost converter, which is controlled through an MPPT based on perturb and observe (P&O) to get the maximum power of the solar panels. The irradiance values were assumed through the Simulink signal builders and the temperature is fixed at 25 °C. The system component was chosen to get the maximum system performance when working together to cover the disadvantages of each source when operating as a stand-alone source. The system is designed to supply a dump load with its demand power. The system covers the disadvantages of each individual power system when working as a separate system. The surplus power from PV is utilized in charging the SC and battery. It keeps their state-of-charge (SOC) in proper value for operation.

3. System Components

3.1. PV Arrays

The equivalent circuit for the PV solar cell is represented in Figure 3 [33,34], where I_L is the current generated inside the solar cell according to the sunlight. As a basic configuration, the solar cell is a P–N junction, so the diode current I_D is taken into consideration.

The output current is calculated by applying Kirchhoff’s law and is displayed as follows:

$$I = I_{\mathrm{L}}-I_0 (\exp \left(\frac{\left(Vo+I{R}_{\mathrm{s}}\right)}{a{V}_{\mathrm{T}}}\right)-1)-\frac{Vo+I{R}_{\mathrm{s}}}{R_{\mathrm{SH}}}$$

(1)

where I denotes the output current; I₀ is the diode saturation current; V denotes the output voltage; a is the identifying factor of the cells; and V_T is called the thermal voltage [35,36]. Solving Equation (1) for short circuit current and R_P value is very large compared to the series resistance. The saturation current as a function of temperature is calculated directly by the following equation [37]:

$$I_0 = I_{0.\mathrm{ref}} {\left(\frac{T_{\mathrm{ref}}}{T}\right)}^3 \exp \left\{\frac{q{E}_{\mathrm{g}}}{ak} \left(\frac{1}{T_{\mathrm{ref}}}- \frac{1}{T}\right)\right\}$$

(2)

where T_ref and T are the reference and ambient temperatures, respectively, and E_g denotes the energy gap of the material. The relation between the photon current generated and the solar irradiance is represented as follows [38]:

$$I_{\mathrm{L}} = \frac{G}{G_{\mathrm{a}}} \left(I_{\mathrm{L}.\mathrm{ref}} + V_{\mathrm{sc}} \Delta T\right)$$

(3)

where: G is the solar irradiance; G_a is the reference solar irradiance, which is equivalent to 1 KW/m² at the standard test condition (STC); $\Delta T$ denotes the temperature difference between the actual temperature and the temperature at STC, which is 25 °C; and V_sc is the temperature coefficient [39]. Rezk et al. represent in [40] the modeling of the I–V curve of the PV under all conditions of irradiance and temperature.

Table 1. Data sheet for the TPB 156x156-72-P-295W.

Module Type	TPB 156x156-72-P-295W
Module power class	295 Wp
Composition	72 (156 × 156 mm) polycrystalline silicon solar cells per module
Max. power (Pmpp) (in W)	295
Max. voltage (Umpp) (in V)	35.3
Max. current (Impp) (in A)	8.36
Open-circuit voltage (Uoc) (in V)	44.3
Short-circuit current (ISC) (in A)	8.67
Cell temperature (TNOCT) (in °C)	46
Module efficiency (in %)	15.2

represents the data sheet of the solar panels used in the proposed system in this paper.

Figure 4 shows the relationship between the generated current and output power, along with the voltage for the type TPB 156x156-72-P-295W PV solar module used in this paper. The maximum value of the current, called I_SC current, when the output terminals are shorted and the maximum value of voltage is the V_oc at the value of zero current.

Several researches discussed in detail the MPPT algorithms and how to use them for maximizing the generated power from PV [41,42,43,44,45]. In this paper, the MPPT used is based on the perturb and observe (P&O) algorithm with the flowchart shown in Figure 5. P&O is the most common technique in which the power is compared at several samples and perturbs the current. This process is repeated until the difference in power is zero. Larminie et al. discussed several techniques of MPPT, including P&O [46].

3.2. Fuel Cell

The advantages of the proton exchange membrane fuel cell (PEMFC) include its high efficiency, reaching up to 45%, high energy density out of small dimensions (up to 2 W/cm²), silent operation, low-temperature operation, fast start-up, and system robustness [47,48]. The most important advantage of the PEMFC is the minimum pollutants, where the hydrogen fuel used in FC has no adverse effects on the environment [49,50]. In spite of the FC advantages, the FC has some disadvantages like its slow response to the load variation, its unstable output voltage, its short lifetime because of the increase in current ripple, and its relatively high cost. The overall equivalent circuit for the FC discussed by Outeiro et al. is shown in Figure 6 [50].

The modeling and simulation of the FC were discussed in [51] as follows:

$$A = \frac{RT}{z\alpha F}$$

(4)

E_oc = E_n K_c

(5)

$$i_o = \frac{zFk\left(P_{{\mathrm{H}}_2} + P_{{\mathrm{O}}_2}\right)}{RH} e^{\frac{-\Delta G}{RT}}$$

(6)

where R is 8.3145 J/(mol K); K_c denotes voltage constant at nominal condition of operation; T is temperature of operation (K); F is 96,485 A s/mol; ΔG is size of the activation barrier, which depends on the type of electrode and catalyst used; h denotes Planck’s constant = 6.626 × 10⁻³⁴ J s; z is number of moving electrons; k denotes Boltzmann’s constant = 1.38 × 10⁻²³ J/K; $P_{{\mathrm{O}}_2}$ denotes partial pressure of oxygen inside the stack (atm); $P_{{\mathrm{H}}_2}$ is partial pressure of hydrogen inside the stack (atm); E_n is Nernst voltage, which is the thermodynamics voltage of the cells and depends on the temperatures and partial pressures of reactants and products inside the stack (V); and α is charge transfer coefficient, which depends on the type of electrodes and catalysts used. For block A in the FC equivalent circuit, the utilization factor for the fuel and the air (H₂ and O₂) is calculated as follow:

$$U_{f{\mathrm{O}}_2} = \frac{n_{{\mathrm{O}}_2}^r}{n_{{\mathrm{O}}_2}^{in}} = \frac{6000RT{N}_i{}_{fc}}{2zF{P}_{air}{V}_{lmp\left(air\right) }y\%}$$

(7)

$$U_{f{\mathrm{H}}_2} = \frac{n_{{\mathrm{H}}_2}^r}{n_{{\mathrm{H}}_2}^{in}} = \frac{6000RT{N}_i{}_{fc}}{zF{P}_{fuel}{V}_{lmp\left(fuel\right) }x\%}$$

(8)

where P_fuel is absolute supply pressure of fuel (atm); P_air is absolute supply pressure of air (atm); N denotes number of cells; V_lpm(air) is air flow rate (L/min); V_lpm(fuel) is fuel flow rate (L/min); y denotes percentage of oxygen in the oxidant (%); x denotes percentage of hydrogen in the fuel (%); and the 60,000 constant comes from the conversion from the L/min flow rate used in the model to m³/s (1 L/min = 1/60,000 m³/s). The Nernst voltage is determined in Block B as follows:

$$E_{Nernst t} = 1.229-(T-298.15) \frac{-44.43}{zF} + \frac{-RT}{zF} \ln (P_{{\mathrm{H}}_2} P_{{\mathrm{O}}_2}^{\frac{1}{2}}), \mathrm{when} T \le 100 °\mathrm{C}$$

(9)

$$E_{Nernst t} = 1.229-(T-298.15) \frac{-44.43}{zF} + \frac{-RT}{zF} \ln (\frac{P_{{\mathrm{H}}_2}{P}_{{\mathrm{O}}_2}^{\frac{1}{2}}}{P_{{\mathrm{H}}_2\mathrm{O}}}), \mathrm{when} T > 100 °\mathrm{C}$$

(10)

The partial pressure for H₂, O₂, and H₂O are calculated also in block B as follows:

$$P_{{\mathrm{H}}_2} = (1-U_{f{\mathrm{H}}_2}) x\% P_{fuel}$$

(11)

$$P_{{\mathrm{H}}_2\mathrm{O}} = (\mathrm{W} + 2y\%U_{f{\mathrm{O}}_2}) P_{air}$$

(12)

$$P_{{\mathrm{O}}_2} = (1-U_{f{\mathrm{O}}_2}) y\% P_{air}$$

(13)

where W denotes percentage of water vapor in the oxidant (%) and $P_{{\mathrm{H}}_2\mathrm{O}}$ is partial pressure of water vapor inside the stack (atm). The updated values of the exchange current i_o and the open circuit voltage are calculated according to the partial pressure and the Nernst voltage. The (I–V) curve of the FC used in this paper is represented in Figure 7. It represents the relation between the current density and the FC voltage.

Table 2. Data sheet parameters of the proton exchange membrane fuel cell (PEMFC).

Parameters
Nominal power (w)	10,287.5
Max power (w)	12,544
Nernst voltage (V)	1.1491
Hydrogen (H2)	98.98%
Oxidation (O2)	42.885
Fuel flow rate (lpm)	114.9
Air flow rate (lpm)	732
System Temp (K)	318
P Fuel (bar)	1.16
P Air (bar)	1

represents the data sheet for FC used in present case study.

3.3. Battery

The main target of using and integrating a battery and a supercapacitor with the renewable energy resources power configuration is to store the surplus of energy produced from the other sources and reuse it whenever there is a shortage in energy [52,53]. In this paper, the proposed design was built based on the lithium-ion battery. The battery parameters are shown in

Table 3. Battery parameters.

Parameters
Nominal voltage (V)	48
Rated capacity (Ah)	40
Initial state-of-charge (%)	65

and the discharge parameters are shown in

Table 4. Battery discharge parameters.

Discharge
Maximum capacity (Ah)	40
Fully charged voltage (V)	55.8714
Nominal discharge current (A)	17.3913
Capacity (Ah) at nominal voltage	36.1739
Exponential zone [Voltage (V), Capacity (Ah)]	[52.3, 1.96]
Discharge current [i1, i2, i3, …] (A)	[20, 80]

.

For batteries, there are three main modeling types: Mathematical model, electro-chemical model, and equivalent circuit model [54]. Honorat et al. discussed the three methods of fast characteristics of automotive lithium-ion second life batteries [55], whereas madani et al. [56] discussed the electrical equivalent circuit for second order batteries. Jiuchun et al. [57] argue that the electrical equivalent circuit is the best model for representing the battery, due to the unsuitability of the mathematical model for actual application and the complexity of the electro-chemical model. Valant et al. [58] tested the modules used in secondary application of grid in lab conditions. Generally, the equivalent circuit of the ideal battery combines the open circuit voltage and the battery internal resistance. Figure 8 represents the equivalent battery circuit and Figure 9 represents the battery performance—where V_b is the battery voltage; i_b is the battery current; Voc is the open circuit voltage as a function of SOC h (t); R_p and C_p are the resistance and the capacitance of the battery polarization; and R_s is the internal resistance.

For discharge mode, the battery voltage equation is represented as follow [59]:

$$V_{batt} = E_0 – K (\frac{Q}{Q-it}) i^{*} - K (\frac{Q}{Q-it}) it + A e^{-Bit} (i^{*} > 0)$$

(14)

For charge mode, the battery voltage equation is represented as follows:

$$V_{batt} = E_0 – K (\frac{Q}{it+0.1 Q}) i^{*} - K (\frac{Q}{Q-it}) it + A e^{-Bit} (i^{*} < 0)$$

(15)

The fully charged state voltage is displayed as follows:

V_full = E₀ − Ri + A

(16)

The exponential section voltage is calculated as follows:

$$V_{exp} = E_0- K (\frac{Q}{Q-Q_{exp}}) (Q_{exp} + i) - Ri + A e^{\frac{-3}{Q_{exp}}{Q}_{exp}}$$

(17)

And finally, the nominal zone cell voltage is calculated as follows:

$$V_{nom} = E_0- K (\frac{Q}{Q-Q_{nom}}) (Q_{nom} + i) - Ri + A e^{\frac{-3}{Q_{exp}}{Q}_{nom}}$$

(18)

where E₀ is constant voltage, in V; K is polarization constant, in Ah⁻¹; i* is low frequency current dynamics, in A; i is battery current, in A; it is extracted capacity, in Ah; Q is maximum battery capacity, in Ah; A is exponential voltage, in V; and B is exponential capacity, in Ah⁻¹. SOC is estimated according to coulomb counting by accumulating the capacity during battery charging/discharging:

$$SOC={SOC}_0 - \frac{1}{Q_n}{{\displaystyle \int }}_0^t\eta idt$$

(19)

3.4. Supercapacitors (SC)

The SC is used with the battery to decrease the peak current in the battery when the load is highly fluctuating because of its high specific power. As the battery cannot supply the needed power at a high rate because of it characteristics, the SC covers this power shortage. SC has a high-efficiency cycle (about 100%) which is suitable for both frequent charge/discharge cycles and storage of energy, compared to the battery, which is used to supply the average needed power. It means that the SC delivers the power faster and has more charge/recharge cycles than the battery [60]. That is why the supercapacitor is used as a complementary element with other electrical sources that have different dynamic behavior and different energy storage quantities [61]. The main parameters of the supercapacitor source used in this paper are shown in

Table 5. Supercapacitor (SC) main parameters.

Parameters
Rated capacitance (F)	15.6
Equivalent DC series resistance (Ohms)	1.50 × 10−1
Rated voltage (V)	291.6
Initial voltage (V)	270
Operating temperature (Celsius)	25

, while the self-discharge parameters are listed in

Table 6. Supercapacitor (SC) self-discharge parameters.

Self-Discharge
Current prior open-circuit (A)	10
Voltage at 0 s, 10 s, 100 s, and 1000 s [Voc, V3, V4, V5] (V)	[48, 47.8, 47.06, 44.65]
Charge current [i1, i2, i3, …] (A)	[10, 20, 100, 500]

.

Figure 10 shows the electrical equivalent circuit for the SC [62], where C is the capacitance of SC, EPR is the equivalent parallel resistances, and ESR is the equivalent series internal resistances of SC.

$$E_{UC}=\frac{1}{2}C\left(V_i^2 - V_f^2\right)E_{UC}$$

(20)

where E_UC is the dragged energy from the SC and $\left(V_i^2-V_f^2\right)$ is the voltage change between the final and initial voltage. The series/parallel configuration of the capacitors in SC was determined by the value of the terminal voltage. The total capacitance and resistance for the SC can be determined as follows:

$$R_{total} = n_s\frac{ESR}{n_p}$$

(21)

$$ESR = \frac{\Delta V_d}{I_d}$$

(22)

$$C_{total} = n_p\frac{C}{n_s}$$

(23)

$$C = I_d\frac{\left(t_2 - t_1\right)}{\left(V_2 - V_1\right)}$$

(24)

where I_d is the discharging current; n_s is the number of connected capacitors in series; and n_p is the number of series strings in parallel. The characteristics of the supercapacitor charge is shown in Figure 11.

4. Energy Management System

As the proposed system in this paper contains multi-electrical power sources like FC and PV, an energy storage element could be used as a power source when discharging. Hence, there is a need for an energy management strategy, based on a computer program to control, monitor, and optimize the system operation to get maximum system performance [63]. The EMS is used to increase the system overall efficiency, decrease the hydrogen fuel consumption in the FC power system when the FC is used as a component of the hybrid system, increase the life cycle of the system component to keep the stability of the DC voltage, and control the SOC and prevent its deep discharge [64]. There are many EMSs and control strategies that are used with renewable hybrid power systems, such as state machine control, fuzzy logic control (FLC), Control loop cascade, proportional–integral–derivative (PID) control approach, and instantaneous optimization approach. The PI cascaded control was promoted in this paper as a microgrid control strategy. This control strategy calculates and sets the reference values of FC current, battery charge, and discharge currents. Figure 12 shows the flowchart of the fuel cell current control with each comparison step between the reference values of SOC, load power with PV power, and finally, the minimum and maximum values for the DC bus voltage (VDC). Regarding the EMS used in the present case study, the classic PI controller gives the simplest way because it has a few number of inputs, is easy to be configured, has feedback, and is inexpensive compared with other EMSs like FLC. FLC has more rules for more accuracy, low speed performance, and much more cost with regard to the programming and hardware interface [65].

The PI control strategy is simulated in MATLAB/Simulink, as illustrated in Figure 13. Figure 13a shows the actual percentage of SOC measured in the simulation program compared with a predetermined value (60%). According to the difference, the program increases/decreases the reference power of the fuel cell. Figure 13b illustrates the shortage power from load/PV comparison, where the behavior of the strategy output is calculated according to the difference between the load and the PV power. Figure 13c shows the reference value of the fuel cell current according to the reference power, and Figure 13d shows the fuel cell reference current according to VDC limits.

The control of the charging/discharging battery current is done according to PI control strategy. It depends on a summation of two PI controllers. One of them is based on the power difference between the load and the PV power, and the other is based on the difference between the actual and the reference of the VDC, which is 270 VDC in this case. According to the result of these two PI controllers, the output of the strategy by charge/discharge the battery. Figure 14 shows the flowchart of the battery charge/discharge procedure.

Figure 15 shows the PI control strategy MATLAB model for battery.

The system is designed to supply a variable three-phase dump load, as shown in Figure 16a, with its needed power. The load profile is assumed to be variable with different levels of power in order to test the performance of the proposed system at variable value of load (from about 0 to 9 kW) along the total duration of simulation. The system is implemented and simulated in MATLAB/Simulink for a total simulation time of 350 s. During this period, the behavior of the system could be divided into three different stages according to the PV power, as shown in

Table 7. Simulation stages and its boundaries.

Stages	Time	PV Power (Watt)
Stage #1	From 0 to 90 s	0
Stage #2	From 90 to 250 s	0 > PV > 7326
Stage #3	From 250 to 350 s	0

.

4.1. Performance during Stage #1

The start of this stage is at 0 s, and its end is determined at 90 s. In this period, the PV power is zero, as shown in Figure 16c. In this stage, the zero PV power is because of no solar irradiance, as shown in Figure 16b. During the period from 0 to 40 s, there is a surplus of power because the load is zero. The fuel cell current is at minimum (i_fc = 20 A) because the SOC initial value (60%) is greater than its reference value (60%), which leads the VDC to increase more than 270 V, which is the set point for the system DC bus voltage. The battery and supercapacitor start to charge, as per battery charging current (Figure 17a).

Figure 18 shows line voltage, phase current, fuel cell power, and battery power. At 40 s, the load starts to increase and the supercapacitor starts to supply the load with the power faster than the fuel cell and battery because of its charge/discharge response. Then, the battery and fuel cell start to supply their power at 43 s and 44 s, as illustrated in Figure 18c,d. The fuel cell power, the battery, and the supercapacitor power follows the load power until the end of this stage at 90 s, according to the PI control strategy.

4.2. Performance during Stage #2

This stage is initiated at 90 s and ends at 250 s. The PV output power increases with the increasing of the irradiance value according to day light. As the temperature is assumed to be constant (t = 25 °C), the PV power is mainly dependent on the PV current shown in Figure 16d. The EMS estimates the difference between the load power P_load and the PV power, and then determines the new values of the fuel cell current and the battery charge/discharge current. In this case, the PV power interferes in controlling the battery charging/discharging, as well as controlling the FC current (Figure 19a).

The PV power reaches its maximum value of 7326 watt at 170 s. At this point, the generated PV power exceeds the load demand, leading to a surplus of power. This surplus power is used to charge the battery and supercapacitor through the PI control strategy, and simultaneously decreases the power consumed from the fuel cell at the same time until 180 s. During the period from 80 to 250 s, the load demand is more than the generated PV power and there is no surplus power. The battery and supercapacitor then discharge and share the load power with the PV array and fuel cell. Figure 20 shows the results for all of the system collected together.

4.3. Performance during Stage #3

This stage starts at 250 s up until 350 s. In this stage, the generated PV power is zero and the load is supplied by the fuel cell power, battery power, and the supercapacitor power, the same as stage 1. At the end of this stage, the load power is zero and the fuel cell supplies power for charging the battery and supercapacitor. As a result, the VDC increases again and reaches the value of 285 VDC by the end of this stage. The system keeps working in this manner until the end of the simulation. Figure 20 shows the performance of all power sources along the overall simulation period from 0 to 350 s.

5. Comparison Study

In order to validate the results of the classic PI control strategy as a satisfying energy management system to control hybrid energy sources working in a microgrid, the results of a classic PI control strategy simulation were compared with the results of a fuzzy control strategy and a high frequency decoupling and state machine control strategy. Qi Li et al. [66] discussed the fuzzy logic control strategy as an energy management system for a FC/battery/supercapacitor hybrid vehicle. It was used for enhancing the fuel to increase the mileage of the journey, and the results show that the system achieved the power requirement at four standard driving cycles. In the current research, the FIS function in MATLAB was configured with three input signals to the FIS, which were load power, PV power, and battery SOC%, while the output was configured as the FC current. Eight rules were assigned to represent the operation of the system during the simulation periods. Figure 21 shows the Fuzzy FIS configuration used in the simulation.

Table 8. Fuzzy control system rules.

Rule	Load	PV	SOC	IFC
1	Low	Low	OK	Low
2	OK	Low	OK	OK
3	OK	OK	OK	Low
4	High	Low	OK	High
5	High	OK	OK	Low
6	High	High	OK	Low
7	High	High	Low	Low
8	Low	Low	High	Low

shows the eight rules of the fuzzy control system which control the fuel cell current output signal. The eight rules contain the most conditions so that the system can act accordingly.

High frequency decoupling control strategy is used to decrease the effect of the transient load change by insulating the PEMFC current from the high frequency transient load change [67]. The configuration of the frequency decoupling and state machine control strategy implemented in this paper is shown in Figure 22.

Figure 23 displays the results of the fuzzy logic control strategy, where Figure 23a shows the hydrogen consumption along the simulation period. Figure 23b shows the SOC of the battery.

Figure 24 displays the results of the high frequency decoupling and state machine control strategy. The hydrogen consumption along the simulation period is 19.9 (g), as shown in Figure 24a. Figure 24b shows the SOC of the battery.

For the main two parameters, hydrogen consumption and SOC (%), Figure 25 shows the comparison between three control strategies. Figure 25a shows the fuel consumption for PI, fuzzy, and high frequency decoupling and state machine. The high frequency decoupling and state machine is the biggest strategy for hydrogen consumption, while the fuzzy and the PI are close.

Table 9. Comparison among considered control strategies.

Method	PI	Fuzzy	High Frequency Decoupling and State Machine
H2 consumption (gram)	12.13	13	19.9
SOC%	56–65	55–65	63.19–65.39

summarizes the comparison among the classic PI control strategy, fuzzy logic control strategy, and high frequency decoupling and state machine control strategy.

6. Conclusions

The microgrid combined with a renewable hybrid power system is a very promising, efficient, and clean power generation system. It can replace the conventional fuels easily. In this study, the obtained results prove that the designed hybrid power system—which combines PV, FC, battery, and SC—works efficiently at decreasing the effects of the FC disadvantages. It solves the problems of the individual source and supplies the load with sufficient and stable power. The PV array supplies the main power and the FC compensates for the power shortage because of shading and night time. The battery and SC are used to solve the problems of slow response of the FC during the fast change of the load power and to remove the peak power from the system. In cases where surplus power exists, this power is used to charge the battery to keep battery SOC% at a healthy level (between 57 and 65.4%), and sustain the VDC within the range of 265 to 285 in good condition. Moreover, the H₂ fuel consumption is 12.13 gm, as the FC is used as supported sources working with the PV. The system was simulated for another two control strategies, fuzzy and high frequency decoupling state machines. The results for comparison prove that the PI control strategy is better than the high frequency decoupling state machine. In addition, for the fuzzy control strategy, although the results were close, the PI is easier for implementation. Future researches could focus on improving the system with regard to cost optimization. It is also suggested that an electric electrolyzer should be attached to the system to use the surplus power in hydrogen production. Further researches could focus on helping environment interests such as global warming and climate change, in addition to using other EMS strategies and optimization techniques to improve the system overhaul performance.