Measuring Test Bench with Adjustable Thermal Connection of Cells to Their Neighbors and a New Model Approach for Parallel-Connected Cells

Abstract

This article presents a test bench with variable temperature control of the individual cells connected in parallel. This allows to reconstruct arising temperature gradients in a battery module and to investigate their effects on the current distribution. The influence of additional contact resistances induced by the test bench is determined and minimized. The contact resistances are reduced from $R_{\mathrm{Tab}+}=81.18$ $\mathsf{\mu }\mathsf{\Omega }$ to $R_{\mathrm{Tab}+}=55.15$ $\mathsf{\mu }\mathsf{\Omega }$ at the positive respectively from $R_{\mathrm{Tab}-}=35.59$ $\mathsf{\mu }\mathsf{\Omega }$ to $R_{\mathrm{Tab}-}=28.2$ $\mathsf{\mu }\mathsf{\Omega }$ at the negative tab by mechanical and chemical treating. An increase of the contact resistance at the positive tab is prevented by air seal of the contact. The resistance of the load cable must not be arbitrarily small, as the cable is used as a shunt for current measurement. In order to investigate their impacts, measurements with two parallel-connected cells and different load cables with a resistance of $R_{\mathrm{Cab}+}=0.3$ m$\mathsf{\Omega }$, $R_{\mathrm{Cab}+}=1.6$ m$\mathsf{\Omega }$ and $R_{\mathrm{Cab}+}=4.35$ m$\mathsf{\Omega }$ are conducted. A shift to lower current differences with decreasing cable resistance but qualitatively the same dynamic of the current distribution is found. An extended dual polarization model is introduced, considering the current distribution within the cells as well as the additional resistances induced by the test bench. The model shows a high correspondence to measurements with two parallel-connected cells, with a Root Mean Square Deviation (RMSD) of ${\xi }_{\mathrm{RMSD}}=0.083$ A.

1. Introduction

Large-scale battery applications like electric vehicles (EV) have to meet high power and energy demands, which is mostly realized by the parallel-connection of lithium-ion cells, e.g., Tesla Model S (74p96s (The abbreviation xpys corresponds to a cell configuration with x cells in parallel and y cells in serial connection)), Tesla Model 3 (46p96s), VW eGolf (3p88s), Nissan Leaf (2p96s), BAIC EU260 (3p90s), Renault Zoe (2p96s) and Audi etron (4p108s) [1,2]. Caused by production-induced distributions of cell resistances and capacities [3,4], inhomogeneous cell currents arise within these parallel cell configurations [5], further leading to State of Charge (SoC) [6,7], Open Circuit Voltage (OCV) [8,9] and temperature gaps [6,10] within the parallel cells. Since the cell currents must be maintained in their corresponding operating window and cannot be measured for space and cost considerations, correlations of the current distribution to cell parameters and cell states are essential for an optimal and safe battery operation.

There is a variety of articles focusing on modeling [11,12,13,14,15], aging [16,17,18], safety [19,20,21], state estimation [22,23] and measurement [24,25,26] of parallel-connected cells. Mostly qualitative effects like OCV [27], SoC [13], temperature [13,26,28,29] and current differences [13] are demonstrated but quantitative relationships are missing, especially with regard to the thermal connection of the cells to neighboring cells and cooling. The cell temperature, as well as the temperature difference between parallel cells, can have a high influence on the current distribution both due to the high sensitivity of the cell resistance to the temperature [30,31] and due to the correlation of heat dissipation to the cell current [32].

Therefore, in Section 2, a test bench with a flexibly adjustable thermal connection of the individual cells to their neighboring cells and cooling is presented. Thus, both the formation of temperature gradients due to the current distribution and the impacts of design-induced temperature gradients in a battery module on the current distribution can be investigated. In Section 3, an extended dual polarization Equivalent Circuit Model (ECM) is introduced and compared to measurements. This simulation model takes into account the influences of the test bench on the current distribution and the parallel-connected cell layers within the cells. In Section 4, the influence of temperature gradients induced by inhomogeneous thermal connections of the cells to neighboring cells and cooling on the current distribution of two parallel-connected cells are investigated. At the end, a conclusion is given.

2. The Test Bench

In this section, the test bench is discussed. First, the interactions and functions of all subsystems are explained and afterwards the temperature control system is presented in more detail. Finally, the possible impacts of the test bench on the current distribution are demonstrated.

2.1. Interactions and Communication of the Subsystems

Figure 1 shows the test bench for one cell with view-optimized modifications (a), a schematic view of the temperature control system (b), a detailed view of the position and orientation of the temperature sensors (c), as well as a detailed view of the electrical connection of the cells to the cell tester highlighting the voltage and current measurement of each cell (d).

The test bench for each cell (10) consists of two Peltier Elements (11), two aluminum plates (3), two CPU coolers (1), two speed controllers (2), a measurement device (4), one micro-controller (6) and a power supply unit (7). The housing is electrically grounded and consists of aluminum profiles (5). The cell tabs are connected to the load cable via a screwed aluminum union joint (13). The cell temperature is captured by two Pt100 sensors (12) of each cell side, $T_{\mathrm{Cell},\mathrm{Center}}$ and $T_{\mathrm{Cell},\mathrm{Top}}$ see Figure 1c. The temperature of the adjacent aluminum plates is measured with one Pt100 sensor $T_{\mathrm{Plate}}$. The cell voltage $U_{\mathrm{cell}}$ is measured at the cell tabs, the cell current $I_{Cell}$ is calculated via the voltage drop at the load cable (14) of each cell, see Figure 1d. The load cables of the cells are connected to a cell tester. This setup enables one to investigate any cell topology; the number of parallel-connected cells is only limited by the size of the climate chamber. The communication and interaction of these subsystems are presented in Figure 2.

The measurements are conducted in a temperature controlled climate chamber and the battery load is controlled by a cell tester. The temperatures of the lithium-ion cells are regulated by Peltier Elements. One side of the Peltier Elements is thermally coupled to the CPU coolers to keep the temperature of this side constant at ambient temperature. In order to ensure temperature homogeneity at the cells, the Peltier Elements are embedded in aluminum plates. In addition, the plates and the cells are isolated by Polystyrene (9). The assembly of these subsystems is presented in Figure 1b. The voltages of the Peltier Elements are adjusted by speed controllers, which in turn are controlled by micro-controllers. These are regulated by a PI controller implemented in Matlab.

Measurement data, including six Pt100 temperature sensors (12), three for each cell side, as well as two voltage signals, are recorded with a frequency of $f=100$ Hz. The signals are transferred by an interface via CAN to a PC and real time processed in Matlab. The power for the speed controllers, the measurement device and CPU coolers is provided by a power supply unit.

In addition, the pressure on the cells is kept constant by a spring construction and the mobility of one aluminum plate. A fluctuation of the pressure due to the correlations of the cell’s thickness to SoC [33,34] and temperature [35] as well as the continuous increase of the cell thickness caused by lithium plating and gassing [36] could otherwise have a negative effect on cell aging [37]. The manufacturers and the corresponding types of the individual components are summarized in

Table 1. Manufacturers and corresponding types of the used components.

Designation	Manufacturer	Type
Lithium-ion cell	Kokam	SLPB776495
Peltier element	Quick Cool	QC-127-2.0-15.0M
CPU cooler	be quiet!	SL 240
Speed controller	EPH-Elektronik	DLR 24/20
Measurement device	imc CANSAS	L-HCI8
Micro-controller	Arduino	Mega 2560
Power supply unit	Thermaltake	TR2 S700
Aluminum profiles	ITEM	Profiltyp 5
CAN interface	Vector	Vn1640 A
Climate chamber	Vötsch	${\mathrm{VC}}^3$ 4100/S
Cell tester	BasyTec	HPC

.

The functionality of the temperature control system, temperature homogeneity of the aluminum plates and the heating rate are explained in more detail in Section 2.2.

2.2. Temperature Control System

The control of the cell temperature as well as the temperature homogeneity at the cells were decisive tasks for the test bench in order to fulfill reliable and trustful measurements. In order to validate these requirements, nine temperature sensors were fixed on the cell adjacent subarea of the aluminum plate, Figure 3a, and an exemplary regulation from $T=10 °$C to $T=30 °$C and further to $T=40 °$C, Figure 3b, was conducted.

Figure 3f–h demonstrates the temperature homogeneity of the aluminum plate. The temperature distribution on the plate was determined by weighting each temperature sensor depending on their distance to the respective point. In the stationary state, the maximum temperature difference within the plate was about $\Delta T=0.71$$°$C. The differences can be caused, on the one hand, by the smaller area of the Peltier Element compared to the aluminum plate and, on the other hand, by the energy exchange with the environment.

Another important requirement of the temperature control system is to realize a higher heating rate of the aluminum plates ${\dot{T}}_{\mathrm{Plate}}$ compared to the maximum heating rate of the cells ${\dot{T}}_{\mathrm{Cell}}$ caused by dissipation ${\dot{Q}}_{\mathrm{Diss},\max }$, which can be estimated by

$$\begin{array}{c}\hfill {\dot{T}}_{\mathrm{Cell}}=\frac{1}{m_{\mathrm{Cell}}{c}_p}·{\dot{\mathrm{Q}}}_{\mathrm{Diss},\max },\end{array}$$

(1)

$$\begin{array}{c}\hfill {\dot{\mathrm{Q}}}_{\mathrm{Diss},\max }=R_{\mathrm{Cell},\max }·I_{\mathrm{Cell}}^2,\end{array}$$

(2)

with the maximum cell resistance $R_{\mathrm{Cell},\max }$, the cell current $I_{\mathrm{Cell}}$, the cell’s heat capacity $c_{\mathrm{p},\mathrm{Cell}}$ and the cell mass $m_{\mathrm{Cell}}$. The cell’s resistance was determined by pulse tests as described in Section 3.2 and ranges between $R_{\mathrm{Cell}}=21.3$ m$\mathsf{\Omega }$ and $R_{\mathrm{Cell}}=99.44$ m$\mathsf{\Omega }$, depending on the SoC, temperature and time. With a maximum cell current of $I_{\mathrm{Cell}}=2C$, the required heating rate can be calculated with Equation (2) from ${\dot{T}}_{\mathrm{Cell}}=23.4$ mK$·{\mathrm{s}}^{-1}$ to ${\dot{T}}_{\mathrm{Cell}}=114$ mK$·{\mathrm{s}}^{-1}$. However, as the maximum currents of $I_{\mathrm{Cell}}=2$C are only permitted at cell temperatures above $T_{\mathrm{Cell}}=10$ $°$C and the voltage limits are reached at about $\mathrm{SoC}=8\%$ for these high currents, the practical limit can be set to ${\dot{T}}_{\mathrm{Cell}}=74.8$ mK$·{\mathrm{s}}^{-1}$.

The heating rate of the aluminum plate is approximately limited to ${\dot{T}}_{\mathrm{Plate}}=250$ mK$·{\mathrm{s}}^{-1}$, as shown in Figure 3c–e. This enables a precise temperature adjustment of the cells and the reconstruction of temperature gradients within a battery module due to varying thermal connections of the cells to neighboring cells and cooling.

2.3. Impacts of the Test Bench on the Current Distribution

The ratios of the resistances and capacities of the parallel-connected cells have one of the main influences on the current distribution. This was shown qualitatively by measurements and simulations in [1], the quantitative influences of these parameters were mathematically proven in previous work [8,9].

For this reason, additional resistors induced by the test bench can significantly influence the current distribution. Due to the electrical connection of the cell tester and the lithium-ion cells, additional resistances arise in series with the cells, which are demonstrated in Figure 4.

The contact resistances at the cell tabs as well as the cable resistances must on the one hand be well-known and on the other hand be kept low, at least their difference. As a result of the first Kirchhoff’s law the following is valid

$$\begin{array}{cc}\hfill & U_{\mathrm{Cab}+,\mathrm{i}}+U_{\mathrm{Tab}+,\mathrm{i}}+U_{\mathrm{Cell},\mathrm{i}}+U_{\mathrm{Tab}-,\mathrm{i}}+U_{\mathrm{Cab}-,\mathrm{i}}\hfill \\ \hfill =& U_{\mathrm{Cab}+,\mathrm{i}+1}+U_{\mathrm{Tab}+,\mathrm{i}+1}+U_{\mathrm{Cell},\mathrm{i}+1}+U_{\mathrm{Tab}-,\mathrm{i}+1}+U_{\mathrm{Cab}-,\mathrm{i}+1}\hfill \\ \hfill =& U_{\mathrm{Cab}+,\mathrm{p}}+U_{\mathrm{Tab}+,\mathrm{p}}+U_{\mathrm{Cell},\mathrm{p}}+U_{\mathrm{Tab}-,\mathrm{p}}+U_{\mathrm{Cab}-,\mathrm{p}},\hfill \end{array}$$

(3)

with the cell voltage $U_{\mathrm{Cell},\mathrm{i}}$, the positive $U_{\mathrm{Tab}+,\mathrm{i}}$ and negative tab voltages $U_{\mathrm{Tab}-,\mathrm{i}}$ as well as the voltages of the positive $U_{\mathrm{Cab}+,\mathrm{i}}$ and negative load cable $U_{\mathrm{Cab}-,\mathrm{i}}$ of cell i. In order to keep these disturbing values of the test bench on the current distribution low, the following conditions must be fulfilled

$$\begin{array}{c}\hfill U_{\mathrm{Cell},1}\approx U_{\mathrm{Cell},2}\approx U_{\mathrm{Cell},\mathrm{p}},\end{array}$$

(4)

$$\begin{array}{c}\hfill U_{\mathrm{Cab}-,\mathrm{i}}+U_{\mathrm{Tab}-,\mathrm{i}}+U_{\mathrm{Cab}+,\mathrm{i}}+U_{\mathrm{Tab}+,\mathrm{i}}<<U_{\mathrm{Cell},\mathrm{i}}.\end{array}$$

(5)

The contact resistance at the tabs were examined and the cable resistances were varied in order to validate their impacts on the current distribution.

2.3.1. Contact Resistance at the Tabs

In order to keep the contact resistance at the cell tabs low, different influences on these resistances were investigated. The contact resistances were calculated by a four terminal measurement using a micro ohmmeter (MPK, 2000e). The influences of surface cleaning, torque and air insulation were researched. Therefore the tabs were treated with a non-woven abrasive cloth and then cleaned with an oxide-dissolving spray (CRC-Kontaktchemie, Kontakt 60). In addition, tests with varied contact pressure and conductive epoxy resin were conducted in order to isolate the tabs. For the investigation of the contact pressure, the resistances of twelve cathode and anode tabs were examined. To research the impacts of air seal, six of the cathode tabs were treated with conductive epoxy resin. The other six cathode tabs and the twelve anode tabs were not sealed with epoxy resin. The results are presented in Figure 5, whereby for each point the mean, minimum and maximum value is shown.

The influences of surface cleaning and contact pressure, as presented in Figure 5a,b, have already been investigated in [38,39] with the same findings. Figure 5c shows the influence of the air seal. While the contact resistances at the cathode tabs with air seal remained almost constant over the test period of 51 days, the resistances without air seal increased 2.5 times from $R_{\mathrm{Tab},+}=57.4$$\mathsf{\mu }\mathsf{\Omega }$ to $R_{\mathrm{Tab},+}=133.6$$\mathsf{\mu }\mathsf{\Omega }$. It is assumed that oxidation on the tabs will lead to this increase. A relaxation of the surface pressure during the test period could additionally have led to an increasing contact resistance. However, since the resistances at the anode tabs remained unchanged, this effect should be not that significant. The anode tabs do not require an air seal due to their nickel coating, which shows up in an unchanged resistance over the test period. Furthermore, the contact resistances at the tabs and therefore the corresponding disturbing voltage drops $U_{\mathrm{Tab}+}$ and $U_{\mathrm{Tab}-}$ are low compared to the cell resistance with

$$max\left(\frac{R_{\mathrm{Tab}}}{R_{\mathrm{Cell}}}\right)<1\%,$$

(6)

which should lead to no significant impacts on the current distribution.

2.3.2. Cable Resistance

In addition to the requirement of low resistance, the load cables were also used as a shunt to determine the cell currents, which were calculated via the voltage drop at the cables. Since this drop correlates to the cable resistance, a trade off between the measurement accuracy and the influence on the current distribution arise. Therefore different cable resistances and their impacts on the current distribution were investigated by measurements with two parallel-connected cells. The cable resistances were examined by four terminal measurements using a multimeter (Keithley, DMM7510) and are given in

Table 2. Investigated cable resistances.

Cell	${\mathit{R}}_{\mathbf{Cab},\mathbf{Type}1}$/m$\mathsf{\Omega }$	${\mathit{R}}_{\mathbf{Cab},\mathbf{Type}2}$/m$\mathsf{\Omega }$	${\mathit{R}}_{\mathbf{Cab},\mathbf{Type}3}$/m$\mathsf{\Omega }$
1	0.28	1.48	4.20
2	0.3	1.59	4.52

.

In relation to the cell resistance, the cable resistances of the first type $R_{\mathrm{Cab},\mathrm{Type}1}$ range from $1.3\%$ to $0.2\%$ depending on the SoC and cell temperature and should have no significant influence on the current distribution. Type 3 $R_{\mathrm{Cab},\mathrm{Type}3}$ uses the complete measuring range of the measuring device, which should lead to the highest measurement accuracy. Type 2 $R_{\mathrm{Cab},\mathrm{Type}2}$ offers a trade off.

The current distribution of two parallel-connected cells with the discussed cables are presented in Figure 6. The temperature of the aluminum plates were kept constant at $T_{\mathrm{Plate}}=30$ $°$C. The cells were discharged with a current load of $I=-10.6$ A, which corresponds to a C-rate of 1C. The discharge started with a $\mathrm{SoC}=0.95$ and lasted until the cell voltage reaches the voltage limit of $U_{\mathrm{Cell}}<2.8$ V. After a break of 30 min, the cells were charged with a C-rate of 1C until the cell voltage reached the voltage limit of $U_{\mathrm{Cell}}=4.2$ V. Thereafter the cells were relaxed for 30 min.

The current distribution is qualitatively the same for the three different cables with a shift to higher current differences within the parallel-connected cells with increasing cable resistance. However, this may also be due to the higher difference between the cable resistances. The differences are most obvious at the current rest and at the end of the discharge phase. This can be caused by the correlation of the time constant to the cell’s resistance, as mathematically shown in previous work [8,9].

3. Simulation

In this section the used ECM is presented and the parametrization of the cells is discussed. At the end simulations are compared to measurements of two parallel-connected cells.

3.1. Equivalent Circuit Model

In Figure 7 the implemented dual polarization model is demonstrated. The model considers the mentioned resistances due to the connection of the cells to the cell tester and the parallel-connection of L cell layers within the lithium-ion cell. ECMs with RC-pairs are widely used for the simulation of the current distribution within parallel-connected cells [1,2,40,41,42,43].

This ECM was connected in parallel and solved as described in previous work [8,9].

3.2. Parametrization

The model was parameterized by Constant-Current Constant-Voltage (CCCV) measurements to estimate the cell’s capacity. With a constant current of 1C until $U_{\mathrm{Cell}}=4.2$ V for charging, respectively $U_{\mathrm{Cell}}=2.8$ V for discharging. The voltage was kept constant until the cell current reached $I_{\mathrm{Cell}}<1/20$C. The serial resistor and the parameters of the RC-pairs were determined by 2C charge and discharge current pulses at 34 different SoCs. The cells were relaxed one hour after each pulse to estimate the OCV and guarantee same start conditions for each pulse. The measurements were repeated at different cell temperatures (The current pulses were reduced to $I_{\mathrm{Cell}}=0.2$C at cell temperatures $T_{\mathrm{Cell}}<10 °$C in order to keep the cells in their operating window.) $T=0$, 5, 10, 20, 30 and $40 °$C. The parametrization process as well as the results of the ECM parameters are presented in more detail in previous work [2].

3.3. Validation

In order to validate the discussed ECM, simulations are compared to measurements in Figure 8. Each of the used cells consists of 40 cell layers, whose resistances and capacities were randomly drawn from Gauss distributions. With the related standard deviations of the cell’s resistance and the cell’s capacity

$$\begin{array}{c}\hfill \frac{{\sigma }_R}{{\mathsf{\mu }}_R}={\omega }_R·\sqrt{L},\end{array}$$

(7)

$$\begin{array}{c}\hfill \frac{{\sigma }_C}{{\mathsf{\mu }}_C}={\omega }_C·\sqrt{L},\end{array}$$

(8)

with the standard deviation of the cell’s resistance ${\sigma }_R$ and the cell’s capacity ${\sigma }_C$, the mean value of the cell’s resistance ${\mathsf{\mu }}_R$ and the cell’s capacity ${\mathsf{\mu }}_C$ as well as the number of parallel-connected cell layers L. The standard deviations of the parameters were multiplied by the square root of L to consider the statistical averaging due to the parallel cell layers. The related standard deviations ${\omega }_R$ and ${\omega }_C$ were set to ${\omega }_R=1\%$ and ${\omega }_C=0.5\%$, which are typical parameter distributions caused by manufacturing tolerances as found in [3,4]. The expected values ${\mathsf{\mu }}_R$ and ${\mathsf{\mu }}_C$ were adjusted according to the parametrization results of each cell. The load cable resistances $R_{\mathrm{Cab}}$ were set according to the values of Table 2. For the tab resistances $R_{\mathrm{Tab}}$, the average values of the measurements in Figure 5c were used.

The results of the simulation in Figure 8 agree well with those of the measurement with an RMSD of ${\xi }_{\mathrm{RMSD}}=0.083$ A. The highest differences appeared at the end of discharge and at the first current rest. The simulated layer currents, Figure 8a, within the cells show a similar distribution with an shift depending on the cell parameters.

4. Impacts of the Module Design

Due to the cell packaging, inhomogeneities in terms of cooling and thermal connection of the cells to their neighbor cells arise within a battery module. The influence of the ambient temperature depends on the cell position in the module, whereby the cells at the edge of the module are mainly affected. This leads to inhomogeneous cell cooling resulting in temperature gradients. Existing tension mats, which thermally isolate the cells, can further intensify arising temperature gradients. Possible scenarios are presented in Figure 9.

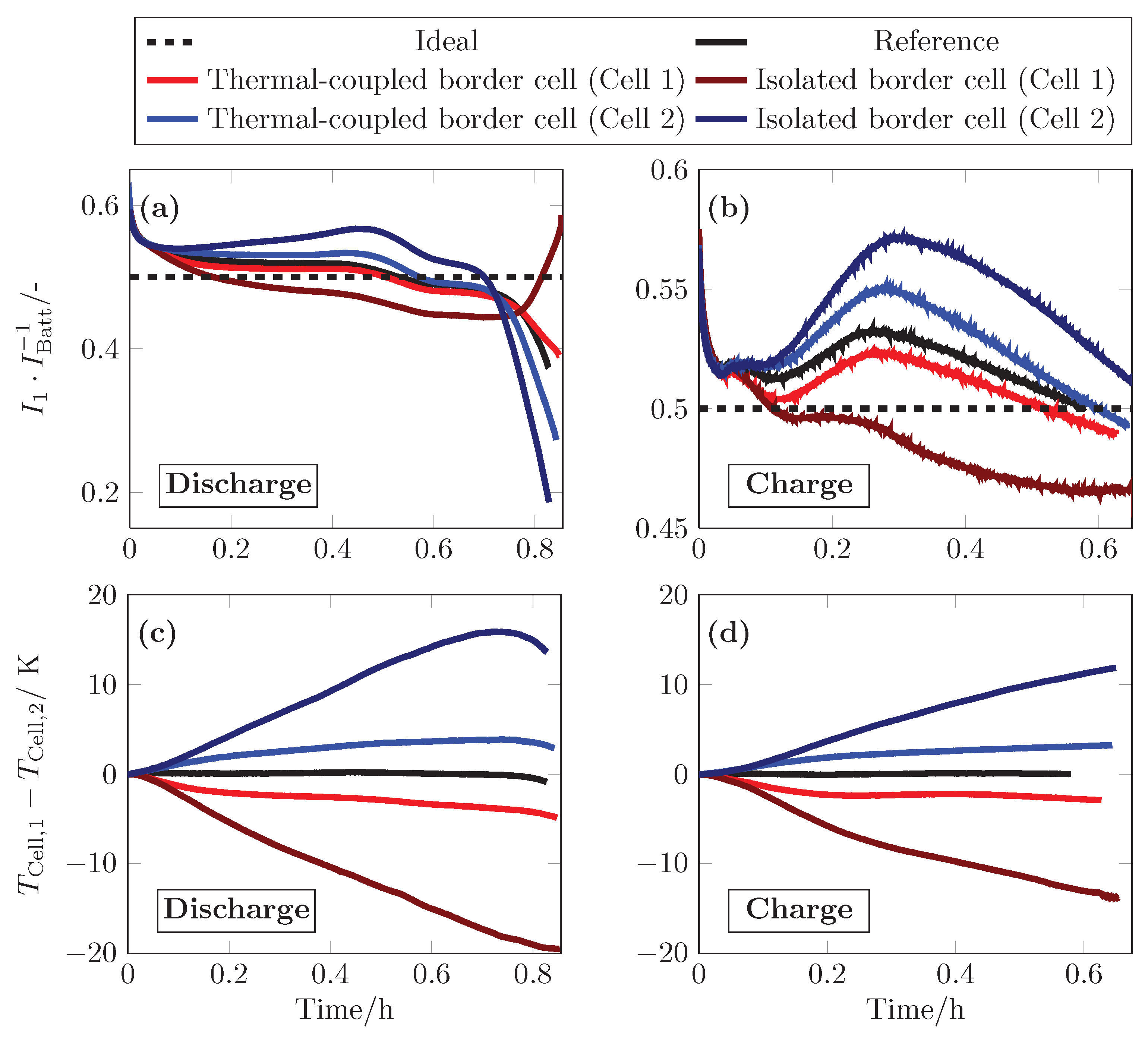
In order to investigate the influence of the cell position and thermal connection of cells, the tension mats were modeled as heat impermeable and the module housing was assumed to be isotherm with a constant temperature at ambient temperature. For each scenario, which considers the effects of the border cell, two measurements were conducted to switch the border position of the two parallel-connected cells. The reference represents conditions at a constant cell temperature, which rather corresponds to most publications.

The current and temperature distribution of these scenarios for two parallel-connected cells are displayed in Figure 10. The cells were fully discharged with $I_{\mathrm{Batt}}=1$C until the cell pack reached the lower voltage limit of $U_{\mathrm{Batt}}=2.8$ V. Thereafter, the cells were further discharged at constant voltage of $U_{\mathrm{Batt}}=2.8$ V until the battery current decreased to $I_{\mathrm{Batt}}=1/20$. After a relaxation of $T_{\mathrm{Break}}=1$ h, the parallel-connected cells were charged with $I_{\mathrm{Batt}}=1$C until the upper voltage limit of $U_{\mathrm{Batt}}=4.2$ V was reached. The ambient temperature and the initial temperature of the aluminum plates were set to $T=20 °$C.

The scenarios show significant differences of the current and temperature distribution of the parallel-connected cells. In the following the scenarios will be separately discussed.

Cell 2—Border Cell

With cell two as border cell, temperature gaps of $\Delta T=3.8 °$C for the thermal-coupled and of $\Delta T=15.8 °$C for the thermal isolated cells raised at discharge. This caused higher current differences and delayed crossing points of the cell currents and resulted in increasing SoC gaps within the parallel cells. For discharging this significantly influenced the current distribution after the crossing point. The OCV bending at low SoC led to a rapid voltage drop of cell one, which resulted in a current peak of cell two. This effect is more distinct with increasing SoC difference, which shows up in an increasing current gap from $I_2=0.73·I_{\mathrm{Batt}}$ to $I_2=0.81·I_{\mathrm{Batt}}$ comparing the thermal-coupled and the isolated scenario. For charging similar effects can be seen. As the current load starts at the point of the highest OCV bending and therefore no distinct SoC gaps have been raised, the rapid current decrease is not seen for charging.

Cell 1—Border Cell

In this scenario the temperature difference showed the same affects on the current distribution, but considering the current of cell one in opposite direction. The temperature difference led to a lower current of cell one and an earlier starting of the crossing point, even compared to the reference measurement. The temperature gap in the thermal-coupled scenario affect more balanced cell currents compared to the reference. This led also to a lower SoC gap, which in turn reduced the current peak of cell two to $I_2=0.61·I_{\mathrm{Batt}}$. The isolation further decreases the current of cell one $I_1$, which caused a higher discharge and charge rate of cell two compared to cell one.

5. Conclusions

In this article a test bench was presented, which enables the individual temperature control of each cell connected in parallel. This allows to reconstruct arising temperature gradients in a battery module due and to investigate their impacts on the dynamic of the current distribution. The aluminum plates adjacent to the cells can be heated and cooled with a rate of about ${\dot{T}}_{\mathrm{Plate}}=250$ mK$·{\mathrm{s}}^{-1}$, which exceeds the maximum heating rate of the cells due to dissipation with ${\dot{T}}_{\mathrm{Cell}}=114$ mK$·{\mathrm{s}}^{-1}$. The influence of the test bench on the current distribution caused by induced additional resistors was determined and minimized. The contact resistance at the cathode tab was reduced from $R_{\mathrm{Tab}+}=81.18$ $\mathsf{\mu }\mathsf{\Omega }$ to $R_{\mathrm{Tab}+}=55.15$ $\mathsf{\mu }\mathsf{\Omega }$ by treating with a non-woven abrasive cloth, cleaning with an oxide-dissolving spray and increasing the pressure from $p=27$ $\mathrm{N}·{\mathrm{mm}}^{-2}$ to $p=93$ $\mathrm{N}·{\mathrm{mm}}^{-2}$. In addition, an increase of the contact resistance during the test period is prevented by air seal of the contact. Without air sealing, the resistance increased from $R_{\mathrm{Tab}+}=57.54$ $\mathsf{\mu }\mathsf{\Omega }$ to $R_{\mathrm{Tab}+}=133.57$ $\mathsf{\mu }\mathsf{\Omega }$ within 51 days at room temperature. The contact resistance at the anode tab was reduced by the same treatments from $R_{\mathrm{Tab}-}=35.59$ $\mathsf{\mu }\mathsf{\Omega }$ to $R_{\mathrm{Tab}-}=28.2$ $\mathsf{\mu }\mathsf{\Omega }$. Due to their nickel coating an air seal was not necessary.

Measurements of two parallel-connected cells with load cable resistances of $R_{\mathrm{Cab}+}=0.3$ m$\mathsf{\Omega }$, $R_{\mathrm{Cab}+}=1.6$ m$\mathsf{\Omega }$ and $R_{\mathrm{Cab}+}=4.35$ m$\mathsf{\Omega }$ showed qualitatively the same dynamic of the current distribution with decreasing current differences within the parallel-connected cells with decreasing cable resistance. An ECM considering the current distribution within the cells as well as the impacts of the induced resistances by the test bench was introduced, parameterized and compared to measurements. The model fitted well to measurements with an RMSD of ${\xi }_{\mathrm{RMSD}}=0.083$ A. Measurements simulating different cell positions in a battery and thermal connections of cells to their neighbor cells were conducted. The consideration of a cell at the module edge showed increasing temperature differences of $\Delta T=3.8 °$C for thermal-coupled cells and of $\Delta T=15.8$ for thermal isolated cells. This temperature difference further increased the initial cell parameter difference and led to higher current and SoC gaps within the parallel-connected cells. The crossing point of the cell current was delayed with increasing $\Delta T$, which in turn caused an increasing current peak of cell two from $I_2=0.73·I_{\mathrm{Batt}}$ to $I_2=0.81·I_{\mathrm{Batt}}$ comparing the thermal-coupled and isolated scenarios.