The Physical Manifestation of Side Reactions in the Electrolyte of Lithium-Ion Batteries and Its Impact on the Terminal Voltage Response
Abstract
:1. Introduction
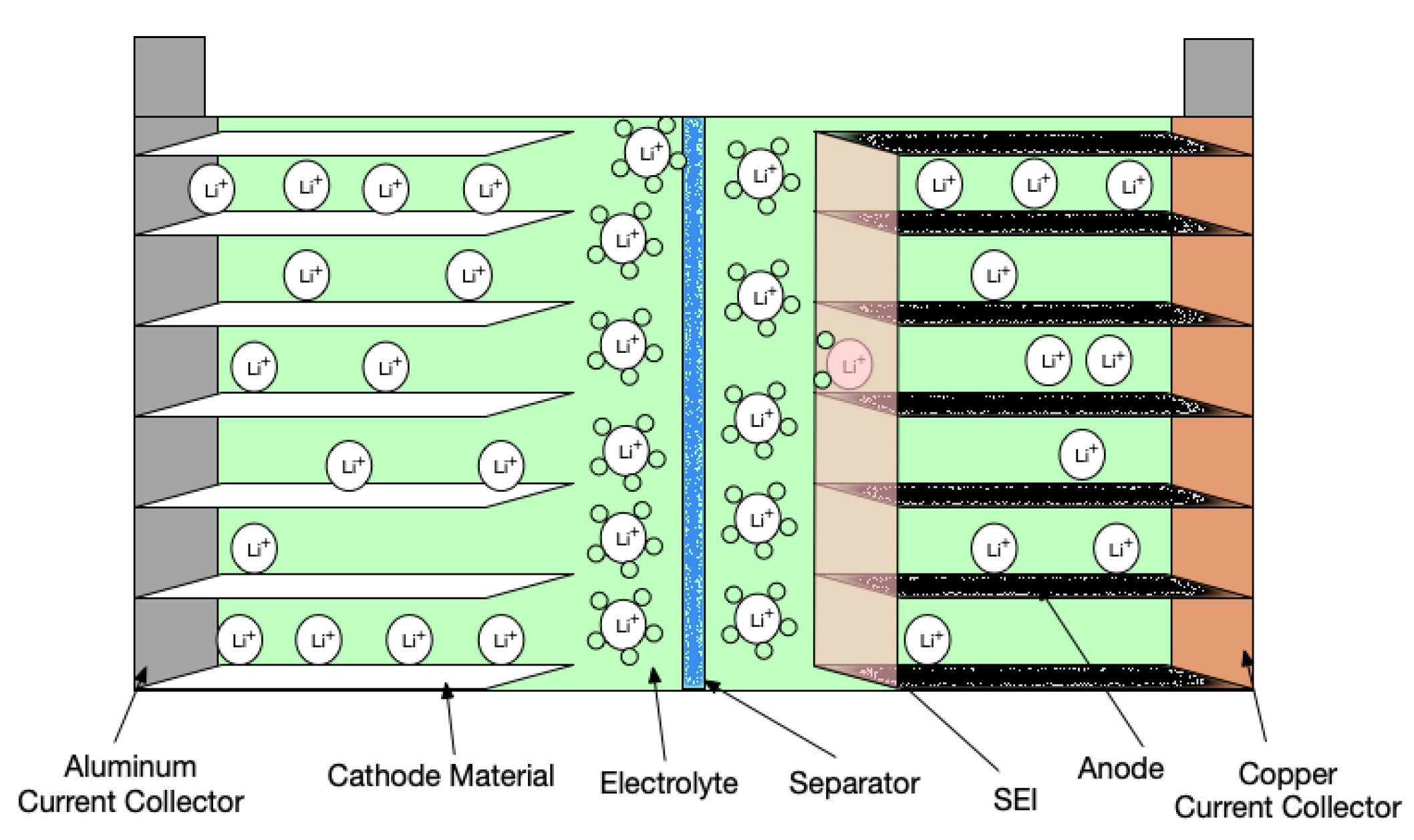
2. Side Reactions
2.1. Electrode–Electrolyte Interface
2.2. Electrode–Current Collector Interface
2.3. Electrolyte
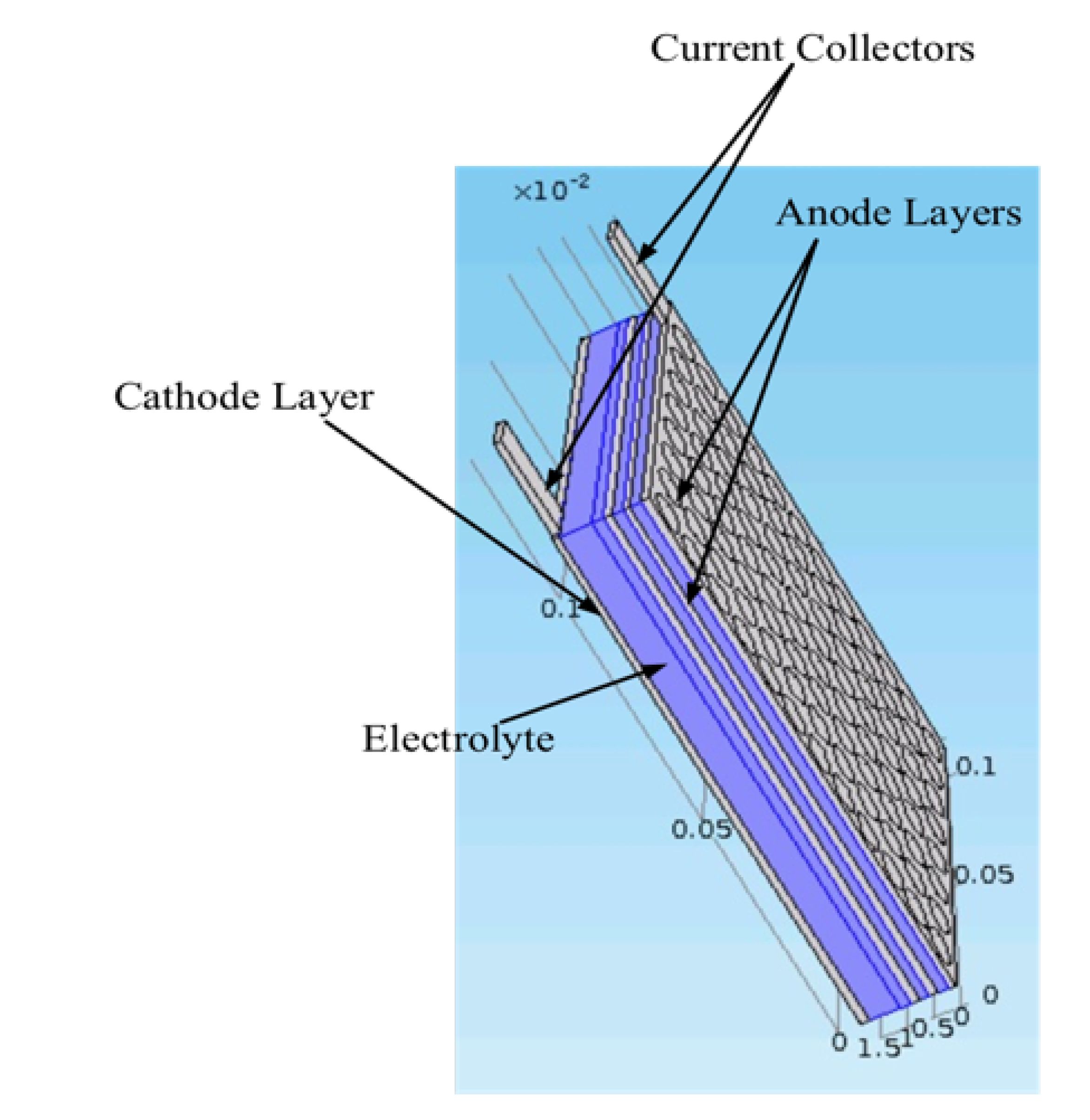
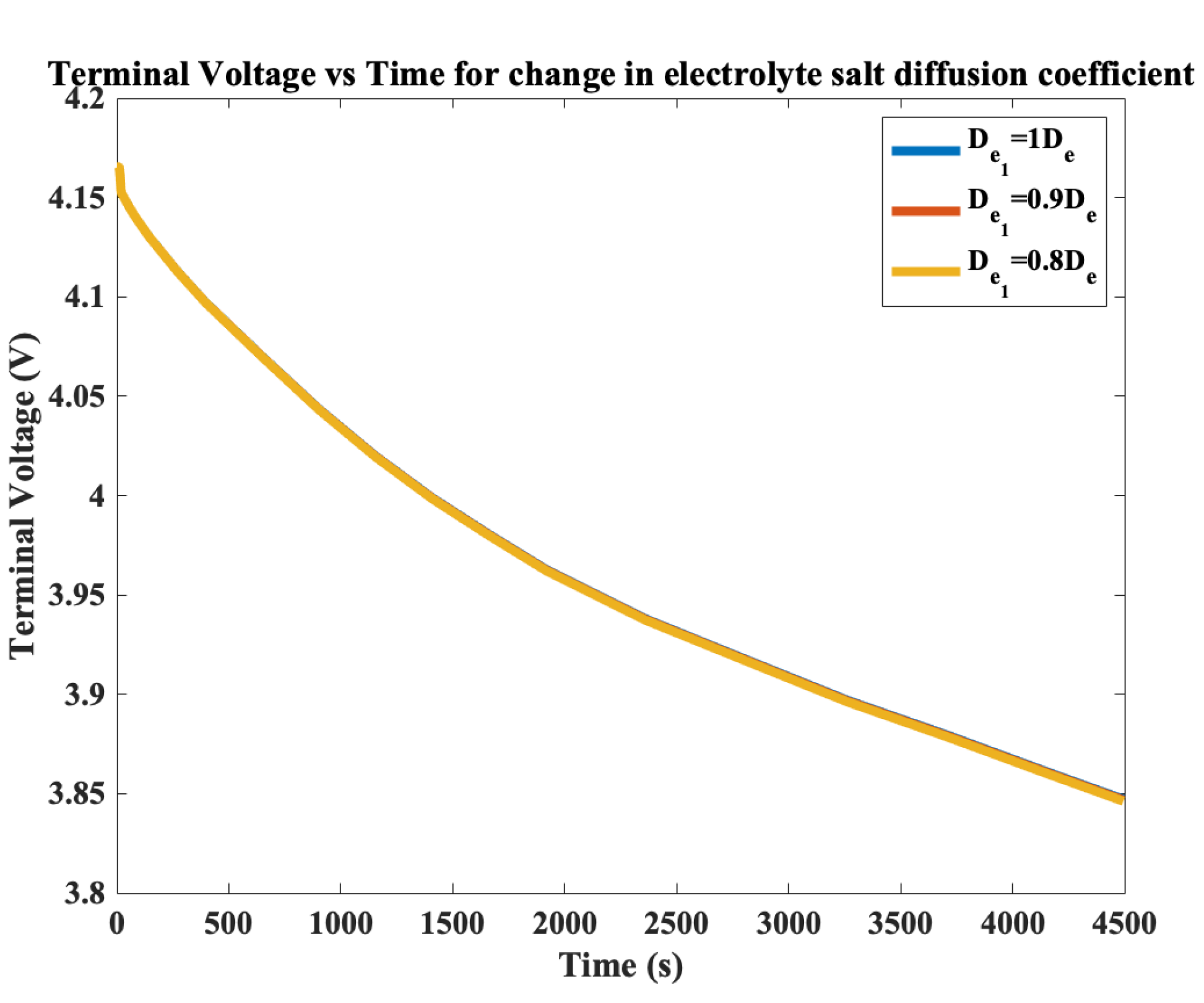
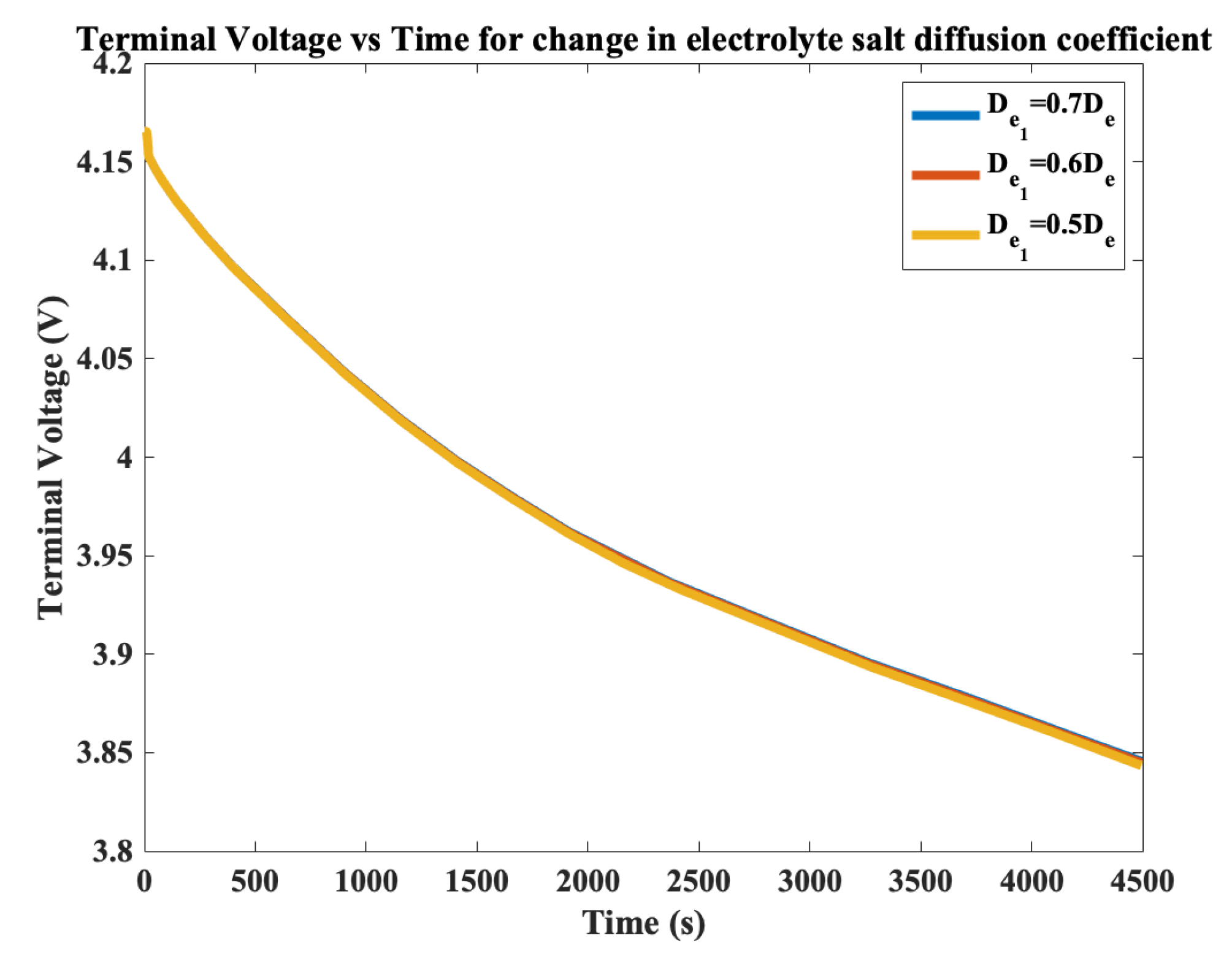
3. Electrolyte Salt Diffusion Coefficient Degradation
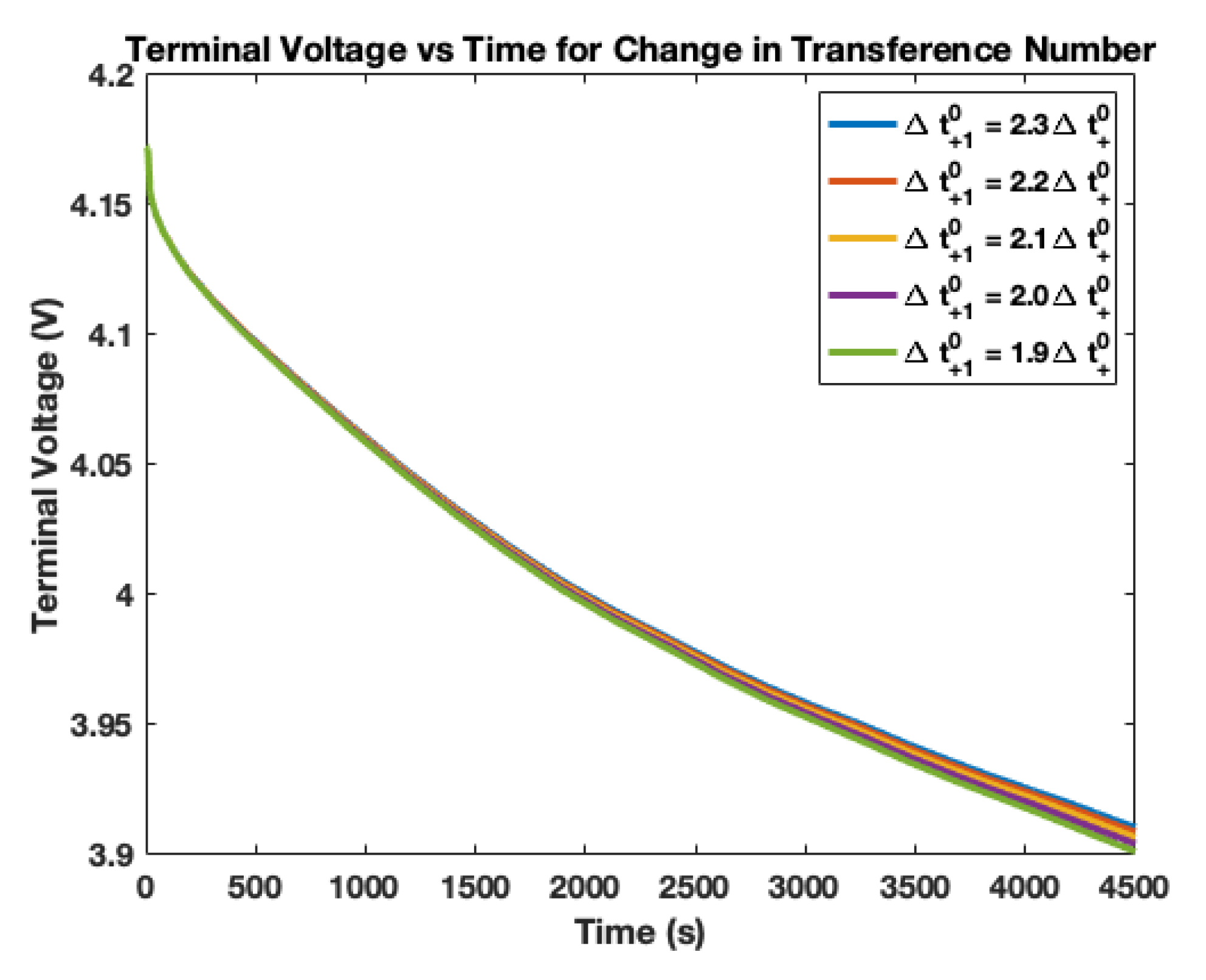
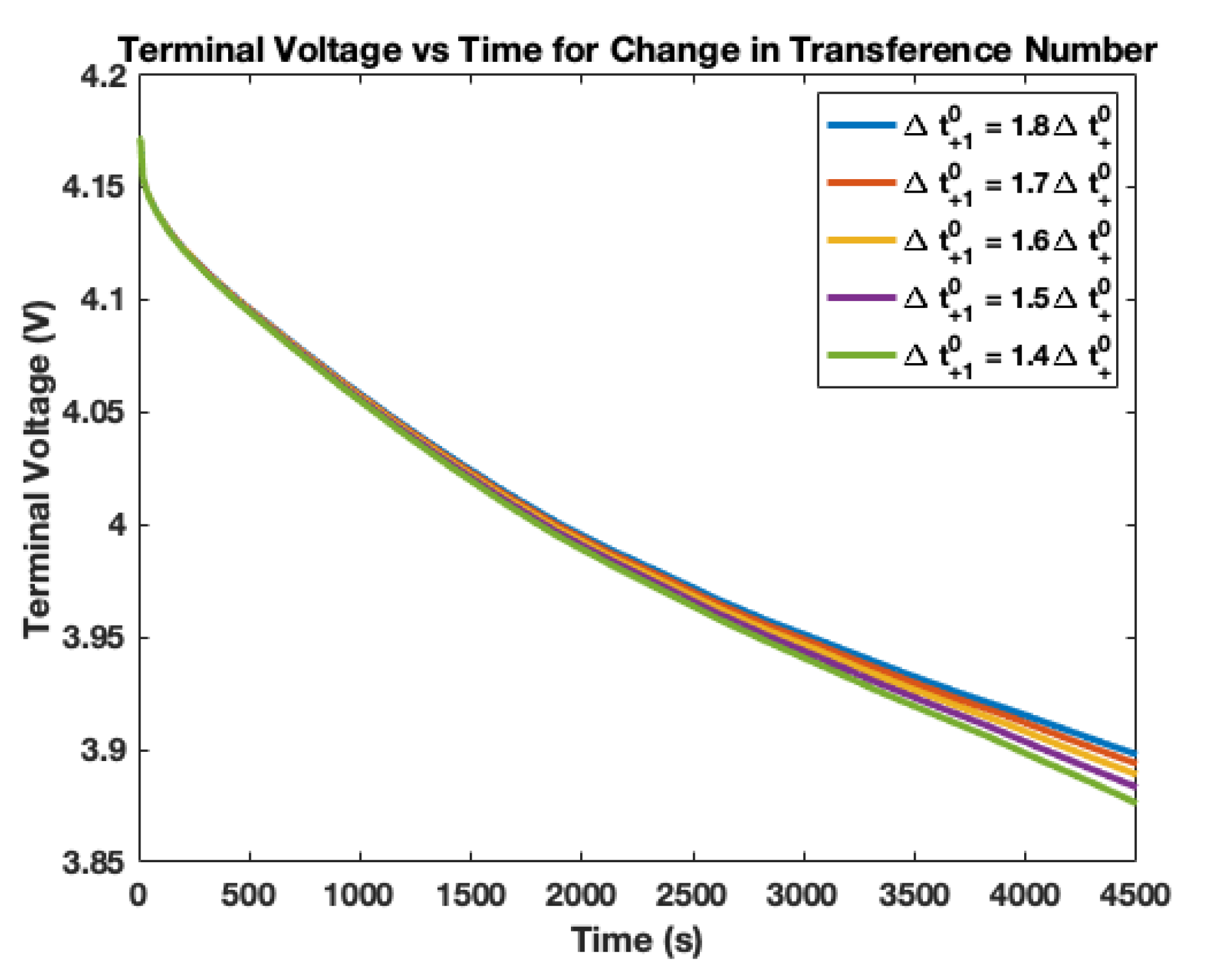
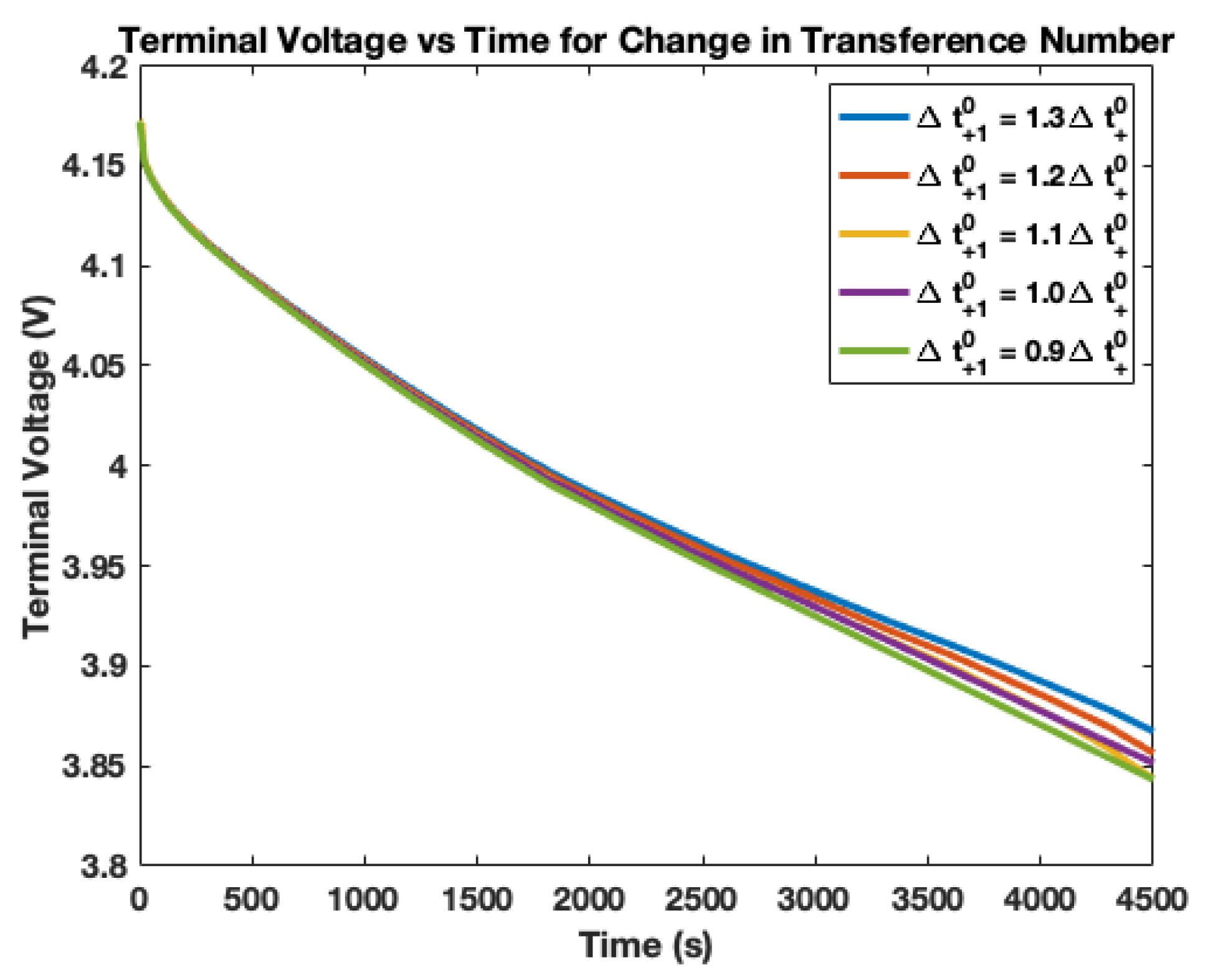
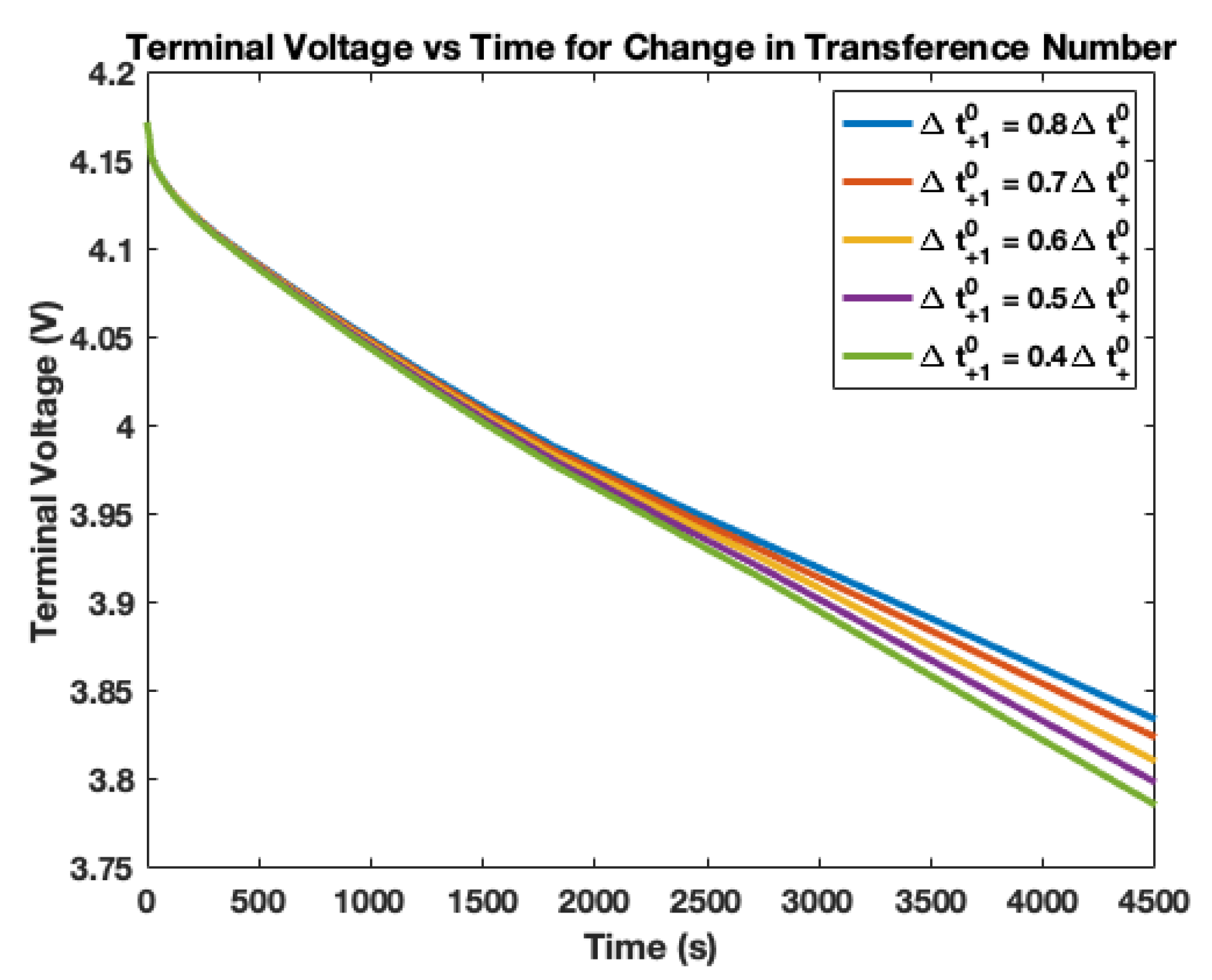
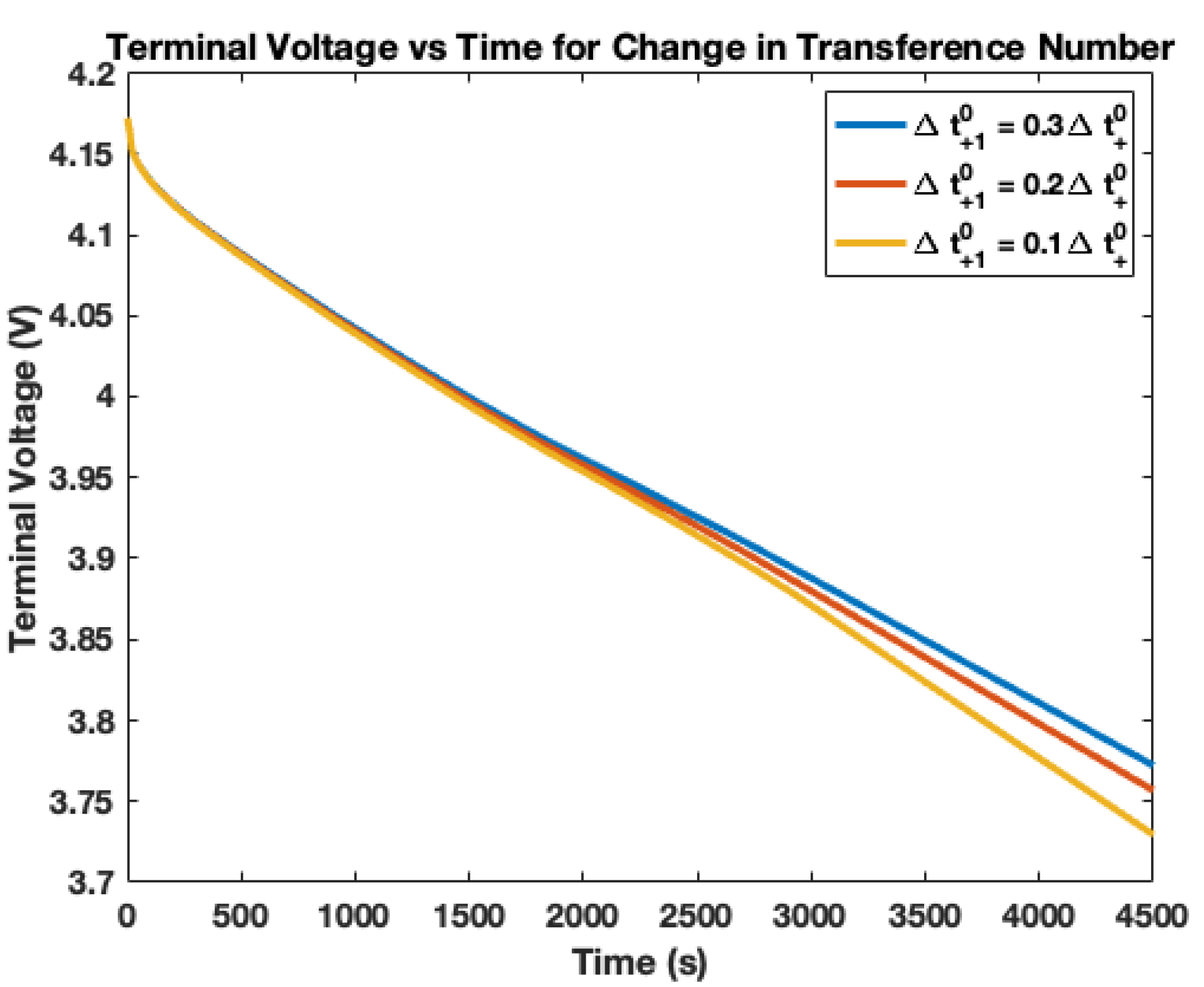
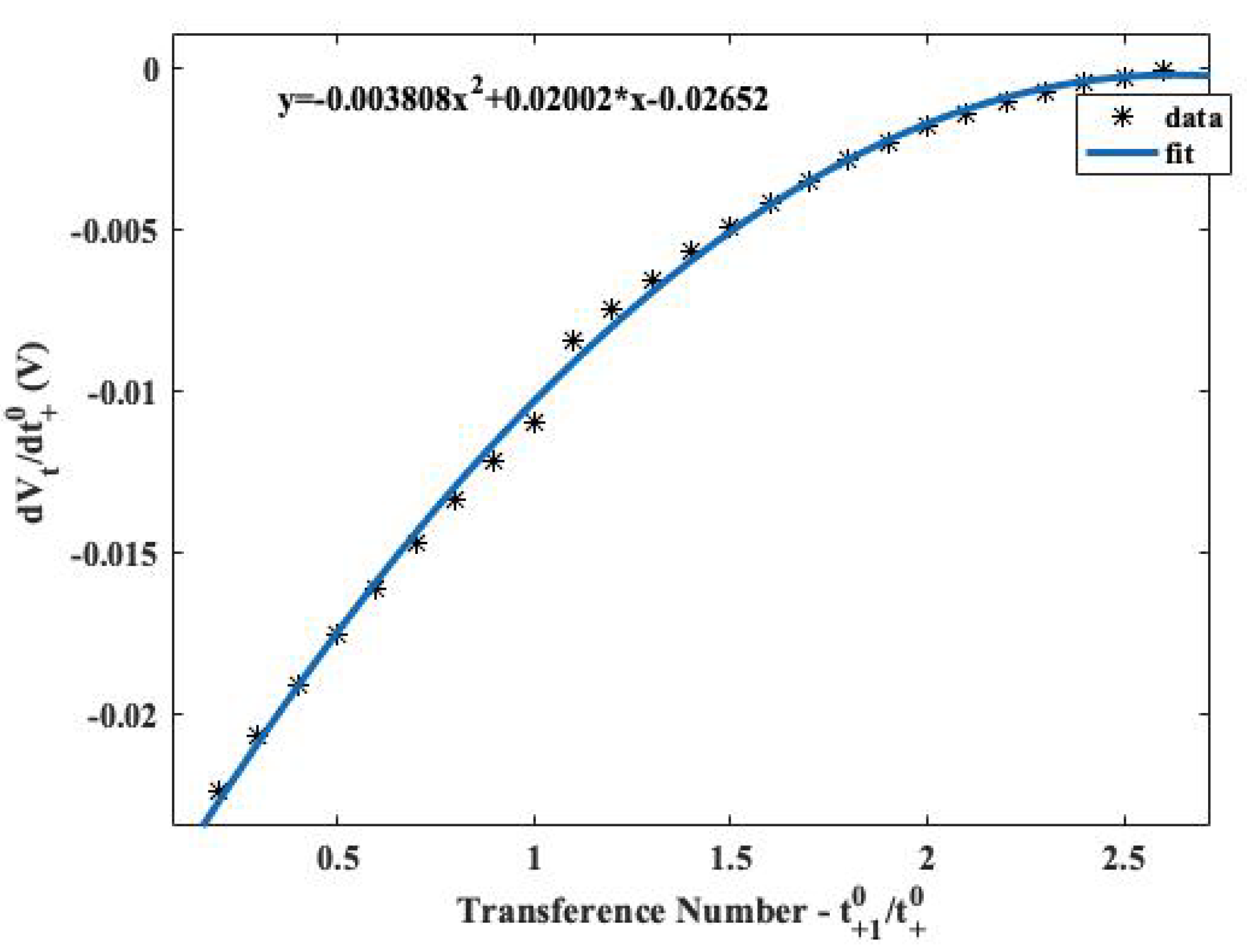
4. Electrolyte Transference Number Degradation
5. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Symbol | Definition | Units |
|---|---|---|
| D | Diffusion Coefficient | m/s |
| Particle Mobility | m/Vs | |
| V | Applied Electromotive Force | V |
| Boltzmann Constant | J/K | |
| T | Temperature | K |
| Electrolyte Phase Volume Fraction | Unitless | |
| Electrolyte Lithium Ion Concentration | mol/m | |
| Effective Electrolyte Diffusion Coefficient | m/s | |
| x | Variable to define position | |
| along the length of the battery | m | |
| t | Time | s |
| Positive Ion (Li) Transference Number | Unitless | |
| F | Faraday’s Constant | C/mol |
| Volumetric Electrochemical Reaction Rate | A/m | |
| at the Surface of the Electrode | ||
| Electrolyte Diffusion Coefficient | m/s | |
| Effective Electrolyte Ionic Conductivity | S/m | |
| Electrolyte Phase Potential | V | |
| Lithium Ion Concentration at the | mol/m | |
| Solid—Electrolyte Interface | ||
| Effective Diffusion Conductivity | S/m | |
| R | Universal Gas Constant | J/mol K |
| Electrolyte Activity Coefficient | Unitless | |
| Solid Phase Potential | V | |
| U | Thermodynamic Equilibrium Potential | V |
| Over Potential | V | |
| Terminal Voltage | V | |
| I | Input Current | A |
| Current Collector—Electrode | ||
| Contact Resistance |
References
- Zheng, X.; Gao, W.; Zhang, X.; He, M.; Lin, X.; Cao, H.; Zhang, Y.; Sun, Z. Spent lithium-ion battery recycling—Reductive ammonia leaching of metals from cathode scrap by sodium sulphite. Waste Manag. 2017, 60, 680–688. [Google Scholar] [CrossRef] [PubMed]
- Gaines, L. Lithium-ion battery recycling processes: Research towards a sustainable course. Sustain. Mater. Technol. 2018, 17, e00068. [Google Scholar] [CrossRef]
- Velázquez-Martínez, O.; Valio, J.; Santasalo-Aarnio, A.; Reuter, M.; Serna-Guerrero, R. A critical review of lithium-ion battery recycling processes from a circular economy perspective. Batteries 2019, 5, 68. [Google Scholar] [CrossRef] [Green Version]
- Doughty, D.; Roth, E.P. A general discussion of Li Ion battery safety. Electrochem. Soc. Interface 2012, 21, 37–44. [Google Scholar] [CrossRef] [Green Version]
- Liu, B.; Jia, Y.; Li, J.; Yin, S.; Yuan, C.; Hu, Z.; Wang, L.; Li, Y.; Xu, J. Safety issues caused by internal short circuits in lithium-ion batteries. J. Mater. Chem. A 2018, 6, 21475–21484. [Google Scholar] [CrossRef]
- Wang, Q.; Jiang, L.; Yu, Y.; Sun, J. Progress of enhancing the safety of lithium ion battery from the electrolyte aspect. Nano Energy 2019, 55, 93–114. [Google Scholar] [CrossRef]
- Rahimi-Eichi, H.; Chow, M. Adaptive parameter identification and State-of-Charge estimation of lithium-ion batteries. In Proceedings of the IECON 2012—38th Annual Conference of the IEEE Industrial Electronics Society, Montreal, QC, Canada, 25–28 October 2012; pp. 4012–4017. [Google Scholar]
- Balagopal, B.; Chow, M.Y. The state of the art approaches to estimate the state of health (SOH) and state of function (SOF) of lithium Ion batteries. In Proceedings of the 2015 IEEE International Conference on Industrial Informatics (INDIN 2015), Cambridge, UK, 22–24 July 2015; pp. 1302–1307. [Google Scholar] [CrossRef]
- Balagopal, B.; Chow, M.Y. Effect of anode conductivity degradation on the Thevenin Circuit Model of lithium ion batteries. In Proceedings of the IECON 2016—42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 24–27 October 2016; pp. 2028–2033. [Google Scholar] [CrossRef]
- Wu, Y. Lithium-ion Batteries: Fundamentals and Applications; CRC Press: Boca Raton, FL, USA, 2015; p. 1. [Google Scholar]
- Jow, T.R.; Delp, S.A.; Allen, J.L.; Jones, J.P.; Smart, M.C. Factors Limiting Li + Charge Transfer Kinetics in Li-Ion Batteries. J. Electrochem. Soc. 2018, 165, A361–A367. [Google Scholar] [CrossRef]
- Logan, E.R.; Tonita, E.M.; Beaulieu, L.Y.; Ma, X.; Li, J.; Dahn, J.R.; Gering, K.L. A Study of the Physical Properties of Li-Ion Battery Electrolytes Containing Esters. J. Electrochem. Soc. 2018, 165, A21–A30. [Google Scholar] [CrossRef]
- Balagopal, B.; Huang, C.S.; Chow, M.Y. Effect of Calendar Aging on Li Ion Battery Degradation and SOH. In Proceedings of the IECON 2017—43rd Annual Conference of the IEEE, Beijing, China, 29 October–1 November 2017; pp. 7647–7652. [Google Scholar]
- Guan, P.; Liu, L. Lithium-ion diffusion in solid electrolyte interface (SEI) predicted by phase field model. Mater. Res. Soc. Symp. Proc. 2015, 1753, 31–37. [Google Scholar] [CrossRef]
- Lee, J.T.; Nitta, N.; Benson, J.; Magasinski, A.; Fuller, T.F.; Yushin, G. Comparative study of the solid electrolyte interphase on graphite in full Li-ion battery cells using X-ray photoelectron spectroscopy, secondary ion mass spectrometry, and electron microscopy. Carbon 2013, 52, 388–397. [Google Scholar] [CrossRef]
- Laresgoiti, I.; Kabitz, S.; Ecker, M.; Sauer, D.U. Modeling mechanical degradation in lithium ion batteries during cycling: Solid electrolyte interphase fracture. J. Power Sources 2015, 300, 112–122. [Google Scholar] [CrossRef]
- Gao, Y.; Jiang, J.; Zhang, C.; Zhang, W.; Ma, Z.; Jiang, Y. Lithium-ion battery aging mechanisms and life model under different charging stresses. J. Power Sources 2017, 356, 103–114. [Google Scholar] [CrossRef]
- Cannarella, J.; Arnold, C.B. Stress evolution and capacity fade in constrained lithium-ion pouch cells. J. Power Sources 2014, 245, 745–751. [Google Scholar] [CrossRef]
- Cannarella, J.; Arnold, C.B. State of health and charge measurements in lithium-ion batteries using mechanical stress. J. Power Sources 2014, 269, 7–14. [Google Scholar] [CrossRef]
- Pinson, M.B.; Bazant, M.Z. Theory of SEI Formation in Rechargeable Batteries: Capacity Fade, Accelerated Aging and Lifetime Prediction. J. Electrochem. Soc. 2012, 160, A243–A250. [Google Scholar] [CrossRef]
- Lawder, M.T.; Northrop, P.W.C.; Subramanian, V.R. Model-Based SEI Layer Growth and Capacity Fade Analysis for EV and PHEV Batteries and Drive Cycles. J. Electrochem. Soc. 2014, 161, A2099–A2108. [Google Scholar] [CrossRef] [Green Version]
- Williard, N.; He, W.; Osterman, M.; Pecht, M. Reliability and failure analysis of Lithium Ion batteries for electronic systems. In Proceedings of the 2012 13th International Conference on Electronic Packaging Technology & High Density Packaging, Guilin, China, 13–16 August 2012; pp. 1051–1055. [Google Scholar] [CrossRef]
- Valo̸en, L.O.; Reimers, J.N. Transport Properties of LiPF6-Based Li-Ion Battery Electrolytes. J. Electrochem. Soc. 2005, 152, A882. [Google Scholar] [CrossRef]
- Balagopal, B.; Huang, C.S.; Chow, M.Y. Effect of Calendar Ageing on SEI growth and its Impact on Electrical Circuit Model Parameters in Lithium Ion Batteries. In Proceedings of the IEEE International Conference on Industrial Electronics for Sustainable Energy Systems, Hamilton, New Zealand, 31 January–2 February 2018. [Google Scholar]
- Hayamizu, K. Direct relations between ion diffusion constants and ionic conductivity for lithium electrolyte solutions. Electrochim. Acta 2017, 254, 101–111. [Google Scholar] [CrossRef]
- Chintapalli, M.; Timachova, K.; Olson, K.R.; Mecham, S.J.; Devaux, D.; Desimone, J.M.; Balsara, N.P. Relationship between Conductivity, Ion Diffusion, and Transference Number in Perfluoropolyether Electrolytes. Macromolecules 2016, 49, 3508–3515. [Google Scholar] [CrossRef] [Green Version]
- Diederichsen, K.M.; McShane, E.J.; McCloskey, B.D. Promising Routes to a High Li+ Transference Number Electrolyte for Lithium Ion Batteries. ACS Energy Lett. 2017, 2, 2563–2575. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Balagopal, B.; Chow, M.-Y. The Physical Manifestation of Side Reactions in the Electrolyte of Lithium-Ion Batteries and Its Impact on the Terminal Voltage Response. Batteries 2020, 6, 53. https://doi.org/10.3390/batteries6040053
Balagopal B, Chow M-Y. The Physical Manifestation of Side Reactions in the Electrolyte of Lithium-Ion Batteries and Its Impact on the Terminal Voltage Response. Batteries. 2020; 6(4):53. https://doi.org/10.3390/batteries6040053
Chicago/Turabian StyleBalagopal, Bharat, and Mo-Yuen Chow. 2020. "The Physical Manifestation of Side Reactions in the Electrolyte of Lithium-Ion Batteries and Its Impact on the Terminal Voltage Response" Batteries 6, no. 4: 53. https://doi.org/10.3390/batteries6040053
APA StyleBalagopal, B., & Chow, M. -Y. (2020). The Physical Manifestation of Side Reactions in the Electrolyte of Lithium-Ion Batteries and Its Impact on the Terminal Voltage Response. Batteries, 6(4), 53. https://doi.org/10.3390/batteries6040053






