Analysis of Electrochemical Impedance Spectroscopy on Zinc-Air Batteries Using the Distribution of Relaxation Times
Abstract
:1. Introduction
2. Materials and Methods
2.1. Electrochemical Impedance Spectroscopy
2.2. Distribution of Relaxation Times
2.3. Determination of the Regularization Parameter
2.4. Preparation of DRT for Electrochemical Analysis
3. Results
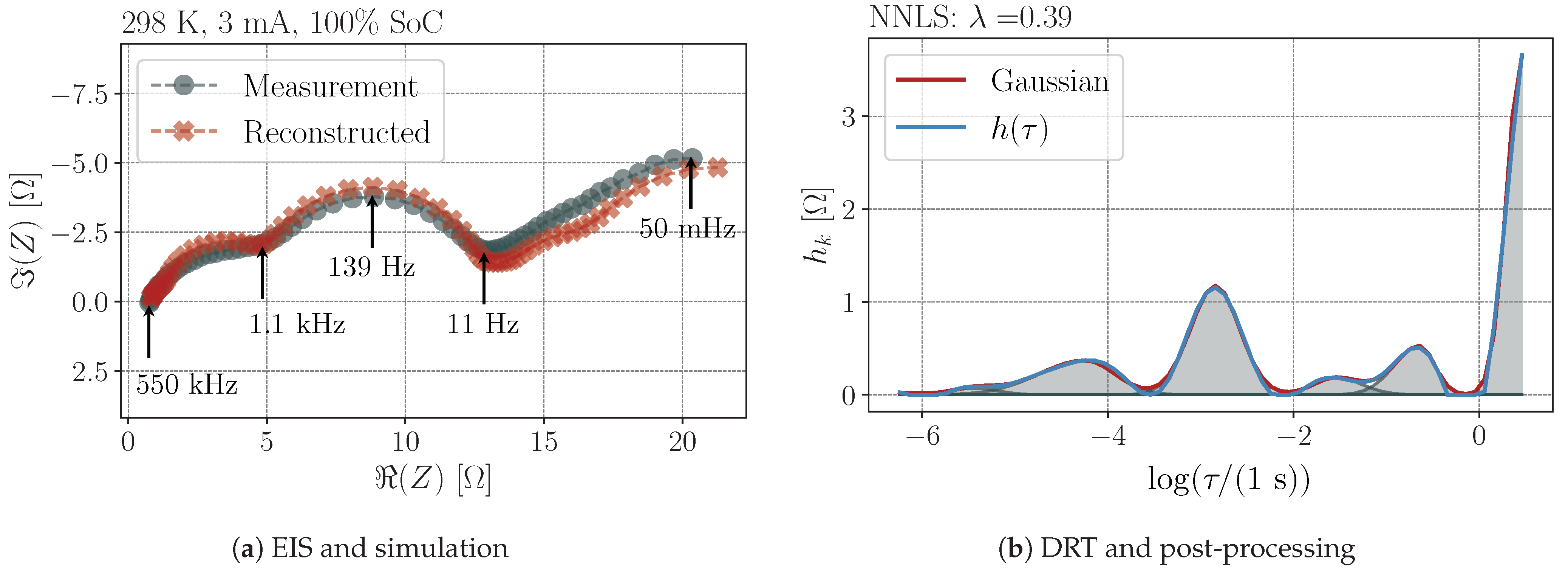
3.1. Regularization
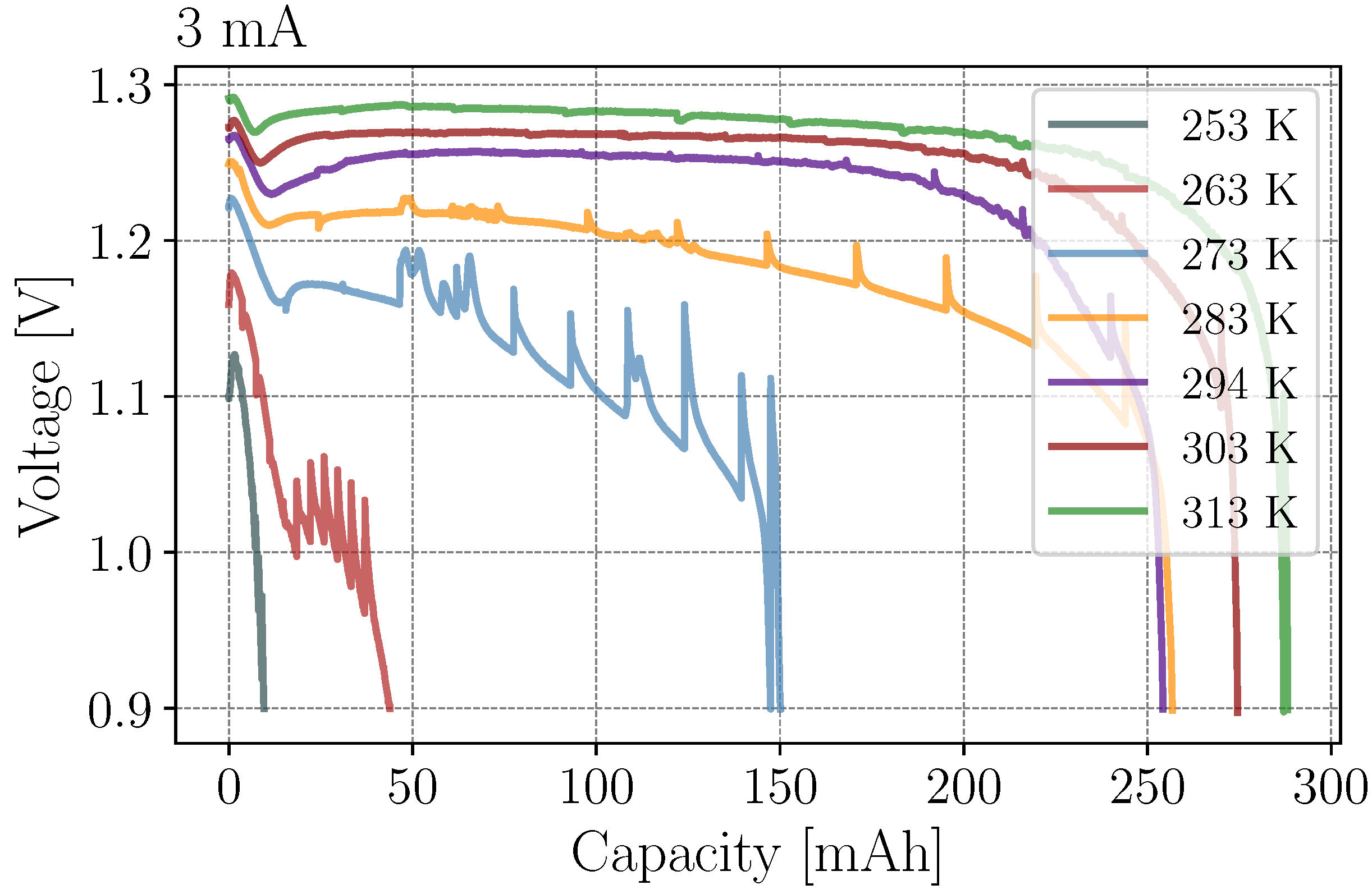
3.2. Temperatures and Currents
- I
- As shown in Figure 1, the initial operating phase could be subdivided into three specific processes. The process I.1 was very fast and has slightly recovered the voltage in respect of the initial voltage drop. This was followed by process I.2, which resulted in a linear decrease of the voltage until a minimum was reached. In process I.3 the voltage gradually recovered and converged to a constant value. All three processes occurred independently of the current, with process I.1 and I.2 also appearing to be time independent.
- II
- The corresponding capacity in the nearly constant voltage operating phase II was depended on the the applied discharge currents, i.e., the greater the discharge current, the smaller the duration.
- III
- After the constant operating phase for currents greater than 4 mA, an additional voltage drop was observable. Especially between 4 mA and 8 mA this phase is clearly detectable.
- IV
- In the final operating phase, the voltage decreased rapidly until it reached the cut-off voltage. As the current increased, the boundary between phase III and IV became unclear.
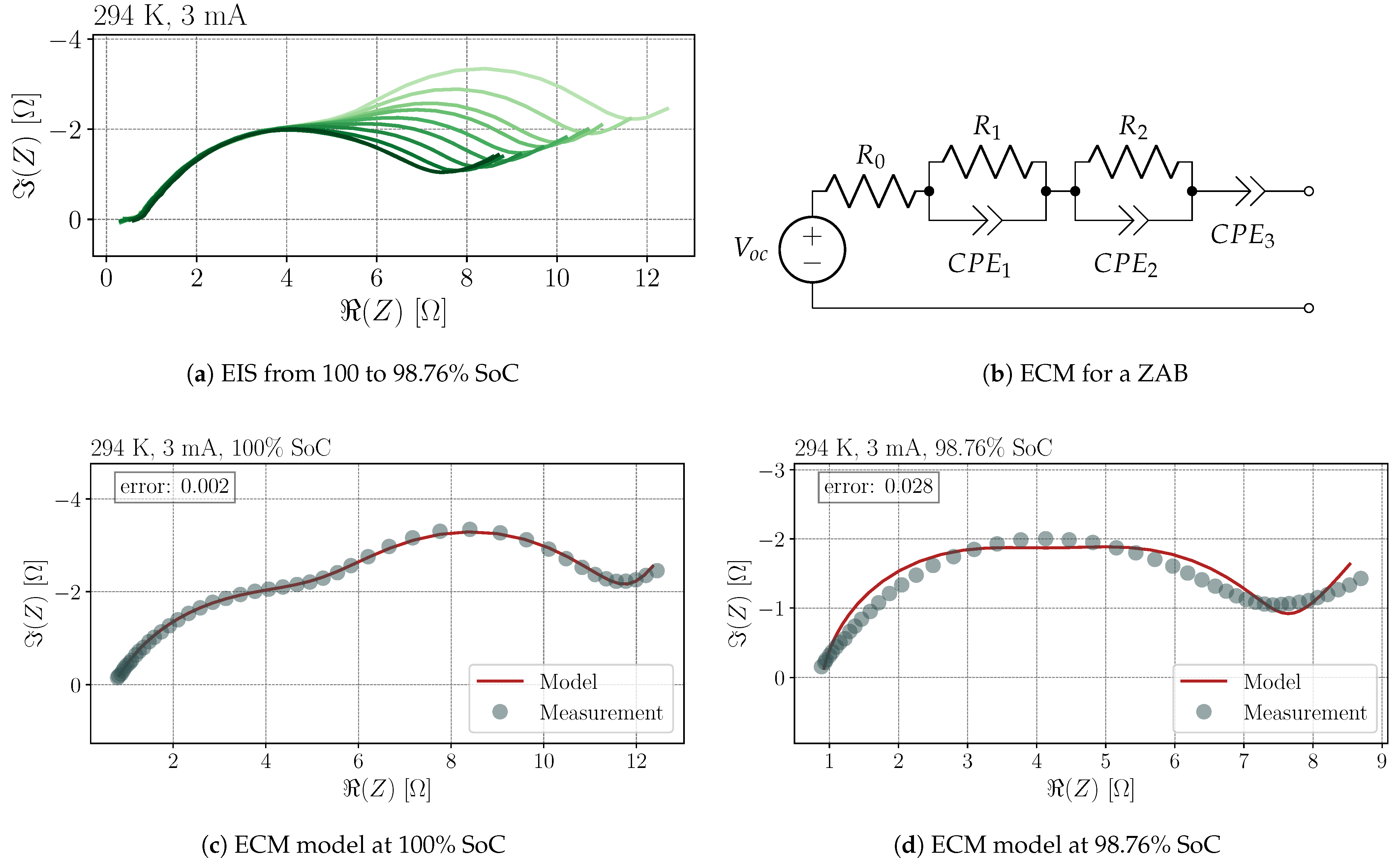
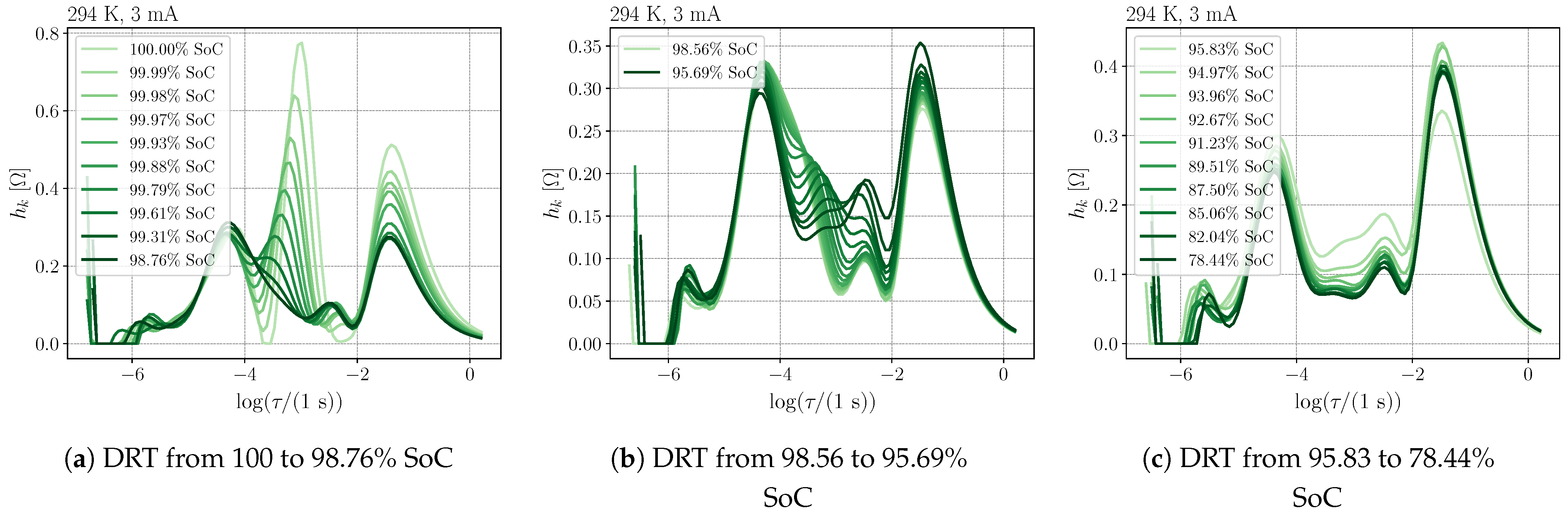
3.3. Process Analysis
4. Discussion
4.1. Capacity
4.2. Operating Phases
4.2.1. Operating Phase I
4.2.2. Operating Phase II
4.2.3. Operating Phase III and IV
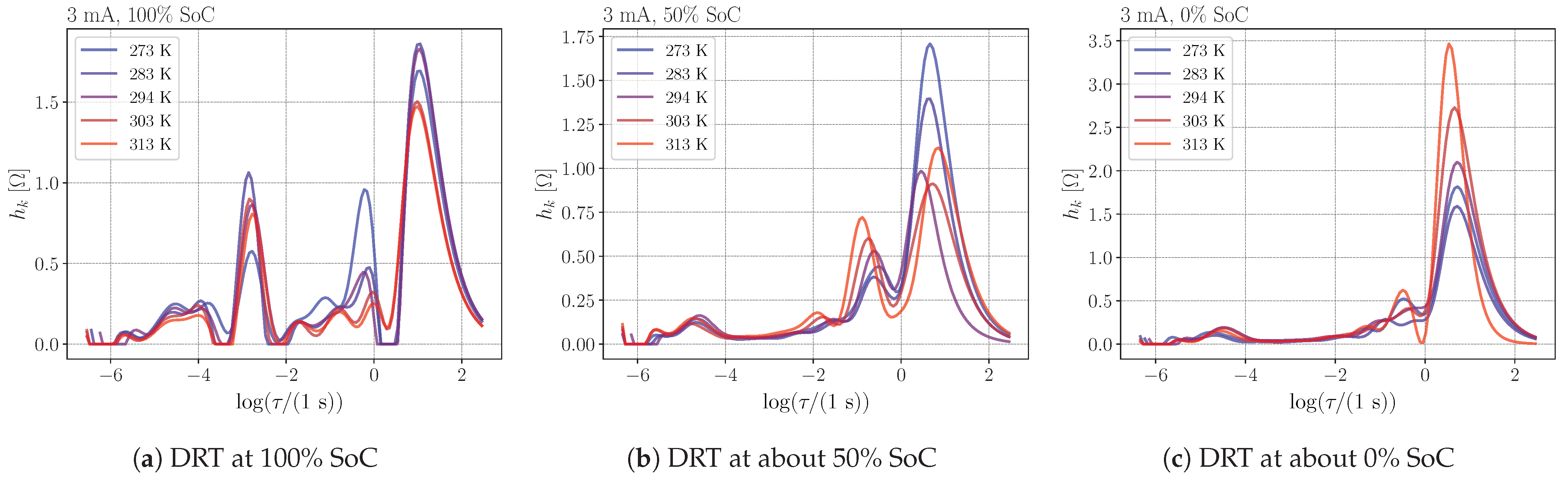
4.3. Temperature
4.4. Shortcomings
- The regularization parameter directly influences the number and heights of the peaks within the DRT (see Figure A3). Each EIS measurement may have its own optimal regularization parameter, so that an estimation of the parameter must be made over all data (cf. Figure 5). It is not guaranteed that there will be an ideal parameter for the entire data set.
- The intersection of the EIS measurement with the real axis is not always given at high frequencies and no exists. The intersection point for the DRT must consequently be estimated for the initial condition, which leads to an additional peak and a minimization of the other peaks according to Equation (12). This shortcoming can be avoided by pre-processing the EIS measurement.
- The extended time constant range and the extended boundary at low frequencies improve the physical interpretation of the DRT but manipulate the height of the peaks.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ECM | Equivalent Circuit Model |
| SoC | State-of-Charge |
| DRT | Distribution of Relaxation Times |
| EIS | Electrochemical Impedance Spectroscopy |
| NNLS | Non-Negative Least Squares |
| CNLS | Complex Nonlinear Least Squares |
| TNC | Truncated Newton Conjugate-Gradient |
| L-BFGS-B | Limited-Memory-Broyden Fletcher Goldfarb Shanno-Boundary |
| RC | Resistor-Capacitor |
| MSE | Mean Squared Error |
| CPE | Constant Phase Element |
Appendix A. Theory


Appendix B. Results

| SoC | in | in | in | in | in | in | |||
|---|---|---|---|---|---|---|---|---|---|
| 100% | 0.80 | 5.36 | 5.37 | 9.4 × | 1.8 × | 1.6 × | 0.77 | 1.03 | 0.80 |
| 98.76% | 0.89 | 3.22 | 3.22 | 2.0 × | 1.8 × | 4.6 × | 0.90 | 0.88 | 0.58 |
References
- Li, M.; Lu, J.; Chen, Z.; Amine, K. 30 Years of Lithium-Ion Batteries. Adv. Mater. 2018, 30, 1800561. [Google Scholar] [CrossRef] [Green Version]
- Caramia, V.; Bozzini, B. Materials science aspects of zinc-air batteries: A review. Mater. Renew. Sustain. Energy 2014, 3, 28. [Google Scholar] [CrossRef] [Green Version]
- Yi, J.; Liang, P.; Liu, X.; Wu, K.; Liu, Y.; Wang, Y.; Xia, Y.; Zhang, J. Challenges, mitigation strategies and perspectives in development of zinc-electrode materials and fabrication for rechargeable zinc–air batteries. Energy Environ. Sci. 2018, 11, 3075–3095. [Google Scholar] [CrossRef] [Green Version]
- Pan, J.; Xu, Y.Y.; Yang, H.; Dong, Z.; Liu, H.; Xia, B.Y. Advanced Architectures and Relatives of Air Electrodes in Zn–Air Batteries. Adv. Sci. 2018, 5, 1700691. [Google Scholar] [CrossRef]
- Zhang, J.; Zhou, Q.; Tang, Y.; Zhang, L.; Li, Y. Zinc-air batteries: Are they ready for prime time? Chem. Sci. 2019, 10, 8924–8929. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fu, J.; Cano, Z.P.; Park, M.G.; Yu, A.; Fowler, M.; Chen, Z. Electrically Rechargeable Zinc–Air Batteries: Progress, Challenges, and Perspectives. Adv. Mater. 2017, 29, 1604685. [Google Scholar] [CrossRef] [PubMed]
- Pei, P.; Wang, K.; Ma, Z. Technologies for extending zinc-air battery’s cyclelife: A review. Appl. Energy 2014, 128, 315–324. [Google Scholar] [CrossRef]
- Gu, P.; Zheng, M.; Zhao, Q.; Xiao, X.; Xue, H.; Pang, H. Rechargeable zinc-air batteries: A promising way to green energy. J. Mater. Chem. A 2017, 5, 7651–7666. [Google Scholar] [CrossRef]
- Shin, J.; Lee, J.; Park, Y.; Choi, J.W. Aqueous zinc ion batteries: Focus on zinc metal anodes. Chem. Sci. 2020, 11, 2028–2044. [Google Scholar] [CrossRef] [Green Version]
- Stock, D.; Dongmo, S.; Damtew, D.; Stumpp, M.; Konovalova, A.; Henkensmeier, D.; Schlettwein, D.; Schröder, D. Design Strategy for Zinc Anodes with Enhanced Utilization and Retention: Electrodeposited Zinc Oxide on Carbon Mesh Protected by Ionomeric Layers. ACS Appl. Energy Mater. 2018, 1, 5579–5588. [Google Scholar] [CrossRef]
- Riede, J.C.; Turek, T.; Kunz, U. Critical zinc ion concentration on the electrode surface determines dendritic zinc growth during charging a zinc air battery. Electrochim. Acta 2018, 269, 217–224. [Google Scholar] [CrossRef]
- Mainar, A.R.; Colmenares, L.C.; Grande, H.J.J.; Blázquez, J.A. Enhancing the cycle life of a Zinc–air battery by means of electrolyte additives and zinc surface protection. Batteries 2018, 4, 46. [Google Scholar] [CrossRef] [Green Version]
- Mainar, A.R.; Colmenares, L.C.; Blázquez, J.A.; Urdampilleta, I. A brief overview of secondary zinc anode development: The key of improving zinc-based energy storage systems. Int. J. Energy Res. 2018, 42, 903–918. [Google Scholar] [CrossRef]
- Stock, D.; Dongmo, S.; Walther, F.; Sann, J.; Janek, J.; Schröder, D. Homogeneous Coating with an Anion-Exchange Ionomer Improves the Cycling Stability of Secondary Batteries with Zinc Anodes. ACS Appl. Mater. Interfaces 2018, 10, 8640–8648. [Google Scholar] [CrossRef]
- Bockelmann, M.; Becker, M.; Reining, L.; Kunz, U.; Turek, T. Passivation of Zinc Anodes in Alkaline Electrolyte: Part I. Determination of the Starting Point of Passive Film Formation. J. Electrochem. Soc. 2018, 165, A3048–A3055. [Google Scholar] [CrossRef]
- Bockelmann, M.; Becker, M.; Reining, L.; Kunz, U.; Turek, T. Passivation of Zinc Anodes in Alkaline Electrolyte: Part II. Influence of Operation Parameters. J. Electrochem. Soc. 2019, 166, A1132–A1139. [Google Scholar] [CrossRef]
- Cai, M.; Park, S.M. Spectroelectrochemical Studies on Dissolution and Passivation of Zinc Electrodes in Alkaline Solutions. J. Electrochem. Soc. 1996, 143, 2125. [Google Scholar] [CrossRef]
- Kim, H.I.; Kim, E.J.; Kim, S.J.; Shin, H.C. Influence of ZnO precipitation on the cycling stability of rechargeable Zn–air batteries. J. Appl. Electrochem. 2015, 45, 335–342. [Google Scholar] [CrossRef]
- Franke-Lang, R.; Arlt, T.; Manke, I.; Kowal, J. X-ray tomography as a powerful method for zinc-air battery research. J. Power Sources 2017, 370, 45–51. [Google Scholar] [CrossRef]
- Wang, H.F.; Xu, Q. Materials Design for Rechargeable Metal-Air Batteries. Matter 2019, 1, 565–595. [Google Scholar] [CrossRef]
- Macdonald, J.R. Impedance spectroscopy. Ann. Biomed. Eng. 1992, 20, 289–305. [Google Scholar] [CrossRef] [PubMed]
- Fu, J.; Zhang, J.; Song, X.; Zarrin, H.; Tian, X.; Qiao, J.; Rasen, L.; Li, K.; Chen, Z. A flexible solid-state electrolyte for wide-scale integration of rechargeable zinc-air batteries. Energy Environ. Sci. 2016, 9, 663–670. [Google Scholar] [CrossRef]
- Sanal, E.; Dost, P.; Sourkounis, C. Electrotechnical investigation of zinc-air cells for determination of cell-parameters for a battery management system. In Proceedings of the 2015 International Conference on Renewable Energy Research and Applications (ICRERA), Palermo, Italy, 22–25 November 2015; pp. 1157–1161. [Google Scholar] [CrossRef]
- Larsson, F.; Rytinki, A.; Ahmed, I.; Albinsson, I.; Mellander, B.E. Overcurrent abuse of primary prismatic zinc–air battery cells studying air supply effects on performance and safety shut-down. Batteries 2017, 3, 1. [Google Scholar] [CrossRef] [Green Version]
- Meng, F.; Zhong, H.; Bao, D.; Yan, J.; Zhang, X. In Situ Coupling of Strung Co 4 N and Intertwined N–C Fibers toward Free-Standing Bifunctional Cathode for Robust, Efficient, and Flexible Zn–Air Batteries. J. Am. Chem. Soc. 2016, 138, 10226–10231. [Google Scholar] [CrossRef] [PubMed]
- Li, G.; Zhang, K.; Mezaal, M.A.; Zhang, R.; Lei, L. Effect of electrolyte concentration and depth of discharge for zinc-air fuel cell. Int. J. Electrochem. Sci. 2015, 10, 6672–6683. [Google Scholar]
- Chotipanich, J.; Arpornwichanop, A.; Yonezawa, T.; Kheawhom, S. Electronic and ionic conductivities enhancement of zinc anode for flexible printed zinc-air battery. Eng. J. 2018, 22, 47–57. [Google Scholar] [CrossRef]
- Kubannek, F.; Turek, T.; Krewer, U. Modeling Oxygen Gas Diffusion Electrodes for Various Technical Applications. Chemie-Ingenieur-Technik 2019, 91, 720–733. [Google Scholar] [CrossRef] [Green Version]
- Tran, T.N.T.; Chung, H.J.; Ivey, D.G. A study of alkaline gel polymer electrolytes for rechargeable zinc–air batteries. Electrochim. Acta 2019, 327, 135021. [Google Scholar] [CrossRef]
- Barsoukov, E.; Macdonald, J.R. (Eds.) Impedance Spectroscopy, 3rd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2018; pp. 1–528. [Google Scholar] [CrossRef]
- Vielstich, W.; Hamann, C.H. Elektrochemie; Wiley-VCH: Weinheim, Germany, 2005; p. 662. [Google Scholar] [CrossRef]
- Weiß, A.; Schindler, S.; Galbiati, S.; Danzer, M.A.; Zeis, R. Distribution of Relaxation Times Analysis of High-Temperature PEM Fuel Cell Impedance Spectra. Electrochim. Acta 2017, 230, 391–398. [Google Scholar] [CrossRef]
- Ivers-Tiffée, E.; Weber, A. Evaluation of electrochemical impedance spectra by the distribution of relaxation times. J. Ceram. Soc. Jpn. 2017, 125, 193–201. [Google Scholar] [CrossRef] [Green Version]
- Schichlein, H.; Müller, A.C.; Voigts, M.; Krügel, A.; Ivers-Tiffée, E. Deconvolution of electrochemical impedance spectra for the identification of electrode reaction mechanisms in solid oxide fuel cells. J. Appl. Electrochem. 2002, 32, 875–882. [Google Scholar] [CrossRef]
- Hahn, M.; Schindler, S.; Triebs, L.C.; Danzer, M.A. Optimized process parameters for a reproducible distribution of relaxation times analysis of electrochemical systems. Batteries 2019, 5, 43. [Google Scholar] [CrossRef] [Green Version]
- Hahn, M.; Rosenbach, D.; Krimalowski, A.; Nazarenus, T.; Moos, R.; Thelakkat, M.; Danzer, M.A. Investigating solid polymer and ceramic electrolytes for lithium-ion batteries by means of an extended Distribution of Relaxation Times analysis. Electrochim. Acta 2020, 344, 136060. [Google Scholar] [CrossRef]
- Danzer, M.A. Generalized distribution of relaxation times analysis for the characterization of impedance spectra. Batteries 2019, 5, 53. [Google Scholar] [CrossRef] [Green Version]
- Ciucci, F.; Chen, C. Analysis of electrochemical impedance spectroscopy data using the distribution of relaxation times: A Bayesian and hierarchical Bayesian approach. Electrochim. Acta 2015, 167, 439–454. [Google Scholar] [CrossRef]
- Schlüter, N.; Ernst, S.; Schröder, U. Direct Access to the Optimal Regularization Parameter in Distribution of Relaxation Times Analysis. ChemElectroChem 2020, 7, 3445–3458. [Google Scholar] [CrossRef]
- Boukamp, B.A. Fourier transform distribution function of relaxation times; application and limitations. Electrochim. Acta 2015, 154, 35–46. [Google Scholar] [CrossRef]
- Boukamp, B.A.; Rolle, A. Analysis and Application of Distribution of Relaxation Times in Solid State Ionics. Solid State Ion. 2017, 302, 12–18. [Google Scholar] [CrossRef]
- Effat, M.B.; Ciucci, F. Bayesian and Hierarchical Bayesian Based Regularization for Deconvolving the Distribution of Relaxation Times from Electrochemical Impedance Spectroscopy Data. Electrochim. Acta 2017, 247, 1117–1129. [Google Scholar] [CrossRef]
- Hörlin, T. Deconvolution and maximum entropy in impedance spectroscopy of noninductive systems. Solid State Ion. 1998, 107, 241–253. [Google Scholar] [CrossRef]
- Liu, J.; Ciucci, F. The Gaussian process distribution of relaxation times: A machine learning tool for the analysis and prediction of electrochemical impedance spectroscopy data. Electrochim. Acta 2020, 331, 135316. [Google Scholar] [CrossRef]
- Liu, J.; Ciucci, F. The Deep-Prior Distribution of Relaxation Times. J. Electrochem. Soc. 2020, 167, 026506. [Google Scholar] [CrossRef]
- Tuncer, E.; Gubanski, S. On dielectric data analysis. Using the Monte Carlo method to obtain relaxation time distribution and comparing non-linear spectral function fits. IEEE Trans. Dielectr. Electr. Insul. 2001, 8, 310–320. [Google Scholar] [CrossRef]
- Ross Macdonald, J. Comparison of parametric and nonparametric methods for the analysis and inversion of immittance data: Critique of earlier work. J. Comput. Phys. 2000, 157, 280–301. [Google Scholar] [CrossRef]
- Bello, A.; Laredo, E.; Grimau, M. Distribution of relaxation times from dielectric spectroscopy using Monte Carlo simulated annealing: α-PVDF. Phys. Rev. B 1999, 60, 12764–12774. [Google Scholar] [CrossRef]
- Tesler, A.B.; Lewin, D.R.; Baltianski, S.; Tsur, Y. Analyzing results of impedance spectroscopy using novel evolutionary programming techniques. J. Electroceram. 2010, 24, 245–260. [Google Scholar] [CrossRef]
- Hershkovitz, S.; Baltianski, S.; Tsur, Y. Harnessing evolutionary programming for impedance spectroscopy analysis: A case study of mixed ionic-electronic conductors. Solid State Ion. 2011, 188, 104–109. [Google Scholar] [CrossRef]
- Saccoccio, M.; Wan, T.H.; Chen, C.; Ciucci, F. Optimal regularization in distribution of relaxation times applied to electrochemical impedance spectroscopy: Ridge and Lasso regression methods—A theoretical and experimental Study. Electrochim. Acta 2014, 147, 470–482. [Google Scholar] [CrossRef]
- Wan, T.H.; Saccoccio, M.; Chen, C.; Ciucci, F. Influence of the Discretization Methods on the Distribution of Relaxation Times Deconvolution: Implementing Radial Basis Functions with DRTtools. Electrochim. Acta 2015, 184, 483–499. [Google Scholar] [CrossRef]
- Žic, M.; Pereverzyev, S.; Subotić, V.; Pereverzyev, S. Adaptive multi-parameter regularization approach to construct the distribution function of relaxation times. GEM Int. J. Geomath. 2020, 11, 1–23. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gavrilyuk, A.L.; Osinkin, D.A.; Bronin, D.I. The use of Tikhonov regularization method for calculating the distribution function of relaxation times in impedance spectroscopy. Russ. J. Electrochem. 2017, 53, 575–588. [Google Scholar] [CrossRef]
- Schlüter, N.; Ernst, S.; Schröder, U. Finding the Optimal Regularization Parameter in Distribution of Relaxation Times Analysis. ChemElectroChem 2019, 6, 6027–6037. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Ahmadi, M.; Collins, L.; Kalinin, S.V. Deconvolving distribution of relaxation times, resistances and inductance from electrochemical impedance spectroscopy via statistical model selection: Exploiting structural-sparsity regularization and data-driven parameter tuning. Electrochim. Acta 2019, 313, 570–583. [Google Scholar] [CrossRef]
- Nickol, A.; Schied, T.; Heubner, C.; Schneider, M.; Michaelis, A.; Bobeth, M.; Cuniberti, G. GITT Analysis of Lithium Insertion Cathodes for Determining the Lithium Diffusion Coefficient at Low Temperature: Challenges and Pitfalls. J. Electrochem. Soc. 2020, 167, 090546. [Google Scholar] [CrossRef]
- Lawson, C.L.; Hanson, R.J. Solving Least Squares Problems; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1995; p. 337. [Google Scholar] [CrossRef]
- Marquardt, D.W. An Algorithm for Least-Squares Estimation of Nonlinear Parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Kraft, D. A Software Package for Sequential Quadratic Programming; Wiss. Berichtswesen d. DFVLR: Köln, Germany, 1988. [Google Scholar]
- Byrd, R.H.; Lu, P.; Nocedal, J.; Zhu, C. A Limited Memory Algorithm for Bound Constrained Optimization. SIAM J. Sci. Comput. 1995, 16, 1190–1208. [Google Scholar] [CrossRef]
- Tikhonov, A.N.; Goncharsky, A.V.; Stepanov, V.V.; Yagola, A.G. Numerical Methods for the Solution of Ill-Posed Problems; Springer: Dordrecht, The Netherlands, 1995. [Google Scholar] [CrossRef]
- Hansen, J.K.; Hogue, J.D.; Sander, G.K.; Renaut, R.A.; Popat, S.C. Non-negatively constrained least squares and parameter choice by the residual periodogram for the inversion of electrochemical impedance spectroscopy data. J. Comput. Appl. Math. 2015, 278, 52–74. [Google Scholar] [CrossRef]
- Korth Pereira Ferraz, P.; Kowal, J. A Comparative Study on the Influence of DC/DC-Converter Induced High Frequency Current Ripple on Lithium-Ion Batteries. Sustainability 2019, 11, 6050. [Google Scholar] [CrossRef] [Green Version]
- Agarwal, P.; Orazem, M. Measurement Models for Electrochemical Impedance Spectroscopy. J. Electrochem. Soc. 1992, 139, 1917. [Google Scholar] [CrossRef]
- Orazem, M.E.; Tribollet, B. Electrochemical Impedance Spectroscopy; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2017; pp. 1–523. [Google Scholar] [CrossRef]
- Deutsches Institut für Normung e.V. International Standard: Primary Batteries—Part 2: Physical and Electrical Specifications (IEC 60086-2:2015); Beuth-Verlag: Berlin, Germany, 2016. [Google Scholar] [CrossRef]
- Ingale, P.; Sakthivel, M.; Drillet, J.F. Test of Diethylmethylammonium Trifluoromethanesulfonate Ionic Liquid as Electrolyte in Electrically Rechargeable Zn/Air Battery. J. Electrochem. Soc. 2017, 164, H5224–H5229. [Google Scholar] [CrossRef]
- Penteado, S.P.; Bento, R.F. Performance analysis of ten brands of batteries for hearing aids. Int. Arch. Otorhinolaryngol. 2013, 17, 291–304. [Google Scholar] [CrossRef] [Green Version]
- Reddy, T.B. Linden’s Handbook of Batteries, 4th ed.; McGraw-Hill Education: New York, NY, USA, 2011. [Google Scholar]
- Clark, S.; Mainar, A.R.; Iruin, E.; Colmenares, L.C.; Blázquez, J.A.; Tolchard, J.R.; Jusys, Z.; Horstmann, B. Designing Aqueous Organic Electrolytes for Zinc–Air Batteries: Method, Simulation, and Validation. Adv. Energy Mater. 2020, 10. [Google Scholar] [CrossRef]
- Stamm, J.; Varzi, A.; Latz, A.; Horstmann, B. Modeling nucleation and growth of zinc oxide during discharge of primary zinc-air batteries. J. Power Sources 2017, 360, 136–149. [Google Scholar] [CrossRef] [Green Version]
- Ma, Z.; Pei, P.; Wang, K.; Wang, X.; Xu, H.; Liu, Y.; Peng, G. Degradation characteristics of air cathode in zinc air fuel cells. J. Power Sources 2015, 274, 56–64. [Google Scholar] [CrossRef]
- Schröder, D.; Arlt, T.; Krewer, U.; Manke, I. Analyzing transport paths in the air electrode of a zinc air battery using X-ray tomography. Electrochem. Commun. 2014, 40, 88–91. [Google Scholar] [CrossRef]
- Tsehaye, M.T.; Alloin, F.; Iojoiu, C.; Tufa, R.A.; Aili, D.; Fischer, P.; Velizarov, S. Membranes for zinc-air batteries: Recent progress, challenges and perspectives. J. Power Sources 2020, 475, 228689. [Google Scholar] [CrossRef]
- Schmitt, T.; Arlt, T.; Manke, I.; Latz, A.; Horstmann, B. Zinc electrode shape-change in secondary air batteries: A 2D modeling approach. J. Power Sources 2019, 432, 119–132. [Google Scholar] [CrossRef] [Green Version]
- Arlt, T.; Schröder, D.; Krewer, U.; Manke, I. In operando monitoring of the state of charge and species distribution in zinc air batteries using X-ray tomography and model-based simulations. Phys. Chem. Chem. Phys. 2014, 16, 22273–22280. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Franke-lang, R.; Kowal, J. Electrochemical Model-Based Investigation of Thick LiFePO4 Electrode Design Parameters. Modelling 2021, 2, 259–287. [Google Scholar] [CrossRef]
- See, D.M.; White, R.E. Temperature and concentration dependence of the specific conductivity of concentrated solutions of potassium hydroxide. J. Chem. Eng. Data 1997, 42, 1266–1268. [Google Scholar] [CrossRef]
- Zhuang, S.; Zhang, H.; Liu, S.; Tu, F.; Zhang, W.; Zhao, C. Optimized perovskite electrocatalyst for bifunctional air electrode by impedance spectroscopy analysis. Int. J. Electrochem. Sci. 2014, 9, 1690–1701. [Google Scholar]
- Hoang, T.K.A.; Doan, T.N.L.; Sun, K.E.K.; Chen, P. Corrosion chemistry and protection of zinc & zinc alloys by polymer-containing materials for potential use in rechargeable aqueous batteries. RSC Adv. 2015, 5, 41677–41691. [Google Scholar] [CrossRef]
- Thomas Goh, F.W.; Liu, Z.; Hor, T.S.A.; Zhang, J.; Ge, X.; Zong, Y.; Yu, A.; Khoo, W. A Near-Neutral Chloride Electrolyte for Electrically Rechargeable Zinc-Air Batteries. J. Electrochem. Soc. 2014, 161, A2080–A2086. [Google Scholar] [CrossRef]








| Current | 253 K | 263 K | 273 K | 283 K | 294 K | 303 K | 313 K |
|---|---|---|---|---|---|---|---|
| 3 mA | 39 mAh | 43 mAh | 202 mAh | 257 mAh | 254 mAh | 275 mAh | 287 mAh |
| 4 mA | - | - | 188 mAh | 231 mAh | 232 mAh | 246 mAh | 287 mAh |
| 5 mA | - | - | 108 mAh | 211 mAh | 221 mAh | 239 mAh | 261 mAh |
| 6 mA | - | - | 89 mAh | 187 mAh | 215 mAh | 220 mAh | 260 mAh |
| SoC in % | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 100 | 4.6 × | 2.5 × | 1.9 × | 9.8 × | 1.2 × | 1.7 × | 1.6 × | 9.2 × | 9.7 |
| 90.2 | 4.6 × | 3.1 × | 2.5 × | - | - | 9.2 × | 1.3 × | - | 3.4 |
| 80.3 | 4.6 × | 3.1 × | 2.1 × | - | - | 1.2 × | 1.5 × | - | 3.4 |
| 70.5 | 4.6 × | 3.1 × | 2.5 × | - | - | 1.4 × | 1.5 × | - | 3.4 |
| 60.7 | 4.6 × | 2.7 × | 1.8 × | 3.5 × | - | 1.7 × | 1.5 × | - | 4.6 |
| 50.5 | 4.6 × | 2.7 × | 1.6 × | 3.1 × | - | 1.7 × | 1.8 × | - | 5.3 |
| 41.0 | 4.6 × | 2.7 × | 1.6 × | - | - | 2.2 × | 2.0 × | - | 5.3 |
| 31.1 | 4.6 × | 2.7 × | 1.6 × | 2.0 × | - | - | 3.7 × | - | 4.6 |
| 21.3 | 4.6 × | 2.7 × | 1.6 × | 1.1 × | - | - | - | - | 4.6 |
| 11.5 | 4.6 × | 3.1 × | 1.8 × | 2.3 × | - | - | 1.8 × | - | 2.5 |
| 1.6 | 4.6 × | 3.6 × | 2.5 × | - | - | 1.4 × | 9.8 × | 3.7 × | 4.6 |
| SoCin % | in | in | in | in | in | in | in | in | in |
| 100 | 0.081 | 0.061 | 0.151 | 0.201 | 0.834 | 0.135 | 0.247 | 0.311 | 1.355 |
| 90.2 | 0.057 | 0.051 | 0.137 | - | - | 0.095 | 0.374 | - | 0.893 |
| 80.3 | 0.029 | 0.057 | 0.134 | - | - | 0.106 | 0.497 | - | 0.931 |
| 70.5 | 0.042 | 0.055 | 0.139 | - | - | 0.125 | 0.549 | - | 0.954 |
| 60.7 | 0.071 | 0.080 | 0.124 | 0.039 | - | 0.153 | 0.581 | - | 0.894 |
| 50.5 | 0.080 | 0.081 | 0.116 | 0.038 | - | 0.154 | 0.601 | - | 0.912 |
| 41.0 | 0.089 | 0.076 | 0.111 | - | - | 0.168 | 0.639 | - | 0.944 |
| 31.1 | 0.072 | 0.074 | 0.103 | 0.031 | - | - | 0.665 | - | 0.988 |
| 21.3 | 0.048 | 0.072 | 0.106 | 0.035 | - | - | - | - | 1.079 |
| 11.5 | 0.033 | 0.051 | 0.115 | 0.030 | - | - | 0.343 | - | 2.317 |
| 1.6 | 0.030 | 0.042 | 0.127 | - | - | 0.097 | 0.256 | 0.382 | 3.039 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Franke-Lang, R.; Kowal, J. Analysis of Electrochemical Impedance Spectroscopy on Zinc-Air Batteries Using the Distribution of Relaxation Times. Batteries 2021, 7, 56. https://doi.org/10.3390/batteries7030056
Franke-Lang R, Kowal J. Analysis of Electrochemical Impedance Spectroscopy on Zinc-Air Batteries Using the Distribution of Relaxation Times. Batteries. 2021; 7(3):56. https://doi.org/10.3390/batteries7030056
Chicago/Turabian StyleFranke-Lang, Robert, and Julia Kowal. 2021. "Analysis of Electrochemical Impedance Spectroscopy on Zinc-Air Batteries Using the Distribution of Relaxation Times" Batteries 7, no. 3: 56. https://doi.org/10.3390/batteries7030056
APA StyleFranke-Lang, R., & Kowal, J. (2021). Analysis of Electrochemical Impedance Spectroscopy on Zinc-Air Batteries Using the Distribution of Relaxation Times. Batteries, 7(3), 56. https://doi.org/10.3390/batteries7030056







