Power and Energy Rating Considerations in Integration of Flow Battery with Solar PV and Residential Load
Abstract
:1. Introduction
2. System Lay-Out and Experimental Details
2.1. Conceptual System and Experimental Set-Up
2.2. Construction of PV Output Profile
2.3. Construction of Residential Load Profile
2.4. Salient Features of the Redox Flow Battery
2.5. Estimation of State of Charge (SoC) of the Battery
2.6. Set-Up of the Experimental Study
3. Results and Discussion
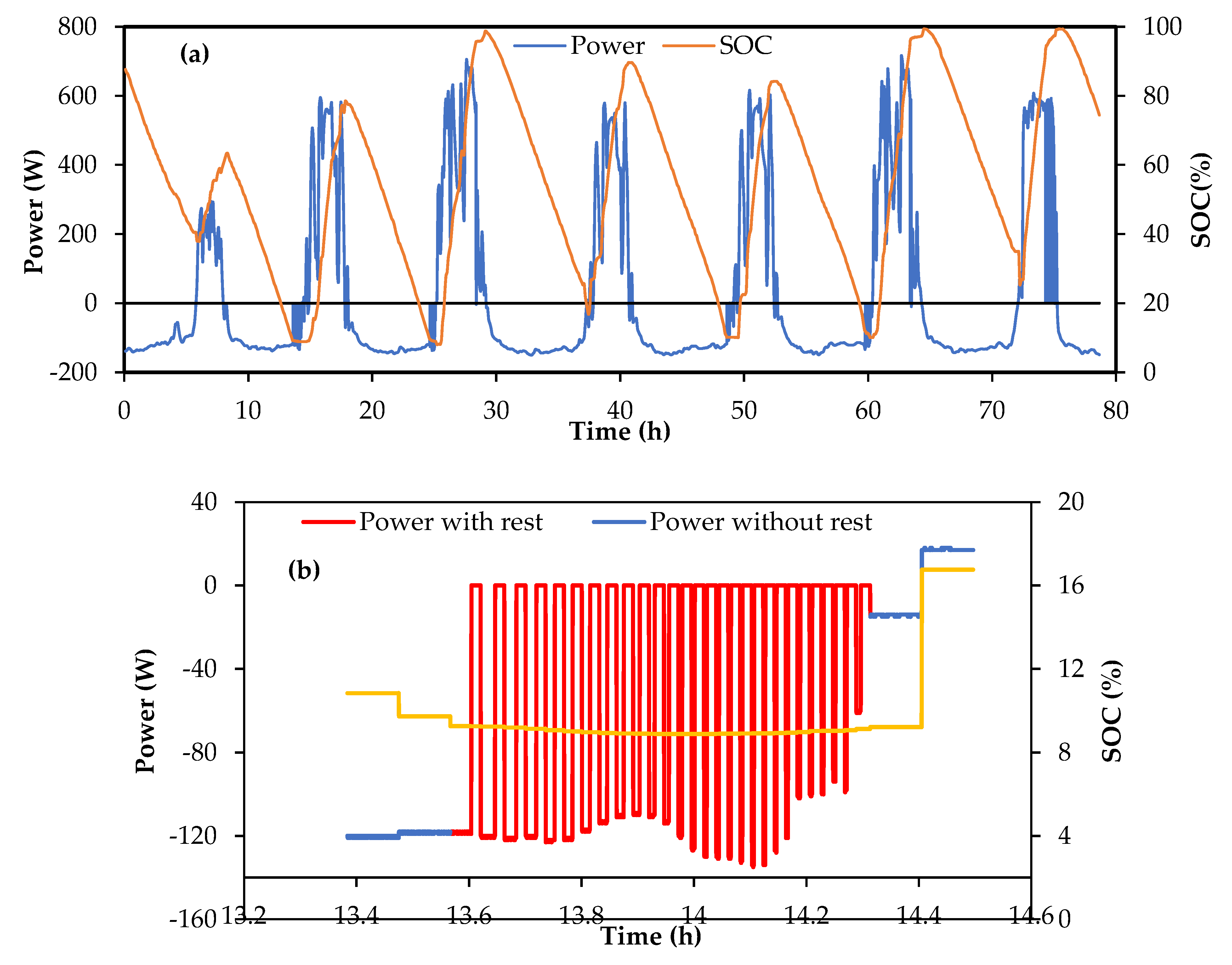
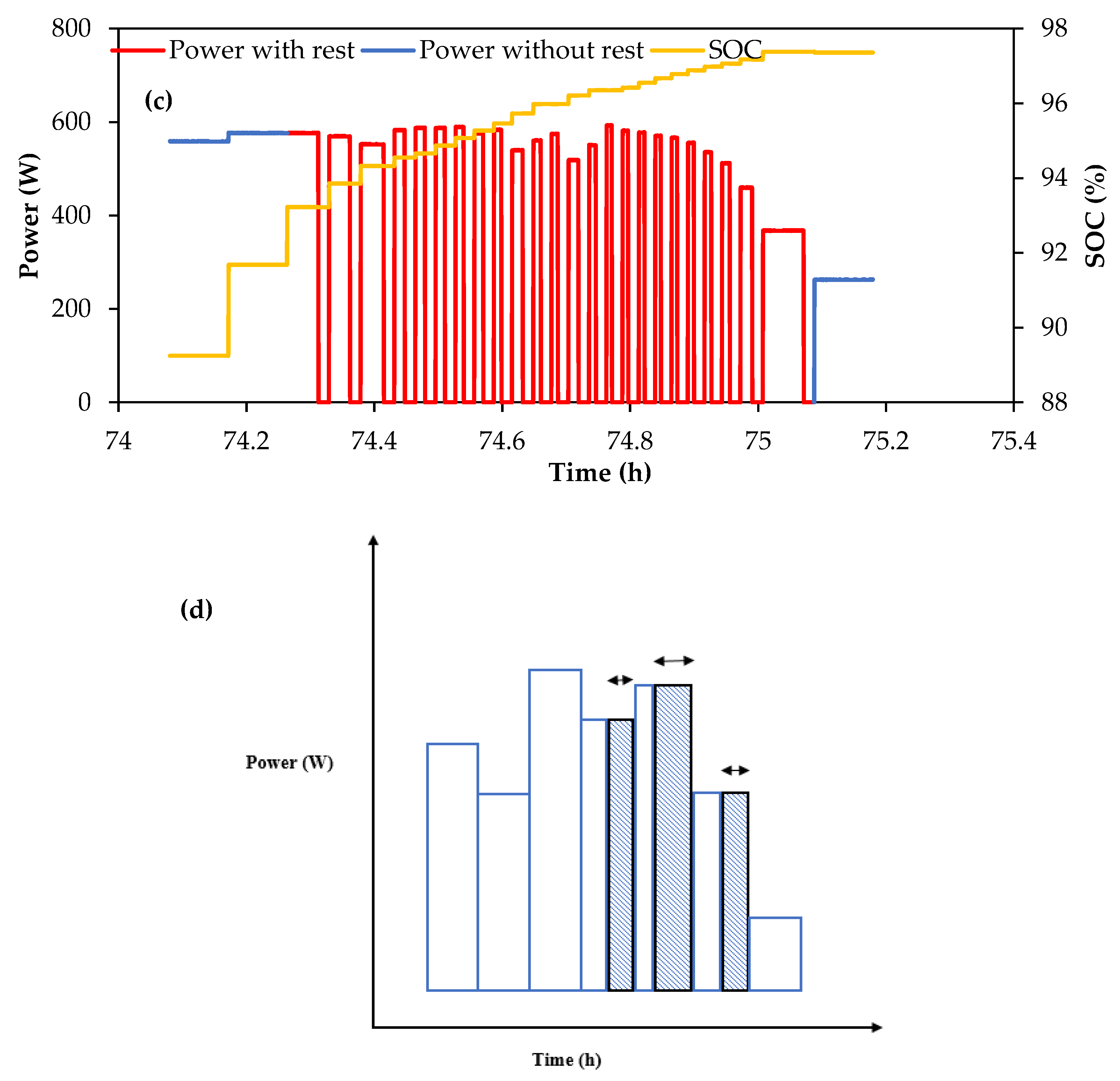
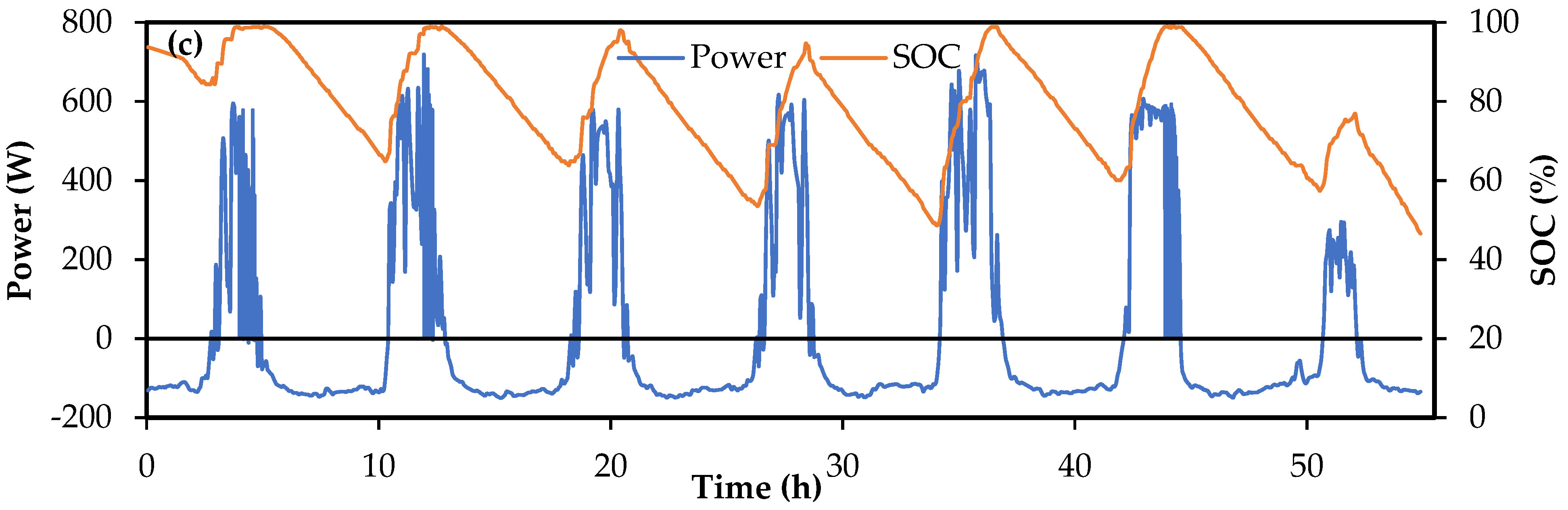
3.1. Battery Performance for the Baseline Case
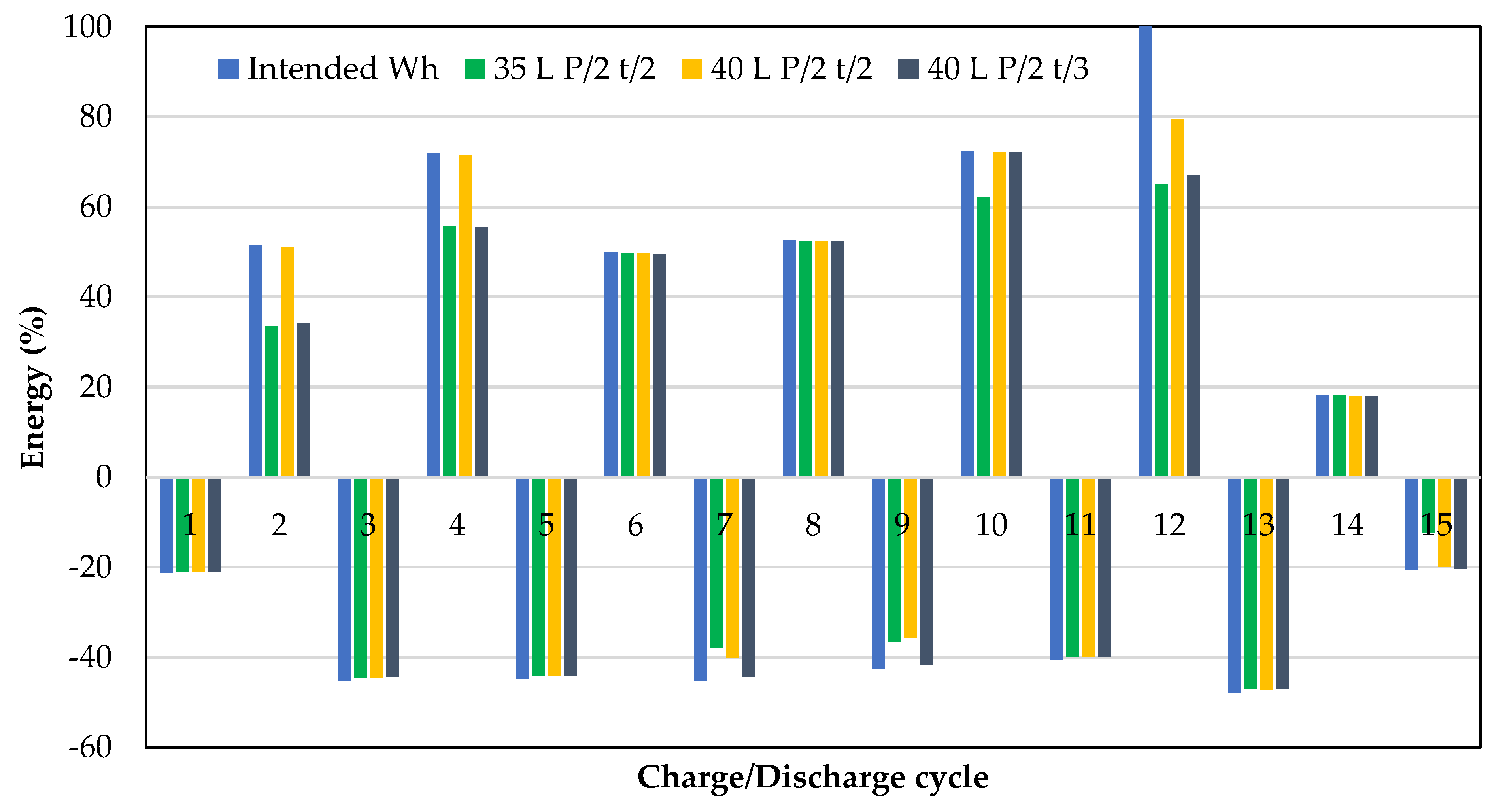
3.2. Power and Energy Scaling Studies
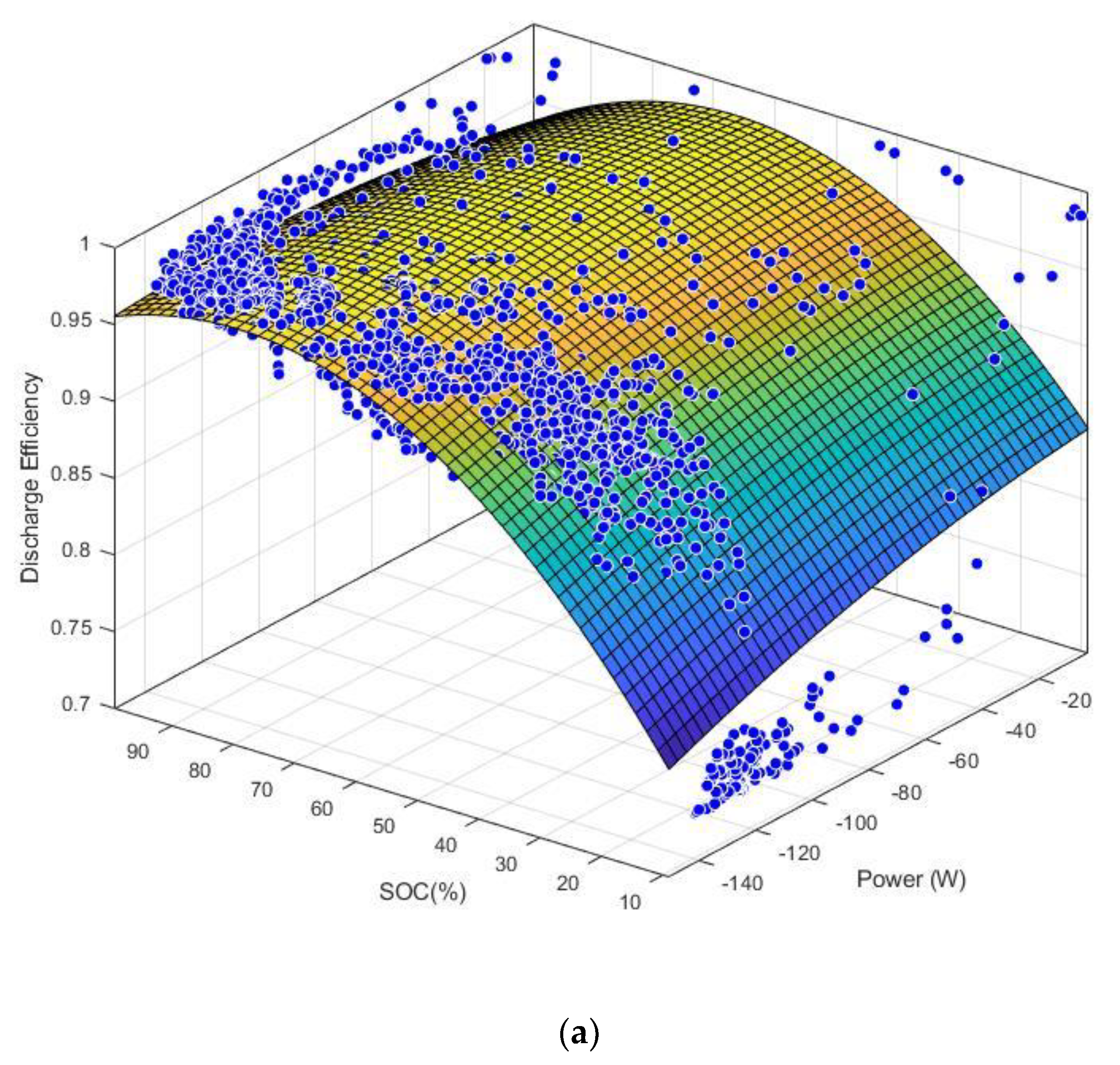
3.3. Charging and Discharging Efficiency
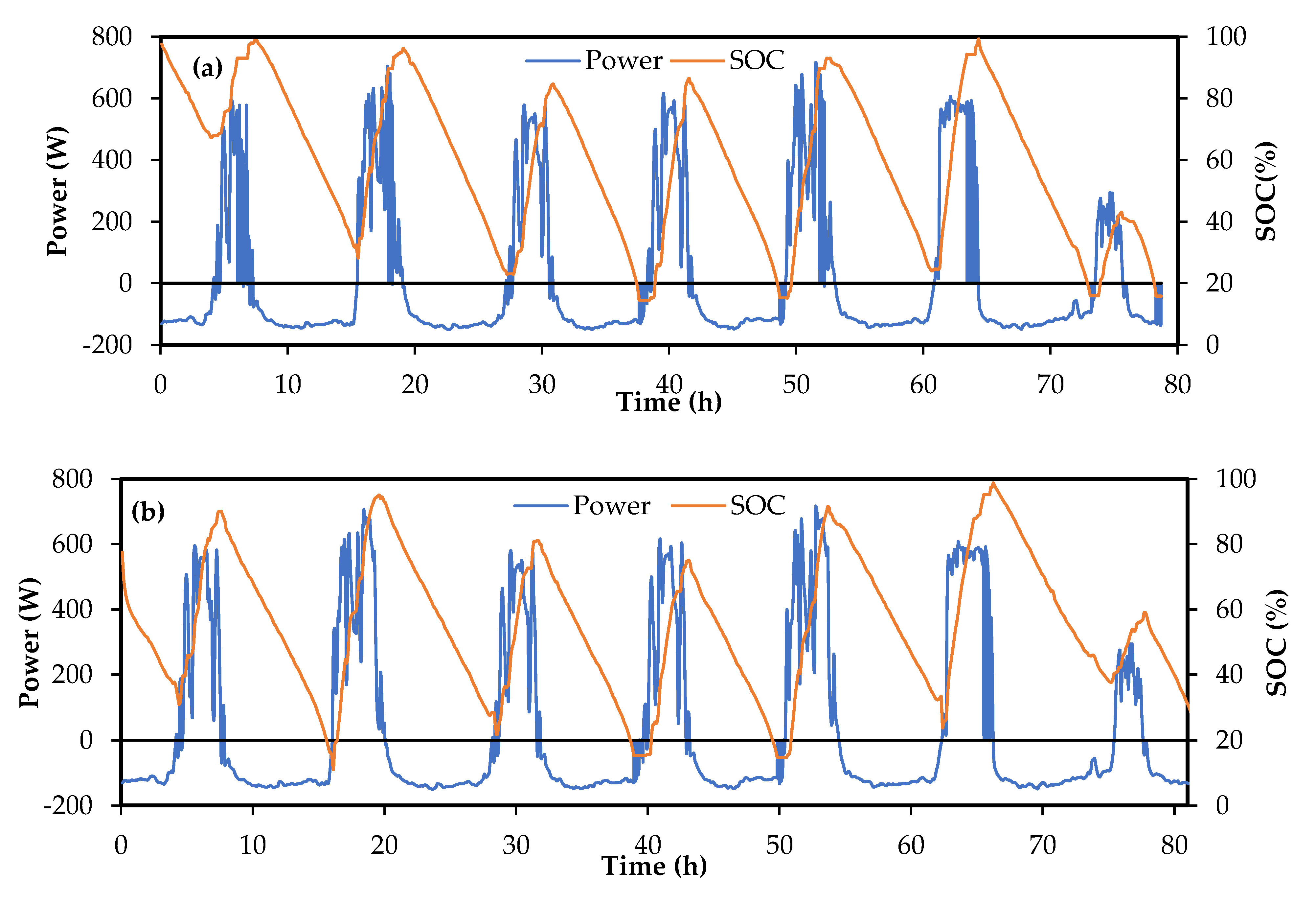
3.4. Lead Acid Battery Performance
4. Conclusions
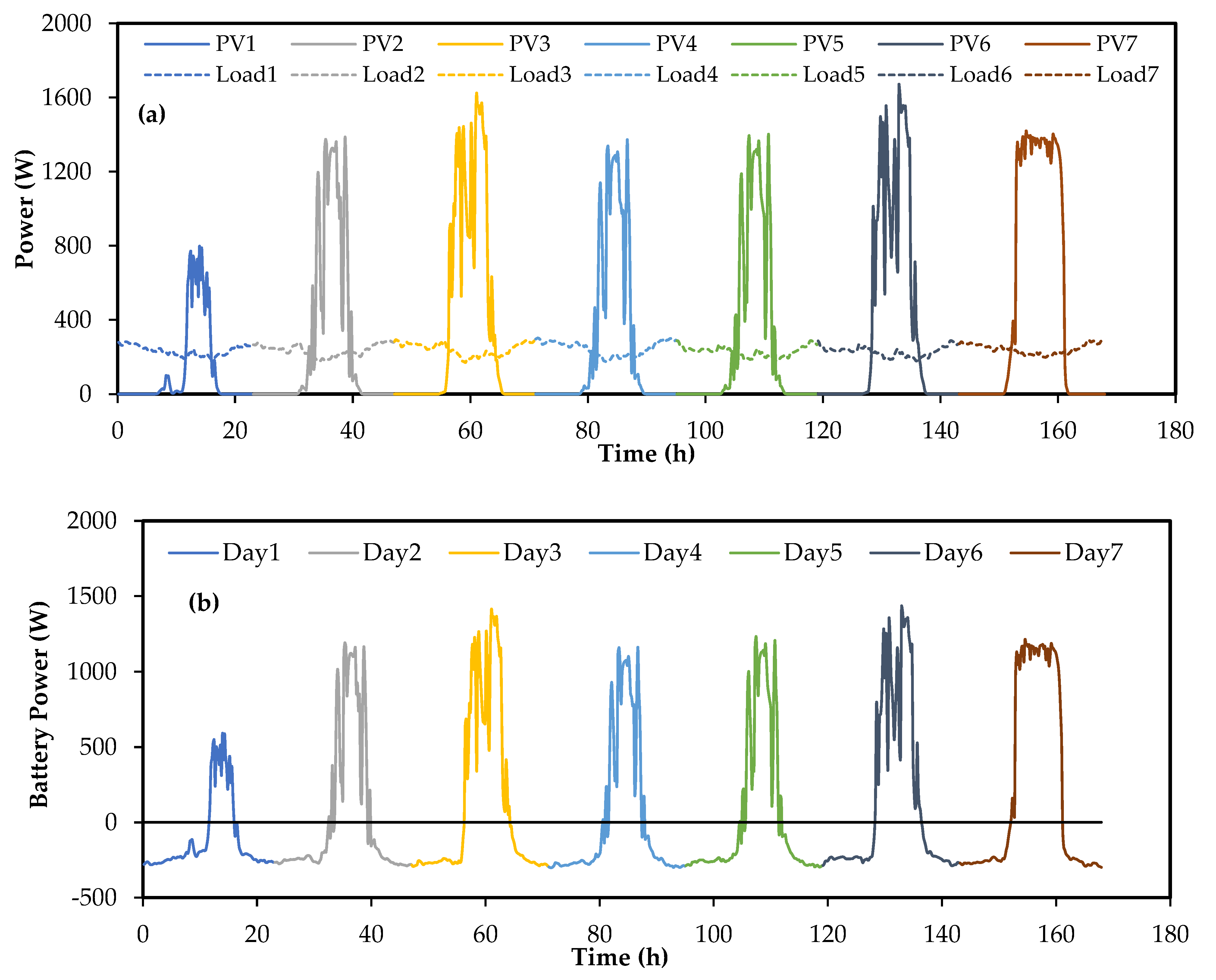
- Typical insolation and load profiles for an integrated solar PV-battery-residential load system have about a quarter of the PV output going directly to meet the load demand during sunshine hours. This means that nearly three-quarters of energy flow to the load occurs through the battery. Account must therefore be taken of charging and discharging energy efficiencies.
- The seven-day power profiles for the integrated system show the vast differences between charging and discharging conditions for the battery of such an integrated system. Average charging power is about three times that of average discharge power. Further, due to the different nature of variations of solar insolation and aggregated residential load, ratio of peak power in charging to that in discharging of the battery is 4.7. Thus, charging conditions are much more severe than discharging. The stack power rating should therefore be based on the charging condition during peak solar insolation. Too low stack power rating can lead to considerable charging failures which can subsequently translate into discharging failures.
- For residential load applications, the daily energy variation is not highly variable. The energy rating of the VRFB system, i.e., electrolyte volume, should be based on the maximum daily discharge load and the range of operable SoC.
- Due to the rather mild discharging conditions of the battery, favorable discharging efficiencies can be maintained in a properly-sized stack for SoC variations in the range of 20 to 90%. A stack operating over this range may be expected to have, given that it is designed for harsh charging conditions, net discharge efficiency of 90% or higher.
- The sizing of the PV plant should be based on both charging and discharging efficiencies of the battery. Given that the stack should be designed for peak charging power, and given that the peak-to-average charging power is nearly two, the stack charging efficiency is likely to between 85 to 90%. With discharge efficiency being in the range of 90 to 95%, a net round trip energy loss of about 80% may be expected.
- Considering the fact that about 75% energy flow occurs through the battery (with a round-trip efficiency of 80%) with the rest going through to load directly with a considerably higher efficiency, and making some allowance for failure to charge, the PV plant should be rated at about 25% more energy than the average daily energy demand from the load.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Global Renewables Outlook: Energy Transformation 2050, International Renewable Energy Agency. 2020. Available online: https://www.irena.org/publications/2020/Apr/Global-Renewables-Outlook-2020 (accessed on 20 June 2020).
- Duffie, A.J.; Beckman, A.W. Solar Engineering of Thermal Processes; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Gur, T.M. Review of electrical energy storage technologies, materials and systems: Challenges and prospects for large scale grid storage. Energy Environ. Sci. 2018, 11, 2696–2967. [Google Scholar] [CrossRef]
- Sufyan, M.; Rahim, N.A.; Aman, M.M.; Tan, C.K.; Raihan, S.R.S. Sizing and applications of battery energy storage technologies in smart grid system: A review. J. Renew. Sustain. Energy 2019, 11, 014105. [Google Scholar] [CrossRef]
- Liu, J.; Chen, X.; Cao, S.; Yang, H. Overview on hybrid solar photovoltaic-electrical energy storage technologies for power supply to buildings. Energy Convers. Manag. 2019, 187, 103–121. [Google Scholar] [CrossRef]
- Huggins, R.A. Energy Storage: Fundamentals, Materials and Applications; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Whitehead, A.H.; Rabbow, T.J.; Trampert, M.; Pokorny, P. Critical safety features of vanadium redox flow battery. J. Power Sources 2017, 351, 1–7. [Google Scholar] [CrossRef]
- Angenendt, G.; Zurmühlen, S.; Axelsen, H.; Sauer, D.U. Comparison of different operation strategies for PV battery home storage systems including forecast-based operation strategies. Appl. Energy 2018, 229, 884–899. [Google Scholar] [CrossRef]
- Litjens, G.B.M.A.; Worrell, E.; van Sark, W.G.J.H.M. Assessment of forecasting methods on performance of photovoltaic-battery systems. Appl. Energy 2018, 221, 358–373. [Google Scholar] [CrossRef]
- Jing, W.; Lai, C.H.; Wong, W.S.; Wong, M.D. A comprehensive study of battery-supercapacitor hybrid energy storage system of standalone PV power system in rural electrification. Appl. Energy 2018, 224, 340–356. [Google Scholar] [CrossRef]
- Gharavi, H.; Ardehali, M.; Ghanbari-Tichi, S. Imperial competitive algorithm optimization of fuzzy multi-objective design of a hybrid green power system with considerations for economics, reliability, and environmental emissions. Renew. Energy 2015, 78, 427–437. [Google Scholar] [CrossRef]
- Hadidian-Moghaddam, M.J.; Arabi-Nowdeh, S.; Bigdeli, M. Optimal sizing of a stand-alone hybrid photovoltaic/wind system using new grey wolf optimizer considering reliability. J. Renew. Sustain. Energy 2016, 8, 035903. [Google Scholar] [CrossRef]
- Hakimi, S.M.; Moghaddas-Tafreshi, S.M. Optimal sizing of a stand-alone hybrid power system via particle swarm optimization for Kahnouj area in south-east of Iran. Renew. Energy 2009, 34, 1855–1862. [Google Scholar] [CrossRef]
- Ekren, O.; Ekren, B.Y. Size optimization of a PV/wind hybrid energy conversion system with battery storage using simulated annealing. Appl. Energy 2010, 87, 592–598. [Google Scholar] [CrossRef]
- Askarzadeh, A. A discrete chaotic harmony search-based simulated annealing algorithm for optimum design of PV/wind hybrid system. Sol. Energy 2013, 97, 93–101. [Google Scholar] [CrossRef]
- Moghaddam, M.J.H.; Kalam, A.; Nowdeh, S.A.; Ahmadi, A.; Babanezhad, M.; Saha, S. Optimal sizing and energy management of stand-alone hybrid photovoltaic/ wind system based on hydrogen storage considering LOEE and LOLE reliability indices using flower pollination algorithm. Renew. Energy 2019, 135, 1412–1434. [Google Scholar] [CrossRef]
- Fetanat, A.; Khorasaninejad, E. Size optimization for hybrid photovoltaic–wind energy system using ant colony optimization for continuous domains based integer programming. Appl. Soft Comput. 2015, 31, 196–209. [Google Scholar] [CrossRef]
- Ajlan, A.; Tan, C.W.; Abdilahi, A.M. Assessment of environmental and economic perspectives for renewable-based hybrid power system in Yemen. Renew. Sustain. Energy Rev. 2017, 75, 559–570. [Google Scholar] [CrossRef]
- Lu, P.; Leung, P.; Su, H.; Yang, W.; Xu, Q. Materials, performance, and systems design for integrated solar flow batteries—A mini review. Appl. Energy 2021, 282, 116210. [Google Scholar] [CrossRef]
- Minke, C.; Turek, T. Materials, System designs and modelling approaches in techno-economic assessment of all-vanadium redox flow batteries—A review. J. Power Sources 2018, 376, 66–81. [Google Scholar] [CrossRef]
- Akter, P.; Li, Y.; Bao, J.; Skyllas-Kazacos, M.; Rahman, M.F. Optimal Charging of Vanadium Redox Flow Battery with Time-Varying Input Power. Batteries 2019, 5, 20. [Google Scholar] [CrossRef] [Green Version]
- Gundlapalli, R.; Jayanti, S. Comparative Study of Kilowatt-Scale Vanadium Redox Flow Battery Stacks Designed with Serpentine Flow Fields and Split Manifolds. Batteries 2021, 7, 30. [Google Scholar] [CrossRef]
- García-Quismondo, E.; Almonacid, I.; Martinez, M.A.C.; Miroslavov, V.; Serrano, E.; Palma, J.; Salmerón, J.P.A. Operational Experience of 5 kW/5 kWh All-Vanadium Flow Batteries in Photovoltaic Grid Applications. Batteries 2019, 5, 52. [Google Scholar] [CrossRef] [Green Version]
- Mongird, K.; Viswanathan, V.; Alam, J.; Vartanian, C.; Sprenkle, V.; Baxter, R. 2020 Grid Energy Storage Technology Cost and Performance Assessment; Technical Report No. DOE/PA-0204; US Department of Energy: Washington, DC, USA, 2020.
- Zhang, Y.; Liu, L.; Xi, J.; Wu, Z.; Qiu, X. The benefits and limitations of electrolyte mixing in vanadium flow batteries. Appl. Energy 2017, 204, 373–381. [Google Scholar] [CrossRef]
- Wang, K.; Liu, L.; Xi, J.; Wu, Z.; Qiu, X. Reduction of capacity decay in vanadium flow batteries by an electrolyte-reflow method. J. Power Sources 2017, 338, 17–25. [Google Scholar] [CrossRef]
- Sun, C.; Negro, E.; Nale, A.; Pagot, G.; Vezzù, K.; Zawodzinski, T.A.; Meda, L.; Gambaro, C.; Di Noto, V. An efficient barrier toward vanadium crossover in redox flow batteries: The bilayer [Nafion/(WO3)x] hybrid inorganic-organic membrane. Electrochim. Acta 2021, 378, 138133. [Google Scholar] [CrossRef]
- Bhattacharjee, A.; Saha, H. Design and experimental validation of a generalized electrical equivalent model of Vanadium redox flow battery for interfacing with renewable energy sources. J. Energy Storage 2017, 13, 220–232. [Google Scholar] [CrossRef]
- Zhang, X.; Li, Y.; Skyllas-Kazacos, M.; Bao, J. Optimal Sizing of Vanadium Redox Flow Battery Systems for Residential Applications Based on Battery Electrochemical Characteristics. Energies 2016, 9, 857. [Google Scholar] [CrossRef] [Green Version]
- Sarkar, T.; Bhattacharjee, A.; Samanta, H.; Bhattacharya, K.; Saha, H. Optimal design and implementation of solar PV-wind-biogas-VRFB storage integrated smart hybrid microgrid for ensuring zero loss of power supply probability. Energy Convers. Manag. 2019, 191, 102–118. [Google Scholar] [CrossRef]
- Behi, B.; Baniasadi, A.; Arefi, A.; Gorjy, A.; Jennings, P.; Pivrikas, A. Cost-benefits analysis of a virtual power plant including solar PV, flow battery, heat pump, and demand management: A western Australia case study. Energies 2020, 13, 2614. [Google Scholar] [CrossRef]
- Solar Park 2000 MW Capacity in the State of Karnataka, Detailed Project Report. 2015. Available online: https://cdkn.org/wp-content/uploads/2017/07/Up-Karnataka-Solar-park-DPR-1.pdf (accessed on 10 November 2019).
- Ali, S. The Future of Indian Electricity Demand: How Much, by Whom, and under What Conditions, Brooking India. 2018. Available online: https://www.brookings.edu/wp-content/uploads/2018/10/The-future-of-Indian-electricity-demand.pdf (accessed on 20 December 2019).
- Available online: http://emarc.watchyourpower.org/energycurve.php (accessed on 20 December 2019).
- Chunekar, A.; Sreenivas, A. Towards an understanding of residential electricity consumption in India. Build. Res. Inf. 2018, 47, 75–90. [Google Scholar] [CrossRef]
- Walker, A.; Kwon, S. Analysis on impact of shared energy storage in residential community: Individual versus shared energy storage. Appl. Energy 2020, 282, 116172. [Google Scholar] [CrossRef]
- Gundlapalli, R.; Jayanti, S. Effective splitting of serpentine flow field for applications in large-scale flow batteries. J. Power Sources 2021, 487, 229409. [Google Scholar] [CrossRef]
- Jayanti, S.; Gundlapalli, R.; Chetty, R.; Jeevandoss, C.R.; Ramanujam, K.; Monder, D.S.; Rengaswamy, R.; Suresh, P.V.; Swarup, K.S.; Varadaraju, U.V.; et al. Characteristics of an Indigenously Developed 1 KW Vanadium Redox Flow Battery Stack. In Proceedings of the 7th International Conference on Advances in Energy Research, Mumbai, India, 10–12 December 2019; Springer: Singapore, 2021. [Google Scholar]
- Gundlapalli, R.; Kumar, S.; Jayanti, S. Stack Design Considerations for Vanadium Redox Flow Battery. INAE Lett. 2018, 3, 149–157. [Google Scholar] [CrossRef]
- Gundlapalli, R.; Jayanti, S. Effect of electrode compression and operating parameters on the performance of large vanadium redox flow battery cells. J. Power Sources 2019, 427, 231–242. [Google Scholar] [CrossRef]




| PV | Load | Battery | |
|---|---|---|---|
| Power (W) | Power (W) | Charge Power (W) | Discharge Power (W) |
| Max–1670 | Max–303 | Max–1432 | Max–303 |
| Min–0 | Min–156 | Min–2.9 | Min–5.9 |
| Avg–640 | Avg–238 | Avg–769 | Avg–238 |
| Energy per day (Wh) | Energy per day (Wh) | Charge energy per day (Wh) | Discharge energy per day (Wh) |
| Max–11,110 | Max–5944 | Max–9240 | Max–4316 |
| Min–2600 | Min–3716 | Min–1720 | Min–1840 |
| Avg–7144 | Avg–5713 | Avg–5450 | Avg–4029 |
| Solar insolation to load (%) | 23.4 | Solar insolation to battery (%) | 76.6% |
| Cycle | PV | Load | Battery |
|---|---|---|---|
| 1 half DC | 47 | 697 | 653 |
| 1 C | 650 | 232 | −419 |
| 2 DC | 51 | 1004 | 957 |
| 2 C | 1545 | 373 | −1173 |
| 3 DC | 35 | 1065 | 1035 |
| 3 C | 2066 | 421 | −1648 |
| 4 DC | 70 | 1090 | 1025 |
| 4 C | 1494 | 354 | −1142 |
| 5 DC | 66 | 1095 | 1034 |
| 5 C | 1521 | 317 | −1205 |
| 6 DC | 36 | 1005 | 973 |
| 6 C | 2082 | 425 | −1660 |
| 7 DC | 52 | 979 | 931 |
| 7 C | 2775 | 486 | −2291 |
| 8 half DC | 13 | 454 | 443 |
| Cycles | Intended Wh | Experimental Wh | Energy Based % Failure | Time Based % Failure |
|---|---|---|---|---|
| 0th Discharge | 653 | 643 | 2 | 0 |
| 1st Charge | 419 | 415 | 1 | 0 |
| 1st Discharge | 957 | 677 | 29 | 28 |
| 2nd Charge | 1173 | 1172 | 0 | 0 |
| 2nd Discharge | 1035 | 850 | 18 | 16 |
| 3rd Charge | 1648 | 1606 | 3 | 1 |
| 3rd Discharge | 1025 | 1011 | 1 | 0 |
| 4th Charge | 1142 | 1136 | 1 | 0 |
| 4th Discharge | 1034 | 977 | 5 | 5 |
| 5th Charge | 1205 | 1199 | 0 | 0 |
| 5th Discharge | 973 | 877 | 10 | 8 |
| 6th Charge | 1660 | 1550 | 7 | 4 |
| 6th Discharge | 931 | 912 | 2 | 0 |
| 7th Charge | 2291 | 1288 | 44 | 40 |
| 7th Discharge | 443 | 437 | 1 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Parmeshwarappa, P.; Gundlapalli, R.; Jayanti, S. Power and Energy Rating Considerations in Integration of Flow Battery with Solar PV and Residential Load. Batteries 2021, 7, 62. https://doi.org/10.3390/batteries7030062
Parmeshwarappa P, Gundlapalli R, Jayanti S. Power and Energy Rating Considerations in Integration of Flow Battery with Solar PV and Residential Load. Batteries. 2021; 7(3):62. https://doi.org/10.3390/batteries7030062
Chicago/Turabian StyleParmeshwarappa, Purnima, Ravendra Gundlapalli, and Sreenivas Jayanti. 2021. "Power and Energy Rating Considerations in Integration of Flow Battery with Solar PV and Residential Load" Batteries 7, no. 3: 62. https://doi.org/10.3390/batteries7030062
APA StyleParmeshwarappa, P., Gundlapalli, R., & Jayanti, S. (2021). Power and Energy Rating Considerations in Integration of Flow Battery with Solar PV and Residential Load. Batteries, 7(3), 62. https://doi.org/10.3390/batteries7030062








