Attention-Based Long Short-Term Memory Recurrent Neural Network for Capacity Degradation of Lithium-Ion Batteries
Abstract
:1. Introduction
2. Lithium-Ion Battery Datasets
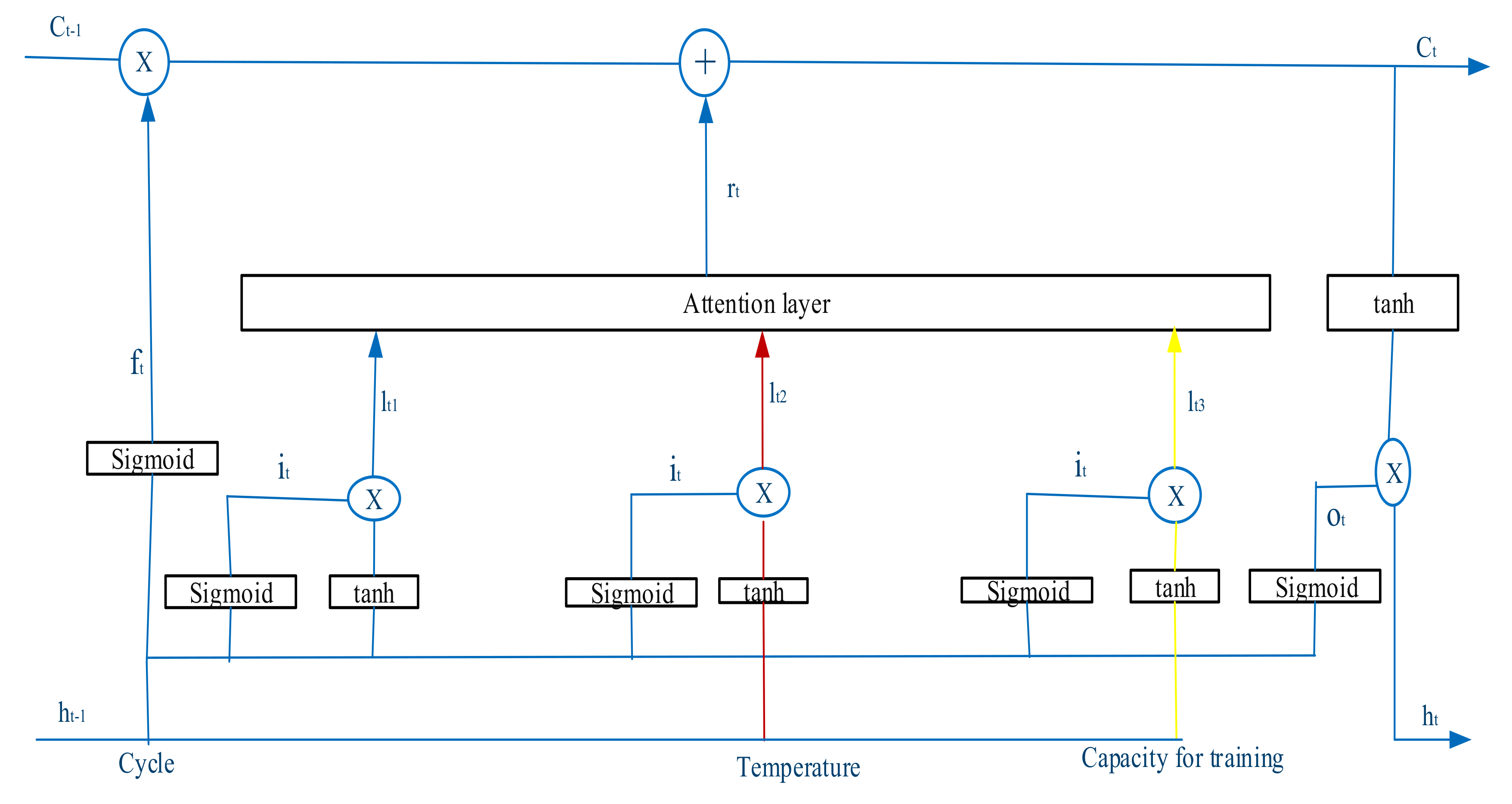
3. Long Short-Term Memory with Attention Mechanism
4. Analysis Results
4.1. Model Performance for Prediction of Capacity Degradation Trend
4.2. Battery EOL Prediction
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Barre, A.; Deguilhem, B.; Grolleau, S.; Gerard, M.; Suard, F.; Riu, D. A review on lithium-ion battery ageing mechanisms and estimations for automotive applications. J. Power Sources 2013, 241, 680–689. [Google Scholar] [CrossRef] [Green Version]
- Wu, L.; Fu, X.; Guan, Y. Review of the remaining useful life prognostics of vehicle lithium-ion batteries using data-driven methodologies. Appl. Sci. 2016, 6, 166. [Google Scholar] [CrossRef] [Green Version]
- Su, C.; Chen, H.J. A review on prognostics approaches for remaining useful life of lithium-ion battery. IOP Conf. Ser. Earth Environ. Sci. 2017, 93, 012040. [Google Scholar] [CrossRef]
- Omariba, Z.B.; Zhang, L.; Sun, D. Review on health management system for lithium-ion batteries of electric vehicles. Electronics 2018, 7, 72. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.; Yu, J.; Kim, M.; Kim, K.; Han, S. Estimation of Li-ion battery state of health based on multilayer perceptron: As an EV application. IFAC-PapersOnLine 2018, 51, 392–397. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiong, R.; He, H.; Pecht, M. Long short-term memory recurrent neural network for remaining useful life prediction of lithium-ion batteries. IEEE Trans. Veh. Technol. 2018, 67, 5695–5705. [Google Scholar] [CrossRef]
- Li, X.; Zhang, L.; Wang, Z.; Dong, P. Remaining useful life prediction for lithium-ion batteries based on a hybrid model combining the long short-term memory and Elman neural networks. J. Energy Storage 2019, 21, 510–518. [Google Scholar] [CrossRef]
- Ren, L.; Zhao, L.; Hong, S.; Zhao, S.; Wang, H.; Zhang, L. Remaining useful life prediction for lithium-ion battery: A deep learning approach. IEEE Access 2018, 6, 50587–50598. [Google Scholar] [CrossRef]
- Yang, J.; Peng, Z.; Wang, H.; Yuan, H.; Wu, L. The remaining useful life estimation of lithium-ion battery based on improved extreme learning machine algorithm. Int. J. Electrochem. Sci. 2018, 13, 4991–5004. [Google Scholar] [CrossRef]
- Wei, J.; Dong, G.; Chen, Z. Remaining useful life prediction and state of health diagnosis for lithium-ion batteries using particle filter and support vector regression. IEEE Trans. Ind. Electron. 2018, 65, 5634–5643. [Google Scholar] [CrossRef]
- Wang, F.K.; Mamo, T. A hybrid model based on support vector regression and differential evolution for remaining useful lifetime prediction of lithium-ion batteries. J. Power Sources 2018, 401, 49–54. [Google Scholar] [CrossRef]
- Yang, D.; Wang, Y.; Pan, R.; Chen, R.; Chen, Z. State-of-health estimation for the lithium-ion battery based on support vector regression. Appl. Energy 2018, 227, 273–283. [Google Scholar] [CrossRef]
- Zhao, Q.; Qin, X.; Zhao, H.; Feng, W. A novel prediction method based on the support vector regression for the remaining useful life of lithium-ion batteries. Microelectron. Reliab. 2018, 85, 99–108. [Google Scholar] [CrossRef]
- Wang, Z.; Zeng, S.; Guo, J.; Qin, T. Remaining capacity estimation of lithium-ion batteries based on the constant voltage charging profile. PLoS ONE 2018, 13, e0200169. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, Y.; Guo, B. Online capacity estimation of lithium-ion batteries based on novel feature extraction and adaptive multi-kernel relevance vector machine. Energies 2015, 8, 12439–12457. [Google Scholar] [CrossRef] [Green Version]
- Liu, D.; Zhou, J.; Pan, D.; Peng, Y.; Peng, X. Lithium-ion battery remaining useful life estimation with an optimized relevance vector machine algorithm with incremental learning. Measurement 2015, 63, 143–151. [Google Scholar] [CrossRef]
- Song, Y.; Liu, D.; Hou, Y.; Yu, J.; Peng, Y. Satellite lithium-ion battery remaining useful life estimation with an iterative updated RVM fused with the KF algorithm. Chin. J. Aeronaut. 2018, 31, 31–40. [Google Scholar] [CrossRef]
- Yang, D.; Zhang, X.; Pan, R.; Wang, Y.; Chen, Z. A novel Gaussian process regression model for state-of-health estimation of lithium-ion battery using charging curve. J. Power Sources 2018, 384, 387–395. [Google Scholar] [CrossRef]
- Yu, J. State of health prediction of lithium-ion batteries: Multiscale logic regression and Gaussian process regression ensemble. Reliab. Eng. Syst. Saf. 2018, 174, 82–95. [Google Scholar] [CrossRef]
- Peng, Y.; Hou, Y.; Song, Y.; Pang, J.; Liu, D. Lithium-ion battery prognostics with hybrid Gaussian process function regression. Energies 2018, 11, 1420. [Google Scholar] [CrossRef] [Green Version]
- Richardson, R.R.; Birkl, C.R.; Osborne, M.A.; Howey, D. Gaussian process regression for in-situ capacity estimation of lithium-ion batteries. IEEE Trans. Ind. Inform. 2019, 15, 127–138. [Google Scholar] [CrossRef] [Green Version]
- Li, F.; Xu, J. A new prognostics method for state of health estimation of lithium-ion batteries based on a mixture of Gaussian process models and particle filter. Microelectron. Reliab. 2015, 55, 1035–1045. [Google Scholar] [CrossRef]
- Li, Y.; Zou, C.; Berecibar, M.; Nanini-Maury, E.; Chan, J.C.W.; van den Bossche, P.; Van Mierlo, J.; Omar, N. Random forest regression for online capacity estimation of lithium-ion batteries. Appl. Energy 2018, 232, 197–210. [Google Scholar] [CrossRef]
- Mansouri, S.S.; Karvelis, P.; Georgoulas, G.; Nikolakpopoulos, G. Remaining useful battery life prediction for UAVs based on machine learning. IFAC-PapersOnLine 2017, 50, 4727–4732. [Google Scholar] [CrossRef]
- Sun, S.; Zhang, J.; Bi, J.; Wang, Y. A machine learning method for predicting driving range of battery electric vehicles. J. Adv. Transp. 2019, 2019, 4109148. [Google Scholar] [CrossRef]
- Saha, B.; Goebel, K. Battery Data Set, NASA AMES Prognostics Data Repository; NASA Ames: Moffett Field, CA, USA, 2007.
- Miao, Q.; Xie, L.; Cui, H.; Liang, W.; Pecht, M. Remaining useful life prediction of lithium-ion battery with unscented particle filter technique. Microelectron. Reliab. 2013, 53, 805–810. [Google Scholar] [CrossRef]
- Birkl, C. Oxford Battery Degradation Dataset 1; University of Oxford: Oxford, UK, 2017. [Google Scholar]
- Severson, K.A.; Attia, P.M.; Jin, N.; Perkins, N.; Jiang, B.; Yang, Z.; Chen, M.H.; Aykol, M.; Herring, P.K.; Fraggedakis, D.; et al. Data-driven prediction of battery cycle life before capacity degradation. Nat. Energy 2019, 4, 383–391. [Google Scholar] [CrossRef] [Green Version]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Raffel, C.; Ellis, D.P. Feed-forward networks with attention can solve some long-term memory problem. arXiv 2015, arXiv:1512.08756. [Google Scholar]
- Wang, F.K.; Mamo, T.; Cheng, X.B. Bi-directional long short-term memory recurrent neural network with attention for stack voltage degradation from proton exchange membrane fuel cells. J. Power Sources 2020, 461, 228170. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]

| Data | Batteries | Ambient Temperature (°C) | Discharge Current (A) | Rated Capacity (Ah) |
|---|---|---|---|---|
| NASA | #5, #6, #7, and #18 | 24 | 2 | 2 |
| CALCE | CS2_35, CS2_37, and CS2_38 | 25 | 1 | 1.1 |
| Oxford | Cell-1, Cell-2, Cell-3, and Cell-7 | 40 | 1 | 0.74 |
| Toyota | #16, #31, #33, #36, and #43 | 30 | 1 | 1.1 |
| Models | #5 | #6 | #7 | #18 | ||||
|---|---|---|---|---|---|---|---|---|
| MAPE (%) | RMSE | MAPE (%) | RMSE | MAPE (%) | RMSE | MAPE (%) | RMSE | |
| SVR | 1.4125 | 0.0123 | 2.1036 | 0.0190 | 0.6628 | 0.0074 | 1.2730 | 0.0112 |
| MLP | 2.1388 | 0.0174 | 1.6934 | 0.0155 | 0.6953 | 0.0081 | 1.7221 | 0.0145 |
| LSTM with attention | 0.5462 | 0.0078 | 1.1559 | 0.0123 | 0.6348 | 0.0074 | 1.1267 | 0.0112 |
| Battery | Training Data | Models | ||
|---|---|---|---|---|
| SVR | MLP | LSTM with Attention | ||
| #5 | 1–80 | 0.0123 | 0.0174 | 0.0078 |
| 1–100 | 0.0111 | 0.0101 | 0.0047 | |
| 1–120 | 0.0060 | 0.0087 | 0.0058 | |
| #6 | 1–80 | 0.0190 | 0.0155 | 0.0123 |
| 1–100 | 0.0119 | 0.0205 | 0.0072 | |
| 1–120 | 0.0137 | 0.0131 | 0.0073 | |
| #7 | 1–80 | 0.0074 | 0.0081 | 0.0074 |
| 1–100 | 0.0049 | 0.0076 | 0.0047 | |
| 1–120 | 0.0089 | 0.0068 | 0.0046 | |
| #18 | 1–80 | 0.0112 | 0.0145 | 0.0112 |
| 1–100 | 0.0156 | 0.0138 | 0.0129 | |
| 1–120 | 0.0103 | 0.0144 | 0.0094 | |
| Battery | Training Data | Models | |||||
|---|---|---|---|---|---|---|---|
| GPR 1 | HGPFR 1 | WD-HGPFR 1 | SVR | MLP | LSTM with Attention | ||
| Cell-1 | 100–3000 | 0.0600 | 0.0408 | 0.0108 | 0.0085 | 0.0101 | 0.0030 |
| 100–3500 | 0.0525 | 0.0181 | 0.0072 | 0.0079 | 0.0119 | 0.0043 | |
| 100–4000 | 0.0598 | 0.0163 | 0.0108 | 0.0058 | 0.0102 | 0.0032 | |
| Cell-7 | 100–3000 | 0.1026 | 0.0147 | 0.0061 | 0.0079 | 0.0041 | 0.0034 |
| 100–3500 | 0.0833 | 0.0444 | 0.0056 | 0.0034 | 0.0071 | 0.0023 | |
| 100–4000 | 0.0681 | 0.0231 | 0.0145 | 0.0069 | 0.0110 | 0.0037 | |
| Data | Training Set | Testing Set | SVR | MLP | LSTM with Attention |
|---|---|---|---|---|---|
| NASA | #5 and #6 | #7 | 0.0446 | 0.0431 | 0.0310 |
| #18 | 0.0322 | 0.0298 | 0.0232 | ||
| CALCE | CS2_35 | CS2_37 | 0.0339 | 0.0341 | 0.0315 |
| CS2_38 | 0.0246 | 0.0243 | 0.0223 | ||
| Oxford | Cell-1, Cell-2, and Cell-3 | Cell-7 | 0.0212 | 0.0211 | 0.0204 |
| Toyota | #16, #31, and #33 | #36 | 0.0030 | 0.0045 | 0.0027 |
| #43 | 0.0053 | 0.0044 | 0.0034 |
| Data | Training Set | Test Set | R | SVR | MLP | LSTM with Attention | |||
|---|---|---|---|---|---|---|---|---|---|
| RE (%) | RE (%) | RE (%) | |||||||
| NASA | #5 and #6 | #7 | 126 | 94 | 25.40 | 92 | 26.98 | 115 | 8.73 |
| #18 | 97 | 95 | 2.06 | 94 | 3.09 | 98 | 1.03 | ||
| CALCE | CS2_35 | CS2_37 | 721 | 745 | 3.33 | 738 | 2.36 | 721 | 0.00 |
| CS2_38 | 780 | 771 | 1.15 | 763 | 2.18 | 778 | 0.25 | ||
| Oxford | Cell-1, Cell-2, and Cell-3 | Cell-7 | 7000 | 5400 | 22.86 | 5400 | 22.86 | 6000 | 14.29 |
| Toyota | #16, #31, and #33 | #36 | 651 | 654 | 0.46 | 653 | 0.31 | 650 | 0.15 |
| #43 | 644 | 653 | 1.40 | 652 | 1.24 | 645 | 0.16 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mamo, T.; Wang, F.-K. Attention-Based Long Short-Term Memory Recurrent Neural Network for Capacity Degradation of Lithium-Ion Batteries. Batteries 2021, 7, 66. https://doi.org/10.3390/batteries7040066
Mamo T, Wang F-K. Attention-Based Long Short-Term Memory Recurrent Neural Network for Capacity Degradation of Lithium-Ion Batteries. Batteries. 2021; 7(4):66. https://doi.org/10.3390/batteries7040066
Chicago/Turabian StyleMamo, Tadele, and Fu-Kwun Wang. 2021. "Attention-Based Long Short-Term Memory Recurrent Neural Network for Capacity Degradation of Lithium-Ion Batteries" Batteries 7, no. 4: 66. https://doi.org/10.3390/batteries7040066
APA StyleMamo, T., & Wang, F.-K. (2021). Attention-Based Long Short-Term Memory Recurrent Neural Network for Capacity Degradation of Lithium-Ion Batteries. Batteries, 7(4), 66. https://doi.org/10.3390/batteries7040066







