1. Introduction
With the ever-increasing prices of energy and fossil fuels such as gasoline, electrified rail traffic is becoming one of the most common public transportation options for urban residents [
1]. In China, Beijing, Shanghai, and Guangzhou, metro loads accounted for from 1.5% to 2.5% of the city’s total load, which had become the largest single electricity load in the cities [
2]. To cope with the increasing energy consumption problem of the urban rail transit system, the energy-saving operation for electric trains has become a hot topic. At present, on-board hybrid energy storage devices (HESDs) were utilized in some modern railway systems, which can supply traction energy and recover regenerative energy to improve the systems’ energy efficiency [
3,
4].
As an emerging technology, on-board HESDs are usually composed of different types of energy storage devices, namely, batteries (BATs), supercapacitors (SCs), and flywheels, where the hybridization solutions to BATs and SCs are widely applied in electric vehicles and rail transportation [
5,
6]. BATs are well known for their high-energy density and large energy-storage abilities, which are often used to absorb regenerative braking energy [
7]. However, BATs are generally bulky and can withstand a limited lifespan in the driving range of electric trains. Li-ion BATs-driven light rail has been applied in the West Japan railway [
8] and Ni-MH BATs-driven was installed in France tramway [
9]. Alternatively, SCs can achieve a high number of cycle lifetime, such as 80,000 to 100,000 cycles, as well as providing instantaneous high power during traction operation, but face many practical problems associated with their low energy density and relatively higher economic cost [
10]. The simplistic and novel hydrothermal approaches were reported to enhance the electrochemical activity of SCs, and all these results indicate a superb cycling performance after 4000 cycles [
11,
12,
13]. In some urban rail transit systems, e.g., the Hong Kong and Warsaw metro systems, the SCs systems were applied, which can store an amount of energy ranging from 2.8 MJ to 45 MJ [
14]. In addition, flywheels feature a higher stored energy density and a greater life span, while complicated mechanical containment systems and irregular vibration hamper energy efficiency [
15]. The application scenario of flywheel energy storage was also mainly concentrated in heavy haul locomotives [
16]. Based on the abovementioned discussion, adding on-board HESDs to form hybrid powertrain trains could improve the responsiveness of the power source to abrupt load changes during train traction operations and meet the peak power demand. However, the application of on-board HESDs consisting of Li-ion BATs and SCs based on the complementary features of the energy sources remains to be further explored.
The train operation consists of four typical movement modes [
17]: (1) motoring mode, (2) cruising mode, (3) coasting mode, and (4) braking mode. During motoring and cruising operation, the train overcomes the drag resistance or the force due to its gradient and consumes the traction energy from the traction substations (TSSs) and on-board HESDs. In the coasting mode, the train is only affected by the drag resistance or the force due to the gradient. Braking efforts are then applied to reduce the train speed and the regenerative braking energy could be recycled by on-board HESDs in the braking operation. The energy-saving operation for electric trains could result in the minimum energy consumption as well as the optimal train speed profile within a given allowable error under the power split of on-board HESDs and train dynamics constraints [
18].
In recent years, some studies considering both the on-board energy storage devices and the energy-saving operation for electric trains have become increasingly popular. Zhang et al. [
19] introduced the Mixed Integer Linear Programming (MILP) model to optimize the speed profile and the capacity configuration for on-board HESDs, which focused on minimum economic costs considering the long-term train operation. In [
20], the authors showed that the capacity of SCs and speed trajectory for Fuel-cell hybrid trains could be co-optimized to achieve minimum net hydrogen consumption. The distance-based model was proposed to obtain the speed trajectory and capacity solution with energy flow constraints [
21]. By considering the capacity constraints of on-board HESDs, a rule-based energy management strategy was tested in CRRC Qingdao Sifang Co. Ltd, which aimed to improve train operation and optimize hydrogen consumption [
22]. Moreover, many researchers derived some highly nonlinear State of Charge (SOC) models for energy storage devices and revealed the working mechanism between them and train operation through numerous experimental studies. In [
23], a novel dynamic programming method was proposed to reveal the optimal operation control of trains with on-board Li-ion BATs. It concluded that the optimal train speed profile would depend on the SOC for Li-ion BATs, considering the track condition and speed limitations. A peak demand cutting strategy was applied to study the optimal energy-saving solution for the electric trains in the Thailand Silom Line, where the initial SOC of the on-board energy storage system had a huge effect on train operation [
24]. Xia et al. [
25] proposed an SOC-based energy management strategy, where the SCs could reduce the power dissipation of the train and voltage stress of the traction power grid. In [
26], a coordinated optimal decision-making method based on train operation and on-board BATs was established, subject to the dynamic performance of the train and SOC. In most previous and proceeding papers, the train operation and power split of on-board HESDs were not jointly optimized, and the initial SOC and capacity were only set as fixed parameters, which reduced the applicability of the model to electrified rail systems.
In addition to the important electrical parameters (SOC and capacity) of on-board HESDs, the degradation behavior of the BATs is also of considerable importance in the energy-saving operation of electric trains. Considering long-term train operation, the impact of the BATs’ degradation on the energy-saving operations of electric trains could not be ignored due to its significant impact on the system’s energy-saving performance. There are two common approaches to exploring the BATs’ degradation: one is to build an electrochemical model, and the other is to develop a traditional empirical model [
27]. Although the former could accurately predict actual degradation behavior within the BATs, it relied heavily on theory and was difficult to apply under practical conditions [
28]. The latter required a large amount of data to fit the model parameters, but could not accurately represent the train operation and load profiles, since it was only valid under specific experimental conditions [
29]. Zhang et al. [
30] carried out a series of overcharge tests for ternary power BATs and evaluated the degradation characteristics of electrochemical models from microscopic perspectives. Li et al. [
31] developed a novel deep learning algorithm to quantify the battery degradation phenomenon and explored the aging characteristics, where the estimation error was no greater than 3%. In [
32], the authors analyzed the effect of complex vibration conditions on the degradation effect of Li-ion BATs during train operation. In [
33], the authors selected different stress factors to explore the health feature of Li-ion BATs from a physics-based perspective. A hybrid estimation method based on incremental capacity and back-propagation neural network was proposed to accurately estimate of the state of health (SOH) of the Li-ion BATs [
34]. The common features of the abovementioned works are that the majority were restricted to the applications of electric vehicles and the impact of BATs’ degradation behavior on the energy-saving operation for electric trains was not fully considered.
The above review shows that the energy-saving operation for electric trains is discussed, while on-board HESDs are not involved or only a few properties of energy storage devices as fixed parameters are taken into account. Numerous studies have been conducted to evaluate the energy-saving potential of on-board energy storage devices, as summarized in
Table 1. Although the integration of on-board HESDs in the traction system are considered to be an important and effective method for energy-saving operations, the energy-saving performance can be greatly affected by other factors. The mechanism is complicated and we need a complete integrative model to fully investigate and evaluate energy-saving performance. Based on the above discussion, this paper focuses on the problem of energy-saving operations for electric trains with on-board HESDs consisting of Li-ion BATs and SCs, while the properties of on-board HESDs (capacity, SOC, and degradation mechanisms) are introduced and investigated. The contributions of this article are outlined as follows.
- (1)
A novel time-based, mixed-integer, linear programming (MILP) model is developed, which could simplify and solve the derivative operations and the product operation of multiple time-varying parameters in complex nonlinear electrified rail transit systems by employing the proposed piecewise linearization (PWL) method. In some of the existing literature, the traction power systems are equivalent to infinite power sources [
35] or the line impedance is neglected [
26]. In this study, the proposed integration power flow model based on the train longitudinal dynamics, power split of on-board HESDs, and line impedance can further improve the accuracy of the system.
- (2)
This paper focuses on three important engineering characteristics of on-board HESDs (i.e., capacity, initial SOC, and degradation), further analyzes how these engineering characteristics affect the energy-saving operation of electric trains from the perspective of operations research, and reveals the intrinsic mechanism. The optimal energy-saving operation of electric trains under the different operating conditions of on-board HESDs can be located, where the corresponding train speed trajectory, power split of on-board HESDs and the solution of minimum net energy consumption (NEC) are all obtained. The optimization results provide clear guidance for real-world engineering applications.
Table 1.
Summary of the relevant studies on the modeling methods.
Table 1.
Summary of the relevant studies on the modeling methods.
| Publication | Objective/ Method | Consider SOC and Capacity | Consider Degradation Mechanism | Consider TSSs Model |
|---|
| Zhang et al. [19] | Minimum NEC/ MILP | Yes only optimized capacity | Yes | No |
| Meng et al. [20] | Minimum net hydrogen consumption/ MILP | Yes only optimized capacity | No | No |
| Sumpavakup et al. [24] | Maximize total saved energy/ Genetic algorithm | Yes only optimized SOC | No | Yes |
| Yang et al. [26] | Minimum cost / Mixed integer nonlinear programming | Yes only optimized SOC | No | No |
| Xiao et al. [36] | Minimum energy consumption/ Dynamic programming | Yes only optimized SOC | No | Yes |
| Wu et al. [35,37] | Minimum NEC/ MILP | Yes only optimized capacity | Yes | No |
| Kim et al. [38] | Minimum energy consumption/ Dynamic programming | Yes only optimized SOC | No | No |
| Zhang et al. (this work) | Minimum NEC/ MILP | Yes optimized | Yes | Yes |
The remainder of this paper is organized as follows.
Section 2 provides a detailed system setup of eanelectric train with on-board HESDs. In
Section 3, the system model is elaborated, where the train longitudinal dynamics, on-board HESDs, the traction power system, energy flow modeling, constraints, and objective are shown.
Section 4 covers the optimization results and a detailed discussion of different case studies. Finally, the conclusion is provided, along with a discussion of future work, in
Section 5.
2. The System Setup of the Electric Train with On-Board HESDs
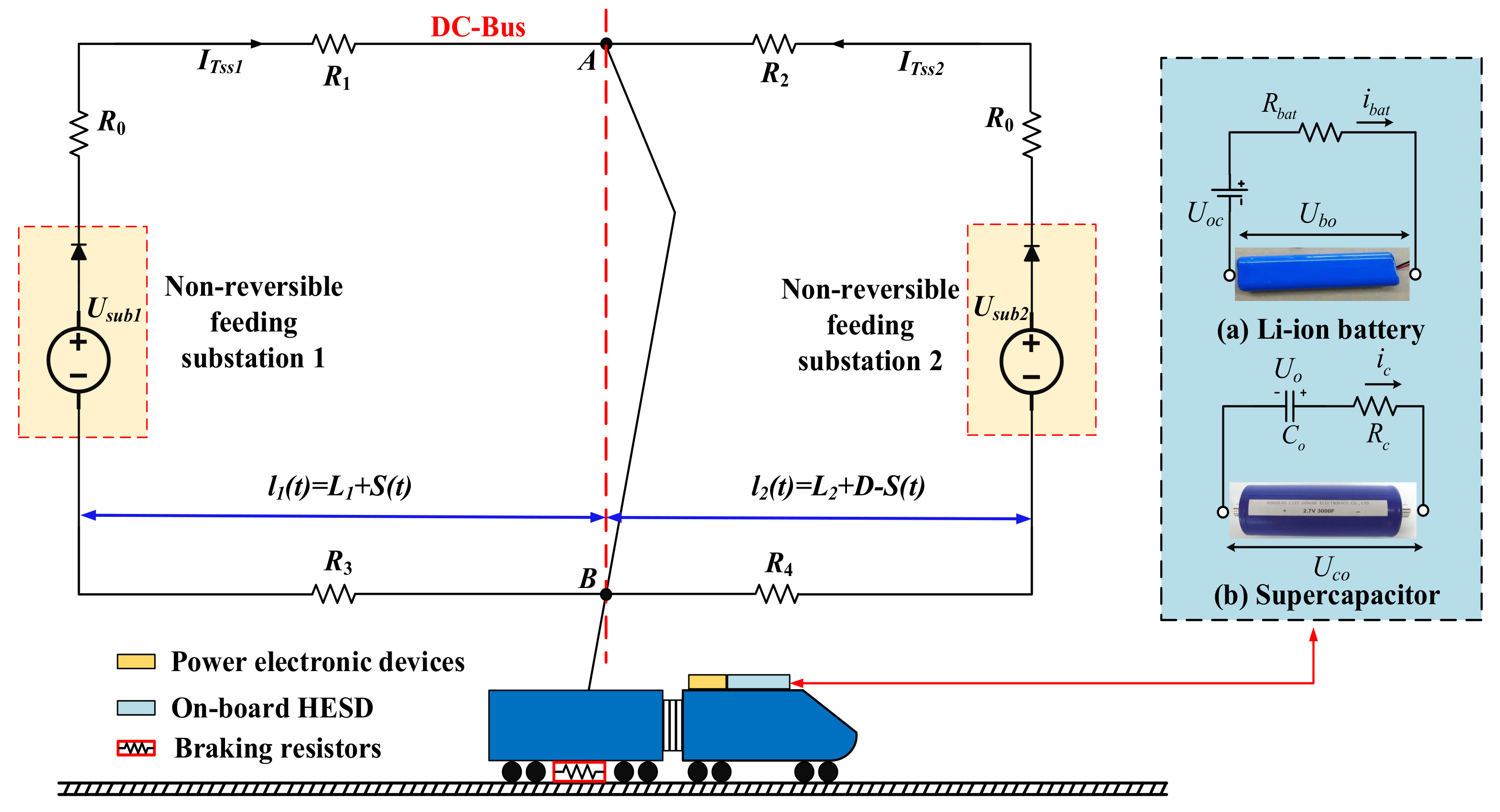
The schematic diagram of an electric train with on-board HESDs is shown in
Figure 1. The system has the following components: Li-ion battery packs (MV06203127NTPCA, manufactured by Microvast Power), supercapacitor modules (BMOD0063-P125-B08, manufactured by Maxwell), DC-DC converters, and the traction motors associated with the braking resistors and non-reversible feeding substations. In the circuit topology, the electric train is supported by Li-ion BATs, SCs, and non-reversible feeding substations, where these energy sources are connected to the electric train load through DC-DC converters or DC bus.
Many researchers have found that the use of on-board HESDs allows for a more flexible system, where SCs and Li-ion BATs can improve the power density and energy density of the integrated system, respectively [
19,
39,
40]. After considering the optimized scenarios and commonly used commercial components, the proposed integrated system in this work is mainly composed of: (1) each cell for Li-ion BATs is 10 Ah and 2.3 V. When the rated charge/discharge rate is 4 C, the rated charging power is −93.3 W and rated discharging power is 93.3 W [
22]; (2) each module for BMOD0063-P125-B08 supercapacitor is 63 F, which is specifically designed for heavy transport applications such as electric trains, trolleys, cranes, etc. The electric energy is 0.14 kWh, and the rated power is 130 kW [
41]; (3) the rated DC output voltage and power of the traction substation are 1500 V and 3 MW, respectively [
36]. The main specifications of each system of the train are shown in
Table 2. It should be noted that detailed models for power electronics and efficiency are not considered, that is, the power dissipated in DC-DC converters is not included in this study.
In addition, the scheme of non-reversible feeding substations means that the regenerative braking energy could not be transmitted back to the grid through the DC bus. Although it is interesting to integrate a reverse power flow into electric transportation systems to generate more efficient energy reuse solutions, its scalability, cost, and complexity due to the high coupling hinder further development [
42]. In addition, the solution to reverse power flow has not been diffused because the troubles of multi-level energy source cooperative control need to be solved.
4. Case Studies and Result Discussion
- •
In
Section 4.1, we aimed to reveal the impact of the different capacity of on-board HESDs on the train operation, where case 1 is assumed to be unequipped with on-board HESDs as a comparison. Here, for the sake of compactness, cases 2–3 are selected, where the parameters can be easily modified in the model. The optimal energy-saving operation for electric trains and power split for on-board HESDs are only displayed when the capacity is changed under capital cost constraints.
- •
Based on the optimization results in
Section 4.1, we aimed to reveal the impact of the different initial SOC on the train operation and further explore the energy-saving potential of on-board HESDs. Similarly, three typical initial SOC values are selected in cases 4–6, which correspond to the minimum allowable value, the middle value, and the maximum allowable value, respectively.
- •
Based on the optimization results in
Section 4.1 and
Section 4.2, on-board HESDs with optimal capacity and initial SOC were selected to reveal the impact of degradation on train operation. Cases 7 and 8 correspond to fresh and end-of-life cells, respectively, which fully demonstrate the significant differences in optimal train operation and power split strategies under different states of health.
The different cases for on-board HESDs configuration scenarios were discussed using a real route based on the data from the Guangzhou Metro Line 7. The route covers 3028 m, two feeding electricity TSSs, and three stations, where the route structure is shown in
Figure 4. The main parameters were tabulated in
Table 3. The mass of the train for AW2 in Guangzhou metro line 7 is 279.1 tons without on-board HESDs, and the maximum operational speed cannot exceed 80 km/h. The maximum acceleration
and deceleration
are both set at
.
The average energy efficiency of on-board HESDs
and
is set to be 0.9 considering negligible transmission loss [
19]. In [
44,
45], the efficiency of the advanced DC and induction motors are about 90–94% and 93–95%, respectively, and then approximately set as 90%. By exploring the model,
is shown to provide a better compromise between computational burden and accuracy. As mentioned in [
17], the maximum traction power and braking power are obtained in the field test, as well as maximum tractive effort and braking effort. All of these parameter values in
Table 3 can be modified according to the field data collected from different types of traction power systems and on-board HESDs. This paper presents a simulation where the used parameters are provided by the Guangzhou metro line 7 for journeys from Guangzhou South Station to Xiecun Station.
Table 4 shows the scheduled information of railway vehicles.
4.1. Impact of Different On-Board HESDs Capacity on Train Operation under Capital Cost Constraints
In this subsection, the influence of different on-board HESDs capacities on power split and train operation under capital cost constraints is investigated. As a comparison, the capacity of on-board HESDs in Case 1 is assumed to be 0 MJ, to indicate that the train is not equipped with on-board HESDs. Concerning cases 2 and 3, the specific capacity configuration of on-board HESDs and optimization results are shown in
Table 5. The initial SOC for the on-board HESDs is 50% for cases 2 and 3, which can be modified in the model.
As shown in
Figure 5 and
Figure 6, the optimal operation of the train and power split show substantial differences when the capacity and power of on-board HESDs are different in cases 1–3. From
Figure 5, when the railway vehicle operates without on-board HESDs in case 1, this means that the trains cannot recover and reuse regenerative braking energy through electrical braking. It should be noted that the train operation conforms to the law of conservation of energy, and when the output power is less than 0, this means that the on-board HESDs are in the charging state. In
Figure 6, it can be observed that the propulsion energy of the train mainly comes from the non-reversible feeding TSSs and discharge energy from on-board HESDs during traction operation. Subsequently, the potential energy of the train caused by height differences can be converted into kinetic energy, on-board HESDs energy, and heat energy. During the train’s braking operations, the kinetic energy can be converted into electrical energy, which can be recovered by the on-board HESDs. In addition, it is evident that the charge/discharge rate of SCs is significantly faster than that of Li-ion BATs due to their respective characteristics. The SCs are discharged to a minimum SOC value, i.e., 30% during traction operation, and charged to a maximum SOC value, i.e., 90% during braking operation, while the SOC of the Li-ion BATs slowly changes throughout the journey.
As shown in
Figure 6 and
Figure 7, the energy consumption and peak power of the feeding TSSs in case 3 are lower than that in case 2, and the on-board HESDs in case 3 can recover and reuse more braking energy, which results in a minimal NEC solution in case 3.
The relationship between the NEC and different maximum power of on-board HESDs under varying capital cost constraints is illustrated in
Figure 8.
Figure 8 shows that, with the increase in the maximum power and capacity of on-board HESDs, the solutions of NEC first drop quickly and then slightly increase. When the maximum power of the Li-ion BATs and the SCs is 1049.6 kW and 1560 kW, respectively, the proposed model obtains the optimization solution and the minimum NEC, which is 44.01 MJ.
Figure 9 illustrates the detailed trend shownig how the total power and mass of on-board HESDs influence the NEC solutions. It clearly indicates that even though the maximum power of on-board HESDs continually increases, the NEC cannot be continuously reduced, and even raises slightly due to the increase in the total mass of on-board HESDs, and the NEC solutions slightly increased from 44.01 MJ to 46.98 MJ. This further reveals that, with the given railway line and journey time, the optimal on-board HESDs’ power split scheme can achieve the unique minimum NEC solution, which allows for railway planners and operators to avoid an unnecessary waste of on-board HESDs capacity and reduce operation costs.
4.2. Impact of Different Initial SOC of On-Board HESDs on Train Operation
This subsection aims to further explore the impact of the different initial SOC for on-board HESDs, which is another important engineering characteristic of on-board HESDs and impacts train optimal operation. In cases 4–6, the maximum power of the Li-ion BATs and the SCs were uniformly set at 1049.6 kW and 1560 kW, respectively. The initial SOC for the on-board HESDs was set to 30%, 60%, and 90% in cases 4–6, respectively. The parameters and optimal results for cases 4–6 are tabulated in
Table 6.
When the initial SOC of on-board HESDs is different, it indicates that on-board HESDs power split schemes for different cases need to meet the constraints of the proposed model and achieve the energy-saving operation for electric trains. In
Figure 10 and
Figure 11, the speed trajectory for case 4 does not demonstrate a notable change compared with case 5, while the power profiles of on-board HESDs and the feeding TSSs have significant differences. As shown in
Figure 11a, when the journey time ranges from 0 s to 24 s, the propulsion energy of the train only comes from the feeding TSSs, and on-board HESDs cannot be allowed to discharge to support traction operations due to their minimum allowable SOC value. Therefore, a higher NEC value is observed in case 4 and the maximal peak power is found from the feeding TSSs consumed by the train. However, it can be observed that on-board HESDs with a higher initial SOC are not always preferred in terms of NEC values. From
Figure 11c, it is easily noted when the train operates from 6 s to 14 s and 104 s to 112 s, the traction energy of the train mainly derives from the on-board HESDs.
This results from on-board HESDs with excessive initial SOC because, for energy-saving operations, they need to be discharged first to obtain sufficient rechargeable capacity for subsequent braking operations. As shown in
Figure 12, although the traction energy consumption from the feeding TSSs in case 4 was significantly higher than that in case 6, the frequent discharging process undermines the energy-saving potential.
Based on the above optimization results,
Figure 13 further depicts the relationship between the different initial SOC of on-board HESDs and the NEC, which helps railway vehicle operators to dynamically adjust the charging/discharging strategy of on-board HESDs and take full advantage of on-board HESDs for energy-efficient operation. In
Figure 13, the initial SOC range of on-board HESDs is from 30% to 90% with an increment step of 10%, and when the initial SOC of Li-ion BATs and SCs is set as 50% and 70%, the proposed model obtains the minimum NEC, i.e., 43.61 MJ. In addition, a lower or excessive initial SOC cannot obtain the optimal NEC solution for the given railway line and journey time conditions. It can be concluded that the optimization results for different initial SOCs show substantial differences, and we need to obtain a trade-off between the initial SOC of Li-ion BATs and SCs to improve the energy-saving potential of on-board HESDs.
4.3. Impact of the Degradation of Li-Ion BATs on Train Operation
The cases above all operate under the assumption that the optimization problem is solved over a horizon (train travel distance) that is a negligible fraction of the total distance to reach the on-board HESDs’ end of life. In other words, the influence of the on-board HESDs’ degradation process on the train operation can be neglected. However, in real operation, on-board HESDs would suffer from degradation considering the long-term train operation. Concerning SCs, they can achieve a longer cycle lifetime, e.g., from 80,000 to 100,000 cycles, as previously mentioned [
10]. Therefore, from the perspective of long-term energy-saving operation, it also seems logical to focus only on exploring the impact of the degradation behavior of Li-ion BATs with a limited lifespan on train operation.
Figure 14 shows the schematic representation of the electrochemical Li-ion battery function, which consists of three regions: an anode (negative electrode), a separator, and a cathode (positive electrode). During the discharging operation, the electrons and ions simultaneously flow from the anode to the cathode through an external circuit and electrolyte, respectively. The process is reversed, and the ion flow is from the cathode to the anode during the charging operation. The performance of Li-ion BATs irreversibly generates deterioration after long-term charging and discharging operations. The determining factors for Li-ion battery degradation are usually defined as capacity fading and internal resistance rising [
46].
- (1)
Capacity fading: During the Li-ion BATs operatiom, the chemical reaction between the anode and the electrolyte and the simultaneous consumption of lithium ions would lead to capacity fading. Keeping the Li-ion BATs at a high cycling rate would enhance the degradation degree [
47]. The capacity fading of Li-ion BATs would shorten the electric trains’ achievable range and it is considered to reach the end-of-life when the available capacity is 80% of the nominal capacity [
48].
- (2)
Internal resistance rising: After long-term cycling of Li-ion BATs, the decrease in accessible surface area due to continuous solid electrolyte interphase (SEI) growth can also cause internal resistance to rise. Charge/discharge operation or high temperatures tend to accelerate the degradation process [
47]. The internal resistance raises, thereby reducing the available output power of the Li-ion BATs, and increased to 160% of its original value under the reference operating conditions, which is typically considered to be the end-of-life [
49,
50].
For the analysis stated above, the presence and extent of different Li-ion BATs degredation mechanisms and their multiple interaction relationships make it very complicated to accurately model and estimate the impact of degradation behaviors on optimal train operation. The purpose of this subsection is to synthesize the key degradation parameters of Li-ion BATs (i.e., their capacity and internal resistance) for a sensitivity analysis from an operations research perspective, as well as to reveal the effect of degradation behavior on NEC values in the context of transportation planning problems. The analytical method combines the advantages of the electrochemical modeling approach and traditional empirical approach, and is thus simpler than the former while being applicable to broader conditions than the latter. Here, we used the optimization results in
Figure 13 as an example to further explore the influence of Li-ion battery degradation behavior on train operation. The parameters and optimal results for cases 7–8 are tabulated in
Table 7.
In case 7, the degradation of the Li-ion BATs was not considered for comparison, and they were treated as fresh cells. Therefore, the capacity fading ratio and the internal resistance rising ratio are 0. From
Figure 15 and
Figure 16, it can be observed that the railway vehicle tends to utilize longer braking distances as well as the charging process for energy-saving operation in case 8 when the journey time ranges from 38 s to 90 s.
Furthermore, the maximum charge/discharge power of the Li-ion BATs in case 8 is significantly less than that in case 7, which indicates that, as the internal resistance increases, the Li-ion BATs should be employed as little as possible to avoid unnecessary internal energy loss. Therefore, it can be concluded that the train needs to dynamically adjust the initial optimal speed trajectory with the increase in the degradation degree of the on-board Li-ion BATs. In other words, the energy-saving potential of degraded Li-ion BATs is more dependent on the power split strategy, especially when the internal resistance increases and the electric trains tend to consume more energy from the feeding TSSs rather than Li-ion BATs. Compared to fresh cells, the degraded Li-ion BATs could no longer implement the initial power split strategy, which leads to greater internal losses.
Based on the above optimization results,
Figure 17 further depicts the relationship between the NEC solutions and capacity fading ratio and resistance rising ratio, whose performances are the key factors concerning the railway energy systems planners and operators after considering the degradation of Li-ion BATs due to the long-term train operation. From
Figure 17, it should be noted that the NEC solutions increase more slowly when the capacity fading ratio of the Li-ion BATs rises. The NEC solutions for the internal resistance rising ratio of Li-ion BATs are more sensitive, and lead to higher NEC solutions in some spaces. The results clearly show that the increase in internal resistance caused by high temperature or over-charge/discharge operations is more worthy of our attention than the capacity degradation, which would greatly reduce the available output power of Li-ion BATs and is the main factor undermining the energy-saving operation for electric trains.
4.4. The Analysis of Energy-Saving Potential
The net energy consumption and energy-saving rate for cases 2–8 are plotted in
Figure 18. Note that the energy-saving rate of the abovementioned cases is calculated in reference to case 1 without on-board HESDs.
Figure 18 shows that by optimizing the capacity and initial SOC of on-board HESDs, it is indeed possible to achieve energy-saving operation for electric trains in the given journey.
When the initial SOC of the on-board HESDs remains unchanged in cases 2 and 3, the NEC decreases and the energy-saving rate rises by increasing the maximum power and capacity of the on-board HESDs. However,
Figure 8 clearly shows that by continuously increasing the power and capacity of the on-board HESDs, the NEC solutions slightly increase due to the increase in total mass. As a result, the minimum NEC can only be obtained when the power and capacity of the on-board HESDs change and the initial SOC remains unchanged. In addition, the lower or excessive initial SOC of the on-board HESDs could undermine the energy-saving potential of integrated systems in cases 4–6 when the optimal capacity is obtained. It is worth mentioning that although the energy-saving rate of railway vehicles could reach up to 41.57% in case 7, after considering the long-term train operation, the energy-saving rate would drop to 31.90% in case 8 due to the degradation of Li-ion BATs. The optimization results provide clear guidance on how to select and utilize on-board HESDs and avoid unnecessary waste in real engineering applications.
5. Conclusions
In this paper, a time-based MILP model was developed, which aims to optimize the energy-saving operation of electric trains equipped with on-board HESDs in DC railway systems. The main attractiveness of the proposed integration power flow model resides in the combination of the optimal energy-saving operation with the emerging on-board HESDs under different constraints. The minimum NEC solution can be obtained to reveal the energy-saving potential of on-board HESDs in practical engineering applications, which are the key factors in railway energy system planners and operators. In addtion, the real-world train operation data from Guangzhou Metro Line No.7 and mature commercial components are applied in the proposed model.
Based on the abovementioned case studies, it can be concluded that different capacity of on-board HESDs would change the energy-saving operation for electric trains and charging/discharging strategy, which leads to notable differences in the train speed trajectory and power split. More specifically, the NEC value is reduced to 44.01 MJ when the maximum power of the Li-ion BATs and the SCs is 1049.6 kW and 1560 kW, respectively. However, the NEC value would not be continuously reduced, and could even rise slightly due to the increase in the total mass of on-board HESDs, which increased slightly from 44.01 MJ to 46.98 MJ. Furthermore, the lower or excessive initial SOC for on-board HESDs would undermine the energy-saving potential of the integrated system. It can be observed that the proposed model obtains the minimum NEC, i.e., 43.61 MJ, under different initial SOC constraints for on-board HESDs. Overall, the research results show that the optimal energy-saving operation equipped with on-board HESDs requires trade-offs under different capacities and initial SOC constraints. Considering the degradation of Li-ion BATs due to the long-term train operation, the increase in internal resistance leads to a lower available output power and higher NEC compared with capacity fading. The degradation changed the energy-saving operation for electric trains and the NEC value, where the energy-saving rate decreased from 41.57% to 31.90%. In short, based on the proposed integration power flow model, the optimization results show significant correlations between on-board HESDs and energy-saving operation for electric trains, which further demonstrate the necessity of research.
In future work, it is our intention to extend the existing research, considering more complex traffic and energy system setups, such as by involving wayside energy storage devices, multiple electric trains and or distributed energy sources such as photovoltaics and wind power.