A State of Charge Estimation Approach for Lithium-Ion Batteries Based on the Optimized Metabolic EGM(1,1) Algorithm
Abstract
1. Introduction
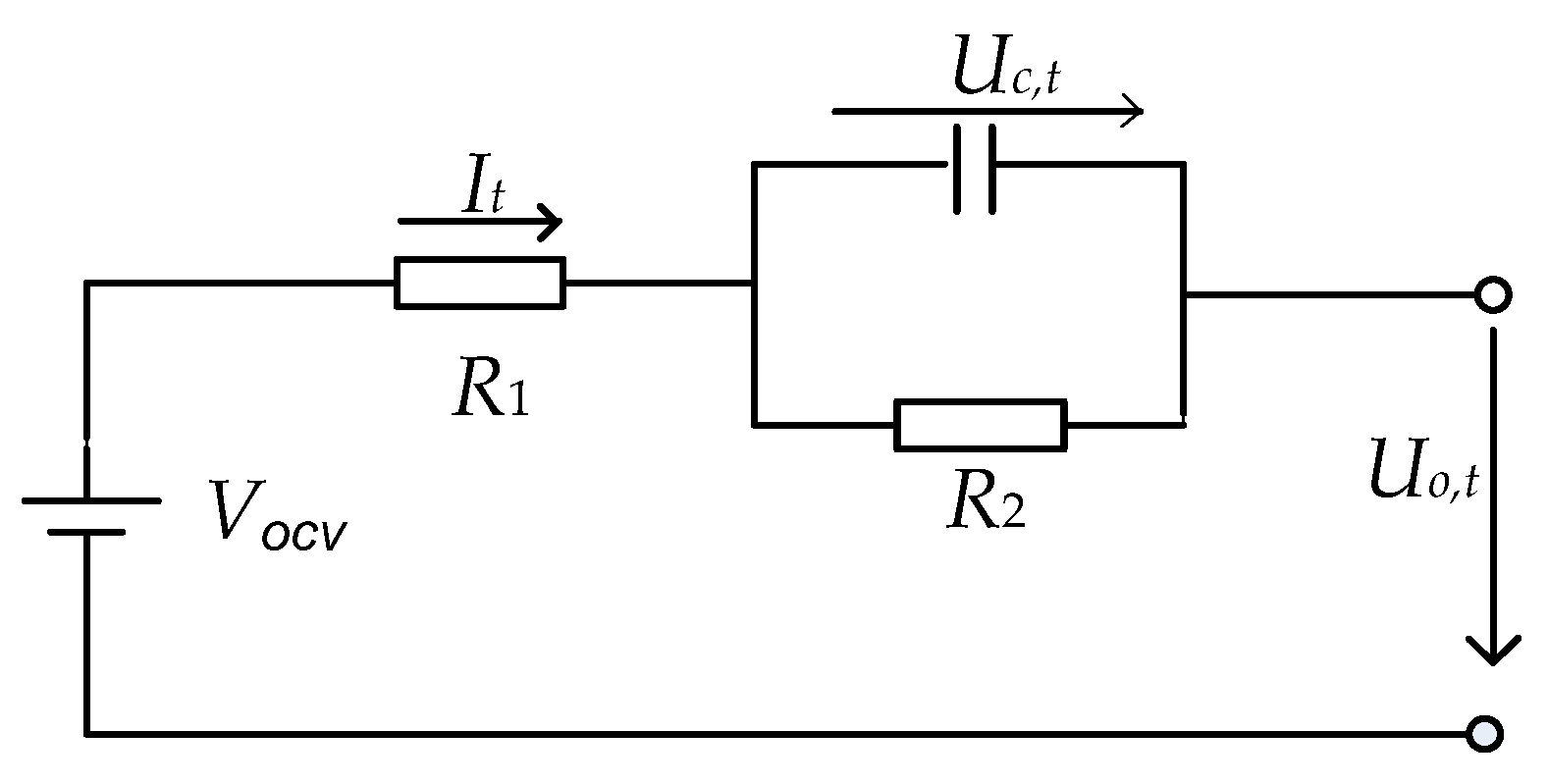
2. Lithium-Ion Batteries’ Modeling
3. Estimation Mechanism Based on Optimized MEGM(1,1)
3.1. General Principle of GM(1,1)
3.2. Principle of Optimized MEGM(1,1)
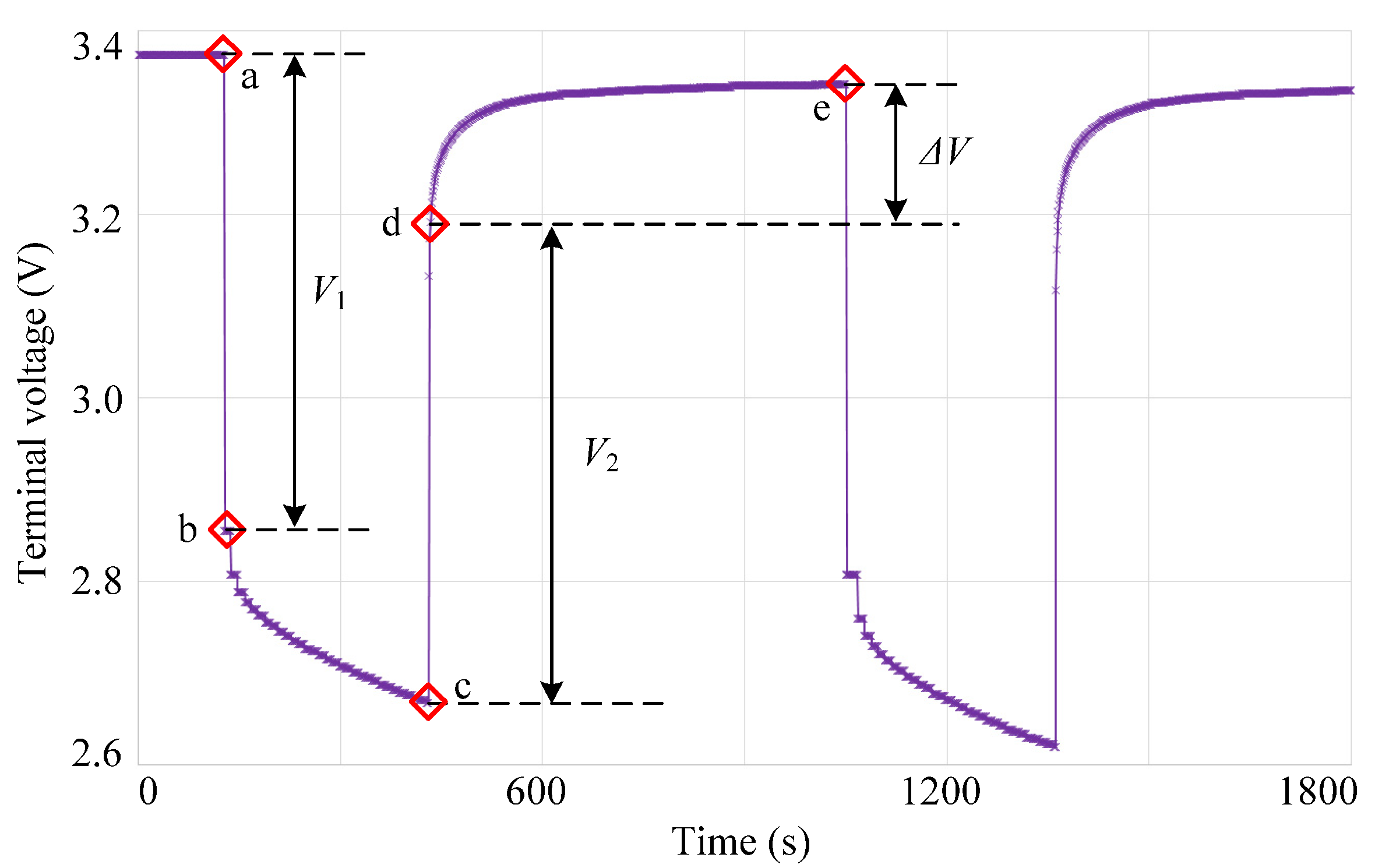
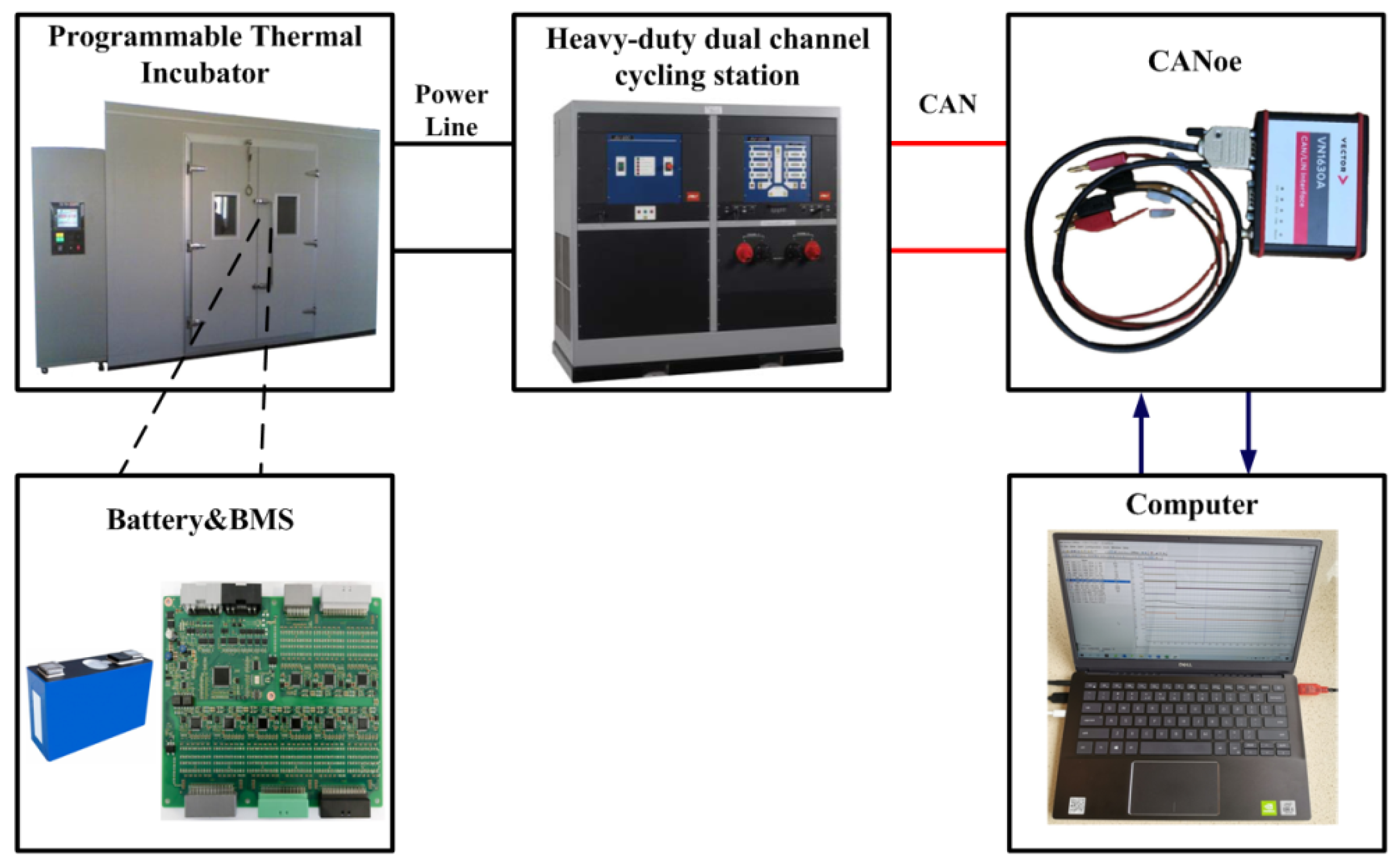
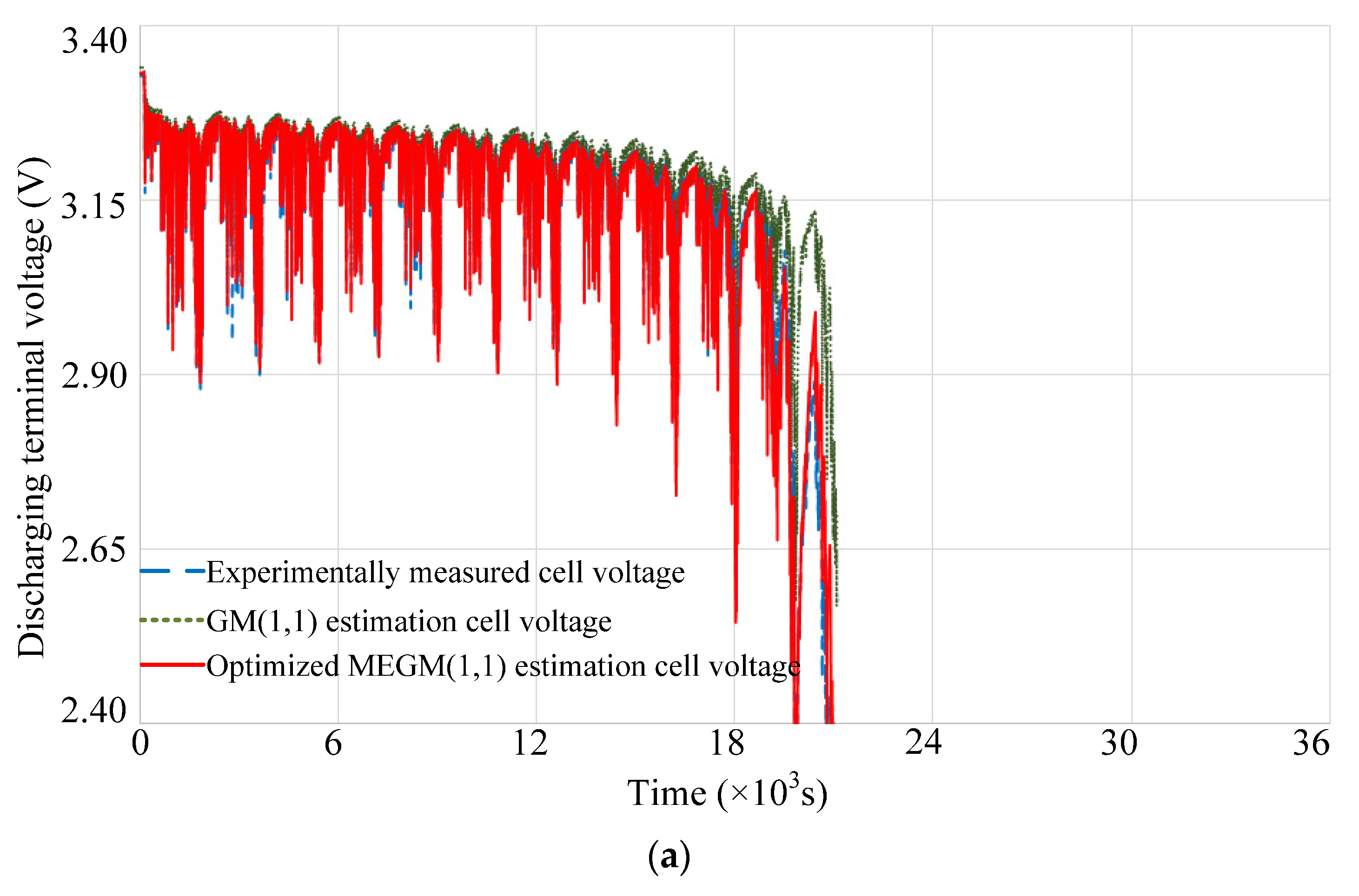
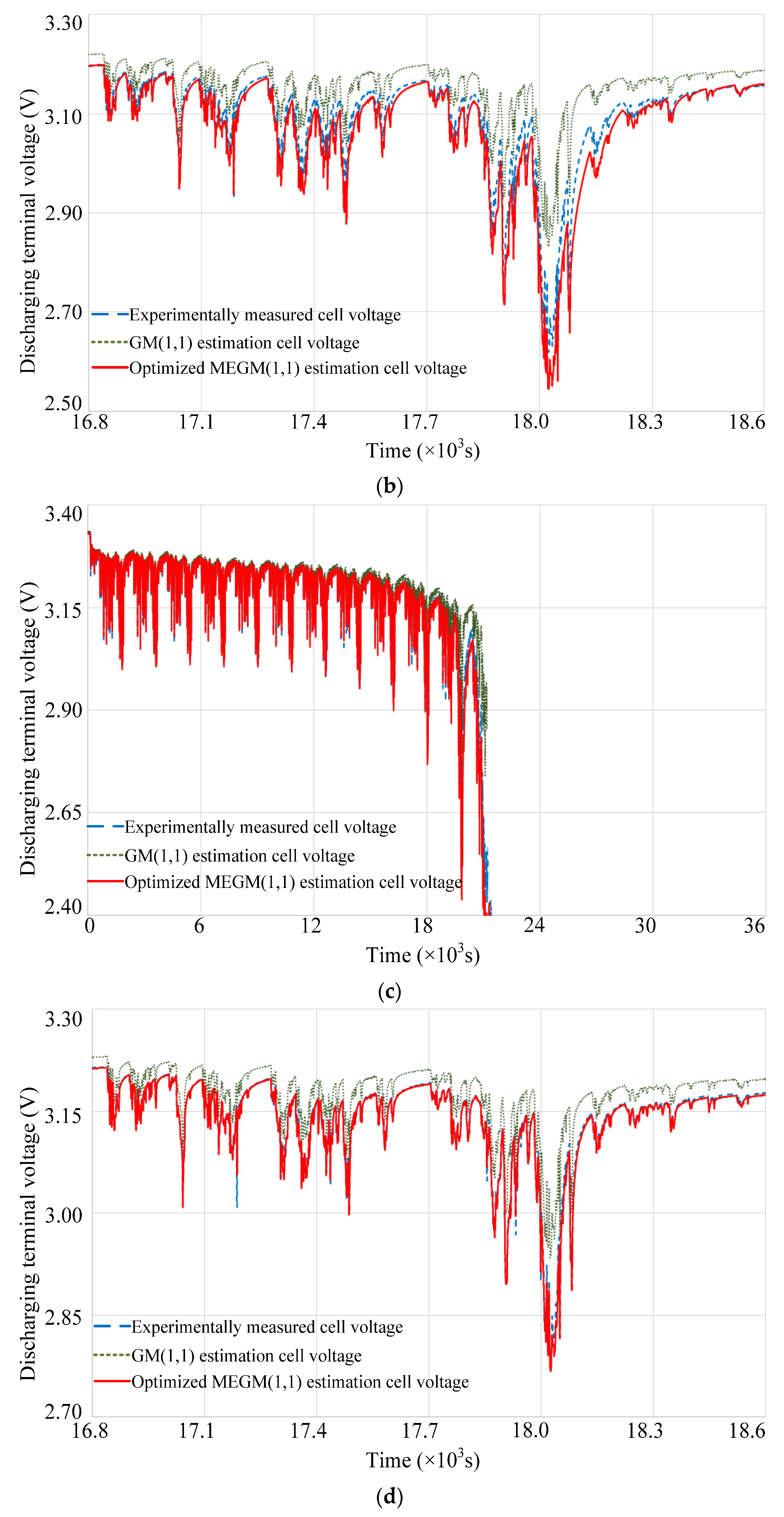
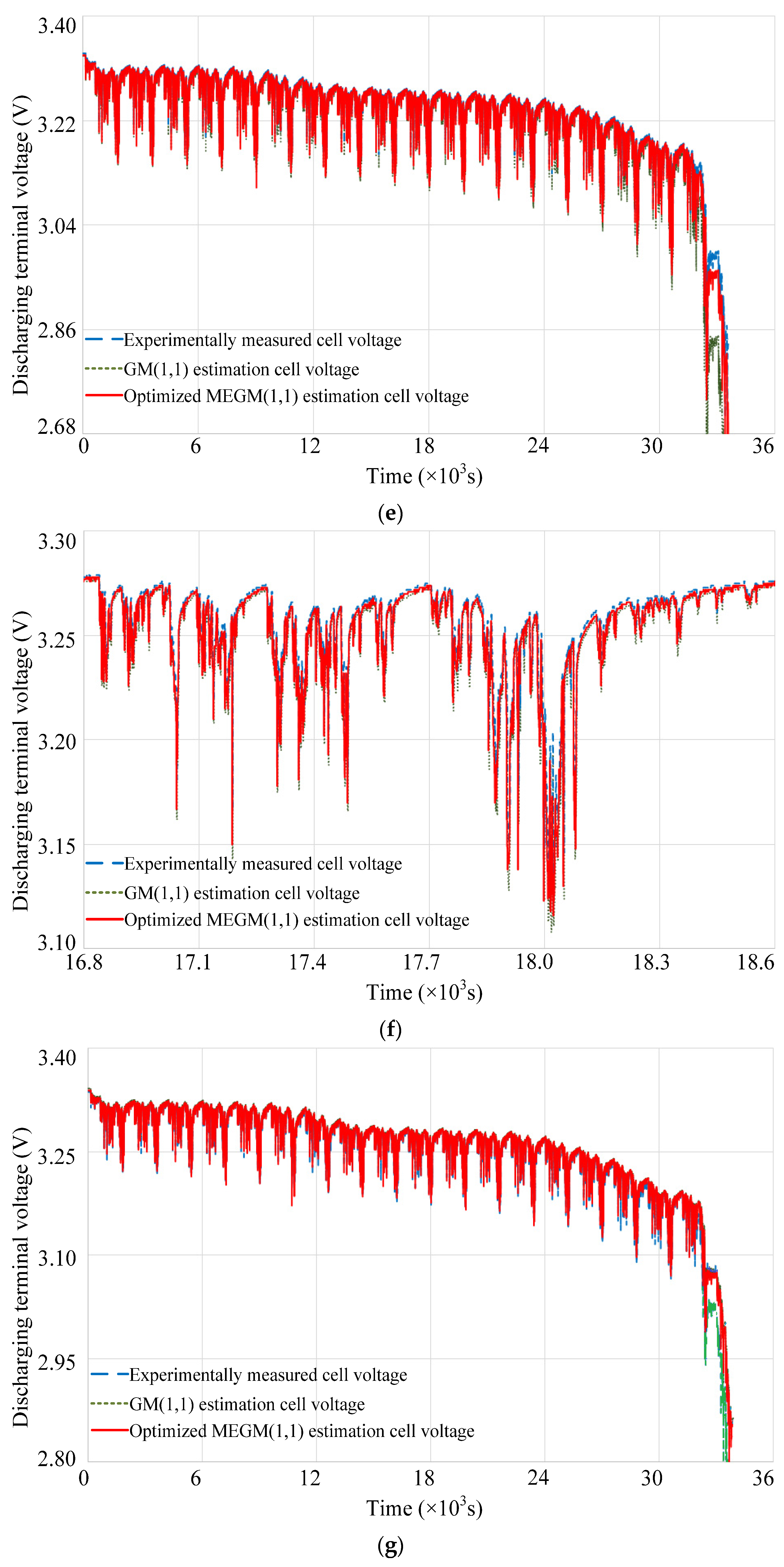
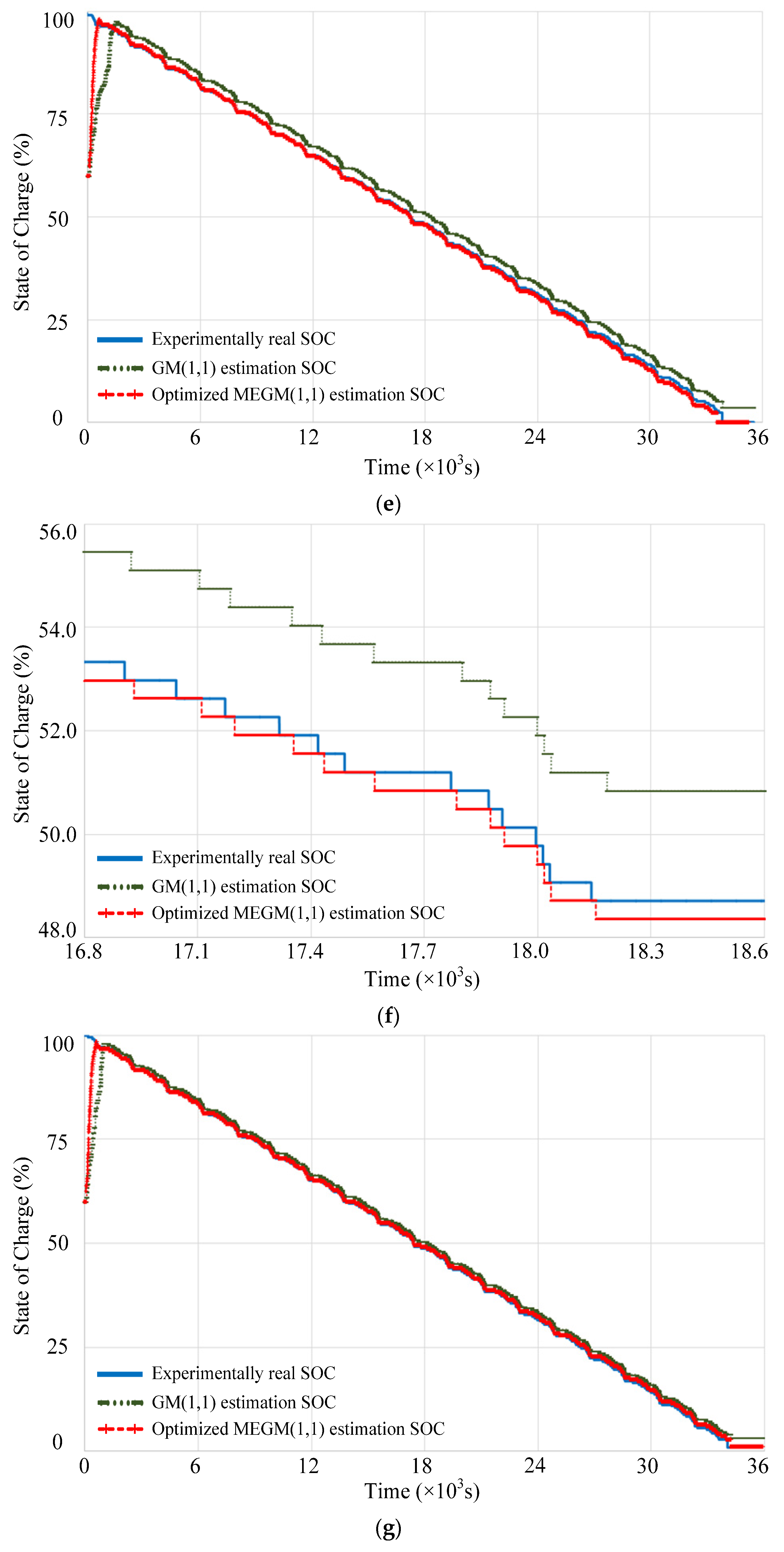
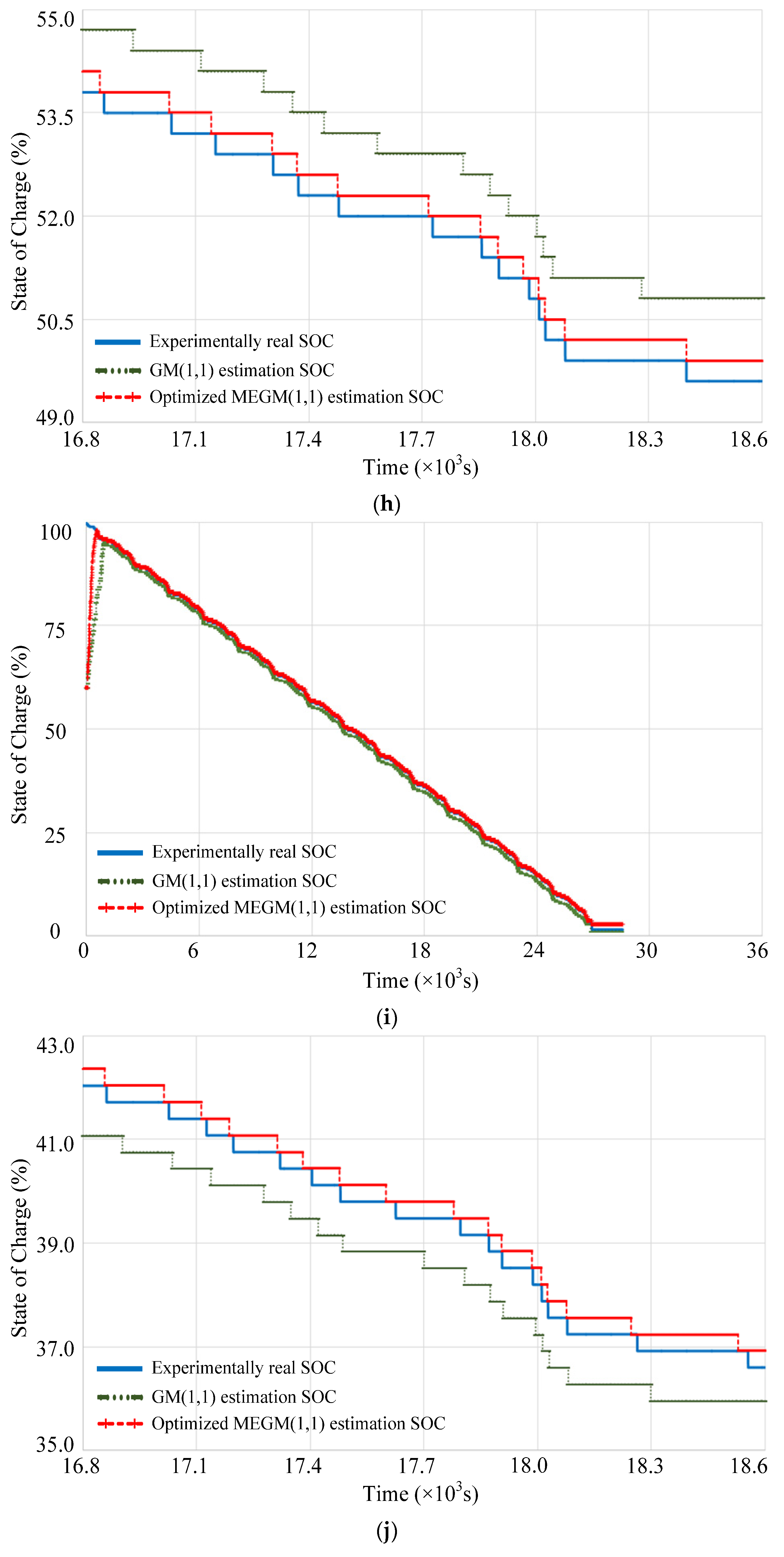
4. Experimental Verification and Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kurzweil, P.; Frenzel, B.; Scheuerpflug, W. A Novel Evaluation Criterion for the Rapid Estimation of the Overcharge and Deep Discharge of Lithium-Ion Batteries Using Differential Capacity. Batteries 2022, 8, 86. [Google Scholar] [CrossRef]
- Li, A.; Yuen, A.C.Y.; Wang, W.; Chen, T.B.Y.; Lai, C.S.; Yang, W.; Wu, W.; Chan, Q.N.; Kook, S.; Yeoh, G.H. Integration of Computational Fluid Dynamics and Artificial Neural Network for Optimization Design of Battery Thermal Management System. Batteries 2022, 8, 69. [Google Scholar] [CrossRef]
- Dubarry, M.; Beck, D. Analysis of Synthetic Voltage vs. Capacity Datasets for Big Data Li-ion Diagnosis and Prognosis. Energies 2021, 14, 2371. [Google Scholar] [CrossRef]
- Zhang, S.; Guo, X.; Dou, X.; Zhang, X. A rapid online calculation method for state of health of lithium-ion battery based on coulomb counting method and differential voltage analysis. J. Power Sources 2020, 479, 228740. [Google Scholar] [CrossRef]
- Solaymani, S. CO2 emissions patterns in 7 top carbon emitter economies: The case of transport sector. Energy 2019, 168, 989–1001. [Google Scholar] [CrossRef]
- Theiler, M.; Schneider, D.; Endisch, C. Kalman Filter Tuning Using Multi-Objective Genetic Algorithm for State and Parameter Estimation of Lithium-Ion Cells. Batteries 2022, 8, 104. [Google Scholar] [CrossRef]
- Sun, Q.; Lv, H.; Wang, S.; Gao, S.; Wei, K. Optimized state of charge estimation of lithium-ion battery in smes/battery hybrid energy storage system for electric vehicles. IEEE Trans. Appl. Supercond. 2021, 31, 3091119. [Google Scholar] [CrossRef]
- Lv, J.; Jiang, B.; Wang, X.; Liu, Y.; Fu, Y. Estimation of the State of Charge of Lithium Batteries Based on Adaptive Unscented Kalman Filter Algorithm. Electronics 2020, 9, 1425. [Google Scholar] [CrossRef]
- Xu, Y.; Hu, M.; Fu, C.; Cao, K.; Su, Z.; Yang, Z. State of Charge Estimation for Lithium-Ion Batteries Based on Temperature-Dependent Second-Order RC Model. Electronics 2019, 8, 1012. [Google Scholar] [CrossRef]
- Hu, M.; Li, Y.; Li, S.; Fu, C.; Qin, D.; Li, Z. Lithium-ion battery modeling and parameter identification based on fractional theory. Energy 2018, 165, 153–163. [Google Scholar] [CrossRef]
- Li, X.; Yuan, C.; Wang, Z. State of health estimation for Li-ion battery via partial incremental capacity analysis based on support vector regression. Energy 2020, 203, 117852. [Google Scholar] [CrossRef]
- Huang, B.; Hu, M.; Chen, L.; Jin, G.; Liao, S.; Fu, C.; Wang, D.; Cao, K. A Novel Electro-Thermal Model of Lithium-Ion Batteries Using Power as the Input. Electronics 2021, 10, 2753. [Google Scholar] [CrossRef]
- Hossain Lipu, M.S.; Hannan, M.A.; Hussain, A.; Ayob, A.; Saad, M.H.M.; Muttaqi, K.M. State of Charge Estimation in Lithium-Ion Batteries: A Neural Network Optimization Approach. Electronics 2020, 9, 1546. [Google Scholar] [CrossRef]
- Li, X.; Huang, Z.; Tian, J.; Tian, Y. State-of-charge estimation tolerant of battery aging based on a physics-based model and an adaptive cubature Kalman filter. Energy 2021, 220, 119767. [Google Scholar] [CrossRef]
- Ye, M.; Guo, H.; Cao, B. A model-based adaptive state of charge estimator for a lithium-ion battery using an improved adaptive particle filter. Appl. Energy 2017, 190, 740–748. [Google Scholar] [CrossRef]
- Lian, B.; Sims, A.; Yu, D.; Wang, C.; Dunn, R.W. Optimizing LiFePO, battery energy storage systems for frequency response in the UK system. IEEE Trans. Sustain. Energy 2016, 8, 385–394. [Google Scholar] [CrossRef]
- Jiang, K.; Gu, P.; Huang, P.; Zhang, Y.; Duan, B.; Zhang, C. The Hazards Analysis of Nickel-Rich Lithium-Ion Battery Thermal Runaway under Different States of Charge. Electronics 2021, 10, 2376. [Google Scholar] [CrossRef]
- Yuan, W.; Jeong, S.; Sean, W.; Chiang, Y. Development of Enhancing Battery Management for Reusing Automotive Lithium-Ion Battery. Energies 2020, 13, 3306. [Google Scholar] [CrossRef]
- Wu, L.; Pang, H.; Geng, Y.; Liu, X.; Liu, J.; Liu, K. Low-complexity state of charge and anode potential prediction for lithium-ion batteries using a simplified electrochemical model-based observer under variable load condition. Int. J. Energy Res. 2022, 46, 11834–11848. [Google Scholar] [CrossRef]
- Armand, M.; Axmann, P.; Bresser, D.; Copley, M.; Edström, K.; Ekberg, C.; Guyomard, D.; Lestriez, B.; Novák, P.; Petranikova, M. Lithium-ion batteries–Current state of the art and anticipated developments. J. Power Sources 2020, 479, 228708. [Google Scholar] [CrossRef]
- Li, Y.; Vilathgamuwa, M.; Xiong, B.; Tang, J.; Su, Y.; Wang, Y. Design of minimum cost degradation-conscious lithium-ion battery energy storage system to achieve renewable power dispatchability. Appl. Energy 2020, 260, 114282. [Google Scholar] [CrossRef]
- Chen, T.; Jin, Y.; Lv, H.; Yang, A.; Liu, M.; Chen, B.; Xie, Y.; Chen, Q. Applications of lithium-ion batteries in grid-scale energy storage systems. Trans. Tianjin Univ. 2020, 26, 208–217. [Google Scholar] [CrossRef]
- Wang, Q.; Shen, J.; He, Y.; Ma, Z. Design and management of lithium-ion batteries: A perspective from modeling, simulation, and optimization. Chin. Phys. B 2020, 29, 068201. [Google Scholar] [CrossRef]
- Li, J.; Ye, M.; Jiao, S.; Meng, W.; Xu, X. A Novel State Estimation Approach Based on Adaptive Unscented Kalman Filter for Electric Vehicles. IEEE Access 2020, 8, 185629–185637. [Google Scholar] [CrossRef]
- Guo, F.; Hu, G.; Xiang, S.; Zhou, P.; Hong, R.; Xiong, N. A multi-scale parameter adaptive method for state of charge and parameter estimation of lithium-ion batteries using dual Kalman filters. Energy 2019, 178, 79–88. [Google Scholar] [CrossRef]
- Wang, Z.; Gladwin, D.T.; Smith, M.J.; Haass, S. Practical state estimation using Kalman filter methods for large-scale battery systems. Appl. Energy 2021, 294, 117022. [Google Scholar] [CrossRef]
- Jiang, Z.; Li, H.; Qu, Z.; Zhang, J. Recent progress in lithium-ion battery thermal management for a wide range of temperature and abuse conditions. Int. J. Hydrogen Energy 2022, 47, 9428–9459. [Google Scholar] [CrossRef]
- Feng, F.; Teng, S.; Liu, K.; Xie, J.; Xie, Y.; Liu, B.; Li, K. Co-estimation of lithium-ion battery state of charge and state of temperature based on a hybrid electrochemical-thermal-neural-network model. J. Power Sources 2020, 455, 227935. [Google Scholar] [CrossRef]
- Shi, Y.; Ahmad, S.; Liu, H.; Lau, K.T.; Zhao, J. Optimization of air-cooling technology for LiFePO4 battery pack based on deep learning. J. Power Sources 2021, 497, 229894. [Google Scholar] [CrossRef]
- Yetik, O.; Karakoc, T.H. Estimation of thermal effect of different busbars materials on prismatic Li-ion batteries based on artificial neural networks. J. Energy Storage 2021, 38, 102543. [Google Scholar] [CrossRef]
- Zhang, C.; Jiang, J.; Gao, Y.; Zhang, W.; Liu, Q.; Hu, X. Charging optimization in lithium-ion batteries based on temperature rise and charge time. Appl. Energy 2017, 194, 569–577. [Google Scholar] [CrossRef]
- Corno, M.; Pozzato, G. Active adaptive battery aging management for electric vehicles. IEEE Trans. Veh. Technol. 2019, 69, 258–269. [Google Scholar] [CrossRef]
- Castaings, A.; Lhomme, W.; Trigui, R.; Bouscayrol, A. Energy management of a multi-source vehicle by λ-control. Appl. Sci. 2020, 10, 6541. [Google Scholar] [CrossRef]
- Eckert, J.J.; Silva, L.C.; Dedini, F.G.; Correa, F.C. Electric Vehicle Powertrain and Fuzzy Control Multi-objective Optimization, considering Dual Hybrid Energy Storage Systems. IEEE Trans. Veh. Technol. 2020, 69, 3773–3782. [Google Scholar] [CrossRef]
- Vidal, C.; Malysz, P.; Kollmeyer, P.; Emadi, A. Machine learning applied to electrified vehicle battery state of charge and state of health estimation: State-of-the-art. IEEE Access 2020, 8, 52796–52814. [Google Scholar] [CrossRef]
- Stroe, D.I.; Schaltz, E. Lithium-Ion Battery State-of-Health Estimation Using the Incremental Capacity Analysis Technique. IEEE Trans. Ind. Appl. 2020, 56, 678–685. [Google Scholar] [CrossRef]
- Fotouhi, A.; Auger, D.J.; Propp, K.; Longo, S. Lithium–Sulfur Battery State-of-Charge Observability Analysis and Estimation. IEEE Trans. Power Electron. 2018, 33, 5847–5859. [Google Scholar] [CrossRef]
- Benveniste, G.; Rallo, H.; Canals, L.; Merino, A.; Amante, B. Comparison of the state of lithium-sulphur and lithium-ion batteries applied to electromobility. J. Environ. Manag. 2018, 226, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Eckert, J.J.; Barbosa, T.P.; da Silva, S.F.; Silva, F.L.; Silva, L.C.; Dedini, F.G. Electric hydraulic hybrid vehicle powertrain design and optimization-based power distribution control to extend driving range and battery life cycle. Energy Convers. Manag. 2022, 252, 115094. [Google Scholar] [CrossRef]
- Castanho, D.; Guerreiro, M.; Silva, L.; Eckert, J.; Antonini Alves, T.; Tadano, Y.d.S.; Stevan, S.L., Jr.; Siqueira, H.V.; Corrêa, F.C. Method for SoC Estimation in Lithium-Ion Batteries Based on Multiple Linear Regression and Particle Swarm Optimization. Energies 2022, 15, 6881. [Google Scholar] [CrossRef]
- Zerrahn, A.; Schill, W.-P.; Kemfert, C. On the economics of electrical storage for variable renewable energy sources. Eur. Econ. Rev. 2018, 108, 259–279. [Google Scholar] [CrossRef]
- Omariba, Z.B.; Zhang, L.; Kang, H.; Sun, D. Parameter Identification and State Estimation of Lithium-Ion Batteries for Electric Vehicles with Vibration and Temperature Dynamics. World Electr. Veh. J. 2020, 11, 50. [Google Scholar] [CrossRef]
- Chen, Q.; Jiang, J.; Ruan, H.; Zhang, C. Simply designed and universal sliding mode observer for the SOC estimation of lithium-ion batteries. IET Power Electron. 2017, 10, 697–705. [Google Scholar] [CrossRef]
- Li, S.; Li, G.; Ma, X. Grey prediction of lithium battery lifetime based on Markov rolling optimization. J. Hefei Univ. Technol. Nat. Sci. 2019, 42, 763–769. [Google Scholar]
- Liu, S.; Dang, Y.; Fang, Z.; Xie, N. Grey System Theory and Its Application, 5th ed.; Science Press: Beijing, China, 2010. [Google Scholar]
- Duan, H.; Wang, D.; Pang, X.; Liu, Y.; Zeng, S. A novel forecasting approach based on Multi-Kernel Nonlinear Multivariable Grey Model: A case report. J. Clean. Prod. 2020, 260, 120929. [Google Scholar] [CrossRef]
- Wei, H.; Chen, X.; Lv, Z.; Wang, Z.; Pan, H.; Chen, L. Online Estimation of Lithium-Ion Battery State of Health Using Grey Neural Network. Power Syst. Technol. 2017, 41, 4038–4044. [Google Scholar]
- Wu, W.; Ma, X.; Wang, Y.; Cai, W.; Zeng, B. Predicting China’s energy consumption using a novel grey Riccati model. Appl. Soft Comput. 2020, 95, 106555. [Google Scholar] [CrossRef]
- Liu, Y.; Wu, Z.X.; Zhou, H.; Zheng, H.; Yu, N.; An, X.P.; Li, J.Y.; Li, M.L. Development of China Light-Duty Vehicle Test Cycle. Int. J. Automot. Technol. 2020, 21, 1233–1246. [Google Scholar] [CrossRef]
- Liu, Y.; Zhou, H.; Xu, Y.; Qin, K.; Yu, H. Feasibility Study of Using WLTC for Fuel Consumption Certification of Chinese Light-Duty Vehicles; SAE International: Warrendale, PA, USA, 2018. [Google Scholar]
- Tucki, K. A Computer Tool for Modelling CO2 Emissions in Driving Cycles for Spark Ignition Engines Powered by Biofuels. Energies 2021, 14, 1400. [Google Scholar] [CrossRef]
- Deng, Z.; Hu, X.; Lin, X.; Che, Y.; Xu, L.; Guo, W. Data-driven state of charge estimation for lithium-ion battery packs based on Gaussian process regression. Energy 2020, 205, 118000. [Google Scholar] [CrossRef]
- Plett, G.L. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs: Part 3. State and parameter estimation. J. Power Sources 2004, 134, 277–292. [Google Scholar] [CrossRef]
- Deng, Z.; Yang, L.; Cai, Y.; Deng, H.; Sun, L. Online available capacity prediction and state of charge estimation based on advanced data-driven algorithms for lithium iron phosphate battery. Energy 2016, 112, 469–480. [Google Scholar] [CrossRef]
- Wang, L. Research on Reliability Predication and Life Cycle Cost Assessment of Low-voltage Switchgear. Ph.D. Thesis, Hebei University of Technology, Tianjin, China, 2017. [Google Scholar]






| Parameters | Values |
|---|---|
| Nominal Capacity (Ah) | 30 |
| Rated Voltage (V) | 3.2 |
| Charge Cutoff Voltage (V) | 3.65 |
| Discharge Cutoff Voltage (V) | 2.5 |
| Charge Temperature (°C) | 0~55 |
| Discharge Temperature (°C) | −25~55 |
| Coefficient | −25 °C | −20 °C | −10 °C | 0 °C | +25 °C | +40 °C | +55 °C |
|---|---|---|---|---|---|---|---|
| K0 | 2.5802 | 2.7285 | 2.9621 | 3.0937 | 3.2595 | 3.2159 | 3.2143 |
| K1 | 1.2526 | 0.958 | 0.7823 | 0.9278 | 1.0965 | 2.8663 | 3.2648 |
| K2 | −0.7987 | −3.2591 | −7.4156 | −9.5828 | −14.302 | −30.61 | −34.814 |
| K3 | −25.623 | 4.133 | 35.141 | 43.355 | 65.984 | 133 | 151.43 |
| K4 | 99.131 | −9.5266 | −91.694 | −99.723 | −141.04 | −277.11 | −314.99 |
| K5 | −146.39 | 24.44 | 116.65 | 109.91 | 140.22 | 273.9 | 310.24 |
| K6 | 73.74 | −23.711 | −57.662 | −46.669 | −52.579 | −103.23 | −116.37 |
| Temperature | Model | RMSE | MAE |
|---|---|---|---|
| −10 °C | GM(1,1) | 0.0175 | 0.0142 |
| MEGM(1,1) | 0.0099 | 0.0079 | |
| 0 °C | GM(1,1) | 0.0174 | 0.0140 |
| MEGM(1,1) | 0.0089 | 0.0061 | |
| +15 °C | GM(1,1) | 0.0163 | 0.0129 |
| MEGM(1,1) | 0.0072 | 0.0051 | |
| +25 °C | GM(1,1) | 0.0144 | 0.0115 |
| MEGM(1,1) | 0.0059 | 0.0046 | |
| +35 °C | GM(1,1) | 0.0157 | 0.0122 |
| MEGM(1,1) | 0.0069 | 0.0048 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Q.; Wang, S.; Gao, S.; Lv, H.; Liu, J.; Wang, L.; Du, J.; Wei, K. A State of Charge Estimation Approach for Lithium-Ion Batteries Based on the Optimized Metabolic EGM(1,1) Algorithm. Batteries 2022, 8, 260. https://doi.org/10.3390/batteries8120260
Sun Q, Wang S, Gao S, Lv H, Liu J, Wang L, Du J, Wei K. A State of Charge Estimation Approach for Lithium-Ion Batteries Based on the Optimized Metabolic EGM(1,1) Algorithm. Batteries. 2022; 8(12):260. https://doi.org/10.3390/batteries8120260
Chicago/Turabian StyleSun, Qiang, Shasha Wang, Shuang Gao, Haiying Lv, Jianghao Liu, Li Wang, Jifei Du, and Kexin Wei. 2022. "A State of Charge Estimation Approach for Lithium-Ion Batteries Based on the Optimized Metabolic EGM(1,1) Algorithm" Batteries 8, no. 12: 260. https://doi.org/10.3390/batteries8120260
APA StyleSun, Q., Wang, S., Gao, S., Lv, H., Liu, J., Wang, L., Du, J., & Wei, K. (2022). A State of Charge Estimation Approach for Lithium-Ion Batteries Based on the Optimized Metabolic EGM(1,1) Algorithm. Batteries, 8(12), 260. https://doi.org/10.3390/batteries8120260







