Analysis of Peukert Generalized Equations Use for Estimation of Remaining Capacity of Automotive-Grade Lithium-Ion Batteries
Abstract
:1. Introduction
2. Theory
3. Experimental Methodology
4. Results
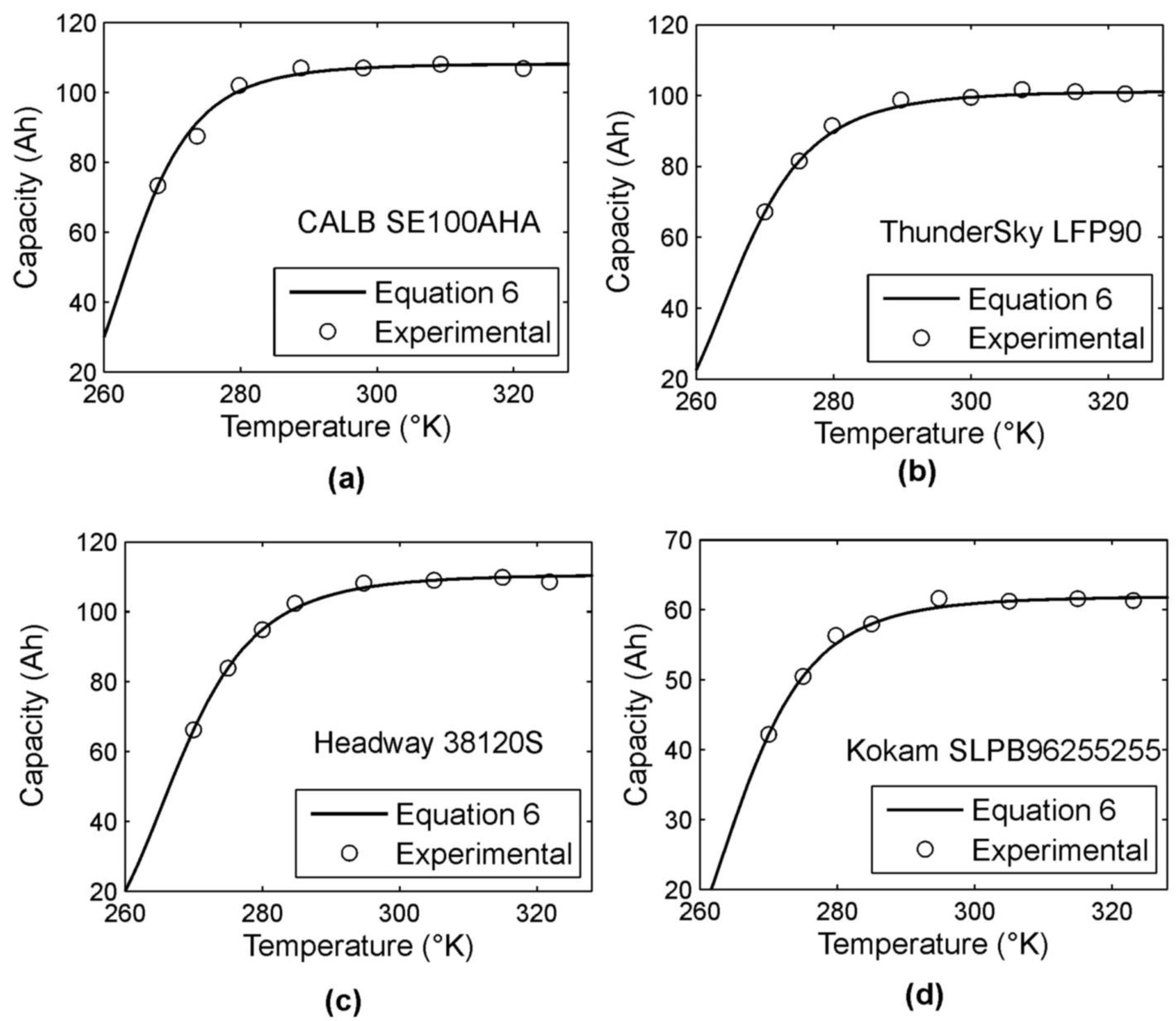
4.1. Studying of Dependence of Released Capacity on a Battery’s Temperature
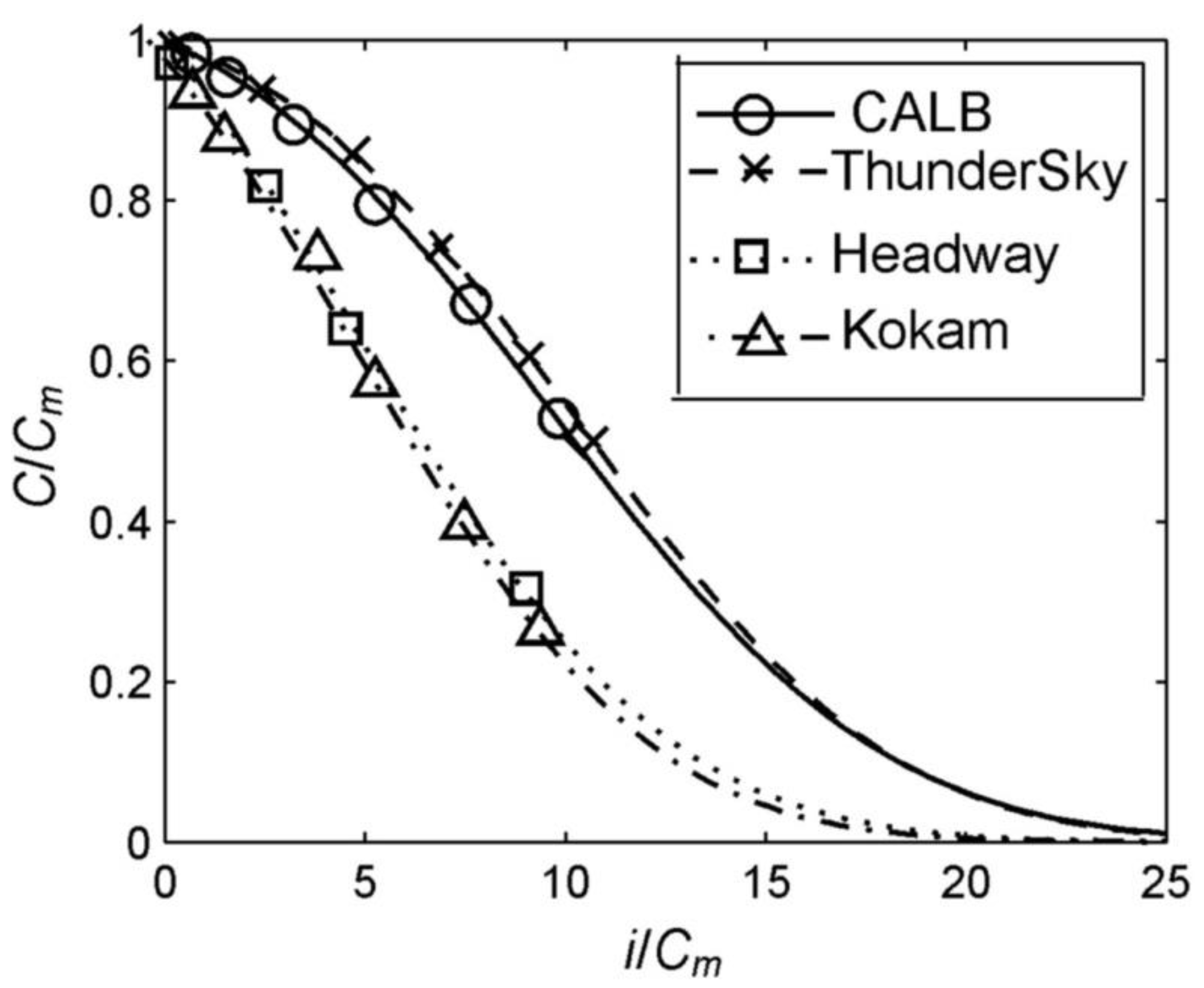
4.2. Studying of Dependence of Batteries’ Released Capacity on Discharging Current
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Blomgren, G.E. The Development and Future of Lithium Ion Batteries. J. Electrochem. Soc. 2017, 164, A5019–A5025. [Google Scholar] [CrossRef]
- Zubi, G.; Dufo-López, R.; Carvalho, M.; Pasaoglu, G. The lithium-ion battery: State of the art and future perspectives. Renew. Sustain. Energy Rev. 2018, 89, 292–308. [Google Scholar] [CrossRef]
- Lipu, M.S.H.; Hannan, M.A.; Hussain, A.; Hoque, M.M.; Ker, P.J.; Saad, M.H.M.; Ayob, A. A review of state of health and remaining useful life estimation methods for lithium-ion battery in electric vehicles: Challenges and recommendations. J. Clean. Prod. 2018, 205, 115–133. [Google Scholar] [CrossRef]
- Kim, S.U.; Albertus, P.; Cook, D.; Monroe, C.W.; Christensen, J. Thermoelectrochemical simulations of performance and abuse in 50-Ah automotive cells. J. Power Sources 2014, 268, 625–633. [Google Scholar] [CrossRef]
- Hannan, M.A.; Lipu, M.S.H.; Hussain, A.; Mohamed, A. A review of lithium-ion battery state of charge estimation and management system in electric vehicle applications: Challenges and recommendations. Renew. Sustain. Energy Rev. 2017, 78, 834–854. [Google Scholar] [CrossRef]
- Arunachalam, H.; Onori, S.; Battiato, I. On Veracity of Macroscopic Lithium-Ion Battery Models. J. Electrochem. Soc. 2015, 162, A1940–A1951. [Google Scholar] [CrossRef]
- Fan, G.; Pan, K.; Canova, M.; Marcicki, J.; Yang, X.G. Modeling of Li-Ion cells for fast simulation of high C-rate and low temperature operations. J. Electrochem. Soc. 2016, 163, A666–A676. [Google Scholar] [CrossRef]
- Cugnet, M.; Laruelle, S.; Grugeon, S.; Sahut, B.; Sabatier, J.; Tarascon, J.-M.; Oustaloup, A. A mathematical model for the simulation of new and aged automotive lead-acid batteries. J. Electrochem. Soc. 2009, 156, A974–A985. [Google Scholar] [CrossRef]
- Hausmann, A.; Depcik, C. Expanding the Peukert equation for battery capacity modeling through inclusion of a temperature dependency. J. Power Sources 2013, 235, 148–158. [Google Scholar] [CrossRef]
- Galushkin, N.E.; Yazvinskaya, N.N.; Galushkin, D.N. Generalized analytical model for capacity evaluation of automotive-grade lithium batteries. J. Electrochem. Soc. 2015, 162, A308–A314. [Google Scholar] [CrossRef]
- Feng, F.; Lu, R.; Wei, G.; Zhu, C. Online estimation of model parameters and state of charge of LiFePO4 batteries using a novel open-circuit voltage at various ambient temperatures. Energies 2015, 8, 2950–2976. [Google Scholar] [CrossRef]
- Tremblay, O.; Dessaint, L.A. Experimental validation of a battery dynamic model for EV applications. World Electr. Veh. J. 2009, 3, 289–298. [Google Scholar] [CrossRef]
- Chen, M.; Rincon-Mora, G.A. Accurate electrical battery model capable of predicting runtime and I-V performance. IEEE Trans. Energy Convers. 2006, 21, 504–511. [Google Scholar] [CrossRef]
- Perez, H.E.; Hu, X.; Dey, S.; Moura, S.J. Optimal charging of Li-ion batteries with coupled electro-thermal-aging dynamics. IEEE Trans. Power Electron. 2017, 66, 7761–7770. [Google Scholar] [CrossRef]
- Zou, Y.; Hu, X.; Ma, H.; Li, S.E. Combined State of Charge and State of Health estimation over lithium-ion battery cell cycle lifespan for electric vehicles. J. Power Sources 2015, 273, 793–803. [Google Scholar] [CrossRef]
- Kong, D.; Wang, G.; Ping, P.; Wen, J. A coupled conjugate heat transfer and CFD model for the thermal runaway evolution and jet fire of 18650 lithium-ion battery under thermal abuse. eTransportation 2022, 12, 100157. [Google Scholar] [CrossRef]
- Golubkov, A.W.; Fuchs, D.; Wagner, J.; Wiltsche, H.; Stangl, C.; Fauler, G.; Voitic, G.; Thalera, A.; Hackere, V. Thermal-runaway experiments on consumer Li-ion batteries with metal-oxide and olivin-type cathodes. RSC Adv. 2014, 4, 3633–3642. [Google Scholar] [CrossRef]
- Cheng, Q.; Sun, D.; Yu, X. Metal hydrides for lithium-ion battery application: A review. J. Alloys Compd. 2018, 769, 167–185. [Google Scholar] [CrossRef]
- Oumellal, Y.; Rougier, A.; Nazri, G.A.; Tarascon, J.-M.; Aymard, L. Metal hydrides for lithium-ion batteries. Nat. Mater. 2008, 7, 916–921. [Google Scholar] [CrossRef]
- Ponrouch, A.; Bitenc, J.; Dominko, R.; Lindahl, N.; Johansson, P.; Palacin, M.R. Multivalent rechargeable batteries. Energy Storage Mater. 2019, 20, 253–262. [Google Scholar] [CrossRef]
- Coleman, M.; Lee, C.K.; Zhu, C.; Hurley, W.G. State-of-charge determination from EMF voltage estimation: Using impedance, terminal voltage, and current for lead-acid and lithium-ion batteries. IEEE Trans. Ind. Electron. 2007, 54, 2550–2557. [Google Scholar] [CrossRef]
- Rakhmatov, D.; Vrudhula, S.; Wallach, D.A. A model for battery lifetime analysis for organizing applications on a pocket computer. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2003, 11, 1019–1030. [Google Scholar] [CrossRef]
- Omar, N.; Daowd, M.; Van den Bossche, P.; Hegazy, O.; Smekens, J.; Coosemans, T.; van Mierlo, J. Rechargeable energy storage systems for plug-in hybrid electric vehicles—Assessment of electrical characteristics. Energies 2012, 5, 2952–2988. [Google Scholar] [CrossRef]
- He, W.; Williard, N.; Chen, C.; Pecht, M. State of charge estimation for electric vehicles batteries using unscented Kalman filtering. Microelectron. Reliab. 2013, 53, 840–847. [Google Scholar] [CrossRef]
- Han, J.; Kim, D.; Sunwoo, M. State-of-charge estimation of lead-acid batteries using an adaptive extended Kalman filter. J. Power Sources 2009, 188, 606–612. [Google Scholar] [CrossRef]
- He, H.; Zhang, X.; Xiong, R.; Xu, Y.; Guo, H. Online model-based estimation of state-of-charge and open-circuit voltage of lithium-ion batteries in electric vehicles. Energy 2012, 39, 310–318. [Google Scholar] [CrossRef]
- He, Y.; Liu, X.T.; Zhang, C.B.; Chen, Z.H. A new model for State-of-Charge (SOC) estimation for high-power Li-ion batteries. Appl. Energy 2013, 101, 808–814. [Google Scholar] [CrossRef]
- Buchmann, I. Batteries in a Portable World; Cadex Electronics Inc.: Richmond, BC, Canada, 2016. [Google Scholar]
- Galushkin, N.E.; Yazvinskaya, N.N.; Ruslyakov, D.V.; Galushkin, D.N. Analysis of Peukert and Liebenow Equations Use for Evaluation of Capacity Released by Lithium-Ion Batteries. Processes 2021, 9, 1753–1763. [Google Scholar]
- Peukert, W. About the dependence of the capacity of the discharge current magnitude and lead acid batterie. Elektrotech. Z. 1897, 20, 287–288. [Google Scholar]
- Pilatowicz, G.; Budde-Meiwes, H.; Schulte, D.; Kowal, J.; Zhang, Y.; Du, X.; Salman, M.; Gonzales, D.; Alden, J.; Sauer, D.U. Simulation of SLI lead-acid batteries for SoC, aging and cranking capability prediction in automotive applications. J. Electrochem. Soc. 2012, 159, A1410–A1419. [Google Scholar] [CrossRef]
- Herstedt, M.; Abraham, D.P.; Kerr, J.B.; Edstrom, K. X-ray photoelectron spectroscopy of negative electrodes from high-power lithium-ion cells showing various levels of power fade. Electrochim. Acta 2004, 49, 5097–5110. [Google Scholar] [CrossRef]
- Galushkin, N.E.; Yazvinskaya, N.N.; Galushkin, D.N. Analysis of generalized Peukert’s equations for capacity calculation of lithium-ion cells. J. Electrochem. Soc. 2020, 167, 013535. [Google Scholar] [CrossRef]
- Pitaevskii, L.P.; Lifshitz, E.M. Physical Kinetics; Pergamon Press: Oxford, UK, 1981; Volume 10, pp. 522–527. [Google Scholar]
- Yazvinskaya, N.N.; Lipkin, M.S.; Galushkin, N.E.; Galushkin, D.N. Peukert Generalized Equations Applicability with Due Consideration of Internal Resistance of Automotive-Grade Lithium-Ion Batteries for Their Capacity Evaluation. Energies 2022, 15, 2825. [Google Scholar] [CrossRef]
- Cugnet, M.G.; Dubarry, M.; Liaw, B.Y. Peukert’s Law of a Lead-Acid Battery Simulated by a Mathematical Model. ECS Trans. 2010, 25, 223–233. [Google Scholar] [CrossRef]
- Doerffel, D.; Sharkh, S.A. A critical review of using the Peukert equation for determining the remaining capacity of lead-acid and lithium-ion batteries. J. Power Sources 2006, 155, 395–400. [Google Scholar] [CrossRef]
- Omar, N.; van den Bossche, P.; Coosemans, T.; Mierlo, J.V. Peukert Revisited—Critical Appraisal and Need for Modification for Lithium-Ion Batteries. Energies 2013, 6, 5625–5641. [Google Scholar] [CrossRef]

| Model | SE100AHA | LFP90 | 38120S | SLPB96255255 |
|---|---|---|---|---|
| Manufacturer | CALB | ThunderSky | Headway | Kokam |
| Cathode material | LiFePO4 | LiFePO4 | LiFePO4 | LiCoO2 |
| Structure | prismatic battery | prismatic battery | cylindrical battery package (1S10P) | pouch battery |
| Nominal capacity (Ah) | 100 | 90 | 100 | 60 |
| Charge current (A) | 40 | 40 | 40 | 30 |
| Upper cutoff (V) | 3.60 | 4.25 | 3.65 | 4.20 |
| End current (A) | 2.5 | 2.25 | 2.5 | 1.5 |
| Lower cutoff (V) | 2.50 | 2.50 | 2.00 | 2.70 |
| Discharge current (for training cycles) (A) | 20 | 18 | 20 | 12 |
| Parameters | CALB LiFePO4 | ThunderSky LiFePO4 | Headway LiFePO4 | Kokam LiCoO2 |
|---|---|---|---|---|
| Cn (Ah) | 100 | 90 | 100 | 60 |
| Cmref (Ah) | 107.05 | 99.18 | 107.74 | 60.72 |
| Tref (°K) | 298 | 298 | 298 | 298 |
| Tk (°K) | 240 | 239 | 238 | 237 |
| β | 5.10 | 4.95 | 5.11 | 5.13 |
| K | 1.010 | 1.021 | 1.027 | 1.020 |
| δ (%) 1 | 1.8 | 1.8 | 1.7 | 1.9 |
| Parameters | CALB LiFePO4 | ThunderSky LiFePO4 | Headway LiFePO4 | Kokam LiCoO2 |
|---|---|---|---|---|
| Equation (10) | ||||
| Cn (Ah) | 100 | 90 | 100 | 60 |
| Cm (Ah) | 106.95 | 104.59 | 107.82 | 59.42 |
| i0or ik (A) | 1107.82 | 1088.23 | 692.93 | 396.04 |
| n | 1.867 | 1.872 | 1.982 | 2.130 |
| δ (%) 1 | 2.3 | 2.2 | 2.4 | 2.3 |
| Equation (11) | ||||
| Cm (Ah) | 106.85 | 104.55 | 107.20 | 59.06 |
| i0or ik (A) | 1140.23 | 1075.35 | 683.30 | 392.61 |
| n | 1.003 | 0.998 | 1.17 | 1.255 |
| δ (%) 1 | 3.2 | 3.4 | 3.3 | 3.4 |
| Equation (12) | ||||
| Cm (Ah) | 107.88 | 105.05 | 110.74 | 61.285 |
| i0 or ik (A) | 1039.26 | 1084.57 | 524.67 | 321.90 |
| n | 1.037 | 1.187 | 0.547 | 0.653 |
| δ (%) 1 | 1.7 | 1.8 | 1.9 | 1.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yazvinskaya, N.N.; Lipkin, M.S.; Galushkin, N.E.; Galushkin, D.N. Analysis of Peukert Generalized Equations Use for Estimation of Remaining Capacity of Automotive-Grade Lithium-Ion Batteries. Batteries 2022, 8, 118. https://doi.org/10.3390/batteries8090118
Yazvinskaya NN, Lipkin MS, Galushkin NE, Galushkin DN. Analysis of Peukert Generalized Equations Use for Estimation of Remaining Capacity of Automotive-Grade Lithium-Ion Batteries. Batteries. 2022; 8(9):118. https://doi.org/10.3390/batteries8090118
Chicago/Turabian StyleYazvinskaya, Nataliya N., Mikhail S. Lipkin, Nikolay E. Galushkin, and Dmitriy N. Galushkin. 2022. "Analysis of Peukert Generalized Equations Use for Estimation of Remaining Capacity of Automotive-Grade Lithium-Ion Batteries" Batteries 8, no. 9: 118. https://doi.org/10.3390/batteries8090118
APA StyleYazvinskaya, N. N., Lipkin, M. S., Galushkin, N. E., & Galushkin, D. N. (2022). Analysis of Peukert Generalized Equations Use for Estimation of Remaining Capacity of Automotive-Grade Lithium-Ion Batteries. Batteries, 8(9), 118. https://doi.org/10.3390/batteries8090118










