On the Theory of the Arrhenius-Normal Model with Applications to the Life Distribution of Lithium-Ion Batteries
Abstract
:1. Introduction
2. Generalizing the Arrhenius Model
3. The Arrhenius-Normal Model
4. The Life Distribution of Li-Ion Batteries
5. Conclusions and Recommendations
Funding
Data Availability Statement
Conflicts of Interest
References
- Pena-Bello, A.; Barbour, E.; Gonzalez, M.C.; Patel, M.K.; Parra, D. Optimized PV-coupled battery systems for combining applications: Impact of battery technology and geography. Renew. Sustain. Energ. Rev. 2019, 112, 978–990. [Google Scholar] [CrossRef]
- Lupangu, C.; Bansal, R.C. A review of technical issues on the development of solar photovoltaic systems. Renew. Sustain. Energy Rev. 2017, 73, 950–965. [Google Scholar] [CrossRef]
- Jinga, W.; Laia, C.H.; Linga, D.K.X.; Wonga, W.S.H.; Wong, M.L.D. Battery lifetime enhancement via smart hybrid energy storage plug-in module in standalone photovoltaic power system. J. Energy Storage 2019, 21, 586–598. [Google Scholar] [CrossRef]
- Gomes, I.S.F.; Perez, Y.; Suomalainen, E. Coupling small batteries and PV generation: A review. Renew. Sust. Energ. Rev. 2020, 126, 109835–109848. [Google Scholar] [CrossRef]
- Borah, R.; Hughson, F.R.; Johnston, J.; Nann, T. On battery materials and methods. Mater. Today Adv. 2020, 6, 100046–100068. [Google Scholar] [CrossRef]
- Boucar, D.; Ramchandra, P. Potential of lithium-ion batteries in renewable energy. Renew. Energy 2015, 76, 375–380. [Google Scholar]
- Meeker, W.Q.; Escobar, L.A. Pitfalls of accelerated testing. IEEE Trans. Reliab. 1998, 47, 114–118. [Google Scholar] [CrossRef]
- Nelson, W. Accelerated Testing: Statistical Models, Test Plans, and Data Analyses, 3rd ed.; John Wiley & Sons: Schenectady, NY, USA, 1990. [Google Scholar]
- Ebeling, C. An Introduction to Reliability and Maintainability Engineering; Waveland Press: Long Grove, IL, USA, 2010. [Google Scholar]
- Park, C.; Padgett, W.J. Stochastic degradation models with several accelerating variables. IEEE Trans. Reliab. 2006, 55, 379–390. [Google Scholar] [CrossRef]
- Haghighi, F.; Bae, S.J. Reliability Estimation from Linear Degradation and Failure Time Data with Competing Risks Under a Step-Stress Accelerated Degradation Test. IEEE Trans. Reliab. 2015, 64, 960–971. [Google Scholar] [CrossRef]
- Nelson, W.; Kielpinski, T.J. Theory for optimum censored accelerated life tests for normal and lognormal life distributions. Dent. Tech. 1976, 18, 105–114.29. [Google Scholar] [CrossRef]
- Gouno, E. Optimum step-stress for temperature accelerated life testing. Qual. Reliab. Eng. Int. 2007, 23, 915–924. [Google Scholar] [CrossRef]
- Park, J.W.; Yum, B.J. Optimal design of accelerated life tests with two stresses. Nav. Res. Logist. 1996, 43, 863–884. [Google Scholar] [CrossRef]
- Tsai, T.R.; Lio, Y.L.; Jiang, N. Optimal decisions on the accelerated degradation test plan under the wiener process. Qual. Technol. Quant. Manag. 2014, 11, 461–470. [Google Scholar] [CrossRef]
- Escobar, L.; Meeker, W. A Review of Accelerated Test Models. Stat. Sci. 2006, 21, 552–577. [Google Scholar] [CrossRef] [Green Version]
- Bai, D.S.; Chun, Y.R.; Cha, M.S. Time-censored ramp tests with stress bound for Weibull life distribution. IEEE Trans. Reliab. 1997, 46, 99–107.32. [Google Scholar] [CrossRef]
- Rinne, H. The Weibull Distribution: A Handbook, 1st ed.; CRC Press: Boca Raton, FL, USA, 2008; p. 808. [Google Scholar]
- Pham, H. (Ed.) Handbook of Reliability Engineering; Springer: London, UK, 2003. [Google Scholar]
- Dennah, D.Y.; Ammach, S.B.; Barakat, E.; Majid, M.A. Life Distribution of Commercial Concentrator III-V Triple-Junction Solar Cells in View of Inverse Power law and Arrhenius Life-stress Relationships. In Proceedings of the 2022 IEEE Green Technologies Conference (GreenTech), Houston, TX, USA, 30 March–1 April 2022; IEEE: Piscataway, NJ, USA, 2022. [Google Scholar]
- Song, K.; Cui, L. Fiducial inference-based failure mechanism consistency analysis for accelerated life and degradation tests. Appl. Math Model 2022, 105, 340–354. [Google Scholar] [CrossRef]
- Soleimani, M.; Kezunovic, M.; Butenko, S. Linear Arrhenius-Weibull Model for Power Transformer Thermal Stress Assessment. IEEE Access 2022, 10, 19013–19021. [Google Scholar] [CrossRef]
- Lee, P.H.; Torng, C.C.; Lin, Y.C. Determination of the optimal accelerated burn-in time under Arrhenius–Lognormal distribution assumption. Appl. Math. Model. 2011, 35, 4023–4030. [Google Scholar] [CrossRef]
- Kielpinski, T.J.; Nelson, W. Optimum censored accelerated life tests for normal and lognormal life distributions. IEEE Trans. Reliab. 1975, 24, 310–320. [Google Scholar] [CrossRef]
- Bai, D.S.; Kim, M.S.; Lee, S.H. Optimum simple step-stress accelerated life tests with censoring. IEEE Trans. Reliab. 1989, 38, 528–532. [Google Scholar] [CrossRef]
- Cousineau, D. Fitting the three-parameter Weibull distribution: Review and evaluation of existing and new methods. IEEE Trans. Dielectr. Electr. Insul. 2008, 16, 281–288. [Google Scholar] [CrossRef]
- Zhang, H.; Gao, Z.; Du, C.; Bi, S.; Fang, Y.; Yun, F.; Fang, S.; Yu, Z.; Cui, Y.; Shen, X. Parameter estimation of three-parameter Weibull probability model based on outlier detection. RSC Adv. 2022, 53, 34154–34164. [Google Scholar] [CrossRef] [PubMed]
- Smith, R.L.; Naylor, J.C. A comparison of maximum likelihood and Bayesian estimators for the three parameter Weibull distribution. J. R Stat. Soc. Ser. C Appl. Stat. 1987, 36, 358–369. [Google Scholar] [CrossRef]
- Stacy, E.W. A generalization of the gamma distribution. Ann. Math. Statist. 1962, 33, 1187–1192. [Google Scholar] [CrossRef]
- Cox, C.; Chu, H.; Schneider, M.F.; Munoz, A. Parametric survival analysis and taxonomy of hazard functions for the generalized gamma distribution. Stat. Med. 2007, 26, 4352–4374. [Google Scholar] [CrossRef]
- Kartsonaki, C. Survival analysis. Diagn. Histopathol. 2016, 22, 263–270. [Google Scholar] [CrossRef] [Green Version]
- Schijve, J. A normal distribution or a weibull distribution for fatigue lives. Fatigue Fract. Eng. Mater. Struct. 1993, 16, 851–859. [Google Scholar] [CrossRef] [Green Version]
- Schijve, J. Fatigue of Structures and Materials; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2001. [Google Scholar]
- Okamura, H.; Dohi, T.; Osaki, S. Software reliability growth models with normal failure time distribution. Reliab. Eng. Syst. Saf. 2013, 116, 135–141. [Google Scholar] [CrossRef]
- Lu, J.C.; Park, J.; Yang, Q. Statistical inference of a time-to-failure distribution derived from linear degradation data. Technometrics 1997, 39, 391–400. [Google Scholar] [CrossRef]
- Schuster, S.F.; Brand, M.J.; Berg, P.; Gleissenberger, M.; Jossen, A. Li-ion cell-to-cell variation during battery electric vehicle operation. J. Power Sources 2015, 297, 242–251. [Google Scholar] [CrossRef]
- Bayle, F.; Mettas, A. Temperature Acceleration Models in Reliablity Predictions: Justification and Improvements. In Proceedings of the 2010 Proceedings-Annual Reliability and Maintainability Symposium (RAMS), San Jose, CA, USA , 25–28 January 2010. [Google Scholar]
- Thiraviam, A.; Mudge, W.; Malone, L. Six challenges in implementation of effective accelerated life tests. In Proceedings of the Reliability and Maintainability Symposium, Fort Worth, TX, USA, 26–29 January 2009; pp. 47–52. [Google Scholar]
- Lande, R. On comparing coefficients of variation. Syst Zool. 1977, 26, 214–217. [Google Scholar] [CrossRef]
- Abdi, H.; Salkind, N. Coefficient of Variation. Encycl. Res. Des. 2012, 1, 169–171. [Google Scholar]
- Espinet-González, P.; Algora, C.; Núñez, N.; Orlando, V.; Vázquez, M.; Bautista, J.; Araki, K. Temperature accelerated life test on commercial concentrator III-V triple-junction solar cells and reliability analysis as a function of the operating temperature. Prog. Photovolt. Res. Appl. 2014, 23, 559–569. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Zhou, T.; Wu, H.; Wu, Y.; Wu, W.; Ren, J. Constant-Step-Stress Accelerated Life Test of White OLED Under Weibull Distribution Case. IEEE Trans. Electron Devices 2012, 59, 715–720. [Google Scholar] [CrossRef]
- Kittaneh, O.A.; Helal, S.; Almorad, H.; Bayoud, H.A.; Abufoudeh, G.; Majid, M.A. Preferable Parametric Model for the Lifetime of the Organic Light-Emitting Diode Under Accelerated Current Stress Tests. IEEE Trans. Electron Devices 2021, 68, 4478–4484. [Google Scholar] [CrossRef]
- Chiodo, E.; Lauria, D.; Andrenacci, N.; Pede, G. Accelerated life tests of complete lithium-ion battery systems for battery life statistics assessment. In Proceedings of the IEEE 2016 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Capri, Italy, 22–24 June 2016; pp. 1073–1078. [Google Scholar]
- Harris, S.J.; Harris, D.J.; Li, C. Failure statistics for commercial lithium-ion batteries: A study of 24 pouch cells. J. Power Sources 2017, 342, 589–597. [Google Scholar] [CrossRef] [Green Version]
- Johnen, M.; Schmitz, C.; Kateri, M.; Kamps, U. Fitting lifetime distributions to interval censored cyclic-aging data of lithium-ion batteries. Comput. Ind. Eng. 2020, 143, 106418. [Google Scholar] [CrossRef]
- Talal, M.; Kittaneh, O.A.; Majid, M.A. Choosing the Best Lifetime Model for Commercial Li-Ion Batteries. J. Energy Storage 2021, 41, 102827. [Google Scholar]
- D’ Agostino, R.B.; Stephens, M.A. Goodness-of-Fit Techniques; Marcel Dekker: New York, NY, USA, 1986. [Google Scholar]
- McKinley, R.L.; Mills, C.N. A comparison of several goodness-of-fit statistics. Appl. Psychol. Meas. 1985, 9, 49–57. [Google Scholar] [CrossRef] [Green Version]
- Schervish, M.J. P-Values: What They Are and What They Are Not. Am. Stat. 1996, 50, 203–206. [Google Scholar] [CrossRef]
- Vidgen, B.; Yasseri, T. P-values: Misunderstood and misused. Front Phys. Front Phys. 2016, 4, 6. [Google Scholar] [CrossRef] [Green Version]
- Kittaneh, O.A.; Almorad, H.; Helal, S.; Majid, M.A. On the efficiency of type I censored samples. IMA J. Math. Control. Inf. 2021, 38, 743–753. [Google Scholar] [CrossRef]
- Lilliefors, H.W. On the Kolmogorov-Smirnov Test for Normality with Mean and Variance Unknown. J. Am. Stat. Assoc. 1967, 62, 399–402. [Google Scholar] [CrossRef]
- Greenwood, P.E.; Nikulin, M.S. A Guide to Chi-Squared Testing; John Wiley & Sons: New York, NY, USA, 1996. [Google Scholar]
- Pettit, A.N.; Stephens, M.A. Modified Cramér-von Mises statistics for censored data. Biometrika 1976, 63, 291–298. [Google Scholar]
- Jarque, C.M.; Bera, A.K. Efficient tests for normality, homoscedasticity and serial independence of regression residuals. Econ. Lett. 1980, 6, 255–259. [Google Scholar] [CrossRef]
- Kittaneh, O.A. Powerful Mathematica Codes for Goodness-of-Fit Tests for Censored Data. In Handbook of Smart Energy Systems; Fathi, M., Zio, E., Pardalos, P.M., Eds.; Springer: Cham, Germany, 2022. [Google Scholar] [CrossRef]
- Kittaneh, O.A. Deriving the efficiency function for type I censored sample from exponential distribution using sup-entropy. J. Stat. 2012, 19, 43–53. [Google Scholar]
- Leung, K.M.; Elashoff, R.M.; Afifi, A.A. Censoring issues in survival analysis. Ann. Rev. Public Health 1997, 18, 83–104. [Google Scholar] [CrossRef] [PubMed]
- Weiping, D.; Xing, Y.; Saxena, S.; Pecht, M. Evaluation of Present Accelerated Temperature Testing and Modeling of Batteries. Appl. Sci. 2018, 8, 10. [Google Scholar]
- Leng, F.; Tan, C.; Pecht, M. Effect of Temperature on the Aging rate of Li Ion Battery Operating above Room Temperature. Sci. Rep. 2015, 5, 12967. [Google Scholar] [CrossRef] [Green Version]
- Yang, K.; Liu, D.; Qian, Z.; Jiang, D.; Wang, R. Computational auxiliary for the progress of sodium-ion solid-state electrolytes. ACS Nano 2021, 15, 17232–17246. [Google Scholar] [CrossRef]
- Miao, L.; Wang, R.; Di, S.; Qian, Z.; Zhang, L.; Xin, W.; Liu, M.; Zhu, Z.; Chu, S.; Du, Y.; et al. Aqueous Electrolytes with Hydrophobic Organic Cosolvents for Stabilizing Zinc Metal Anodes. ACS Nano 2022, 16, 9667–9678. [Google Scholar] [CrossRef] [PubMed]
| Distribution | Coef. of Var. |
|---|---|
| Weibull | = |
| Lognormal ) | = |
| Gamma | |
| Log-logistic |
| Type of Battery | Li-Ion |
|---|---|
| Nominal capacity | 4.4 Ah |
| Active material of the anodes | synthetic graphite |
| Active material of the cathode | LCO (Li Cobalt Oxide) |
| Number of cells tested | 24 cells |
| Temperature | 25 °C |
| Discharge rate | 10 C |
| 255 | 379 | 497 | 541 |
| 301 | 408 | 509 | 560 |
| 326 | 409 | 515 | |
| 338 | 430 | 518 | |
| 340 | 449 | 537 | |
| 341 | 475 | 541 |
| 123 | 151 | 167 | 180 | 191 | |
| 200 | 208 | 216 | 224 | 232 | |
| 239 | 246 | 254 | 262 | 270 | |
| 280 | 290 | 303 | 319 | 346 | |
| 62 | 76 | 84 | 90 | 95 | |
| 100 | 104 | 108 | 112 | 116 | |
| 120 | 123 | 127 | 131 | 135 | |
| 140 | 145 | 151 | 159 | 174 | |
| 31 | 38 | 42 | 45 | 48 | |
| 50 | 52 | 54 | 56 | 58 | |
| 60 | 61 | 63 | 65 | 67 | |
| 70 | 72 | 75 | 80 | 86 |
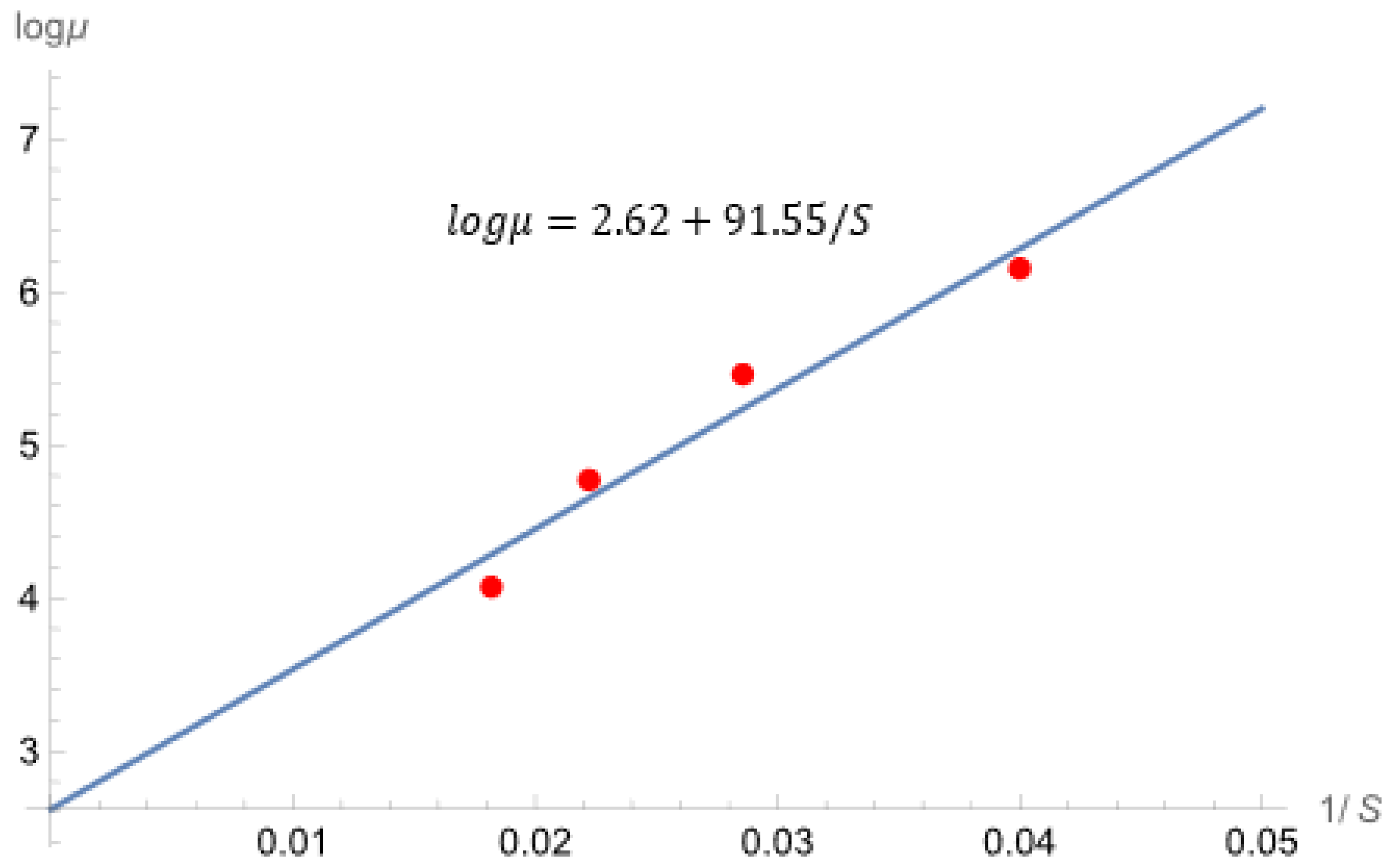
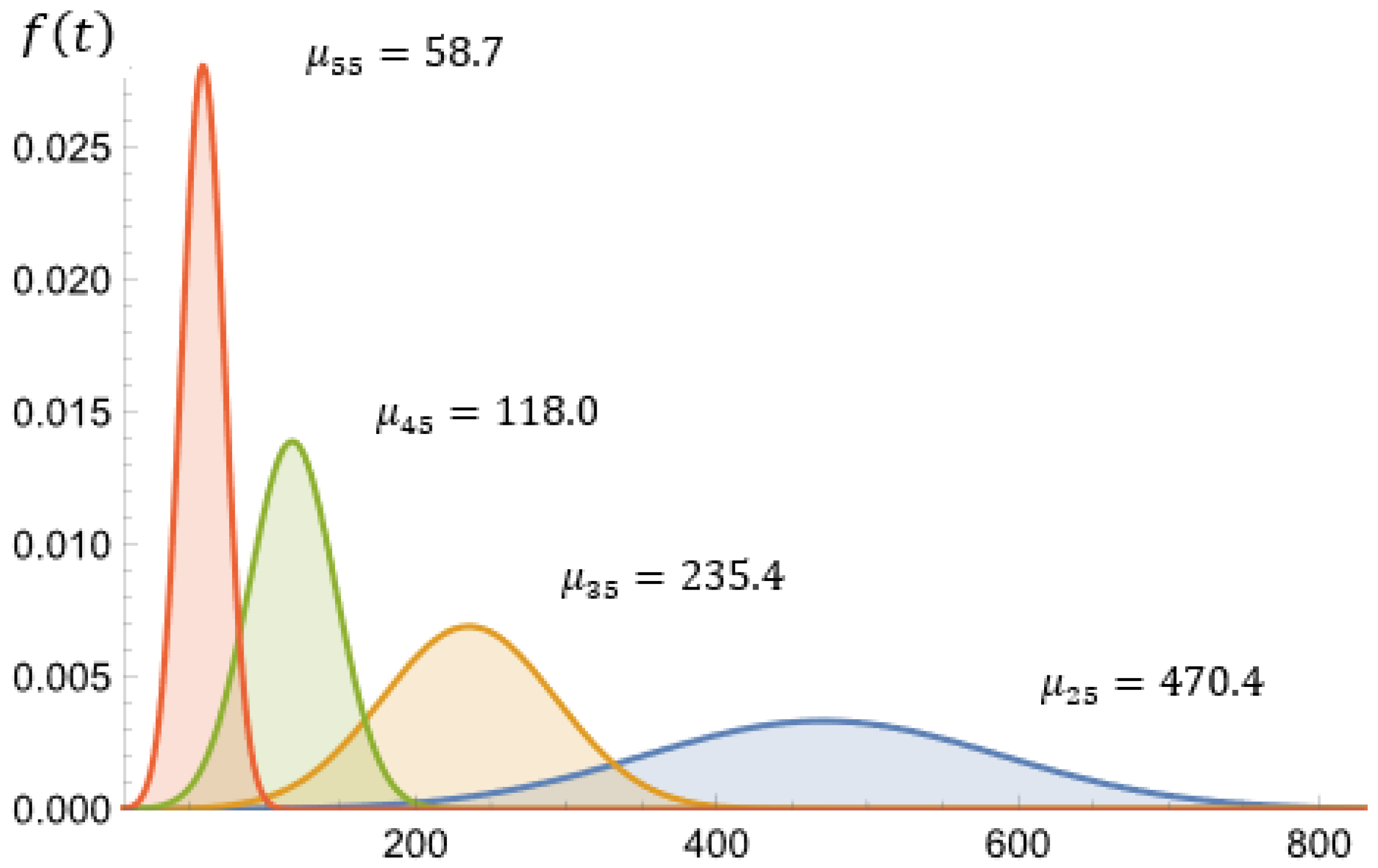
| Stress | ||||
|---|---|---|---|---|
| 20 | 470.4 | 119.3 | 0.2536 | |
| 20 | 235.4 | 57.7 | 0.2451 | |
| 20 | 118.0 | 28.7 | 0.2432 | |
| 20 | 58.7 | 14.2 | 0.2419 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kittaneh, O. On the Theory of the Arrhenius-Normal Model with Applications to the Life Distribution of Lithium-Ion Batteries. Batteries 2023, 9, 55. https://doi.org/10.3390/batteries9010055
Kittaneh O. On the Theory of the Arrhenius-Normal Model with Applications to the Life Distribution of Lithium-Ion Batteries. Batteries. 2023; 9(1):55. https://doi.org/10.3390/batteries9010055
Chicago/Turabian StyleKittaneh, Omar. 2023. "On the Theory of the Arrhenius-Normal Model with Applications to the Life Distribution of Lithium-Ion Batteries" Batteries 9, no. 1: 55. https://doi.org/10.3390/batteries9010055





