2. Theory: Statistical Thermodynamics of the Ising Model
While we are solely looking at the original Ising model as developed by Lenz [
1] and Ising [
2], it should be mentioned that a number of extensions exist, such as the inclusion of next-nearest neighbor and higher order interactions [
9] or the consideration of more than two states per spin [
10]. For a comprehensive overview, we recommend standard text books on statistical mechanics [
11] as well as specialized literature [
12,
13]. In the absence of an external magnetic field, the Hamiltonian
H evaluates the total interaction energy (i.e., potential energy only without a kinetic contribution) for a system of interacting spins placed on a regular lattice where each spin can only interact with its nearest neighbor spins. In such a setting,
H results from summation of pair energies (
):
where the sum runs over all pairs of nearest neighbor spins
with two possible values for the spin number
, corresponding to the spin-up and spin-down state. Once all spins are prepared in a particular configuration with specified values for the spin numbers (e.g.,
),
H returns the resulting system energy of this particular configuration. The coupling constant
carries units of an energy and specifies the interaction strength between nearest neighboring spins
i and
j such that the spins become decoupled, i.e., independent, for
. Interactions between different particle types as it becomes relevant for mixtures or in case of impurities could be modeled by using different
-values. In the last identity of Equation (
1), we assumed isotropic interactions, i.e., uniform coupling constants
between all pairs in all directions. We implicitly assumed regular, i.e., ideal or uniform lattices where each spin is assigned to a single lattice site without any vacancies or impurities in between. Explicit expressions for the Hamiltonian of the 1D- and 2D-Ising model in case of free boundary (FBC) and periodic boundary conditions (PBC) are given in Equations (A1a), (A1b) and (A2a)–(A2c). PBC are typically applied in order to reduce the impact of boundary or surface effects in case of finite-size systems. However, in the thermodynamic limit, i.e., for infinite lattice sizes, the impact of the boundary conditions on the system’s (thermodynamic) behavior and thus the difference between FBC and PBC has to vanish. Schematic examples for 1D- and 2D-systems with FBC and PBC are shown in
Figure A1 in
Appendix A.1. In 1D, FBC corresponds to a linear chain with open ends, i.e., all spins except for the first and last one in the chain share two nearest neighbors, while PBC corresponds to a closed ring where the last spin
N also interacts with the first spin 1 such that all spins have two nearest neighbors. In 2D, a number of
spins are arranged onto a regular lattice, with
spins in x-direction (=number of columns) and
spins in y-direction (=number of rows), corresponding to a matrix of dimensions
. In two dimensions, FBC correspond to a planar graph, with
horizontal and
vertical interactions, yielding
interactions in total for the special case of quadratic (
) lattices with
. In this case, all inner spins have four nearest neighbors, while spins at the boundary can have two or three neighbors. When PBC are applied in both the x- and y-direction, the resulting lattice is wrapped around a torus with all spins having four neighbors. In such an arrangement, we equally have
horizontal and
vertical interactions, yielding a total of
interactions in case of a quadratic system. For the sake of completeness it should be noted that also hybrid boundary conditions can be used where PBC are applied in one and FBC in the other direction, yielding a lattice with cylindrical topology.
Once the interactions of the spin system are specified in form of the Hamiltonian
H (cf. Equation (
1)), the partition function in the canonical ensemble
at constant number of spins
and temperature
T is obtained via summation of Boltzmann factors
for all possible spin configurations:
where
denotes the collection of all possible spin configurations the system can populate,
is the collection of all nearest neighbor pairs, and
is the inverse temperature with Boltzmann constant
. All thermodynamic quantities of interest such as internal energy
U, entropy
S, isochoric heat capacity
(in the following, simply denoted as
C) or chemical potential
can be obtained rigorously from appropriate partial differentiation of
Z (see Equations (A3a)–(A3e)). Since the total number of possible spin configurations (=number of micro(scopic) states) is
, i.e., the set
involves a total of
different configurations, it is evident that the number of terms involved in
Z grows rapidly with increasing spin number
and becomes very large even for small systems. Due to this scaling behavior, it is typically not practicable to evaluate
Z by exact enumeration for general systems of arbitrary size even with state of the art computational resources. Here, simulation-based approaches such as Markov chain Monte Carlo (MC) can make an important contribution to estimate quantities such as
C with high accuracy [
14,
15]. Only for very simple systems such as the 1D-Ising model, it is possible to find exact closed analytic expressions for
Z which are summarized in Equations (A11a) and (A11b) for the cases of FBC and PBC together with corresponding expressions for the Helmholtz (free) energy
in Equations (A12a) and (A12b). In 2D, a closed analytical solution exists for the limiting case of infinite lattices which was derived by Lars Onsager [
16] with high mathematical effort (see Equation (
7)). For 2D-systems of finite size, exact solutions for
Z exist in case of PBC [
17,
18,
19] but to the best of our knowledge not for FBC [
20,
21]. This means it is (currently) not possible to directly write down an expression for
Z as function of (inverse) temperature
and
in case of a finite-size
-2D-model with FBC of arbitrary system size. It is of course possible, at least in principle, to calculate
Z for any 2D-system of arbitrary size on the basis of Equation (
2). However as mentioned before, with increasing lattice size, the evaluation becomes increasingly computationally intensive due to the combinatorial part of the calculation given by the power law scaling of the number of possible configurations. Alternatively to summing over all possible spin configurations
as conducted in Equation (
2), one can first cluster the configurations into a set of discrete energy levels
and then sum over this set of distinct energy levels instead:
where the weights (=frequencies, multiplicities, degeneracies)
associated with energy levels
have to fulfill the closure relation
. The energy level of a specific configuration is calculated from Equation (
1) according to
. The quantity introduced in this way and defined by the combined collection of energy levels
and corresponding weights
is called the density of states (DOS). The DOS refers to the number of different states at a particular energy level and can be interpreted as an energy spectrum of the corresponding Ising model. It should be noted that the DOS itself is temperature-independent while all derived quantities such as
A,
U and
C depend on
T. Calculation of
Z based on the DOS is completely equivalent to the former calculation according to Equation (
2) and therefore also allows exact evaluation of
Z. Corresponding expressions for the calculation of derived thermodynamic quantities involving the DOS are summarized in Equations (A7a)–(A7c). It should be stressed that even though the number of distinct energy levels
n is typically much smaller than the number of possible spin configurations
(i.e., the set
is smaller than the set
), and consequently the sum in Equation (
3) involves considerably fewer terms as compared to Equation (
2), practical calculation of
Z via the DOS formulation is, from a computational point of view, not superior per se towards the first route, since in both cases all possible configurations
have to be generated anyway. However, the DOS formulation allows a compact representation of the partition function itself. Another difference between the two formulations for
Z is that computation according to Equation (
2) involves a number of
individual sums (see Equation (A15b)) while the summation over energy levels according to Equation (
3) involves a single summation only.
Figure 1 shows estimated DOS for a couple of small quadratic (
) 2D-Ising systems with FBC (left) and PBC (right). In case of FBC, all DOS distributions are symmetric around the maximal value at
, whereas for PBC, this symmetry is found for even
N only. The minimum energy of the DOS distribution for a generic
-system is given by
for FBC and
for PBC, respectively, with a weight of
for both cases, corresponding to the two equivalent configurations with all spins being either in the up- or down-state.
In the following, we will take a closer look at the thermodynamic behavior of the 2D-Ising model, using the minimal
-system (FBC) as an explicit example which is shown in
Figure A1b and
Figure A3. In this case, there are
distinguishable configurations, i.e., microscopic states, but the DOS only involves three distinct energy states given by
such that
configurations have the minimal energy of
,
configurations have the maximal energy of
and the majority of
configurations have an energy value of
(cf.
Figure 1a and
Figure A3). The canonical partition function can then be written as (see also Equation (A15b) in the
Appendix A.3):
In order to rationalize the following discussion, it is advantageous to (re)define a normalized partition function with respect to the lowest-energy state (ground state)
, first:
from which expressions for the populated fractions associated with the
nth discrete energy state can be defined as:
For each temperature, the condition
with
must be fulfilled. It is important to emphasize that the meaning of a state here refers to a particular macroscopic (=energy) state and the fractions
measure the probability of finding the
-system in one of these three discrete energy states
,
or
. On the other hand, one could also calculate the probability for each of the 16 individual configurations, i.e., microscopic states (see Equation (
A5)). Such a simple three-state model as the
-system can be applied in a wide range of applications such as protein thermodynamics where states 0, 1 and 2 could correspond to the native (i.e., folded) state, intermediate (i.e., partially folded) state and denatured (i.e., unfolded) state of a protein, respectively [
22]. The equilibrium constants
, defined above, are a measure for the ratio of two probabilities and are closely related to the free energy barrier between ground state 0 and (excited) state
i via
. In principle, the equilibrium constant for the transition from the ground state to the second (excited) state (
) could be further split into two sequential transitions according to
such that
which will not be performed in the following however. In case of the
-system, the free energy barriers
relative to the ground state which comprise an energetic and entropic part according to
are given by
and
. The energetic contribution is simply given by
. The entropy difference which is related to the ratio of the weights of the corresponding states according to
reflects the fact that the state
has a six-times higher weight compared to the ground state
.
Figure 2a shows the fractions
of the three states as function of temperature where the latter is represented in reduced (dimensionless) form as
. At low temperatures (
, i.e.,
), only
corresponding to the ground state
is populated, while at increasing temperatures (
, i.e.,
), though all three states become thermally accessible,
associated with the zero-energy state
dominates due to its six-times higher statistical weight
compared to the other states. As revealed by
Figure 2b, at
when the system is in the ground state, free energy
A and internal energy
U coincide (
) and the entropic part is zero. It should be stressed that it is the entropic part of the free energy given by
which becomes zero due to
, while the entropy itself becomes
due to the two possible and equivalent configurations (all spins up or all spins down) associated with the ground state. With increasing
T,
A becomes more negative and the entropic part dominates the free energy while the absolute value of
U (i.e., the interactions between the spins) asymptotically decreases to zero. In this case, when all states are accessible and the system behaves as a collection of non-interacting spins, entropy becomes
with
. Different ways to estimate entropy are outlined in the
Appendix A.2.
For comparison,
Figure 3 shows an analogue decomposition analysis for the
-FBC-Ising model which in this case comprises a total of 39 distinct energy states with ground state energy
(cf.
Figure 1a). As pointed out earlier, the number of energy levels is significantly smaller than the number of different spin configurations
.
As the system size
further increases, the system can adopt an ever-increasing number of discrete energetic states while the spacing between these energy levels decreases. In the extreme case of the thermodynamic limit (
), an infinite number of states (=number of fractions
), i.e., a continuum of states is required. For this case, for which the difference between FBC and PBC as present for finite-size system vanishes, the following expression for the reduced free energy per spin
was derived by Lars Onsager [
16]:
Focusing on the reduced quantity
instead of the dimensional free energy
A itself which is an extensive quantity and therefore scales with
allows for a comparison between finite-size systems of all dimensions including the limiting case of
. This is shown in
Figure 4 which shows a set of curves for
as function of inverse temperature for a couple of quadratic (
) 2D-Ising models together with the limiting Onsager expression. In the low-temperature (LT) regime (i.e., high
) in case of FBC,
can be well-approximated by the scaling law
with
which is linear in
with slope
multiplied by a system-size dependent factor [
23]. This LT-approximation holds increasingly better for increasing
N (see dashed lines in
Figure 4a). For high temperatures (HT), i.e.,
, all curves independent of system size
N converge to the same limiting value
.
A main characteristic of the 2D-Ising model and major difference compared to the 1D-Ising model is that it features a phase transition when the number of spins increases to infinity. This phase transition is characterized by a discontinuity or singularity at a critical temperature in different physical observables when monitored as function of temperature such as (isochoric) heat capacity or the derivative of the (spontaneous) magnetization. For a 2D-lattice of infinite size and in the absence of a magnetic field, this critical temperature
is given by [
16,
24]:
As revealed for example by MC simulations, below this critical temperature (
), a phase exists comprising large domains where most of the spins have identical spin numbers
(either
or
) together with small isolated clusters with opposite
[
25]. Such a phase can coexist with a phase of opposite magnetization, i.e., where all spins are reversed. For
on the other hand, only a single homogenous (“disordered”) phase exists.
Figure 5 shows the temperature-dependence of the reduced heat capacity per spin
calculated for a couple of quadratic (
) 2D-Ising systems based on their DOS for FBC (a) and PBC (b). For comparison, the limiting heat capacity for the 1D-Ising model, given by
is also shown (purple dashed-dotted curve). The finite height of this curve over the whole temperature range demonstrates the absence of a phase transition in case of the 1D-Ising model. Since the first part of Equation (
7) is almost identical to the limiting value of
for the 1D-Ising model (
, cf. Equation (
A14a)) it can be concluded that it is the second part of the Onsager expression for
, i.e., the integral which gives rise to the phase transition. The black curve in
Figure 5 which shows the aforementioned singularity at the critical temperature
according to Equation (
8) (black dashed line) corresponds to the limiting reduced heat capacity for a 2D-lattice. It was derived from the Onsager expression Equation (
7) according to
but can not be expressed in closed form. Here, we applied an automatic differentiation approach based on (hyper-) dual numbers to obtain
[
26]. Despite the fact that, both for the FBC and PBC case, the curves for
clearly seem to converge towards the limiting Onsager solution with increasing
N (peaks become higher and corresponding peak temperature gets closer to
), the heat capacity values for all finite-size
systems will remain finite and a singularity is only found for macroscopic systems in the thermodynamic limit, i.e., for
. Different methods for estimating the critical temperature of the infinite system based on extrapolation from a couple of finite-size systems will be discussed in more detail in the context of another planned publication. In addition to the temperature at the peak maximum of the heat capacity curve, other characteristic parameters can be deduced from the profile giving access to insights into the thermodynamic behavior of the system. In analogy to calorimetric experiments [
22], the integration of the heat capacity profile over the whole temperature range delivers the so-called calorimetric change in internal energy and entropy:
with
. Using the state function property of
U and
S as it was performed in the first equality, the value of the integral between the given temperature bounds on the right-hand side can be evaluated without the need to actually integrate the heat capacity profile mathematically. For a
-system based on FBC, one obtains
with
and
and
with
and
. For quadratic PBC-systems, one obtains
due to the different value for the ground state energy
while
remains the same as for FBC. In order to compare the behavior of FBC and PBC when the number of spins
increases, it is beneficial to divide Equations (9a) and (9b) by
:
with
and the dimensionless per-spin quantities
and
. The integrals now involve the reduced heat capacity per spin
as plotted in
Figure 5. From Equation (
10a), one can see that the difference for
between FBC and PBC as present for finite lattice sizes vanishes in the thermodynamic limit as expected.
on the other hand is identical for both boundary types at all lattice sizes. One also sees that
which corresponds to the area under the curve
remains finite even for infinite lattice size despite the singularity at the aforementioned critical temperature
(see black curve in
Figure 5) and takes a value of
in this case. The conditions given by Equations (10a), (10b) can be used as diagnostic test for assessing the quality of the presented modeling approach for
in an integral sense.
3. Materials and Methods
The central idea as tested in this work is based on the question if it is possible to develop a free energy expression on the basis of 1D-Ising chains that can reproduce the results of a finite-size 2D-Ising model with FBC at least qualitatively. Here, we focus on the description of quadratic
-Ising models with
spins. The goal is to obtain an analytic and, in the best case, simple expression for the reduced free energy per spin
which approximates the exact solution as good as possible for any
-Ising model and therefore allows fast estimation without the rapidly growing computational effort for increasing lattice sizes as it is the case for the exact evaluation based on Equation (
2). The model should be applicable to small lattice dimensions
N on the one hand but should also feature a phase transition in case of infinite
N as described by the Onsager solution (see Equation (
7)). While the modeling takes place on the basis of the reduced free energy
, the reduced heat capacity per spin
follows straightforwardly at any (inverse) temperature from the second derivative with respect to
:
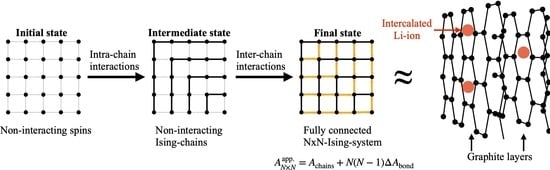
. The general idea is illustrated in
Figure 6 for the example of a
-FBC-system.
Initially, the number of
non-interacting spins corresponding to the desired
-system is placed on the lattice (=initial state 0). As a first step, a total of
interactions are added by summarizing the spins to
N non-interacting, i.e., independent Ising chains as shown in
Figure 6 (=state 1). In this scheme, the chains are labeled beginning from chain-ID 1, corresponding to the minimal length of 1 (i.e., a single spin) to chain-ID
N, corresponding to the longest chain, consisting of
spins. In this notion, the added
interactions correspond to intra-chain bonds since they connect neighboring spins within a chain. For the remainder of the work, the expressions “interactions” and “bonds” are used synonymously. In order to obtain a fully connected 2D-Ising system, another equal amount of
interactions have to be added to the graph, corresponding to inter-chain bonds since they establish interactions between adjacent chains, i.e., to couple neighboring spins assigned to different chains. This could be performed in a series of steps by successively adding more layers of inter-chain bonds. A specific example is shown in
Figure 6 where chains are connected via a set of edge bonds such that the edge spin of chain
i is connected via 2 bonds to 2 spins of chain
, resulting in a weakly coupled graph (=state 2). We emphasize that this procedure to go from state 1 (non-interacting Ising chains) to the final state of a fully coupled
-system is by no means unique, i.e., there are several ways of adding the remaining
inter-chain bonds and as it turns out, this part represents the actual challenge. From a statistical-mechanical point of view, the described approach (denoted by superscript “app.”) corresponds to a free energy construction of the kind:
In such an additive construction scheme, the final free energy estimate
for the interacting
-system results from addition of different free energy contributions
, associated with the inclusion of specific inter-chain bonds of type
k to the reference system of non-interacting Ising chains
. If
represents the free energy contribution for the addition of a single bond of type
k, the corresponding coefficients
have to add up to the total number of remaining inter-chain bonds:
. Explicit expressions for
and
will be derived in the following. Ideally, the constructed
would correspond to the exact
for the
-FBC-system as calculated from the corresponding exact 2D-partition function based on Equation (
2). Equation (
11) can be equivalently formulated in terms of partition functions:
with the relations
,
and
. From the latter relation it follows that
actually does not represent an absolute partition function but rather a partition function ratio corresponding to the inclusion of a single bond of type
k into the graph which is emphasized by the use of a lowercase letter
z.
3.1. Free Energy of Independent Ising Chains
The first step corresponding to state 1 in
Figure 6 is to summarize the
non-interacting spins on the lattice to
N independent Ising chains which implies the inclusion of
intra-chain bonds to the graph. The first and smallest chain has a length of 1, i.e., an isolated spin while the last chain
N is the longest with a length of
spins. Since the chains are independent, the combined partition function for the whole set of
N chains is given exactly by the product of the partition functions of the individual chains, i.e., it factorizes into
N partition functions:
with
according to Equation (
A11a) where the special case
corresponds to the partition function of a single isolated spin. In terms of free energy, the corresponding expression reads as:
with
according to Equation (
A12a) and
. Using the Gaussian sum formula, Equation (
14) can be simplified to give the following expression for the (reduced) free energy:
which is identical to the expression for the reduced free energy per spin of a single 1D-Ising chain of length
N with FBC (compare Equation (A12c)).
3.2. Inclusion of Inter-Chain Interactions
In this work, we applied a simplified variant of the presented approach discussed above where only one bond type in Equation (
11) with a single value for the free energy contribution
is considered. In this case, one adds all inter-chain bonds simultaneously and thus transitions directly from state 1 to the final state of a fully connected
-system without any intermediate steps (compare
Figure 6):
where
is given by Equation (15b). For the
-FBC-system in
Figure 6 this would correspond to the addition of 20 equal bonds to the graph in state 1, where the free energy contribution of each added bond is identical and given by
. At this point it should be stressed that although only one bond type is considered,
is not a constant, but a function of
N and
. Further, it should be emphasized that the decomposition of the free energy into an intra-chain and an inter-chain part does not involve any approximation so far and is exact (i.e.,
) as long as one calculates the bond contribution
consistently:
with
. For infinite lattice size, the equation changes into:
where
is now a function of temperature only,
is given by the Onsager expression Equation (
7) and
. From the comparison of the Onsager expression with Equation (16b), it can be seen that the second term of the latter equation which involves
should be given by the integral of the Onsager expression in case of
and is thus responsible for the phase transition.
Based on Equation (16b), an equivalent decomposition can also be obtained for the heat capacity via
:
where
was derived from Equation (15b). For infinite lattice size this expression becomes:
where
only depends on
.
From the derived expressions it becomes evident that the initial problem of expressing the free energy of a (finite-size) 2D-Ising model by means of 1D-Ising chains is now reduced to the estimation of
as function of system size
N and (inverse) temperature
. A requirement for the calculation of
is that the function
is two times differentiable with respect to
. The route taken in this work was to compute
according to Equation (
17) from the exact
for a couple of finite-size
-systems and then perform an approximation based on a two-dimensional fit in
N- and
-space. For the calculation of
, we used the optimized code of Karandashev et al. [
27] which evaluates the exact partition function
Z of a given 2D-Ising model at specified temperature and is publically available [
28]. Since the code returns
,
and
with
, the (reduced) heat capacity was computed from a finite-differences (second-order forward) approach. We validated this code for small system dimensions through comparison with self-written (non-optimized) code which evaluates the exact partition functions of
-systems based on the DOS formalism by systematically generating all possible
configurations using the Python itertools-module [
29]. Relative deviations in
between the two implementations for the considered temperature range were found to be in the order of
.
Among different investigated modeling approaches for
, the following has been found to be the most suitable: (i) calculation of exact values for
according to Equation (
17) for a couple of
-systems (e.g.,
to
) within a defined discretized (inverse) temperature interval; (ii) fitting the results with the inverse power law or generalized hyperbola function Equation (
21a) in
N-space with the four temperature-dependent model parameters
, separately for every discrete
-value (the reader has to be aware of not to confuse the model parameter
a with the reduced free energy
):
with
,
and
(analogously for the other model parameters
) and the following abbreviations:
As can be seen from Equation (
21a), for positive exponent
c, the asymptotic value of
for infinite lattice dimension is given by the temperature-dependent offset parameter
d:
; (iii) interpolation of the discretized model parameter values in
-space using cubic splines. Using Equations (21a)–(21c) and (22a)–(22c), the reduced free energy and heat capacity can then be calculated according to Equation (16b) and Equation (19b), respectively, at any temperature and system size.
The quality of the predicted approximations was assessed through a comparison with the exact results for
and
as obtained with the code of Karandashev et al. As mentioned above, alternative and lower-complexity modeling approaches for
, such as a second-degree polynomial function in inverse lattice dimension
with only three
-dependent model parameters were also tested but found not to be suitable (data not shown). Nonlinear fitting of Equation (
21a) was performed using the optimize-package of the open-source Python library SciPy [
30]. For piecewise cubic splines interpolation, the SciPy interpolate-package has been used. The routine returns not only the interpolated function value itself for the fitting parameters (e.g.,
) but also the corresponding first (
) and second derivative (
) at this temperature as required for the evaluation of Equations (21b), (21c) and (22a)–(22c). At this point, it should be emphasized again that the approximation of the modeling approach is introduced by specifying a specific functional form for
(in our case the generalized hyperbola Equation (
21a)) and not through Equations (16a), (16b) which are exact. For the sake of completeness, it should be noted that the analytical expression
further enables a direct and straightforward calculation of the chemical potential
for arbitrary quadratic systems as function of lattice size and temperature (see
Appendix A.4).
4. Results and Discussion
Figure 7 demonstrates the success of the described modeling procedure for
(see methods section for details) involving fitting with the hyperbola-based approach in Equation (
21a) to system sizes
to
. Therefore, exact reference solutions for
were calculated for these systems using the code of Karandashev et al. [
27] at 200 equidistant temperature points in the interval
for each system. The shown results for systems
to
were not incorporated into the fitting process and thus represent (interpolated) predictions. However, it has been found that it is also necessary to prescribe the Onsager solution for infinite
N by constraining the offset parameter
d of the fitting function via:
where Equation (
18) has been applied in the second equality. By doing this,
d becomes fixed such that only three free adjustable model parameters (
) remain. Without constraining
d, the (reduced) heat capacity profile will become unphysical for increasing
N and will not converge towards the correct Onsager solution in thermodynamic limit (see
Figure A4 in the
Appendix A.5). Furthermore, the exponent
c was restricted to positive values. As can be seen from
Figure 7,
shows a pronounced dependence on system size and temperature, both of which seem to be well reproduced by our approach. As expected, the free energy contribution of an added bond diminishes with increasing temperature.
The corresponding adjusted model parameters are shown in
Figure 8 as function of inverse temperature. It can be seen that all parameters are bound and well-behaved within the studied temperature-range.
Figure 9 shows the modeling results for the reduced free energy per spin
and reduced heat capacity per spin
based on Equation (16b) and Equation (19b), respectively, as functions of inverse temperature for selected
-systems. By construction through constraining the model parameter
d, both
and
become identical to the corresponding Onsager expressions for
. While the agreement between the tested model approach and corresponding exact results are close to perfect in case of
, a fact which is also confirmed by the very low percentage relative deviation (
) in
Figure 10, deviations for
are more pronounced. This behavior is due to the fact that
is proportional to the second derivative of
and thus is very sensitive to small local changes in the curvature of
. For all system sizes, some artifacts are present in
around the critical temperature which cause the curves to become increasingly rugged near the maximum as
N increases and makes an unambiguous determination of the peak maximum and the corresponding peak temperature difficult. These numerical artifacts can be mainly attributed to two origins: (i) a side effect of the imposed constraint to match the Onsager solution for infinite
N and (ii) the limited number of temperature points as used for interpolation. The latter can be seen when more temperature points are used which increases the resolution in
-space at the expense of increased computational effort. Although a higher
-resolution reduces the artifacts near the critical temperature and makes the curves smoother around the maximum, this creates small local disturbances (see
Figure A5 in the
Appendix A.5). For large
N-values outside the fitting range, the maximum of the approximated
-curve is already determined by the critical temperature
, whereas the peak temperature of the exact curve does not yet match it (see result for the
-system in
Figure 9b). However, despite these deviations in the shape of the profiles, the evaluation of the integral conditions in Equations (10a), (10b) yielded a maximal violation in the order of
from the nominal value. In this context, the impact of including the exact results from more
-systems in the fitting process at the same temperature resolution was also investigated (see
Figure A6 in the
Appendix A.5). For small system sizes the aforementioned artifacts close to
become more pronounced when more systems were taken into account for fitting (at same
-resolution) while for the prediction of larger system sizes the description near the peak becomes better. However, the qualitative behavior is identical for the studied cases where a different number of reference solutions was involved.
Figure 10 further shows that the deviations in
disappear for very high and low temperatures at all system sizes. Although it appears that local extrema emerge at certain intervals which increase with increasing
N, in the limiting case for infinite
N, all deviations must by construction decrease to zero for all temperatures.
As already mentioned in the introduction, a separate publication will focus on the adaption of the Ising model such that it can be applied to the description of intercalation phenomena such as the intercalation of Li-ions into an electrode host matrix. Here, we will only briefly illustrate a possible roadmap for such a modeling attempt. In the simplest case, one could study a one-dimensional cut through a (finite-sized) crystal lattice composed of
N lattice sites where each site can be either occupied by an ion (
) or empty (
). Such a description could be used for example to model the diffusion of Li-ions diffusion into tunnel-like structures of
[
31,
32]. Therefore, a Hamiltonian based on pairwise ion-ion interactions could be constructed in the following way:
with the pair energy
between lattice sites
i and
j. Equation (
23) involves a total of
pair interactions in case of FBC, comprising
possible nearest neighbor interactions between adjacent lattice sites,
possible next-nearest neighbor interactions between lattice sites which have another site in between and so on. Due to the long-range nature of electrostatic interactions it might be necessary to include interactions which go beyond nearest neighbors which is a clear difference compared to the classic Ising model (compare Equation (
A1a)) and the simplifying assumption of a uniform coupling constant
might not be applicable. A possible modeling approach of the distance-dependence of
for interaction sites which are
sites apart could be derived in analogy to Coulomb’s law according to
. Here, the coupling constant
between ions sitting directly next to each other (i.e.,
) could be treated as adjustable model parameter. Another degree of freedom could be introduced by the multiplication of
J with a distance-dependent screening parameter
to better incorporate the effect of the electrode matrix on the alteration of the ion-ion interactions. For computational reasons it might be necessary to define a certain cut-off distance beyond which the interactions are assumed to be zero which can be included into
in combination with a special switching function. Of course, both
and
could further be treated as temperature-dependent. Due to the inherent periodicity of the crystal, inclusion of PBC might yield a more realistic description for finite-size systems. For a 1D-crystal with
N lattice sites, the corresponding canonical partition function
involves a total of
possible configurations, including states with
ions and can (in principle) be calculated for every lattice size according to Equation (
2). In 1D, the transfer matrix method offers a route to obtain a closed analytic solution for
[
33]. However, in order to apply this kind of model for intercalation of Li-ions into other host materials where two- or three-dimensional diffusion takes place such as graphitic carbon [
34] or
spinel [
35], respectively, efficient approximative approaches for the evaluation of the higher-dimensional Ising model are required which was the main motivation of the present work. For these situations, a similar approach as presented in this work will be followed, comprising calculation of exact partition functions (or free energies
) for a couple of finite-size
-systems, followed by approximation of
with a suitable analytic expression and extrapolation to other lattice dimensions of interest. In contrast to the classic Ising model, it is known that such a proposed model based on the Hamiltonian above features a phase transition even in 1D due to the presence of long-range interactions [
36,
37]. The advantages of such a simple but at the same time physically based model and its implications for battery modeling are versatile: it could be used not only to predict the most probable electrode composition at a particular temperature but also transition temperatures between different phases from the heat capacity profile. Through the combination with experimentally or computationally determined ionic conductivities or diffusion coefficients, a link to transport properties of ionic species within crystal lattices can be achieved. Microscopic origins of hysteresis effects during dis-/charging which are highly relevant for battery energy efficiency and are thought to be related to lattice reorganization, could be possibly incorporated into such a model through further factorization of the coupling constant.