Modeling Silicon-Dominant Anodes: Parametrization, Discussion, and Validation of a Newman-Type Model
Abstract
:1. Introduction
2. Experimental Procedure
3. Modeling
3.1. Equilibrium Potential
3.2. Voltage Hysteresis
3.3. Electrolyte Properties
3.4. Electrical Conductivity
3.5. Solid-Phase Concentration
3.6. Solid-Phase Diffusivity
3.7. Electrode Kinetics
4. Results and Discussion
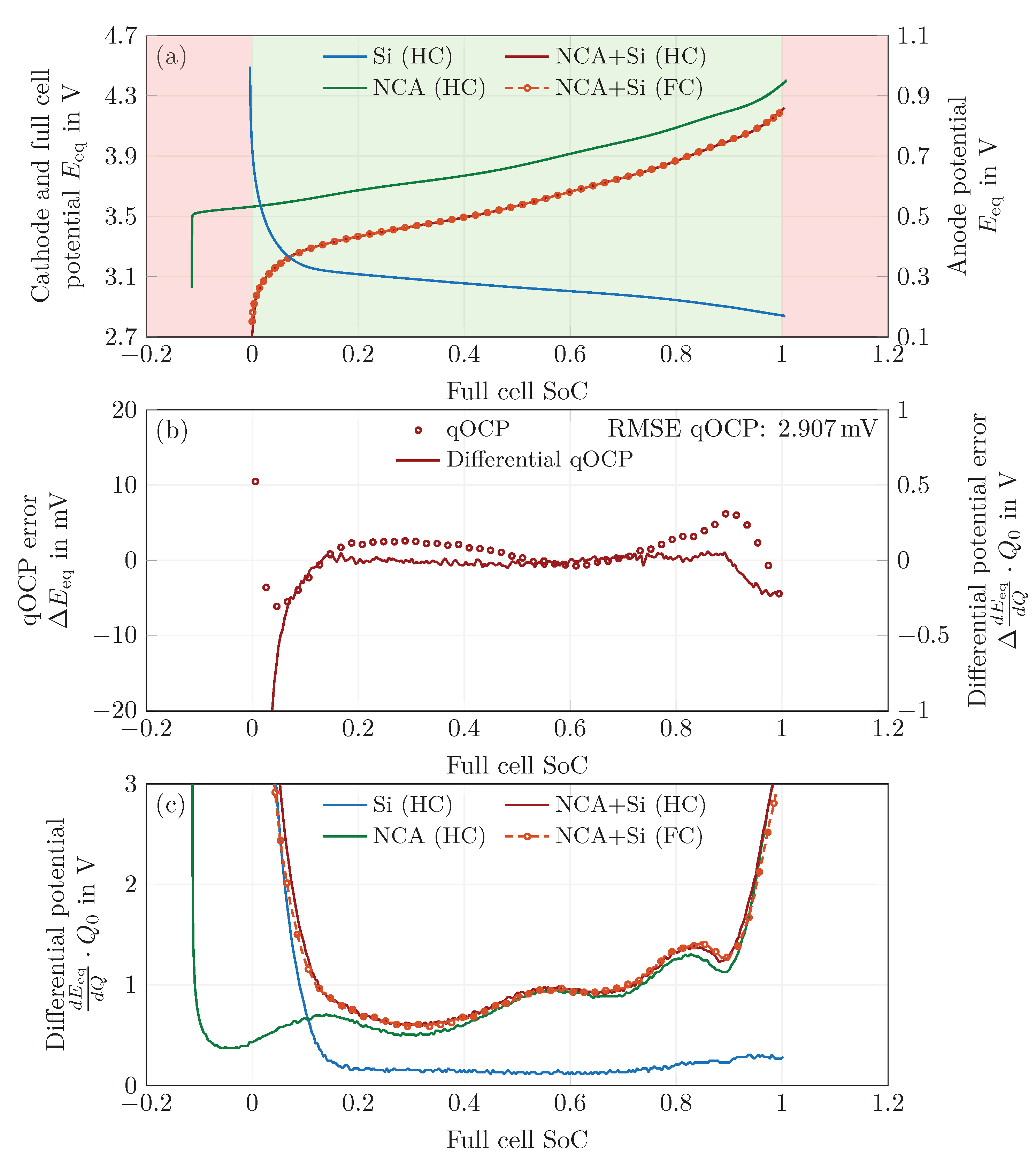
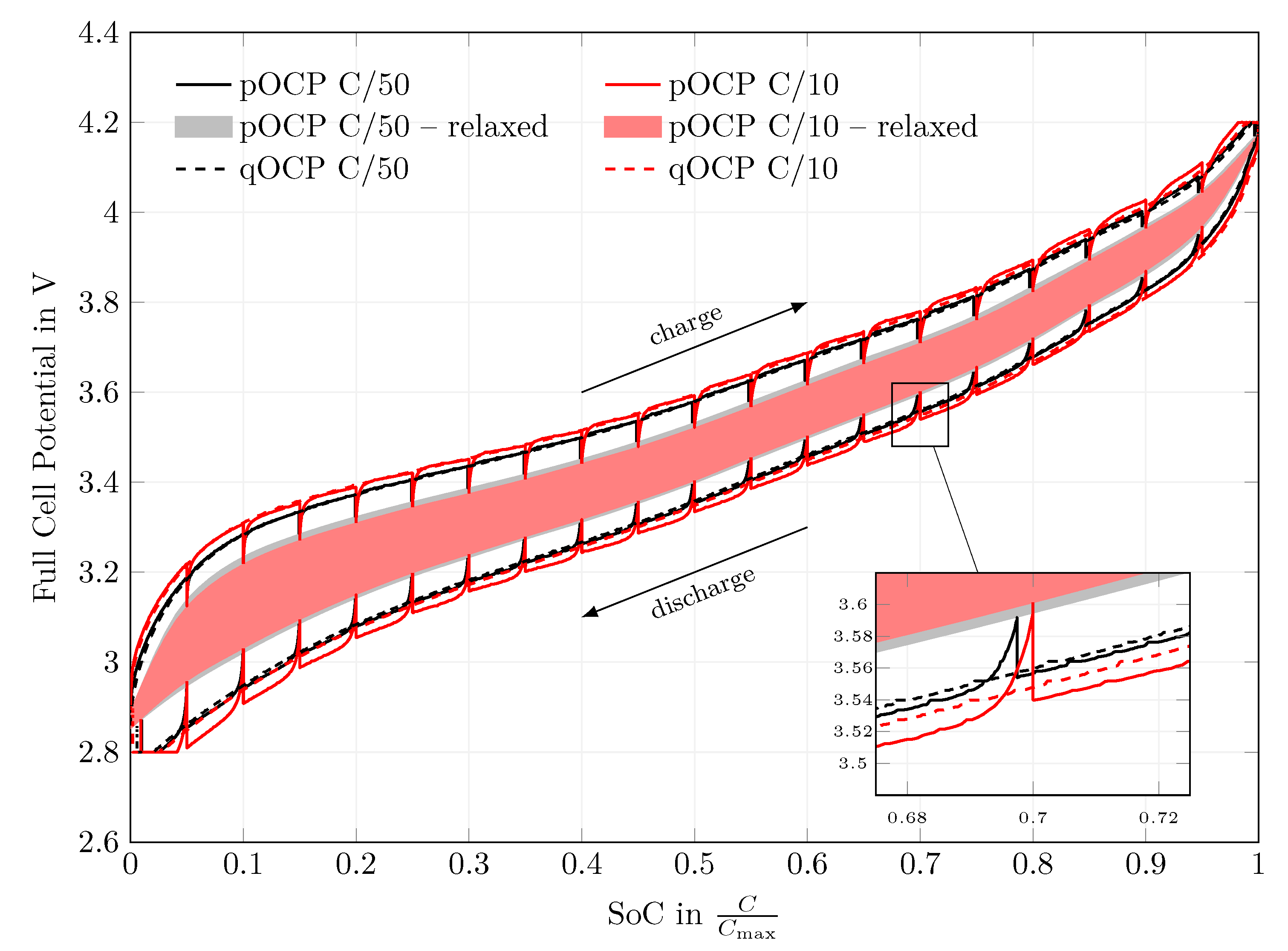
4.1. Open-Circuit Potential Measurements
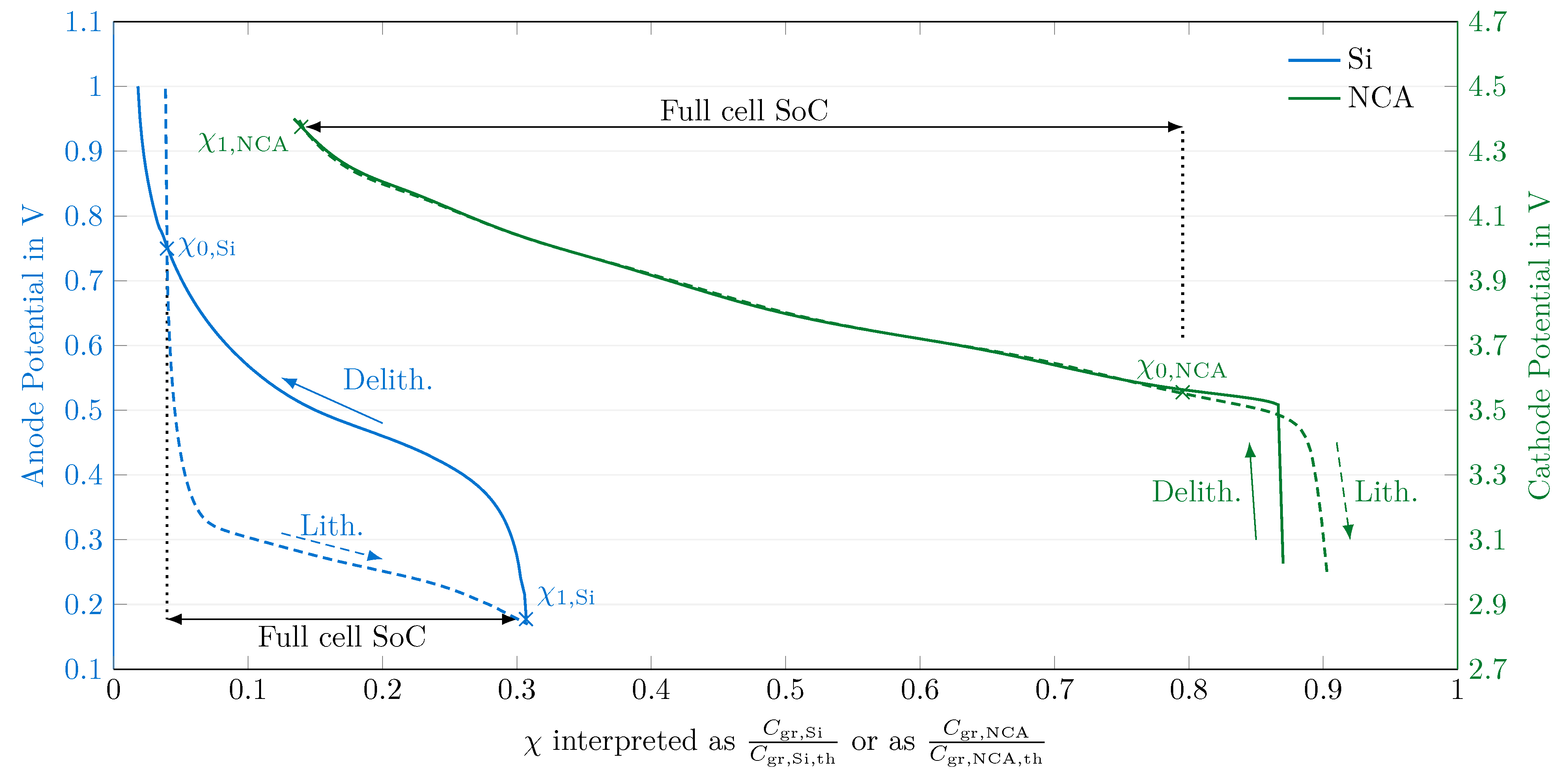
4.2. Electrode Balancing
4.3. Transformation to the Degree of Lithiation
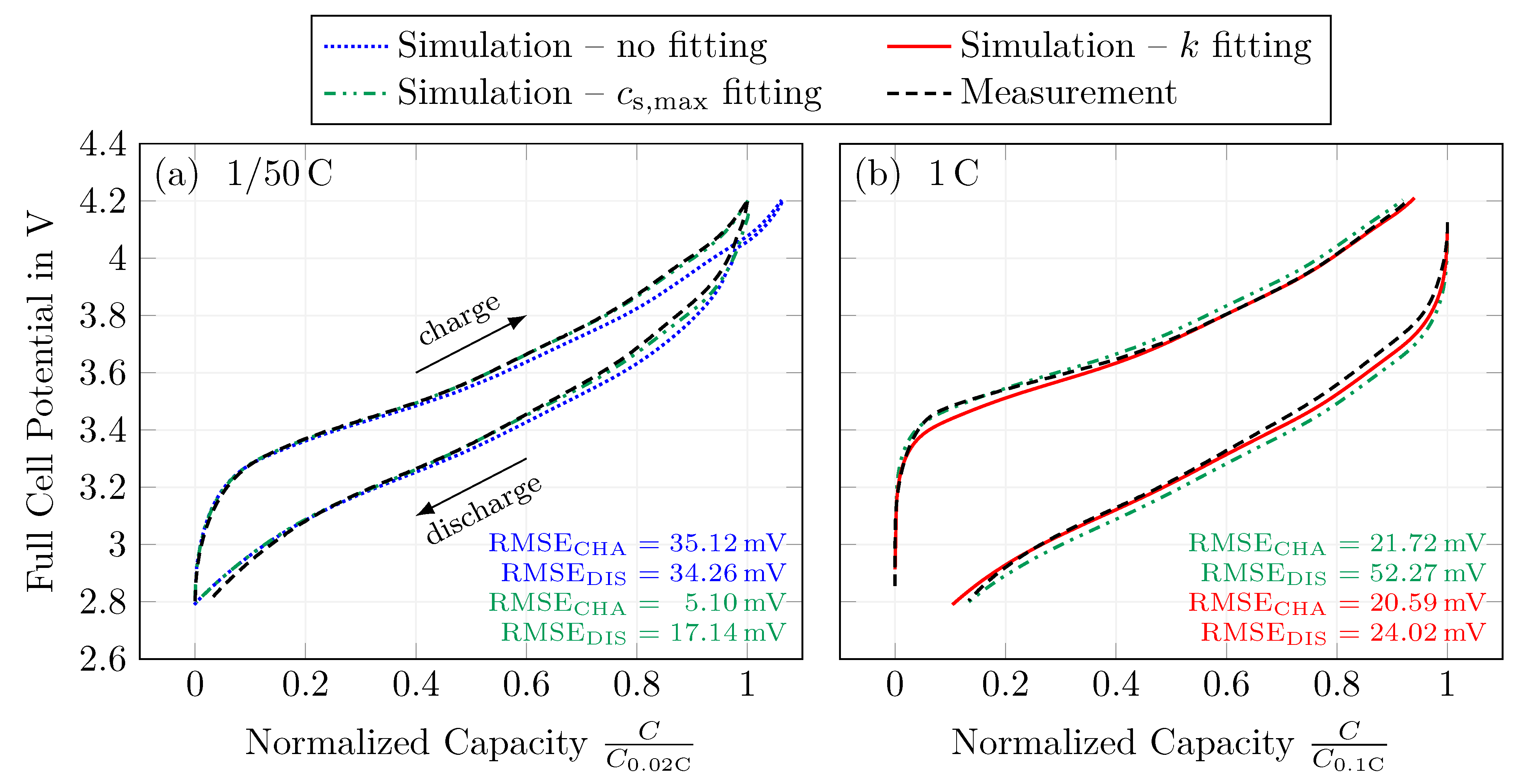
4.4. Fitting of Solid-Phase Concentrations
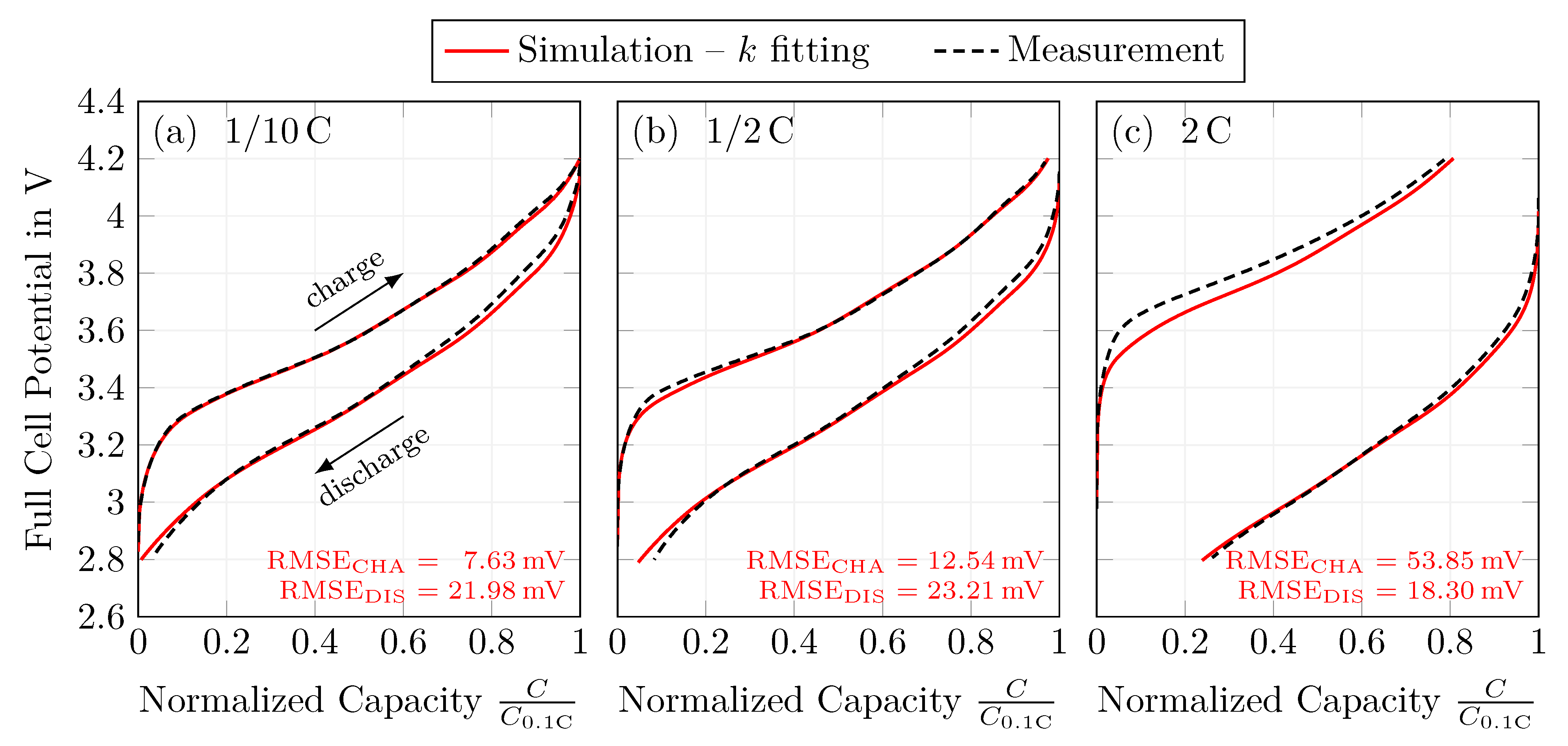
4.5. Rate Capability
5. Conclusions and Outlook
- Si is partially lithiated to a similar degree as in this study and as such does not undergo further amorphization or crystallization.
- Model equations have not been adjusted, for example with respect to complex electrode kinetics, solid state diffusion, or volumetric changes.
- Voltage hysteresis is accounted for via two equilibrium curves rather than a dedicated hysteresis model.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Acronyms | |
| AM | active material |
| CC | constant current |
| CV | constant voltage |
| DoL | degree of lithiation |
| DVA | differential voltage analysis |
| GITT | galvanostatic intermittent titration technique |
| Li | lithium |
| LIB | lithium-ion battery |
| NCA | nickel-cobalt-aluminum-oxide |
| PITT | potentiostatic intermittent titration technique |
| pOCP | pulsed open-circuit potential |
| qOCP | quasi open-circuit potential |
| RMSE | root-mean-squared error |
| SEI | solid-electrolyte interphase |
| Si | silicon |
| SoC | state of charge |
| Roman Symbols | |
| C | capacity, Ah |
| c | concentration, mol m |
| D | diffusivity, m s |
| activity, no unit | |
| equilibrium potential, V | |
| Faraday’s constant, 96,485 A s mol | |
| i | current density, A m |
| exchange current density, A m | |
| pore-wall flux, mol m s | |
| k | reaction rate constant, m s |
| L | through-plane thickness, m |
| MacMullin number, no unit | |
| r | r-axis or r-dimension (pseudo dimension), m |
| universal gas constant, 8.314 J mol K | |
| particle radius, m | |
| T | temperature, K |
| t | time, s |
| transference number, no unit | |
| x | x-axis or x-dimension, m |
| Greek Symbols | |
| charge transfer coefficient, no unit | |
| stoichiometry, no unit | |
| volume fraction, no unit | |
| overpotential, V | |
| conductivity, S m | |
| electrical potential, V | |
| density, kg m | |
| Subscripts & Superscripts | |
| a | anodic |
| app | applied |
| c | cathodic |
| eff | effective |
| gr | gravimetric |
| l | liquid phase |
| max | maximum |
| ref | reference |
| s | solid phase |
| surf | surface |
| th | theoretical |
| tot | total |
Appendix A. Model Equations and Parameters
| Spatial gradients | (r in spherical pseudo dimension) | (A1) |
| Mass balance | (A2) | |
| Mass balance | (A3) | |
| Potentials | (A4) | |
| (A5) | ||
| Charge balance | (A6) | |
| Electrode kinetics | (A7) | |
| (A8) | ||
| (A9) | ||
| Effective transport parameters | (A10) | |
| Boundary conditions | (A11) | |
| (A12) | ||
| (A13) | ||
| (A14) | ||
| (A15) | ||
| (A16) |
| Anode | Separator | Cathode | |
|---|---|---|---|
| Geometry | |||
| Thickness coating L | 46 μm m,c | 2 × 260 μm | 68 |
| particle radius | 2.25 μm L1 | 3.0755 μm | |
| Active material volume fraction | 0.32 | 0.61 | |
| Electrolyte volume fraction (porosity) | 0.50 c | 0.55 | 0.32 |
| MacMullin number | 5.385 | 1.29 | 7.333 |
| Thermodynamics | |||
| Equilibrium potential | Figure 1 m | Figure 1 m | |
| Stoichiometry 100% SoC | 0.3068 f | 0.1396 | |
| 0% SoC | 0.0396 | 0.7954 | |
| Max. concentration | 322,067 mol m−3 c,f | 46,400 mol m−3 c,f | |
| Transport | |||
| Solid diffusivity | 2 × 10−15 m2 s−1 L3 | 1 × 10−14 m2 s−1 L7 | |
| Electric conductivity | 33 S m−1 L3 | 1 S m−1 L6 | |
| Kinetics | |||
| Reaction rate constant k | 5.78 × 10−12 m s−1 L2,f | 1.64 × 10−10 m s−1 L4,f | |
| Anodic charge transfer coefficient | 0.5 a | 0.5 a | |
| Cathodic charge transfer coefficient | 0.5 a | 0.5 a | |
| Electrolyte * | |||
| Salt diffusivity in m2 s−1 *, | |||
| Ionic conductivity in S m−1 *, | |||
| Activity (no unit) *, | |||
| Transference number transference number | |||
| Reference concentration | 1 mol m−3 | ||
Appendix B. Additional Measurement Results

References
- Scrosati, B. History of lithium batteries. J. Solid State Electrochem. 2011, 15, 1623–1630. [Google Scholar] [CrossRef]
- Yoshino, A. The birth of the lithium-ion battery. Angew. Chem. Int. Ed. Engl. 2012, 51, 5798–5800. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.G.; Wang, W.; Xiao, J.; Xu, W.; Graff, G.L.; Yang, G.; Choi, D.; Wang, D.; Li, X.; Liu, J. Silicon-Based Anodes for Li-ion Batteries. In Encyclopedia of Sustainability Science and Technology; Meyers, R.A., Ed.; Springer: New York, NY, USA, 2012; pp. 9293–9316. [Google Scholar] [CrossRef]
- Wetjen, M.; Pritzl, D.; Jung, R.; Solchenbach, S.; Ghadimi, R.; Gasteiger, H.A. Differentiating the Degradation Phenomena in Silicon-Graphite Electrodes for Lithium-Ion Batteries. J. Electrochem. Soc. 2017, 164, A2840–A2852. [Google Scholar] [CrossRef]
- Wetjen, M.; Solchenbach, S.; Pritzl, D.; Hou, J.; Tileli, V.; Gasteiger, H.A. Morphological Changes of Silicon Nanoparticles and the Influence of Cutoff Potentials in Silicon-Graphite Electrodes. J. Electrochem. Soc. 2018, 165, A1503–A1514. [Google Scholar] [CrossRef]
- Xu, Q.; Wang, Q.; Chen, D.; Zhong, Y.; Wu, Z.; Song, Y.; Wang, G.; Liu, Y.; Zhong, B.; Guo, X. Silicon/graphite composite anode with constrained swelling and a stable solid electrolyte interphase enabled by spent graphite. Green Chem. 2021, 23, 4531–4539. [Google Scholar] [CrossRef]
- Sturm, J.; Rheinfeld, A.; Zilberman, I.; Spingler, F.B.; Kosch, S.; Frie, F.; Jossen, A. Modeling and simulation of inhomogeneities in a 18650 nickel-rich, silicon-graphite lithium-ion cell during fast charging. J. Power Sources 2019, 412, 204–223. [Google Scholar] [CrossRef]
- Schmitt, J.; Schindler, M.; Jossen, A. Change in the half-cell open-circuit potential curves of silicon–graphite and nickel-rich lithium nickel manganese cobalt oxide during cycle aging. J. Power Sources 2021, 506, 230240. [Google Scholar] [CrossRef]
- Schindler, M.; Sturm, J.; Ludwig, S.; Durdel, A.; Jossen, A. Comprehensive Analysis of the Aging Behavior of Nickel-Rich, Silicon-Graphite Lithium-Ion Cells Subject to Varying Temperature and Charging Profiles. J. Electrochem. Soc. 2021, 168, 060522. [Google Scholar] [CrossRef]
- Ko, M.; Chae, S.; Cho, J. Challenges in Accommodating Volume Change of Si Anodes for Li-Ion Batteries. ChemElectroChem 2015, 2, 1645–1651. [Google Scholar] [CrossRef]
- Jantke, D.; Bernhard, R.; Hanelt, E.; Buhrmester, T.; Pfeiffer, J.; Haufe, S. Silicon-Dominant Anodes Based on Microscale Silicon Particles under Partial Lithiation with High Capacity and Cycle Stability. J. Electrochem. Soc. 2019, 166, A3881–A3885. [Google Scholar] [CrossRef]
- Obrovac, M.N.; Krause, L.J. Reversible Cycling of Crystalline Silicon Powder. J. Electrochem. Soc. 2007, 154, A103. [Google Scholar] [CrossRef]
- Haufe, S.; Bernhard, R.; Pfeiffer, J. Revealing the Failure Mechanism of Partially Lithiated Silicon-Dominant Anodes Based on Microscale Silicon Particles. J. Electrochem. Soc. 2021, 168, 080531. [Google Scholar] [CrossRef]
- Doyle, M.; Fuller, T.F.; Newman, J. Modeling of Galvanostatic Charge and Discharge of the Lithium/Polymer/Insertion Cell. J. Electrochem. Soc. 1993, 140, 1526–1533. [Google Scholar] [CrossRef]
- Fuller, T.F.; Doyle, M.; Newman, J. Relaxation Phenomena in Lithium–Ion–Insertion Cells. J. Electrochem. Soc. 1994, 141, 982–990. [Google Scholar] [CrossRef]
- Rheinfeld, A.; Sturm, J.; Noel, A.; Wilhelm, J.; Kriston, A.; Pfrang, A.; Jossen, A. Quasi-Isothermal External Short Circuit Tests Applied to Lithium-Ion Cells: Part II. Modeling and Simulation. J. Electrochem. Soc. 2019, 166, A151–A177. [Google Scholar] [CrossRef]
- Dees, D.W.; Battaglia, V.S.; Bélanger, A. Electrochemical modeling of lithium polymer batteries. J. Power Sources 2002, 110, 310–320. [Google Scholar] [CrossRef]
- Jiang, Y.; Offer, G.; Jiang, J.; Marinescu, M.; Wang, H. Voltage Hysteresis Model for Silicon Electrodes for Lithium Ion Batteries, Including Multi-Step Phase Transformations, Crystallization and Amorphization. J. Electrochem. Soc. 2020, 167, 130533. [Google Scholar] [CrossRef]
- Lory, P.F.; Mathieu, B.; Genies, S.; Reynier, Y.; Boulineau, A.; Hong, W.; Chandesris, M. Probing Silicon Lithiation in Silicon-Carbon Blended Anodes with a Multi-Scale Porous Electrode Model. J. Electrochem. Soc. 2020, 167, 120506. [Google Scholar] [CrossRef]
- Swamy, T.; Chiang, Y.M. Electrochemical Charge Transfer Reaction Kinetics at the Silicon-Liquid Electrolyte Interface. J. Electrochem. Soc. 2015, 162, A7129–A7134. [Google Scholar] [CrossRef]
- Wang, M.; Xiao, X.; Huang, X. Study of lithium diffusivity in amorphous silicon via finite element analysis. J. Power Sources 2016, 307, 77–85. [Google Scholar] [CrossRef]
- Chandrasekaran, R.; Magasinski, A.; Yushin, G.; Fuller, T.F. Analysis of Lithium Insertion/Deinsertion in a Silicon Electrode Particle at Room Temperature. J. Power Sources 2010, 157, A1139. [Google Scholar] [CrossRef]
- Chandrasekaran, R.; Fuller, T.F. Analysis of the Lithium-Ion Insertion Silicon Composite Electrode/Separator/Lithium Foil Cell. J. Electrochem. Soc. 2011, 158, A859. [Google Scholar] [CrossRef]
- Golmon, S.; Maute, K.; Lee, S.H.; Dunn, M.L. Stress generation in silicon particles during lithium insertion. Appl. Phys. Lett. 2010, 97, 033111. [Google Scholar] [CrossRef]
- Wang, M.; Xiao, X. Investigation of the chemo-mechanical coupling in lithiation/delithiation of amorphous Si through simulations of Si thin films and Si nanospheres. J. Power Sources 2016, 326, 365–376. [Google Scholar] [CrossRef]
- Wang, M.; Xiao, X.; Huang, X. A multiphysics microstructure-resolved model for silicon anode lithium-ion batteries. J. Power Sources 2017, 348, 66–79. [Google Scholar] [CrossRef]
- Dhillon, S.; Hernández, G.; Wagner, N.P.; Svensson, A.M.; Brandell, D. Modelling capacity fade in silicon-graphite composite electrodes for lithium-ion batteries. Electrochim. Acta 2021, 377, 138067. [Google Scholar] [CrossRef]
- Dasari, H.; Eisenbraun, E. Predicting Capacity Fade in Silicon Anode-Based Li-Ion Batteries. Energies 2021, 14, 1448. [Google Scholar] [CrossRef]
- Lu, B.; Song, Y.; Zhang, Q.; Pan, J.; Cheng, Y.T.; Zhang, J. Voltage hysteresis of lithium ion batteries caused by mechanical stress. Phys. Chem. Chem. Phys. PCCP 2016, 18, 4721–4727. [Google Scholar] [CrossRef]
- Chevrier, V.L.; Dahn, J.R. First Principles Model of Amorphous Silicon Lithiation. J. Electrochem. Soc. 2009, 156, A454. [Google Scholar] [CrossRef]
- McDowell, M.T.; Lee, S.W.; Harris, J.T.; Korgel, B.A.; Wang, C.; Nix, W.D.; Cui, Y. In situ TEM of two-phase lithiation of amorphous silicon nanospheres. Nano Lett. 2013, 13, 758–764. [Google Scholar] [CrossRef]
- Bordes, A.; de Vito, E.; Haon, C.; Boulineau, A.; Montani, A.; Marcus, P. Multiscale Investigation of Silicon Anode Li Insertion Mechanisms by Time-of-Flight Secondary Ion Mass Spectrometer Imaging Performed on an In Situ Focused Ion Beam Cross Section. Chem. Mater. 2016, 28, 1566–1573. [Google Scholar] [CrossRef]
- Chockla, A.M.; Harris, J.T.; Akhavan, V.A.; Bogart, T.D.; Holmberg, V.C.; Steinhagen, C.; Mullins, C.B.; Stevenson, K.J.; Korgel, B.A. Silicon nanowire fabric as a lithium ion battery electrode material. J. Am. Chem. Soc. 2011, 133, 20914–20921. [Google Scholar] [CrossRef]
- McDowell, M.T.; Cui, Y. Single Nanostructure Electrochemical Devices for Studying Electronic Properties and Structural Changes in Lithiated Si Nanowires. Adv. Energy Mater. 2011, 1, 894–900. [Google Scholar] [CrossRef]
- Pollak, E.; Salitra, G.; Baranchugov, V.; Aurbach, D. In Situ Conductivity, Impedance Spectroscopy, and Ex Situ Raman Spectra of Amorphous Silicon during the Insertion/Extraction of Lithium. J. Phys. Chem. C 2007, 111, 11437–11444. [Google Scholar] [CrossRef]
- Kim, J.W.; Ryu, J.H.; Lee, K.T.; Oh, S.M. Improvement of silicon powder negative electrodes by copper electroless deposition for lithium secondary batteries. J. Power Sources 2005, 147, 227–233. [Google Scholar] [CrossRef]
- Wang, M. Simulation of Amorphous Silicon Anode in Lithium-Ion Batteries. Ph.D. Thesis, Michigan State University, East Lansing, MI, USA, 2017. [Google Scholar]
- Bucci, G.; Nadimpalli, S.P.; Sethuraman, V.A.; Bower, A.F.; Guduru, P.R. Measurement and modeling of the mechanical and electrochemical response of amorphous Si thin film electrodes during cyclic lithiation. J. Mech. Phys. Solids 2014, 62, 276–294. [Google Scholar] [CrossRef]
- Sivonxay, E.; Aykol, M.; Persson, K.A. The lithiation process and Li diffusion in amorphous SiO2 and Si from first-principles. Electrochim. Acta 2020, 331, 135344. [Google Scholar] [CrossRef]
- Dees, D.W.; Gallagher, K.G.; Abraham, D.P.; Jansen, A.N. Electrochemical Modeling the Impedance of a Lithium-Ion Positive Electrode Single Particle. J. Electrochem. Soc. 2013, 160, A478–A486. [Google Scholar] [CrossRef]
- Li, J.; Xiao, X.; Yang, F.; Verbrugge, M.W.; Cheng, Y.T. Potentiostatic Intermittent Titration Technique for Electrodes Governed by Diffusion and Interfacial Reaction. J. Phys. Chem. C 2012, 116, 1472–1478. [Google Scholar] [CrossRef]
- Sethuraman, V.A.; Srinivasan, V.; Newman, J. Analysis of Electrochemical Lithiation and Delithiation Kinetics in Silicon. J. Electrochem. Soc. 2013, 160, A394–A403. [Google Scholar] [CrossRef]
- Guidelli, R.; Compton, R.G.; Felio, J.M.; Gileadi, E.; Lipkowski, J.; Schmickler, W. Defining the transfer coefficient in electrochemistry: An assessment (IUPAC Technical Report). Pure Appl. Chem. 2014, 86, 245–258. [Google Scholar] [CrossRef]
- Baggetto, L.; Niessen, R.A.H.; Roozeboom, F.; Notten, P.H.L. High Energy Density All-Solid-State Batteries: A Challenging Concept Towards 3D Integration. Adv. Funct. Mater. 2008, 18, 1057–1066. [Google Scholar] [CrossRef]
- Tjandra, R.; Thanagasundram, S.; Tseng, K.J.; Jossen, A. Improved lithium-ion battery model with hysteresis effect. In Proceedings of the 2014 IEEE Transportation Electrification Conference and Expo (ITEC), Dearborn, MI, USA, 15–18 June 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 1–8. [Google Scholar] [CrossRef]
- Valøen, L.O.; Reimers, J.N. Transport Properties of LiPF6-Based Li-Ion Battery Electrolytes. J. Electrochem. Soc. 2005, 152, A882–A891. [Google Scholar] [CrossRef]
- Marinho, B.; Ghislandi, M.; Tkalya, E.; Koning, C.E.; de With, G. Electrical conductivity of compacts of graphene, multi-wall carbon nanotubes, carbon black, and graphite powder. Powder Technol. 2012, 221, 351–358. [Google Scholar] [CrossRef]
- Amin, R.; Ravnsbæk, D.B.; Chiang, Y.M. Characterization of Electronic and Ionic Transport in Li1-xNi0.8Co0.15Al0.05O2 (NCA). J. Electrochem. Soc. 2015, 162, A1163–A1169. [Google Scholar] [CrossRef]
- Ashwin, T.R.; McGordon, A.; Widanage, W.D.; Jennings, P.A. Modified electrochemical parameter estimation of NCR18650BD battery using implicit finite volume method. J. Power Sources 2017, 341, 387–395. [Google Scholar] [CrossRef]
- Grundmann, M. The Physics of Semiconductors; Springer International Publishing: Cham, Switzerland, 2016. [Google Scholar] [CrossRef]
- Pearson, G.L.; Bardeen, J. Electrical Properties of Pure Silicon and Silicon Alloys Containing Boron and Phosphorus. Phys. Rev. 1949, 75, 865–883. [Google Scholar] [CrossRef]
- Fan, S.; Plascencia, G.; Utigard, T. High Temperature Electric Conductivity of Pure Silicon. Can. Metall. Q. 2008, 47, 509–512. [Google Scholar] [CrossRef]
- Dees, D.W.; Kawauchi, S.; Abraham, D.P.; Prakash, J. Analysis of the Galvanostatic Intermittent Titration Technique (GITT) as applied to a lithium-ion porous electrode. J. Power Sources 2009, 189, 263–268. [Google Scholar] [CrossRef]
- Park, J.H.; Yoon, H.; Cho, Y.; Yoo, C.Y. Investigation of Lithium Ion Diffusion of Graphite Anode by the Galvanostatic Intermittent Titration Technique. Materials 2021, 14, 4683. [Google Scholar] [CrossRef]
- Tsai, P.C.; Wen, B.; Wolfman, M.; Choe, M.J.; Pan, M.S.; Su, L.; Thornton, K.; Cabana, J.; Chiang, Y.M. Single-particle measurements of electrochemical kinetics in NMC and NCA cathodes for Li-ion batteries. Energy Environ. Sci. 2018, 11, 860–871. [Google Scholar] [CrossRef]
- Chan, C.K.; Peng, H.; Liu, G.; McIlwrath, K.; Zhang, X.F.; Huggins, R.A.; Cui, Y. High-performance lithium battery anodes using silicon nanowires. Nat. Nanotechnol. 2008, 3, 31–35. [Google Scholar] [CrossRef] [PubMed]
- Pan, K.; Zou, F.; Canova, M.; Zhu, Y.; Kim, J.H. Systematic electrochemical characterizations of Si and SiO anodes for high-capacity Li-Ion batteries. J. Power Sources 2019, 413, 20–28. [Google Scholar] [CrossRef]
- Smith, A.J.; Dahn, H.M.; Burns, J.C.; Dahn, J.R. Long-Term Low-Rate Cycling of LiCoO2 /Graphite Li-Ion Cells at 55 ∘C. J. Electrochem. Soc. 2012, 159, A705–A710. [Google Scholar] [CrossRef]
- Dahn, H.M.; Smith, A.J.; Burns, J.C.; Stevens, D.A.; Dahn, J.R. User-Friendly Differential Voltage Analysis Freeware for the Analysis of Degradation Mechanisms in Li-Ion Batteries. J. Electrochem. Soc. 2012, 159, A1405–A1409. [Google Scholar] [CrossRef]
- Xie, W.; Yang, S. Charging Optimization of Lithium-Ion Batteries Based on Charge Transfer Limitation and Mass Transport Limitation. J. Electrochem. Soc. 2023, 170, 010506. [Google Scholar] [CrossRef]
- Li, J.; Dahn, J.R. An In Situ X-Ray Diffraction Study of the Reaction of Li with Crystalline Si. J. Power Sources 2007, 154, A156. [Google Scholar] [CrossRef]
- Graf, M.; Berg, C.; Bernhard, R.; Haufe, S.; Pfeiffer, J.; Gasteiger, H.A. Effect and Progress of the Amorphization Process for Microscale Silicon Particles under Partial Lithiation as Active Material in Lithium-Ion Batteries. J. Electrochem. Soc. 2022, 169, 020536. [Google Scholar] [CrossRef]
- Nitta, N.; Wu, F.; Lee, J.T.; Yushin, G. Li-ion battery materials: Present and future. Mater. Today 2015, 18, 252–264. [Google Scholar] [CrossRef]
- Landesfeind, J.; Hattendorff, J.; Ehrl, A.; Wall, W.A.; Gasteiger, H.A. Tortuosity Determination of Battery Electrodes and Separators by Impedance Spectroscopy. J. Electrochem. Soc. 2016, 163, A1372–A1387. [Google Scholar] [CrossRef]
- Habedank, J.B.; Kraft, L.; Rheinfeld, A.; Krezdorn, C.; Jossen, A.; Zaeh, M.F. Increasing the Discharge Rate Capability of Lithium-Ion Cells with Laser-Structured Graphite Anodes: Modeling and Simulation. J. Electrochem. Soc. 2018, 165, A1563–A1573. [Google Scholar] [CrossRef]

| Ref. | Focal Area | Silicon | Dimensionality |
|---|---|---|---|
| [18] | Voltage hysteresis via asymmetric reactions | pure | 0D model |
| [19] | Current distribution & inhomogeneous lithation | composite | p2D |
| [20] | Kinetic limitations & rate capability | pure | 0D impedance model |
| [21] | Phase boundaries & diffusivity | pure | 2D SPM |
| [22] | Volume change & (de)insertion process | dominant | 1D SPM |
| [23] | Volume change & electrolyte displacement | dominant | p2D |
| [24] | Mechanical stress & stress-induced diffusion | pure | 1D SPM |
| [25] | Mechanical stress & geometry dependency | dominant | 1D thin-film & SPM |
| [26] | Coupling of electrochemistry and mechanics | pure | 2D MSM |
| [27,28] | Capacity fade via SEI interaction | composite | 1D model |
| [29] | Voltage hysteresis via mechanical stress | pure | 0D model |
| [30] | First principles model of silicon lithiation | pure | 0D DFT calculation |
| This work | Parametrization & validation of an electrode in a full-cell setup | dominant | p2D |
| Parameter | Unit | Value Range | Value Selected for This Work | References | ||
|---|---|---|---|---|---|---|
| Electrical conductivity | 0.2 × 10−9 | to | 5 × 103 | 33 | [23,33,34,35,36,37] | |
| Solid-phase diffusivity | 1 × 10−20 | to | 1 × 10−11 a | 2 × 10−15 | [21,38,39] | |
| Exchange current density | 1 × 10−3 | to | 1 × 105 | 2.2 b | [19,20,22,38,40,41] | |
| Charge transfer coefficient | – | 0.2 | to | 3.42 | 0.5 | [22,42,43] |
| SoC | Anode | Cathode | |||
|---|---|---|---|---|---|
| DoL | DoL | ||||
| in – | in V | in – | in V | ||
| 0% | 0.7531 | 3.5518 | dis | ||
| 0.7267 | 3.5635 | cha | |||
| 0.7399 | 3.5577 | ave | |||
| 100% | 0.1932 | 4.3797 | dis | ||
| 0.1710 | 4.3764 | cha | |||
| 0.1821 | 4.3781 | ave | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Durdel, A.; Friedrich, S.; Hüsken, L.; Jossen, A. Modeling Silicon-Dominant Anodes: Parametrization, Discussion, and Validation of a Newman-Type Model. Batteries 2023, 9, 558. https://doi.org/10.3390/batteries9110558
Durdel A, Friedrich S, Hüsken L, Jossen A. Modeling Silicon-Dominant Anodes: Parametrization, Discussion, and Validation of a Newman-Type Model. Batteries. 2023; 9(11):558. https://doi.org/10.3390/batteries9110558
Chicago/Turabian StyleDurdel, Axel, Sven Friedrich, Lukas Hüsken, and Andreas Jossen. 2023. "Modeling Silicon-Dominant Anodes: Parametrization, Discussion, and Validation of a Newman-Type Model" Batteries 9, no. 11: 558. https://doi.org/10.3390/batteries9110558
APA StyleDurdel, A., Friedrich, S., Hüsken, L., & Jossen, A. (2023). Modeling Silicon-Dominant Anodes: Parametrization, Discussion, and Validation of a Newman-Type Model. Batteries, 9(11), 558. https://doi.org/10.3390/batteries9110558








