SoC Estimation in Lithium-Ion Batteries with Noisy Measurements and Absence of Excitation
Abstract
:1. Introduction
2. Model Description and Problem Formulation
2.1. Equivalent Circuit Model
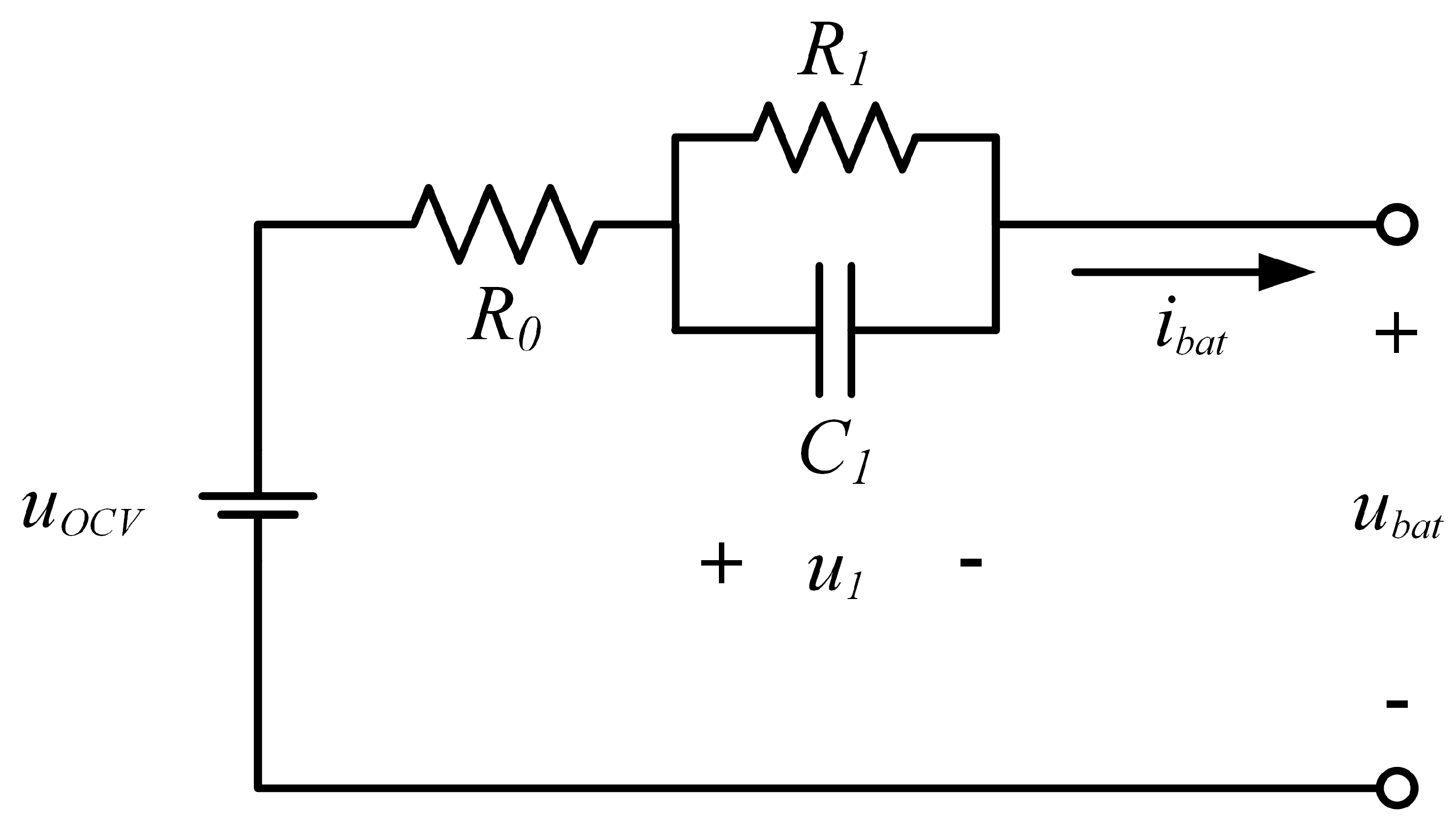
2.2. Estimation Objective
2.3. Limiting Observability Assumptions of Existing Observers
2.4. What If a Higher-Order Model Was Considered?
3. Proposal
3.1. Transforming the Problem
3.2. Estimator Equations
4. Numerical Simulations
4.1. Methodology
4.2. Case 1: Persistence of Excitation Current Signal
4.3. Case 2: Non-Persistence of Excitation Current Signal
4.4. Case 3: Sensor Noise
4.5. Case 4: Variable OCV
4.6. Case 5: Vehicle Load Profile
5. Conclusions and Future Work
- Test of the performance against full unknown parameters. In the test performed, the time constant of the circuit, , was assumed to be known. We think that practical applications would benefit if the GPEBO did not need to know this parameter.
- Experimental validation. Independent test to characterise the cell (as in [48]) to compare it against the estimated value of the parameters.
- Experiment with temperature sensitivity. With temperature affecting the value of many ECM parameters, it would be interesting to test the performance of GPEBO with different temperatures.
- Automatic tuning. Automatic tuning would solve the main drawback that we have experienced, which is finding a gain that ensures performance.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ANN | Artificial Neural Network |
| BMS | Battery Monitoring System |
| DFN | Doyle-Fuller-Newman |
| DREM | dynamic regressor extension and mixing |
| ECM | equivalent circuit model |
| EKF | Extended Kalman Filter |
| ESS | Energy Storage System |
| EV | Electric Vehicle |
| GPEBO | Generalized Parameter Estimation-based Observers |
| HGO | High Gain Observer |
| KF | Kalman Filter |
| Li-ion | Lithium-Ion |
| LIBs | lithium-ion batteries |
| OCV | Open Circuit Voltage |
| SMO | Sliding mode observer |
| SoC | State of Charge |
| SPM | Single Particle Model |
| SVM | Support Vector Machine |
| UCO | Uniform Completely Observable |
| UKF | Unscented Kalman Filter |
| WLTP | Worldwide Harmonised Light Vehicles Test Procedure |
References
- IEA. Electric Vehicles. IEA. Available online: https://www.iea.org/energy-system/transport/electric-vehicles (accessed on 19 October 2023).
- Carignano, M.; Costa-Castelló, R. Toyota Mirai: Powertrain Model and Assessment of the Energy Management. IEEE Trans. Veh. Technol. 2023, 72, 7000–7010. [Google Scholar] [CrossRef]
- IEA. Renewables—Energy System. IEA. Available online: https://www.iea.org/energy-system/renewables (accessed on 19 October 2023).
- Tarascon, J.M.; Armand, M. Issues and challenges facing rechargeable lithium batteries. Nature 2001, 414, 359–367. [Google Scholar] [CrossRef]
- Asri, L.I.M.; Ariffin, W.N.S.F.W.; Zain, A.S.M.; Nordin, J.; Saad, N.S. Comparative Study of Energy Storage Systems (ESSs). J. Phys. Conf. Ser. 2021, 1962, 012035. [Google Scholar] [CrossRef]
- Lee, S.B.; Thiagarajan, R.S.; Subramanian, V.R.; Onori, S. Advanced Battery Management Systems: Modeling and Numerical Simulation for Control. In Proceedings of the 2022 American Control Conference (ACC), Atlanta, GA, USA, 8–10 June 2022; pp. 4403–4414. [Google Scholar]
- Cai, W.; Yan, C.; Yao, Y.X.; Xu, L.; Xu, R.; Jiang, L.L.; Huang, J.Q.; Zhang, Q. Rapid Lithium Diffusion in Order@Disorder Pathways for Fast-Charging Graphite Anodes. Small Struct. 2020, 1, 2000010. [Google Scholar] [CrossRef]
- Sun, C.; Ji, X.; Weng, S.; Li, R.; Huang, X.; Zhu, C.; Xiao, X.; Deng, T.; Fan, L.; Chen, L.; et al. 50C Fast-Charge Li-Ion Batteries using a Graphite Anode. Adv. Mater. 2022, 34, 2206020. [Google Scholar] [CrossRef]
- Yue, X.; Zhang, J.; Dong, Y.; Chen, Y.; Shi, Z.; Xu, X.; Li, X.; Liang, Z. Reversible Li Plating on Graphite Anodes through Electrolyte Engineering for Fast-Charging Batteries. Angew. Chem. Int. Ed. 2023, 62, e202302285. [Google Scholar] [CrossRef]
- Zheng, L.; Zhang, L.; Zhu, J.; Wang, G.; Jiang, J. Co-estimation of state-of-charge, capacity and resistance for lithium-ion batteries based on a high-fidelity electrochemical model. Appl. Energy 2016, 180, 424–434. [Google Scholar] [CrossRef]
- Weng, C.; Sun, J.; Peng, H. A unified open-circuit-voltage model of lithium-ion batteries for state-of-charge estimation and state-of-health monitoring. J. Power Sources 2014, 258, 228–237. [Google Scholar] [CrossRef]
- Pattipati, B.; Balasingam, B.; Avvari, G.V.; Pattipati, K.R.; Bar-Shalom, Y. Open circuit voltage characterization of lithium-ion batteries. J. Power Sources 2014, 269, 317–333. [Google Scholar] [CrossRef]
- Movassagh, K.; Raihan, A.; Balasingam, B.; Pattipati, K. A Critical Look at Coulomb Counting Approach for State of Charge Estimation in Batteries. Energies 2021, 14, 4074. [Google Scholar] [CrossRef]
- Sesidhar, D.V.S.R.; Badachi, C.; Green, R.C., II. A review on data-driven SOC estimation with Li-Ion batteries: Implementation methods & future aspirations. J. Energy Storage 2023, 72, 108420. [Google Scholar]
- Alazki, H.; Cortés-Vega, D.; García, P. Diseño robusto de un observador de perturbaciones con saturaciones: Aplicación al control de regulación de la glucosa en pacientes con diabetes tipo 1. Rev. Iberoam. Autom. Inform. Ind. 2023, 1–9. [Google Scholar] [CrossRef]
- Plett, G.L. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs: Part 3. State and parameter estimation. J. Power Sources 2004, 134, 277–292. [Google Scholar] [CrossRef]
- Hu, C.; Youn, B.D.; Chung, J. A multiscale framework with extended Kalman filter for lithium-ion battery SOC and capacity estimation. Appl. Energy 2012, 92, 694–704. [Google Scholar] [CrossRef]
- Liu, C.z.; Zhu, Q.; Li, L.; Liu, W.q.; Wang, L.Y.; Xiong, N.; Wang, X.y. A State of Charge Estimation Method Based on H∞ Observer for Switched Systems of Lithium-Ion Nickel–Manganese–Cobalt Batteries. IEEE Trans. Ind. Electron. 2017, 64, 8128–8137. [Google Scholar] [CrossRef]
- Sun, F.; Hu, X.; Zou, Y.; Li, S. Adaptive unscented Kalman filtering for state of charge estimation of a lithium-ion battery for electric vehicles. Energy 2011, 36, 3531–3540. [Google Scholar] [CrossRef]
- Huang, C.; Wang, Z.; Zhao, Z.; Wang, L.; Lai, C.S.; Wang, D. Robustness Evaluation of Extended and Unscented Kalman Filter for Battery State of Charge Estimation. IEEE Access 2018, 6, 27617–27628. [Google Scholar] [CrossRef]
- Wang, S.; Jia, X.; Takyi-Aninakwa, P.; Stroe, D.I.; Fernandez, C. Review—Optimized Particle Filtering Strategies for High-Accuracy State of Charge Estimation of LIBs. J. Electrochem. Soc. 2023, 170, 050514. [Google Scholar] [CrossRef]
- Kim, I.S. The novel state of charge estimation method for lithium battery using sliding mode observer. J. Power Sources 2006, 163, 584–590. [Google Scholar] [CrossRef]
- Chen, X.; Shen, W.; Cao, Z.; Kapoor, A. A novel approach for state of charge estimation based on adaptive switching gain sliding mode observer in electric vehicles. J. Power Sources 2014, 246, 667–678. [Google Scholar] [CrossRef]
- Anderson, J.L.; Moré, J.J.; Puleston, P.F.; Roda, V.; Costa-Castelló, R. Control Super-Twisting con adaptación basada en cruce por cero. Análisis de estabilidad y validación. Rev. Iberoam. Autom. Inform. Ind. 2022, 20, 104–114. [Google Scholar] [CrossRef]
- Mukhopadhyay, S.; Zhang, F. A high-gain adaptive observer for detecting Li-ion battery terminal voltage collapse. Automatica 2014, 50, 896–902. [Google Scholar] [CrossRef]
- Jenkins, B.; Krupadanam, A.; Annaswamy, A.M. Fast Adaptive Observers for Battery Management Systems. IEEE Trans. Control Syst. Technol. 2020, 28, 776–789. [Google Scholar] [CrossRef]
- Limoge, D.W.; Annaswamy, A.M. An Adaptive Observer Design for Real-Time Parameter Estimation in Lithium-Ion Batteries. IEEE Trans. Control Syst. Technol. 2020, 28, 505–520. [Google Scholar] [CrossRef]
- Blondel, P.; Postoyan, R.; Raël, S.; Benjamin, S.; Desprez, P. Nonlinear Circle-Criterion Observer Design for an Electrochemical Battery Model. IEEE Trans. Control Syst. Technol. 2019, 27, 889–897. [Google Scholar] [CrossRef]
- Martí-Florences, M.; Cecilia, A.; Costa-Castelló, R. Modelling and Estimation in Lithium-Ion Batteries: A Literature Review. Energies 2023, 16, 6846. [Google Scholar] [CrossRef]
- Ghaeminezhad, N.; Ouyang, Q.; Wei, J.; Xue, Y.; Wang, Z. Review on state of charge estimation techniques of lithium-ion batteries: A control-oriented approach. J. Energy Storage 2023, 72, 108707. [Google Scholar] [CrossRef]
- Clemente, A.; Costa-Castelló, R. Redox Flow Batteries: A Literature Review Oriented to Automatic Control. Energies 2020, 13, 4514. [Google Scholar] [CrossRef]
- Puleston, T.; Clemente, A.; Costa-Castelló, R.; Serra, M. Modelling and Estimation of Vanadium Redox Flow Batteries: A Review. Batteries 2022, 8, 121. [Google Scholar] [CrossRef]
- Doyle, M.; Fuller, T.F.; Newman, J. Modeling of Galvanostatic Charge and Discharge of the Lithium/Polymer/Insertion Cell. J. Electrochem. Soc. 1993, 140, 1526–1533. [Google Scholar] [CrossRef]
- Moura, S.J.; Argomedo, F.B.; Klein, R.; Mirtabatabaei, A.; Krstic, M. Battery State Estimation for a Single Particle Model with Electrolyte Dynamics. IEEE Trans. Control. Syst. Technol. 2017, 25, 453–468. [Google Scholar] [CrossRef]
- Brosa Planella, F.; Ai, W.; Boyce, A.M.; Ghosh, A.; Korotkin, I.; Sahu, S.; Sulzer, V.; Timms, R.; Tranter, T.G.; Zyskin, M.; et al. A continuum of physics-based lithium-ion battery models reviewed. Prog. Energy 2022, 4, 042003. [Google Scholar] [CrossRef]
- Sarkar, S.; Zohra Halim, S.; El-Halwagi, M.M.; Khan, F.I. Electrochemical models: Methods and applications for safer lithium-ion battery operation. J. Electrochem. Soc. 2022, 169, 100501. [Google Scholar] [CrossRef]
- Wu, L.; Lyu, Z.; Huang, Z.; Zhang, C.; Wei, C. Physics-based battery SOC estimation methods: Recent advances and future perspectives. J. Energy Chem. 2024, 89, 27–40. [Google Scholar] [CrossRef]
- van Dao, Q.; Dinh, M.C.; Kim, C.S.; Park, M.; Doh, C.H.; Bae, J.H.; Lee, M.K.; Liu, J.; Bai, Z. Design of an Effective State of Charge Estimation Method for a Lithium-Ion Battery Pack Using Extended Kalman Filter and Artificial Neural Network. Energies 2021, 14, 2634. [Google Scholar]
- Li, M.; Li, C.; Zhang, Q.; Liao, W.; Rao, Z. State of charge estimation of Li-ion batteries based on deep learning methods and particle-swarm-optimized Kalman filter. J. Energy Storage 2023, 64, 107191. [Google Scholar] [CrossRef]
- Islam, S.M.R.; Park, S.Y.; Balasingam, B. Circuit parameters extraction algorithm for a lithium-ion battery charging system incorporated with electrochemical impedance spectroscopy. In Proceedings of the 2018 IEEE Applied Power Electronics Conference and Exposition (APEC), San Antonio, TX, USA, 4–8 March 2018; pp. 3353–3358. [Google Scholar]
- Bensaad, Y.; Friedrichs, F.; Baumhöfer, T.; Eswein, M.; Bähr, J.; Fill, A.; Birke, K.P. Embedded real-time fractional-order equivalent circuit model for internal resistance estimation of lithium-ion cells. J. Energy Storage 2023, 67, 107516. [Google Scholar] [CrossRef]
- Aguirre-Zapata, E.; Garcia-Tirado, J.; Morales, H.; di Sciascio, F.; Amicarelli, A.N. Metodología para el modelado y la estimación de parámetros del proceso de crecimiento de Lobesia botrana. Rev. Iberoam. Autom. Inform. Ind. 2022, 20, 68–79. [Google Scholar] [CrossRef]
- Xing, Y.; Na, J.; Costa-Castelló, R. Real-Time Adaptive Parameter Estimation for a Polymer Electrolyte Membrane Fuel Cell. IEEE Trans. Ind. Inform. 2019, 15, 6048–6057. [Google Scholar] [CrossRef]
- Ioannou, P.A.; Sun, J. Robust Adaptive Control; PTR Prentice-Hall: Upper Saddle River, NJ, USA, 1996; Volume 1. [Google Scholar]
- Chiasson, J.; Vairamohan, B. Estimating the state of charge of a battery. IEEE Trans. Control. Syst. Technol. 2005, 13, 465–470. [Google Scholar] [CrossRef]
- Wang, L.; Ortega, R.; Bobtsov, A. Observability is sufficient for the design of globally exponentially stable state observers for state-affine nonlinear systems. Automatica 2023, 149, 110838. [Google Scholar] [CrossRef]
- Tran, M.K.; DaCosta, A.; Mevawalla, A.; Panchal, S.; Fowler, M. Comparative Study of Equivalent Circuit Models Performance in Four Common Lithium-Ion Batteries: LFP, NMC, LMO, NCA. Batteries 2021, 7, 51. [Google Scholar] [CrossRef]
- Baccouche, I.; Jemmali, S.; Manai, B.; Nikolian, A.; Omar, N.; Essoukri Ben Amara, N. Li–ion battery modeling and characterization: An experimental overview on NMC battery. Int. J. Energy Res. 2022, 46, 3843–3859. [Google Scholar] [CrossRef]
- Yu, Q.Q.; Xiong, R.; Wang, L.Y.; Lin, C. A Comparative Study on Open Circuit Voltage Models for Lithium-ion Batteries. Chin. J. Mech. Eng. 2018, 31, 65. [Google Scholar] [CrossRef]
- Pillai, P.; Sundaresan, S.; Kumar, P.; Pattipati, K.R.; Balasingam, B. Open-Circuit Voltage Models for Battery Management Systems: A Review. Energies 2022, 15, 6803. [Google Scholar] [CrossRef]
- Rugh, W.J. Linear System Theory; Prentice-Hall, Inc.: Hoboken, NJ, USA, 1996. [Google Scholar]
- Kalman, R.E.; Bucy, R.S. New results in linear filtering and prediction theory. J. Basic Eng. 1961, 82, 34–45. [Google Scholar] [CrossRef]
- Ortega, R.; Bobtsov, A.; Nikolaev, N.; Schiffer, J.; Dochain, D. Generalized parameter estimation-based observers: Application to power systems and chemical–biological reactors. Automatica 2021, 129, 109635. [Google Scholar] [CrossRef]
- Wang, L.; Ortega, R.; Bobtsov, A.; Romero, J.G.; Yi, B. Identifiability implies robust, globally exponentially convergent on-line parameter estimation. Int. J. Control. 2023, 1–17. [Google Scholar] [CrossRef]
- Ortega, R.; Nikiforov, V.; Gerasimov, D. On modified parameter estimators for identification and adaptive control. A unified framework and some new schemes. Annu. Rev. Control 2020, 50, 278–293. [Google Scholar] [CrossRef]
- Sastry, S.; Bodson, M.; Bartram, J.F. Adaptive control: Stability, convergence, and robustness. J. Acoust. Soc. Am. 1990, 88, 588–589. [Google Scholar] [CrossRef]
- Moreu, J.M.; Annaswamy, A.M. A Stable High-Order Tuner for General Convex Functions. IEEE Control Syst. Lett. 2022, 6, 566–571. [Google Scholar] [CrossRef]
- Clemente, A.; Cecilia, A.; Costa-Castelló, R. Online state of charge estimation for a vanadium redox flow battery with unequal flow rates. J. Energy Storage 2023, 60, 106503. [Google Scholar] [CrossRef]
- Cecilia, A.; Serra, M.; Costa-Castelló, R. Real-time parameter estimation of polymer electrolyte membrane fuel cell in absence of excitation. Int. J. Hydrogen Energy 2023, in press. [Google Scholar] [CrossRef]
- Welch, G.; Bishop, G. An Introduction to the Kalman Filter; Technical Report 95-041; University of North Carolina at Chapel Hill: Chapel Hill, NC, USA, 1995. [Google Scholar]
- WLTPfacts.eu. What Is WLTP: The Worldwide Harmonised Light Vehicle Test Procedure? WLTPfacts.eu. Available online: https://www.wltpfacts.eu/what-is-wltp-how-will-it-work/ (accessed on 6 September 2017).
- TransportPolicy.net. International: Light-Duty: Worldwide Harmonized Light Vehicles Test Procedure (WLTP)|Transport Policy. Available online: https://www.transportpolicy.net/standard/international-light-duty-worldwide-harmonized-light-vehicles-test-procedure-wltp/ (accessed on 10 October 2023).
- Larminie, J.; Lowry, J. Electric Vehicle Technology Explained; John Wiley & Sons Ltd.: Chichester, UK, 2003. [Google Scholar]
- Catálogo Proace Electric. Available online: https://www.toyota.es/coches/proace-ev/proace-electric-brochure (accessed on 21 April 2023).












| Parameter | Name | Units |
|---|---|---|
| Open Circuit Voltage | V | |
| RC net voltage | V | |
| Battery voltage | V | |
| Series Resistance | ||
| Polarisation Resistance [48] | ||
| Polarisation Capacitance [48] | F |
| Cell | Number | Nominal Capacity | Nominal Voltage | Voltage Range |
|---|---|---|---|---|
| Typology | of Cells | (mAh) | (V) | (V) |
| Cylindrical | 1 | 2600 | 3.20 | 2.00–3.65 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Martí-Florences, M.; Piñol, A.C.; Clemente, A.; Costa-Castelló, R. SoC Estimation in Lithium-Ion Batteries with Noisy Measurements and Absence of Excitation. Batteries 2023, 9, 578. https://doi.org/10.3390/batteries9120578
Martí-Florences M, Piñol AC, Clemente A, Costa-Castelló R. SoC Estimation in Lithium-Ion Batteries with Noisy Measurements and Absence of Excitation. Batteries. 2023; 9(12):578. https://doi.org/10.3390/batteries9120578
Chicago/Turabian StyleMartí-Florences, Miquel, Andreu Cecilia Piñol, Alejandro Clemente, and Ramon Costa-Castelló. 2023. "SoC Estimation in Lithium-Ion Batteries with Noisy Measurements and Absence of Excitation" Batteries 9, no. 12: 578. https://doi.org/10.3390/batteries9120578
APA StyleMartí-Florences, M., Piñol, A. C., Clemente, A., & Costa-Castelló, R. (2023). SoC Estimation in Lithium-Ion Batteries with Noisy Measurements and Absence of Excitation. Batteries, 9(12), 578. https://doi.org/10.3390/batteries9120578






