Influence of Switching on the Aging of High Energy Lithium-Ion Cells
Abstract
:1. Introduction
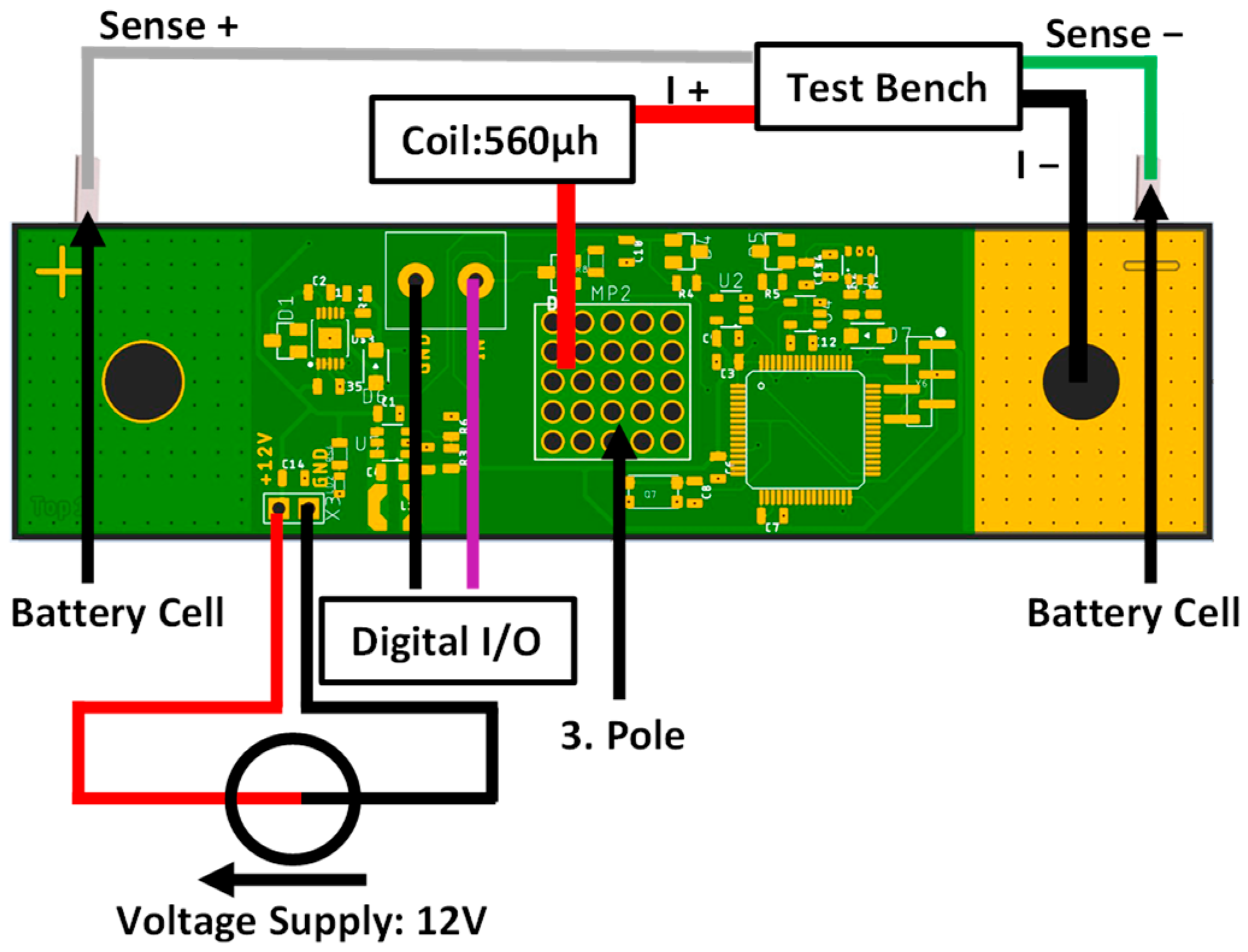
2. Materials and Methods
3. Results and Discussion
3.1. Influence of Temperature
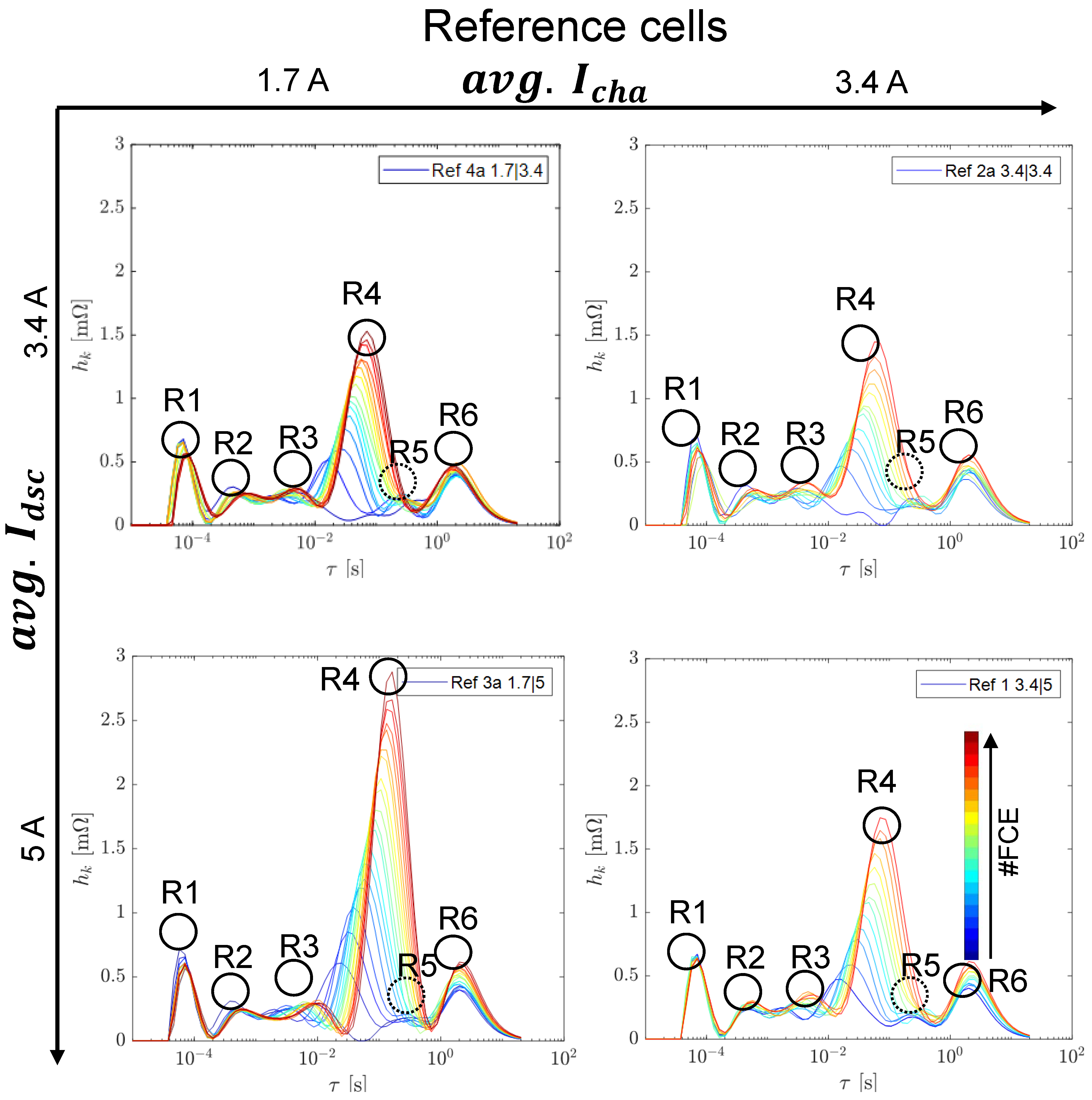
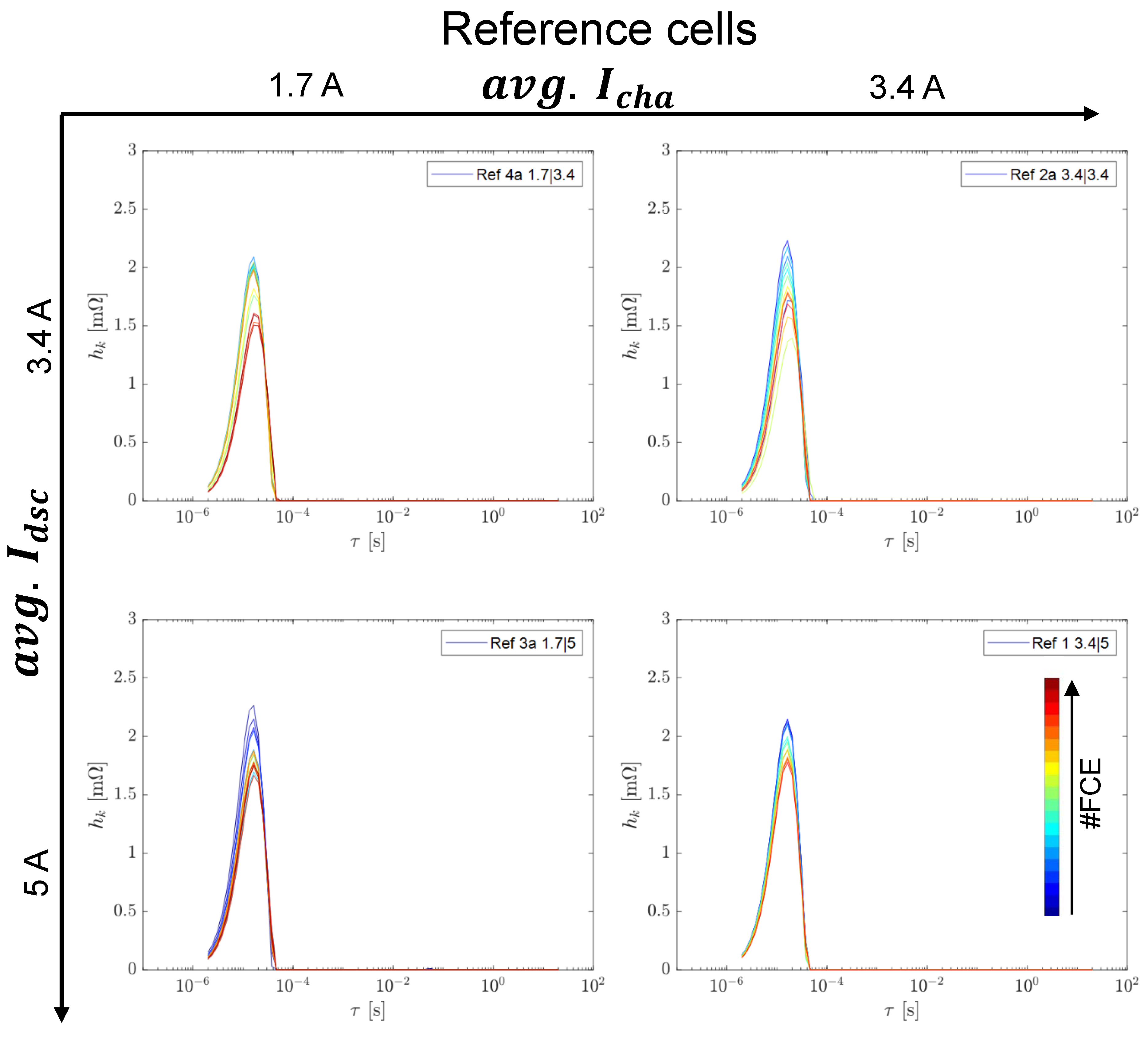
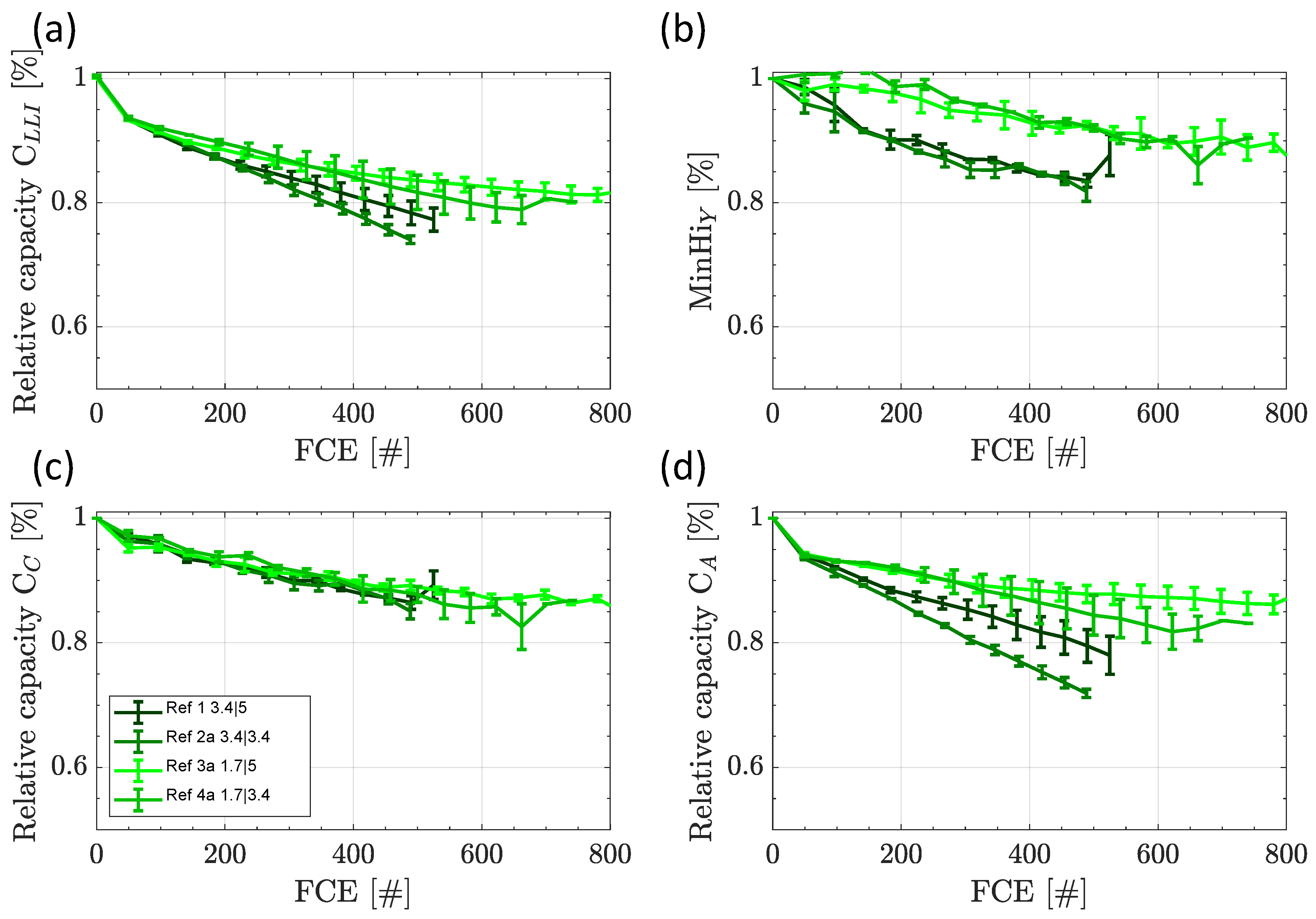
3.2. Reference Tests
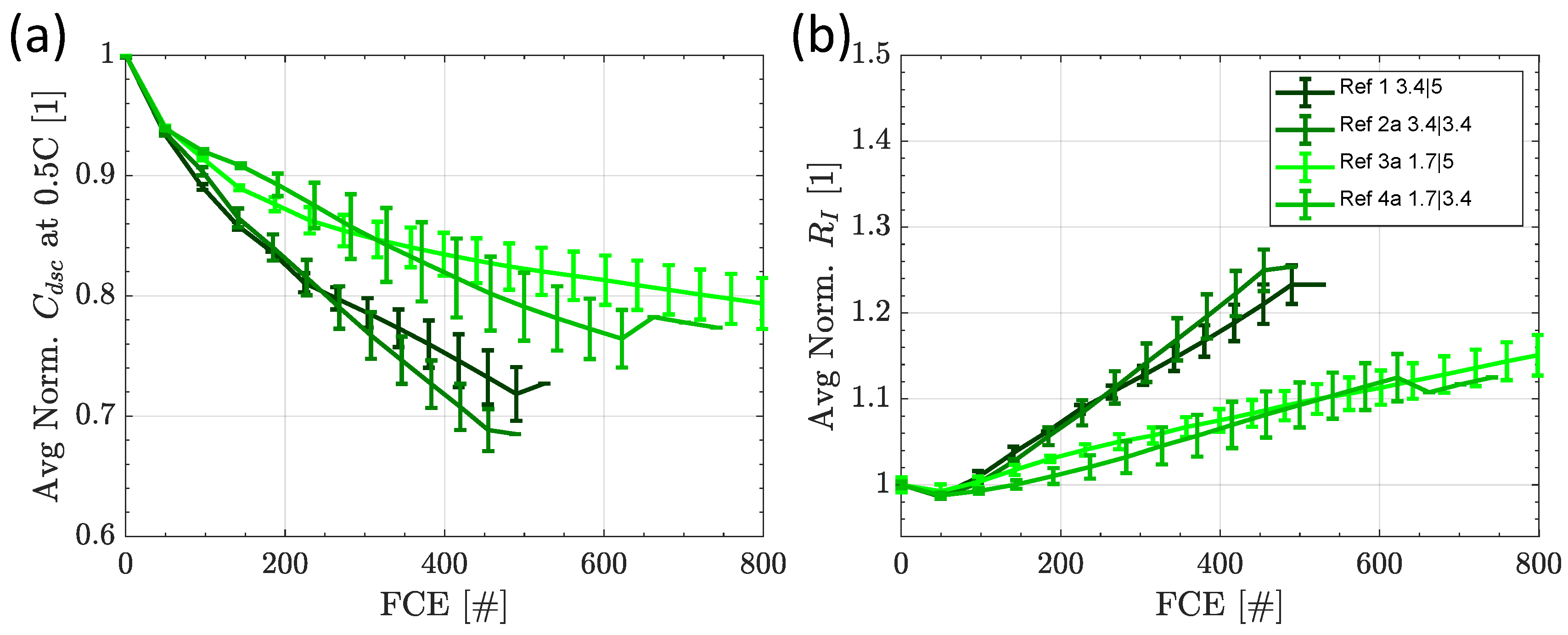
3.2.1. Capacity and Internal Resistance
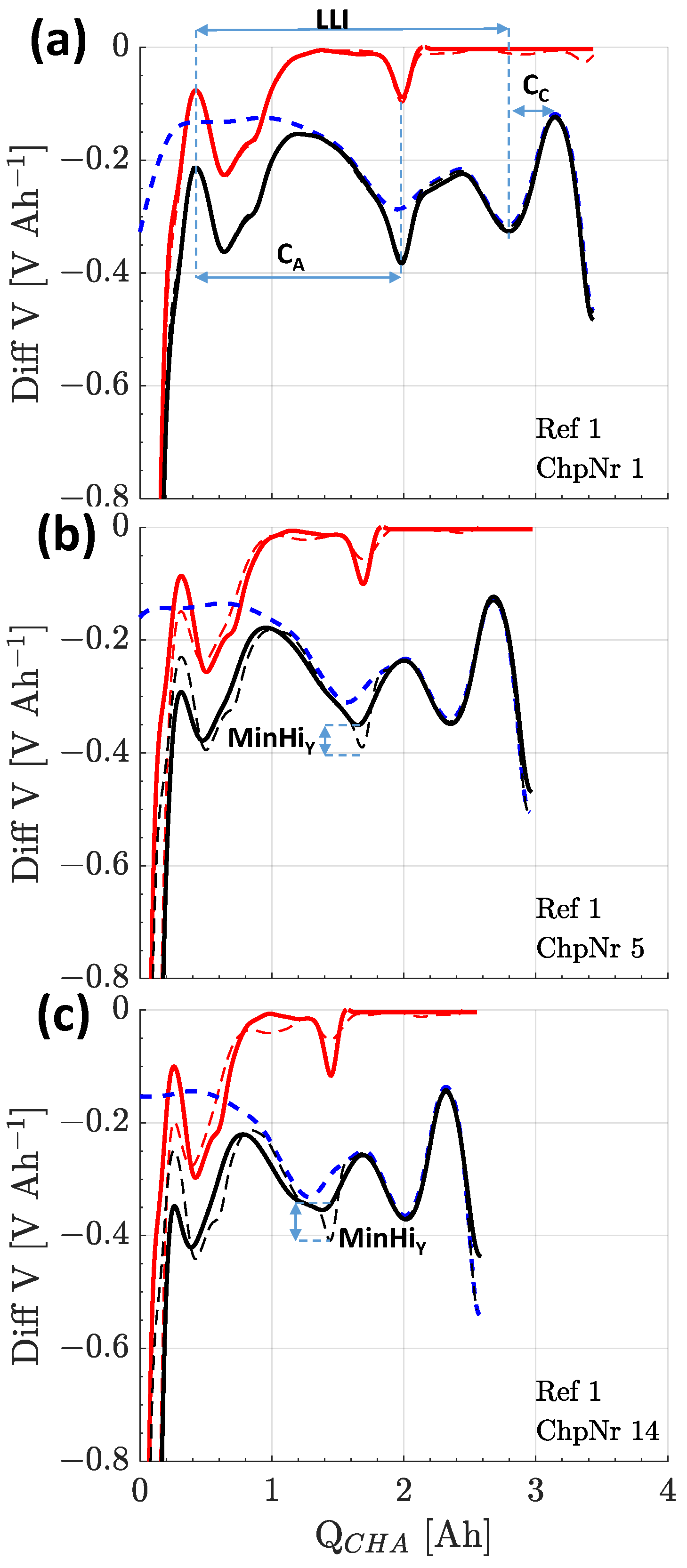
3.2.2. Differential Voltage Analysis
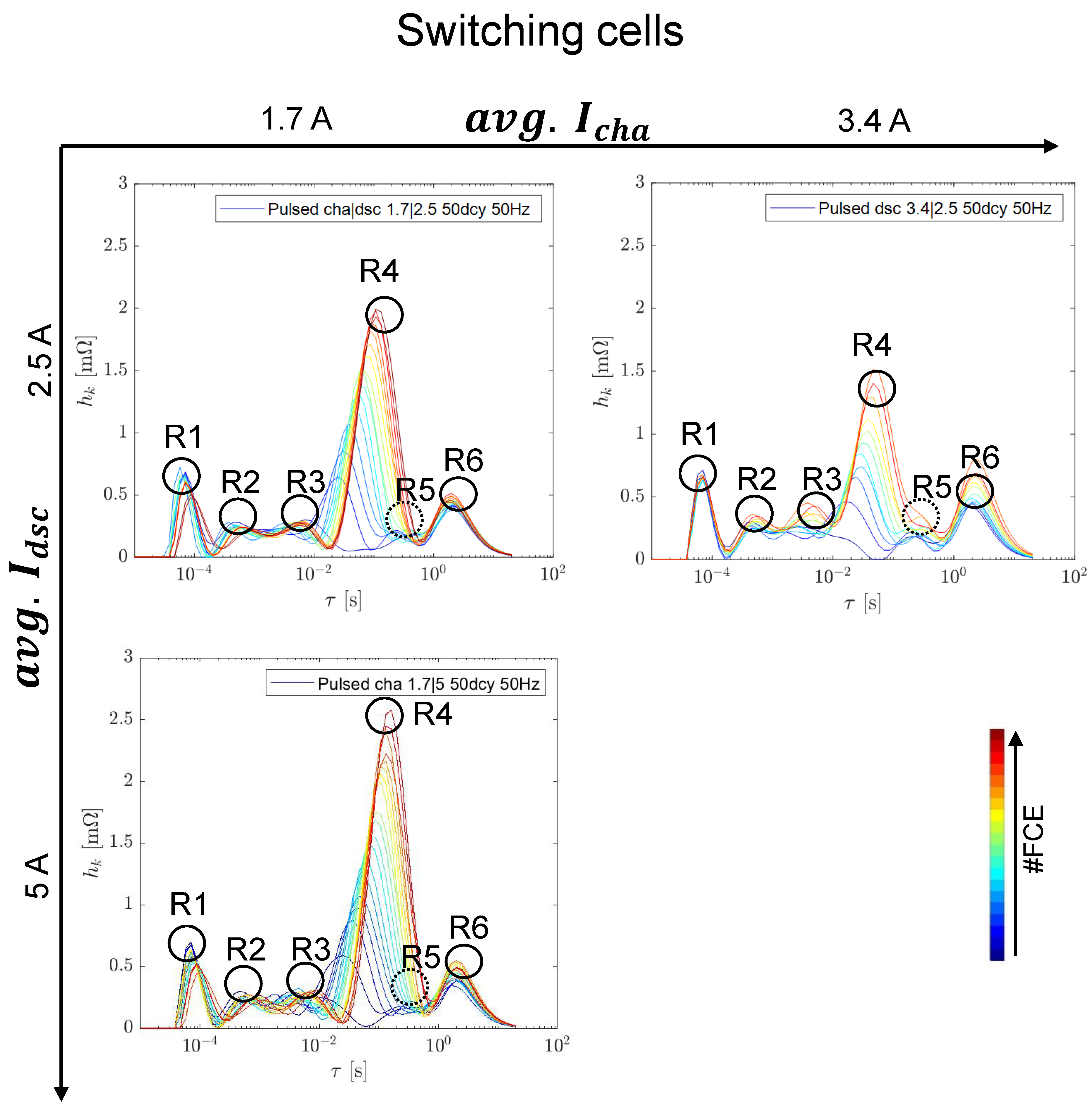
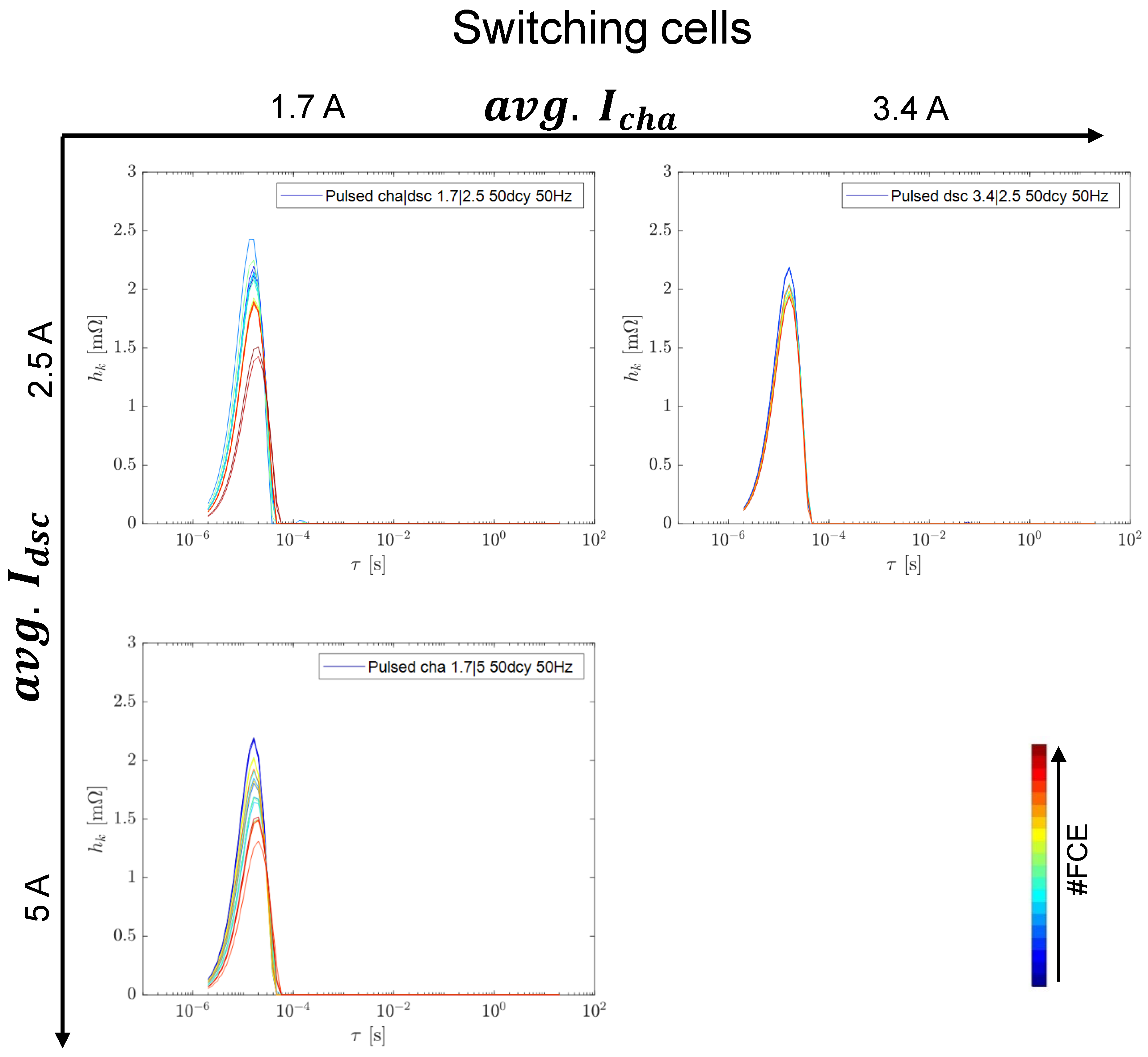
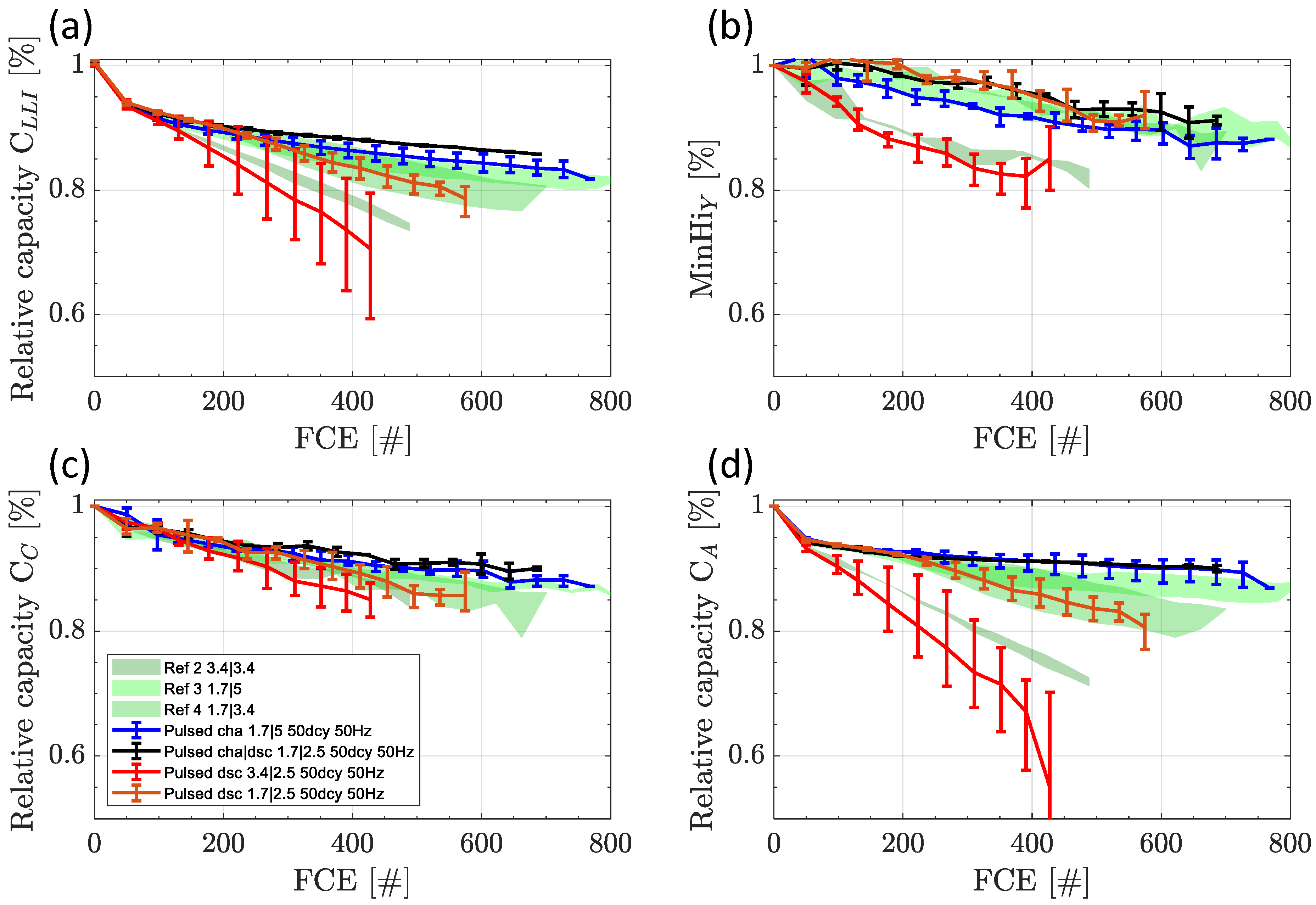
3.3. Switching Tests at 50 Hz and 50% Duty Cycle
3.3.1. Capacity and Internal Resistance
3.3.2. Differential Voltage Analysis
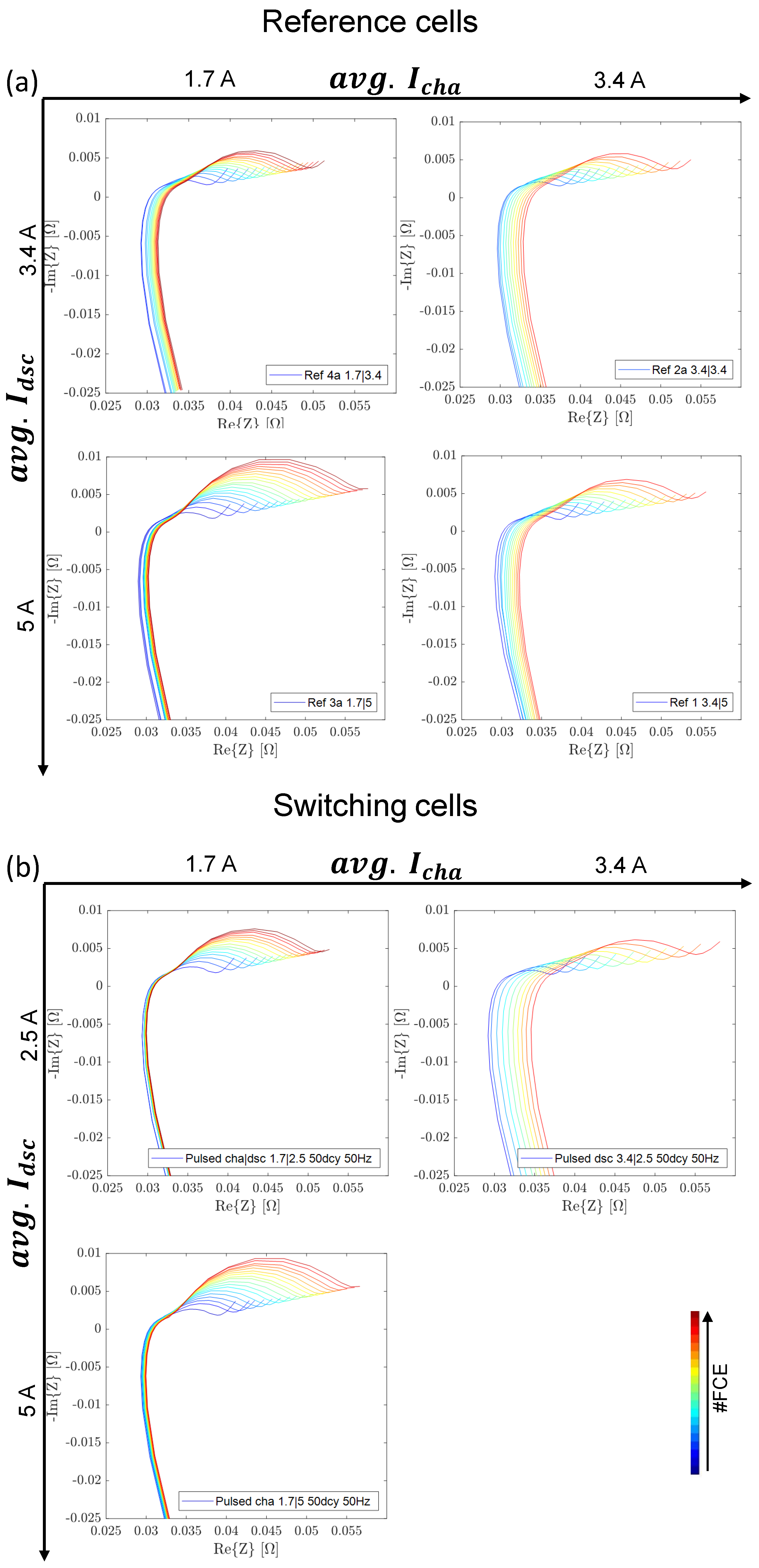
3.3.3. EIS Comparison including Reference Tests
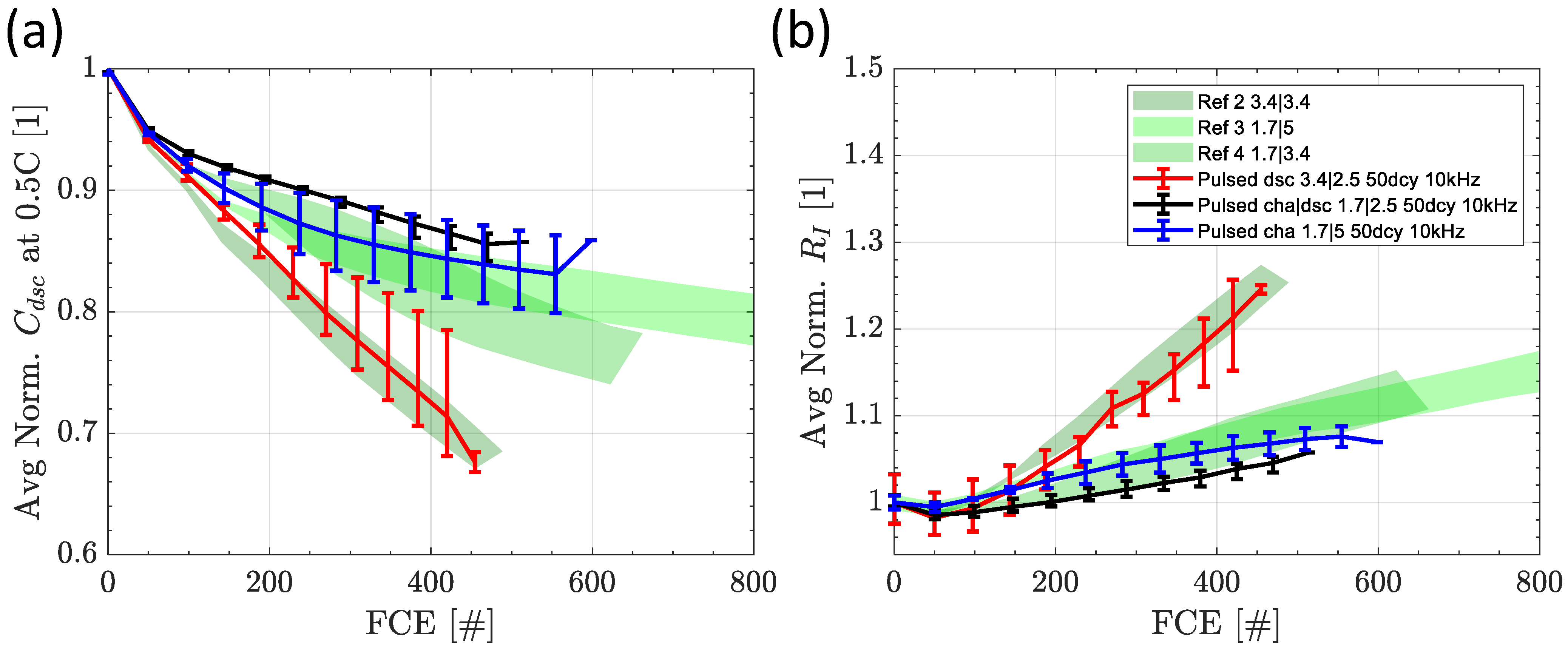
3.4. Switching Tests at 10 kHz
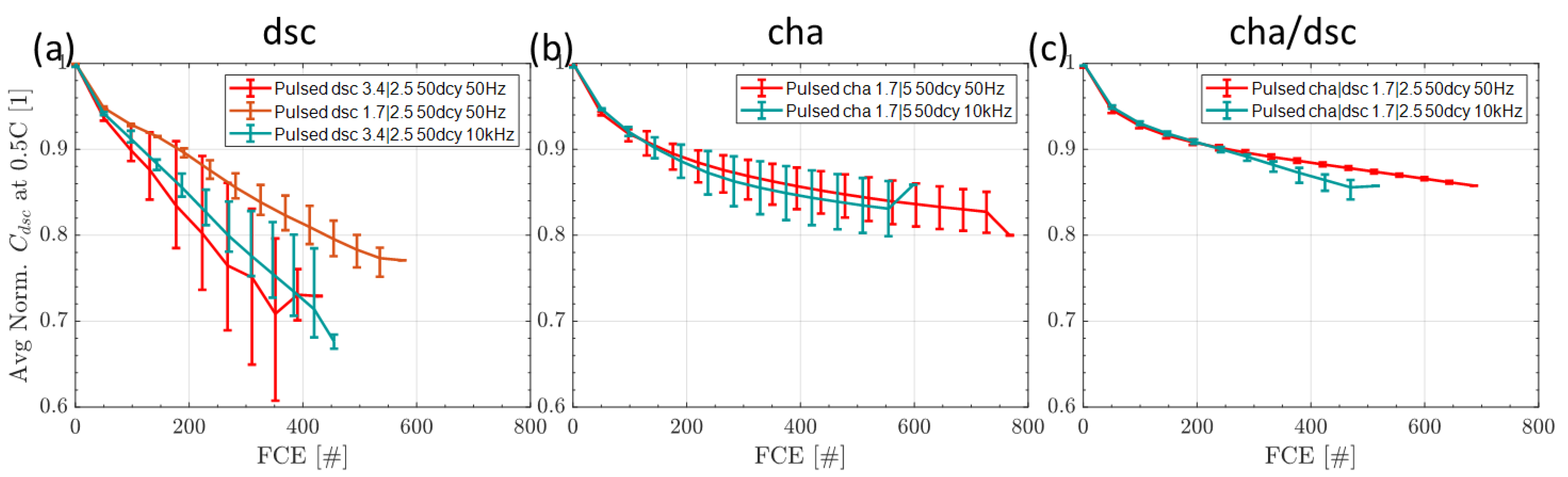
3.4.1. Influence of Switching Strategy at 50% Duty Cycle
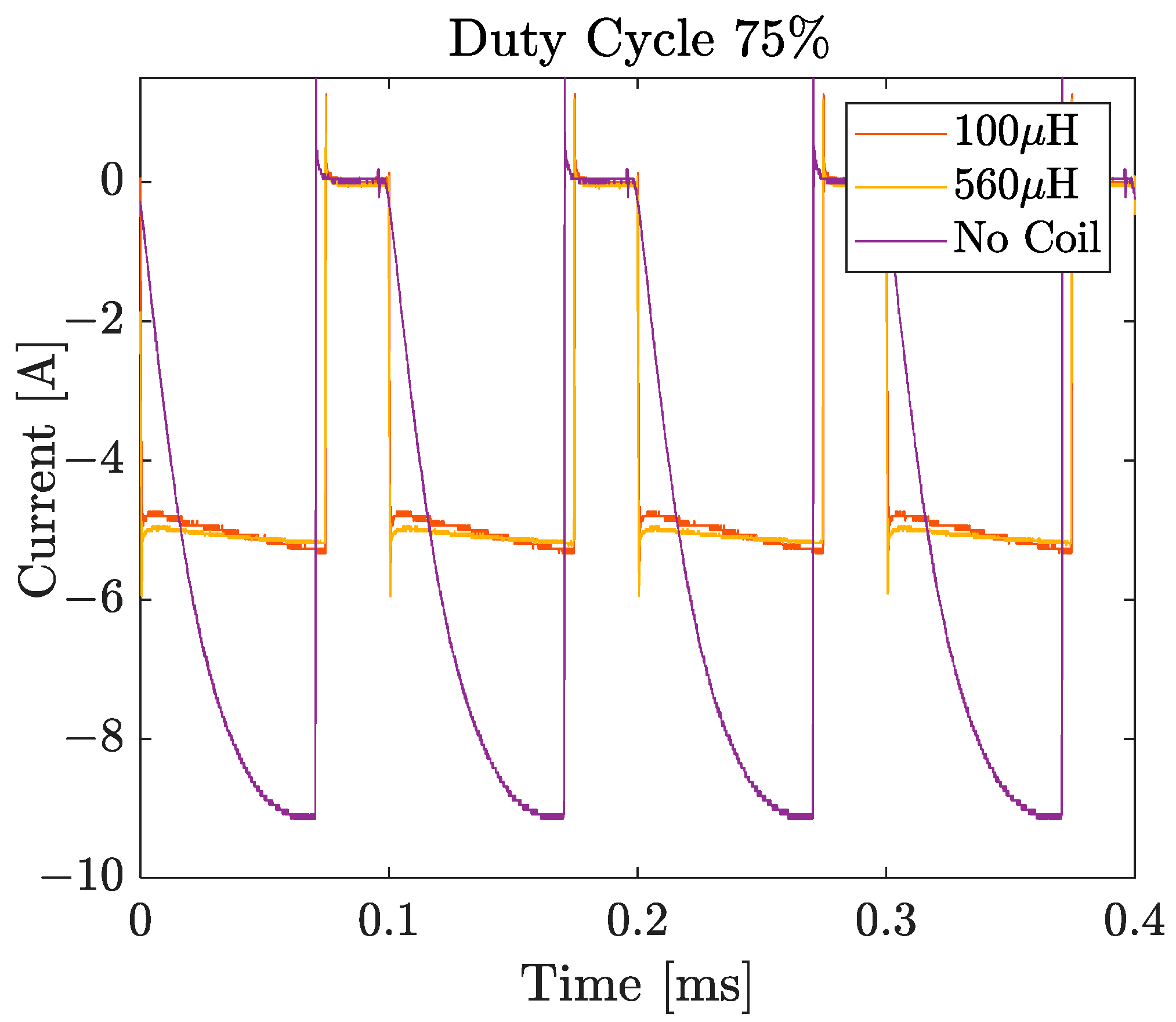
3.4.2. Influence of Duty Cycle at 10 kHz
3.4.3. Comparison of the Switching Frequency at 50% Duty Cycle
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Ferraz, P.K.P.; Schmidt, R.; Kober, D.; Kowal, J. A high frequency model for predicting the behavior of lithium-ion batteries connected to fast switching power electronics. J. Energy Storage 2018, 18, 40–49. [Google Scholar] [CrossRef]
- Korte, C.; Specht, E.; Hiller, M.; Goetz, S. Efficiency evaluation of MMSPC/CHB topologies for automotive applications. In Proceedings of the 2017 IEEE 12th International Conference on Power Electronics and Drive Systems (PEDS), Honolulu, HI, USA, 12–15 December 2017; IEEE: Piscataway, NJ, USA, 2017; Volume 122017, pp. 324–330. ISBN 978-1-5090-2364-6. [Google Scholar]
- Bughneda, A.; Salem, M.; Richelli, A.; Ishak, D.; Alatai, S. Review of Multilevel Inverters for PV Energy System Applications. Energies 2021, 14, 1585. [Google Scholar] [CrossRef]
- Jiang, X.; Doumbia, M.L. Comparative Study of Grid-Connected Multilevel Inverters for High Power Phtovoltaic Systems. In Proceedings of the 2019 IEEE 7th International Conference on Smart Energy Grid Engineering (SEGE), Oshawa, ON, Canada, 12–14 August 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 184–190. ISBN 978-1-7281-2440-7. [Google Scholar]
- Komsiyska, L.; Buchberger, T.; Diehl, S.; Ehrensberger, M.; Hanzl, C.; Hartmann, C.; Hölzle, M.; Kleiner, J.; Lewerenz, M.; Liebhart, B.; et al. Critical Review of Intelligent Battery Systems: Challenges, Implementation, and Potential for Electric Vehicles. Energies 2021, 14, 5989. [Google Scholar] [CrossRef]
- Uno, M.; Tanaka, K. Influence of High-Frequency Charge–Discharge Cycling Induced by Cell Voltage Equalizers on the Life Performance of Lithium-Ion Cells. IEEE Trans. Veh. Technol. 2011, 60, 1505–1515. [Google Scholar] [CrossRef]
- Chang, F.; Roemer, F.; Lienkamp, M. Influence of Current Ripples in Cascaded Multilevel Topologies on the Aging of Lithium Batteries. IEEE Trans. Power Electron. 2020, 35, 11879–11890. [Google Scholar] [CrossRef]
- Qin, Y.; Chen, X.; Tomaszewska, A.; Chen, H.; Wei, Y.; Zhu, H.; Li, Y.; Cui, Z.; Huang, J.; Du, J.; et al. Lithium-ion batteries under pulsed current operation to stabilize future grids. Cell Rep. Phys. Sci. 2022, 3, 100708. [Google Scholar] [CrossRef]
- Wong, D.; Shrestha, B.; Wetz, D.A.; Heinzel, J.M. Impact of high rate discharge on the aging of lithium nickel cobalt aluminum oxide batteries. J. Power Source 2015, 280, 363–372. [Google Scholar] [CrossRef]
- Soares, R.; Bessman, A.; Wallmark, O.; Lindbergh, G.; Svens, P. An Experimental Setup with Alternating Current Capability for Evaluating Large Lithium-Ion Battery Cells. Batteries 2018, 4, 38. [Google Scholar] [CrossRef] [Green Version]
- Prasad, R.; Namuduri, C.; Kollmeyer, P. Onboard unidirectional automotive G2V battery charger using sine charging and its effect on li-ion batteries. In Proceedings of the 2015 IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 20–24 September 2015; pp. 6299–6305. [Google Scholar]
- Korth Pereira Ferraz, P.; Kowal, J. A Comparative Study on the Influence of DC/DC-Converter Induced High Frequency Current Ripple on Lithium-Ion Batteries. Sustainability 2019, 11, 6050. [Google Scholar] [CrossRef] [Green Version]
- Ngaleu, G.; Theiler, M.; Straßer, X.; Hanzl, C.; Komsiyska, L.; Endisch, C.; Lewerenz, M. Influence of Switching on the Aging of High Power Lithium-Ion Cells. Batteries 2022, 8, 33. [Google Scholar] [CrossRef]
- Sturm, J.; Rheinfeld, A.; Zilberman, I.; Spingler, F.B.; Kosch, S.; Frie, F.; Jossen, A. Modeling and simulation of inhomogeneities in a 18650 nickel-rich, silicon-graphite lithium-ion cell during fast charging. J. Power Source 2019, 412, 204–223. [Google Scholar] [CrossRef] [Green Version]
- Heenan, T.M.M.; Jnawali, A.; Kok, M.D.R.; Tranter, T.G.; Tan, C.; Dimitrijevic, A.; Jervis, R.; Brett, D.J.L.; Shearing, P.R. An Advanced Microstructural and Electrochemical Datasheet on 18650 Li-Ion Batteries with Nickel-Rich NMC811 Cathodes and Graphite-Silicon Anodes. J. Electrochem. Soc. 2020, 167, 140530. [Google Scholar] [CrossRef]
- Wu, Y.; Long, X.; Lu, J.; Wu, Y.; Zhou, R.; Liu, L. Effect of temperature on the high-rate pulse charging of lithium-ion batteries. J. Electroanal. Chem. 2022, 922, 116773. [Google Scholar] [CrossRef]
- Hahn, M.; Schindler, S.; Triebs, L.-C.; Danzer, M.A. Optimized Process Parameters for a Reproducible Distribution of Relaxation Times Analysis of Electrochemical Systems. Batteries 2019, 5, 43. [Google Scholar] [CrossRef] [Green Version]
- Lewerenz, M.; Fuchs, G.; Becker, L.; Sauer, D.U. Irreversible calendar aging and quantification of the reversible capacity loss caused by anode overhang. J. Energy Storage 2018, 18, 149–159. [Google Scholar] [CrossRef]
- Gyenes, B.; Stevens, D.A.; Chevrier, V.L.; Dahn, J.R. Understanding Anomalous Behavior in Coulombic Efficiency Measurements on Li-Ion Batteries. J. Electrochem. Soc. 2015, 162, A278–A283. [Google Scholar] [CrossRef]
- Ecker, M.; Shafiei Sabet, P.; Sauer, D.U. Influence of operational condition on lithium plating for commercial lithium-ion batteries—Electrochemical experiments and post-mortem-analysis. Appl. Energy 2017, 206, 934–946. [Google Scholar] [CrossRef]
- Lewerenz, M.; Münnix, J.; Schmalstieg, J.; Käbitz, S.; Knips, M.; Sauer, D.U. Systematic aging of commercial LiFePO 4 |Graphite cylindrical cells including a theory explaining rise of capacity during aging. J. Power Source 2017, 345, 254–263. [Google Scholar] [CrossRef]
- Ecker, M.; Nieto, N.; Käbitz, S.; Schmalstieg, J.; Blanke, H.; Warnecke, A.; Sauer, D.U. Calendar and cycle life study of Li(NiMnCo)O2-based 18650 lithium-ion batteries. J. Power Source 2014, 248, 839–851. [Google Scholar] [CrossRef]
- Mathieu, R.; Briat, O.; Gyan, P.; Vinassa, J.-M. Comparison of the impact of fast charging on the cycle life of three lithium-ion cells under several parameters of charge protocol and temperatures. Appl. Energy 2021, 283, 116344. [Google Scholar] [CrossRef]
- Zilberman, I.; Sturm, J.; Jossen, A. Reversible self-discharge and calendar aging of 18650 nickel-rich, silicon-graphite lithium-ion cells. J. Power Source 2019, 425, 217–226. [Google Scholar] [CrossRef]
- Ji, S.-G.; Umirov, N.; Kim, H.-Y.; Kim, S.-S. Relationship between Mechanical and Electrochemical Property in Silicon Alloy Designed by Grain Size as Anode for Lithium-Ion Batteries. J. Electrochem. Soc. 2022, 169, 60520. [Google Scholar] [CrossRef]
- Lewerenz, M.; Rahe, C.; Fuchs, G.; Endisch, C.; Sauer, D.U. Evaluation of shallow cycling on two types of uncompressed automotive Li (Ni1/3Mn1/3Co1/3)O2-Graphite pouch cells. J. Electrochem. Soc. 2020, 30, 101529. [Google Scholar] [CrossRef]
- Lewerenz, M.; Dechent, P.; Sauer, D.U. Investigation of capacity recovery during rest period at different states-of-charge after cycle life test for prismatic Li(Ni1/3Mn1/3Co1/3)O2-graphite cells. J. Energy Storage 2019, 21, 680–690. [Google Scholar] [CrossRef]
- Epding, B.; Rumberg, B.; Jahnke, H.; Stradtmann, I.; Kwade, A. Investigation of significant capacity recovery effects due to long rest periods during high current cyclic aging tests in automotive lithium ion cells and their influence on lifetime. J. Energy Storage 2019, 22, 249–256. [Google Scholar] [CrossRef]
- Spingler, F.B.; Naumann, M.; Jossen, A. Capacity Recovery Effect in Commercial LiFePO4/Graphite Cells. J. Electrochem. Soc. 2020, 167, 40526. [Google Scholar] [CrossRef]
- Lewerenz, M.; Warnecke, A.; Sauer, D.U. Post-mortem analysis on LiFePO 4 |Graphite cells describing the evolution & composition of covering layer on anode and their impact on cell performance. J. Power Source 2017, 369, 122–132. [Google Scholar] [CrossRef]
- Rajagopalan Kannan, D.R.; Weatherspoon, M.H. The effect of pulse charging on commercial lithium nickel cobalt oxide (NMC) cathode lithium-ion batteries. J. Power Source 2020, 479, 229085. [Google Scholar] [CrossRef]
- Illig, J.; Ender, M.; Weber, A.; Ivers-Tiffée, E. Modeling graphite anodes with serial and transmission line models. J. Power Source 2015, 282, 335–347. [Google Scholar] [CrossRef]
- Piao, T.; Park, S.-M.; Doh, C.-H.; Moon, S.-I. Intercalation of Lithium Ions into Graphite Electrodes Studied by AC Impedance Measurements. J. Electrochem. Soc. 1999, 146, 2794. [Google Scholar] [CrossRef] [Green Version]
- Danzer, M.A. Generalized Distribution of Relaxation Times Analysis for the Characterization of Impedance Spectra. Batteries 2019, 5, 53. [Google Scholar] [CrossRef] [Green Version]
- Boukamp, B.A. Derivation of a Distribution Function of Relaxation Times for the (fractal) Finite Length Warburg. Electrochim. Acta 2017, 252, 154–163. [Google Scholar] [CrossRef]
- Nagasubramanian, G. Two- and three-electrode impedance studies on 18650 Li-ion cells. J. Power Source 2000, 87, 226–229. [Google Scholar] [CrossRef] [Green Version]



| Producer | LG |
|---|---|
| Cell type | INR18650 MJ1 |
| Cathode | NMC: Li(Ni0.8Mn0.1Co0.1)O2 |
| Anode | Silicon-Graphite |
| Nom. Capacity (0.5 C) | 3.4 Ah |
| Max. discharge voltage | 2.5 V |
| Max. charge voltage | 4.2 V |
| Max. charge current | 3.4 A |
| Max. discharge current | 10 A |
| Energy density | 252 Wh/kg |
| Storage voltage (SOC) before test | 3.6 V (33 %) |
| Test-Name | # Test Cells | Imax [A] | Iavg [A] | ||||
|---|---|---|---|---|---|---|---|
| cha | dsc | cha | dsc | ||||
| Ref1 | 2 | 3.4 | 5 | 3.4 | 5 | ||
| Ref2 | 2 | 3.4 | 3.4 | 3.4 | 3.4 | ||
| Ref3 | 2 | 1.7 | 5 | 1.7 | 5 | ||
| Ref4 | 2 | 1.7 | 3.4 | 1.7 | 3.4 | ||
| 50 Hz | 50% dcy | Pulsed dsc/cha | 2 | 3.4 | 5 | 1.7 | 2.5 |
| 50 Hz | 50% dcy | Pulsed cha | 3 | 3.4 | 5 | 1.7 | 5 |
| 50 Hz | 50% dcy | Pulsed dsc | 6 | 3.4 | 5 | 3.4 | 2.5 |
| 50 Hz | 50% dcy | Pulsed dsc low current | 3 | 1.7 | 5 | 1.7 | 2.5 |
| 10 kHz | 50% dcy | Pulsed dsc/cha | 3 | 3.4 | 5 | 1.7 | 2.5 |
| 10 kHz | 75% dcy | Pulsed dsc/cha | 2 | 3.4 | 5 | 2.55 | 3.75 |
| 10 kHz | 25% dcy | Pulsed cha | 1 | 3.4 | 5 | 0.85 | 5 |
| 10 kHz | 50% dcy | Pulsed cha | 2 | 3.4 | 5 | 1.7 | 5 |
| 10 kHz | 75% dcy | Pulsed cha | 1 | 3.4 | 5 | 2.55 | 5 |
| 10 kHz | 25% dcy | Pulsed dsc | 5 | 3.4 | 5 | 3.4 | 1.25 |
| 10 kHz | 50% dcy | Pulsed dsc | 4 | 3.4 | 5 | 3.4 | 2.5 |
| 10 kHz | 75% dcy | Pulsed dsc | 3 | 3.4 | 5 | 3.4 | 3.75 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Straßer, X.; Ngaleu, G.W.; Hanzl, C.; Azzam, M.; Endisch, C.; Lewerenz, M. Influence of Switching on the Aging of High Energy Lithium-Ion Cells. Batteries 2023, 9, 139. https://doi.org/10.3390/batteries9020139
Straßer X, Ngaleu GW, Hanzl C, Azzam M, Endisch C, Lewerenz M. Influence of Switching on the Aging of High Energy Lithium-Ion Cells. Batteries. 2023; 9(2):139. https://doi.org/10.3390/batteries9020139
Chicago/Turabian StyleStraßer, Xenia, Guy Williams Ngaleu, Christian Hanzl, Mohamed Azzam, Christian Endisch, and Meinert Lewerenz. 2023. "Influence of Switching on the Aging of High Energy Lithium-Ion Cells" Batteries 9, no. 2: 139. https://doi.org/10.3390/batteries9020139
APA StyleStraßer, X., Ngaleu, G. W., Hanzl, C., Azzam, M., Endisch, C., & Lewerenz, M. (2023). Influence of Switching on the Aging of High Energy Lithium-Ion Cells. Batteries, 9(2), 139. https://doi.org/10.3390/batteries9020139









