General Decoupling and Sampling Technique for Reduced-Sensor Battery Management Systems in Modular Reconfigurable Batteries
Abstract
:1. Introduction
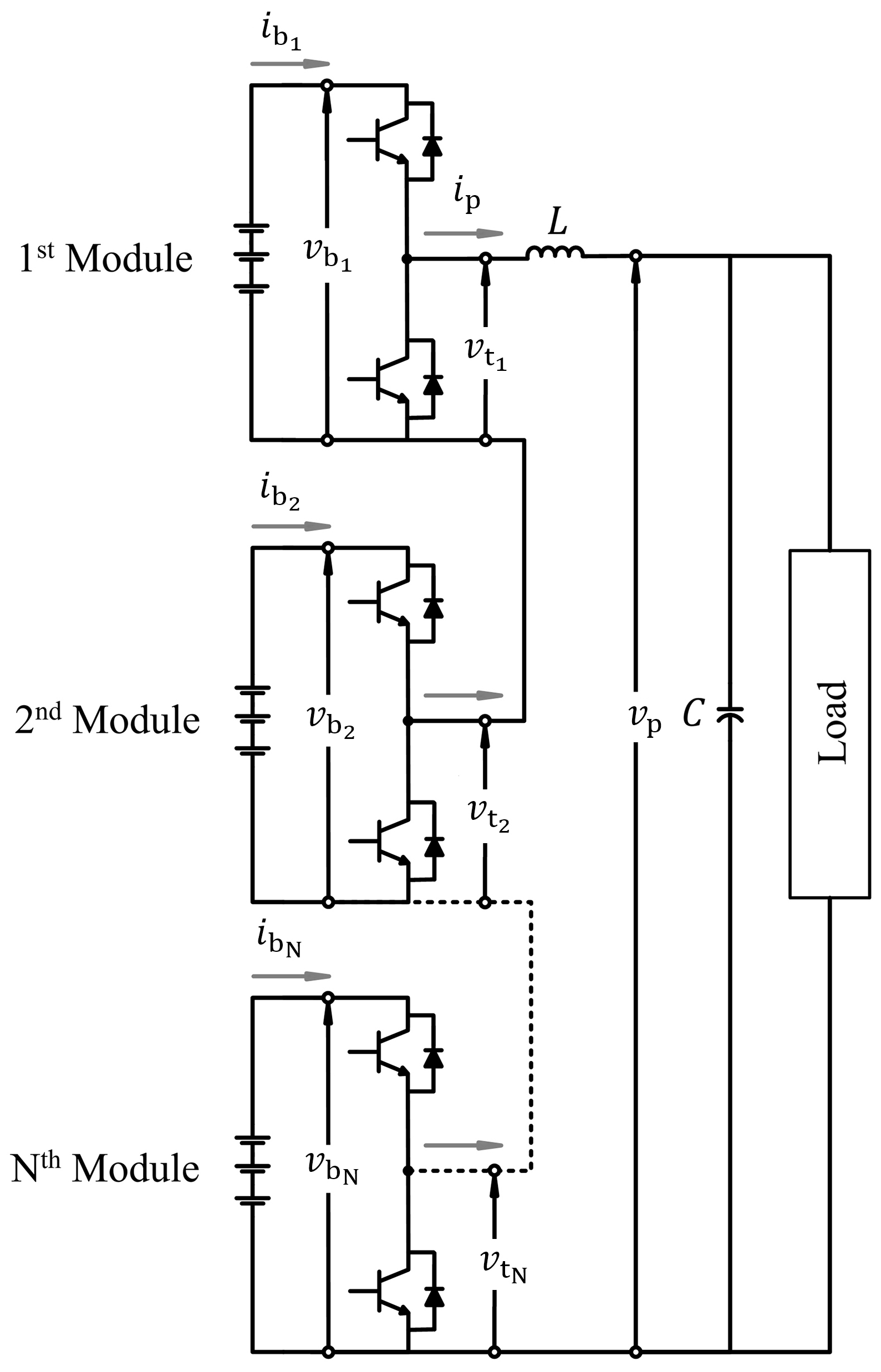
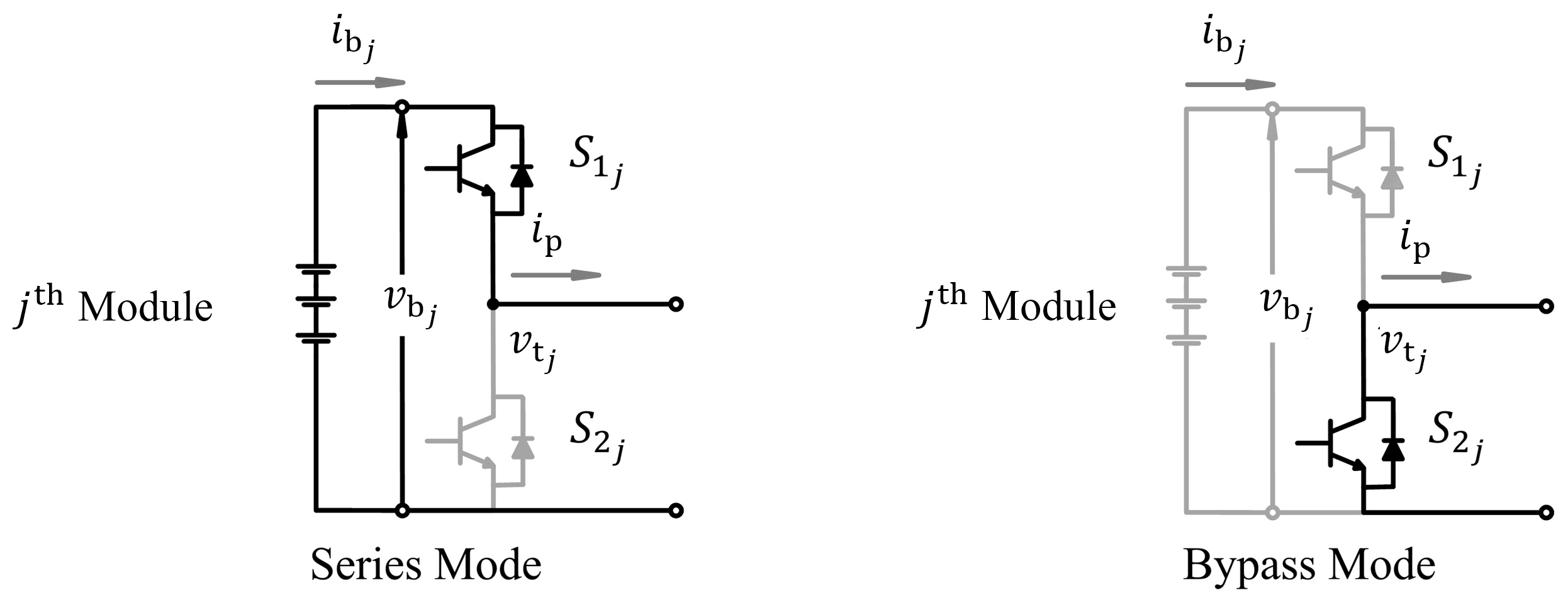
2. System Description
3. Framework of the Reduced-Sensor Parameter Estimation
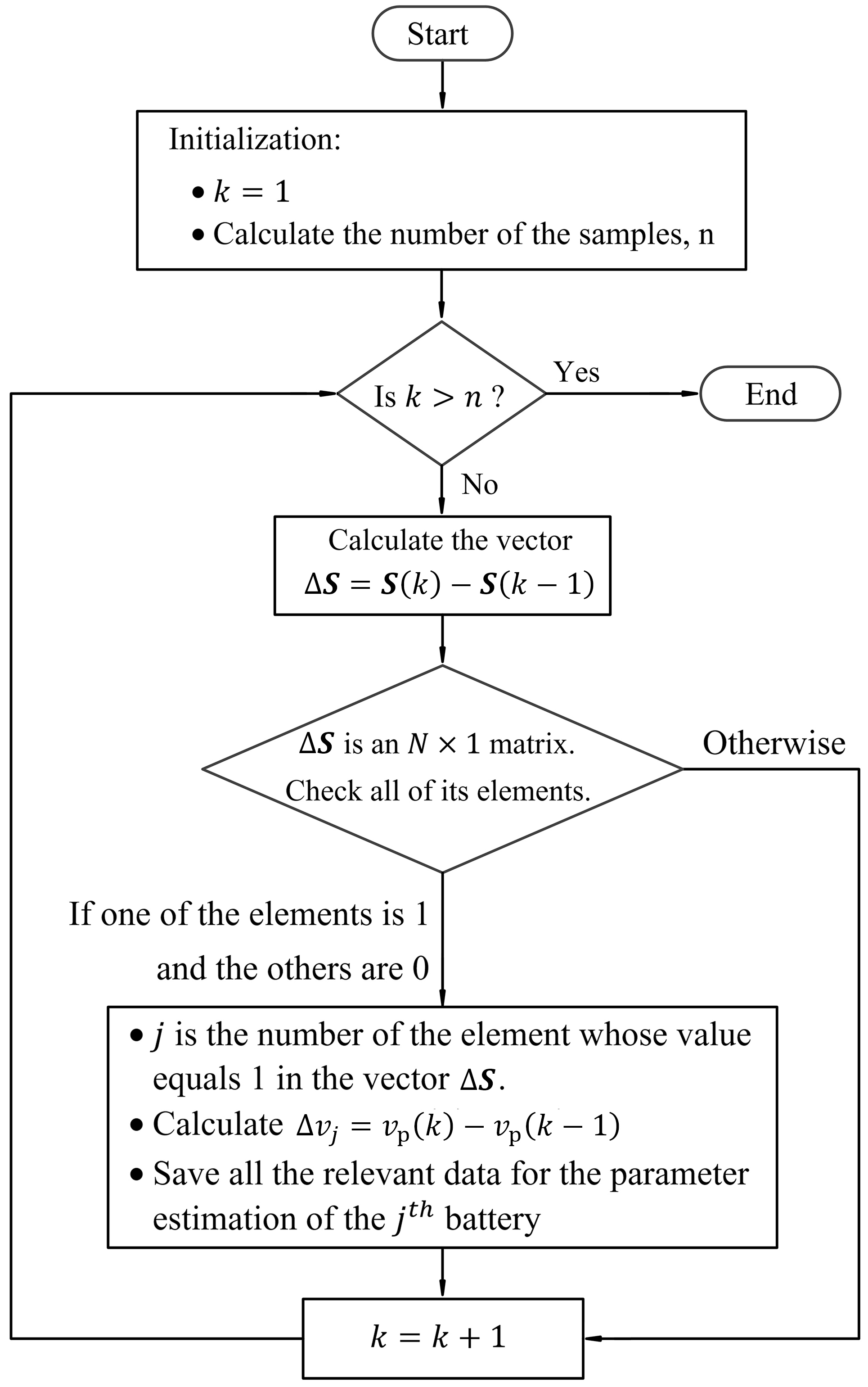
3.1. Decoupling Algorithm
3.2. The Estimation Algorithm
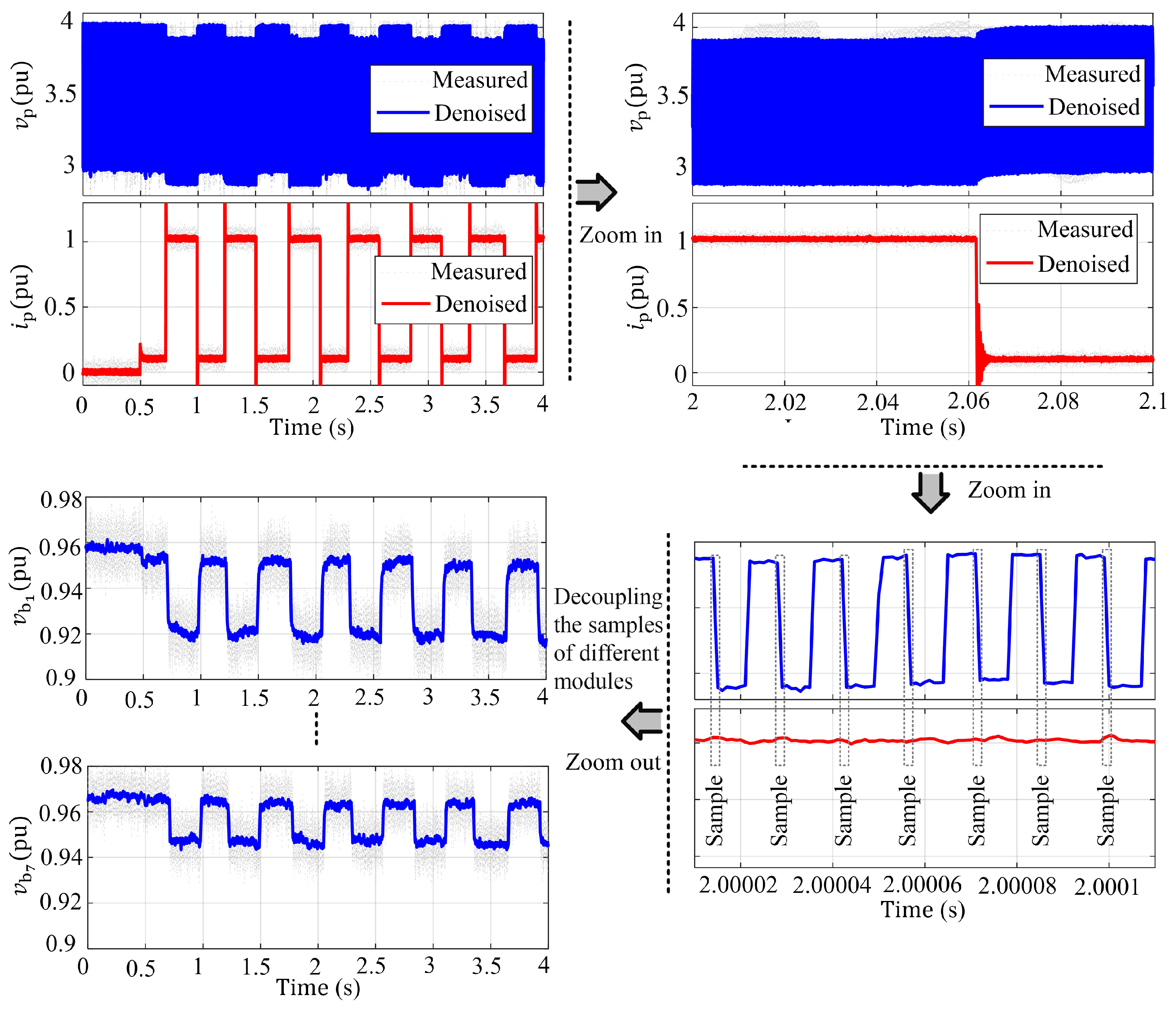
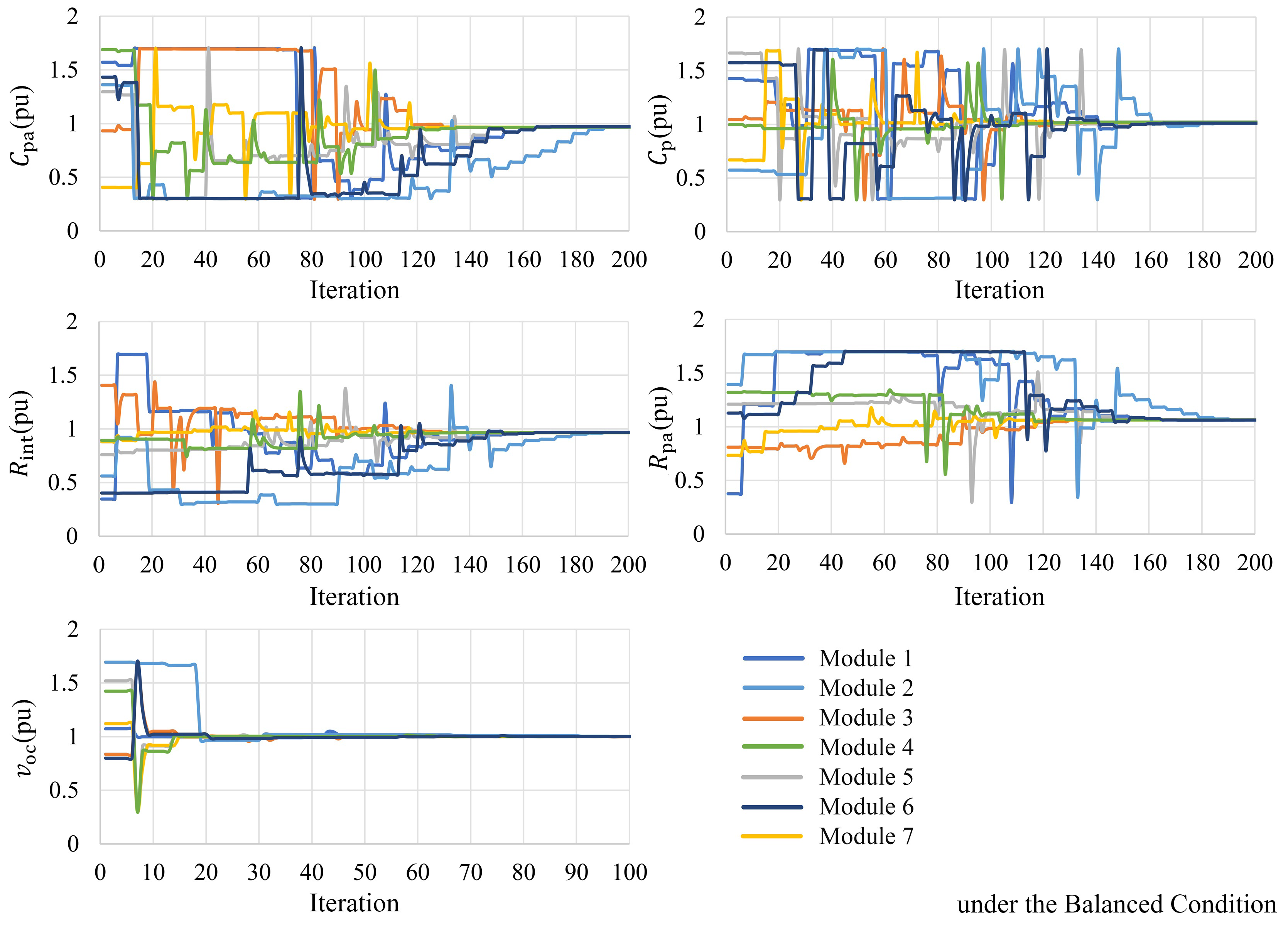
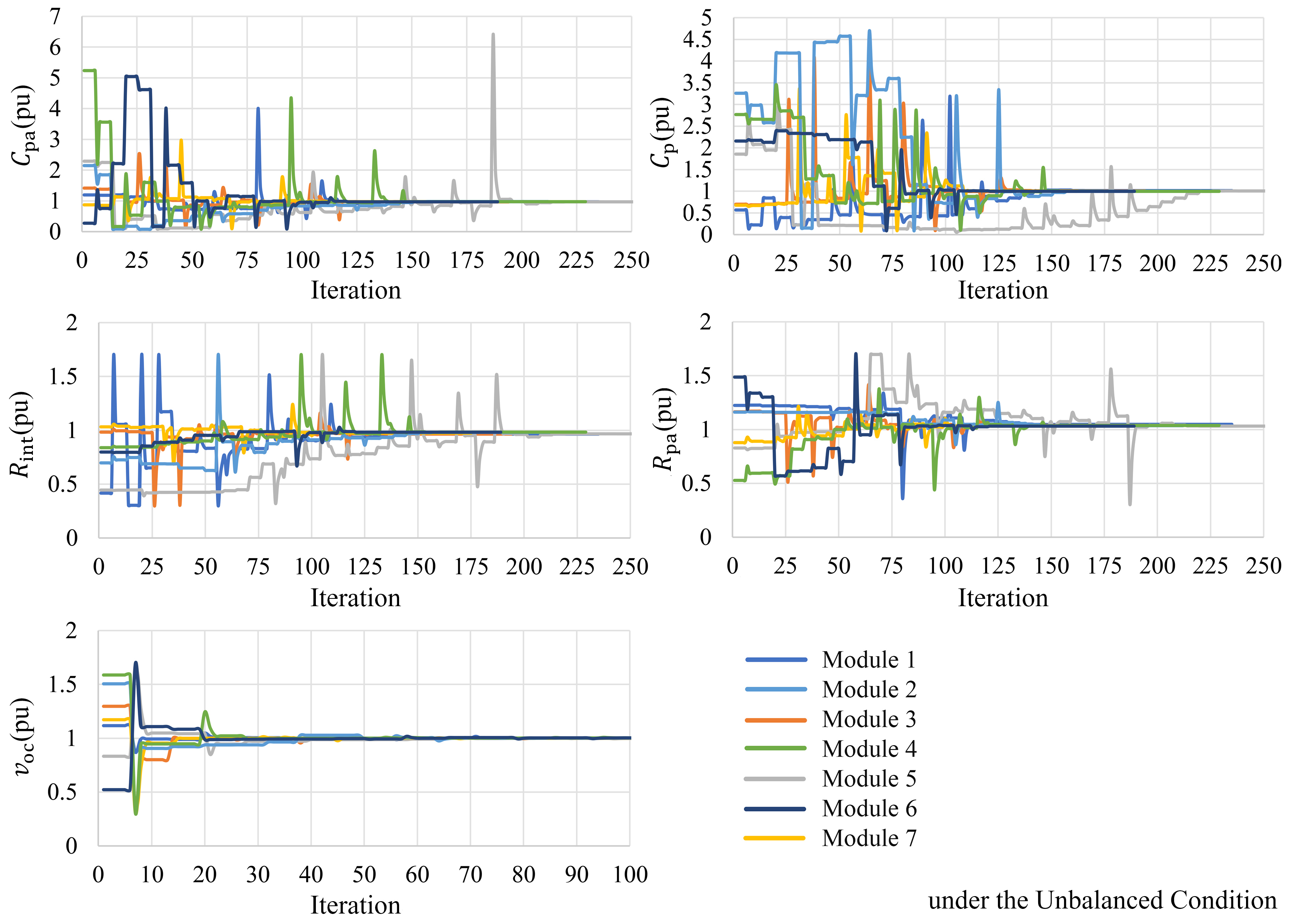
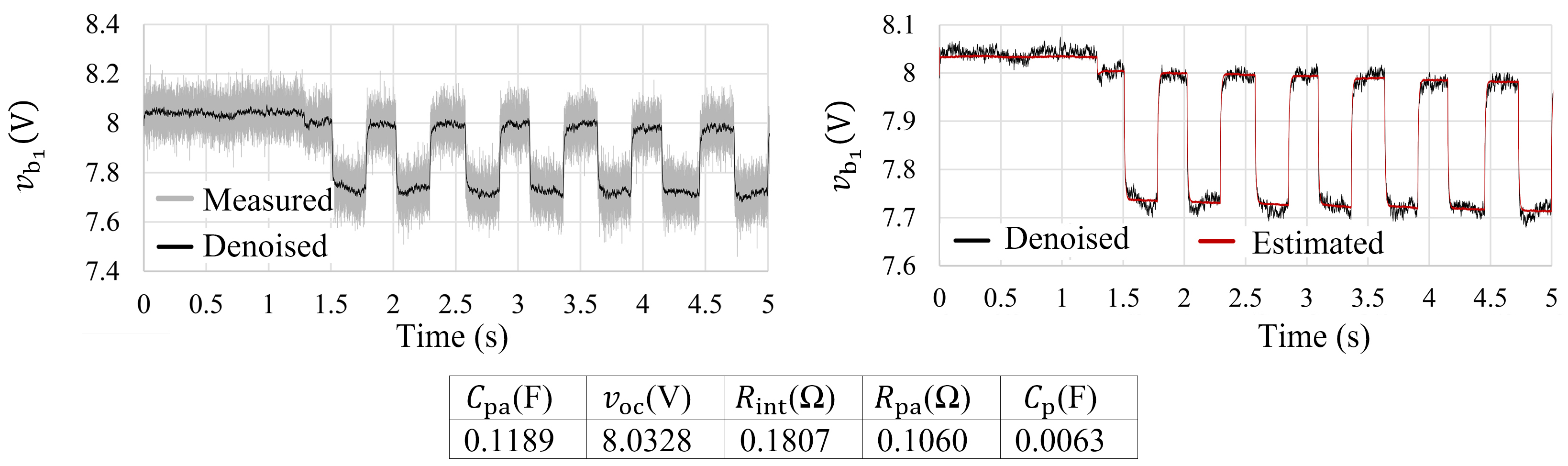
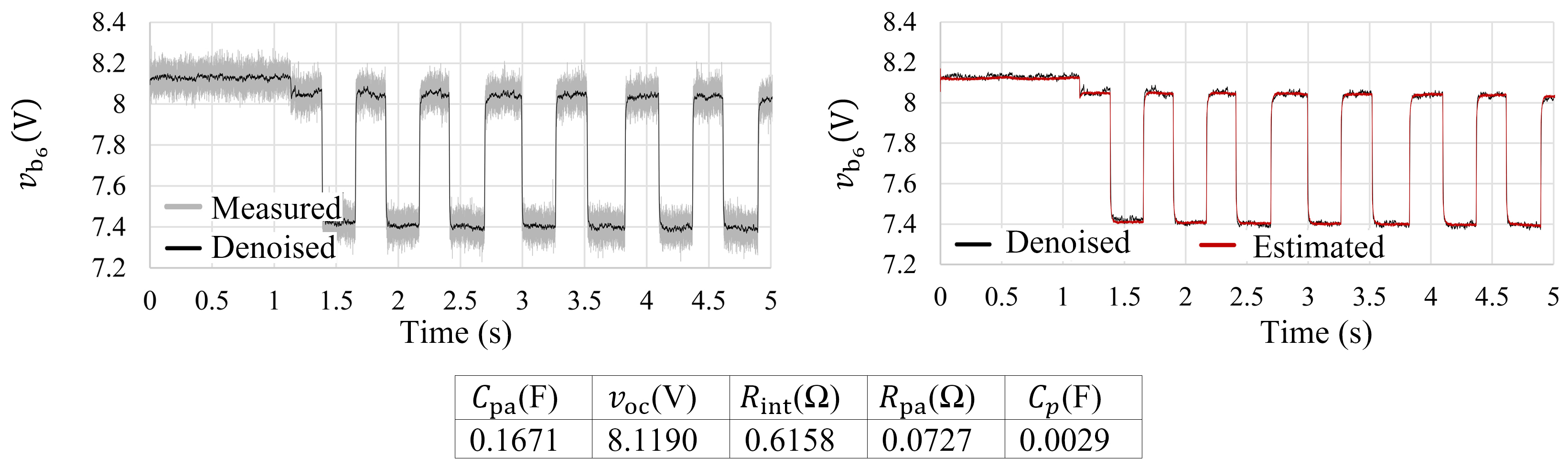
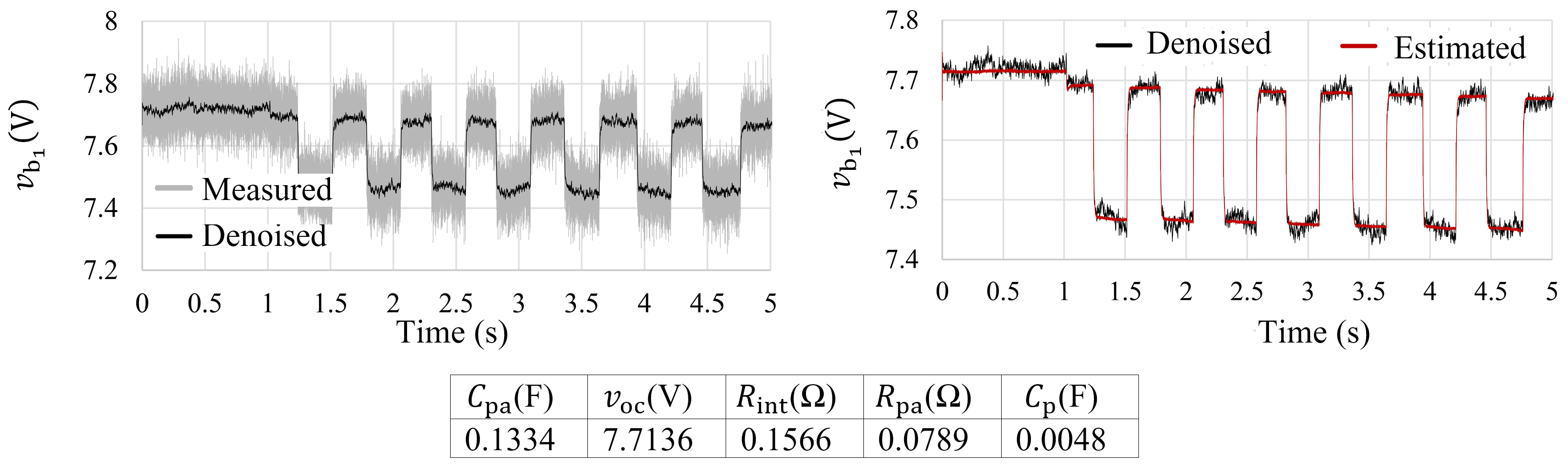
4. Results
- The first scenario investigates the behavior of a balanced system where all the modules have relatively similar states (their SOC and SOH as a case in point) and parameters. There are only small inevitable inherent tolerances among their parameters due to manufacturing tolerances.
- In the second scenario, the uniform parameters of the modules are disturbed to simulate a possible imbalance in the system. The ohmic resistance of the sixth battery module () is intentionally increased by externally connecting an extra 0.43 Ω resistance in series to the battery. The added ohmic resistance can emulate an aged or possibly faulty battery. Additionally, is changed from 10 kHz to 1 kHz to study the effect of sampling frequency. Changing the battery resistance challenges the ability of the proposed technique to track the asymmetric voltage profiles and evaluate the estimation accuracy for parameters which are beyond normal ranges.
- The third scenario focuses on existence of imbalance in the modules’ voltages. Therefore, battery modules 2 to 7 are charged to 8 V, whereas the first module is manually discharged to a lower open-circuit voltage (approximately 7.7 V). As a result of a higher charge depletion, other ECM parameters of Module One also change slightly. This scenario can emulate a SOC imbalance in the system, which can challenge the ability of the proposed decoupling technique to distinguish the profiles of different modules. Moreover, in the last two scenarios, estimation results of the other modules remain similar, showing that an existing imbalance in one module does not significantly impact the accuracy of the decoupling method for other modules.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| EV | Electric Vehicle |
| BMS | Battery Management System |
| ECM | Equivalent Circuit Model |
| SOC | State Of Charges |
| SOH | State Of Health |
| DC | Direct Current |
| AC | Alternating Current |
| MMCs | Modular Multilevel Converters |
| OCVs | Open-Circuit Voltages |
| RC | Resistance-Capacitance |
| FETs | Field-Effect Transistors |
| PWM | Pulse-Width Modulation |
| MOSFETs | Metal-Oxide-Semiconductor Field-Effect Transistors |
| IGBTs | Insulated-Gate Bipolar Transistors |
| FPGA | Field-Programmable Gate Array |
References
- Buberger, J.; Kersten, A.; Kuder, M.; Eckerle, R.; Weyh, T.; Thiringer, T. Total CO2-equivalent life-cycle emissions from commercially available passenger cars. Renew. Sustain. Energy Rev. 2022, 159, 112158. [Google Scholar] [CrossRef]
- Fassio, E.; Ciociola, A.; Giordano, D.; Noussan, M.; Vassio, L.; Mellia, M. Environmental and Economic Comparison of ICEV and EV in Car Sharing. In Proceedings of the 2021 IEEE International Intelligent Transportation Systems Conference (ITSC), Indianapolis, IN, USA, 19–22 September 2021; pp. 1621–1626. [Google Scholar] [CrossRef]
- Fang, J.; Zhang, R.; Li, H.; Tang, Y. Frequency Derivative-Based Inertia Enhancement by Grid-Connected Power Converters with a Frequency-Locked-Loop. IEEE Trans. Smart Grid 2019, 10, 4918–4927. [Google Scholar] [CrossRef]
- Fang, J.; Li, H.; Tang, Y.; Blaabjerg, F. On the Inertia of Future More-Electronics Power Systems. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 7, 2130–2146. [Google Scholar] [CrossRef]
- Vermeer, W.; Mouli, G.R.C.; Bauer, P. A Comprehensive Review on the Characteristics and Modelling of Lithium-ion Battery Ageing. IEEE Trans. Transp. Electrif. 2021, 8, 2205–2232. [Google Scholar] [CrossRef]
- He, C.; Zhu, J.; Li, S.; Chen, Z.; Wu, W. Sizing and Locating Planning of EV Centralized-Battery-Charging-Station Considering Battery Logistics System. IEEE Trans. Ind. Appl. 2022, 58, 5184–5197. [Google Scholar] [CrossRef]
- Hussain, A.; Bui, V.H.; Kim, H.M. Optimal Sizing of Battery Energy Storage System in a Fast EV Charging Station Considering Power Outages. IEEE Trans. Transp. Electrif. 2020, 6, 453–463. [Google Scholar] [CrossRef]
- Gao, F.; Gu, X.; Ma, Z.; Zhang, C. Redistributed Pulsewidth Modulation of MMC Battery Energy Storage System Under Submodule Fault Condition. IEEE Trans. Power Electron. 2020, 35, 2284–2294. [Google Scholar] [CrossRef]
- Salari, O.; Zaad, K.H.; Bakhshai, A.; Jain, P. Reconfigurable hybrid energy storage system for an electric vehicle DC–AC inverter. IEEE Trans. Power Electron. 2020, 35, 12846–12860. [Google Scholar] [CrossRef]
- Chen, P.; Xiao, F.; Liu, J.; Zhu, Z.; Ren, Q. Unbalanced operation principle and fast balancing charging strategy of a cascaded modular multilevel converter–bidirectional dc–dc converter in the shipboard applications. IEEE Trans. Transp. Electrif. 2020, 6, 1265–1278. [Google Scholar] [CrossRef]
- Ronanki, D.; Williamson, S.S. Modular Multilevel Converters for Transportation Electrification: Challenges and Opportunities. IEEE Trans. Transp. Electrif. 2018, 4, 399–407. [Google Scholar] [CrossRef]
- Zhou, L.; Zheng, Y.; Ouyang, M.; Lu, L. A study on parameter variation effects on battery packs for electric vehicles. J. Power Sources 2017, 364, 242–252. [Google Scholar] [CrossRef]
- Xiong, R.; Yang, R.; Chen, Z.; Shen, W.; Sun, F. Online Fault Diagnosis of External Short Circuit for Lithium-Ion Battery Pack. IEEE Trans. Ind. Electron. 2020, 67, 1081–1091. [Google Scholar] [CrossRef]
- Lin, T.; Chen, Z.; Zheng, C.; Huang, D.; Zhou, S. Fault Diagnosis of Lithium-Ion Battery Pack Based on Hybrid System and Dual Extended Kalman Filter Algorithm. IEEE Trans. Transp. Electrif. 2021, 7, 26–36. [Google Scholar] [CrossRef]
- Andrea, D. Battery Management Systems for Large Lithium-Ion Battery Packs; Artech House: Norwood, MA, USA, 2010. [Google Scholar]
- Uzair, M.; Abbas, G.; Hosain, S. Characteristics of Battery Management Systems of Electric Vehicles with Consideration of the Active and Passive Cell Balancing Process. World Electr. Veh. J. 2021, 12, 120. [Google Scholar] [CrossRef]
- Naguib, M.; Kollmeyer, P.; Emadi, A. Lithium-Ion Battery Pack Robust State of Charge Estimation, Cell Inconsistency, and Balancing: Review. IEEE Access 2021, 9, 50570–50582. [Google Scholar] [CrossRef]
- Hu, X.; Xu, L.; Lin, X.; Pecht, M. Battery lifetime prognostics. Joule 2020, 4, 310–346. [Google Scholar] [CrossRef]
- Istardi, D.; Putra, I.Z. The Weakest Cell Identification in Li-Ion battery packs using Discharging Technique Performance. In Proceedings of the 2018 International Conference on Applied Engineering (ICAE), Batam, Indonesia, 3–4 October 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Afonso, J.L.; Tanta, M.; Pinto, J.G.O.; Monteiro, L.F.; Machado, L.; Sousa, T.J.; Monteiro, V. A Review on Power Electronics Technologies for Power Quality Improvement. Energies 2021, 14, 8585. [Google Scholar] [CrossRef]
- He, L.; Yang, Z.; Gu, Y.; Liu, C.; He, T.; Shin, K.G. SoH-Aware Reconfiguration in Battery Packs. IEEE Trans. Smart Grid 2018, 9, 3727–3735. [Google Scholar] [CrossRef]
- Balachandran, A.; Jonsson, T.; Eriksson, L. Design and Analysis of Battery-Integrated Modular Multilevel Converters for Automotive Powertrain Applications. In Proceedings of the 2021 23rd European Conference on Power Electronics and Applications (EPE’21 ECCE Europe), Novi Sad, Serbia, 28–30 October 2021; pp. P.1–P.12. [Google Scholar] [CrossRef]
- Kacetl, J.; Fang, J.; Kacetl, T.; Tashakor, N.; Goetz, S. Design and Analysis of Modular Multilevel Reconfigurable Battery Converters for Variable Bus Voltage Powertrains. IEEE Trans. Power Electron. 2022, 38, 130–142. [Google Scholar] [CrossRef]
- Ma, Z.; Gao, F.; Gu, X.; Li, N.; Niu, D. An Online SOH Testing Method of MMC Battery Energy Storage System. In Proceedings of the 2018 IEEE 19th Workshop on Control and Modeling for Power Electronics (COMPEL), Padova, Italy, 25–28 June 2018; pp. 1–7. [Google Scholar] [CrossRef]
- De Simone, D.; Piegari, L. Modular multilevel converters for battery electric vehicles: Variable dc voltage control to optimize battery lifetime. In Proceedings of the 2020 IEEE 14th International Conference on Compatibility, Power Electronics and Power Engineering (CPE-POWERENG), Setúbal, Portugal, 8–10 July 2020; Volume 1, pp. 137–142. [Google Scholar] [CrossRef]
- Qiu, S.; Shi, B. An Enhanced Battery Interface of MMC-BESS. In Proceedings of the 2019 IEEE 10th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Xi’an, China, 3–6 June 2019; pp. 434–439. [Google Scholar] [CrossRef]
- Gao, F.; Zhang, L.; Zhou, Q.; Chen, M.; Xu, T.; Hu, S. State-of-charge balancing control strategy of battery energy storage system based on modular multilevel converter. In Proceedings of the 2014 IEEE Energy Conversion Congress and Exposition (ECCE), Pittsburgh, PA, USA, 14–18 September 2014; pp. 2567–2574. [Google Scholar] [CrossRef]
- Ma, Z.; Gao, F.; Gu, X.; Li, N.; Wu, Q.; Wang, X.; Wang, X. Multilayer SOH Equalization Scheme for MMC Battery Energy Storage System. IEEE Trans. Power Electron. 2020, 35, 13514–13527. [Google Scholar] [CrossRef]
- Altaf, F.; Egardt, B.; Johannesson Mårdh, L. Load Management of Modular Battery Using Model Predictive Control: Thermal and State-of-Charge Balancing. IEEE Trans. Control Syst. Technol. 2017, 25, 47–62. [Google Scholar] [CrossRef]
- Soong, T.; Lehn, P.W. Assessment of Fault Tolerance in Modular Multilevel Converters with Integrated Energy Storage. IEEE Trans. Power Electron. 2016, 31, 4085–4095. [Google Scholar] [CrossRef]
- Hillers, A.; Biela, J. Fault-tolerant operation of the modular multilevel converter in an energy storage system based on split batteries. In Proceedings of the 2014 16th European Conference on Power Electronics and Applications, Lappeenranta, Finland, 26–28 August 2014; pp. 1–8. [Google Scholar] [CrossRef]
- Quraan, M.; Tricoli, P.; D’Arco, S.; Piegari, L. Efficiency Assessment of Modular Multilevel Converters for Battery Electric Vehicles. IEEE Trans. Power Electron. 2017, 32, 2041–2051. [Google Scholar] [CrossRef]
- Singer, A.; Helling, F.; Weyh, T.; Jungbauer, J.; Pfisterer, H.J. Modular multilevel parallel converter based split battery system (M2B) for stationary storage applications. In Proceedings of the 2017 19th European Conference on Power Electronics and Applications (EPE’17 ECCE Europe), Warsaw, Poland, 11–14 September 2017; pp. P.1–P.10. [Google Scholar] [CrossRef]
- Ma, Z.; Gao, F.; Zhang, C.; Li, W.; Niu, D. Variable DC-Link Voltage Regulation of Single-Phase MMC Battery Energy-Storage System for Reducing Additional Charge Throughput. IEEE Trans. Power Electron. 2021, 36, 14267–14281. [Google Scholar] [CrossRef]
- Fonseca, J.M.L.; Reddy, S.R.P.; Rajashekara, K.; Potti, K.R.R. Reduced Capacitor Energy Requirements in Battery Energy Storage Systems based on Modular Multilevel Converters. IEEE Trans. Ind. Appl. 2022, 58, 7608–7619. [Google Scholar] [CrossRef]
- Guo, P.; Xu, Q.; Yue, Y.; Ma, F.; He, Z.; Luo, A.; Guerrero, J.M. Analysis and Control of Modular Multilevel Converter with Split Energy Storage for Railway Traction Power Conditioner. IEEE Trans. Power Electron. 2020, 35, 1239–1255. [Google Scholar] [CrossRef]
- Zhao, F.; Xiao, G.; Zhu, T.; Zhao, T.; Zheng, X.; Wu, Z. Harmonic Analysis and Suppression Method of Output Current Distortion for Medium-Voltage Motor Drives with Modular Multilevel Converter. IEEE Trans. Power Electron. 2020, 35, 744–759. [Google Scholar] [CrossRef]
- Thakur, S.S.; Odavic, M.; Allu, A.; Zhu, Z.Q.; Atallah, K. Theoretical Harmonic Spectra of PWM Waveforms Including DC Bus Voltage Ripple—Application to a Low-Capacitance Modular Multilevel Converter. IEEE Trans. Power Electron. 2020, 35, 9291–9305. [Google Scholar] [CrossRef]
- Wang, Y.; Aksoz, A.; Geury, T.; El Baghdadi, M.; Hegazy, O. Performance Enhancement of a Battery-Grid Connected SiC MMC for DC Microgrid Systems. In Proceedings of the 2021 Sixteenth International Conference on Ecological Vehicles and Renewable Energies (EVER), Monte-Carlo, Monaco, 5–7 May 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Mittal, N.; Singh, B.; Singh, S.; Dixit, R.; Kumar, D. Multilevel inverters: A literature survey on topologies and control strategies. In Proceedings of the 2012 2nd International Conference on Power, Control and Embedded Systems, Allahabad, India, 17–19 December 2012; pp. 1–11. [Google Scholar] [CrossRef]
- Fang, J.; Blaabjerg, F.; Liu, S.; Goetz, S.M. A review of multilevel converters with parallel connectivity. IEEE Trans. Power Electron. 2021, 36, 12468–12489. [Google Scholar] [CrossRef]
- Chen, J.; Jiang, D.; Sun, W.; Pei, X. Common-Mode Voltage Reduction Scheme for MMC with Low Switching Frequency in AC–DC Power Conversion System. IEEE Trans. Ind. Inform. 2021, 18, 278–287. [Google Scholar] [CrossRef]
- Priya, M.; Ponnambalam, P.; Muralikumar, K. Modular-multilevel converter topologies and applications—A review. IET Power Electron. 2019, 12, 170–183. [Google Scholar] [CrossRef]
- Debnath, S.; Qin, J.; Bahrani, B.; Saeedifard, M.; Barbosa, P. Operation, control, and applications of the modular multilevel converter: A review. IEEE Trans. Power Electron. 2014, 30, 37–53. [Google Scholar] [CrossRef]
- Kersten, A.; Kuder, M.; Grunditz, E.; Geng, Z.; Wikner, E.; Thiringer, T.; Weyh, T.; Eckerle, R. Inverter and Battery Drive Cycle Efficiency Comparisons of CHB and MMSP Traction Inverters for Electric Vehicles. In Proceedings of the 2019 21st European Conference on Power Electronics and Applications (EPE’19 ECCE Europe), Genova, Italy, 3–5 September 2019; pp. P.1–P.12. [Google Scholar] [CrossRef]
- Dai, S.; Zhang, F.; Zhao, X. Series-connected battery equalization system: A systematic review on variables, topologies, and modular methods. Int. J. Energy Res. 2021, 45, 19709–19728. [Google Scholar] [CrossRef]
- Arabsalmanabadi, B.; Tashakor, N.; Zhang, Y.; Al-Haddad, K.; Goetz, S. Parameter estimation of batteries in MMCs with parallel connectivity using PSO. In Proceedings of the IECON 2021—47th Annual Conference of the IEEE Industrial Electronics Society, Toronto, ON, Canada, 13–16 October 2021; pp. 1–6. [Google Scholar]
- Raman, S.R.; Xue, X.; Cheng, K.E. Review of charge equalization schemes for Li-ion battery and super-capacitor energy storage systems. In Proceedings of the 2014 International Conference on Advances in Electronics Computers and Communications, Bangalore, India, 10–11 October 2014; pp. 1–6. [Google Scholar]
- Lu, L.; Han, X.; Li, J.; Hua, J.; Ouyang, M. A review on the key issues for lithium-ion battery management in electric vehicles. J. Power Sources 2013, 226, 272–288. [Google Scholar] [CrossRef]
- Tan, X.; Tan, Y.; Zhan, D.; Yu, Z.; Fan, Y.; Qiu, J.; Li, J. Real-time state-of-health estimation of lithium-ion batteries based on the equivalent internal resistance. IEEE Access 2020, 8, 56811–56822. [Google Scholar] [CrossRef]
- Cao, J.; Emadi, A. Batteries Need Electronics. IEEE Ind. Electron. Mag. 2011, 5, 27–35. [Google Scholar] [CrossRef]
- Givi, H.; Hosseini, E.; Farjah, E. Estimation of batteries voltages and resistances in modular multilevel converter with half-bridge modules using modified PSO algorithm. In Proceedings of the 2021 12th Power Electronics, Drive Systems, and Technologies Conference (PEDSTC), Babol, Iran, 2–4 February 2021; pp. 1–7. [Google Scholar]
- Poblete, P.; Pizarro, G.; Droguett, G.; Núñez, F.; Judge, P.D.; Pereda, J. Distributed Neural Network Observer for Submodule Capacitor Voltage Estimation in Modular Multilevel Converters. IEEE Trans. Power Electron. 2022, 37, 10306–10318. [Google Scholar] [CrossRef]
- Kacetl, T.; Kacetl, J.; Fang, J.; Jaensch, M.; Goetz, S. Degradation-Reducing Control for Dynamically Reconfigurable Batteries. arXiv 2022, arXiv:2202.11757. [Google Scholar]
- Konstantinou, G.; Wickramasinghe, H.R.; Townsend, C.D.; Ceballos, S.; Pou, J. Estimation methods and sensor reduction in modular multilevel converters: A review. In Proceedings of the 2018 8th International Conference on Power and Energy Systems (ICPES), Galadari Hotel, Colombo, Sri Lanka, 21–22 December 2018; pp. 23–28. [Google Scholar]
- da Silva, G.S.; Vieira, R.P.; Rech, C. Discrete-time sliding-mode observer for capacitor voltage control in modular multilevel converters. IEEE Trans. Ind. Electron. 2017, 65, 876–886. [Google Scholar] [CrossRef]
- Nademi, H.; Das, A.; Norum, L.E. Modular multilevel converter with an adaptive observer of capacitor voltages. IEEE Trans. Power Electron. 2014, 30, 235–248. [Google Scholar] [CrossRef]
- Wang, Z.; Peng, L. Grouping capacitor voltage estimation and fault diagnosis with capacitance self-updating in modular multilevel converters. IEEE Trans. Power Electron. 2020, 36, 1532–1543. [Google Scholar] [CrossRef]
- Rong, F.; Gong, X.; Li, X.; Huang, S. A new voltage measure method for MMC based on sample delay compensation. IEEE Trans. Power Electron. 2017, 33, 5712–5723. [Google Scholar] [CrossRef]
- Abushafa, O.; Gadoue, S.; Dhaidah, M.; Aktinson, D. Capacitor voltage estimation in modular multilevel converters using a Kalman filter algorithm. In Proceedings of the 2015 IEEE International Conference on Industrial Technology (ICIT), Seville, Spain, 17–19 March 2015; pp. 3016–3021. [Google Scholar]
- Abushafa, O.S.H.M.; Dahidah, M.S.A.; Gadoue, S.M.; Atkinson, D.J. Submodule Voltage Estimation Scheme in Modular Multilevel Converters with Reduced Voltage Sensors Based on Kalman Filter Approach. IEEE Trans. Ind. Electron. 2018, 65, 7025–7035. [Google Scholar] [CrossRef]
- Chakraborty, R.; Samantaray, J.; Dey, A.; Chakrabarty, S. Capacitor Voltage Estimation of MMC Using a Discrete-Time Sliding Mode Observer Based on Discrete Model Approach. IEEE Trans. Ind. Appl. 2022, 58, 494–504. [Google Scholar] [CrossRef]
- Asoodar, M.; Nahalparvari, M.; Danielsson, C.; Söderström, R.; Nee, H.P. Online Health Monitoring of DC-Link Capacitors in Modular Multilevel Converters for FACTS and HVDC Applications. IEEE Trans. Power Electron. 2021, 36, 13489–13503. [Google Scholar] [CrossRef]
- Purkayastha, B.; Bhattacharya, T. Simplified Approach for Acquisition of Submodule Capacitor Voltages of the Modular Multilevel Converter Using Low Sampling Rate Sensing and Estimation. IEEE Trans. Power Electron. 2022, 37, 13428–13438. [Google Scholar] [CrossRef]
- Han, W.; Zou, C.; Zhou, C.; Zhang, L. Estimation of Cell SOC Evolution and System Performance in Module-Based Battery Charge Equalization Systems. IEEE Trans. Smart Grid 2019, 10, 4717–4728. [Google Scholar] [CrossRef]
- Chen, H.; Tian, E.; Wang, L. State-of-Charge Estimation of Lithium-Ion Batteries Subject to Random Sensor Data Unavailability: A Recursive Filtering Approach. IEEE Trans. Ind. Electron. 2021, 69, 5175–5184. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, Z.; Zhang, L.; Liu, P.; Zhang, Z. A novel consistency evaluation method for series-connected battery systems based on real-world operation data. IEEE Trans. Transp. Electrif. 2020, 7, 437–451. [Google Scholar] [CrossRef]
- Chen, L.; Ding, Y.; Wang, H.; Wang, Y.; Liu, B.; Wu, S.; Li, H.; Pan, H. Online Estimating State of Health of Lithium-Ion Batteries Using Hierarchical Extreme Learning Machine. IEEE Trans. Transp. Electrif. 2021, 8, 965–975. [Google Scholar] [CrossRef]
- Xiong, R.; Li, L.; Tian, J. Towards a smarter battery management system: A critical review on battery state of health monitoring methods. J. Power Sources 2018, 405, 18–29. [Google Scholar] [CrossRef]
- Wang, Y.; Tian, J.; Sun, Z.; Wang, L.; Xu, R.; Li, M.; Chen, Z. A comprehensive review of battery modeling and state estimation approaches for advanced battery management systems. Renew. Sustain. Energy Rev. 2020, 131, 110015. [Google Scholar] [CrossRef]
- Cen, Z.; Kubiak, P. Lithium-ion battery SOC/SOH adaptive estimation via simplified single particle model. Int. J. Energy Res. 2020, 44, 12444–12459. [Google Scholar] [CrossRef]
- Huang, S.C.; Tseng, K.H.; Liang, J.W.; Chang, C.L.; Pecht, M.G. An online SOC and SOH estimation model for lithium-ion batteries. Energies 2017, 10, 512. [Google Scholar] [CrossRef]
- Barré, A.; Deguilhem, B.; Grolleau, S.; Gérard, M.; Suard, F.; Riu, D. A review on lithium-ion battery ageing mechanisms and estimations for automotive applications. J. Power Sources 2013, 241, 680–689. [Google Scholar] [CrossRef]
- Carkhuff, B.G.; Demirev, P.A.; Srinivasan, R. Impedance-Based Battery Management System for Safety Monitoring of Lithium-Ion Batteries. IEEE Trans. Ind. Electron. 2018, 65, 6497–6504. [Google Scholar] [CrossRef]
- Shen, M.; Gao, Q. A review on battery management system from the modeling efforts to its multiapplication and integration. Int. J. Energy Res. 2019, 43, 5042–5075. [Google Scholar] [CrossRef]
- Kersten, A.; Kuder, M.; Han, W.; Thiringer, T.; Lesnicar, A.; Weyh, T.; Eckerle, R. Online and On-Board Battery Impedance Estimation of Battery Cells, Modules or Packs in a Reconfigurable Battery System or Multilevel Inverter. In Proceedings of the IECON 2020 The 46th Annual Conference of the IEEE Industrial Electronics Society, Singapore, 18–21 October 2020; pp. 1884–1891. [Google Scholar] [CrossRef]
- Balachandran, A.; Jonsson, T.; Eriksson, L.; Larsson, A. Experimental Evaluation of Battery Impedance and Submodule Loss Distribution for Battery Integrated Modular Multilevel Converters. In Proceedings of the 2022 24th European Conference on Power Electronics and Applications (EPE’22 ECCE Europe), Hannover, Germany, 5–9 September 2022; pp. 1–10. [Google Scholar]
- Tashakor, N.; Arabsalmanabadi, B.; Naseri, F.; Goetz, S. Low-Cost Parameter Estimation Approach for Modular Converters and Reconfigurable Battery Systems Using Dual Kalman Filter. IEEE Trans. Power Electron. 2021, 37, 6323–6334. [Google Scholar] [CrossRef]
- Einhorn, M.; Conte, F.V.; Kral, C.; Fleig, J. Comparison, Selection, and Parameterization of Electrical Battery Models for Automotive Applications. IEEE Trans. Power Electron. 2013, 28, 1429–1437. [Google Scholar] [CrossRef]
- Meng, J.; Stroe, D.I.; Ricco, M.; Luo, G.; Teodorescu, R. A simplified model-based state-of-charge estimation approach for lithium-ion battery with dynamic linear model. IEEE Trans. Ind. Electron. 2018, 66, 7717–7727. [Google Scholar] [CrossRef]
- Xiong, R.; Cao, J.; Yu, Q.; He, H.; Sun, F. Critical review on the battery state of charge estimation methods for electric vehicles. IEEE Access 2017, 6, 1832–1843. [Google Scholar] [CrossRef]
- Lelie, M.; Braun, T.; Knips, M.; Nordmann, H.; Ringbeck, F.; Zappen, H.; Sauer, D.U. Battery Management System Hardware Concepts: An Overview. Appl. Sci. 2018, 8, 534. [Google Scholar] [CrossRef]
- Pizarro, G.; Poblete, P.; Droguett, G.; Pereda, J.; Núñez, F. Extended Kalman Filtering for Full-State Estimation and Sensor Reduction in Modular Multilevel Converters. IEEE Trans. Ind. Electron. 2022, 70, 1927–1938. [Google Scholar] [CrossRef]
- Zhang, W.; Wang, L.; Wang, L.; Liao, C.; Zhang, Y. Joint State-of-Charge and State-of-Available-Power Estimation Based on the Online Parameter Identification of Lithium-Ion Battery Model. IEEE Trans. Ind. Electron. 2022, 69, 3677–3688. [Google Scholar] [CrossRef]
- Mukhopadhyay, S.; Usman, H.M.; Rehman, H. Real Time Li-Ion Battery Bank Parameters Estimation via Universal Adaptive Stabilization. IEEE Open J. Control Syst. 2022, 1, 268–293. [Google Scholar] [CrossRef]
- Xie, F.; Czogalla, O. Lightweight Parameter Estimation for the Third-Order Lithium-Ion Battery Model Based on Non-iterative Algorithm. In Proceedings of the 2020 IEEE Transportation Electrification Conference & Expo (ITEC), Virtual, 22–26 June 2020; pp. 164–168. [Google Scholar] [CrossRef]
- Lee, S.; Mohtat, P.; Siegel, J.B.; Stefanopoulou, A.G.; Lee, J.W.; Lee, T.K. Estimation Error Bound of Battery Electrode Parameters with Limited Data Window. IEEE Trans. Ind. Inform. 2020, 16, 3376–3386. [Google Scholar] [CrossRef]
- Bhat, C.; Channegowda, J.; Naraharisetti, K. An Improved Equivalent Circuit Parameter Estimation Using Electrochemical Model for Lead-Acid Battery. In Proceedings of the 2022 IEEE Delhi Section Conference (DELCON), Virtual, 11–13 February 2022; pp. 1–4. [Google Scholar] [CrossRef]
- Shrivastava, P.; Soon, T.K.; Yamani Bin Idris, M.; Mekhilef, S. Lithium-ion Battery Model Parameter Identification Using Modified Adaptive Forgetting Factor-Based Recursive Least Square Algorithm. In Proceedings of the 2021 IEEE 12th Energy Conversion Congress & Exposition—Asia (ECCE-Asia), Singapore, 24–27 May 2021; pp. 2169–2174. [Google Scholar] [CrossRef]
- Tashakor, N.; Arabsalmanabadi, B.; Hosseini, E.; Al-Haddad, K.; Goetz, S. Estimation of Battery Parameters in Cascaded Half-Bridge Converters with Reduced Voltage Sensors. In Proceedings of the 2022 24th European Conference on Power Electronics and Applications (EPE’22 ECCE Europe), Hannover, Germany, 5–9 September 2022; pp. 1–11. [Google Scholar]
- He, H.; Xiong, R.; Fan, J. Evaluation of lithium-ion battery equivalent circuit models for state of charge estimation by an experimental approach. Energies 2011, 4, 582–598. [Google Scholar] [CrossRef]
- Bessman, A.; Soares, R.; Wallmark, O.; Svens, P.; Lindbergh, G. Aging effects of AC harmonics on lithium-ion cells. J. Energy Storage 2019, 21, 741–749. [Google Scholar] [CrossRef]
- Uno, M.; Tanaka, K. Influence of high-frequency charge–discharge cycling induced by cell voltage equalizers on the life performance of lithium-ion cells. IEEE Trans. Veh. Technol. 2011, 60, 1505–1515. [Google Scholar] [CrossRef]
- De Jongh, P.; Notten, P. Effect of current pulses on lithium intercalation batteries. Solid State Ionics 2002, 148, 259–268. [Google Scholar] [CrossRef]
- Chang, F.; Roemer, F.; Lienkamp, M. Influence of current ripples in cascaded multilevel topologies on the aging of lithium batteries. IEEE Trans. Power Electron. 2020, 35, 11879–11890. [Google Scholar] [CrossRef]
- Kacetl, T.; Kacetl, J.; Tashakor, N.; Fang, J.; Goetz, S.M. Bandwidth-Increased Ripple-Mitigating Scheduling Algorithm for Dynamically Reconfigurable Batteries. IEEE Access 2022, 10, 104202–104214. [Google Scholar] [CrossRef]
- Kacetl, T.; Kacetl, J.; Tashakor, N.; Goetz, S. A Simplified Model for the Battery Ageing Potential Under Highly Rippled Load. In Proceedings of the 2022 24th European Conference on Power Electronics and Applications (EPE’22 ECCE Europe), Hannover, Germany, 5–9 September 2022; pp. 1–10. [Google Scholar]
- Chen, M.; Rincon-Mora, G.A. Accurate electrical battery model capable of predicting runtime and IV performance. IEEE Trans. Energy Convers. 2006, 21, 504–511. [Google Scholar] [CrossRef]
- Yazdani, A.; Iravani, R. Voltage-Sourced Converters in Power Systems: Modeling, Control, and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Li, Y.; Wang, Y.; Li, B.Q. Generalized Theory of Phase-Shifted Carrier PWM for Cascaded H-Bridge Converters and Modular Multilevel Converters. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 589–605. [Google Scholar] [CrossRef]
- Abdelrahman, A.S.; Erdem, Z.; Attia, Y.; Youssef, M.Z. Wide bandgap devices in electric vehicle converters: A performance survey. Can. J. Electr. Comput. Eng. 2018, 41, 45–54. [Google Scholar] [CrossRef]
- Sivkov, O.; Novak, M.; Novak, J. Comparison between Si IGBT and SiC MOSFET Inverters for AC Motor Drive. In Proceedings of the 2018 18th International Conference on Mechatronics-Mechatronika (ME), Brno, Czech Republic, 5–7 December 2018; pp. 1–5. [Google Scholar]
- Rogers, M.J.; Motto, E.R.; Steiner, M. Performance comparison of state-of-the-art 300a/1700v si igbt and SiC mosfet power modules. IEEE Power Electron. Mag. 2020, 7, 44–51. [Google Scholar] [CrossRef]
- Li, Y.; Zhu, H.; Zheng, J.; Chen, Y. A Multivariate Regression Method for Battery Remaining Capacity Based on Model Parameter Identification. In Proceedings of the 2021 3rd International Academic Exchange Conference on Science and Technology Innovation (IAECST), Guangzhou, China, 10–21 December 2021; pp. 1120–1124. [Google Scholar] [CrossRef]
- Ahmed, R.; Rahimifard, S.; Habibi, S. Offline Parameter Identification and SOC Estimation for New and Aged Electric Vehicles Batteries. In Proceedings of the 2019 IEEE Transportation Electrification Conference and Expo (ITEC), Novi, MI, USA, 21 June 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Hossain, M.; Haque, M.E.; Arif, M.T. Online Model Parameter and State of Charge Estimation of Li-Ion Battery Using Unscented Kalman Filter Considering Effects of Temperatures and C-Rates. IEEE Trans. Energy Convers. 2022, 37, 2498–2511. [Google Scholar] [CrossRef]
- Nocedal, J.; Öztoprak, F.; Waltz, R.A. An interior point method for nonlinear programming with infeasibility detection capabilities. Optim. Methods Softw. 2014, 29, 837–854. [Google Scholar] [CrossRef]
- Adhikaree, A.; Kim, T.; Vagdoda, J.; Ochoa, A.; Hernandez, P.J.; Lee, Y. Cloud-based battery condition monitoring platform for large-scale lithium-ion battery energy storage systems using internet-of-things (IoT). In Proceedings of the 2017 IEEE Energy Conversion Congress and Exposition (ECCE), Cincinnati, OH, USA, 1–5 October 2017; pp. 1004–1009. [Google Scholar] [CrossRef]




| Parameter | Value |
|---|---|
| N | 7 |
| m | 200 |
| = | 10 kHz |
| C | 2 mF |
| L | 0.2 mH |
| R | 0.05 Ω |
| 5∼40 Ω | |
| 2.1∼14.28 V | |
| 0.3∼3.4 F | |
| 0.033∼0.374 Ω | |
| 0.027∼0.306 Ω | |
| 0.001∼0.034 F |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tashakor, N.; Dusengimana, J.; Bayati, M.; Kersten, A.; Schotten, H.; Götz, S. General Decoupling and Sampling Technique for Reduced-Sensor Battery Management Systems in Modular Reconfigurable Batteries. Batteries 2023, 9, 99. https://doi.org/10.3390/batteries9020099
Tashakor N, Dusengimana J, Bayati M, Kersten A, Schotten H, Götz S. General Decoupling and Sampling Technique for Reduced-Sensor Battery Management Systems in Modular Reconfigurable Batteries. Batteries. 2023; 9(2):99. https://doi.org/10.3390/batteries9020099
Chicago/Turabian StyleTashakor, Nima, Janvier Dusengimana, Mahdi Bayati, Anton Kersten, Hans Schotten, and Stefan Götz. 2023. "General Decoupling and Sampling Technique for Reduced-Sensor Battery Management Systems in Modular Reconfigurable Batteries" Batteries 9, no. 2: 99. https://doi.org/10.3390/batteries9020099
APA StyleTashakor, N., Dusengimana, J., Bayati, M., Kersten, A., Schotten, H., & Götz, S. (2023). General Decoupling and Sampling Technique for Reduced-Sensor Battery Management Systems in Modular Reconfigurable Batteries. Batteries, 9(2), 99. https://doi.org/10.3390/batteries9020099







