Prediction of the Heat Generation Rate of Lithium-Ion Batteries Based on Three Machine Learning Algorithms
Abstract
:1. Introduction
2. Data and Methods
2.1. Data Collection and Preprocessing
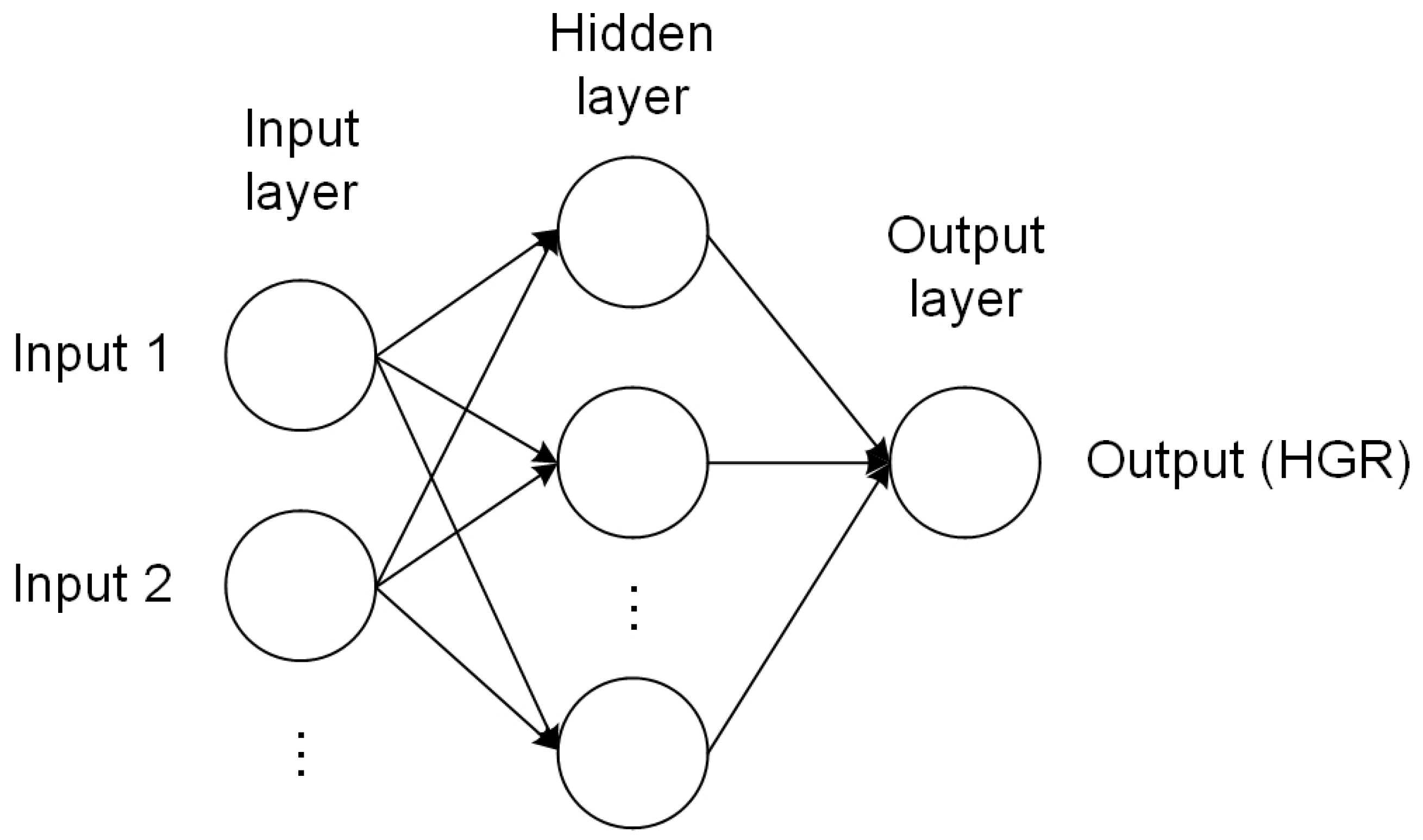
2.2. Machine Learning Modeling
2.3. Evaluation of the Methods
3. Results
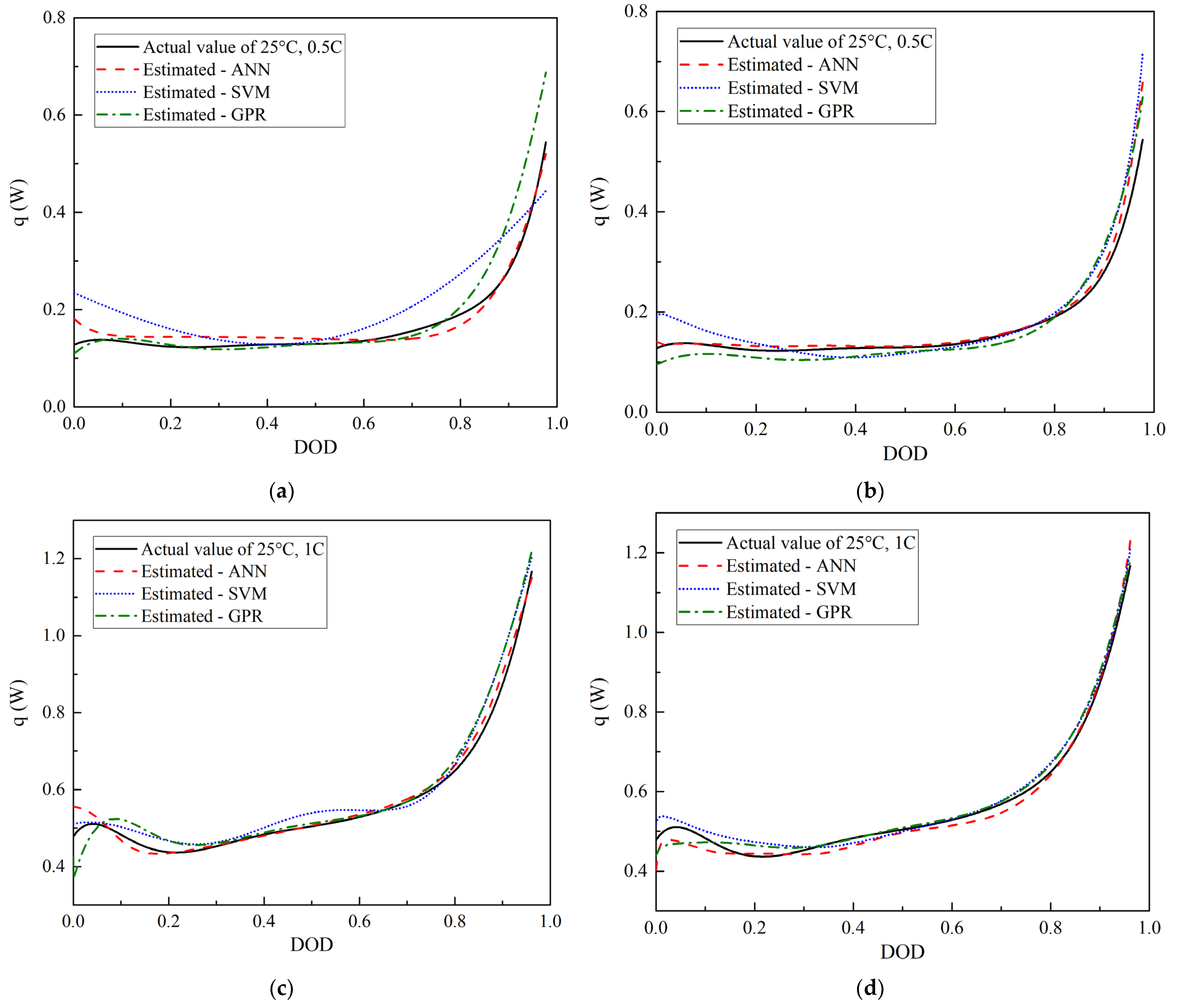
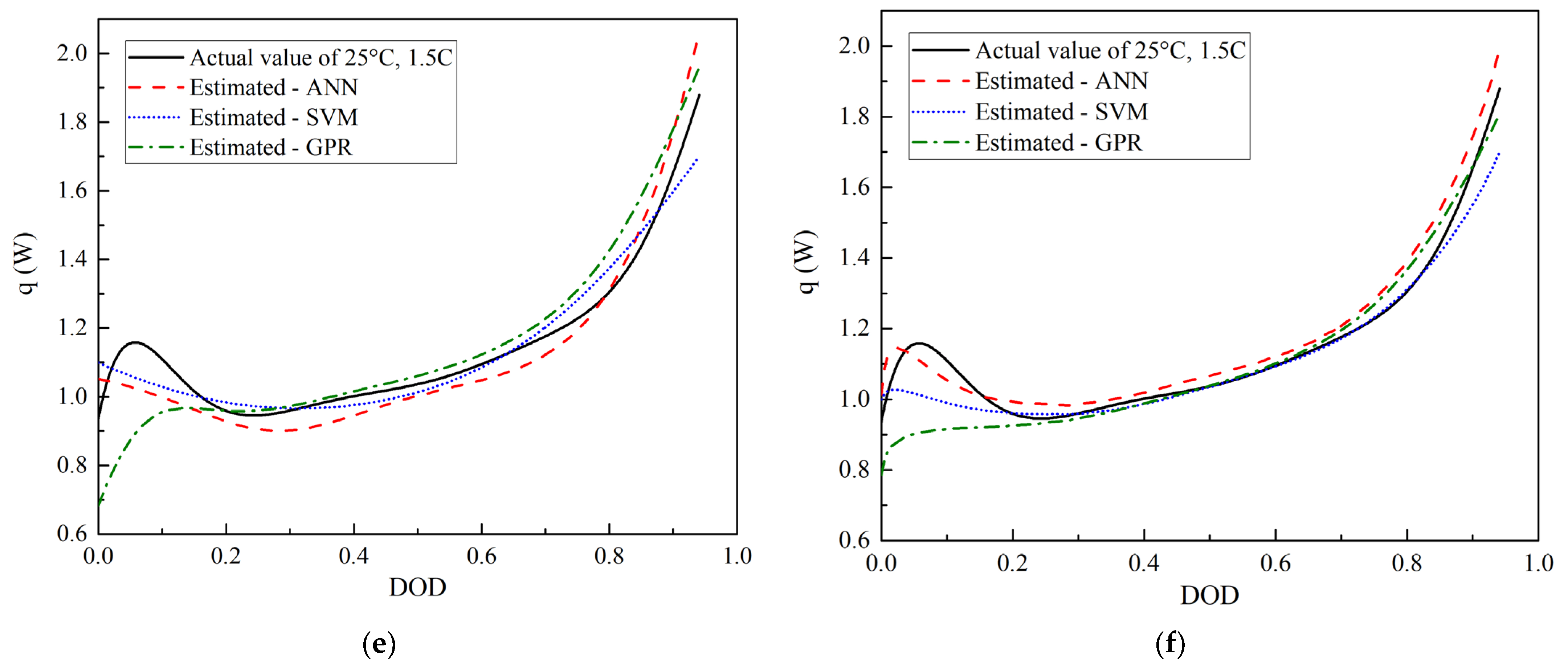
3.1. HGR Prediction at Different Discharge Currents
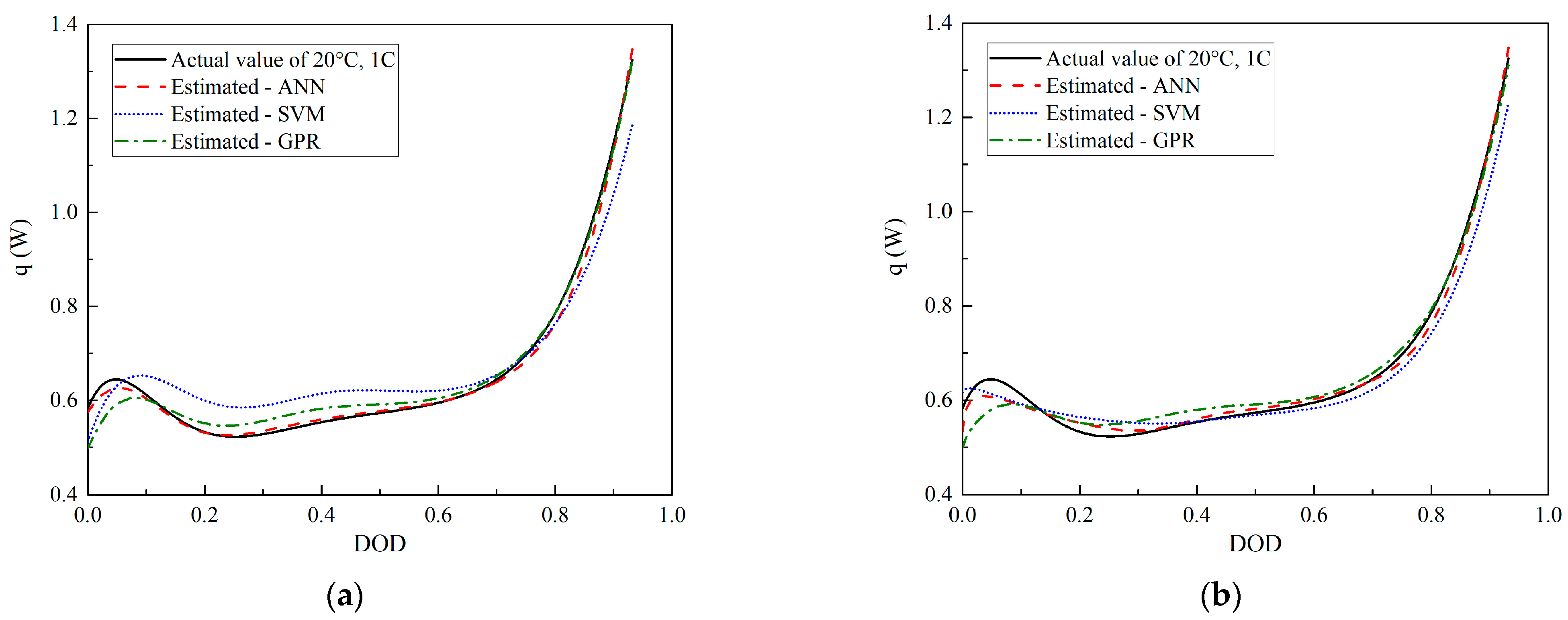
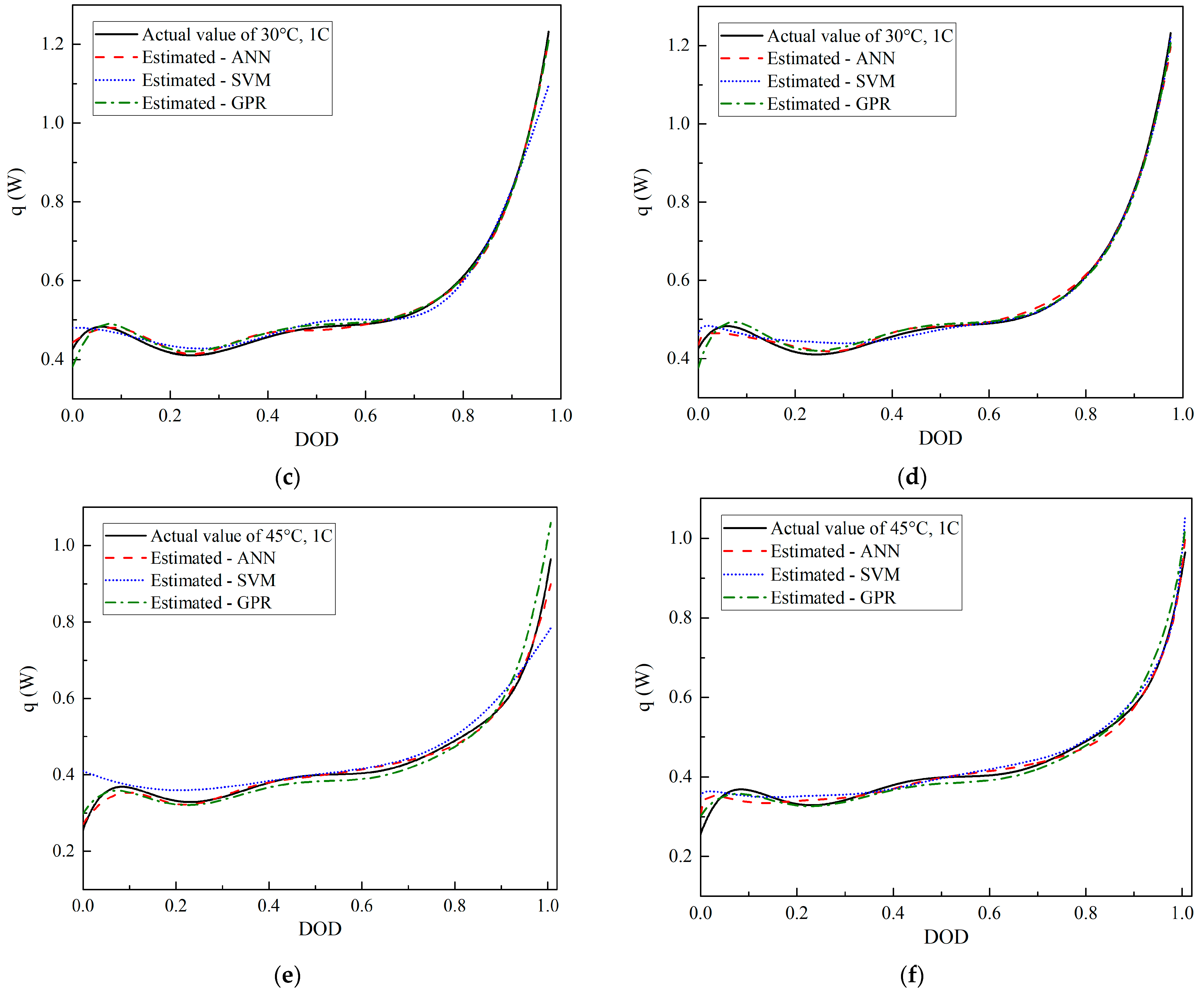
3.2. HGR Prediction at Different Ambient Temperatures
4. Discussion
5. Conclusions
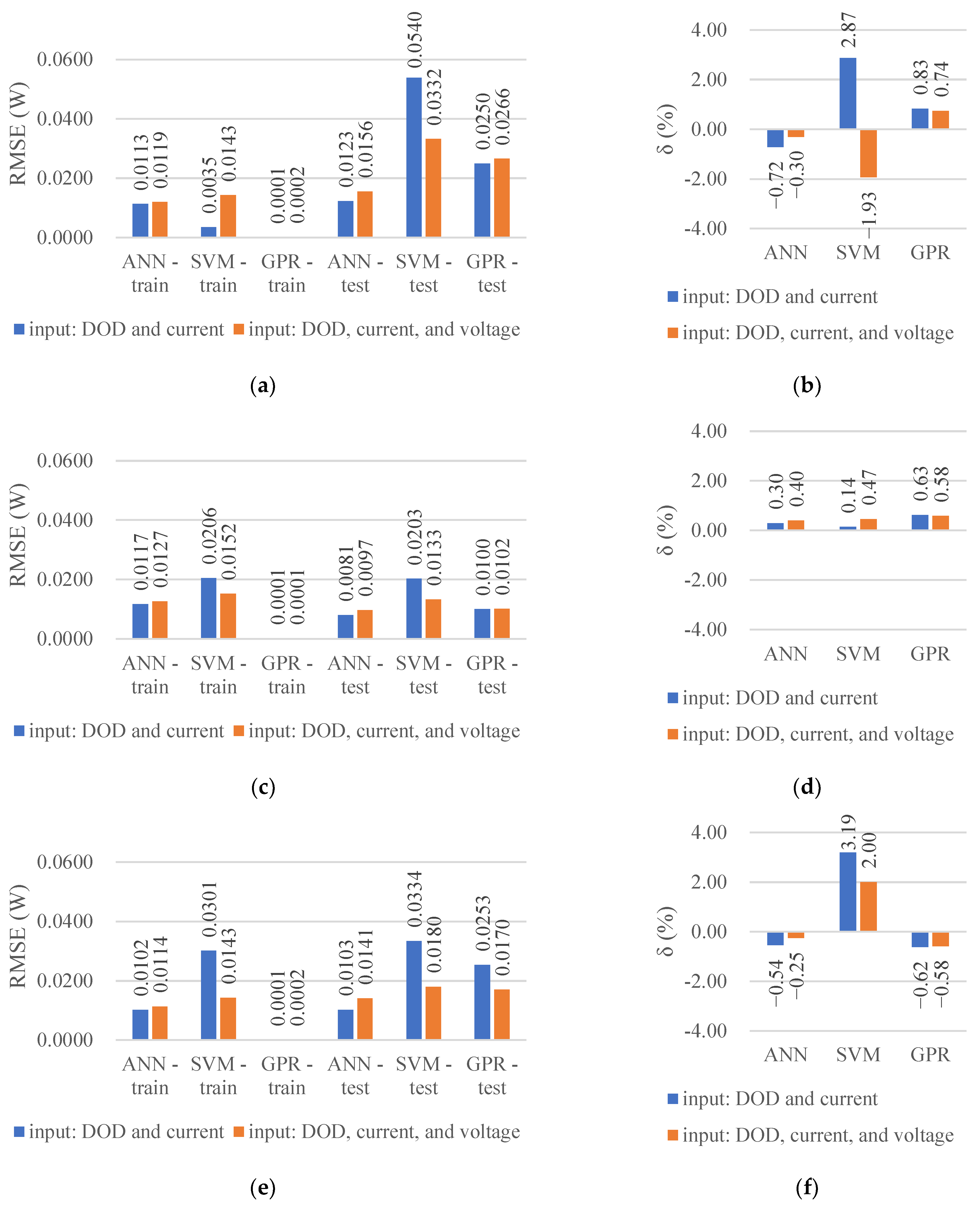
- The prediction performances of the three algorithms for the extrapolation cases were not as good as those for the interpolation cases. Particularly, ideal results may not be obtained for the predictions of the 0.5 C and 1.5 C discharge even after the discharge voltage was added to the inputs. For example, the R2 values of the interpolation cases were greater than 0.96, whereas that of the GPR for the 1.5 C discharge after adding the discharge voltage as an input was only 0.82 (Table 2). Therefore, in practical applications, the boundary of the test conditions must be broadened and extrapolation regression must be avoided as much as possible.
- The prediction accuracy of the SVM and GPR can be improved by adding the discharge voltage to the input parameters of the DOD and discharge current/ambient temperature. For example, in the prediction of different discharge currents, the minimum R2 value increased from 0.53 to 0.82, and the maximum reached 0.98 (Table 2). The effect of adding the input parameter on the accuracy of the ANN was minimal. However, more tests are required to obtain the discharge voltage data under the conditions to be predicted when the input is added, which increases the time consumption.
- The absolute values of the relative error of the average HGRs predicted by the three algorithms were mostly within 5%, indicating that all three algorithms can be applied to predict the battery HGR. The ANN exhibited the best performance among the three algorithms and accurately predicted the interpolation and extrapolation cases without additional input parameters. The R2 values were within the range of 0.89–1.00 (Table 2 and Table 3), the architectures used were simple, and the computation cost was relatively small. Therefore, the ANN is the most preferred among the three machine learning algorithms for similar battery HGR prediction problems.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ANN | Artificial neural network; |
| DOD | Depth of discharge; |
| GPR | Gaussian process regression; |
| HGR | Heat generation rate; |
| LSTM | Long short-term memory; |
| NARX | Non-linear autoregressive exogenous; |
| NN | Neural network; |
| R2 | R-squared, or the coefficient of determination; |
| RBF | Radial basis function; |
| RMSE | Root mean square error; |
| RUL | Remaining useful life; |
| SOC | State of charge; |
| SOH | State of health; |
| SVM | Support vector machine; |
| TMS | Thermal management system. |
References
- Dunn, B.; Kamath, H.; Tarascon, J.-M. Electrical Energy Storage for the Grid: A Battery of Choices. Science 2011, 334, 928–935. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Diouf, B.; Pode, R. Potential of Lithium-Ion Batteries in Renewable Energy. Renew. Energy 2015, 76, 375–380. [Google Scholar] [CrossRef]
- Beauregard, G.P.; Phoenix, A.Z. Report of Investigation: Hybrids plus Plug in Hybrid Electric Vehicle; Electric Transportation Engineering Corporation (eTec): Idaho Falls, ID, USA, 2008. [Google Scholar]
- Smith, B. Chevrolet Volt Battery Incident Summary Report; National Highway Traffic Safety Administration: Washington, DC, USA, 2012.
- Hart, C.A.; Sumwalt, R.L.; Rosekind, M.R.; Weener, E.F. Aircraft Incident Report: Auxiliary Power Unit Battery Fire, Japan Airlines Boeing 787-8, JA829J, Boston, Massachusetts, 7 January 2013; National Transportation Safety Board: Washington, DC, USA, 2014.
- Goto, N.; Endo, S.; Ishikawa, T.; Tamura, S.; Shuto, Y.; Tanaka, K. Aircraft Serious Incident Investigation Report: All Nippon Airways Co. Ltd., JA804A; Japan Transport Safety Board: Tokyo, Japan, 2014. [Google Scholar]
- Feng, X.; Ouyang, M.; Liu, X.; Lu, L.; Xia, Y.; He, X. Thermal Runaway Mechanism of Lithium Ion Battery for Electric Vehicles: A Review. Energy Storage Mater. 2018, 10, 246–267. [Google Scholar] [CrossRef]
- Newman, J.; Tiedemann, W. Porous-Electrode Theory with Battery Applications. AIChE J. 1975, 21, 25–41. [Google Scholar] [CrossRef] [Green Version]
- Doyle, M.; Fuller, T.F.; Newman, J. Modeling of Galvanostatic Charge and Discharge of the Lithium/Polymer/Insertion Cell. J. Electrochem. Soc. 1993, 140, 1526. [Google Scholar] [CrossRef]
- Evans, T.I.; Nguyen, T.V.; White, R.E. A Mathematical Model of a Lithium/Thionyl Chloride Primary Cell. J. Electrochem. Soc. 1989, 136, 328–339. [Google Scholar] [CrossRef]
- Guo, M.; White, R.E. Mathematical Model for a Spirally-Wound Lithium-Ion Cell. J. Power Sources 2014, 250, 220–235. [Google Scholar] [CrossRef]
- Bernardi, D.; Pawlikowski, E.; Newman, J. A General Energy Balance for Battery Systems. J. Electrochem. Soc. 1985, 132, 5–12. [Google Scholar] [CrossRef] [Green Version]
- Mevawalla, A.; Shabeer, Y.; Tran, M.K.; Panchal, S.; Fowler, M.; Fraser, R. Thermal Modelling Utilizing Multiple Experimentally Measurable Parameters. Batteries 2022, 8, 147. [Google Scholar] [CrossRef]
- Jindal, P.; Katiyar, R.; Bhattacharya, J. Evaluation of Accuracy for Bernardi Equation in Estimating Heat Generation Rate for Continuous and Pulse-Discharge Protocols in LFP and NMC Based Li-Ion Batteries. Appl. Therm. Eng. 2022, 201, 117794. [Google Scholar] [CrossRef]
- Wang, S.; Wu, T.; Xie, H.; Li, C.; Zhang, J.; Jiang, L.; Wang, Q. Effects of Current and Ambient Temperature on Thermal Response of Lithium Ion Battery. Batteries 2022, 8, 203. [Google Scholar] [CrossRef]
- Vaidyanathan, H.; Kelly, W.H.; Rao, G. Heat Dissipation in a Lithium Ion Cell. J. Power Sources 2001, 93, 112–122. [Google Scholar] [CrossRef]
- Yu, G.; Zhang, X.; Wang, C.; Zhang, W.; Yang, C. Convective Dimensionless Method for Measurement of Heat Generation in a Lithium Thionyl Chloride Battery. J. Electrochem. Soc. 2013, 160, A2027–A2032. [Google Scholar] [CrossRef]
- Bazinski, S.J.; Wang, X. Predicting Heat Generation in a Lithium-Ion Pouch Cell through Thermography and the Lumped Capacitance Model. J. Power Sources 2016, 305, 97–105. [Google Scholar] [CrossRef]
- Sheng, L.; Zhang, Z.; Su, L.; Zhang, H.; Zhang, H.; Li, K.; Fang, Y.; Ye, W. A Calibration Calorimetry Method to Investigate the Thermal Characteristics of a Cylindrical Lithium-Ion Battery. Int. J. Therm. Sci. 2021, 165, 106891. [Google Scholar] [CrossRef]
- Chen, K.; Unsworth, G.; Li, X. Measurements of Heat Generation in Prismatic Li-Ion Batteries. J. Power Sources 2014, 261, 28–37. [Google Scholar] [CrossRef]
- Drake, S.J.; Martin, M.; Wetz, D.A.; Ostanek, J.K.; Miller, S.P.; Heinzel, J.M.; Jain, A. Heat Generation Rate Measurement in a Li-Ion Cell at Large C-Rates through Temperature and Heat Flux Measurements. J. Power Sources 2015, 285, 266–273. [Google Scholar] [CrossRef]
- Liu, G.; Ouyang, M.; Lu, L.; Li, J.; Han, X. Analysis of the Heat Generation of Lithium-Ion Battery during Charging and Discharging Considering Different Influencing Factors. J. Therm. Anal. Calorim. 2014, 116, 1001–1010. [Google Scholar] [CrossRef]
- Osswald, P.J.; del Rosario, M.; Garche, J.; Jossen, A.; Hoster, H.E. Fast and Accurate Measurement of Entropy Profiles of Commercial Lithium-Ion Cells. Electrochim. Acta 2015, 177, 270–276. [Google Scholar] [CrossRef]
- Li, Y.; Liu, K.; Foley, A.M.; Zülke, A.; Berecibar, M.; Nanini-Maury, E.; Van Mierlo, J.; Hoster, H.E. Data-Driven Health Estimation and Lifetime Prediction of Lithium-Ion Batteries: A Review. Renew. Sustain. Energy Rev. 2019, 113, 109254. [Google Scholar] [CrossRef]
- Boulesteix, A.-L.; Schmid, M. Machine Learning versus Statistical Modeling. Biom. J. 2014, 56, 588–593. [Google Scholar] [CrossRef] [PubMed]
- Chandran, V.; Patil, C.K.; Karthick, A.; Ganeshaperumal, D.; Rahim, R.; Ghosh, A. State of Charge Estimation of Lithium-Ion Battery for Electric Vehicles Using Machine Learning Algorithms. World Electr. Veh. J. 2021, 12, 38. [Google Scholar] [CrossRef]
- Zhang, Q.; Yang, L.; Guo, W.; Qiang, J.; Peng, C.; Li, Q.; Deng, Z. A Deep Learning Method for Lithium-Ion Battery Remaining Useful Life Prediction Based on Sparse Segment Data via Cloud Computing System. Energy 2022, 241, 122716. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, X.; Chen, W.; Han, W.; Zhou, S.; Pecht, M. State of Health Prediction Based on Multi-Kernel Relevance Vector Machine and Whale Optimization Algorithm for Lithium-Ion Battery. Trans. Inst. Meas. Control. 2021, 01423312211042009. [Google Scholar] [CrossRef]
- Wang, J.; Deng, Z.; Li, J.; Peng, K.; Xu, L.; Guan, G.; Abudula, A. State of Health Trajectory Prediction Based on Multi-Output Gaussian Process Regression for Lithium-Ion Battery. Batteries 2022, 8, 134. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, L.; Yu, H.; Yang, X.; Zhang, T.; Chen, S.; Liang, F.; Wang, H.; Lu, X.; Yang, S.; et al. Early Prediction of the Health Conditions for Battery Cathodes Assisted by the Fusion of Feature Signal Analysis and Deep-Learning Techniques. Batteries 2022, 8, 151. [Google Scholar] [CrossRef]
- Afzal, A.; Bhutto, J.K.; Alrobaian, A.; Razak Kaladgi, A.; Khan, S.A. Modelling and Computational Experiment to Obtain Optimized Neural Network for Battery Thermal Management Data. Energies 2021, 14, 7370. [Google Scholar] [CrossRef]
- Liu, K.; Li, K.; Peng, Q.; Guo, Y.; Zhang, L. Data-Driven Hybrid Internal Temperature Estimation Approach for Battery Thermal Management. Complexity 2018, 2018, e9642892. [Google Scholar] [CrossRef] [Green Version]
- Hasan, M.M.; Ali Pourmousavi, S.; Jahanbani Ardakani, A.; Saha, T.K. A Data-Driven Approach to Estimate Battery Cell Temperature Using a Nonlinear Autoregressive Exogenous Neural Network Model. J. Energy Storage 2020, 32, 101879. [Google Scholar] [CrossRef]
- Zhu, S.; He, C.; Zhao, N.; Sha, J. Data-Driven Analysis on Thermal Effects and Temperature Changes of Lithium-Ion Battery. J. Power Sources 2021, 482, 228983. [Google Scholar] [CrossRef]
- Arora, S.; Shen, W.; Kapoor, A. Neural Network Based Computational Model for Estimation of Heat Generation in LiFePO4 Pouch Cells of Different Nominal Capacities. Comput. Chem. Eng. 2017, 101, 81–94. [Google Scholar] [CrossRef]
- Cao, R.; Zhang, X.; Yang, H.; Wang, C. Experimental Study on Heat Generation Characteristics of Lithium-Ion Batteries Using a Forced Convection Calorimetry Method. Appl. Therm. Eng. 2023, 219, 119559. [Google Scholar] [CrossRef]
- Zhang, J.; Huang, J.; Li, Z.; Wu, B.; Nie, Z.; Sun, Y.; An, F.; Wu, N. Comparison and Validation of Methods for Estimating Heat Generation Rate of Large-Format Lithium-Ion Batteries. J. Therm. Anal. Calorim. 2014, 117, 447–461. [Google Scholar] [CrossRef]
- Ge, M.-F.; Liu, Y.; Jiang, X.; Liu, J. A Review on State of Health Estimations and Remaining Useful Life Prognostics of Lithium-Ion Batteries. Measurement 2021, 174, 109057. [Google Scholar] [CrossRef]
- Zhang, G.; Eddy Patuwo, B.; Hu, M.Y. Forecasting with Artificial Neural Networks: The State of the Art. Int. J. Forecast. 1998, 14, 35–62. [Google Scholar] [CrossRef]
- An-na, W.; Yue, Z.; Yun-tao, H.; Yun-lu, L.I. A Novel Construction of SVM Compound Kernel Function. In Proceedings of the 2010 International Conference on Logistics Systems and Intelligent Management (ICLSIM), Harbin, China, 9–10 January 2010; Volume 3, pp. 1462–1465. [Google Scholar]
- Rodriguez, J.D.; Perez, A.; Lozano, J.A. Sensitivity Analysis of K-Fold Cross Validation in Prediction Error Estimation. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 569–575. [Google Scholar] [CrossRef]
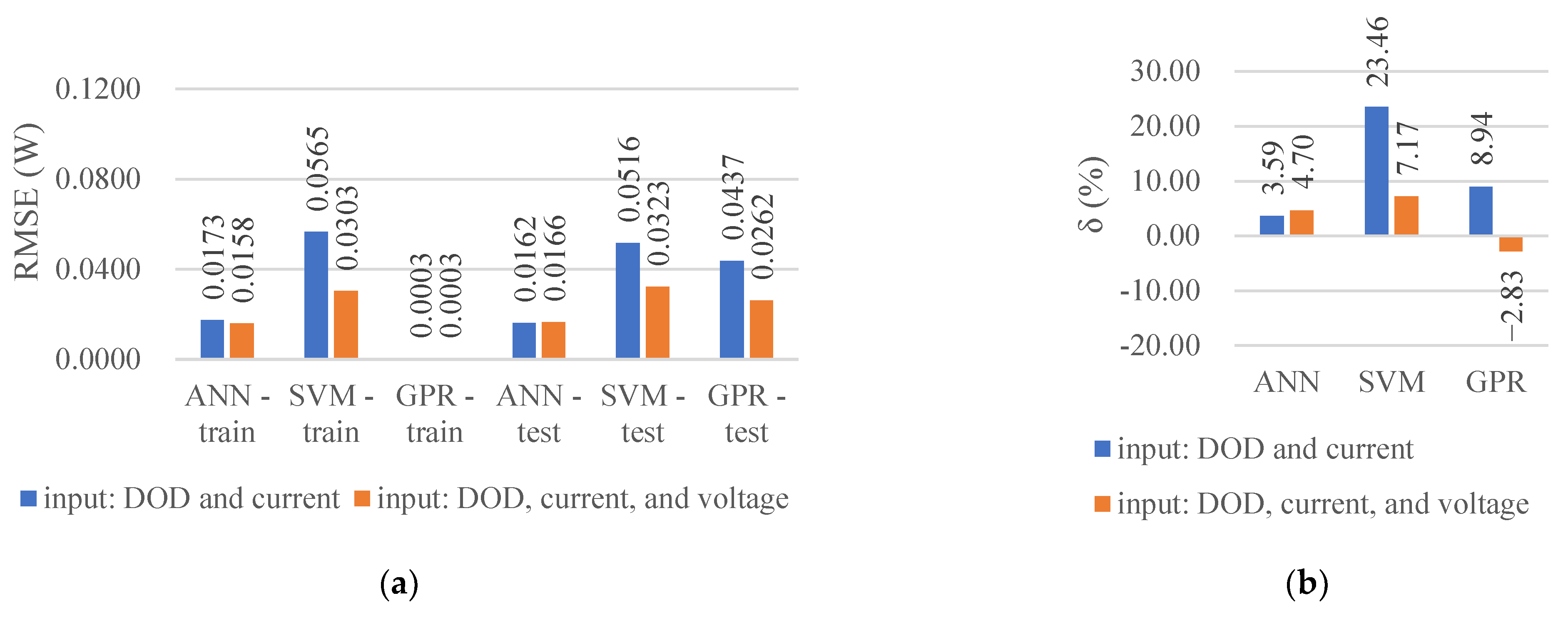

| No. | Operation Conditions | Do the Inputs Contain Discharge Voltage? | Training Data | Number of Training Samples | Number of Testing Samples | Interpolation/Extrapolation |
|---|---|---|---|---|---|---|
| 1 | 0.5 C | No | 0.75 C, 1 C, 1.25 C, and 1.5 C | 3820 | 978 | extrapolation |
| 2 | Yes | |||||
| 3 | 1 C | No | 0.5 C, 0.75 C, 1.25 C, and 1.5 C | 3836 | 962 | interpolation |
| 4 | Yes | |||||
| 5 | 1.5 C | No | 0.5 C, 0.75 C, 1 C, and 1.25 C | 3856 | 942 | extrapolation |
| 6 | Yes | |||||
| 7 | 20 °C | No | 25, 30, 35, 40, and 45 °C | 4930 | 933 | extrapolation |
| 8 | Yes | |||||
| 9 | 30 °C | No | 20, 25, 35, 40, and 45 °C | 4887 | 976 | interpolation |
| 10 | Yes | |||||
| 11 | 40 °C | No | 20, 25, 30, 35, and 40 °C | 4856 | 1007 | extrapolation |
| 12 | Yes |
| No. | Operation Conditions | Do the Inputs Contain Discharge Voltage? | ANN Architecture | Covariance Function of GPR | R2 | ||
|---|---|---|---|---|---|---|---|
| ANN | SVM | GPR | |||||
| 1 | 0.5 C | No | 1 hidden layer–5 neurons | Matern 3/2 | 0.95 | 0.53 | 0.67 |
| 2 | Yes | 1 hidden layer–8 neurons | Matern 3/2 | 0.95 | 0.82 | 0.88 | |
| 3 | 1 C | No | 1 hidden layer–3 neurons | Matern 5/2 | 0.99 | 0.96 | 0.97 |
| 4 | Yes | 1 hidden layer–5 neurons | Exponential | 0.98 | 0.98 | 0.98 | |
| 5 | 1.5 C | No | 1 hidden layer–10 neurons | Matern 3/2 | 0.89 | 0.94 | 0.72 |
| 6 | Yes | 1 hidden layer–4 neurons | Matern 3/2 | 0.94 | 0.93 | 0.82 | |
| No. | Operation Conditions | Do the Inputs Contain Discharge Voltage? | ANN Architecture | Covariance Function of GPR | R2 | ||
|---|---|---|---|---|---|---|---|
| ANN | SVM | GPR | |||||
| 7 | 20 °C | No | 1 hidden layer–15 neurons | Matern 3/2 | 0.99 | 0.90 | 0.98 |
| 8 | Yes | 1 hidden layer–5 neurons | Matern 3/2 | 0.99 | 0.96 | 0.97 | |
| 9 | 30 °C | No | 1 hidden layer–9 neurons | Matern 3/2 | 1.00 | 0.98 | 1.00 |
| 10 | Yes | 1 hidden layer–5 neurons | Rational quadratic | 1.00 | 0.99 | 1.00 | |
| 11 | 45 °C | No | 1 hidden layer–6 neurons | Matern 3/2 | 0.99 | 0.92 | 0.96 |
| 12 | Yes | 1 hidden layer–7 neurons | Matern 3/2 | 0.99 | 0.98 | 0.98 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, R.; Zhang, X.; Yang, H. Prediction of the Heat Generation Rate of Lithium-Ion Batteries Based on Three Machine Learning Algorithms. Batteries 2023, 9, 165. https://doi.org/10.3390/batteries9030165
Cao R, Zhang X, Yang H. Prediction of the Heat Generation Rate of Lithium-Ion Batteries Based on Three Machine Learning Algorithms. Batteries. 2023; 9(3):165. https://doi.org/10.3390/batteries9030165
Chicago/Turabian StyleCao, Renfeng, Xingjuan Zhang, and Han Yang. 2023. "Prediction of the Heat Generation Rate of Lithium-Ion Batteries Based on Three Machine Learning Algorithms" Batteries 9, no. 3: 165. https://doi.org/10.3390/batteries9030165
APA StyleCao, R., Zhang, X., & Yang, H. (2023). Prediction of the Heat Generation Rate of Lithium-Ion Batteries Based on Three Machine Learning Algorithms. Batteries, 9(3), 165. https://doi.org/10.3390/batteries9030165





