Accurate Prediction Approach of SOH for Lithium-Ion Batteries Based on LSTM Method
Abstract
:1. Introduction
2. Lithium-Ion Batteries Health Management
2.1. Factors Influencing SOH
- (1)
- Lithium metal deposition.
- (2)
- Decomposition of positive and negative electrode materials.
- (3)
- Growth of SEI film.
- (4)
- Decomposition of electrolyte.
- (5)
- Diaphragm blockage or disruption.
- (6)
- Dislodged positive and negative electrode materials.
2.2. Capacity Decay Simulation
3. Data Description
3.1. Lifetime Experimental Data
3.1.1. NASA Lithium Battery Life Experiment Data
3.1.2. CALCE Lithium-Ion Battery Life Test Data
3.2. Data Pre-Processing
4. Battery Health Status Prediction
4.1. Principle of RNN
4.2. LSTM Network
- (1)
- Calculation of the forget gate.
- (2)
- Calculation of the input gate.
- (3)
- Update of the internal state.
- (4)
- Calculation of the output gate.
4.3. Discussion and Analysis of Results
4.4. Open Issues
- The current research results of this paper can only make the LSTM curve predict the trend of battery health status. For the case of a high cycle number, it is probably impossible to accurately estimate the remaining capacity. In the following section, the mathematical fitting can be a method to find out the law of battery capacity decline in a high cycle number.
- In this paper, we used a NASA dataset and CALCE dataset. This can basically support the validation of the proposed method at present, but it may also have some limitations. We will further update the LSTM network model in this paper using other datasets from the literature in our continued studies.
- The LSTM model presented in this paper predicts the battery life, but it has not given an evaluation of the battery health status or distinguished whether the battery is suitable. Therefore, batteries in different health states will be classified and evaluated in future research.
5. Conclusions
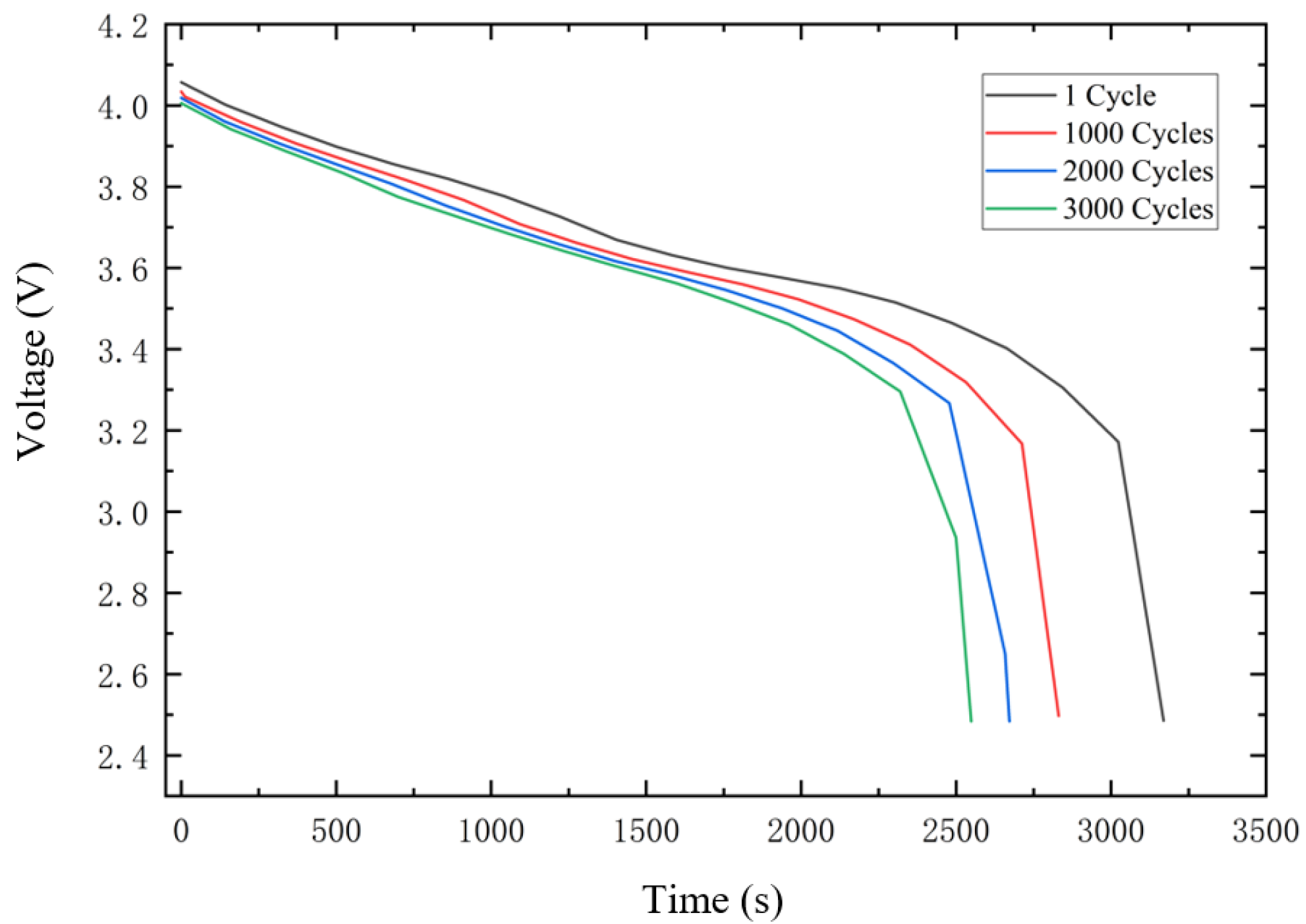
- The hazards of the degradation mechanisms associated with lithium-ion batteries are specifically described, and relevant measures to slow down or avoid degradation of the battery health state are presented. Parasitic side reactions occurring at the negative electrode during charging, which lead to a reduction of recyclable lithium, are mainly considered in the capacity degradation model. The cell discharge voltage and capacity changes are investigated for different cycle counts, with a larger potential drop along the SEI layer at the negative membrane compared to the collector and a faster reduction of electrolyte volume fraction at this location.
- The improved structure and implementation principle of LSTM is compared with RNN, which is more suitable for predicting of long-time sequences. The LSTM network model is constructed for the battery capacity sequence as a reference indicator of SOH and is experimentally validated using pre-processed battery life cycle datasets from NASA and CALCE datasets. The experimental results for different datasets show that the LSTM approach has high accuracy for the direct prediction of SOH. Although the ability to predict the temperature at the stage when the battery capacity fluctuates is reduced, the trend of the battery capacity degradation can be accurately predicted. The LSTM model shows good adaptive performance.
- In this paper, an accurate prediction approach of SOH for lithium-ion batteries based on the LSTM method has been proposed. It can solve the problem of accurately predicting the SOH of lithium-ion batteries, which is a crucial factor in determining the RUL of the batteries. The proposed approach can help users to better manage and maintain their batteries, avoid potential safety hazards, and optimize battery performance and efficiency. Future applications are expected to focus on users such as electric vehicle manufacturers, battery maintenance and repair service providers, and energy storage system operators.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dai, Q.; Kelly, J.C.; Gaines, L.; Wang, M. Life Cycle Analysis of Lithium-Ion Batteries for Automotive Applications. Batteries 2019, 5, 48. [Google Scholar] [CrossRef] [Green Version]
- Chen, Z.; Xu, K.; Wei, J.; Dong, G. Voltage fault detection for lithium-ion battery pack using local outlier factor. Measurement 2019, 146, 544–556. [Google Scholar] [CrossRef]
- Rauf, H.; Khalid, M.; Arshad, N. Machine learning in state of health and remaining useful life estimation: Theoretical and technological development in battery degradation modelling. Renew. Sust. Energy Rev. 2022, 156, 111903. [Google Scholar] [CrossRef]
- Goh, H.H.; Lan, Z.; Zhang, D.; Dai, W.; Kurniawan, T.A.; Goh, K.C. Estimation of the state of health (SOH) of batteries using discrete curvature feature extraction. J. Energy Storage 2022, 50, 104646. [Google Scholar] [CrossRef]
- Chen, L.; Lu, Z.; Lin, W.; Li, J.; Pan, H. A new state-of-health estimation method for lithium-ion batteries through the intrinsic relationship between ohmic internal resistance and capacity. Measurement 2018, 116, 586–595. [Google Scholar] [CrossRef]
- Li, X.; Ding, Q.; Sun, J.-Q. Remaining useful life estimation in prognostics using deep convolution neural networks. Reliab. Eng. Syst. Saf. 2018, 172, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Hu, C.; Ye, H.; Jain, G.; Schmidt, C. Remaining useful life assessment of lithium-ion batteries in implantable medical devices. J. Power. Sources 2018, 375, 118–130. [Google Scholar] [CrossRef]
- Wang, D.; Kong, J.-Z.; Zhao, Y.; Tsui, K.-L. Piecewise model based intelligent prognostics for state of health prediction of rechargeable batteries with capacity regeneration phenomena. Measurement 2019, 147, 106836. [Google Scholar] [CrossRef]
- Lin, H.; Kang, L.; Xie, D.; Linghu, J.; Li, J. Online state-of-health estimation of lithium-ion battery based on incremental capacity curve and BP neural network. Batteries 2022, 8, 29. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, S.; Chen, T.; Huang, L. State of Health Assessment of Lithium-ion Batteries Based on Deep Gaussian Process Regression Considering Heterogeneous Features. J. Energy Storage 2023, 61, 106797. [Google Scholar] [CrossRef]
- Yu, J. State of health prediction of lithium-ion batteries: Multiscale logic regression and gaussian process regression ensemble. Reliab. Eng. Syst. Saf. 2018, 174, 82–95. [Google Scholar] [CrossRef]
- Zhang, W.; Li, X.; Li, X. Deep learning-based prognostic approach for lithium-ion batteries with adaptive time-series prediction and on-line validation. Measurement 2020, 164, 108052. [Google Scholar] [CrossRef]
- Richardson, R.R.; Osborne, M.A.; Howey, D.A. Gaussian process regression for forecasting battery state of health. J. Power Sources 2017, 357, 209–219. [Google Scholar] [CrossRef]
- Xu, X.; Chen, N. A state-space-based prognostics model for lithium-ion battery degradation. Reliab. Eng. Syst. Saf. 2017, 159, 47–57. [Google Scholar] [CrossRef]
- Yang, J.-H.; Chen, K.-C. Evaluation of Electrochemical Parameters for Cycle Aging LiCoO2 lithium-Ion Batteries by Quantifying the Incremental Capacity Curve. J. Electrochem. Soc. 2022, 169, 020517. [Google Scholar] [CrossRef]
- Wei, J.; Dong, G.; Chen, Z. Remaining useful life prediction and state of health diagnosis for lithium-ion batteries using particle filter and support vector regression. IEEE Trans. Industr. Electron. 2018, 65, 5634–5643. [Google Scholar] [CrossRef]
- Li, X.; Zhang, W.; Xu, N.-X.; Ding, Q. Deep learning-based machinery fault diagnostics with domain adaptation across sensors at different places. IEEE Trans. Industr. Electron. 2020, 67, 6785–6794. [Google Scholar] [CrossRef]
- Zhang, W.; Li, X.; Ding, Q. Deep residual learning-based fault diagnosis method for rotating machinery. ISA Trans. 2019, 95, 295–305. [Google Scholar] [CrossRef]
- Zhang, W.; Li, X.; Jia, X.-D.; Ma, H.; Luo, Z.; Li, X. Machinery fault diagnosis with imbalanced data using deep generative adversarial networks. Measurement 2020, 152, 107377. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, X.-Q.; Chen, X.; Zhu, G.-L.; Yan, C.; Huang, J.-Q.; Peng, H.-J. A generalizable, data-driven online approach to forecast capacity degradation trajectory of lithium batteries. J. Energy Chem. 2022, 68, 548–555. [Google Scholar] [CrossRef]
- Li, X.; Zhang, W.; Ding, Q.; Li, X. Diagnosing rotating machines with weakly supervised data using deep transfer learning. IEEE Trans. Industr. Inf. 2019, 16, 1688–1697. [Google Scholar] [CrossRef]
- Wu, J.; Wang, Y.; Zhang, X.; Chen, Z. A novel state of health estimation method of li-ion battery using group method of data handling. J. Power Sources 2016, 327, 457–464. [Google Scholar] [CrossRef]
- Ma, Y.; Shan, C.; Gao, J.; Chen, H. A novel method for state of health estimation of lithium-ion batteries based on improved LSTM and health indicators extraction. Appl. Energy 2022, 251, 123973. [Google Scholar] [CrossRef]
- Chang, Y.; Fang, H.; Zhang, Y. A new hybrid method for the prediction of the remaining useful life of a lithium-ion battery. Appl. Energy 2017, 206, 1564–1578. [Google Scholar] [CrossRef]
- Li, X.; Zhang, W.; Ding, Q. Deep learning-based remaining useful life estimation of bearings using multi-scale feature extraction. Reliab. Eng. Syst. Saf. 2019, 182, 208–218. [Google Scholar] [CrossRef]
- Li, T.; Gao, Y.; Wang, K.; Guo, S.; Liu, H.; Kang, H. Diagnostic assessment of deep learning algorithms for diabetic retinopathy screening. Inf. Sci. 2019, 501, 511–522. [Google Scholar]
- Sikorska, J.Z.; Hodkiewicz, M.; Ma, L. Prognostic modelling options for remaining useful life estimation by industry. Mech. Syst. Signal Process. 2011, 25, 1803–1836. [Google Scholar] [CrossRef]
- Wu, J.; Zhang, C.; Chen, Z. An online method for lithium-ion battery remaining useful life estimation using importance sampling and neural networks. Appl. Energy 2016, 173, 134–140. [Google Scholar] [CrossRef]
- Sbarufatti, C.; Corbetta, M.; Giglio, M.; Cadini, F. Adaptive prognosis of lithium-ion batteries based on the combination of particle filters and radial basis function neural networks. J. Power Sources 2017, 344, 128–140. [Google Scholar] [CrossRef]
- Chemali, E.; Kollmeyer, P.J.; Preindl, M.; Ahmed, R.; Emadi, A. Long short-term memory networks for accurate state-of-charge estimation of li-ion batteries. IEEE Trans. Industr. Electron. 2018, 65, 6730–6739. [Google Scholar] [CrossRef]
- Li, X.; Zhang, W.; Ding, Q. Understanding and improving deep learning-based rolling bearing fault diagnosis with attention mechanism. Signal Process. 2019, 161, 136–154. [Google Scholar] [CrossRef]
- Li, X.; Zhang, W.; Ding, Q. Cross-domain fault diagnosis of rolling element bearings using deep generative neural networks. IEEE Trans. Industr. Electron. 2019, 66, 5525–5534. [Google Scholar] [CrossRef]
- Li, X.; Zhang, W.; Ding, Q.; Sun, J.-Q. Multi-layer domain adaptation method for rolling bearing fault diagnosis. Signal Process. 2019, 157, 180–197. [Google Scholar] [CrossRef] [Green Version]
- Bouktif, S.; Fiaz, A.; Ouni, A.; Serhani, M.A. Multi-Sequence LSTM-RNN Deep Learning and Metaheuristics for Electric Load Forecasting. Energies 2020, 13, 391. [Google Scholar] [CrossRef] [Green Version]












| Aging Factors | Degradation Mechanisms | Degradation Model |
|---|---|---|
| Number of cycles | SEI membrane growth | Increased impedance and loss of lithium storage |
| Temperature | Electrolyte decomposition, SEI film growth, electroplating, lithium dendrite formation | Increased impedance, loss of lithium storage, loss of active material |
| Overcharge and overdischarge | SEI film growth, electrolyte decomposition, graphite shedding, electroplating, lithium dendrite formation, transition metal dissolution, collector corrosion | Increased impedance, loss of lithium storage, loss of active material |
| Charge and discharge rate | SEI film growth, graphite shedding, plating, lithium dendrite formation, electrode particle cracking | Increased impedance, loss of lithium storage, loss of active material |
| Mechanical stress | SEI film growth, electrode particle cracking | Increased impedance, loss of lithium storage, loss of active material |
| Prediction Starting Point | RMSE | MAPE | |
|---|---|---|---|
| CS-35 | 40% | 0.05783 | 5.75% |
| 50% | 0.06409 | 7.00% | |
| 60% | 0.08223 | 9.58% | |
| CS-36 | 40% | 0.07342 | 11.61% |
| 50% | 0.09677 | 14.71% | |
| 60% | 0.09911 | 17.79% | |
| CS-37 | 40% | 0.06182 | 8.27% |
| 50% | 0.09898 | 13.01% | |
| 60% | 0.10735 | 15.21% | |
| CS-38 | 40% | 0.06039 | 6.39% |
| 50% | 0.07191 | 8.84% | |
| 60% | 0.08088 | 9.98% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Ji, T.; Yu, S.; Liu, G. Accurate Prediction Approach of SOH for Lithium-Ion Batteries Based on LSTM Method. Batteries 2023, 9, 177. https://doi.org/10.3390/batteries9030177
Zhang L, Ji T, Yu S, Liu G. Accurate Prediction Approach of SOH for Lithium-Ion Batteries Based on LSTM Method. Batteries. 2023; 9(3):177. https://doi.org/10.3390/batteries9030177
Chicago/Turabian StyleZhang, Lijun, Tuo Ji, Shihao Yu, and Guanchen Liu. 2023. "Accurate Prediction Approach of SOH for Lithium-Ion Batteries Based on LSTM Method" Batteries 9, no. 3: 177. https://doi.org/10.3390/batteries9030177
APA StyleZhang, L., Ji, T., Yu, S., & Liu, G. (2023). Accurate Prediction Approach of SOH for Lithium-Ion Batteries Based on LSTM Method. Batteries, 9(3), 177. https://doi.org/10.3390/batteries9030177









