Lithium-Ion Battery State-of-Charge Estimation Using Electrochemical Model with Sensitive Parameters Adjustment
Abstract
1. Introduction
- (1)
- A simplification of the P2D model, SPME, is combined with PF for Li-ion battery SOC estimation, which involves a trade-off of both the modeling accuracy and simplicity.
- (2)
- The elementary effect test (EET) is used for the parameter sensitivity analysis (SA) of EM to improve the calculational efficiency, and only highly sensitive parameters are identified by PSO.
- (3)
- The performance of the proposed method is validated on three different driving cycles and compared with the EKF and the SPME without PF.
2. Electrochemical Model
2.1. P2D Model
- (1)
- Electrolyte lithium ions diffusion equations in positive electrode, negative electrode, and separator according to Fick’s second law.
- (2)
- Solid phase lithium ions diffusion equations in electrodes due to Fick’s second law.
- (3)
- Electrolyte ohm equations in electrodes and separator.
- (4)
- Solid phase ohm equations in positive electrode and negative electrode.
- (5)
- Charge conservation equations, including positive electrode, negative electrode, and separator.
- (6)
- Butler–Volmer (BV) kinetic equations at the surface of particles in electrodes.
- (7)
2.2. SPM with Electrolyte Dynamics
- (1)
- The solid phase lithium ion concentration is uniformly distributed in each electrode along the spatial x-axis, i.e., it is assumed that and are constant on the coordinate x.
- (2)
- The exchange current density is replaced by its average value along the x-axis approximately, i.e., is assumed to be independent of x.
- (3)
- The moles of lithium ions in electrolyte and solid phases, , , are conserved in sum. The molar fluxes can be written as proportional to current density I thanks to the combination of this assumption and assumption (1).
- (4)
- The electrolyte activity coefficient is constant on the x-axis and can be approximated by . Besides, the electrolyte ionic conductivity is assumed to be constant.
3. Global Sensitivity Analysis and Parameter Identification
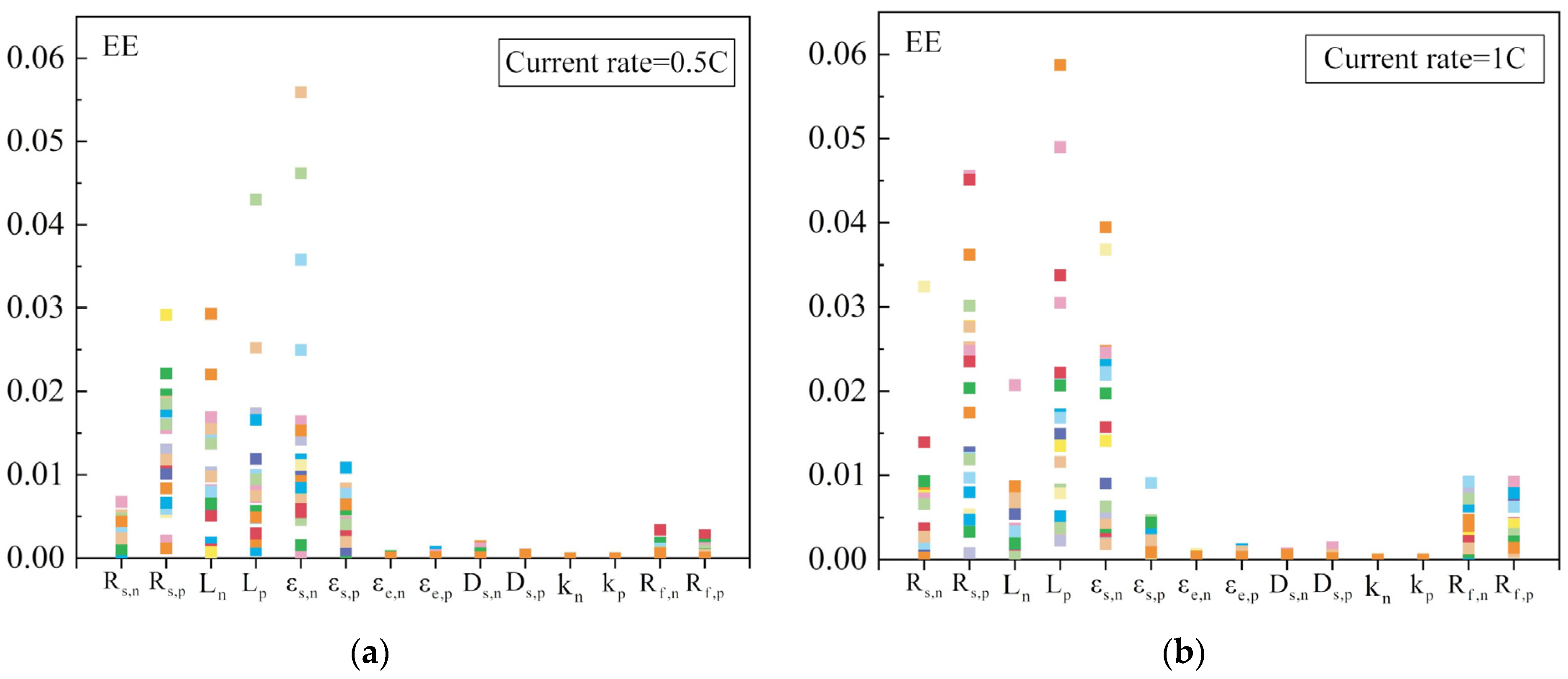
3.1. Global Sensitivity Analysis
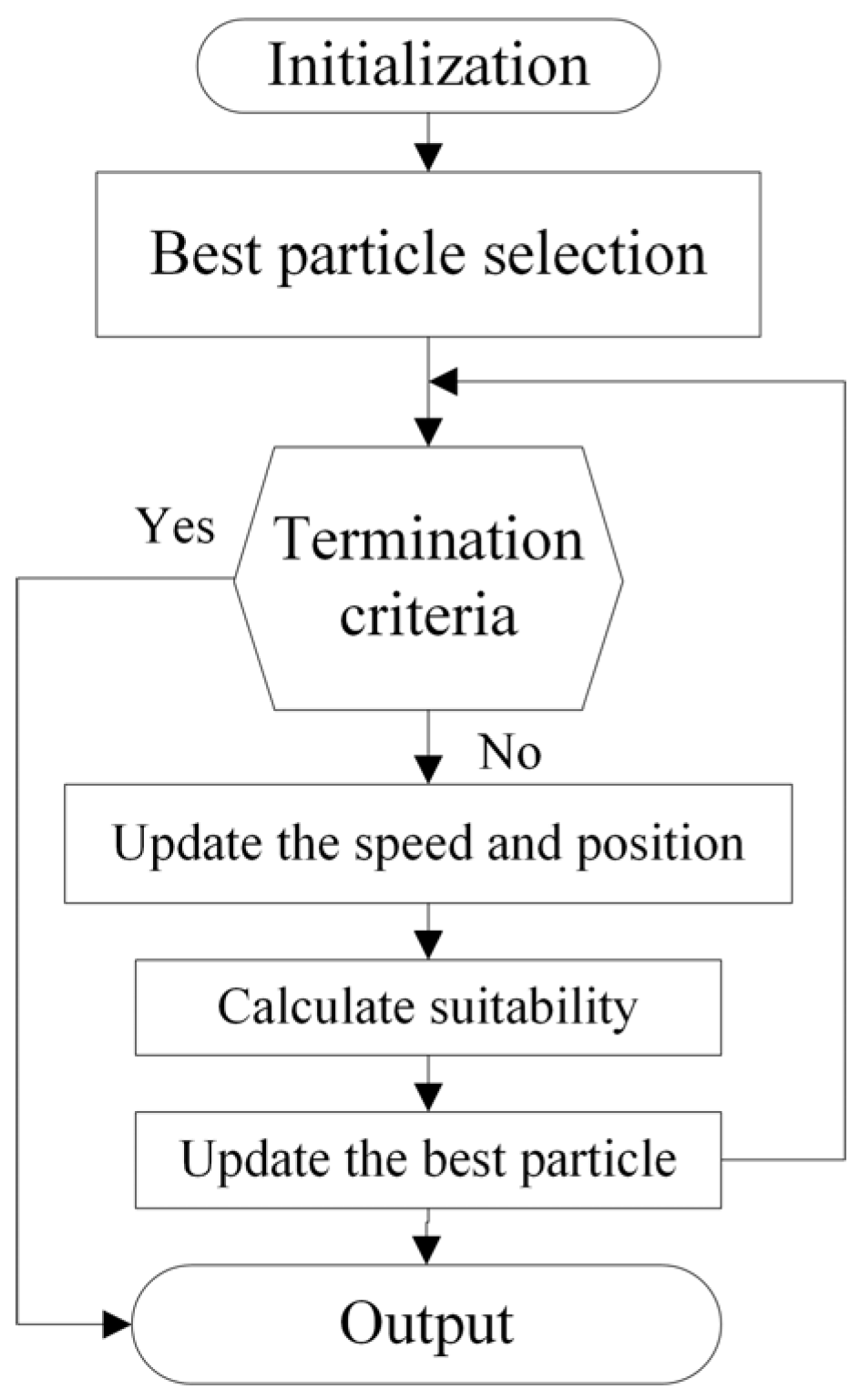
3.2. Parameter Identification Based on PSO
4. Li-Ion Battery SOC Estimation
4.1. Ampere-Hour Integration Method
4.2. Model-Based Method
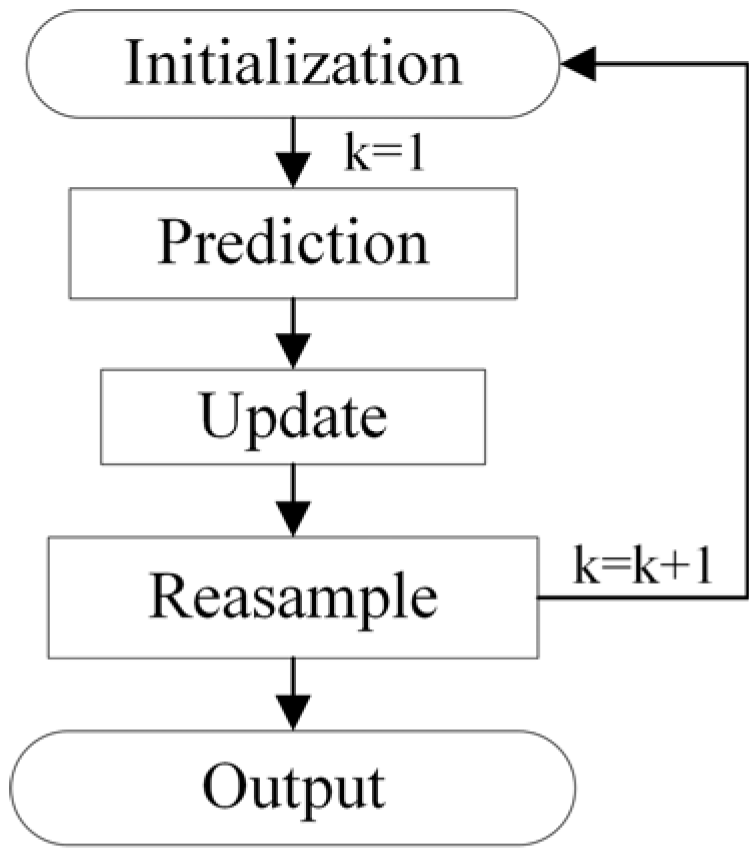
4.3. Particle Filter
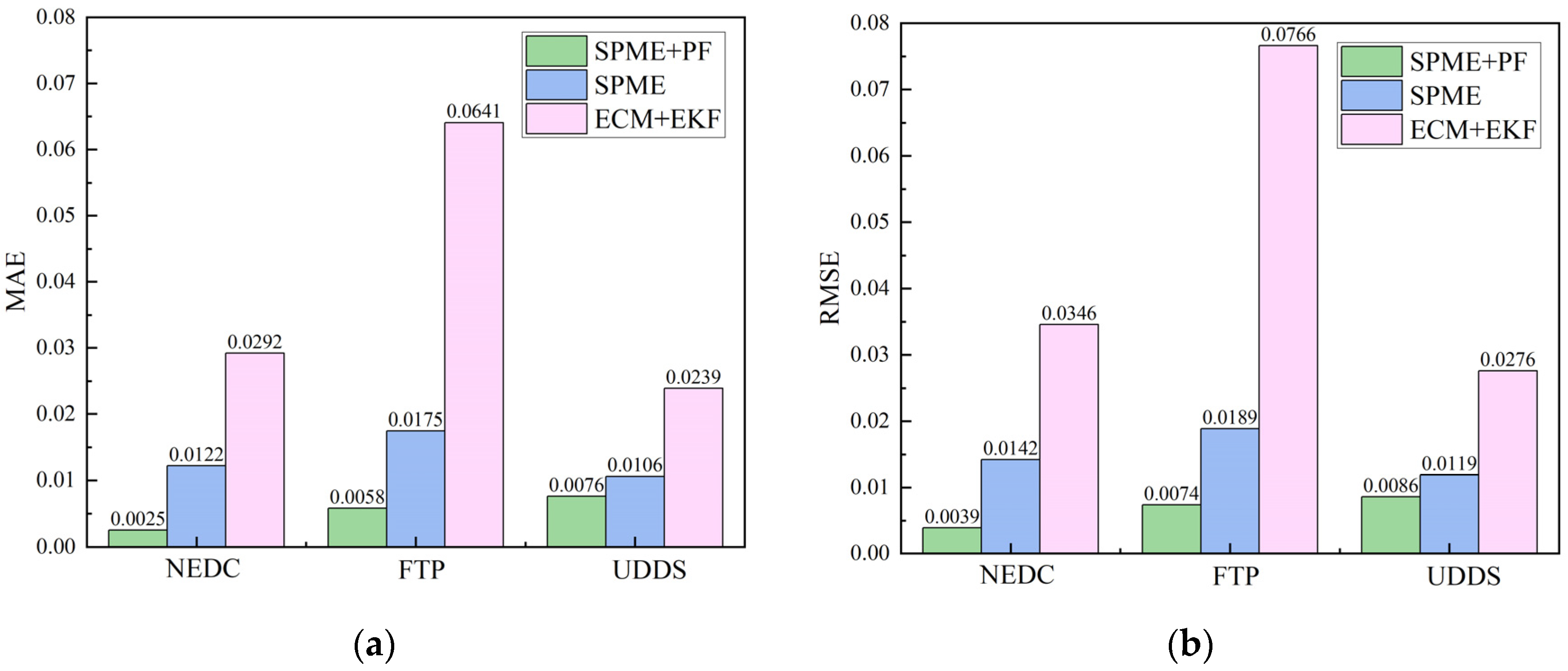
5. Validation and Discussion
5.1. Parameter Identification
5.2. Model Validation
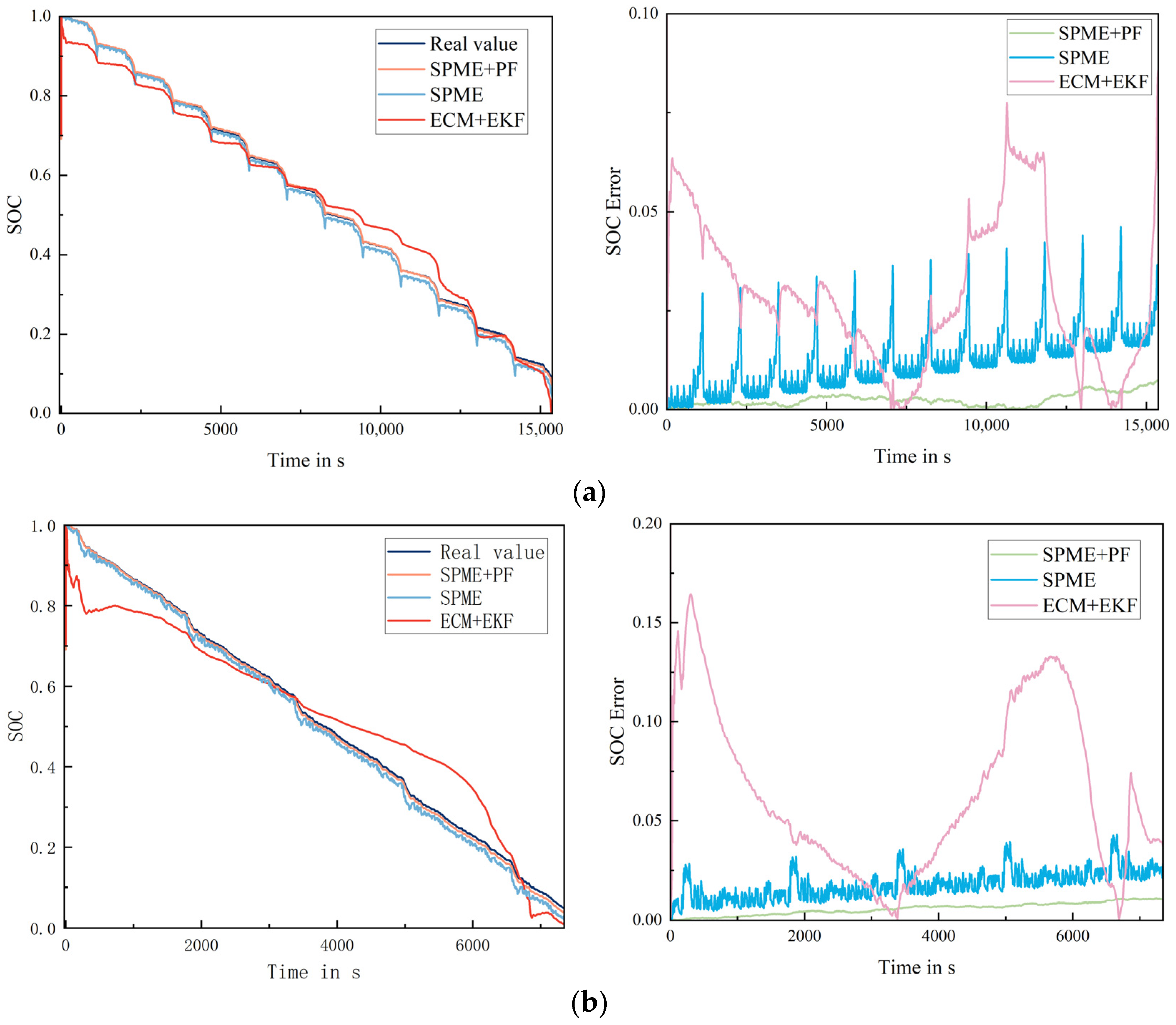
5.3. SOC Estimation Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Nomenclature of Parameters in EM. | |||
| volume fraction of active material | a | specific surface area of the active particles | |
| c | lithium-ions concentration | resistivity of the SEI film | |
| D | lithium-ions diffusion coefficient | V | terminal voltage of battery |
| lithium-ions transfer number | L | thickness of active material | |
| F | Faraday’s constant | S | area of electrode |
| I | external current density | average lithium-ions concentration | |
| electrolyte activity coefficient | EE | elementary effect | |
| z | state vector | y | output vector |
| r | coordinate axis along the radius of the solid-phase particle | x | coordinate axis along the battery |
| p | parameter | average value | |
| X | position of particle | V | velocity of particle |
| u | noice sequences of states | q | noice sequences of observations |
| P | position of personal best particle | G | position of global best particle |
| i | current density of active material | average concentration flux of lithium-ions | |
| active particles molar flux of lithium-ions | Subscripts | ||
| radius of solid particles | n | negative electrode | |
| electrolyte ionic conductivity | p | positive electrode | |
| electrical potential | a | anode | |
| R | molar gas constant | c | cathode |
| T | battery temperature | s | solid phase |
| solid phase conductivity | e | electrolyte | |
| exchange current density | ss | surface of solid particles | |
| reaction transfer coefficients | f | filler | |
| electrochemical reactions overpotential | 0% | SOC = 0% | |
| k | electrochemical reaction rate | 100% | SOC = 100% |
| maximum solid phase lithium-ions concentration | Superscripts | ||
| open circuit potential | eff | effective | |
| s | deviation value | derivatioon | |
| w | weights | + | predicted value |
References
- Ding, Y.; Cano, Z.P.; Yu, A.; Lu, J.; Chen, Z. Automotive Li-Ion Batteries: Current Status and Future Perspectives. Electrochem. Energy Rev. 2019, 2, 1–28. [Google Scholar] [CrossRef]
- Armand, M.; Tarascon, J.-M. Building better batteries. Nature 2008, 451, 652–657. [Google Scholar] [CrossRef] [PubMed]
- Chaturvedi, N.A.; Klein, R.; Christensen, J.; Ahmed, J.; Kojic, A. Algorithms for Advanced Battery-Management Systems: Modeling, estimation, and control challenges for lithium-ion batteries. IEEE Control Syst. 2010, 30, 49–68. [Google Scholar] [CrossRef]
- Lin, X.; Kim, Y.; Mohan, S.; Siegel, J.B.; Stefanopoulou, A.G. Modeling and Estimation for Advanced Battery Management. Annu. Rev. Control. Robot. Auton. Syst. 2019, 2, 393–426. [Google Scholar] [CrossRef]
- Liu, L.; Feng, X.; Rahe, C.; Li, W.; Lu, L.; He, X.; Sauer, D.U.; Ouyang, M. Internal short circuit evaluation and corresponding failure mode analysis for lithium-ion batteries. J. Energy Chem. 2021, 61, 269–280. [Google Scholar] [CrossRef]
- Shen, M.; Gao, Q. A review on battery management system from the modeling efforts to its multiapplication and integration. Int. J. Energy Res. 2019, 43, 5042–5075. [Google Scholar] [CrossRef]
- Ng, K.S.; Moo, C.-S.; Chen, Y.-P.; Hsieh, Y.-C. Enhanced coulomb counting method for estimating state-of-charge and state-of-health of lithium-ion batteries. Appl. Energy 2009, 86, 1506–1511. [Google Scholar] [CrossRef]
- Yang, N.; Zhang, X.; Li, G. State of charge estimation for pulse discharge of a LiFePO4 battery by a revised Ah counting. Electrochimica Acta 2015, 151, 63–71. [Google Scholar] [CrossRef]
- Chaoui, H.; Mandalapu, S. Comparative Study of Online Open Circuit Voltage Estimation Techniques for State of Charge Estimation of Lithium-Ion Batteries. Batteries 2017, 3, 12. [Google Scholar] [CrossRef]
- Xing, Y.; He, W.; Pecht, M.; Tsui, K.L. State of charge estimation of lithium-ion batteries using the open-circuit voltage at various ambient temperatures. Appl. Energy 2014, 113, 106–115. [Google Scholar] [CrossRef]
- Wei, Z.; Zhao, J.; Zou, C.; Lim, T.M.; Tseng, K.J. Comparative study of methods for integrated model identification and state of charge estimation of lithium-ion battery. J. Power Sources 2018, 402, 189–197. [Google Scholar] [CrossRef]
- Meng, J.; Luo, G.; Gao, F. Lithium Polymer Battery State-of-Charge Estimation Based on Adaptive Unscented Kalman Filter and Support Vector Machine. IEEE Trans. Power Electron. 2015, 31, 2226–2238. [Google Scholar] [CrossRef]
- Tulsyan, A.; Tsai, Y.; Gopaluni, R.B.; Braatz, R.D. State-of-charge estimation in lithium-ion batteries: A particle filter approach. J. Power Sources 2016, 331, 208–223. [Google Scholar] [CrossRef]
- Lotfi, N.; Landers, R.G.; Li, J.; Park, J. Reduced-Order Electrochemical Model-Based SOC Observer With Output Model Uncertainty Estimation. IEEE Trans. Control. Syst. Technol. 2016, 25, 1217–1230. [Google Scholar] [CrossRef]
- Allam, A.; Onori, S. An Interconnected Observer for Concurrent Estimation of Bulk and Surface Concentration in the Cathode and Anode of a Lithium-ion Battery. IEEE Trans. Ind. Electron. 2018, 65, 7311–7321. [Google Scholar] [CrossRef]
- Liu, Y.; Ma, R.; Pang, S.; Xu, L.; Zhao, D.; Wei, J.; Huangfu, Y.; Gao, F. A Nonlinear Observer SOC Estimation Method Based on Electrochemical Model for Lithium-Ion Battery. IEEE Trans. Ind. Appl. 2020, 57, 1094–1104. [Google Scholar] [CrossRef]
- Tran, M.-K.; DaCosta, A.; Mevawalla, A.; Panchal, S.; Fowler, M. Comparative Study of Equivalent Circuit Models Performance in Four Common Lithium-Ion Batteries: LFP, NMC, LMO, NCA. Batteries 2021, 7, 51. [Google Scholar] [CrossRef]
- Yang, J.; Cai, Y.; Pan, C.; Mi, C. A novel resistor-inductor network-based equivalent circuit model of lithium-ion batteries under constant-voltage charging condition. Appl. Energy 2019, 254, 113726. [Google Scholar] [CrossRef]
- Du, X.; Meng, J.; Zhang, Y.; Huang, X.; Wang, S.; Liu, P.; Liu, T. An Information Appraisal Procedure: Endows Reliable Online Parameter Identification to Lithium-Ion Battery Model. IEEE Trans. Ind. Electron. 2021, 69, 5889–5899. [Google Scholar] [CrossRef]
- Hentunen, A.; Lehmuspelto, T.; Suomela, J. Time-Domain Parameter Extraction Method for Thévenin-Equivalent Circuit Battery Models. IEEE Trans. Energy Convers. 2014, 29, 558–566. [Google Scholar] [CrossRef]
- Wei, Z.; Zou, C.; Leng, F.; Soong, B.H.; Tseng, K.-J. Online Model Identification and State-of-Charge Estimate for Lithium-Ion Battery with a Recursive Total Least Squares-Based Observer. IEEE Trans. Ind. Electron. 2018, 65, 1336–1346. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, L.Y.; Li, X.; Chen, W.; Yin, G.G.; Jiang, J. Robust and Adaptive Estimation of State of Charge for Lithium-Ion Batteries. IEEE Trans. Ind. Electron. 2015, 62, 4948–4957. [Google Scholar] [CrossRef]
- Meng, J.; Luo, G.; Ricco, M.; Swierczynski, M.; Stroe, D.-I.; Teodorescu, R. Overview of Lithium-Ion Battery Modeling Methods for State-of-Charge Estimation in Electrical Vehicles. Appl. Sci. 2018, 8, 659. [Google Scholar] [CrossRef]
- Doyle, M.; Fuller, T.F.; Newman, J. Modeling of Galvanostatic Charge and Discharge of the Lithium/Polymer/Insertion Cell. J. Electrochem. Soc. 1993, 140, 1526–1533. [Google Scholar] [CrossRef]
- Fuller, T.F.; Doyle, M.; Newman, J. Simulation and Optimization of the Dual Lithium Ion Insertion Cell. J. Electrochem. Soc. 1994, 141, 1–10. [Google Scholar] [CrossRef]
- Zou, C.; Manzie, C.; Nesic, D. A Framework for Simplification of PDE-Based Lithium-Ion Battery Models. IEEE Trans. Control. Syst. Technol. 2015, 24, 1594–1609. [Google Scholar] [CrossRef]
- Kwon, K.H.; Shin, C.B.; Kang, T.H.; Kim, C.-S. A two-dimensional modeling of a lithium-polymer battery. J. Power Sources 2006, 163, 151–157. [Google Scholar] [CrossRef]
- Martínez-Rosas, E.; Vasquez-Medrano, R.; Flores-Tlacuahuac, A. Modeling and simulation of lithium-ion batteries. Comput. Chem. Eng. 2011, 35, 1937–1948. [Google Scholar] [CrossRef]
- Reimers, J.N. Algorithmic Improvements and PDE Decoupling, for the Simulation of Porous Electrode Cells. J. Electrochem. Soc. 2013, 160, A811–A818. [Google Scholar] [CrossRef]
- Torchio, M.; Magni, L.; Gopaluni, R.B.; Braatz, R.D.; Raimondo, D.M. LIONSIMBA: A Matlab Framework Based on a Finite Volume Model Suitable for Li-Ion Battery Design, Simulation, and Control. J. Electrochem. Soc. 2016, 163, A1192–A1205. [Google Scholar] [CrossRef]
- Marcicki, J.; Canova, M.; Conlisk, A.T.; Rizzoni, G. Design and parametrization analysis of a reduced-order electrochemical model of graphite/LiFePO4 cells for SOC/SOH estimation. J. Power Sources 2013, 237, 310–324. [Google Scholar] [CrossRef]
- Haran, B.S.; Popov, B.N.; White, R.E. Determination of the hydrogen diffusion coefficient in metal hydrides by impedance spectroscopy. J. Power Sources 1998, 75, 56–63. [Google Scholar] [CrossRef]
- Wang, Y.; Fang, H.; Sahinoglu, Z.; Wada, T.; Hara, S. Adaptive Estimation of the State of Charge for Lithium-Ion Batteries: Nonlinear Geometric Observer Approach. IEEE Trans. Control. Syst. Technol. 2014, 23, 948–962. [Google Scholar] [CrossRef]
- Di Domenico, D.; Stefanopoulou, A.; Fiengo, G. Lithium-Ion Battery State of Charge and Critical Surface Charge Estimation Using an Electrochemical Model-Based Extended Kalman Filter. J. Dyn. Syst. Meas. Control. 2010, 132, 061302. [Google Scholar] [CrossRef]
- Santhanagopalan, S.; White, R.E. Online estimation of the state of charge of a lithium ion cell. J. Power Sources 2006, 161, 1346–1355. [Google Scholar] [CrossRef]
- Lai, Q.; Ahn, H.J.; Kim, Y.; Na Kim, Y.; Lin, X. New data optimization framework for parameter estimation under uncertainties with application to lithium-ion battery. Appl. Energy 2021, 295, 117034. [Google Scholar] [CrossRef]
- Bonfitto, A.; Feraco, S.; Tonoli, A.; Amati, N.; Monti, F. Estimation Accuracy and Computational Cost Analysis of Artificial Neural Networks for State of Charge Estimation in Lithium Batteries. Batteries 2019, 5, 47. [Google Scholar] [CrossRef]
- Santhanagopalan, S.; Guo, Q.; White, R.E. Parameter Estimation and Model Discrimination for a Lithium-Ion Cell. J. Electrochem. Soc. 2007, 154, A198. [Google Scholar] [CrossRef]
- Thirugnanam, K.; Saini, H.; Kumar, P. Mathematical modeling of Li-ion battery for charge/discharge rate and capacity fading characteristics using genetic algorithm approach. In Proceedings of the 2012 IEEE Transportation Electrification Conference and Expo, ITEC, Dearborn, MI, USA, 18–20 June 2012. [Google Scholar] [CrossRef]
- Hu, Y.; Yurkovich, S.; Guezennec, Y.; Yurkovich, B. Electro-thermal battery model identification for automotive applications. J. Power Sources 2011, 196, 449–457. [Google Scholar] [CrossRef]
- Shekar, A.C.; Anwar, S. Real-Time State-of-Charge Estimation via Particle Swarm Optimization on a Lithium-Ion Electrochemical Cell Model. Batteries 2019, 5, 4. [Google Scholar] [CrossRef]
- Rahman, A.; Anwar, S.; Izadian, A. Electrochemical model parameter identification of a lithium-ion battery using particle swarm optimization method. J. Power Sources 2016, 307, 86–97. [Google Scholar] [CrossRef]
- Xiong, R.; Li, L.; Li, Z.; Yu, Q.; Mu, H. An electrochemical model based degradation state identification method of Lithium-ion battery for all-climate electric vehicles application. Appl. Energy 2018, 219, 264–275. [Google Scholar] [CrossRef]
- Moura, S.J.; Chaturvedi, N.A.; Krstić, M. Adaptive Partial Differential Equation Observer for Battery State-of-Charge/State-of-Health Estimation Via an Electrochemical Model. J. Dyn. Syst. Meas. Control. 2013, 136, 011015. [Google Scholar] [CrossRef]
- Moura, S.J.; Argomedo, F.B.; Klein, R.; Mirtabatabaei, A.; Krstic, M. Battery State Estimation for a Single Particle Model With Electrolyte Dynamics. IEEE Trans. Control. Syst. Technol. 2016, 25, 453–468. [Google Scholar] [CrossRef]
- Zeng, X.; Xu, L.; Deng, Z.; Feng, F.; Hu, X. Global Sensitivity Analysis of Battery Single Particle Model Parameters. In Proceedings of the 2019 IEEE Vehicle Power and Propulsion Conference (VPPC), Hanoi, Vietnam, 14–17 October 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Meng, J.; Ricco, M.; Luo, G.; Swierczynski, M.; Stroe, D.-I.; Stroe, A.-I.; Teodorescu, R. An Overview and Comparison of Online Implementable SOC Estimation Methods for Lithium-Ion Battery. IEEE Trans. Ind. Appl. 2017, 54, 1583–1591. [Google Scholar] [CrossRef]
- Chen, D.; Meng, J.; Huang, H.; Wu, J.; Liu, P.; Lu, J.; Liu, T. An Empirical-Data Hybrid Driven Approach for Remaining Useful Life prediction of lithium-ion batteries considering capacity diving. Energy 2022, 245, 123222. [Google Scholar] [CrossRef]
- Meng, J.; Stroe, D.-I.; Ricco, M.; Luo, G.; Teodorescu, R. A Simplified Model-Based State-of-Charge Estimation Approach for Lithium-Ion Battery With Dynamic Linear Model. IEEE Trans. Ind. Electron. 2018, 66, 7717–7727. [Google Scholar] [CrossRef]





| Governing Equations | Boundary Conditions |
|---|---|
| Electrolyte Diffusion Equation | |
| Solid Phase Diffusion Equation | |
| Electrolyte Ohm Equation | |
| Solid Phase Ohm Equation | |
| Charge Conservation Equation | |
| BV Kinetic Equation | |
| Geometric Parameters | Unit |
|---|---|
| 1 | |
| 1 | |
| Performance Parameters | Unit |
| 1 | |
| Fixed Parameters | Unit |
| 1 |
| Category | Specification |
|---|---|
| Nominal capacity | 2.6 Ah |
| Nominal voltage | 3.6 V |
| Max. charging current | 2.6 A |
| Cut-off voltage | 4.2 V |
| Charging temperature | 0–45 °C |
| Discharging temperature | −10–55 °C |
| Weight | 45 g |
| Parameters | Unit | Negative | Separator | Positive |
|---|---|---|---|---|
| 0.0772 | 0.0747 | |||
| 1 | 0.5 | 0.5 | ||
| 1 | 0.5 | 0.45 | 0.5 | |
| 31,389 | 56,250 | |||
| 29,505.68 | 14,126.37 | |||
| 1200 | ||||
| 0.04211 | 0.03096 | |||
| 0.93 | ||||
| 1 | 0.363 | |||
| 96,487 | ||||
| 8.314 | ||||
| 298.15 | ||||
| Parameters | Unit | Negative | Positive |
|---|---|---|---|
| m | |||
| 1 | 0.5052 | 0.55 | |
| 1 | 0.4382 | 0.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Meng, J.; Peng, Q.; Liu, T.; Zeng, X.; Chen, G.; Li, Y. Lithium-Ion Battery State-of-Charge Estimation Using Electrochemical Model with Sensitive Parameters Adjustment. Batteries 2023, 9, 180. https://doi.org/10.3390/batteries9030180
Wang J, Meng J, Peng Q, Liu T, Zeng X, Chen G, Li Y. Lithium-Ion Battery State-of-Charge Estimation Using Electrochemical Model with Sensitive Parameters Adjustment. Batteries. 2023; 9(3):180. https://doi.org/10.3390/batteries9030180
Chicago/Turabian StyleWang, Jingrong, Jinhao Meng, Qiao Peng, Tianqi Liu, Xueyang Zeng, Gang Chen, and Yan Li. 2023. "Lithium-Ion Battery State-of-Charge Estimation Using Electrochemical Model with Sensitive Parameters Adjustment" Batteries 9, no. 3: 180. https://doi.org/10.3390/batteries9030180
APA StyleWang, J., Meng, J., Peng, Q., Liu, T., Zeng, X., Chen, G., & Li, Y. (2023). Lithium-Ion Battery State-of-Charge Estimation Using Electrochemical Model with Sensitive Parameters Adjustment. Batteries, 9(3), 180. https://doi.org/10.3390/batteries9030180









