Research on Multi-Time Scale SOP Estimation of Lithium–Ion Battery Based on H∞ Filter
Abstract
:1. Introduction
2. Battery Modeling and Parameter Identification
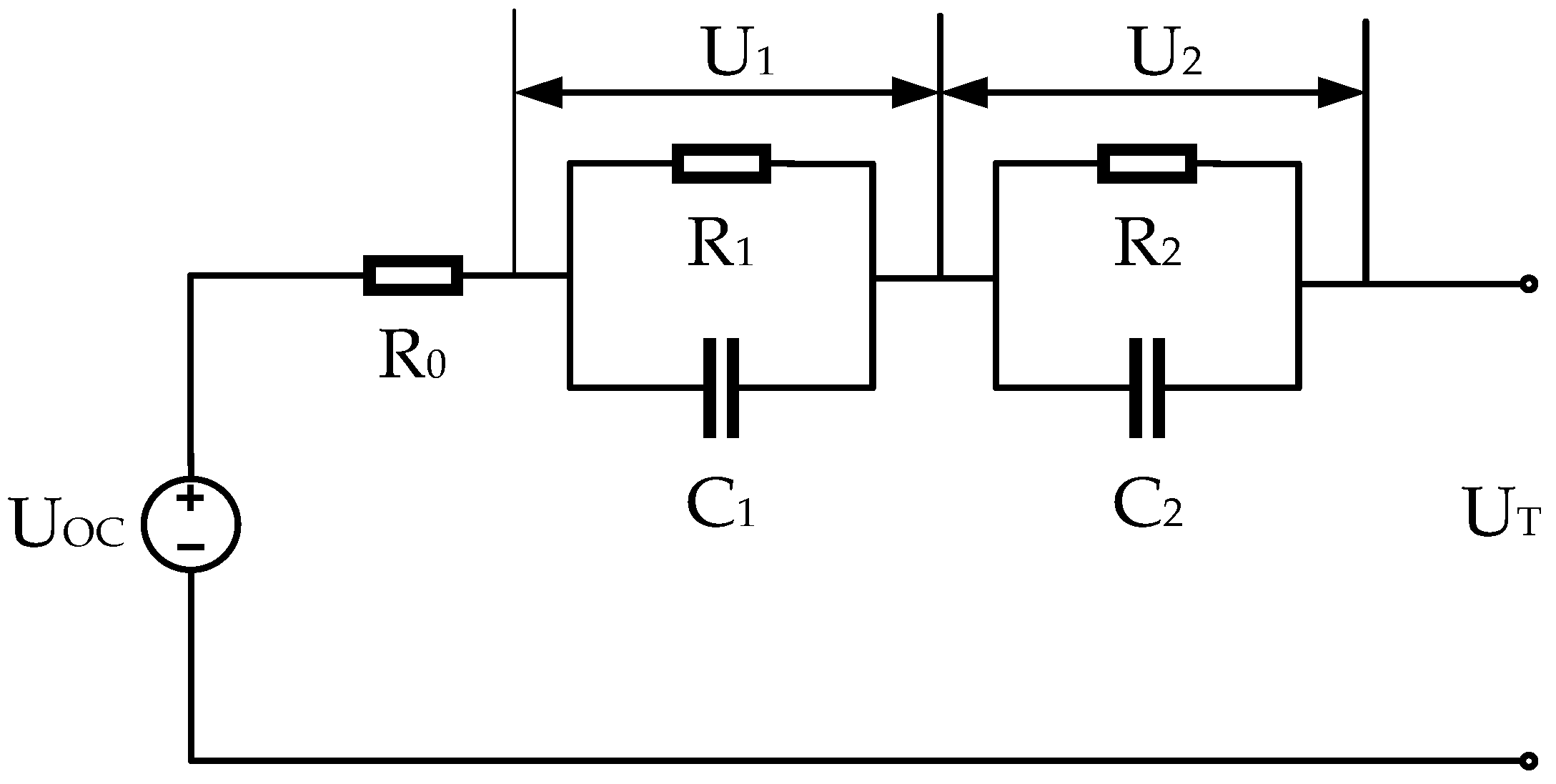
2.1. Battery Modeling
2.2. Forgetting Factor Recursive Least Squares (FFRLS)
3. Joint Multi-Time Scale SOC-SOP Estimation
3.1. H∞ Filtering
3.2. Multi-Time Scale SOP Estimation
3.2.1. Continuous Peak Current Based on Voltage Constraints
3.2.2. Continuous Peak Current Based on SOC Constraints
3.2.3. Continuous Peak Charge/Discharge Current under Multiple Constraints
3.2.4. Algorithm Flow
4. Validations and Discussion
4.1. Experimental Setup and Test Procedure
- Battery capacity test
- (1)
- Charge the battery with a current from 0.5 C to 4.2 V, and then change it to a constant voltage of 4.2 V to charge the battery. When the charging current drops to 50 mA, stop charging, and the battery is considered to be fully charged;
- (2)
- Let stand for 2 h;
- (3)
- Discharge at a constant current of 0.2 C until the terminal voltage is less than 2.75 V, and integrate the discharge current with time, that is, use the ampere-hour integration method to obtain the current discharge capacity;
- (4)
- Repeat steps (1) to (3) three times. If the error of the capacity obtained for three times is less than 2%, take the average of the three discharge capacities as the maximum usable capacity, otherwise repeat steps (1) to (3) until the requirements are met.
- Open-circuit voltage test
- (1)
- Charge the battery to 4.2 V with a current of 0.5 C, and then convert it to a constant voltage of 4.2 V to charge the battery pack. When the charging current drops to 50 mA, stop charging, and then the battery is considered to be fully charged;
- (2)
- After standing for 2 h, the measured terminal voltage is OCV when fully charged (i.e., SOC = 100%);
- (3)
- Discharge at 1C constant current for 3 min, and then let it stand for 2 h. The terminal voltage after standing for 2 h is the OCV under the current SOC state;
- (4)
- Repeat the third step until the terminal voltage of the tested object is less than 2.75 V and stop discharging, and collect the experimental data.
- UDDS working condition test
- (1)
- Charge the battery with a current of 0.5 C to 4.2 V, and then change it to a constant voltage of 4.2 V to charge the battery. When the charging current drops to 50 mA, stop charging, and the battery is considered to be fully charged;
- (2)
- Let stand for 2 h;
- (3)
- Input the UDDS working condition excitation current (as shown in Figure 7) into the battery test system to conduct the cyclic working condition test until the terminal voltage of the tested object is less than 2.75 V and stop discharging, and collect the experimental data.
4.2. Validation of FFRLS Parameter Identification Results
4.3. Verification of SOC Estimation
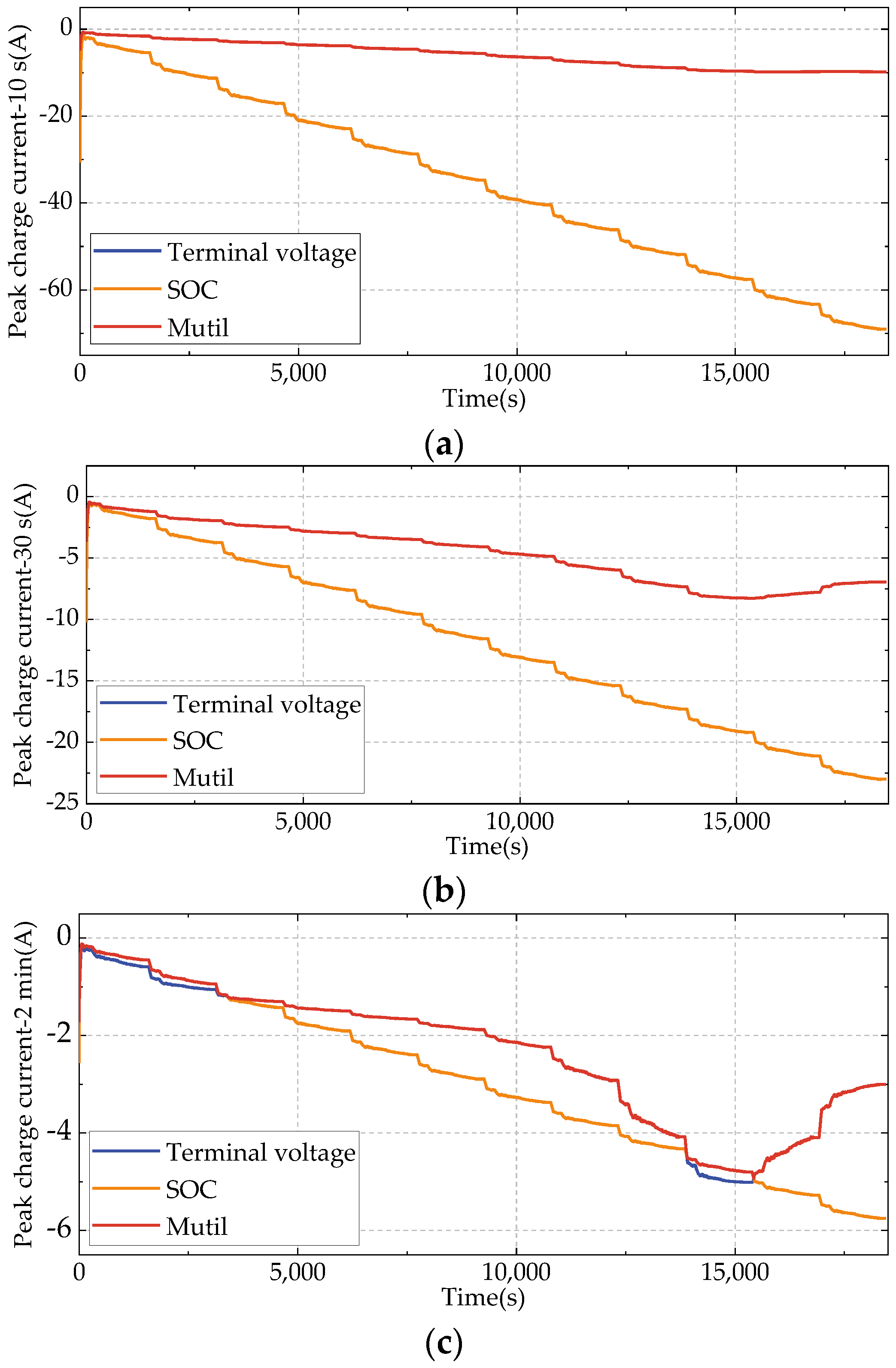
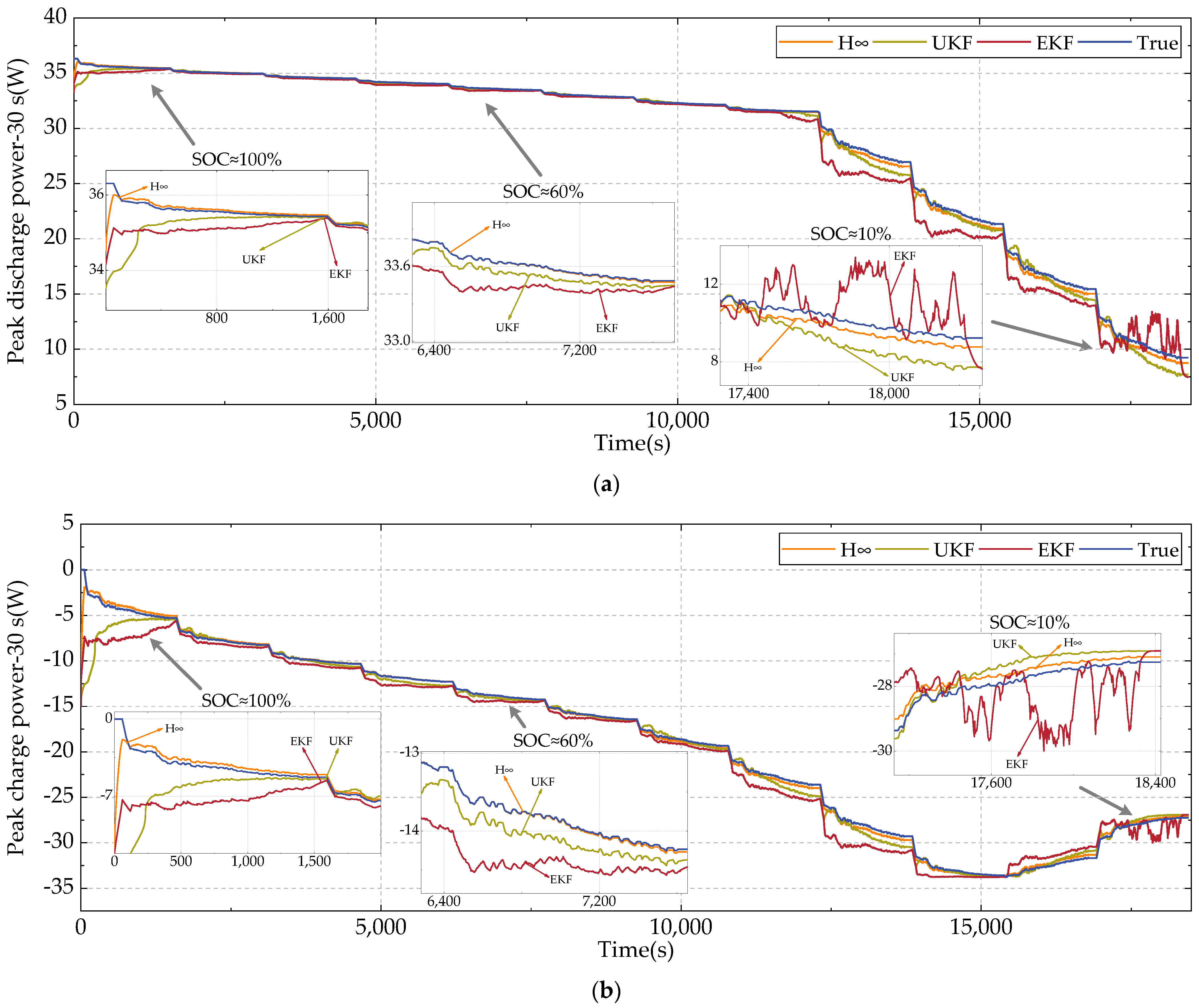
4.4. Validation Results of Online SOP Estimation
4.4.1. Discharge SOP Estimation
4.4.2. Charging SOP Estimation
4.4.3. Comparison of SOP Estimates
5. Conclusions
- (1)
- To address the significant computational workload required by traditional online identification methods, it is proposed in this paper to address the online identification of model parameters through the recursive least squares method with forgetting factor, which achieves a high accuracy and a strong tracking capability under the condition of low computational workload;
- (2)
- To eliminate the unavoidable measurement noise from current, voltage, and other sensors, H∞ filtering is performed for process noise and measurement noise. SOC estimation is also carried out;
- (3)
- To resolve problems such as insufficient constraints, the low accuracy of SOC estimation, and single time scale, a multi-constraint SOP estimation method based on multiple time scales is proposed in this paper.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| SOP | State of Power |
| SOC | State of Charge |
| MARE | Mean Absolute Relative Error |
| RNN | Recurrent Neural Network |
| KF | Kalman Filter |
| EKF | Extended Kalman Filter |
| DEKF | Double Extended Kalman filter |
| BP | Back Propagation |
| HPPC | Hybrid Pulse Power Characteristic |
| MPC | Model Predictive Control |
| SOH | State of Health |
| SOF | Functional State |
| LIB | Lithium–Ion Battery |
| FFRLS | Forgetting Factor Recursive Least Squares |
| OCV | Open-Circuit Voltage |
| RE | Relative Error |
| RMSE | Root Mean Square Error |
References
- Jin, X.N.; Gu, Q.M.; Pan, Y.W.; Hua, Y. Online state of power estimation methods for lithium-ion batteries in EV. China J. Power Sources 2019, 43, 1448–1452. [Google Scholar]
- Xiong, R.; Sun, F.C.; Gong, X.Z. A data-driven based adaptivestate of charge estimator of lithium-ion polymer battery used inelectric vehicles. Appl. Energy 2014, 113, 1421–1433. [Google Scholar] [CrossRef]
- Wen, G.B.; Rehman, S.; Tranter, T.G.; Ghosh, D.; Chen, Z.; Gostick, J.T.; Pope, M.A. Insights into Multiphase Reactions during Self-Discharge of Li-S Batteries. Chem. Mater. Publ. Am. Chem. Soc. 2020, 32, 4518–4526. [Google Scholar] [CrossRef]
- Bhattacharjee, A.; Mohanty, R.K.; Ghosh, A. Design of an optimized thermal management system for Li-Ion batteries under different discharging conditions. Energies 2020, 13, 5695. [Google Scholar] [CrossRef]
- Liu, X.T.; He, Y.; Zeng, J.G.; Zheng, X.X. State-of-Power estimation for Li-ion battery considering the effect of temperature. Trans. China Electrotech. Soc. 2016, 31, 155–163. [Google Scholar]
- Yoon, S.; Hwang, I.; Lee, C.W.; Ko, H.S.; Han, K.H. Power capability analysis in lithium ion batteries using electrochemical impedance spectroscopy. J. Electroanal. Chem. 2011, 655, 32–38. [Google Scholar] [CrossRef]
- Chen, C.; Pi, Z.Y.; Zhao, Y.L.; Liao, X.; Zhang, M.M. State of charge estimation with adaptive cataclysm genetic algo-rithm-recurrent neural network for Li-ion batteries. J. Electr. Eng. 2022, 17, 86–94. [Google Scholar]
- Qian, J.W.; Du, C.; Tian, X.; Zhu, Y.B. An improved fuzzy neural network method based on T-S model to estimate state of charge of lithium batteries. China J. Power Sources 2020, 44, 1270–1273. [Google Scholar]
- Tang, X.; Liu, K.; Li, K.; Widanage, W.D.; Kendrick, E.; Gao, F. Recovering large-scale battery aging dataset with machine learning. Patterns 2021, 2, 1000302. [Google Scholar] [CrossRef]
- Li, W.; Sengupta, N.; Dechent, P.; Howey, D.; Annaswamy, A.; Sauer, D.U. One-shot battery degradation trajectory prediction with deep learning. J. Power Sources 2021, 506, 230024. [Google Scholar] [CrossRef]
- Mastali, M.; Vazquez-Arenas, J.; Fraser, R.; Fowler, M.; Afshar, S.; Stevens, M. Battery state of the charge estimation using Kalman filtering. J. Power Sources 2013, 239, 294–307. [Google Scholar] [CrossRef]
- Huang, C.; Wang, Z.; Zhao, Z.; Wang, L.; Lai, C.S.; Wang, D. Robustness evaluation of extended and unscented kalman filter for battery state of charge estimation. IEEE Access 2018, 6, 27617–27628. [Google Scholar] [CrossRef]
- Andre, D.; Appel, C.; Soczka-Guth, T.; Sauer, D.U. Advanced mathematical methods of SOC and SOH estimation for lithium-ion batteries. J. Power Sources 2013, 224, 20–27. [Google Scholar] [CrossRef]
- Xiong, R.; Cao, J.Y.; Yu, Q.Q.; He, H.W.; Sun, F.C. Critical review on the battery state of charge estimation methods for electric vehicles. IEEE Access 2017, 6, 1832–1843. [Google Scholar] [CrossRef]
- Xiong, R.; He, H.W.; Sun, F.C.; Liu, X.L.; Liu, Z.T. Model-based state of charge and peak power capability joint estimation of lithium-ion battery in plug-in hybrid electric vehicles. J. Power Sources 2013, 229, 159–169. [Google Scholar] [CrossRef]
- Li, W.; Fan, Y.; Ringbeck, F.; Jöst, D.; Han, X.; Ouyang, M.; Sauer, D.U. Electrochemical model-based state estimation for lithium-ion batteries with adaptive unscented Kalman filter. J. Power Sources 2020, 476, 228534. [Google Scholar] [CrossRef]
- Wang, T.; Chen, S.; Ren, H.; Zhao, Y. Model-based unscented Kalman filter observer design for lithium-ion battery state of charge estimation. Int. J. Energy Res. 2012, 42, 1603–1614. [Google Scholar] [CrossRef]
- Zou, C.; Klintberg, A.; Wei, Z.; Fridholm, B.; Wik, T.; Egardt, B. Power capability prediction for lithium-ion batteries using economic nonlinear model predictive control. J. Power Sources 2018, 396, 580–589. [Google Scholar] [CrossRef]
- Sun, B.X.; Gao, K.; Jiang, C.J.; Luo, M.; He, T.T.; Zheng, F.D.; Guo, H.Y. Research on discharge peak power prediction of battery based on ANFIS and subtraction clustering. Trans. China Electrotech. Soc. 2015, 30, 272–280. [Google Scholar]
- Zhu, H.; Zhang, W.B.; Deng, Y.W.; Li, M.; Ji, X. Peak power estimation of power battery discharge based on SA + BP hybrid algorithm. J. Jiangsu Univ. 2020, 41, 192–198. [Google Scholar]
- Plett, G.L. High-performance battery-pack power estimation using a dynamic cell model. IEEE Trans. Veh. Technol. 2004, 53, 1586–1593. [Google Scholar] [CrossRef] [Green Version]
- Xavier, M.A.; de Souza, A.K.; Plett, G.L.; Trimboli, M.S. A low-cost MPC-based algorithm for battery power limit estimation. In Proceedings of the 2020 American Control Conference (ACC), Denver, CO, USA, 1–3 July 2020; pp. 1161–1166. [Google Scholar]
- Zhang, W.; Shi, W.; Ma, Z. Adaptive unscented Kalman filter based state of energy and power capability estimation approach for lithium-ion battery. J. Power Sources 2015, 289, 50–62. [Google Scholar] [CrossRef]
- Pei, L.; Zhu, C.; Wang, T.; Lu, R.; Chan, C.C. Online peak power prediction based on a parameter and state estimator for lithium-ion batteries in electric vehicles. Energy 2014, 66, 766–778. [Google Scholar] [CrossRef]
- Tang, X.; Wang, Y.; Yao, K.; He, Z.; Gao, F. Model migration based battery power capability evaluation considering uncertainties of temperature and aging. J. Power Sources 2019, 440, 227141. [Google Scholar] [CrossRef]
- Zhang, W.J.; Wang, L.Y.; Wang, L.F.; Liao, C.L.; Zhang, Y.W. Joint State-of-Charge and State-of-Available-Power Estimation Based on the Online Parameter Identification of Lithium-Ion Battery Model. IEEE Trans. Ind. Electron. 2022, 69, 3677–3688. [Google Scholar] [CrossRef]
- Guo, R.H.; Shen, W.X. A data-model fusion method for online state of power estimation of lithium-ion batteries at high discharge rate in electric vehicles. Energy 2022, 254, 124270. [Google Scholar] [CrossRef]
- Hu, X.S.; Jiang, H.; Feng, F.; Liu, B. An enhanced multi-state estimation hierarchy for advanced lithium-ion battery management. Appl. Energy 2020, 257, 114019. [Google Scholar] [CrossRef]
- Dong, G.; Wei, J.; Chen, Z. Kalman filter for onboard state of charge estimation and peak power capability analysis of lithium-ion batteries. J. Power Sources 2016, 328, 615–626. [Google Scholar] [CrossRef]
- Rahimifard, S.; Ahmed, R.; Habibi, S. Interacting multiple model strategy for electric vehicle batteries state of charge/health/power estimation. IEEE Access 2021, 9, 109875–109888. [Google Scholar] [CrossRef]
- Li, Q.; Wang, T.; Li, S.; Chen, W.; Liu, H.; Breaz, E.; Gao, F. Online extremum seeking-based optimized energy management strategy for hybrid electric tram considering fuel cell degradation. Appl. Energy 2021, 285, 116505–118153. [Google Scholar] [CrossRef]
- Shrivastava, P.; Soon, T.K.; Idris, M.Y.I.B.; Mekhilef, S. Overview of model-based online state-of-charge estimation using Kalman filter family for lithium-ion batteries. Renew. Sustain. Energy Rev. 2019, 113, 109233. [Google Scholar] [CrossRef]
- Mevawalla, A.; Panchal, S.; Tran, M.K.; Fowler, M.; Fraser, R. One dimensional fast computational partial differential model for heat transfer in lithium-ion batteries. J. Power Sources 2021, 37, 102471. [Google Scholar] [CrossRef]
- Yang, N.; Song, Z.; Hofmann, H.; Sun, J. Robust state of health estimation of lithium-ion batteries using convolutional neural network and random forest. J. Energy Storage 2022, 48, 103857. [Google Scholar] [CrossRef]
- Li, X.; Wang, Z.; Zhang, L. Co-estimation of capacity and state-of-charge for lithium-ion batteries in electric vehicles. Energy 2019, 174, 33–44. [Google Scholar] [CrossRef]






















| Time Scale | RMSE (W) | MARE (%) | Title 1 | Title 2 | Title 3 |
|---|---|---|---|---|---|
| 10 s | 0.4298 | 0.25 | entry 1 | data | data |
| 30 s | 0.7652 | 0.83 | entry 2 | data | data |
| 2 min | 1.3047 | 1.21 |
| Time Scale | RMSE (W) | MARE (%) | Title 1 | Title 2 | Title 3 |
|---|---|---|---|---|---|
| 10 s | 0.9019 | 0.77 | entry 1 | data | data |
| 30 s | 1.5034 | 1.02 | entry 2 | data | data |
| 2 min | 2.2763 | 1.53 |
| Technique | Discharge (s) | Charge (s) |
|---|---|---|
| H∞ | 80 | 90 |
| UKF | 821 | 1088 |
| EKF | 1426 | 1605 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, R.; Li, K.; Liu, P.; Zhang, X. Research on Multi-Time Scale SOP Estimation of Lithium–Ion Battery Based on H∞ Filter. Batteries 2023, 9, 191. https://doi.org/10.3390/batteries9040191
Li R, Li K, Liu P, Zhang X. Research on Multi-Time Scale SOP Estimation of Lithium–Ion Battery Based on H∞ Filter. Batteries. 2023; 9(4):191. https://doi.org/10.3390/batteries9040191
Chicago/Turabian StyleLi, Ran, Kexin Li, Pengdong Liu, and Xiaoyu Zhang. 2023. "Research on Multi-Time Scale SOP Estimation of Lithium–Ion Battery Based on H∞ Filter" Batteries 9, no. 4: 191. https://doi.org/10.3390/batteries9040191
APA StyleLi, R., Li, K., Liu, P., & Zhang, X. (2023). Research on Multi-Time Scale SOP Estimation of Lithium–Ion Battery Based on H∞ Filter. Batteries, 9(4), 191. https://doi.org/10.3390/batteries9040191






