Structural and Dynamic Characterization of Li–Ionic Liquid Electrolyte Solutions for Application in Li-Ion Batteries: A Molecular Dynamics Approach
Abstract
:1. Introduction
2. Methods and IL Systems
3. Results and Discussions
3.1. Neat Pyrrolidinium-Anion Ionic Liquids
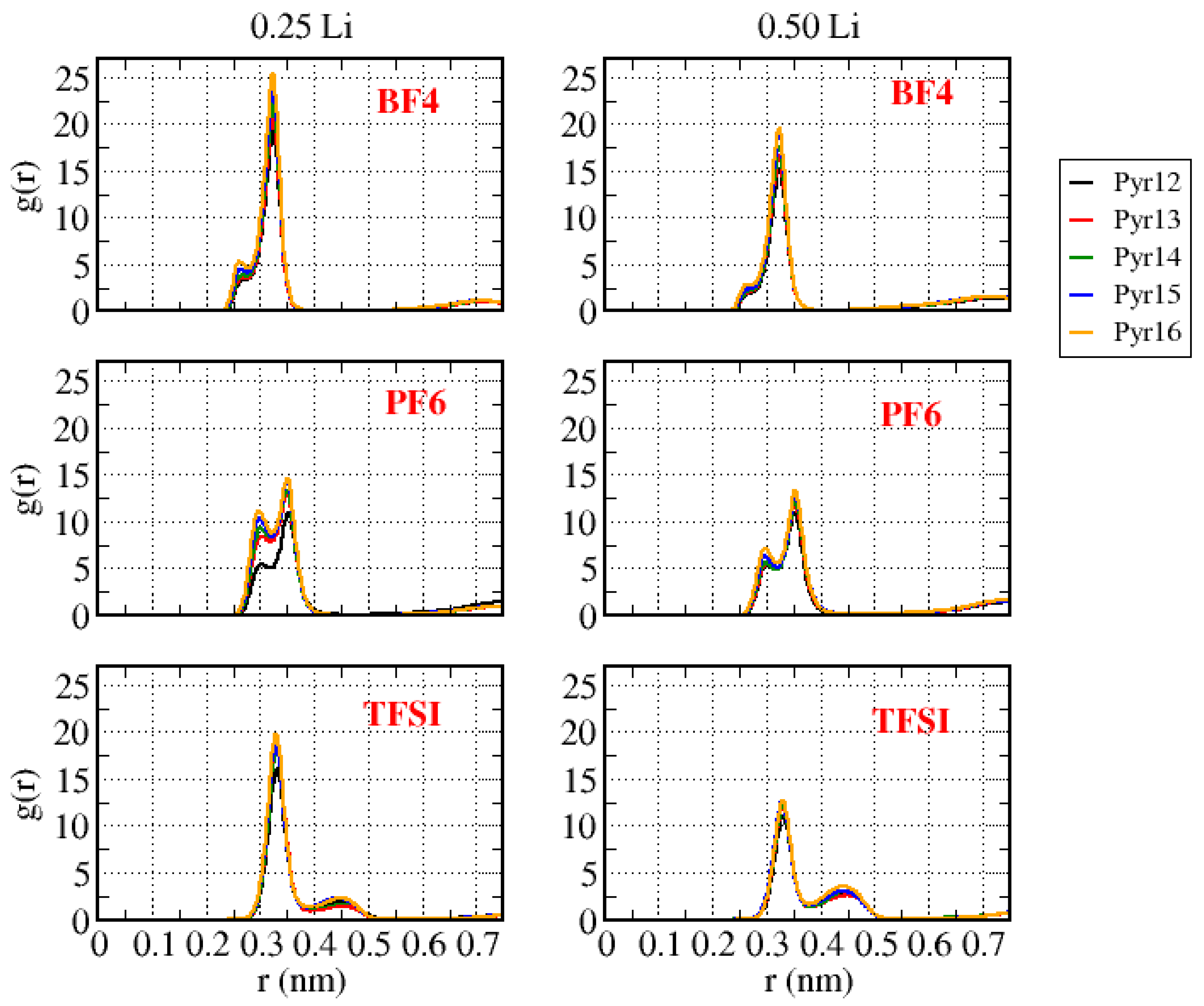
3.2. Li-Ionic Liquid Electrolyte Solutions
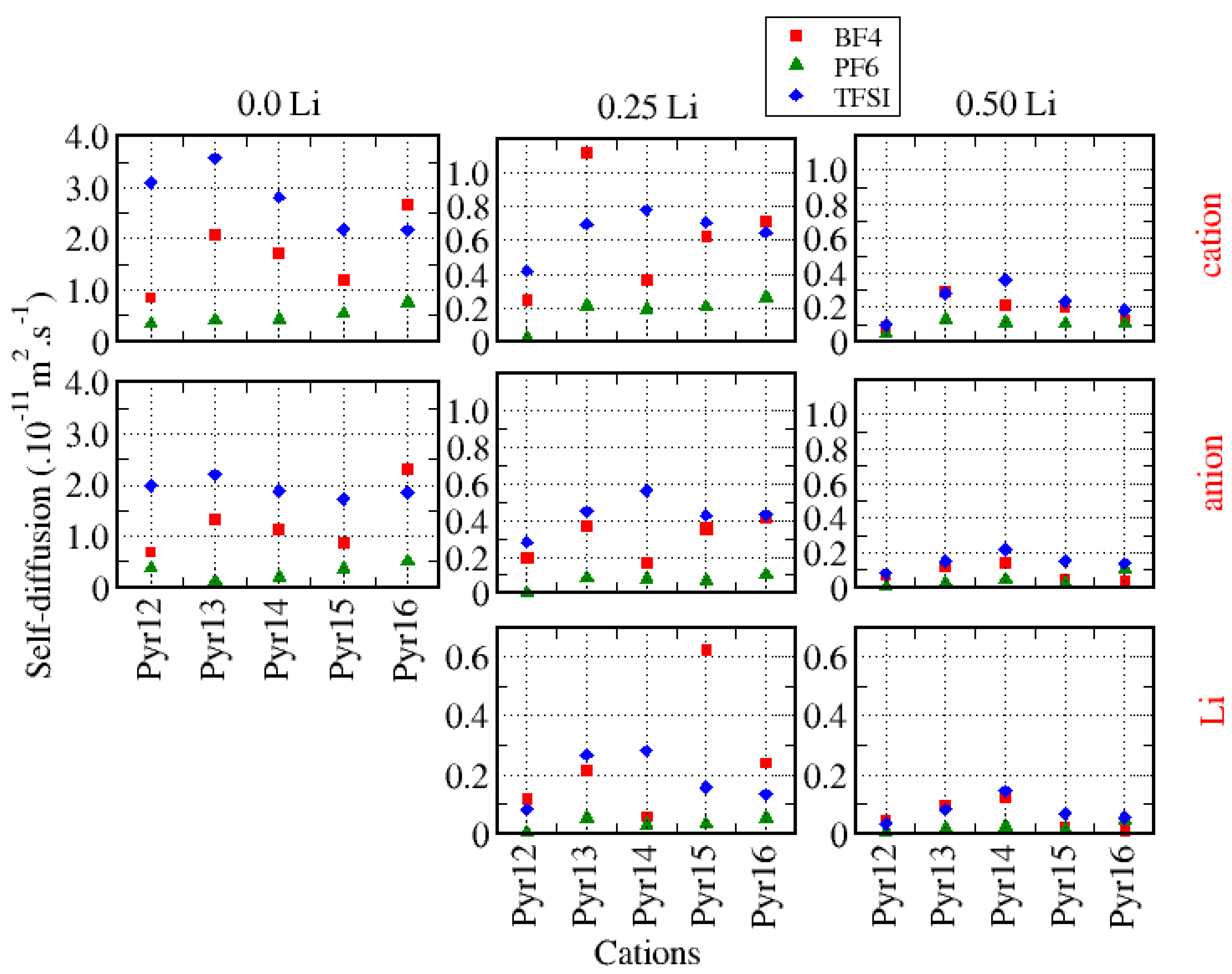
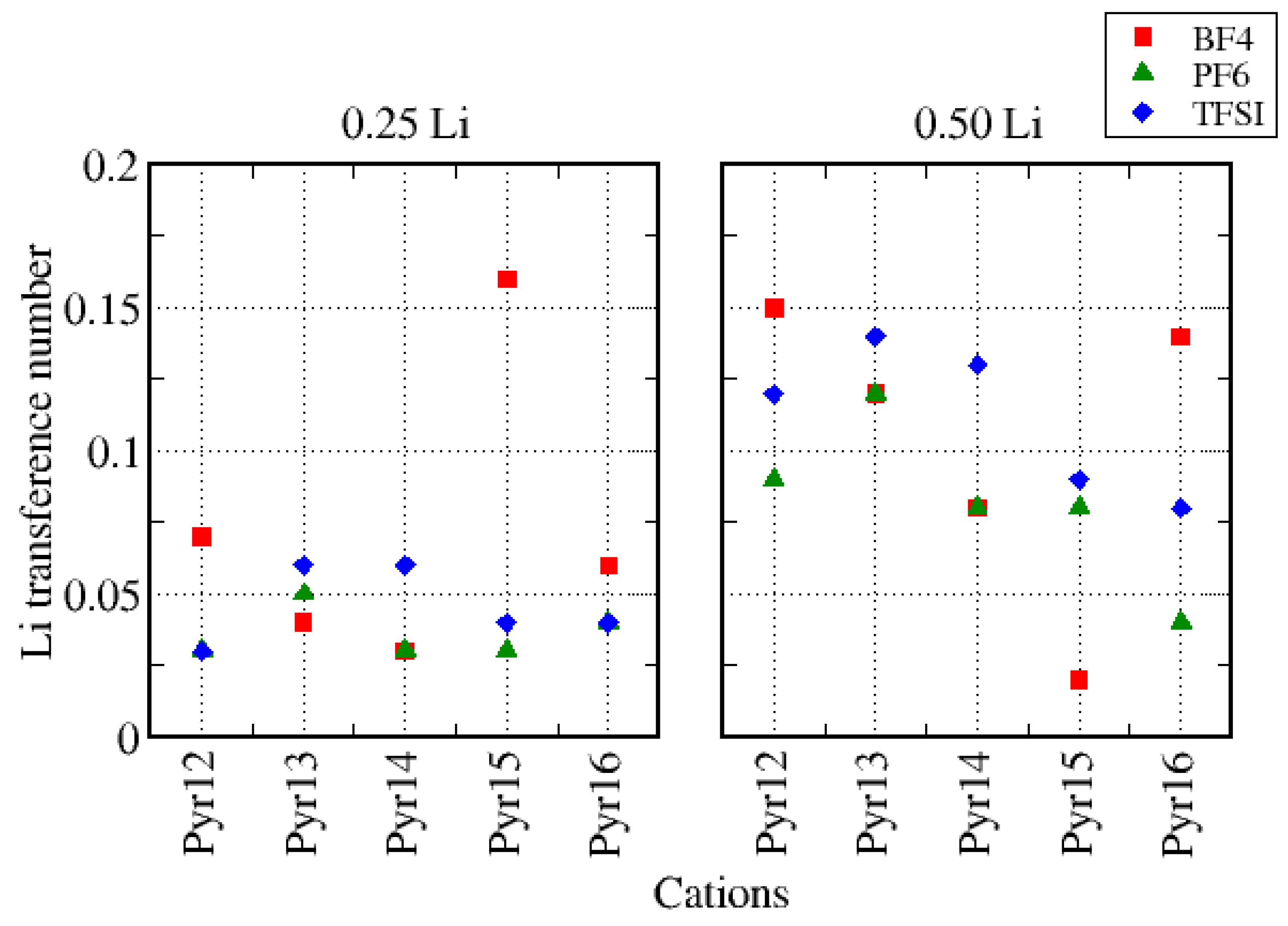
3.3. Dynamical Properties
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Thum, A.; Heuer, A.; Shimizu, K.; Canongia Lopes, J.N. Solvate ionic liquids based on lithium bis(trifluoromethanesulfonyl)imide-glyme systems: Coordination in MD simulations with scaled charges. Phys. Chem. Chem. Phys 2020, 22, 525–535. [Google Scholar] [CrossRef] [PubMed]
- Borodin, O. Polarizable Force Field Development and Molecular Dynamics Simulations of Ionic Liquids. J. Phys. Chem. B 2009, 113, 11463–11478. [Google Scholar] [CrossRef] [PubMed]
- Paredes, X.; Fernández, J.; Pádua, A.A.H.; Malfreyt, P.; Malberg, F.; Kirchner, B.; Pensado, A.S. Bulk and Liquid-Vapor Interface of Pyrrolidinium-Based Ionic Liquids: A Molecular Simulation Study. J. Phys. Chem. B 2014, 118, 731–742. [Google Scholar] [CrossRef] [PubMed]
- Choi, J.A.; Sun, Y.K.; Shim, E.G.; Scrosati, B.; Kim, D.W. Effect of 1-butyl-1-methylpyrrolidinium hexafluorophosphate as a flame-retarding additive on the cycling performance and thermal properties of lithium-ion batteries. Electrochim. Acta 2011, 56, 10179–10184. [Google Scholar] [CrossRef]
- Tiago, G.A.O.; Matias, I.A.S.; Ribeiro, A.P.C.; Martins, L.M.D.R.S. Application of Ionic Liquids in Electrochemistry–Recent Advances. Molecules 2020, 25, 5812. [Google Scholar] [CrossRef] [PubMed]
- Farahipour, R.; Mehrkesh, A.; Karunanithi, A.T. A systematic screening methodology towards exploration of ionic liquids for CO2 capture processes. Chem. Engin. Sci. 2016, 145, 126–132. [Google Scholar] [CrossRef]
- Gnezdilov, O.I.; Filippov, A.; Khan, I.A.; Shah, F.U. Translational and reorientational dynamics of ionic liquid-based fluorine-free lithium-ion battery electrolytes. J. Mol. Liq. 2022, 345, 117001. [Google Scholar] [CrossRef]
- Judeinstein, P.; Zeghal, M.; Constantin, D.; Iojoiu, C.; Coasne, B. Interplay of Structure and Dynamics in Lithium/Ionic Liquid Electrolytes: Experiment and Molecular Simulation. J. Phys. Chem. B 2021, 125, 1618–1631. [Google Scholar] [CrossRef]
- Méndez-Morales, T.; Carrete, J.; Bouzón-Capelo, S.; Pérez-Rodríguez, M.; Cabeza, O.; Gallego, L.J.; Varela, L.M. MD Simulations of the Formation of Stable Clusters in Mixtures of Alkaline Salts and Imidazolium-Based Ionic Liquids. J. Phys. Chem. B 2013, 117, 3207–3220. [Google Scholar] [CrossRef]
- Ray, P.; Vogl, T.; Balducci, A.; Kirchner, B. Structural Investigations on Lithium-Doped Protic and Aprotic Ionic Liquids. J. Phys. Chem. B 2017, 121, 5279–5292. [Google Scholar] [CrossRef] [PubMed]
- Sánchez, L.G.; Espel, J.R.; Onick, F.; Meindersma, G.W.; Haan, A.B. Density, Viscosity, and Surface Tension of Synthesis Grade Imidazolium, Pyridinium, and Pyrrolidinium Based Room Temperature Ionic Liquids. J. Chem. Eng. Data 2009, 54, 2803–2812. [Google Scholar] [CrossRef]
- Kunze, M.; Jeong, S.; Paillard, E.; Winter, M.; Passerini, S. Melting Behavior of Pyrrolidinium Based Ionic Liquids and Their Binary Mixtures. J. Phys. Chem. C 2010, 114, 12364–12369. [Google Scholar] [CrossRef]
- Brutti, S. Pyr1,x-TFSI Ionic Liquids (x = 1–8): A Computational Chemistry Study. Appl. Sci. 2020, 10, 8552. [Google Scholar] [CrossRef]
- Molinari, N.; Mailoa, J.P.; Kozinsky, B. General Trend of a Negative Li Effective Charge in Ionic Liquid Electrolytes. J. Phys. Chem. Lett. 2019, 10, 2313–2319. [Google Scholar] [CrossRef]
- Postupna, O.O.; Kolesnik, Y.V.; Kalugin, O.N.; Prezhdo, O.V. Microscopic Structure and Dynamics of LiBF4 Solutions in Cyclic and Linear Carbonates. J. Phys. Chem. B 2011, 115, 14563–14571. [Google Scholar] [CrossRef]
- Pires, J.; Timperman, L.; Jacquemin, J.; Balducci, A.; Anouti, M. Density, conductivity, viscosity, and excess properties of (pyrrolidinium nitrate-based Protic Ionic Liquid + propylene carbonate) binary mixture. J. Chem. Thermodyn. 2013, 59, 10–19. [Google Scholar] [CrossRef]
- Xiao, W.; Yang, Q.; Zhu, S. Comparing ion transport in ionic liquids and polymerized ionic liquids. Sci. Rep. 2020, 10, 7825–7837. [Google Scholar] [CrossRef]
- Sharma, S.; Kashyap, H.K. Interfacial Structure of Pyrrolidinium Cation Based Ionic Liquids at Charged Carbon Electrodes: The Role of Linear and Nonlinear Alkyl Tails. J. Phys. Chem. C 2017, 121, 13202–13210. [Google Scholar] [CrossRef]
- Philippi, F.; Welton, T. Targeted modifications in ionic liquids—From understanding to design. Phys. Chem. Chem. Phys. 2021, 23, 6993–7021. [Google Scholar] [CrossRef]
- MacGrath, L.M.; Rohan, J.F. Pyrrolidinium Containing Ionic Liquid Electrolytes for Li-Based Batteries. Molecules 2020, 25, 6002. [Google Scholar] [CrossRef]
- Murugesan, S.; Quintero, O.A.; Chou, B.P.; Xiao, P.; Park, K.; Hall, J.W.; Jones, R.A.; Henkelman, G.; Goodenough, J.B.; Stevenson, K.J. Wide electrochemical window ionic salt for use in electropositive metal electrodeposition and solid state Li-ion batteries. J. Mater. Chem. A 2014, 2, 1294–1302. [Google Scholar] [CrossRef]
- Ray, A.; Saruhan, B. Application of Ionic Liquids for Batteries and Supercapacitors. Materials 2021, 14, 2942. [Google Scholar] [CrossRef]
- Hayamizu, K.; Tsuzuki, S.; Seki, S.; Fujii, K.; Suenaga, M.; Umebayashi, Y. Studies on the translational and rotational motions of ionic liquids composed of N-methyl-N-propyl-pyrrolidinium (P13) cation and bis(trifluoromethanesulfonyl)amide and bis(fluorosulfonyl)amide anions and their binary systems including lithium salts. J. Chem. Phys. 2010, 133, 194505. [Google Scholar] [CrossRef]
- Celeste, A.; Silvestri, L.; Agostini, M.; Sadd, M.; Palumbo, S.; Panda, J.K.; Matic, A.; Pellegrini, V.; Brutti, S. Enhancement of Functional Properties of Liquid Electrolytes for Lithium-Ion Batteries by Addition of Pyrrolidinium-Based Ionic Liquids with Long Alkyl-Chains. Batter. Supercaps 2020, 3, 1059–1068. [Google Scholar] [CrossRef]
- Al-Rashed, O.A.; Nazzer, A.A. Ionic liquids with superior protection for mild steel in acidic media: Effects of anion, cation, and alkyl chain length. J. Mol. Liquids 2019, 288, 111015–111026. [Google Scholar] [CrossRef]
- Lesch, V.; Heuer, A.; Holm, C.; Smiatek, J. Properties of Apolar Solutes in Alkyl Imidazolium-Based Ionic Liquids: The Importance of Local Interactions. ChemPhysChem 2016, 17, 387–394. [Google Scholar] [CrossRef]
- Ray, P.; Balducci, A.; Kirchner, B. Molecular Dynamics Simulations of Lithium-Doped Ionic-Liquid Electrolytes. J. Phys. Chem. B 2018, 122, 10535–10547. [Google Scholar] [CrossRef]
- Méndez-Morales, T.; Carrete, J.S.; Pérez-Rodríguez, M.; Cabeza, O.; Gallego, L.J.; Lynden-Bell, R.M.; Varela, L.M. Molecular dynamics simulations of the structure of the graphene-ionic liquid/alkali salt mixtures interface. Phys. Chem. Chem. Phys. 2014, 16, 13271–13278. [Google Scholar] [CrossRef]
- Liu, H.; Maginn, E. Effect of ion structure on conductivity in lithium-doped ionic liquid electrolytes: A molecular dynamics study. J. Chem. Phys. 2013, 139, 114508. [Google Scholar] [CrossRef]
- Huang, J. Confinement Induced Dilution: Electrostatic Screening Length Anomaly in Concentrated Electrolytes in Confined Space. J. Phys. Chem. C 2018, 122, 3428–3433. [Google Scholar] [CrossRef]
- Lesch, V.; Li, Z.; Bedrov, D.; Borodin, O.; Heuer, A. The influence of cations on lithium ion coordination and transport in ionic liquid electrolytes: A MD simulation study. Phys. Chem. Chem. Phys. 2016, 18, 382–393. [Google Scholar] [CrossRef]
- Haskins, J.B.; Bennett, W.R.; Wu, J.J.; Hernández, D.M.; Borodin, O.; Momk, J.D.; Bauschlincher, C.W., Jr.; Lawson, J.W. Computational and Experimental Investigation of Li-Doped Ionic Liquid Electrolytes: [pyr14][TFSI], [pyr13][FSI], and [EMIM][BF4]. J. Phys. Chem. B 2014, 118, 11295–11309. [Google Scholar] [CrossRef]
- Rüther, T.; Bhatt, A.I.; Best, A.S.; Harris, K.R.; Hollenkamp, A.F. Electrolytes for Lithium (Sodium) Batteries Based on Ionic Liquids: Highlighting the Key Role Played by the Anion. Batter. Supercaps 2020, 3, 793–827. [Google Scholar] [CrossRef]
- Seo, D.M.; Boyle, P.D.; Allen, J.L.; Han, S.D.; Jónsson, E.; Johansson, P.; Henderson, W.A. Solvate Structures and Computational/Spectroscopic Characterization of LiBF4 Electrolytes. J. Phys. Chem. C 2014, 118, 18377–18386. [Google Scholar] [CrossRef]
- Canongia Lopes, J.N.; Deschamps, J.; Pádua, A.A.H. Modeling Ionic Liquids Using a Systematic All-Atom Force Field. J. Phys. Chem. B 2004, 108, 2038–2047. [Google Scholar] [CrossRef]
- Jorgersen, W.L.; Maxwell, D.S.; Tirado-Rives, J. Development and Testing of the OPLS All-Atom Force Field on Conformational Energetics and Properties of Organic Liquids. J. Am. Chem. Soc. 1996, 118, 11225–11236. [Google Scholar] [CrossRef]
- Ponder, J.W.; Case, D.A. Force fields for protein simulations. Adv. Prot. Chem. 2003, 66, 27–85. [Google Scholar]
- Canongia Lopes, J.N.; Pádua, A.A.H. Nanostructural Organization in Ionic Liquids. J. Phys. Chem. B 2006, 110, 3330–3335. [Google Scholar] [CrossRef]
- Canongia Lopes, J.N.; Shimizu, K.; Pádua, A.A.H.; Umebayashi, Y.; Fukuda, S.; Fujii, K.; Ishiguro, S. A Tale of Two Ions: The Conformational Landscapes of Bis(trifluoromethanesulfonyl)amide and N,N-Dialkylpyrrolidinium. J. Phys. Chem. B 2008, 112, 1465–1472. [Google Scholar] [CrossRef]
- Canongia Lopes, J.N.; Pádua, A.A.H. CL&P: A generic and systematic force field for ionic liquids modeling. Theor. Chem. Acc. 2012, 131, 1129–1140. [Google Scholar]
- Chen, M.; Pendrill, R.; Widmalm, G.; Brady, J.W.; Wohlert, J. Molecular Dynamics Simulations of the Ionic Liquid 1-n-Butyl-3-Methylimidazolium Chloride and Its Binary Mixtures with Ethanol. J. Chem. Theory Comput. 2014, 10, 4465–4479. [Google Scholar] [CrossRef]
- McDaniel, J.G.; Choi, E.; Son, C.Y.; Schmidt, J.R.; Yethiraj, A. Ab Initio Force Fields for Imidazolium-Based Ionic Liquids. J. Phys. Chem. B 2016, 120, 7024–7036. [Google Scholar] [CrossRef]
- Köderman, T.; Paschek, D.; Ludwig, R. Ionic Liquids: Dissecting the Enthalpies of Vaporization. ChemPhysChem 2008, 9, 549–555. [Google Scholar] [CrossRef]
- Chaban, V.; Voroshylova, I.V. Systematic Refinement of Canongia Lopes-Pádua Force Field for Pyrrolidinium-Based Ionic Liquids. J. Phys. Chem. B 2015, 119, 6242–6249. [Google Scholar] [CrossRef]
- Barbosa, G.D.; Liu, X.; O’Hara, K.E.; Bara, J.E.; Turner, C.H. Charge scaling parameter evaluation for multivalent ionic liquids with fixed point charge force fields. J. Ion. Liq. 2022, 2, 100020. [Google Scholar] [CrossRef]
- van der Spoel, D.; Lindahl, E.; Hess, B.; Groenhof, G.; Mark, A.E.; Berendsen, H.J.C. GROMACS: Fast, Flexible and Free. J. Comp. Chem. 2005, 26, 1701–1719. [Google Scholar] [CrossRef] [PubMed]
- Lindahl, E.; Abraham, M.J.; Hess, B.; van der Spoel, D. Gromacs 2020-3 Version. Available online: https://zenodo.org/record/3923644#.ZD9WLfZByUl (accessed on 26 February 2023).
- Chen, J.; Mia, J.G.; Chan, K.Y. Comparison of different mixing rules for prediction of density and residual internal energy of binary and ternary Lennard-Jones mixtures. Fluid Phase Equilibria 2001, 178, 87–95. [Google Scholar] [CrossRef]
- Essman, U.; Perera, L.; Berkowitz, M.L.; Darden, T.; Lee, H.; Pedersen, L.G. A smooth particle mesh Ewald method. J. Chem. Phys. 1995, 103, 8577–8592. [Google Scholar] [CrossRef]
- Hess, B.; Bekker, H.; Berendsen, H.J.C.; Fraaije, J.G.E.M. LINCS: A Linear Constraint Solver for molecular simulations. J. Comp. Chem. 1997, 18, 1463–1472. [Google Scholar] [CrossRef]
- Avogadro: An Open-Source Molecular Builder and Visualization Tool; Version 1.2.0. Available online: http://avogadro.cc/ (accessed on 26 February 2023).
- Hanwell, M.D.; Curtis, D.E.; Lonie, D.C.; Vandermeersch, T.; Zurek, E.; Hutchison, G.R. Avogadro: An advanced semantic chemical editor, visualization, and analysis platform. J. Cheminform. 2012, 4, 1–17. [Google Scholar] [CrossRef]
- Neese, F. The ORCA program system. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2003, 2, 73–78. [Google Scholar] [CrossRef]
- Johnson, E.R.; Becke, A.D. A post-Hartree-Fock model of intermolecular interactions. J. Chem. Phys. 2005, 123, 024101. [Google Scholar] [CrossRef] [PubMed]
- Hehre, W.J.; Ditchfield, R.; Pople, J.A. Self—consistent molecular orbital methods. XII. Further extensions of Gaussian—type basis sets for use in molecular orbital studies of organic molecules. J. Chem. Phys. 1972, 56, 2257–2261. [Google Scholar] [CrossRef]
- Breneman, C.M.; Wilberg, K.B. Determining Atom-Centered Monopoles from Molecular Electrostatic Potentials. The Need for High Sampling Density in Formamide Conformational Analysis. J.Comput. Chem. 1990, 11, 361–373. [Google Scholar] [CrossRef]
- Bussi, G.; Donadio, D.; Parrinello, M. Canonical sampling through velocity rescaling. J. Chem. Phys. 2007, 126, 014101. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; Postma, J.P.M.; DiNola, A.; Haak, J.R. Molecular dynamics with coupling to an external bath. J. Chem. Phys. 1984, 81, 3684–3690. [Google Scholar] [CrossRef]
- Parrinello, M.; Rahman, A. Polymorphic transitions in single crystals: A new molecular dynamics method. J. Appl. Phys. 1981, 52, 7182–7190. [Google Scholar] [CrossRef]
- Golding, J.; Hamid, N.; MacFarlane, D.R.; Forsyt, M.; Forsyt, C.; Collings, C.; Huang, J. N-Methyl-N-alkylpyrrolidinium Hexafluorophosphate Salts: Novel Molten Salts and Plastic Crystal Phases. Chem. Mater. 2001, 13, 558–564. [Google Scholar] [CrossRef]
- Forsyt, S.; Golding, J.; MacFarlane, D.R.; Forsyt, M. N-methyl-N-alkylpyrrolidinium tetrafluoroborate salts: Ionic solvents and solid electrolytes. Electrochim. Acta 2001, 46, 1753–1757. [Google Scholar] [CrossRef]
- Li, S.; Bañuelos, J.L.; Guo, J.; Anovitz, L.; Rother, G.; Shaw, R.W.; Hillesheim, P.C.; Dai, S.; Baker, G.A.; Cummings, P.T. Alkyl Chain Length and Temperature Effects on Structural Properties of Pyrrolidinium-Based Ionic Liquids: A Combined Atomistic Simulation and Small-Angle X-ray Scattering Study. J. Phys. Chem. Lett. 2012, 3, 125–130. [Google Scholar] [CrossRef]
- Nasrabadi, A.T.; Gelb, L.D. Structural and Transport Properties of Tertiary Ammonium Triflate Ionic Liquids: A Molecular Dynamics Study. J. Phys. Chem. B 2017, 121, 1908–1921. [Google Scholar] [CrossRef]
- Lourenço, T.C.; Zhang, Y.; Costa, L.T.; Maginn, E.J. A molecular dynamics study of lithium-containing aprotic heterocyclic ionic liquid electrolytes. J. Chem. Phys. 2018, 148, 193834. [Google Scholar] [CrossRef]
- Tong, J.; Xiao, X.; Liang, X.; von Solms, N.; Huo, F.; He, H.; Zhang, S. Insights into the solvation and dynamic behaviors of a lithium salt in organic-and ionic liquid-based electrolytes. Phys. Chem. Chem. Phys. 2019, 21, 19216–19225. [Google Scholar] [CrossRef]
- Yamaguchi, S.; Yamada, H.; Takeoka, Y.; Rikukawa, M.; Yoshizawa-Fugita, M. Synthesis of pyrrolidinium-based plastic crystals exhibiting high ionic conductivity at ambient temperature. New J. Chem. 2019, 43, 4008–4012. [Google Scholar] [CrossRef]
- Tong, J.; Wu, S.; von Solms, N.; Liang, X.; Huo, F.; Zhou, H.; Zhang, S. The Effect of Concentration of Lithium Salt on the Structural and Transport Properties of Ionic Liquid-Based Electrolytes. Front. Chem. 2020, 7, 945. [Google Scholar] [CrossRef]
- Kashyap, H.K.; Santos, C.S.; Murthy, N.S.; Hettige, J.J.; Kerr, K.; Ramati, S.; Gwon, J.; Gohdo, M.; Lall-Ramnarine, I.; Wishart, J.F.; et al. Structure of 1-Alkyl-1-methylpyrrolidinium Bis(trifluoromethylsulfonyl)amide Ionic Liquids with Linear, Branched, and Cyclic Alkyl Groups. J. Phys. Chem. B 2013, 117, 15328–15337. [Google Scholar] [CrossRef]
- Saitoh, K.; Takai, Y.; Sato, T.; Takuma, M.; Takahashi, Y. Optimization of LIB Electrolyte and Exploration of Novel Compounds via the Molecular Dynamics Method. Batteries 2022, 8, 27. [Google Scholar] [CrossRef]
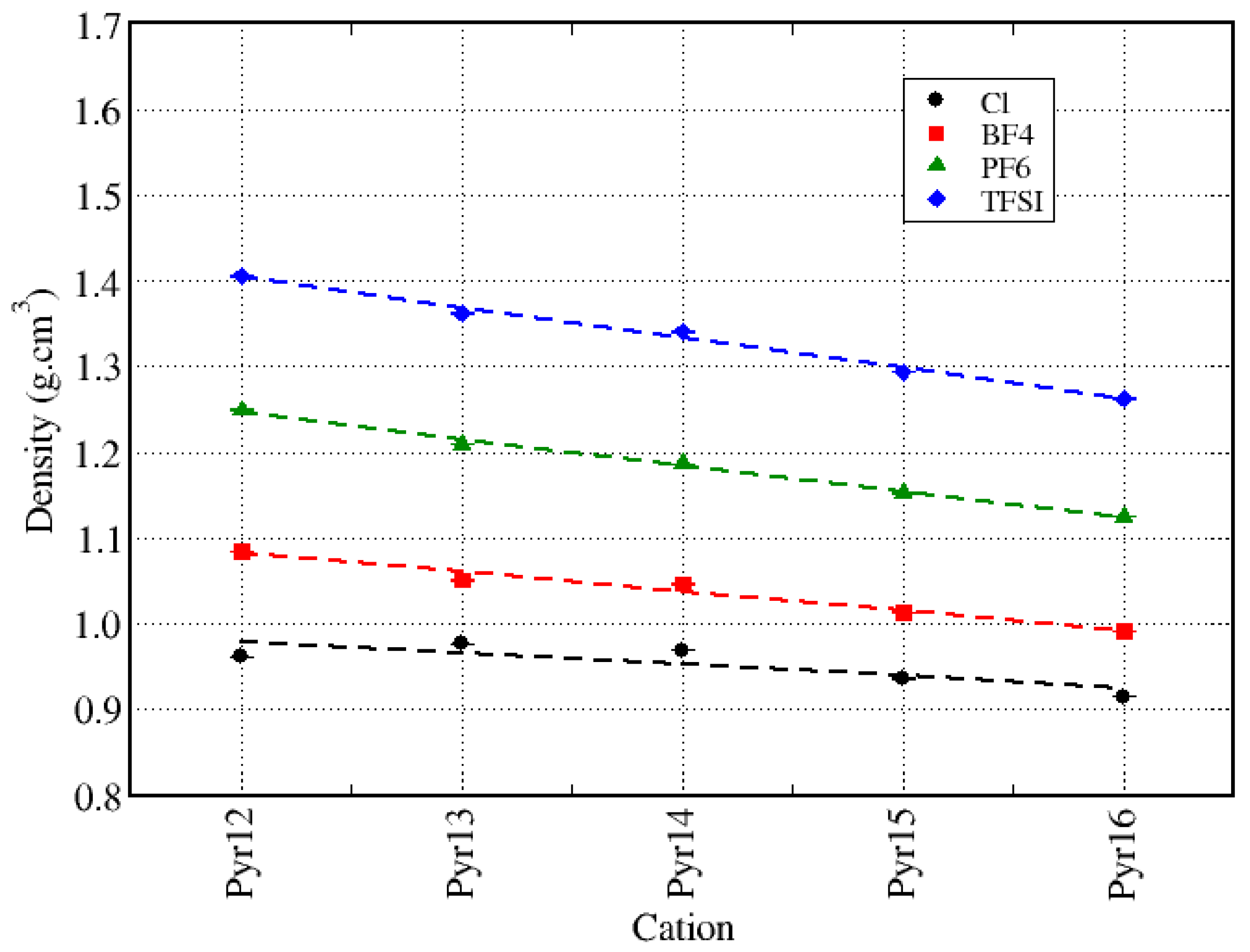

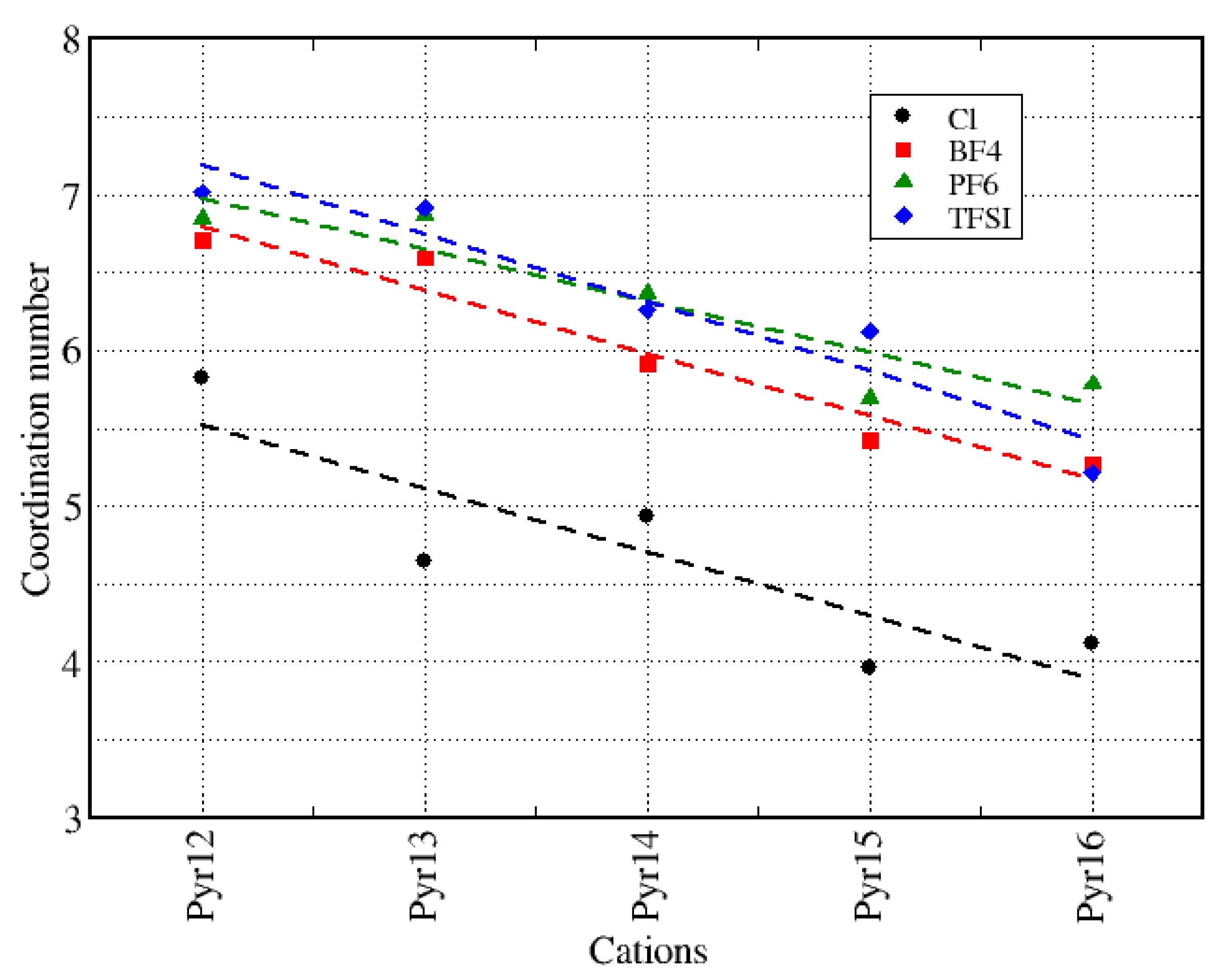
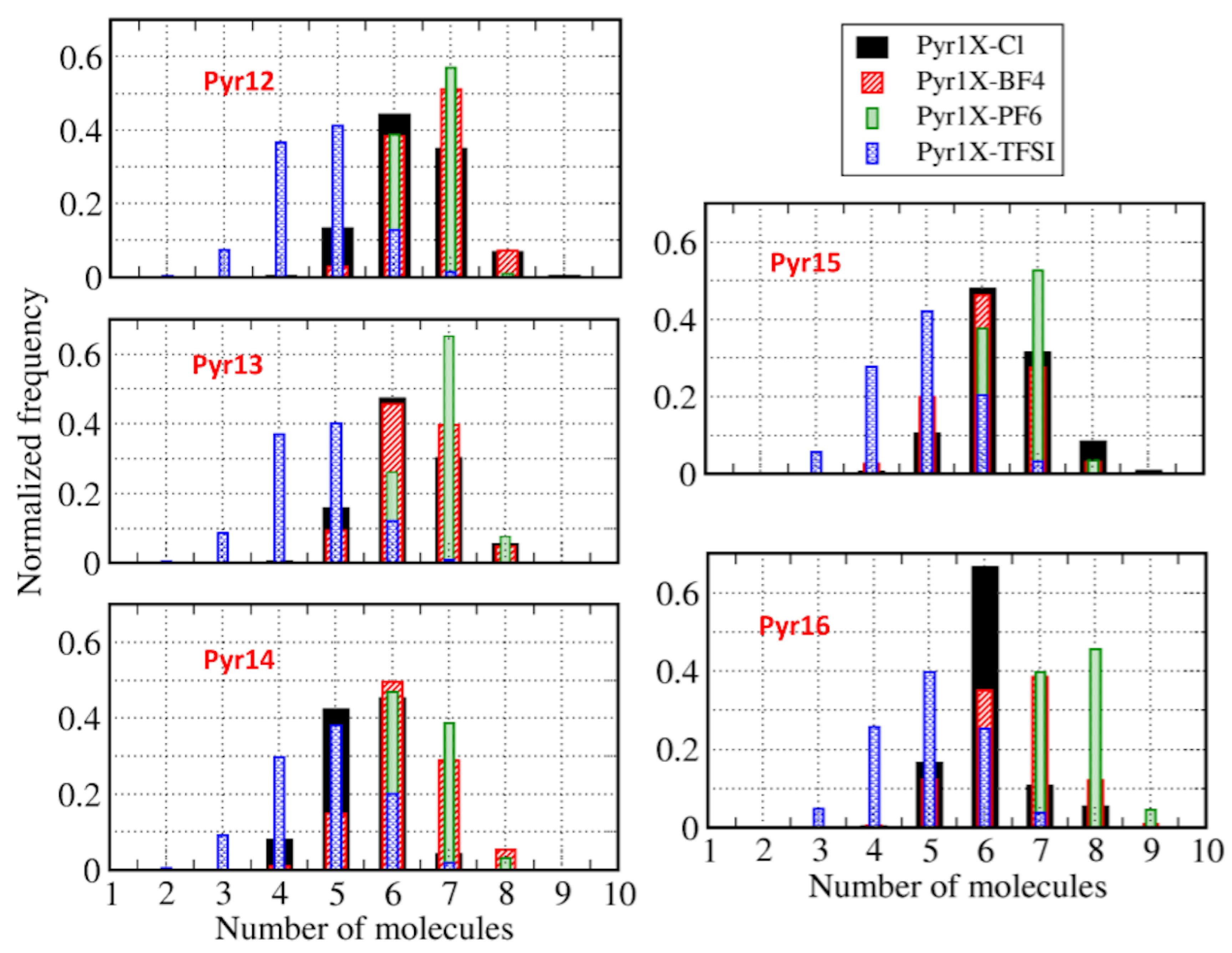
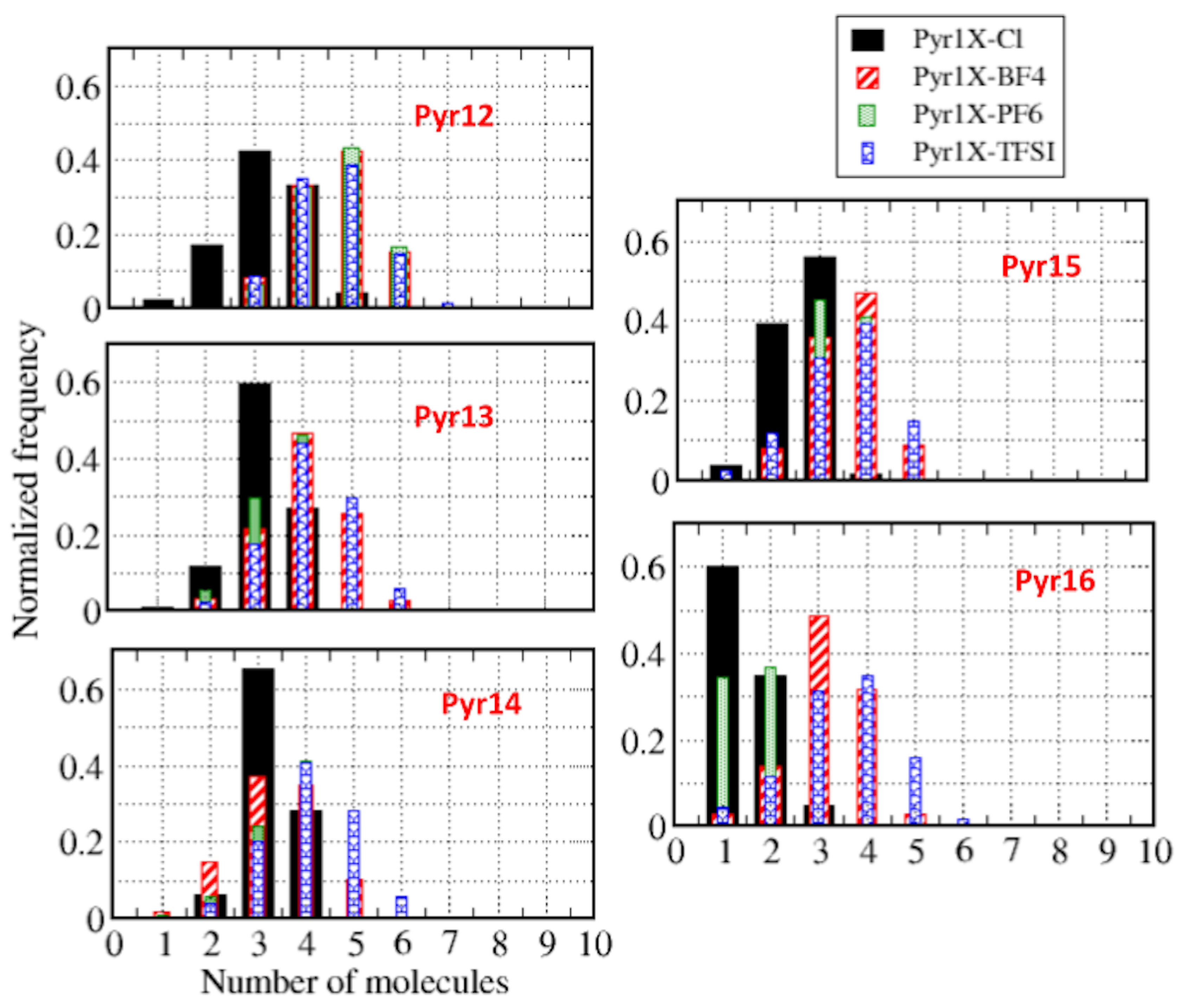

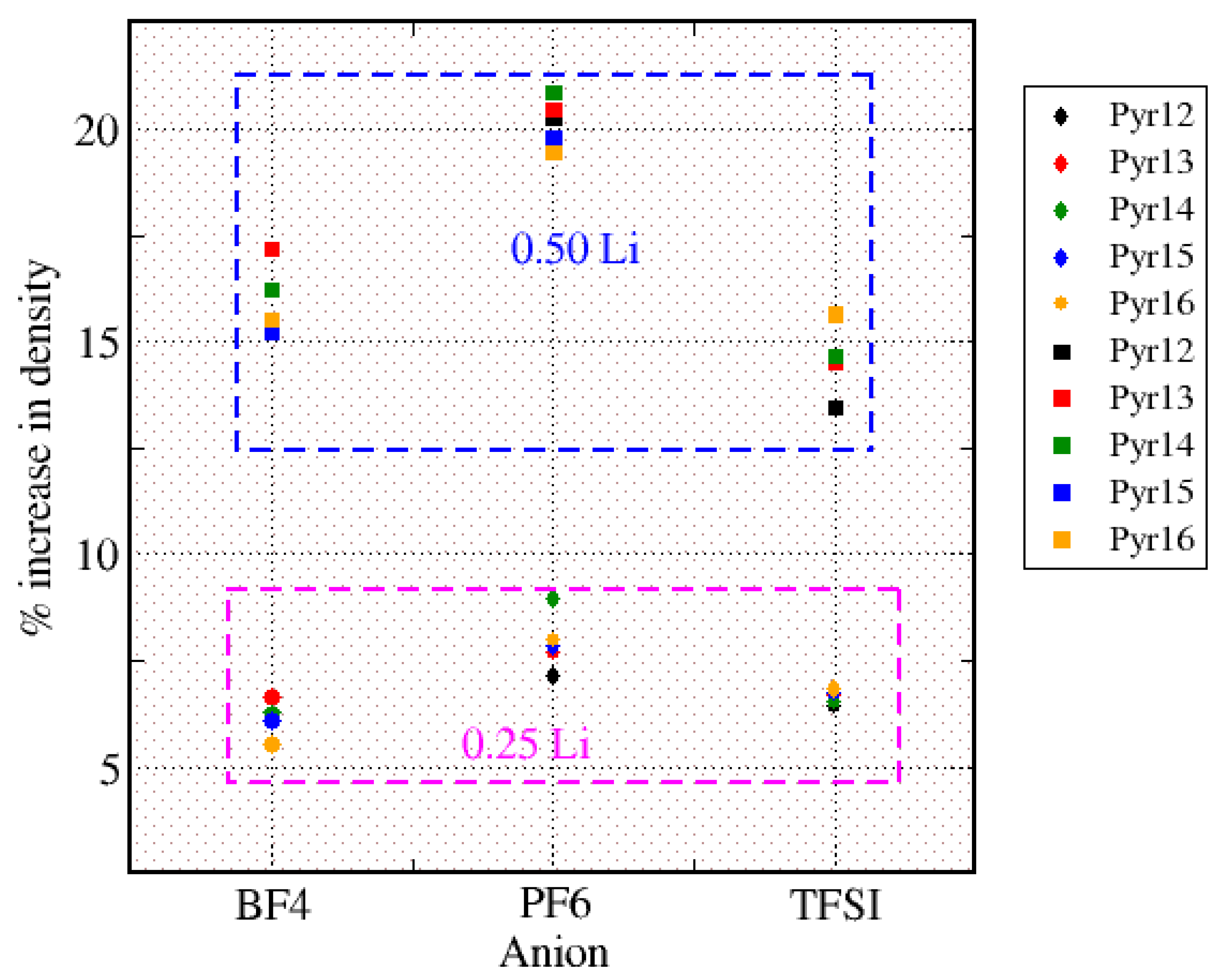
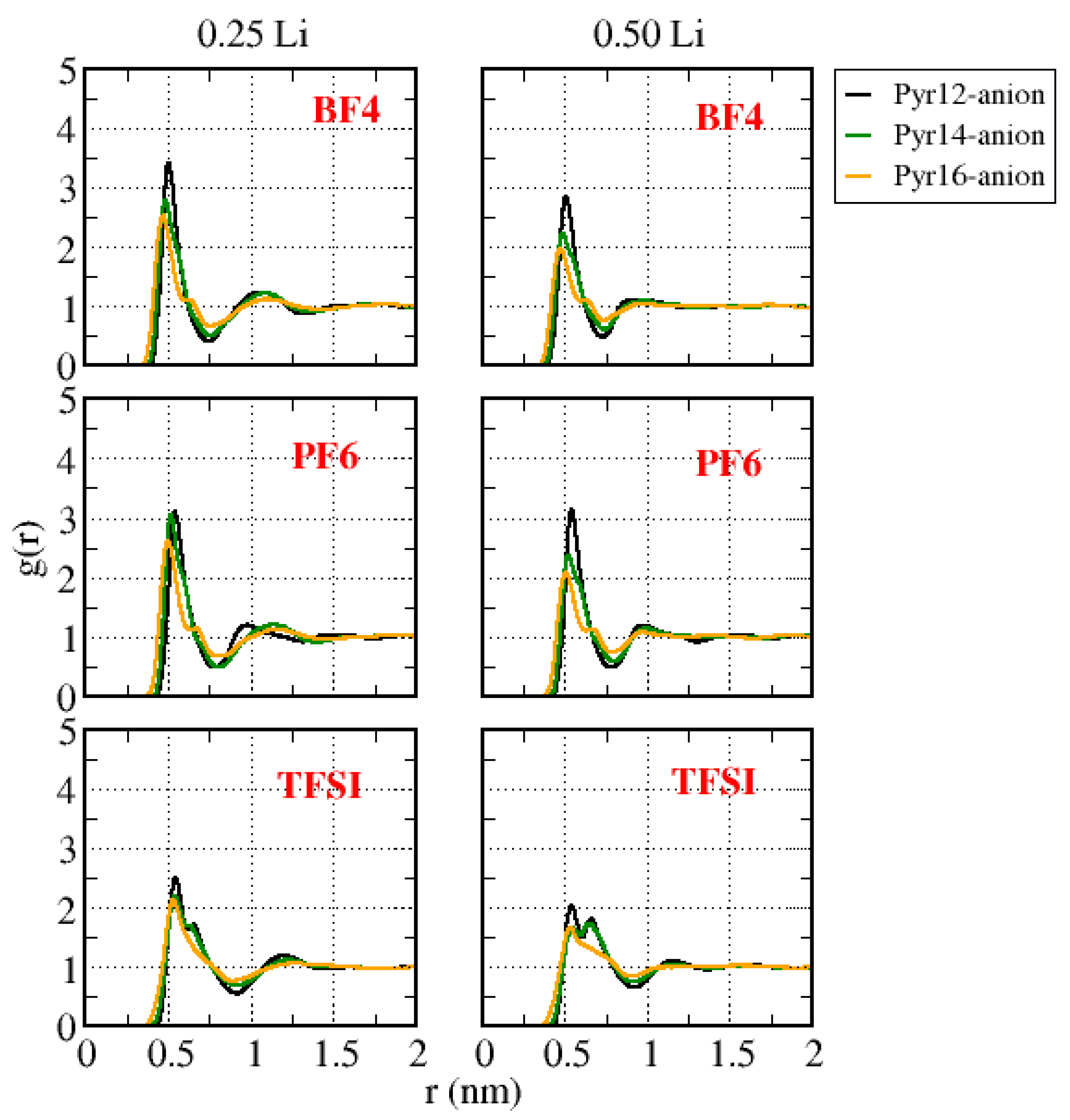
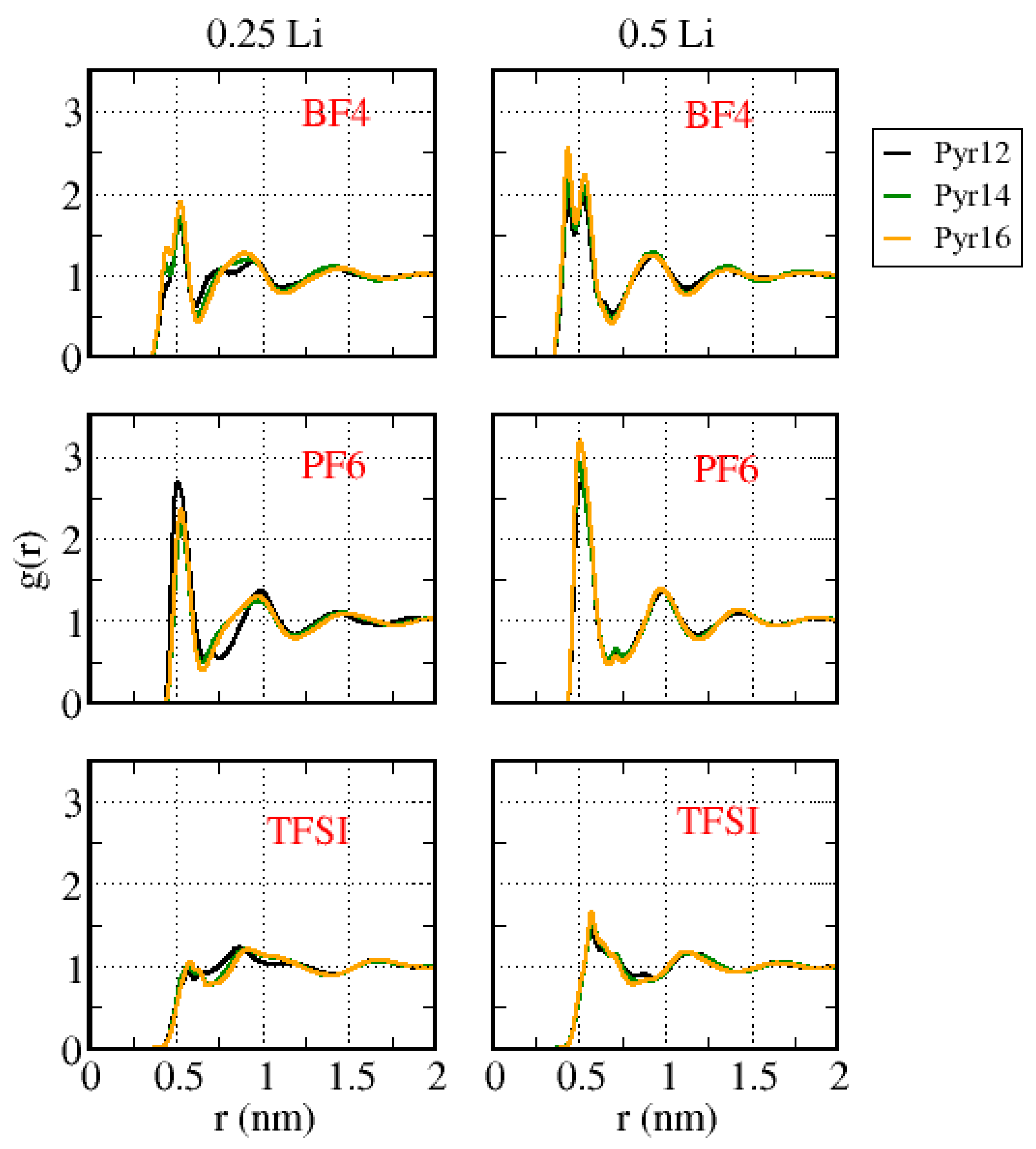

| Cations | Molar Mass (g/mol) | Anion | Molar Mass (g/mol) |
|---|---|---|---|
| Pyr12 | 114.2 | Cl | 35.4 |
| Pyr13 | 128.2 | BF4 | 86.8 |
| Pyr14 | 142.3 | PF6 | 144.9 |
| Pyr15 | 156.3 | TFSI | 280.1 |
| Pyr16 | 170.3 | - | - |
| (400 K) | Haskings [32] (390 K) | Chaban [44] (355 K) | Kashyap [68] (295 K) | |
|---|---|---|---|---|
| This Work | sim/exp | sim/exp | sim/exp | |
| Pyr13–TFSI | 1.362 | 1.264/- | -/1.378 | - |
| Pyr14–Cl | 0.969 | -/1.049 | 0.910/- | - |
| Pyr14–BF4 | 1.047 | 1.315/1.313 | 1.004/- | - |
| Pyr14–TFSI | 1.341 | 1.346/1.398 | 1.453/1.390 | |
| Pyr15–TFSI | 1.294 | - | - | 1.418/1.360 |
| Pyr16–TFSI | 1.263 | - | - | 1.387/1.320 |
| Cl | BF4 | PF6 | TFSI | |
|---|---|---|---|---|
| Pyr12 | 4.4 | 5.0 | 5.4 | 5.5 |
| Pyr13 | 4.2 | 5.0 | 5.4 | 5.5 |
| Pyr14 | 4.2 | 4.9 | 5.1 | 5.5 |
| Pyr15 | 4.1 | 4.7 | 5.1 | 5.3 |
| Pyr16 | 4.3 | 4.7 | 5.1 | 5.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salvador, M.A.; Maji, R.; Rossella, F.; Degoli, E.; Ruini, A.; Magri, R. Structural and Dynamic Characterization of Li–Ionic Liquid Electrolyte Solutions for Application in Li-Ion Batteries: A Molecular Dynamics Approach. Batteries 2023, 9, 234. https://doi.org/10.3390/batteries9040234
Salvador MA, Maji R, Rossella F, Degoli E, Ruini A, Magri R. Structural and Dynamic Characterization of Li–Ionic Liquid Electrolyte Solutions for Application in Li-Ion Batteries: A Molecular Dynamics Approach. Batteries. 2023; 9(4):234. https://doi.org/10.3390/batteries9040234
Chicago/Turabian StyleSalvador, Michele A., Rita Maji, Francesco Rossella, Elena Degoli, Alice Ruini, and Rita Magri. 2023. "Structural and Dynamic Characterization of Li–Ionic Liquid Electrolyte Solutions for Application in Li-Ion Batteries: A Molecular Dynamics Approach" Batteries 9, no. 4: 234. https://doi.org/10.3390/batteries9040234
APA StyleSalvador, M. A., Maji, R., Rossella, F., Degoli, E., Ruini, A., & Magri, R. (2023). Structural and Dynamic Characterization of Li–Ionic Liquid Electrolyte Solutions for Application in Li-Ion Batteries: A Molecular Dynamics Approach. Batteries, 9(4), 234. https://doi.org/10.3390/batteries9040234







