A Lithium-Ion Battery Capacity and RUL Prediction Fusion Method Based on Decomposition Strategy and GRU
Abstract
:1. Introduction
- (1)
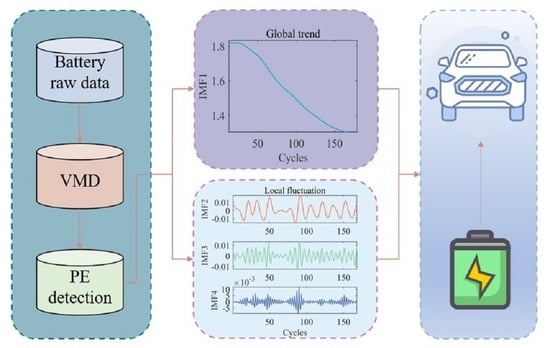
- An innovative hybrid approach for capacity and RUL prediction is developed. The measured capacity data is decoupled by the VMD algorithm into a global degradation trend sequence and local fluctuation sequences, followed by a double Gaussian aging model to predict global degradation trends and a GRU NN to predict local changes. This hybrid method overcomes to some extent the effects of measurement noise and sudden changes in capacity.
- (2)
- The modal components are determined by PE detection and then adaptively categorized into different trend types, which safeguards the subsequent prediction and enhances the noise immunity of the forecasting system.
- (3)
- A novel double Gaussian model for battery capacity aging is proposed with excellent fitting properties, for which the Levenberg–Marquardt and PF (LM-PF) algorithm overcomes the parameter sensitivity problem. The learning rate of the GRU is optimized by the beetle antennae search (BAS) algorithm.
2. Methodology
2.1. Related Theory of VMD Algorithm
2.2. PE Algorithm
- (1)
- A sequence of time series of length N is reconstructed in phase space and yields a matrix Y.
- (2)
- Rearranging each reconstructed component in ascending order gives the column indices of the positions of the elements in the vector and forms a set of symbolic sequences.
- (3)
- Calculating the probability of each symbolic sequence, i.e., , and the formula for calculating the permutation entropy of a time sequence X is
- (4)
- When , achieves a maximum value . Usually, can be normalized using :
2.3. Optimization of the VMD Algorithm with PE Detection
- (a)
- The initial parameters are set for VMD and PE, where the initial number of decompositions is set to 1.
- (b)
- VMD processing is performed on the input signal to generate IMFs, and the PE values of the resulting IMFs are calculated.
- (c)
- The presence of IMFs with PE values up to the threshold is verified.
- (d)
- If the conditions of the algorithm are met, the IMFs and the corresponding entropy values at that moment are output, and the VMD algorithm stops.
- (e)
- Otherwise, the modal component is updated and the number of decompositions is increased by 1.
- (f)
- Steps (b) to (d) are repeated until the stopping condition is satisfied, and the algorithm stops.
2.4. LM-PF Algorithm for Optimising Double Gaussian Model
- Step 1:
- The LM algorithm is applied to obtain the initial for PF.
- Step 2:
- The set of particles is generated from the prior distribution , where denotes the whole amount of particles, and all particles are initialized with a weight of .
- Step 3:
- is updated to get a new set of particles , where is the operating cycle, and is the complete amount of aging cycle; represents the importance density function.
- Step 4:
- The important weight is calculated by Equation (15) for each particle in the particle set, and the weights are normalized according to Equation (16).
- Step 5:
- A fresh batch of particles is created by resampling, where is constructed from an estimate of the model parameters for particle at cycle number .
- Step 6:
- An estimate of the capacity is obtained.
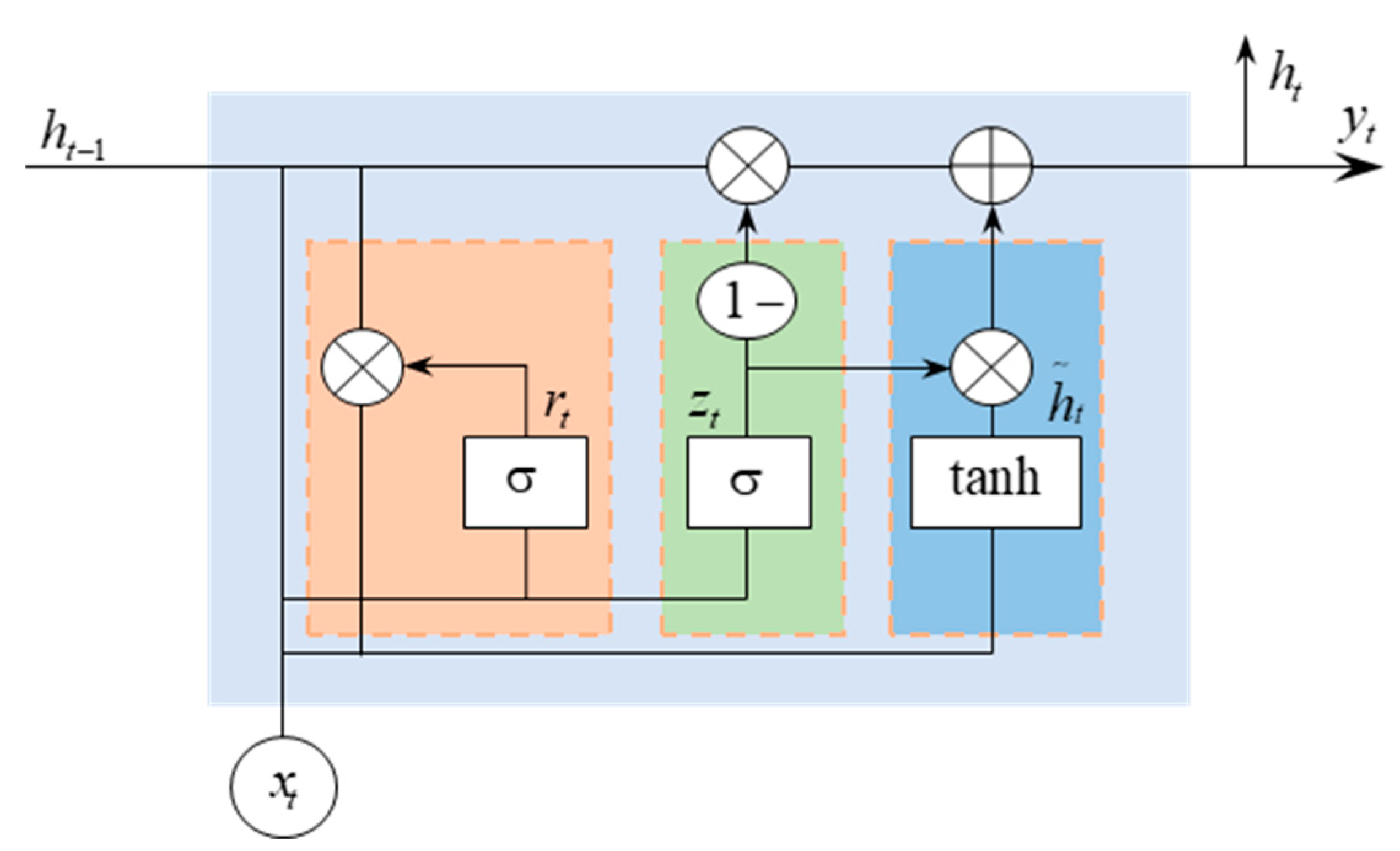
2.5. GRU NN and BAS Algorithm
3. Experimental Setup
3.1. Laboratory Apparatus and Experiment Data
- (1)
- The 18650 cylindrical batteries include batteries S5, 5, and 6, while CX2-37 is a rectangular battery. The anode and cathode of battery S5 consist of graphite and LiFePO4, while batteries 5 and 6 have a graphite anode and an LNCA cathode material. In contrast, CX2-37 utilizes LiCoO2 as the cathode material. Moreover, the battery S5 is rated at 2.4 Ah; thus, the EOL criterion is designed as 1.68 Ah. Batteries 5 and 6 have a rated capacity of 2 Ah, with a 1.4 Ah EOL criterion. The rated capacity of CX2-37 is only 1.35 Ah, with its EOL threshold considered to be 0.945 Ah.
- (2)
- The aging test of battery S5 was tested at a 25 °C constant temperature; the datasets for batteries 5 and 6 were collected at a 24 °C constant temperature, while that of CX2-37 was tested at room temperature.
- (3)
- A constant current of 1.2 A was applied to charge the battery S5 up to 4.2 V, and then the voltage was kept constant at 4.2 V until the current decreased to 48 mA. The discharge process involved applying a 2.4 A constant current, and the voltage was discharged to 3.2 V. NASA batteries 5 and 6 were charged at a 1.5 A constant current; their voltage rose to 4.2 V, and then the voltage was maintained constant at 4.2 V until the current fell to 20 mA. The discharge procedure comprised the provision of a 2 A constant current and lowering the voltage to 2.7 V and 2.5 V, respectively. CX2-37 was charged at a constant current rate of 0.5 C to 4.2 V, and then the voltage was maintained until the current dropped to 0.05 A. It was discharged at a constant current rate of 1 C until the voltage fell to 2.7 V.
3.2. Experimental Procedures
- Step 1:
- On the basis of the experimental data, the decomposition number and IMFs for capacity data were obtained by the improved PE−VMD algorithm.
- Step 2:
- The derived IMFs were adaptively divided into global degradation trend sequence and local fluctuation sequences according to their PE values.
- Step 3:
- Both the global degenerate trend sequence and the local fluctuation sequences were equally divided into the corresponding training and testing sets.
- Step 4:
- A double Gaussian capacity fading model was constructed to predict the global deterioration trend on the basis of the training set of the global degradation trend sequence adopting the LM-PF algorithm.
- Step 5:
- The training set of local fluctuation sequences was utilized, and the GRU local prediction model was trained to capture the local variations in capacity. The BAS algorithm was responsible for optimizing the learning rate of the GRU model.
- Step 6:
- The test set data were input, and the future global trend and future local fluctuation data were predicted by the double Gaussian capacity degradation model and GRU local prediction model, respectively.
- Step 7:
- The final capacity prediction result was generated by adding the predicted future local fluctuation data to the future global trend data.
- Step 8:
- The RUL was calculated from the EOL values.
3.3. Evaluation Criteria
4. Experimental Verification and Analysis
4.1. Battery Capacity Decomposition Based on PE−VMD
4.2. Capacity Prediction
4.3. RUL Prediction
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cao, J.; Harrold, D.; Fan, Z.; Morstyn, T.; Healey, D.; Li, K. Deep Reinforcement Learning-Based Energy Storage Arbitrage with Accurate Lithium-Ion Battery Degradation Model. IEEE Trans. Smart Grid 2020, 11, 4513–4521. [Google Scholar] [CrossRef]
- Ding, X.L.; Wang, Z.P.; Zhang, L.; Wang, C. Longitudinal Vehicle Speed Estimation for Four-Wheel-Independently-Actuated Electric Vehicles Based on Multi-Sensor Fusion. IEEE Trans. Veh. Technol. 2020, 69, 12797–12806. [Google Scholar] [CrossRef]
- Xu, J.N.; Wang, T.S.; Pei, L.; Mao, S.T.; Zhu, C.B. Parameter identification of electrolyte decomposition state in lithium-ion batteries based on a reduced pseudo two-dimensional model with Padé approximation. J. Power Sources 2020, 460, 228093. [Google Scholar] [CrossRef]
- Sadabadi, K.K.; Jin, X.; Rizzoni, G. Prediction of remaining useful life for a composite electrode lithium ion battery cell using an electrochemical model to estimate the state of health. J. Power Sources 2021, 481, 228861. [Google Scholar] [CrossRef]
- Duong, P.L.T.; Raghavan, N. Heuristic Kalman optimized particle filter for remaining useful life prediction of lithium-ion battery. Microelectron. Reliab. 2018, 81, 232–243. [Google Scholar] [CrossRef]
- Sun, J.L.; Tang, C.Y.; Li, X.; Wang, T.R.; Jiang, T.; Tang, Y.; Chen, S.H.; Qiu, S.S.; Zhu, C.B. A remaining charging electric quantity based pack available capacity optimization method considering aging inconsistency. eTransportation 2022, 11, 100149. [Google Scholar] [CrossRef]
- Dong, G.Z.; Chen, Z.H.; Wei, J.W.; Ling, Q. Battery Health Prognosis Using Brownian Motion Modeling and Particle Filtering. IEEE Trans. Ind. Electron. 2018, 65, 8646–8655. [Google Scholar] [CrossRef]
- Zhang, H.; Miao, Q.; Zhang, X.; Liu, Z.W. An improved unscented particle filter approach for lithium-ion battery remaining useful life prediction. Microelectron. Reliab. 2018, 81, 288–298. [Google Scholar] [CrossRef]
- Hong, G.X.; Song, W.Q.; Gao, Y.; Zio, E.; Kudreyko, A. An iterative model of the generalized Cauchy process for predicting the remaining useful life of lithium-ion batteries. Measurement 2022, 187, 110269. [Google Scholar] [CrossRef]
- Elsheikh, A.H. Applications of machine learning in friction stir welding: Prediction of joint properties, real-time control and tool failure diagnosis. Eng. Appl. Artif. Intell. 2023, 121, 105961. [Google Scholar] [CrossRef]
- Elsheikh, A.H.; Shanmugan, S.; Sathyamurthy, R.; Thakur, A.K.; Issa, M.; Panchal, H.; Muthuramalingam, T.; Kumar, R.; Sharifpur, M. Low-cost bilayered structure for improving the performance of solar stills: Performance/cost analysis and water yield prediction using machine learning. Sustain. Energy Technol. Assess. 2022, 49, 101783. [Google Scholar] [CrossRef]
- Moustafa, E.B.; Elsheikh, A. Predicting Characteristics of Dissimilar Laser Welded Polymeric Joints Using a Multi-Layer Perceptrons Model Coupled with Archimedes Optimizer. Polymers 2023, 15, 233. [Google Scholar] [CrossRef]
- Elsheikh, A.H.; El-Said, E.M.S.; Elaziz, M.A.; Fujii, M.; El-Tahan, H.R. Water distillation tower: Experimental investigation, economic assessment, and performance prediction using optimized machine-learning model. J. Clean. Prod. 2023, 388, 135896. [Google Scholar] [CrossRef]
- Hu, W.Y.; Zhao, S.S. Remaining useful life prediction of lithium-ion batteries based on wavelet denoising and transformer neural network. Front. Energy Res. 2022, 10, 969168. [Google Scholar] [CrossRef]
- Wu, J.J.; Cheng, X.K.; Huang, H.; Fang, C.; Zhang, L.; Zhao, X.K.; Zhang, L.; Xing, J.J. Remaining useful life prediction of Lithium-ion batteries based on PSO-RF algorithm. Front. Energy Res. 2023, 10, 937035. [Google Scholar] [CrossRef]
- Zhang, L.J.; Ji, T.; Yu, S.H.; Liu, G.C. Accurate Prediction Approach of SOH for Lithium-Ion Batteries Based on LSTM Method. Batteries 2023, 9, 177. [Google Scholar] [CrossRef]
- Wang, Z.K.; Zeng, S.K.; Guo, J.B.; Qin, T.C. Remaining capacity estimation of lithium-ion batteries based on the constant voltage charging profile. PLoS ONE 2018, 13, e0200169. [Google Scholar] [CrossRef] [Green Version]
- Li, X.Y.; Wang, Z.P.; Yan, J.Y. Prognostic health condition for lithium battery using the partial incremental capacity and Gaussian process regression. J. Power Sources 2019, 421, 56–67. [Google Scholar] [CrossRef]
- Lee, C.-J.; Kim, B.-K.; Kwon, M.-K.; Nam, K.; Kang, S.-W. Real-Time Prediction of Capacity Fade and Remaining Useful Life of Lithium-Ion Batteries Based on Charge/Discharge Characteristics. Electronics 2021, 10, 846. [Google Scholar] [CrossRef]
- Ji, Y.F.; Chen, Z.W.; Shen, Y.; Yang, K.; Wang, Y.R.; Cui, J. An RUL prediction approach for lithium-ion battery based on SADE-MESN. Appl. Soft Comput. 2021, 104, 107195. [Google Scholar] [CrossRef]
- Cadini, F.; Sbarufatti, C.; Cancelliere, F. Giglio, State-of-life prognosis and diagnosis of lithium-ion batteries by data-driven particle filters. Appl. Energy 2019, 235, 661–672. [Google Scholar] [CrossRef]
- Zhao, S.S.; Zhang, C.L.; Wang, Y.Z. Lithium-ion battery capacity and remaining useful life prediction using board learning system and long short-term memory neural network. J. Energy Storage 2022, 52, 104901. [Google Scholar] [CrossRef]
- Chen, Z.W.; Shi, N.; Ji, Y.F.; Niu, M.; Wang, Y.R. Lithium-ion batteries remaining useful life prediction based on BLS-RVM. Energy 2021, 234, 121269. [Google Scholar] [CrossRef]
- Chen, X.W.; Liu, Z. A long short-term memory neural network based Wiener process model for remaining useful life prediction. Reliability Reliab. Eng. Syst. Saf. 2022, 226, 108651. [Google Scholar] [CrossRef]
- Zhang, Y.Z.; Xiong, R.; He, H.W.; Pecht, M. Validation and verification of a hybrid method for remaining useful life prediction of lithium-ion batteries. J. Cleaner Prod. 2019, 212, 240–249. [Google Scholar] [CrossRef]
- Yu, J.B. State-of-Health Monitoring and Prediction of Lithium-Ion Battery Using Probabilistic Indication and State-Space Model. IEEE Trans. Instrum. Meas. 2015, 64, 2937–2949. [Google Scholar] [CrossRef]
- Yu, J.B. State of health prediction of lithium-ion batteries: Multiscale logic regression and Gaussian process regression ensemble. Reliab. Eng. Syst. Saf. 2018, 174, 82–95. [Google Scholar] [CrossRef]
- Ma, Q.H.; Zheng, Y.; Yang, W.D.; Zhang, Y.; Zhang, H. Remaining useful life prediction of lithium battery based on capacity regeneration point detection. Energy 2021, 234, 121233. [Google Scholar] [CrossRef]
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef]
- Ma, C.Y.; Li, Y.B.; Wang, X.Z.; Cai, Z.Q. Early fault diagnosis of rotating machinery based on composite zoom permutation entropy. Reliab. Eng. Syst. Saf. 2023, 230, 108967. [Google Scholar] [CrossRef]
- Mansourian, N.; Sarafan, S.; Azar, F.T.; Ghirmai, T.; Cao, H. Novel QRS detection based on the Adaptive Improved Permutation Entropy. Biomed. Signal Process. Control 2023, 80, 104270. [Google Scholar] [CrossRef]
- Rajabi, S.; Azari, M.S.; Santini, S.; Flammini, F. Fault diagnosis in industrial rotating equipment based on permutation entropy, signal processing and multi-output neuro-fuzzy classifier. Expert Syst. Appl. 2022, 206, 117754. [Google Scholar] [CrossRef]
- Cho, K.; van Merrienboer, B.; Bahdanau, D.; Bengio, Y. On the Properties of Neural Machine Translation: Encoder-Decoder Approaches. arXiv 2014, arXiv:1409.1259. [Google Scholar]
- Saha, B.; Goebel, K. Battery Data Set, NASA Ames Prognostics Data Repository; NASA Ames Research Center: Moffett Field, CA, USA, 2007.
- Pecht, M. Battery Data Set; Center for Advanced Life Cycle Engineering CALCE, University of Maryland: College Park, MD, USA.
- Li, L.L.; Liu, Z.F.; Tseng, M.L.; Chiu, A.S.F. Enhancing the Lithium-ion battery life predictability using a hybrid method. Appl. Soft Comput. 2019, 74, 110–121. [Google Scholar] [CrossRef]
- Xue, Z.W.; Zhang, Y.; Cheng, C.; Ma, G.J. Remaining useful life prediction of lithium-ion batteries with adaptive unscented kalman filter and optimized support vector regression. Neurocomputing 2020, 376, 95–102. [Google Scholar] [CrossRef]
- Chen, L.P.; Xu, L.J.; Zhou, Y.L. Novel Approach for Lithium-Ion Battery On-Line Remaining Useful Life Prediction Based on Permutation Entropy. Energies 2018, 11, 820. [Google Scholar] [CrossRef] [Green Version]










| (a) Battery S5 | ||||||||
| IMFs | IMF1 | IMF2 | IMF3 | IMF4 | ||||
| K | Hpe | R2 | Hpe | R2 | Hpe | R2 | Hpe | R2 |
| K = 1 | 0.1575 | 0.9995 | ||||||
| K = 2 | 0.1445 | 0.9802 | 0.2995 | 0.7015 | ||||
| K = 3 | 0.1373 | 0.9801 | 0.3022 | 0.7021 | 0.6042 | 0.0129 | ||
| K = 4 | 0.0412 | 0.9799 | 0.2719 | 0.7121 | 0.3622 | 0.0625 | 0.7102 | 0.0122 |
| (b) Battery 5 | ||||||||
| IMFs | IMF1 | IMF2 | IMF3 | IMF4 | ||||
| K | Hpe | R2 | Hpe | R2 | Hpe | R2 | Hpe | R2 |
| K = 1 | 0.0832 | 0.9982 | ||||||
| K = 2 | 0.0885 | 0.9981 | 0.6475 | 0.0642 | ||||
| K = 3 | 0.0542 | 0.9977 | 0.4435 | 0.1163 | 0.6485 | 0.0517 | ||
| K = 4 | 0.0542 | 0.9977 | 0.4409 | 0.1156 | 0.6386 | 0.0514 | 0.7519 | 0.0312 |
| (c) Battery 6 | ||||||||
| IMFs | IMF1 | IMF2 | IMF3 | |||||
| K | Hpe | R2 | Hpe | R2 | Hpe | R2 | ||
| K = 1 | 0.1027 | 0.9963 | ||||||
| K = 2 | 0.0832 | 0.9961 | 0.6359 | 0.0792 | ||||
| K = 3 | 0.0387 | 0.9955 | 0.4841 | 0.1179 | 0.7651 | 0.0518 | ||
| (d) Battery CX2-37 | ||||||||
| IMFs | IMF1 | IMF2 | IMF3 | IMF4 | ||||
| K | Hpe | R2 | Hpe | R2 | Hpe | R2 | Hpe | R2 |
| K = 1 | 0.3944 | 0.9994 | ||||||
| K = 2 | 0.2920 | 0.9985 | 0.5623 | 0.0726 | ||||
| K = 3 | 0.1533 | 0.9984 | 0.4554 | 0.0740 | 0.6097 | 0.0285 | ||
| K = 4 | 0.0771 | 0.9981 | 0.3956 | 0.0793 | 0.5845 | 0.0366 | 0.8078 | 0.0265 |
| Battery | RMSE | MAPE (%) |
|---|---|---|
| Battery S5 | 0.0103 | 0.4288 |
| Battery B5 | 0.0083 | 0.4555 |
| Battery B6 | 0.0142 | 0.6446 |
| Battery CX2-37 | 0.0053 | 0.4289 |
| Battery | Algorithm | RMSE | MAPE (%) |
|---|---|---|---|
| Battery S5 | PF | 0.0173 | 0.7342 |
| GRU | 0.0435 | 1.8197 | |
| Battery 5 | PF | 0.0172 | 0.8059 |
| GRU | 0.0149 | 0.8081 | |
| Battery 6 | PF | 0.0243 | 1.0916 |
| GRU | 0.0243 | 1.2754 | |
| Battery CX2-37 | PF | 0.0109 | 0.8720 |
| GRU | 0.0101 | 0.8022 |
| Battery | EOL Cycle | Actual RUL | Predicted RUL | AE |
|---|---|---|---|---|
| Battery S5 | 292 | 137 | 138 | 1 |
| Battery 5 | 124 | 54 | 54 | 0 |
| Battery 6 | 108 | 43 | 42 | 1 |
| Battery CX2-37 | 1021 | 436 | 434 | 2 |
| Battery | Methods | Training Cycles | RMSE | AE |
|---|---|---|---|---|
| Battery 5 | QPSO−SVM [36] | 110 | 0.03 | 5 |
| BLS−RVM [23] | 100 | 0.0105 | 1 | |
| PSO−PF [5] | 80 | 0.0026 | 10 | |
| RVR−UKF [37] | 80 | 0.0381 | 14 | |
| AEKF−GASVR [37] | 80 | 0.0304 | 18 | |
| AUKF−GASVR [37] | 80 | 0.0192 | 3 | |
| EMD−ARIMA [38] | 80 | 0.0356 | 8 | |
| EMD-LR−GPR [27] | 70 | 0.0168 | 16 | |
| VMD−PF−GRU | 70 | 0.0091 | 0 | |
| Battery 6 | BLS−RVM [23] | 100 | 0.0138 | 3 |
| QPSO−SVM [36] | 80 | 0.07 | 8 | |
| PSO-PF [5] | 80 | 0.0022 | 6 | |
| RVR−UKF [37] | 80 | 0.1265 | 17 | |
| AEKF−GASVR [37] | 80 | 0.0593 | 8 | |
| AUKF−GASVR [37] | 80 | 0.0483 | 7 | |
| EMD−LR−GPR [27] | 70 | 0.0292 | 21 | |
| VMD−PF−GRU | 65 | 0.0187 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Li, Y.; Luo, L.; Zhang, C. A Lithium-Ion Battery Capacity and RUL Prediction Fusion Method Based on Decomposition Strategy and GRU. Batteries 2023, 9, 323. https://doi.org/10.3390/batteries9060323
Liu H, Li Y, Luo L, Zhang C. A Lithium-Ion Battery Capacity and RUL Prediction Fusion Method Based on Decomposition Strategy and GRU. Batteries. 2023; 9(6):323. https://doi.org/10.3390/batteries9060323
Chicago/Turabian StyleLiu, Huihan, Yanmei Li, Laijin Luo, and Chaolong Zhang. 2023. "A Lithium-Ion Battery Capacity and RUL Prediction Fusion Method Based on Decomposition Strategy and GRU" Batteries 9, no. 6: 323. https://doi.org/10.3390/batteries9060323
APA StyleLiu, H., Li, Y., Luo, L., & Zhang, C. (2023). A Lithium-Ion Battery Capacity and RUL Prediction Fusion Method Based on Decomposition Strategy and GRU. Batteries, 9(6), 323. https://doi.org/10.3390/batteries9060323