Battery State of Health Estimate Strategies: From Data Analysis to End-Cloud Collaborative Framework
Abstract
:1. Introduction
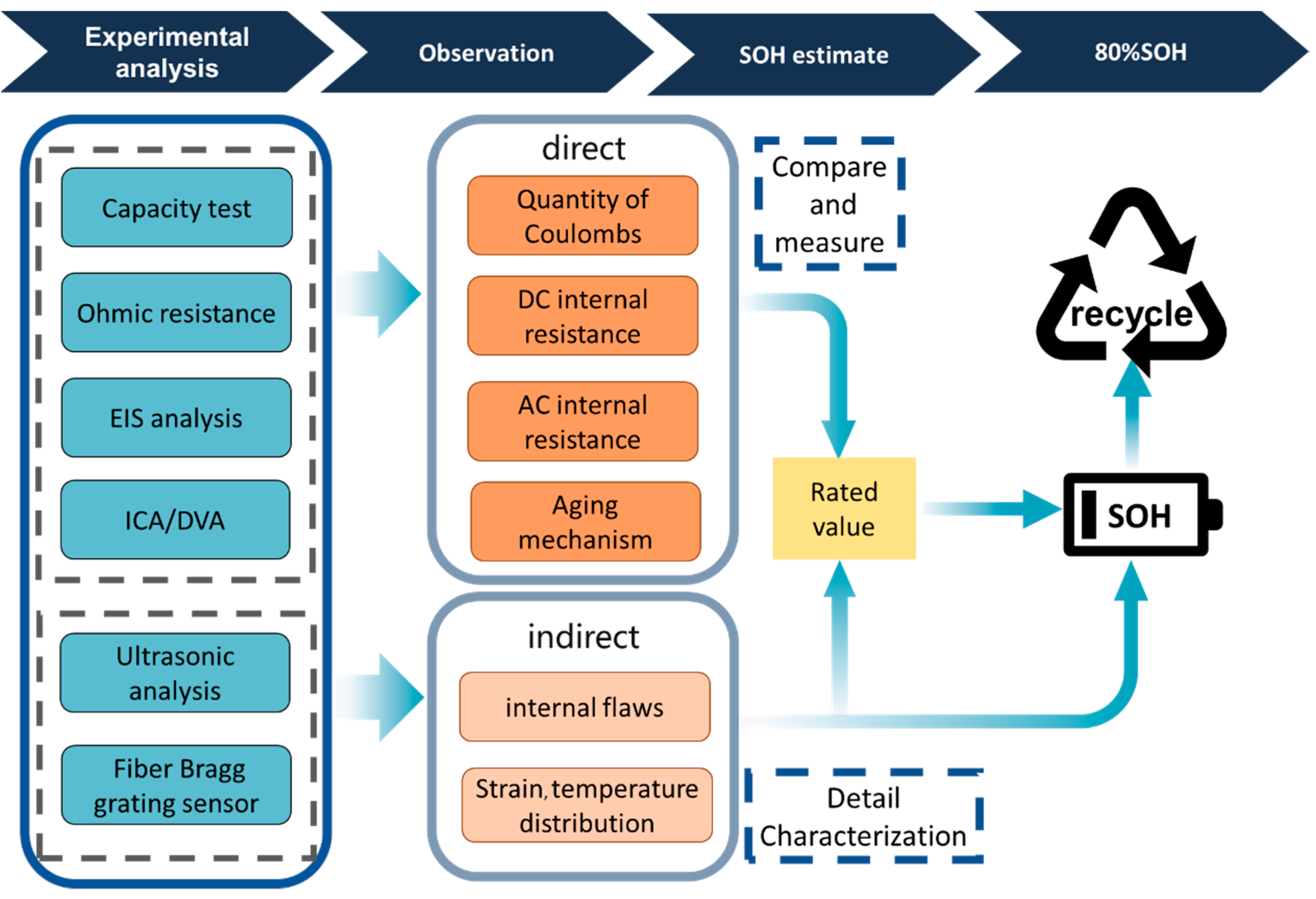
2. Experimental Analysis Methods for SOH Estimation
2.1. Direct Experimental Methods
2.1.1. Capacity Test Technique
- Step 1: CC-CV charging at C/3 and 4.2 V;
- Step 2: CC discharge till 2.5 V at 0.1 C.
2.1.2. Ohmic Resistance
2.1.3. Electrochemical Impedance Spectroscopy
2.1.4. Incremental Capacity Analysis (ICA) and Differential Voltage Analysis (DVA)
2.2. Advanced Sensors Experiment
2.2.1. Ultrasonic Technique
2.2.2. Fiber Bragg Grating Technique
2.3. Other Experimental Method
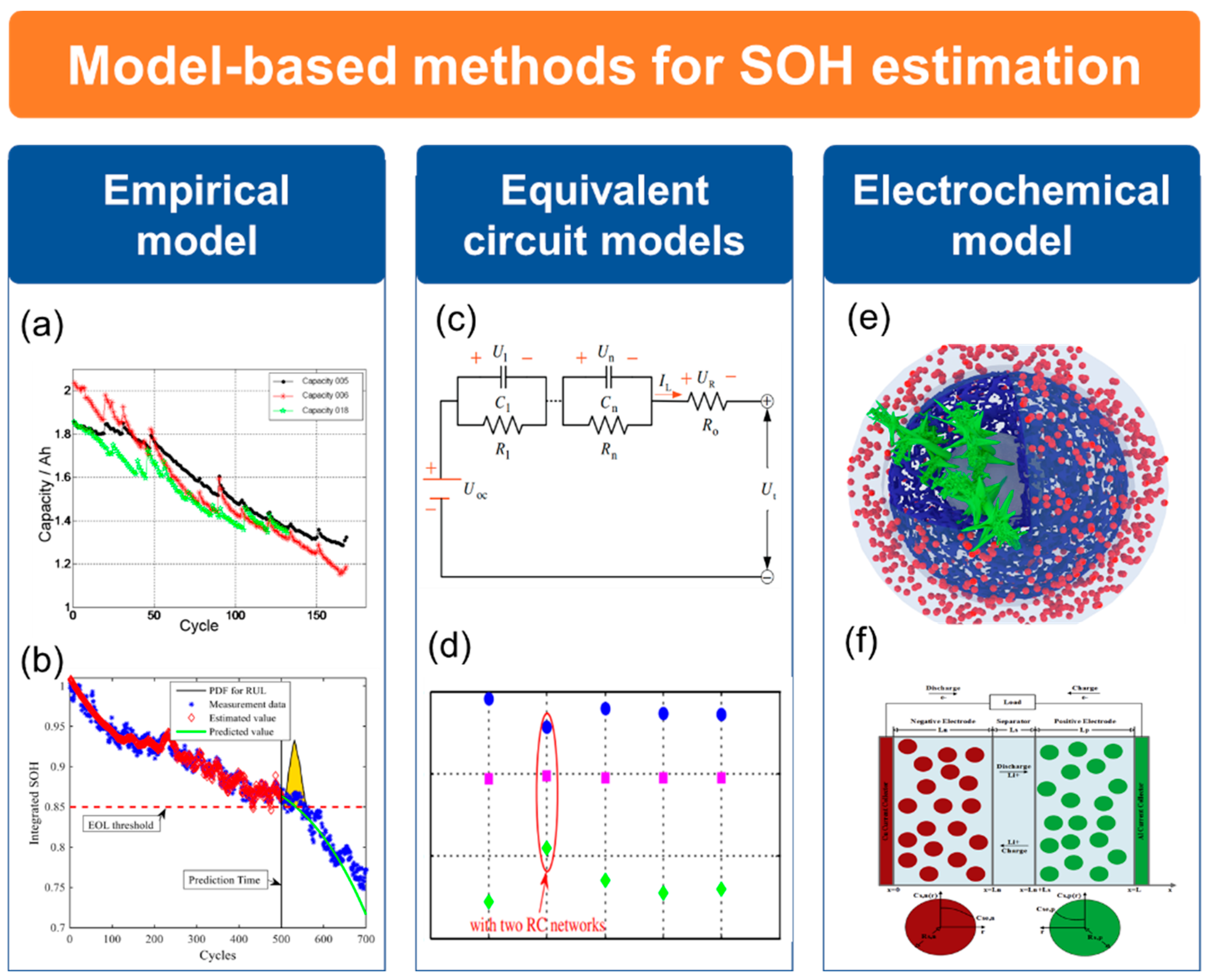
3. Model-Based Methods for SOH Estimation
3.1. Empirical Models
3.2. Equivalent Circuit Models
3.3. Electrochemical Models
4. Machine Learning Methods for SOH Estimation
4.1. Probabilistic-Based Algorithms
4.2. Non-Probabilistic Algorithms
4.2.1. Supervised Learning
4.2.2. Un-Supervised Learning
4.3. Sime-Probabilistic Algorithms
5. Applications of Knowledge-Based AI and Knowledge Graphs
6. Multi-Model Fusion and End-Cloud Collaborative Framework for SOH Estimation
6.1. Cloud-Side Highly Accurate Model
6.2. End-Side Highly Real-Time Model
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lanz, L.; Noll, B.; Schmidt, T.S.; Steffen, B. Comparing the Levelized Cost of Electric Vehicle Charging Options in Europe. Nat. Commun. 2022, 13, 5277. [Google Scholar] [CrossRef]
- Xu, H. Facilitating Full and Effective Implementation of the Paris Agreement for Carbon Neutrality Vision. Carbon Neutrality 2022, 1, 3. [Google Scholar] [CrossRef]
- Needell, Z.A.; McNerney, J.; Chang, M.T.; Trancik, J.E. Potential for Widespread Electrification of Personal Vehicle Travel in the United States. Nat. Energy 2016, 1, 16112. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Feng, L.; Palmer, P.I.; Liu, Y.; Fang, S.; Bösch, H.; O’Dell, C.W.; Tang, X.; Yang, D.; Liu, L.; et al. Large Chinese Land Carbon Sink Estimated from Atmospheric Carbon Dioxide Data. Nature 2020, 586, 720–723. [Google Scholar] [CrossRef]
- Jain, R.K.; Qin, J.; Rajagopal, R. Data-Driven Planning of Distributed Energy Resources amidst Socio-Technical Complexities. Nat. Energy 2017, 2, 17112. [Google Scholar] [CrossRef]
- Guo, J.; Zhang, P.; Wu, D.; Liu, Z.; Ge, H.; Zhang, S.; Yang, X. A New Collaborative Optimization Method for a Distributed Energy System Combining Hybrid Energy Storage. Sustain. Cities Soc. 2021, 75, 103330. [Google Scholar] [CrossRef]
- Huang, Y.; Duan, J.; Zheng, X.; Wen, J.; Dai, Y.; Wang, Z.; Luo, W.; Huang, Y. Lithium Metal-Based Composite: An Emerging Material for Next-Generation Batteries. Matter 2020, 3, 1009–1030. [Google Scholar] [CrossRef]
- Han, X.; Lu, L.; Zheng, Y.; Feng, X.; Li, Z.; Li, J.; Ouyang, M. A Review on the Key Issues of the Lithium Ion Battery Degradation among the Whole Life Cycle. eTransportation 2019, 1, 100005. [Google Scholar] [CrossRef]
- Hu, X.; Xu, L.; Lin, X.; Pecht, M. Battery Lifetime Prognostics. Joule 2020, 4, 310–346. [Google Scholar] [CrossRef]
- Lai, X.; Huang, Y.; Gu, H.; Deng, C.; Han, X.; Feng, X.; Zheng, Y. Turning Waste into Wealth: A Systematic Review on Echelon Utilization and Material Recycling of Retired Lithium-Ion Batteries. Energy Storage Mater 2021, 40, 96–123. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, T.; Gao, Q.; Han, Z.; Jin, Y.; Li, L.; Yang, K.; Xu, Y.; Liu, X.; Xu, X.; et al. Assessment and Management of Health Status in Full Life Cycle of Echelon Utilization for Retired Power Lithium Batteries. J. Clean Prod. 2022, 379, 134583. [Google Scholar] [CrossRef]
- Birkl, C.R.; Roberts, M.R.; McTurk, E.; Bruce, P.G.; Howey, D.A. Degradation Diagnostics for Lithium Ion Cells. J. Power Sources 2017, 341, 373–386. [Google Scholar] [CrossRef]
- Heiskanen, S.K.; Kim, J.; Lucht, B.L. Generation and Evolution of the Solid Electrolyte Interphase of Lithium-Ion Batteries. Joule 2019, 3, 2322–2333. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, L.; Gao, X.; Pan, Y.; Liu, X.; Feng, X. Modeling of Lithium Plating in Lithium Ion Batteries Based on Monte Carlo Method. J. Power Sources 2022, 541, 231568. [Google Scholar] [CrossRef]
- Zhang, L.; Yu, H.; Wang, W.; Xie, H.; Wang, M.; Yang, S.; Chen, S.; Liu, X. Revealing the Lithium Dendrite Deposition/Dissolution Progression Based on Monte Carlo Method. J. Energy Storage 2022, 55, 105473. [Google Scholar] [CrossRef]
- Al-Zubaidi R-Smith, N.; Leitner, M.; Alic, I.; Toth, D.; Kasper, M.; Romio, M.; Surace, Y.; Jahn, M.; Kienberger, F.; Ebner, A.; et al. Assessment of Lithium Ion Battery Ageing by Combined Impedance Spectroscopy, Functional Microscopy and Finite Element Modelling. J. Power Sources 2021, 512, 230459. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, L.; Yu, H.; Wang, J.; Li, J.; Yang, K.; Zhao, Y.; Wang, H.; Wu, B.; Brandon, N.P.; et al. Bridging Multiscale Characterization Technologies and Digital Modeling to Evaluate Lithium Battery Full Lifecycle. Adv. Energy Mater 2022, 12, 2200889. [Google Scholar] [CrossRef]
- Dubarry, M.; Svoboda, V.; Hwu, R.; Liaw, B.Y. Incremental Capacity Analysis and Close-to-Equilibrium OCV Measurements to Quantify Capacity Fade in Commercial Rechargeable Lithium Batteries. Electrochem. Solid-State Lett. 2006, 9, A454–A457. [Google Scholar] [CrossRef]
- Dubarry, M.; Liaw, B.Y. Identify Capacity Fading Mechanism in a Commercial LiFePO4 Cell. J. Power Sources 2009, 194, 541–549. [Google Scholar] [CrossRef]
- Dubarry, M.; Beck, D. Perspective on Mechanistic Modeling of Li-Ion Batteries. Acc. Mater Res. 2022, 3, 843–853. [Google Scholar] [CrossRef]
- Wu, B.; Widanage, W.D.; Yang, S.; Liu, X. Battery Digital Twins: Perspectives on the Fusion of Models, Data and Artificial Intelligence for Smart Battery Management Systems. Energy AI 2020, 1, 100016. [Google Scholar] [CrossRef]
- Xu, P.; Dai, Q.; Gao, H.; Liu, H.; Zhang, M.; Li, M.; Chen, Y.; An, K.; Meng, Y.S.; Liu, P.; et al. Efficient Direct Recycling of Lithium-Ion Battery Cathodes by Targeted Healing. Joule 2020, 4, 2609–2626. [Google Scholar] [CrossRef]
- Tian, J.; Xu, R.; Wang, Y.; Chen, Z. Capacity Attenuation Mechanism Modeling and Health Assessment of Lithium-Ion Batteries. Energy 2021, 221, 119682. [Google Scholar] [CrossRef]
- Schuster, S.F.; Bach, T.; Fleder, E.; Müller, J.; Brand, M.; Sextl, G.; Jossen, A. Nonlinear Aging Characteristics of Lithium-Ion Cells under Different Operational Conditions. J. Energy Storage 2015, 1, 44–53. [Google Scholar] [CrossRef]
- Ng, K.S.; Moo, C.S.; Chen, Y.P.; Hsieh, Y.C. Enhanced Coulomb Counting Method for Estimating State-of-Charge and State-of-Health of Lithium-Ion Batteries. Appl. Energy 2009, 86, 1506–1511. [Google Scholar] [CrossRef]
- Fan, L.; Wang, P.; Cheng, Z. A Remaining Capacity Estimation Approach of Lithium-Ion Batteries Based on Partial Charging Curve and Health Feature Fusion. J. Energy Storage 2021, 43, 103115. [Google Scholar] [CrossRef]
- Divakar, B.P.; Cheng, K.W.E.; Wu, H.J.; Xu, J.; Ma, H.B.; Ting, W.; Ding, K.; Choi, W.F.; Huang, B.F.; Leung, C.H. Battery Management System and Control Strategy for Hybrid and Electric Vehicle. In Proceedings of the 2009 3rd International Conference on Power Electronics Systems and Applications (PESA), Hong Kong, China, 1 September 2009; pp. 1–6. [Google Scholar]
- Tang, X.; Zhou, Y.; Gao, F.; Lai, X. Joint Estimation of State-of-Charge and State-of-Health for All Cells in the Battery Pack Using “Leader-Follower” Strategy. eTransportation 2023, 15, 100213. [Google Scholar] [CrossRef]
- Remmlinger, J.; Buchholz, M.; Meiler, M.; Bernreuter, P.; Dietmayer, K. State-of-Health Monitoring of Lithium-Ion Batteries in Electric Vehicles by on-Board Internal Resistance Estimation. J. Power Sources 2011, 196, 5357–5363. [Google Scholar] [CrossRef]
- Chen, L.; Zhang, M.; Ding, Y.; Wu, S.; Li, Y.; Liang, G.; Li, H.; Pan, H. Estimation the Internal Resistance of Lithium-Ion-Battery Using a Multi-Factor Dynamic Internal Resistance Model with an Error Compensation Strategy. Energy Rep. 2021, 7, 3050–3059. [Google Scholar] [CrossRef]
- Waag, W.; Fleischer, C.; Sauer, D.U. Critical Review of the Methods for Monitoring of Lithium-Ion Batteries in Electric and Hybrid Vehicles. J. Power Sources 2014, 258, 321–339. [Google Scholar] [CrossRef]
- Zhou, L.; Zhao, Y.; Li, D.; Wang, Z. State-of-Health Estimation for LiFePO4Battery System on Real-World Electric Vehicles Considering Aging Stage. IEEE Trans. Transp. Electrif. 2022, 8, 1724–1733. [Google Scholar] [CrossRef]
- Chiang, Y.H.; Sean, W.Y.; Ke, J.C. Online Estimation of Internal Resistance and Open-Circuit Voltage of Lithium-Ion Batteries in Electric Vehicles. J. Power Sources 2011, 196, 3921–3932. [Google Scholar] [CrossRef]
- Wang, J.; Liu, S.; Lin, C.; Wang, F.; Liu, C.; Su, Y.; Chen, S.; Wu, F. Experimental Study on the Internal Resistance and Heat Generation Characteristics of Lithium Ion Power Battery with NCM/C Material System. SAE Int. J. Passeng. Cars Electron. Electr. Syst. 2018, 11, 131–138. [Google Scholar] [CrossRef]
- Xiong, R.; Tian, J.; Mu, H.; Wang, C. A Systematic Model-Based Degradation Behavior Recognition and Health Monitoring Method for Lithium-Ion Batteries. Appl. Energy 2017, 207, 372–383. [Google Scholar] [CrossRef]
- Gaberšček, M. Understanding Li-Based Battery Materials via Electrochemical Impedance Spectroscopy. Nat. Commun. 2021, 12, 6513. [Google Scholar] [CrossRef]
- Ciucci, F. Modeling Electrochemical Impedance Spectroscopy. Curr. Opin. Electrochem. 2019, 13, 132–139. [Google Scholar] [CrossRef]
- Jones, P.K.; Stimming, U.; Lee, A.A. Impedance-Based Forecasting of Lithium-Ion Battery Performance amid Uneven Usage. Nat. Commun. 2022, 13, 4806. [Google Scholar] [CrossRef]
- Wang, X.; Wei, X.; Chen, Q.; Zhu, J.; Dai, H. Lithium-Ion Battery Temperature on-Line Estimation Based on Fast Impedance Calculation. J. Energy Storage 2019, 26, 100952. [Google Scholar] [CrossRef]
- Al Nazer, R.; Cattin, V.; Granjon, P.; Montaru, M.; Ranieri, M. Broadband Identification of Battery Electrical Impedance for HEVs. IEEE Trans. Veh. Technol. 2013, 62, 2896–2905. [Google Scholar] [CrossRef] [Green Version]
- Robinson, R.S. System Noise as a Signal Source for Impedance Measurements on Batteries Connected to Operating Equipment. J. Power Sources 1993, 42, 381–388. [Google Scholar] [CrossRef]
- Li, W.; Huang, Q.A.; Yang, C.; Chen, J.; Tang, Z.; Zhang, F.; Li, A.; Zhang, L.; Zhang, J. A Fast Measurement of Warburg-like Impedance Spectra with Morlet Wavelet Transform for Electrochemical Energy Devices. Electrochim. Acta. 2019, 322, 134760. [Google Scholar] [CrossRef]
- Hoshi, Y.; Yakabe, N.; Isobe, K.; Saito, T.; Shitanda, I.; Itagaki, M. Wavelet Transformation to Determine Impedance Spectra of Lithium-Ion Rechargeable Battery. J. Power Sources 2016, 315, 351–358. [Google Scholar] [CrossRef]
- Guo, D.; Yang, G.; Zhao, G.; Yi, M.; Feng, X.; Han, X.; Lu, L.; Ouyang, M. Determination of the Differential Capacity of Lithium-Ion Batteries by the Deconvolution of Electrochemical Impedance Spectra. Energies 2020, 13, 915. [Google Scholar] [CrossRef] [Green Version]
- Yao, L.; Xu, S.; Tang, A.; Zhou, F.; Hou, J.; Xiao, Y.; Fu, Z. A Review of Lithium-Ion Battery State of Health Estimation and Prediction Methods. World Electr. Veh. J. 2021, 12, 113. [Google Scholar] [CrossRef]
- Liu, J.; Duan, Q.; Ma, M.; Zhao, C.; Sun, J.; Wang, Q. Aging Mechanisms and Thermal Stability of Aged Commercial 18650 Lithium Ion Battery Induced by Slight Overcharging Cycling. J. Power Sources 2020, 445, 227263. [Google Scholar] [CrossRef]
- Zhu, J.; Dewi Darma, M.S.; Knapp, M.; Sørensen, D.R.; Heere, M.; Fang, Q.; Wang, X.; Dai, H.; Mereacre, L.; Senyshyn, A.; et al. Investigation of Lithium-Ion Battery Degradation Mechanisms by Combining Differential Voltage Analysis and Alternating Current Impedance. J. Power Sources 2020, 448, 227575. [Google Scholar] [CrossRef]
- Galeotti, M.; Cinà, L.; Giammanco, C.; Cordiner, S.; Di Carlo, A. Performance Analysis and SOH (State of Health) Evaluation of Lithium Polymer Batteries through Electrochemical Impedance Spectroscopy. Energy 2015, 89, 678–686. [Google Scholar] [CrossRef]
- Randau, S.; Weber, D.A.; Kötz, O.; Koerver, R.; Braun, P.; Weber, A.; Ivers-Tiffée, E.; Adermann, T.; Kulisch, J.; Zeier, W.G.; et al. Benchmarking the Performance of All-Solid-State Lithium Batteries. Nat. Energy 2020, 5, 259–270. [Google Scholar] [CrossRef]
- Li, W.; Lutz, D.M.; Wang, L.; Takeuchi, K.J.; Marschilok, A.C.; Takeuchi, E.S. Peering into Batteries: Electrochemical Insight Through In Situ and Operando Methods over Multiple Length Scales. Joule 2021, 5, 77–88. [Google Scholar] [CrossRef]
- Wang, Y.; Marchetti, B.; Zhou, X.D. Call Attention to Using DRT and EIS to Quantify the Contributions of Solid Oxide Cell Components to the Total Impedance. Int. J. Hydrog. Energy 2022, 47, 35437–35448. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, Y.; Yan, M.; Chen, F. Reconstruction of Relaxation Time Distribution from Linear Electrochemical Impedance Spectroscopy. J. Power Sources 2015, 283, 464–477. [Google Scholar] [CrossRef]
- Lu, Y.; Zhao, C.-Z.; Huang, J.-Q.; Zhang, Q. The Timescale Identification Decoupling Complicated Kinetic Processes in Lithium Batteries. Joule 2022, 6, 1172–1198. [Google Scholar] [CrossRef]
- Westerhoff, U.; Kurbach, K.; Lienesch, F.; Kurrat, M. Analysis of Lithium-Ion Battery Models Based on Electrochemical Impedance Spectroscopy. Energy Technol. 2016, 4, 1620–1630. [Google Scholar] [CrossRef] [Green Version]
- Paul, T.; Chi, P.W.; Wu, P.M.; Wu, M.K. Computation of Distribution of Relaxation Times by Tikhonov Regularization for Li Ion Batteries: Usage of L-Curve Method. Sci. Rep. 2021, 11, 12624. [Google Scholar] [CrossRef]
- Li, X.; Ahmadi, M.; Collins, L.; Kalinin, S.V. Deconvolving Distribution of Relaxation Times, Resistances and Inductance from Electrochemical Impedance Spectroscopy via Statistical Model Selection: Exploiting Structural-Sparsity Regularization and Data-Driven Parameter Tuning. Electrochim. Acta. 2019, 313, 570–583. [Google Scholar] [CrossRef]
- Wang, X.; Kou, Y.; Wang, B.; Jiang, Z.; Wei, X.; Dai, H. Fast Calculation of Broadband Battery Impedance Spectra Based on S Transform of Step Disturbance and Response. IEEE Trans. Transp. Electrif. 2022, 8, 3659–3672. [Google Scholar] [CrossRef]
- Raijmakers, L.H.J.; Shivakumar, K.M.; Donkers, M.C.F.; Lammers, M.J.G.; Bergveld, H.J. Crosstalk Interferences on Impedance Measurements in Battery Packs**This Work Has Received Financial Support from the Dutch Ministry of Economic Affairs under the Grant A Green Deal in Energy Materials (ADEM) and from the Horizon 2020 Programme of the European Union under the Grant Integrated Components for Complexity Control in Affordable Electrified Cars (3Ccar-662192). IFAC-Pap. 2016, 49, 42–47. [Google Scholar] [CrossRef]
- Howey, D.A.; Mitcheson, P.D.; Yufit, V.; Offer, G.J.; Brandon, N.P. Online Measurement of Battery Impedance Using Motor Controller Excitation. IEEE Trans. Veh. Technol. 2014, 63, 2557–2566. [Google Scholar] [CrossRef]
- Wang, X.; Wei, X.; Chen, Q.; Dai, H. A Novel System for Measuring Alternating Current Impedance Spectra of Series-Connected Lithium-Ion Batteries with a High-Power Dual Active Bridge Converter and Distributed Sampling Units. IEEE Trans. Ind. Electron. 2021, 68, 7380–7390. [Google Scholar] [CrossRef]
- Buteau, S.; Dahn, J.R. Analysis of Thousands of Electrochemical Impedance Spectra of Lithium-Ion Cells through a Machine Learning Inverse Model. J. Electrochem. Soc. 2019, 166, A1611–A1622. [Google Scholar] [CrossRef]
- Si, X.-S.; Wang, W.; Hu, C.-H.; Zhou, D.-H. Remaining Useful Life Estimation—A Review on the Statistical Data Driven Approaches. Eur. J. Oper. Res. 2011, 213, 1–14. [Google Scholar] [CrossRef]
- Jiang, B.; Zhu, J.; Wang, X.; Wei, X.; Shang, W.; Dai, H. A Comparative Study of Different Features Extracted from Electrochemical Impedance Spectroscopy in State of Health Estimation for Lithium-Ion Batteries. Appl. Energy 2022, 322, 119502. [Google Scholar] [CrossRef]
- Fu, Y.; Xu, J.; Shi, M.; Mei, X. A Fast Impedance Calculation-Based Battery State-of-Health Estimation Method. IEEE Trans. Ind. Electron. 2022, 69, 7019–7028. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, D.; Schaltz, E.; Stroe, D.I.; Gismero, A.; Yang, B. Degradation Mechanism Analysis and State-of-Health Estimation for Lithium-Ion Batteries Based on Distribution of Relaxation Times. J. Energy Storage 2022, 55, 105386. [Google Scholar] [CrossRef]
- Lewerenz, M.; Marongiu, A.; Warnecke, A.; Sauer, D.U. Differential Voltage Analysis as a Tool for Analyzing Inhomogeneous Aging: A Case Study for LiFePO4|Graphite Cylindrical Cells. J. Power Sources 2017, 368, 57–67. [Google Scholar] [CrossRef]
- Xiong, R.; Pan, Y.; Shen, W.; Li, H.; Sun, F. Lithium-Ion Battery Aging Mechanisms and Diagnosis Method for Automotive Applications: Recent Advances and Perspectives. Renew. Sustain. Energy Rev. 2020, 131, 110048. [Google Scholar] [CrossRef]
- Dubarry, M.; Truchot, C.; Cugnet, M.; Liaw, B.Y.; Gering, K.; Sazhin, S.; Jamison, D.; Michelbacher, C. Evaluation of Commercial Lithium-Ion Cells Based on Composite Positive Electrode for Plug-in Hybrid Electric Vehicle Applications. Part I: Initial Characterizations. J. Power Sources 2011, 196, 10328–10335. [Google Scholar] [CrossRef]
- Ma, B.; Yang, S.; Zhang, L.; Wang, W.; Chen, S.; Yang, X.; Xie, H.; Yu, H.; Wang, H.; Liu, X. Remaining Useful Life and State of Health Prediction for Lithium Batteries Based on Differential Thermal Voltammetry and a Deep-Learning Model. J. Power Sources 2022, 548, 232030. [Google Scholar] [CrossRef]
- Weng, C.; Feng, X.; Sun, J.; Peng, H. State-of-Health Monitoring of Lithium-Ion Battery Modules and Packs via Incremental Capacity Peak Tracking. Appl. Energy 2016, 180, 360–368. [Google Scholar] [CrossRef] [Green Version]
- Berecibar, M.; Garmendia, M.; Gandiaga, I.; Crego, J.; Villarreal, I. State of Health Estimation Algorithm of LiFePO4 Battery Packs Based on Differential Voltage Curves for Battery Management System Application. Energy 2016, 103, 784–796. [Google Scholar] [CrossRef]
- Gao, Y.; Jiang, J.; Zhang, C.; Zhang, W.; Ma, Z.; Jiang, Y. Lithium-Ion Battery Aging Mechanisms and Life Model under Different Charging Stresses. J. Power Sources 2017, 356, 103–114. [Google Scholar] [CrossRef]
- Alvarez Anton, J.C.; Garcia Nieto, P.J.; Blanco Viejo, C.; Vilan Vilan, J.A. Support Vector Machines Used to Estimate the Battery State of Charge. IEEE Trans. Power Electron. 2013, 28, 5919–5926. [Google Scholar] [CrossRef]
- Ma, Z.; Jiang, J.; Shi, W.; Zhang, W.; Mi, C.C. Investigation of Path Dependence in Commercial Lithium-Ion Cells for Pure Electric Bus Applications: Aging Mechanism Identification. J. Power Sources 2015, 274, 29–40. [Google Scholar] [CrossRef]
- Qiao, D.; Wang, X.; Lai, X.; Zheng, Y.; Wei, X.; Dai, H. Online Quantitative Diagnosis of Internal Short Circuit for Lithium-Ion Batteries Using Incremental Capacity Method. Energy 2022, 243, 123082. [Google Scholar] [CrossRef]
- Tomaszewska, A.; Chu, Z.; Feng, X.; O’Kane, S.; Liu, X.; Chen, J.; Ji, C.; Endler, E.; Li, R.; Liu, L.; et al. Lithium-Ion Battery Fast Charging: A Review. eTransportation 2019, 1, 100011. [Google Scholar] [CrossRef]
- Xu, C.; Reeves, P.J.; Jacquet, Q.; Grey, C.P. Phase Behavior during Electrochemical Cycling of Ni-Rich Cathode Materials for Li-Ion Batteries. Adv. Energy Mater 2021, 11, 2003404. [Google Scholar] [CrossRef]
- Dubarry, M.; Truchot, C.; Liaw, B.Y.; Gering, K.; Sazhin, S.; Jamison, D.; Michelbacher, C. Evaluation of Commercial Lithium-Ion Cells Based on Composite Positive Electrode for Plug-in Hybrid Electric Vehicle Applications. Part II. Degradation Mechanism under 2 C Cycle Aging. J. Power Sources 2011, 196, 10336–10343. [Google Scholar] [CrossRef]
- Krupp, A.; Ferg, E.; Schuldt, F.; Derendorf, K.; Agert, C. Incremental Capacity Analysis as a State of Health Estimation Method for Lithium-Ion Battery Modules with Series-Connected Cells. Batteries 2021, 7, 2. [Google Scholar] [CrossRef]
- Bensaad, Y.; Friedrichs, F.; Sieg, J.; Bähr, J.; Fill, A.; Birke, K.P. Multidimensional Estimation of Inhomogeneous Lithium-Ion Cell Aging via Modal Differential Voltage Analysis. J. Energy Storage 2023, 63, 107108. [Google Scholar] [CrossRef]
- Fly, A.; Chen, R. Rate Dependency of Incremental Capacity Analysis (DQ/DV) as a Diagnostic Tool for Lithium-Ion Batteries. J. Energy Storage 2020, 29, 101329. [Google Scholar] [CrossRef]
- McBrayer, J.D.; Rodrigues, M.T.F.; Schulze, M.C.; Abraham, D.P.; Apblett, C.A.; Bloom, I.; Carroll, G.M.; Colclasure, A.M.; Fang, C.; Harrison, K.L.; et al. Calendar Aging of Silicon-Containing Batteries. Nat. Energy 2021, 6, 866–872. [Google Scholar] [CrossRef]
- Lewerenz, M.; Sauer, D.U. Evaluation of Cyclic Aging Tests of Prismatic Automotive LiNiMnCoO2-Graphite Cells Considering Influence of Homogeneity and Anode Overhang. J. Energy Storage 2018, 18, 421–434. [Google Scholar] [CrossRef]
- Burow, D.; Sergeeva, K.; Calles, S.; Schorb, K.; Börger, A.; Roth, C.; Heitjans, P. Inhomogeneous Degradation of Graphite Anodes in Automotive Lithium Ion Batteries under Low-Temperature Pulse Cycling Conditions. J. Power Sources 2016, 307, 806–814. [Google Scholar] [CrossRef]
- Matadi, B.P.; Geniès, S.; Delaille, A.; Waldmann, T.; Kasper, M.; Wohlfahrt-Mehrens, M.; Aguesse, F.; Bekaert, E.; Jiménez-Gordon, I.; Daniel, L.; et al. Effects of Biphenyl Polymerization on Lithium Deposition in Commercial Graphite/NMC Lithium-Ion Pouch-Cells during Calendar Aging at High Temperature. J. Electrochem. Soc. 2017, 164, A1089–A1097. [Google Scholar] [CrossRef]
- Fath, J.P.; Dragicevic, D.; Bittel, L.; Nuhic, A.; Sieg, J.; Hahn, S.; Alsheimer, L.; Spier, B.; Wetzel, T. Quantification of Aging Mechanisms and Inhomogeneity in Cycled Lithium-Ion Cells by Differential Voltage Analysis. J. Energy Storage 2019, 25, 100813. [Google Scholar] [CrossRef]
- Lewerenz, M.; Fuchs, G.; Becker, L.; Sauer, D.U. Irreversible Calendar Aging and Quantification of the Reversible Capacity Loss Caused by Anode Overhang. J. Energy Storage 2018, 18, 149–159. [Google Scholar] [CrossRef]
- Bloom, I.; Jansen, A.N.; Abraham, D.P.; Knuth, J.; Jones, S.A.; Battaglia, V.S.; Henriksen, G.L. Differential Voltage Analyses of High-Power, Lithium-Ion Cells 1. Technique and Application. J. Power Sources 2005, 139, 295–303. [Google Scholar] [CrossRef]
- Bloom, I.; Walker, L.K.; Basco, J.K.; Abraham, D.P.; Christophersen, J.P.; Ho, C.D. Differential Voltage Analyses of High-Power Lithium-Ion Cells. 4. Cells Containing NMC. J. Power Sources 2010, 195, 877–882. [Google Scholar] [CrossRef]
- Liu, P.; Wang, J.; Hicks-Garner, J.; Sherman, E.; Soukiazian, S.; Verbrugge, M.; Tataria, H.; Musser, J.; Finamore, P. Aging Mechanisms of LiFePO[Sub 4] Batteries Deduced by Electrochemical and Structural Analyses. J. Electrochem. Soc. 2010, 157, A499. [Google Scholar] [CrossRef]
- Lin, C.P.; Cabrera, J.; Yu, D.Y.W.; Yang, F.; Tsui, K.L. SOH Estimation and SOC Recalibration of Lithium-Ion Battery with Incremental Capacity Analysis & Cubic Smoothing Spline. J. Electrochem. Soc. 2020, 167, 090537. [Google Scholar] [CrossRef]
- Li, X.; Wang, Z.; Zhang, L.; Zou, C.; Dorrell, D.D. State-of-Health Estimation for Li-Ion Batteries by Combing the Incremental Capacity Analysis Method with Grey Relational Analysis. J. Power Sources 2019, 410–411, 106–114. [Google Scholar] [CrossRef]
- Tang, X.; Zou, C.; Yao, K.; Chen, G.; Liu, B.; He, Z.; Gao, F. A Fast Estimation Algorithm for Lithium-Ion Battery State of Health. J. Power Sources 2018, 396, 453–458. [Google Scholar] [CrossRef]
- She, C.; Wang, Z.; Sun, F.; Liu, P.; Zhang, L. Battery Aging Assessment for Real-World Electric Buses Based on Incremental Capacity Analysis and Radial Basis Function Neural Network. IEEE Trans. Ind. Inf. 2020, 16, 3345–3354. [Google Scholar] [CrossRef]
- Dubarry, M.; Truchot, C.; Liaw, B.Y. Synthesize Battery Degradation Modes via a Diagnostic and Prognostic Model. J. Power Sources 2012, 219, 204–216. [Google Scholar] [CrossRef]
- Weng, C.; Cui, Y.; Sun, J.; Peng, H. On-Board State of Health Monitoring of Lithium-Ion Batteries Using Incremental Capacity Analysis with Support Vector Regression. J. Power Sources 2013, 235, 36–44. [Google Scholar] [CrossRef]
- Wang, L.; Pan, C.; Liu, L.; Cheng, Y.; Zhao, X. On-Board State of Health Estimation of LiFePO4 Battery Pack through Differential Voltage Analysis. Appl. Energy 2016, 168, 465–472. [Google Scholar] [CrossRef]
- Galiounas, E.; Tranter, T.G.; Owen, R.E.; Robinson, J.B.; Shearing, P.R.; Brett, D.J.L. Battery State-of-Charge Estimation Using Machine Learning Analysis of Ultrasonic Signatures. Energy AI 2022, 10, 100188. [Google Scholar] [CrossRef]
- Kim, J.-Y.; Jo, J.-H.; Byeon, J.-W. Ultrasonic Monitoring Performance Degradation of Lithium Ion Battery. Microelectron. Reliab. 2020, 114, 113859. [Google Scholar] [CrossRef]
- Gold, L.; Bach, T.; Virsik, W.; Schmitt, A.; Müller, J.; Staab, T.E.M.; Sextl, G. Probing Lithium-Ion Batteries’ State-of-Charge Using Ultrasonic Transmission—Concept and Laboratory Testing. J. Power Sources 2017, 343, 536–544. [Google Scholar] [CrossRef]
- Robinson, J.B.; Owen, R.E.; Kok, M.D.R.; Maier, M.; Majasan, J.; Braglia, M.; Stocker, R.; Amietszajew, T.; Roberts, A.J.; Bhagat, R.; et al. Identifying Defects in Li-Ion Cells Using Ultrasound Acoustic Measurements. J. Electrochem. Soc. 2020, 167, 120530. [Google Scholar] [CrossRef]
- Robinson, J.B.; Maier, M.; Alster, G.; Compton, T.; Brett, D.J.L.; Shearing, P.R. Spatially Resolved Ultrasound Diagnostics of Li-Ion Battery Electrodes. Phys. Chem. Chem. Phys. 2019, 21, 6354–6361. [Google Scholar] [CrossRef] [Green Version]
- Chang, J.J.; Zeng, X.F.; Wan, T.L. Real-Time Measurement of Lithium-Ion Batteries’ State-of-Charge Based on Air-Coupled Ultrasound. AIP Adv. 2019, 9, 085116. [Google Scholar] [CrossRef] [Green Version]
- Sood, B.; Osterman, M.; Pecht, M. Product Safety Engineering Society. Annual IEEE Computer Conference. In Proceedings of the Annual IEEE Symposium on Product Compliance Engineering (ISPCE), Austin, TE, USA, 7–9 October 2013; ISBN 9781467329422. [Google Scholar]
- Li, X.; Wu, C.; Fu, C.; Zheng, S.; Tian, J. State Characterization of Lithium-Ion Battery Based on Ultrasonic Guided Wave Scanning. Energies 2022, 15, 6027. [Google Scholar] [CrossRef]
- Hsieh, A.G.; Bhadra, S.; Hertzberg, B.J.; Gjeltema, P.J.; Goy, A.; Fleischer, J.W.; Steingart, D.A. Electrochemical-Acoustic Time of Flight: In Operando Correlation of Physical Dynamics with Battery Charge and Health. Energy Environ. Sci. 2015, 8, 1569–1577. [Google Scholar] [CrossRef]
- Davies, G.; Knehr, K.W.; Van Tassell, B.; Hodson, T.; Biswas, S.; Hsieh, A.G.; Steingart, D.A. State of Charge and State of Health Estimation Using Electrochemical Acoustic Time of Flight Analysis. J. Electrochem. Soc. 2017, 164, A2746–A2755. [Google Scholar] [CrossRef]
- Su, Z.; Ye, L.; Lu, Y. Guided Lamb Waves for Identification of Damage in Composite Structures: A Review. J. Sound Vib. 2006, 295, 753–780. [Google Scholar] [CrossRef]
- Ladpli, P.; Kopsaftopoulos, F.; Chang, F.K. Estimating State of Charge and Health of Lithium-Ion Batteries with Guided Waves Using Built-in Piezoelectric Sensors/Actuators. J. Power Sources 2018, 384, 342–354. [Google Scholar] [CrossRef]
- Ladpli, P.; Liu, C.; Kopsaftopoulos, F.; Chang, F.K. Estimating Lithium-Ion Battery State of Charge and Health with Ultrasonic Guided Waves Using an Efficient Matching Pursuit Technique. In Proceedings of the ITEC Asia-Pacific 2018—IEEE Transportation Electrification Conference and Expo, Asia-Pacific: E-Mobility: A Journey from Now and Beyond, Bangkok, Thailand, 6–9 June 2018; Institute of Electrical and Electronics Engineers Inc.: Piscateville, NJ, USA, 2018. [Google Scholar]
- Wu, Y.; Wang, Y.; Yung, W.K.C.; Pecht, M. Ultrasonic Health Monitoring of Lithium-Ion Batteries. Electronics 2019, 8, 751. [Google Scholar] [CrossRef] [Green Version]
- Matuck, L.; Pinto, J.L.; Marques, C.; Nascimento, M. Simultaneous Strain and Temperature Discrimination in 18650 Li-Ion Batteries Using Polarization-Maintaining Fiber Bragg Gratings. Batteries 2022, 8, 233. [Google Scholar] [CrossRef]
- Albero Blanquer, L.; Marchini, F.; Seitz, J.R.; Daher, N.; Bétermier, F.; Huang, J.; Gervillié, C.; Tarascon, J.M. Optical Sensors for Operando Stress Monitoring in Lithium-Based Batteries Containing Solid-State or Liquid Electrolytes. Nat. Commun. 2022, 13, 1–14. [Google Scholar] [CrossRef]
- Goutam, S.; Timmermans, J.M.; Omar, N.; Van den Bossche, P.; Van Mierlo, J. Comparative Study of Surface Temperature Behavior of Commercial Li-Ion Pouch Cells of Different Chemistries and Capacities by Infrared Thermography. Energies 2015, 8, 8175–8192. [Google Scholar] [CrossRef] [Green Version]
- Han, G.; Yan, J.; Guo, Z.; Greenwood, D.; Marco, J.; Yu, Y. A Review on Various Optical Fibre Sensing Methods for Batteries. Renew. Sustain. Energy Rev. 2021, 150, 111514. [Google Scholar] [CrossRef]
- Wei, Z.; Zhao, J.; He, H.; Ding, G.; Cui, H.; Liu, L. Future Smart Battery and Management: Advanced Sensing from External to Embedded Multi-Dimensional Measurement. J. Power Sources 2021, 489, 229462. [Google Scholar] [CrossRef]
- Huang, J.; Albero Blanquer, L.; Bonefacino, J.; Logan, E.R.; Alves Dalla Corte, D.; Delacourt, C.; Gallant, B.M.; Boles, S.T.; Dahn, J.R.; Tam, H.Y.; et al. Operando Decoding of Chemical and Thermal Events in Commercial Na(Li)-Ion Cells via Optical Sensors. Nat. Energy 2020, 5, 674–683. [Google Scholar] [CrossRef]
- Wu, Y.; Long, X.; Lu, J.; Zhou, R.; Liu, L.; Wu, Y. Long-Life in-Situ Temperature Field Monitoring Using Fiber Bragg Grating Sensors in Electromagnetic Launch High-Rate Hardcase Lithium-Ion Battery. J. Energy Storage 2023, 57, 106207. [Google Scholar] [CrossRef]
- Nascimento, M.; Ferreira, M.S.; Pinto, J.L. Real Time Thermal Monitoring of Lithium Batteries with Fiber Sensors and Thermocouples: A Comparative Study. Measurement 2017, 111, 260–263. [Google Scholar] [CrossRef]
- Nascimento, M.; Novais, S.; Ding, M.S.; Ferreira, M.S.; Koch, S.; Passerini, S.; Pinto, J.L. Internal Strain and Temperature Discrimination with Optical Fiber Hybrid Sensors in Li-Ion Batteries. J. Power Sources 2019, 410–411, 1–9. [Google Scholar] [CrossRef]
- Peng, J.; Jia, S.; Yang, S.; Kang, X.; Yu, H.; Yang, Y. State Estimation of Lithium-Ion Batteries Based on Strain Parameter Monitored by Fiber Bragg Grating Sensors. J. Energy Storage 2022, 52, 104950. [Google Scholar] [CrossRef]
- Nedjalkov, A.; Meyer, J.; Gräfenstein, A.; Schramm, B.; Angelmahr, M.; Schwenzel, J.; Schade, W. Refractive Index Measurement of Lithium Ion Battery Electrolyte with Etched Surface Cladding Waveguide Bragg Gratings and Cell Electrode State Monitoring by Optical Strain Sensors. Batteries 2019, 5, 30. [Google Scholar] [CrossRef] [Green Version]
- Rente, B.; Fabian, M.; Vidakovic, M.; Liu, X.; Li, X.; Li, K.; Sun, T.; Grattan, K.T.V. Lithium-Ion Battery State-of-Charge Estimator Based on FBG-Based Strain Sensor and Employing Machine Learning. IEEE Sens. J. 2021, 21, 1453–1460. [Google Scholar] [CrossRef]
- Raghavan, A.; Kiesel, P.; Sommer, L.W.; Schwartz, J.; Lochbaum, A.; Hegyi, A.; Schuh, A.; Arakaki, K.; Saha, B.; Ganguli, A.; et al. Embedded Fiber-Optic Sensing for Accurate Internal Monitoring of Cell State in Advanced Battery Management Systems Part 1: Cell Embedding Method and Performance. J. Power Sources 2017, 341, 466–473. [Google Scholar] [CrossRef] [Green Version]
- Ganguli, A.; Saha, B.; Raghavan, A.; Kiesel, P.; Arakaki, K.; Schuh, A.; Schwartz, J.; Hegyi, A.; Sommer, L.W.; Lochbaum, A.; et al. Embedded Fiber-Optic Sensing for Accurate Internal Monitoring of Cell State in Advanced Battery Management Systems Part 2: Internal Cell Signals and Utility for State Estimation. J. Power Sources 2017, 341, 474–482. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Li, K.; Liu, X.; Li, X.; Zhang, L.; Rente, B.; Sun, T.; Grattan, K.T.V. A Hybrid Machine Learning Framework for Joint SOC and SOH Estimation of Lithium-Ion Batteries Assisted with Fiber Sensor Measurements. Appl. Energy 2022, 325, 119787. [Google Scholar] [CrossRef]
- Meyer, J.; Nedjalkov, A.; Pichler, E.; Kelb, C.; Schade, W. Development of a Polymeric Arrayed Waveguide Grating Interrogator for Fast and Precise Lithium-Ion Battery Status Monitoring. Batteries 2019, 5, 66. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Farfan-Ramos, L.; Zhang, Y.; Salman, M. Automotive Battery State-of-Health Monitoring: A Parity Relation Based Approach. IFAC Proc. Vol. 2012, 8, 1179–1184. [Google Scholar] [CrossRef]
- Cannarella, J.; Arnold, C.B. State of Health and Charge Measurements in Lithium-Ion Batteries Using Mechanical Stress. J. Power Sources 2014, 269, 7–14. [Google Scholar] [CrossRef]
- Panchal, S.; Mcgrory, J.; Kong, J.; Fraser, R.; Fowler, M.; Dincer, I.; Agelin-Chaab, M. Cycling Degradation Testing and Analysis of a LiFePO4 Battery at Actual Conditions. Int. J. Energy Res. 2017, 41, 2565–2575. [Google Scholar] [CrossRef]
- Gomez, J.; Nelson, R.; Kalu, E.E.; Weatherspoon, M.H.; Zheng, J.P. Equivalent Circuit Model Parameters of a High-Power Li-Ion Battery: Thermal and State of Charge Effects. J. Power Sources 2011, 196, 4826–4831. [Google Scholar] [CrossRef]
- Xiong, R.; He, H.; Sun, F.; Liu, X.; Liu, Z. Model-Based State of Charge and Peak Power Capability Joint Estimation of Lithium-Ion Battery in Plug-in Hybrid Electric Vehicles. J. Power Sources 2013, 229, 159–169. [Google Scholar] [CrossRef]
- Smith, K.; Wang, C.Y. Solid-State Diffusion Limitations on Pulse Operation of a Lithium Ion Cell for Hybrid Electric Vehicles. J. Power Sources 2006, 161, 628–639. [Google Scholar] [CrossRef]
- Subramanian, V.R.; Diwakar, V.D.; Tapriyal, D. Efficient Macro-Micro Scale Coupled Modeling of Batteries. J. Electrochem. Soc. 2005, 152, A2002. [Google Scholar] [CrossRef]
- Zhang, L.; Mu, Z.; Sun, C. Remaining Useful Life Prediction for Lithium-Ion Batteries Based on Exponential Model and Particle Filter. IEEE Access 2018, 6, 17729–17740. [Google Scholar] [CrossRef]
- Sun, Y.; Hao, X.; Pecht, M.; Zhou, Y. Remaining Useful Life Prediction for Lithium-Ion Batteries Based on an Integrated Health Indicator. Microelectron. Reliab. 2018, 88–90, 1189–1194. [Google Scholar] [CrossRef]
- He, H.; Xiong, R.; Guo, H.; Li, S. Comparison Study on the Battery Models Used for the Energy Management of Batteries in Electric Vehicles. In Energy Conversion and Management; Elsevier: Amsterdam, The Netherlands, 2012; Volume 64, pp. 113–121. [Google Scholar]
- Zhang, L.; Chen, S.; Wang, W.; Yu, H.; Xie, H.; Wang, H.; Yang, S.; Zhang, C.; Liu, X. Enabling Dendrite-Free Charging for Lithium Batteries Based on Transport-Reaction Competition Mechanism in CHAIN Framework. J. Energy Chem. 2022, 75, 408–421. [Google Scholar] [CrossRef]
- Liu, B.; Tang, X.; Gao, F. Joint Estimation of Battery State-of-Charge and State-of-Health Based on a Simplified Pseudo-Two-Dimensional Model. Electrochim. Acta. 2020, 344, 136098. [Google Scholar] [CrossRef]
- Jiang, S.; Song, Z. A Review on the State of Health Estimation Methods of Lead-Acid Batteries. J. Power Sources 2022, 517, 230710. [Google Scholar] [CrossRef]
- Han, X.; Ouyang, M.; Lu, L.; Li, J.; Zheng, Y.; Li, Z. A Comparative Study of Commercial Lithium Ion Battery Cycle Life in Electrical Vehicle: Aging Mechanism Identification. J. Power Sources 2014, 251, 38–54. [Google Scholar] [CrossRef]
- Schmalstieg, J.; Käbitz, S.; Ecker, M.; Sauer, D.U. A Holistic Aging Model for Li(NiMnCo)O2 Based 18650 Lithium-Ion Batteries. J. Power Sources 2014, 257, 325–334. [Google Scholar] [CrossRef]
- Ecker, M.; Gerschler, J.B.; Vogel, J.; Käbitz, S.; Hust, F.; Dechent, P.; Sauer, D.U. Development of a Lifetime Prediction Model for Lithium-Ion Batteries Based on Extended Accelerated Aging Test Data. J. Power Sources 2012, 215, 248–257. [Google Scholar] [CrossRef]
- Singh, P.; Chen, C.; Tan, C.M.; Huang, S.C. Semi-Empirical Capacity Fading Model for SoH Estimation of Li-Ion Batteries. Appl. Sci. 2019, 9, 3012. [Google Scholar] [CrossRef] [Green Version]
- Fuller, T.F.; Doyle, M.; Newman, J. Simulation and Optimization of the Dual Lithium Ion Insertion Cell. J. Electrochem. Soc. 1994, 141, 1. [Google Scholar] [CrossRef] [Green Version]
- Doyle, M.; Newman, J. Modeling the Performance of Rechargeable Lithium-Based Cells: Design Correlations for Limiting Cases. J. Power Sources 1995, 54, 46–51. [Google Scholar] [CrossRef]
- Doyle, M.; Fuller, T.F.; Newman, J. Modeling of Galvanostatic Charge and Discharge of the Lithium/Polymer/Insertion Cell. J. Electrochem. Soc. 1993, 140, 1526. [Google Scholar] [CrossRef]
- Doyle, M.; Newman, J.; Gozdz, A.S.; Schmutz, C.N.; Tarascon, J. Comparison of Modeling Predictions with Experimental Data from Plastic Lithium Ion Cells. J. Electrochem. Soc. 1996, 143, 1890. [Google Scholar] [CrossRef]
- Li, J.; Adewuyi, K.; Lotfi, N.; Landers, R.G.; Park, J. A Single Particle Model with Chemical/Mechanical Degradation Physics for Lithium Ion Battery State of Health (SOH) Estimation. Appl. Energy 2018, 212, 1178–1190. [Google Scholar] [CrossRef]
- Verma, M.K.S.; Basu, S.; Patil, R.S.; Hariharan, K.S.; Adiga, S.P.; Kolake, S.M.; Oh, D.; Song, T.; Sung, Y. On-Board State Estimation in Electrical Vehicles: Achieving Accuracy and Computational Efficiency through an Electrochemical Model. IEEE Trans. Veh. Technol. 2020, 69, 2563–2575. [Google Scholar] [CrossRef]
- Li, J.; Wang, D.; Deng, L.; Cui, Z.; Lyu, C.; Wang, L.; Pecht, M. Aging Modes Analysis and Physical Parameter Identification Based on a Simplified Electrochemical Model for Lithium-Ion Batteries. J. Energy Storage 2020, 31, 101538. [Google Scholar] [CrossRef]
- Prasad, G.K.; Rahn, C.D. Model Based Identification of Aging Parameters in Lithium Ion Batteries. J. Power Sources 2013, 232, 79–85. [Google Scholar] [CrossRef]
- Katrašnik, T.; Mele, I.; Zelič, K. Multi-Scale Modelling of Lithium-Ion Batteries: From Transport Phenomena to the Outbreak of Thermal Runaway. Energy Convers. Manag. 2021, 236, 114036. [Google Scholar] [CrossRef]
- Li, W.; Demir, I.; Cao, D.; Jöst, D.; Ringbeck, F.; Junker, M.; Sauer, D.U. Data-Driven Systematic Parameter Identification of an Electrochemical Model for Lithium-Ion Batteries with Artificial Intelligence. Energy Storage Mater 2022, 44, 557–570. [Google Scholar] [CrossRef]
- Stetzel, K.D.; Aldrich, L.L.; Trimboli, M.S.; Plett, G.L. Electrochemical State and Internal Variables Estimation Using a Reduced-Order Physics-Based Model of a Lithium-Ion Cell and an Extended Kalman Filter. J. Power Sources 2015, 278, 490–505. [Google Scholar] [CrossRef] [Green Version]
- Zou, C.; Manzie, C.; Nešić, D.; Kallapur, A.G. Multi-Time-Scale Observer Design for State-of-Charge and State-of-Health of a Lithium-Ion Battery. J. Power Sources 2016, 335, 121–130. [Google Scholar] [CrossRef]
- Dey, S.; Ayalew, B.; Pisu, P. Combined Estimation of State-of-Charge and State-of-Health of Li-Ion Battery Cells Using SMO on Electrochemical Model. In Proceedings of the IEEE Workshop on Applications of Computer Vision; IEEE Computer Society, Nantes, France, 29 June–2 July 2014. [Google Scholar]
- Pradhan, S.K.; Chakraborty, B. Battery Management Strategies: An Essential Review for Battery State of Health Monitoring Techniques. J. Energy Storage 2022, 51, 104427. [Google Scholar] [CrossRef]
- Zhou, X.; Stein, J.L.; Ersal, T. Battery State of Health Monitoring by Estimation of the Number of Cyclable Li-Ions. Control Eng. Pr. 2017, 66, 51–63. [Google Scholar] [CrossRef]
- Yuan, S.; Jiang, L.; Yin, C.; Wu, H.; Zhang, X. A Transfer Function Type of Simplified Electrochemical Model with Modified Boundary Conditions and Padé Approximation for Li-Ion Battery: Part 1. Lithium Concentration Estimation. J. Power Sources 2017, 352, 245–257. [Google Scholar] [CrossRef]
- Ramadesigan, V.; Northrop, P.W.C.; De, S.; Santhanagopalan, S.; Braatz, R.D.; Subramanian, V.R. Modeling and Simulation of Lithium-Ion Batteries from a Systems Engineering Perspective. J. Electrochem. Soc. 2012, 159, R31–R45. [Google Scholar] [CrossRef]
- Cen, Z.; Kubiak, P. Lithium-Ion Battery SOC/SOH Adaptive Estimation via Simplified Single Particle Model. Int. J. Energy Res. 2020, 44, 12444–12459. [Google Scholar] [CrossRef]
- Khaleghi Rahimian, S.; Rayman, S.; White, R.E. Extension of Physics-Based Single Particle Model for Higher Charge-Discharge Rates. J. Power Sources 2013, 224, 180–194. [Google Scholar] [CrossRef]
- Bracale, A.; De Falco, P.; Di Noia, L.P.; Rizzo, R. Probabilistic State of Health and Remaining Useful Life Prediction for Li-Ion Batteries. In Proceedings of the 2021 IEEE Texas Power and Energy Conference, TPEC 2021, College Station, TX, USA, 2 February 2021; Institute of Electrical and Electronics Engineers Inc.: Piscateville, NJ, USA, 2021. [Google Scholar]
- Ng, S.S.Y.; Xing, Y.; Tsui, K.L. A Naive Bayes Model for Robust Remaining Useful Life Prediction of Lithium-Ion Battery. Appl. Energy 2014, 118, 114–123. [Google Scholar] [CrossRef]
- Li, Y.; Liu, K.; Foley, A.M.; Zülke, A.; Berecibar, M.; Nanini-Maury, E.; Van Mierlo, J.; Hoster, H.E. Data-Driven Health Estimation and Lifetime Prediction of Lithium-Ion Batteries: A Review. Renew. Sustain. Energy Rev. 2019, 113, 109254. [Google Scholar] [CrossRef]
- Zhao, J.; Xuebin, L.; Daiwei, Y.; Jun, Z.; Wenjin, Z. Lithium-Ion Battery State of Health Estimation Using Meta-Heuristic Optimization and Gaussian Process Regression. J. Energy Storage 2023, 58, 106319. [Google Scholar] [CrossRef]
- Zhou, Y.; Dong, G.; Tan, Q.; Han, X.; Chen, C.; Wei, J. State of Health Estimation for Lithium-Ion Batteries Using Geometric Impedance Spectrum Features and Recurrent Gaussian Process Regression. Energy 2023, 262, 125514. [Google Scholar] [CrossRef]
- Jin, H.; Cui, N.; Cai, L.; Meng, J.; Li, J.; Peng, J.; Zhao, X. State-of-Health Estimation for Lithium-Ion Batteries with Hierarchical Feature Construction and Auto-Configurable Gaussian Process Regression. Energy 2023, 262, 125503. [Google Scholar] [CrossRef]
- Yang, D.; Zhang, X.; Pan, R.; Wang, Y.; Chen, Z. A Novel Gaussian Process Regression Model for State-of-Health Estimation of Lithium-Ion Battery Using Charging Curve. J. Power Sources 2018, 384, 387–395. [Google Scholar] [CrossRef]
- Liu, D.; Pang, J.; Zhou, J.; Peng, Y.; Pecht, M. Prognostics for State of Health Estimation of Lithium-Ion Batteries Based on Combination Gaussian Process Functional Regression. Microelectron. Reliab. 2013, 53, 832–839. [Google Scholar] [CrossRef]
- Richardson, R.R.; Osborne, M.A.; Howey, D.A. Gaussian Process Regression for Forecasting Battery State of Health. J. Power Sources 2017, 357, 209–219. [Google Scholar] [CrossRef]
- Richardson, R.R.; Osborne, M.A.; Howey, D.A. Battery Health Prediction under Generalized Conditions Using a Gaussian Process Transition Model. J. Energy Storage 2019, 23, 320–328. [Google Scholar] [CrossRef]
- Li, X.; Yuan, C.; Wang, Z.; He, J.; Yu, S. Lithium Battery State-of-Health Estimation and Remaining Useful Lifetime Prediction Based on Non-Parametric Aging Model and Particle Filter Algorithm. eTransportation 2022, 11, 100156. [Google Scholar] [CrossRef]
- He, W.; Williard, N.; Osterman, M.; Pecht, M. Prognostics of Lithium-Ion Batteries Based on Dempster-Shafer Theory and the Bayesian Monte Carlo Method. J. Power Sources 2011, 196, 10314–10321. [Google Scholar] [CrossRef]
- Tang, X.; Zou, C.; Yao, K.; Lu, J.; Xia, Y.; Gao, F. Aging Trajectory Prediction for Lithium-Ion Batteries via Model Migration and Bayesian Monte Carlo Method. Appl. Energy 2019, 254, 113591. [Google Scholar] [CrossRef] [Green Version]
- Tang, X.; Yao, K.; Zou, C.; Liu, B.; Gao, F. Predicting Battery Aging Trajectory via a Migrated Aging Model and Bayesian Monte Carlo Method. In Energy Procedia; Elsevier: Amsterdam, The Netherlands, 2019; Volume 158, pp. 2456–2461. [Google Scholar]
- Liu, W.; Shen, Y.; Shen, L. Degradation Modeling for Lithium-Ion Batteries with an Exponential Jump-Diffusion Model. Mathematics 2022, 10, 2991. [Google Scholar] [CrossRef]
- Li, Y.; Zou, C.; Berecibar, M.; Nanini-Maury, E.; Chan, J.C.W.; van den Bossche, P.; Van Mierlo, J.; Omar, N. Random Forest Regression for Online Capacity Estimation of Lithium-Ion Batteries. Appl. Energy 2018, 232, 197–210. [Google Scholar] [CrossRef]
- Yang, N.; Song, Z.; Hofmann, H.; Sun, J. Robust State of Health Estimation of Lithium-Ion Batteries Using Convolutional Neural Network and Random Forest. J. Energy Storage 2022, 48, 103857. [Google Scholar] [CrossRef]
- Lin, M.; Wu, D.; Meng, J.; Wu, J.; Wu, H. A Multi-Feature-Based Multi-Model Fusion Method for State of Health Estimation of Lithium-Ion Batteries. J. Power Sources 2022, 518, 230774. [Google Scholar] [CrossRef]
- De Falco, P.; Di Noia, L.P.; Rizzo, R. State of Health Prediction of Lithium-Ion Batteries Using Accelerated Degradation Test Data. IEEE Trans. Ind. Appl. 2020, 57, 6483–6493. [Google Scholar]
- Haris, M.; Hasan, M.N.; Qin, S. Early and Robust Remaining Useful Life Prediction of Supercapacitors Using BOHB Optimized Deep Belief Network. Appl. Energy 2021, 286, 116541. [Google Scholar] [CrossRef]
- Wei, M.; Gu, H.; Ye, M.; Wang, Q.; Xu, X.; Wu, C. Remaining Useful Life Prediction of Lithium-Ion Batteries Based on Monte Carlo Dropout and Gated Recurrent Unit. Energy Rep. 2021, 7, 2862–2871. [Google Scholar] [CrossRef]
- Liu, D.; Xie, W.; Liao, H.; Peng, Y. An Integrated Probabilistic Approach to Lithium-Ion Battery Remaining Useful Life Estimation. IEEE Trans. Instrum. Meas. 2015, 64, 660–670. [Google Scholar] [CrossRef]
- Sui, X.; He, S.; Vilsen, S.B.; Meng, J.; Teodorescu, R.; Stroe, D.I. A Review of Non-Probabilistic Machine Learning-Based State of Health Estimation Techniques for Lithium-Ion Battery. Appl. Energy 2021, 300, 117346. [Google Scholar] [CrossRef]
- Lombardo, T.; Duquesnoy, M.; El-Bouysidy, H.; Årén, F.; Gallo-Bueno, A.; Jørgensen, P.B.; Bhowmik, A.; Demortière, A.; Ayerbe, E.; Alcaide, F.; et al. Artificial Intelligence Applied to Battery Research: Hype or Reality? Chem. Rev. 2022, 122, 10899–10969. [Google Scholar] [CrossRef]
- Zhu, J.; Wang, Y.; Huang, Y.; Bhushan Gopaluni, R.; Cao, Y.; Heere, M.; Mühlbauer, M.J.; Mereacre, L.; Dai, H.; Liu, X.; et al. Data-Driven Capacity Estimation of Commercial Lithium-Ion Batteries from Voltage Relaxation. Nat. Commun. 2022, 13, 2261. [Google Scholar] [CrossRef]
- Vapnik, V. The Support Vector Method of Function Estimation. In Nonlinear Modeling; Springer: Boston, MA, USA, 1998; pp. 55–85. [Google Scholar] [CrossRef]
- Feng, X.; Weng, C.; He, X.; Han, X.; Lu, L.; Ren, D.; Ouyang, M. Online State-of-Health Estimation for Li-Ion Battery Using Partial Charging Segment Based on Support Vector Machine. IEEE Trans. Veh. Technol. 2019, 68, 8583–8592. [Google Scholar] [CrossRef]
- Klass, V.; Behm, M.; Lindbergh, G. A Support Vector Machine-Based State-of-Health Estimation Method for Lithium-Ion Batteries under Electric Vehicle Operation. J. Power Sources 2014, 270, 262–272. [Google Scholar] [CrossRef]
- Shu, X.; Li, G.; Zhang, Y.; Shen, J.; Chen, Z.; Liu, Y. Online Diagnosis of State of Health for Lithium-Ion Batteries Based on Short-Term Charging Profiles. J. Power Sources 2020, 471, 228478. [Google Scholar] [CrossRef]
- Patil, M.A.; Tagade, P.; Hariharan, K.S.; Kolake, S.M.; Song, T.; Yeo, T.; Doo, S. A Novel Multistage Support Vector Machine Based Approach for Li Ion Battery Remaining Useful Life Estimation. Appl. Energy 2015, 159, 285–297. [Google Scholar] [CrossRef]
- Li, Y.; Wang, S.; Chen, W.; Han, W. Holistic Comparison of Different Kernel Functions for Support Vector Regression Based on State-of-Health Prediction of Lithium-Ion Battery. In Proceedings of the 11th International Conference on Prognostics and System Health Management (PHM-2020 Jinan), Jinan, China, 23–25 October 2020; Institute of Electrical and Electronics Engineers Inc.: Piscateville, NJ, USA, 2020; pp. 40–46. [Google Scholar]
- Xiang, M.; He, Y.; Zhang, H.; Zhang, C.; Wang, L.; Wang, C.; Sui, C. State-of-Health Prognosis for Lithium-Ion Batteries Considering the Limitations in Measurements via Maximal Information Entropy and Collective Sparse Variational Gaussian Process. IEEE Access 2020, 8, 188199–188217. [Google Scholar] [CrossRef]
- Hu, C.; Jain, G.; Zhang, P.; Schmidt, C.; Gomadam, P.; Gorka, T. Data-Driven Method Based on Particle Swarm Optimization and k-Nearest Neighbor Regression for Estimating Capacity of Lithium-Ion Battery. Appl. Energy 2014, 129, 49–55. [Google Scholar] [CrossRef]
- Ma, Y.; Yao, M.; Liu, H.; Tang, Z. State of Health Estimation and Remaining Useful Life Prediction for Lithium-Ion Batteries by Improved Particle Swarm Optimization-Back Propagation Neural Network. J. Energy Storage 2022, 52, 104750. [Google Scholar] [CrossRef]
- Toughzaoui, Y.; Toosi, S.B.; Chaoui, H.; Louahlia, H.; Petrone, R.; Le Masson, S.; Gualous, H. State of Health Estimation and Remaining Useful Life Assessment of Lithium-Ion Batteries: A Comparative Study. J. Energy Storage 2022, 51, 104520. [Google Scholar] [CrossRef]
- Gu, X.; See, K.W.; Li, P.; Shan, K.; Wang, Y.; Zhao, L.; Lim, K.C.; Zhang, N. A Novel State-of-Health Estimation for the Lithium-Ion Battery Using a Convolutional Neural Network and Transformer Model. Energy 2023, 262, 125501. [Google Scholar] [CrossRef]
- Bao, X.; Chen, L.; Lopes, A.M.; Li, X.; Xie, S.; Li, P.; Chen, Y. Hybrid Deep Neural Network with Dimension Attention for State-of-Health Estimation of Lithium-Ion Batteries. Energy 2023, 278, 127734. [Google Scholar] [CrossRef]
- Shen, S.; Sadoughi, M.; Chen, X.; Hong, M.; Hu, C. A Deep Learning Method for Online Capacity Estimation of Lithium-Ion Batteries. J. Energy Storage 2019, 25, 100817. [Google Scholar] [CrossRef]
- Eddahech, A.; Briat, O.; Bertrand, N.; Delétage, J.-Y.; Vinassa, J.-M. Behavior and State-of-Health Monitoring of Li-Ion Batteries Using Impedance Spectroscopy and Recurrent Neural Networks. International Journal of Electrical Power & Energy Systems 2012, 42, 487–494. [Google Scholar] [CrossRef]
- Wang, H.K.; Zhang, Y.; Huang, M. A Conditional Random Field Based Feature Learning Framework for Battery Capacity Prediction. Sci. Rep. 2022, 12, 13221. [Google Scholar] [CrossRef]
- Kwon, S.; Han, D.; Park, J.; Lee, P.Y.; Kim, J. Joint State-of-Health and Remaining-Useful-Life Prediction Based on Multi-Level Long Short-Term Memory Model Prognostic Framework Considering Cell Voltage Inconsistency Reflected Health Indicators. J. Energy Storage 2022, 55, 105731. [Google Scholar] [CrossRef]
- Zhang, Y.; Xiong, R.; He, H.; Pecht, M.G. Long Short-Term Memory Recurrent Neural Network for Remaining Useful Life Prediction of Lithium-Ion Batteries. IEEE Trans. Veh. Technol. 2018, 67, 5695–5705. [Google Scholar] [CrossRef]
- Wang, F.K.; Amogne, Z.E.; Chou, J.H.; Tseng, C. Online Remaining Useful Life Prediction of Lithium-Ion Batteries Using Bidirectional Long Short-Term Memory with Attention Mechanism. Energy 2022, 254, 124344. [Google Scholar] [CrossRef]
- Ma, Y.; Shan, C.; Gao, J.; Chen, H. A Novel Method for State of Health Estimation of Lithium-Ion Batteries Based on Improved LSTM and Health Indicators Extraction. Energy 2022, 251, 123973. [Google Scholar] [CrossRef]
- Ren, P.; Wang, S.; Chen, X.; Zhou, H.; Fernandez, C.; Stroe, D.I. A Novel Multiple Training-Scale Dynamic Adaptive Cuckoo Search Optimized Long Short-Term Memory Neural Network and Multi-Dimensional Health Indicators Acquisition Strategy for Whole Life Cycle Health Evaluation of Lithium-Ion Batteries. Electrochim. Acta. 2022, 435, 141404. [Google Scholar] [CrossRef]
- González-Muñiz, A.; Díaz, I.; Cuadrado, A.A.; García-Pérez, D. Health Indicator for Machine Condition Monitoring Built in the Latent Space of a Deep Autoencoder. Reliab. Eng. Syst. Saf. 2022, 224, 108482. [Google Scholar] [CrossRef]
- Sun, Y.; Zhang, J.; Zhang, K.; Qi, H.; Zhang, C. Battery State of Health Estimation Method Based on Sparse Auto-Encoder and Backward Propagation Fading Diversity among Battery Cells. Int. J. Energy Res. 2021, 45, 7651–7662. [Google Scholar] [CrossRef]
- Wu, J.; Chen, J.; Feng, X.; Xiang, H.; Zhu, Q. State of Health Estimation of Lithium-Ion Batteries Using Autoencoders and Ensemble Learning. J. Energy Storage 2022, 55, 105708. [Google Scholar] [CrossRef]
- Jiang, Y.; Chen, Y.; Yang, F.; Peng, W. State of Health Estimation of Lithium-Ion Battery with Automatic Feature Extraction and Self-Attention Learning Mechanism. J. Power Sources 2023, 556, 232466. [Google Scholar] [CrossRef]
- Xu, Z.; Guo, Y.; Saleh, J.H. A Physics-Informed Dynamic Deep Autoencoder for Accurate State-of-Health Prediction of Lithium-Ion Battery. Neural. Comput. Appl. 2022, 34, 15997–16017. [Google Scholar] [CrossRef]
- Lee, P.Y.; Kwon, S.; Kang, D.; Cho, I.; Kim, J. Principle Component Analysis-Based Optimized Feature Extraction Merged with Nonlinear Regression Model for Improved State-of-Health Prediction. J. Energy Storage 2022, 48, 104026. [Google Scholar] [CrossRef]
- Banguero, E.; Correcher, A.; Pérez-Navarro, Á.; García, E.; Aristizabal, A. Diagnosis of a Battery Energy Storage System Based on Principal Component Analysis. Renew Energy 2020, 146, 2438–2449. [Google Scholar] [CrossRef]
- Liu, C.; Wen, X.; Zhong, J.; Liu, W.; Chen, J.; Zhang, J.; Wang, Z.; Liao, Q. Characterization of Aging Mechanisms and State of Health for Second-Life 21700 Ternary Lithium-Ion Battery. J. Energy Storage 2022, 55, 105511. [Google Scholar] [CrossRef]
- Li, X.; Yuan, C.; Wang, Z. State of Health Estimation for Li-Ion Battery via Partial Incremental Capacity Analysis Based on Support Vector Regression. Energy 2020, 203, 117852. [Google Scholar] [CrossRef]
- Zhao, G.; Zhang, C.; Duan, B.; Shang, Y.; Kang, Y.; Zhu, R. State-of-Health Estimation with Anomalous Aging Indicator Detection of Lithium-Ion Batteries Using Regression Generative Adversarial Network. IEEE Trans. Ind. Electron. 2022, 70, 2685–2695. [Google Scholar] [CrossRef]
- Kim, S.; Choi, Y.Y.; Choi, J.I. Impedance-Based Capacity Estimation for Lithium-Ion Batteries Using Generative Adversarial Network. Appl. Energy 2022, 308, 118317. [Google Scholar] [CrossRef]
- Yao, X.-Y.; Chen, G.; Hu, L.; Pecht, M. A Multi-Model Feature Fusion Model for Lithium-Ion Battery State of Health Prediction. J. Energy Storage 2022, 56, 106051. [Google Scholar] [CrossRef]
- Wei, Y.; Wu, D. Prediction of State of Health and Remaining Useful Life of Lithium-Ion Battery Using Graph Convolutional Network with Dual Attention Mechanisms. Reliab. Eng. Syst. Saf. 2023, 230, 108947. [Google Scholar] [CrossRef]
- Gou, B.; Xu, Y.; Feng, X. An Ensemble Learning-Based Data-Driven Method for Online State-of-Health Estimation of Lithium-Ion Batteries. IEEE Trans. Transp. Electrif. 2021, 7, 422–436. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, L.; Yu, H.; Yang, X.; Zhang, T.; Chen, S.; Liang, F.; Wang, H.; Lu, X.; Yang, S.; et al. Early Prediction of the Health Conditions for Battery Cathodes Assisted by the Fusion of Feature Signal Analysis and Deep-Learning Techniques. Batteries 2022, 8, 151. [Google Scholar] [CrossRef]
- Chen, X.; Duan, Y.; Houthooft, R.; Schulman, J.; Sutskever, I.; Abbeel, P. InfoGAN: Interpretable Representation Learning by Information Maximizing Generative Adversarial Nets. Adv. Neural Inf. Process. Syst. 2016, 29. [Google Scholar]
- Yang, G.; Ma, Q.; Sun, H.; Zhang, X. State of Health Estimation Based on GAN-LSTM-TL for Lithium-Ion Batteries. Int. J. Electrochem. Sci. 2022, 17, 21128. [Google Scholar] [CrossRef]
- Huo, Q.; Ma, Z.; Zhao, X.; Zhang, T.; Zhang, Y. Bayesian Network Based State-of-Health Estimation for Battery on Electric Vehicle Application and Its Validation through Real-World Data. IEEE Access 2021, 9, 11328–11341. [Google Scholar] [CrossRef]
- Dong, G.; Han, W.; Wang, Y. Dynamic Bayesian Network-Based Lithium-Ion Battery Health Prognosis for Electric Vehicles. IEEE Trans. Ind. Electron. 2021, 68, 10949–10958. [Google Scholar] [CrossRef]
- He, Z.; Gao, M.; Ma, G.; Liu, Y.; Chen, S. Online State-of-Health Estimation of Lithium-Ion Batteries Using Dynamic Bayesian Networks. J. Power Sources 2014, 267, 576–583. [Google Scholar] [CrossRef]
- Nie, Z.; Zheng, S.; Liu, Y.; Chen, Z.; Li, S.; Lei, K.; Pan, F. Automating Materials Exploration with a Semantic Knowledge Graph for Li-Ion Battery Cathodes. Adv. Funct. Mater 2022, 32, 2201437. [Google Scholar] [CrossRef]
- Ong, L.; Karmakar, G.; Atherton, J.; Zhou, X.; Lim, M.Q.; Chadzynski, A.; Li, L.; Wang, X.; Kraft, M. Embedding Energy Storage Systems into a Dynamic Knowledge Graph. Ind. Eng. Chem. Res. 2022, 61, 8390–8398. [Google Scholar] [CrossRef]
- Zhang, Z.; Sun, Y.; Zhang, L.; Cheng, H.; Cao, R.; Liu, X.; Yang, S. Enabling Online Search and Fault Inference for Batteries Based on Knowledge Graph. Batteries 2023, 9, 124. [Google Scholar] [CrossRef]
- Kalaycı, T.E.; Bricelj, B.; Lah, M.; Pichler, F.; Scharrer, M.K.; Rubeša-Zrim, J. A Knowledge Graph-Based Data Integration Framework Applied to Battery Data Management. Sustainability 2021, 13, 1583. [Google Scholar] [CrossRef]
- Yao, X.Y.; Chen, G.; Pecht, M.; Chen, B. A Novel Graph-Based Framework for State of Health Prediction of Lithium-Ion Battery. J. Energy Storage 2023, 58, 106437. [Google Scholar] [CrossRef]
- Chen, Z.; Mi, C.C.; Fu, Y.; Xu, J.; Gong, X. Online Battery State of Health Estimation Based on Genetic Algorithm for Electric and Hybrid Vehicle Applications. J. Power Sources 2013, 240, 184–192. [Google Scholar] [CrossRef]
- Lyu, C.; Lai, Q.; Ge, T.; Yu, H.; Wang, L.; Ma, N. A Lead-Acid Battery’s Remaining Useful Life Prediction by Using Electrochemical Model in the Particle Filtering Framework. Energy 2017, 120, 975–984. [Google Scholar] [CrossRef]
- Li, J.; Herdem, M.S.; Nathwani, J.; Wen, J.Z. Methods and Applications for Artificial Intelligence, Big Data, Internet of Things, and Blockchain in Smart Energy Management. Energy AI 2023, 11, 100208. [Google Scholar] [CrossRef]
- Qin, P.; Zhao, L.; Liu, Z. State of Health Prediction for Lithium-Ion Battery Using a Gradient Boosting-Based Data-Driven Method. J. Energy Storage 2022, 47, 103644. [Google Scholar] [CrossRef]
- Hu, X.; Che, Y.; Lin, X.; Onori, S. Battery Health Prediction Using Fusion-Based Feature Selection and Machine Learning. IEEE Trans. Transp. Electrif. 2021, 7, 382–398. [Google Scholar] [CrossRef]
- Yang, S.; Zhang, Z.; Cao, R.; Wang, M.; Cheng, H.; Zhang, L.; Jiang, Y.; Li, Y.; Chen, B.; Ling, H.; et al. Implementation for a Cloud Battery Management System Based on the CHAIN Framework. Energy AI 2021, 5, 100088. [Google Scholar] [CrossRef]
- Yang, S.; He, R.; Zhang, Z.; Cao, Y.; Gao, X.; Liu, X. CHAIN: Cyber Hierarchy and Interactional Network Enabling Digital Solution for Battery Full-Lifespan Management. Matter 2020, 3, 27–41. [Google Scholar] [CrossRef]
- Gao, X.; Liu, X.; He, R.; Wang, M.; Xie, W.; Brandon, N.P.; Wu, B.; Ling, H.; Yang, S. Designed High-Performance Lithium-Ion Battery Electrodes Using a Novel Hybrid Model-Data Driven Approach. Energy Storage Mater 2021, 36, 435–458. [Google Scholar] [CrossRef]
- Wang, W.; Ma, B.; Hua, X.; Zou, B.; Zhang, L.; Yu, H.; Yang, K.; Yang, S.; Liu, X. End-Cloud Collaboration Approach for State-of-Charge Estimation in Lithium Batteries Using CNN-LSTM and UKF. Batteries 2023, 9, 114. [Google Scholar] [CrossRef]




| Strategies | Models | Ref. | Data | Topic | Indicators |
|---|---|---|---|---|---|
| Probabilistic based | Naïve Bayes | [165] | Lab data | RUL | 16.1 cycles (RMSE 0.17%) |
| GPR | [168] | Lab data | SOH | RMSE < 1.29% | |
| GPR | [169] | Lab data | SOH | MSE < 0.34% | |
| GPR | [170] | Lab data | SOH | RMSE < 3.45% | |
| Monte Carlo | [175] | Lab data | SOH | RMSE < 2.02% | |
| Monte Carlo | [176] | Lab data | SOH | RMSE < 1.88% | |
| RF | [179] | Lab data | SOH | RMSE < 1.26% | |
| RF | [180] | Lab data | SOH | MAE = 0.72% | |
| Non-Probabilistic based | SVR | [217] | Lab data | SOH | MAE < 1.64% |
| SVR | [32] | vehicle data | SOH | maximum error < 0.5% | |
| KNN | [196] | Lab data | SOH | RMSE < 1.53% | |
| CNN | [199] | Lab data | SOH | RMSE < 0.3% | |
| DCNN | [201] | Lab data | SOH | RMSE < 0.36% | |
| AE | [212] | Lab data | SOH | RMSE < 0.87% Average RMSE = 0.48% | |
| AE | [213] | Lab data | SOH | RMSE = 0.6% | |
| PCA | [216] | Lab data | SOH | RMSE < 1.37% | |
| Semi-probability model | GAN | [218] | Lab data | SOH | RMSE < 1.82% |
| GAN | [219] | Lab data | SOH | RMSE < 1.61mAh | |
| Others | LSTM | [206] | Lab data | SOH | RMSE < 1.06% |
| LSTM | [207] | Lab data | SOH | RMSE < 0.401% | |
| GNN | [220] | Lab data | SOH | RMSE < 0.40% | |
| GNN | [221] | Lab data | SOH and RUL | RMSE < 1.62% | |
| EL | [222,223] | Lab data | SOH | RMSE < 1.67% Average RMSE around 0.78% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, K.; Zhang, L.; Zhang, Z.; Yu, H.; Wang, W.; Ouyang, M.; Zhang, C.; Sun, Q.; Yan, X.; Yang, S.; et al. Battery State of Health Estimate Strategies: From Data Analysis to End-Cloud Collaborative Framework. Batteries 2023, 9, 351. https://doi.org/10.3390/batteries9070351
Yang K, Zhang L, Zhang Z, Yu H, Wang W, Ouyang M, Zhang C, Sun Q, Yan X, Yang S, et al. Battery State of Health Estimate Strategies: From Data Analysis to End-Cloud Collaborative Framework. Batteries. 2023; 9(7):351. https://doi.org/10.3390/batteries9070351
Chicago/Turabian StyleYang, Kaiyi, Lisheng Zhang, Zhengjie Zhang, Hanqing Yu, Wentao Wang, Mengzheng Ouyang, Cheng Zhang, Qi Sun, Xiaoyu Yan, Shichun Yang, and et al. 2023. "Battery State of Health Estimate Strategies: From Data Analysis to End-Cloud Collaborative Framework" Batteries 9, no. 7: 351. https://doi.org/10.3390/batteries9070351
APA StyleYang, K., Zhang, L., Zhang, Z., Yu, H., Wang, W., Ouyang, M., Zhang, C., Sun, Q., Yan, X., Yang, S., & Liu, X. (2023). Battery State of Health Estimate Strategies: From Data Analysis to End-Cloud Collaborative Framework. Batteries, 9(7), 351. https://doi.org/10.3390/batteries9070351









