A Self-Charging Concentration Cell: Theory
Abstract
:1. Introduction
2. Theory
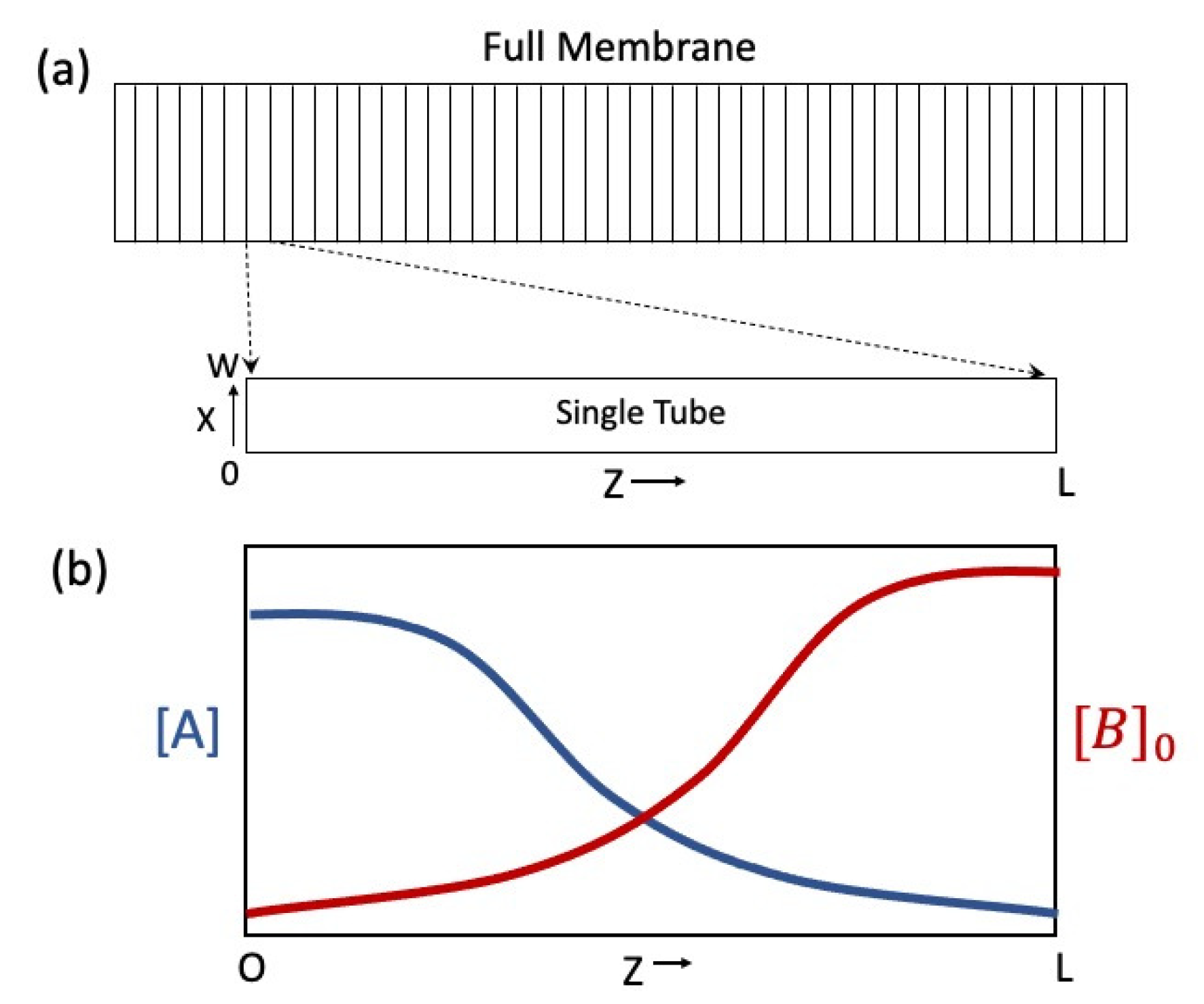
2.1. AMS Model: Tube Array
- (1)
- The concentration pertains to volume, while , , , and pertain to the surrounding surfaces. As such, this is a boundary value problem, in which the specifics of and can depend heavily on the size and shape of the reaction vessel (membrane channels). Numerical simulations bear this out [12].
- (2)
- (3)
- While Equations (4) and (5) indicate that the magnitude of is proportional to , numerically large gradients do not necessarily translate to larger emfs because the Nernst relation (Equation (6)) dictates that it is the ratio that determines emf, not their individual magnitudes. (For instance, contrast the following two scenarios: (i) M and M versus (ii) M and M. The concentrations of the latter are 50–400 times greater than the former, but the Nernst emf of the former is greater than the latter by a factor of 2).
2.2. Maximizing AMS Density Gradients
- Limit 1: Trivially, if the AMS tube has an initially uniform axial concentration of B (i.e., ) and also uniform binding strength (i.e., ), then the concentration of A in solution will also be uniform (i.e., ), thus the AMS fails.Conclusion: At least one of the parameters, or must vary axially.
- Limit 2: If the binding is too strong, such that effectively, , then, assuming remains finite, the first term on the rhs of Equation (4) goes to zero, while the second term becomes irrelevant because A–B binding is effectively permanent, in which case there is no ongoing interplay between the walls and solute. Thus, A diffuses to uniform concentration (), and again, the AMS fails.Conclusion: Very strong surface binding should be avoided.
- Limit 3: In the opposite limit (very weak, effectively no surface binding), the walls are operationally inert, and therefore lack any chemical asymmetry, so and along the tube. As a result, A molecules diffuse freely, uniformly filling the tube, rendering .Conclusion: Weak binding should likewise be avoided.
- Limit 4: If , then regardless of the reactivity of A for B, the concentration of B will not change appreciably (), in which case Equation (3) gives . In this scenario, species A has been stripped from the solution, precipitated out as ; thus, the AMS fails.Conclusion: should be avoided.
- Limit 5: In the opposite limit, if , then the initial concentration of A is effectively unchanged (i.e., ). Without sculpting by [B(z)], the concentration of A will become uniform along the length of the tube via diffusion, in which case , and again the AMS fails.Conclusion: should be avoided.
- (i)
- (ii)
- (iii)
- (iv)
- (v)
- (vi)
2.3. Dimensionless Constants and the Buckingham Pi Theorem
- (1)
- : total number of A molecules in the AMS tube. (Dimensions: None).
- (2)
- : initial density distribution of binding sites B as a function of axial location (z) along the tube walls. (Dimensions: m).
- (3)
- : residence time of A on binding site B as a function of axial location (z) along the tube. Here, appears as a proxy for or . (Dimensions: s).
- (4)
- w: diameter of AMS tube. (Dimensions: m).
- (5)
- L: axial length of AMS tube. (Dimension: m).
- (6)
- : Diffusion coefficient for species A in solution. (Dimensions: m/s) Typical value: m/s for small molecules and ions in water.
- (1)
- ;
- (2)
- ;
- (3)
- ; and
- (4)
- .
2.4. Equilibrium Current Densities in the AMS
3. Discussion
3.1. Liquid Chromatography and Concentration Gradient Corrosion
3.2. Analogy to Solid State Diodes
3.3. AMCC Energy and Power Density
4. Conclusions and Future Directions
- Traditional thermodynamics predicts the AMS effect. Analysing for the surface reaction (A + B⇄) identifies the primary factors upon which depends; specifically, the initial binding site density () and the Gibbs free energy (), in Equations (3)–(5). Because and can be engineered to vary with z, must likewise vary ().
- The AMS effect can be understood to arise as a balance between oppositely directed particle current densities in the membrane ( vs. ). These generate a one-dimensional profile for akin to that of an isothermal atmosphere (Section 2.4).
- Equilibrium solute concentrations in the AMS tube can be modeled in 1–3 dimensions using the time-independent (equilibrium) diffusion equation (Appendix A). The solution of the 2-D AMS has a well-known analog: the Laplace equation solution for the electrostatic parallel plate capacitor. From this, one can deduce that a concentration gradient must form in the AMS.
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
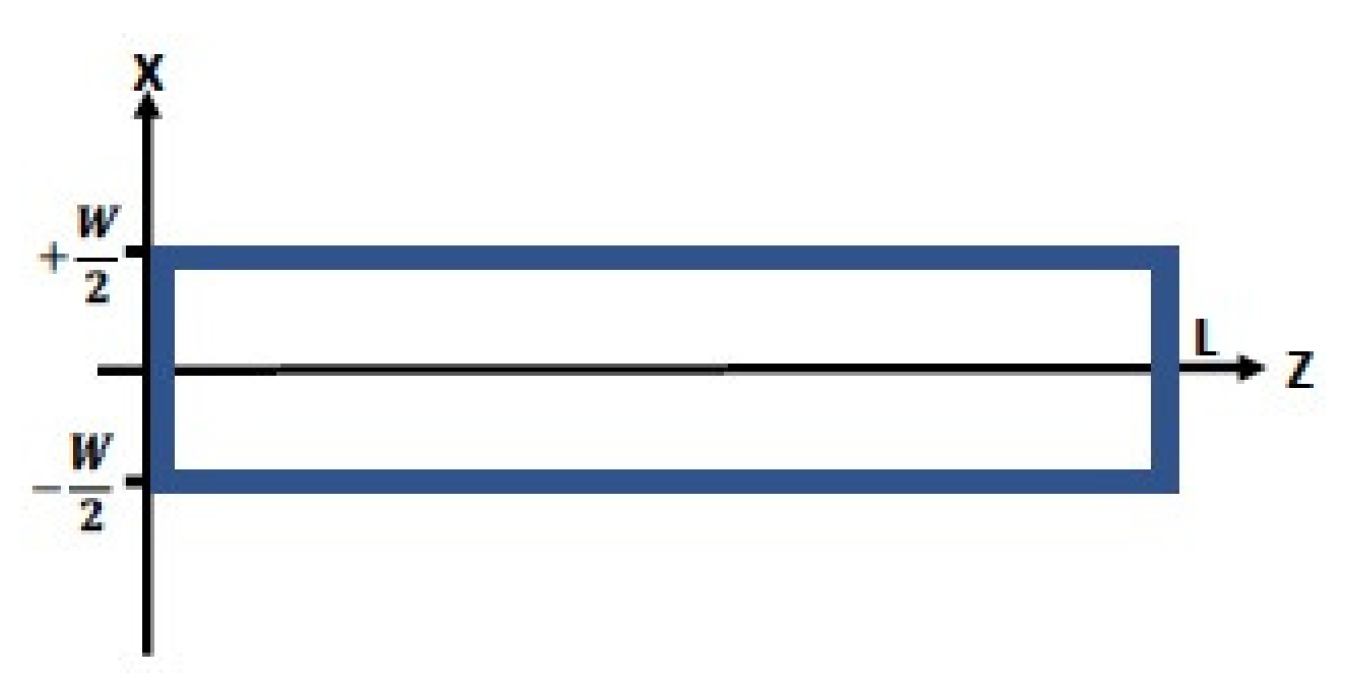
Appendix A. Time-Independent Diffusion Equation and AMS
- (1)
- Mirror (bilateral) symmetry across the z axis, i.e., .
- (2)
- No y-dependence for , thus (), in which case the Laplacian operator is reduced from 3-D to 2-D and the AMS assumes slot geometry. If y-dependence is desired for a full 3-D description, the 2-D tube might at least be made a square channel, thereby symmetrizing the x and y solutions. (Going forward, 2-D slot geometry is assumed).
- (3)
- The ends of the AMS (z = 0 and z = L) are chemically identical to their immediate lateral walls. (The solid endcaps can be replaced with chemically treated fine screens. This would preserve the mathematical boundary conditions, while permitting the flow of solution into and out of the cell).
- (i)
- Bottom Boundary (; ): (variable);
- (ii)
- Top Boundary (; ): (variable);
- (iii)
- Endcap 1 (; ): (constant); and
- (iv)
- Endcap 2 (; ): (constant).
- (a)
- ; and
- (b)
- .
- (c)
- ; and
- (d)
- .
- (1)
- The interior solution is uniquely determined by on the boundary; in this case, the solution-surface interface.
- (2)
- For the 2-D case, the value of at a spatial point (x,z) is the average of values on its surrounding circle: .
- (3)
- Solutions have no local maxima or minima in the interior; all extrema are on the boundaries.
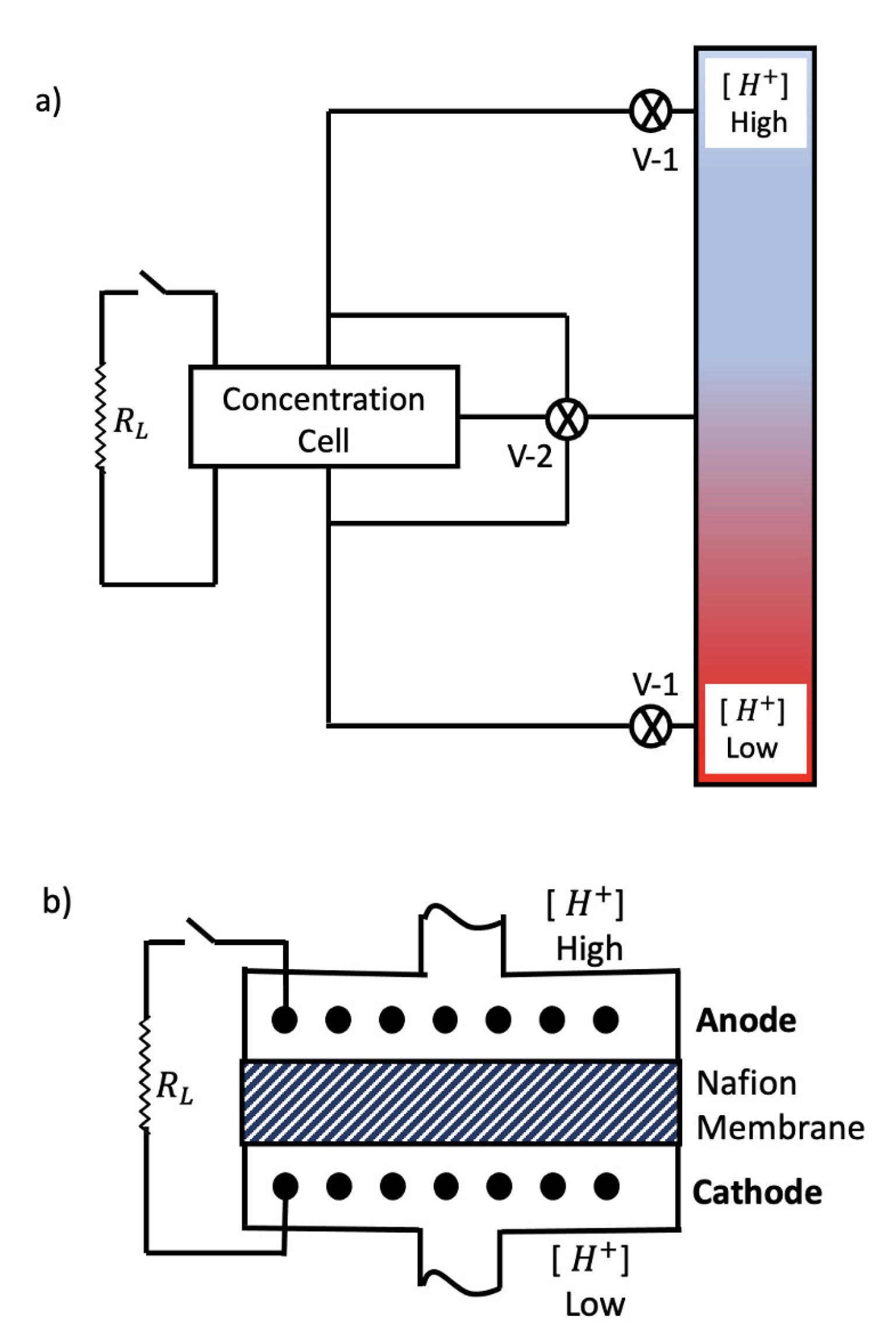
Appendix B. Physical Example of AMCC
while the cathode’s reduction half-reaction (low [H]) is:Cl + Ag⟶ AgCl + e;
AgCl + e⟶ Ag + Cl.
which is emblematic of a concentration cell.Cl⟶ Cl,
References
- Newman, J.; Thomas-Alyea, K.E. Electrochemical Systems, 3rd ed.; John Wiley and Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Bokris, J.O.M.; Reddy, A.K.N. Electrochemistry 1: Ionics, 2nd ed.; Kluwer: New York, NY, USA, 2002. [Google Scholar]
- Hibbert, D.B. Introduction to Electrochemistry; Macmillan: Houndmills, UK, 1993. [Google Scholar]
- Andrews, J.; Jelley, N. Energy Science: Principles, Technologies, and Impacts; Oxford University Press: Oxford, UK, 2017. [Google Scholar]
- Zito, R. Energy Storage: A New Approach; Wiley: Hoboken, NJ, USA, 2010. [Google Scholar]
- Weinstein, J.N.; Leitz, F.B. Electric power from differences in salinity: The dialytic battery. Science 1976, 191, 557. [Google Scholar] [CrossRef] [PubMed]
- Clampitt, B.H.; Kiviat, F.E. Energy recovery from saline water by means of electrochemical cells. Science 1976, 194, 719. [Google Scholar]
- Rahmstrof, S. Thermohaline circulation: The current climate. Nature 2003, 421, 699. [Google Scholar] [CrossRef]
- Campbell, N.A.; Williamson, B.; Heyden, R.J. Biology: Exploring Life; Pearson/Prentice Hall: Boston, MA, USA, 2006. [Google Scholar]
- Gerstner, W.; Kistler, W. Spiking Neuron Models: Single Neurons, Populations, Plasticity; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Sheehan, D.P.; Hebert, M.R.; Keogh, D.M. Concentration cell powered by a chemically asymmetric membrane: Experiment. Sust. Ener. Assess. Technol. 2022, 52, 102194. [Google Scholar] [CrossRef]
- Sheehan, D.P.; Watson, A.J.; Welsh, T.M.; Gibson, C.C.; Miller, D.W.; Glick, J. Numerical simulations of diffusion-driven concentration gradients in chemically asymmetric membranes: Implications for sustainable energy and the second law of thermodynamics. 2023, in preparation. 2023; in preparation. [Google Scholar]
- Sheehan, W.F. Chemistry: A Physical Approach; Allyn and Bacon: Boston, MA, USA, 1964. [Google Scholar]
- Sheehan, W.F. Physical Chemistry, 2nd ed.; Allyn and Bacon: Boston, MA, USA, 1970. [Google Scholar]
- Kolasinski, K.W. Surface Science: Foundations of Catalysis and Nanoscience, 2nd ed.; Wiley: Hoboken, NJ, USA, 2008. [Google Scholar]
- Masel, R.I. Prinicples of Adsorption and Reaction on Solid Surfaces; John Wiley and Sons: New York, NY, USA, 1996. [Google Scholar]
- Sheehan, D.P. Dynamically-maintained, steady-state pressure gradients. Phys. Rev. E 1998, 57, 6660. [Google Scholar] [CrossRef] [Green Version]
- Sheehan, D.P. Nonequilibrium heterogeneous catalysis in the long mean-free-path regime. Phys. Rev. E 2013, 88, 032125. [Google Scholar] [CrossRef] [Green Version]
- Sheehan, D.P. A Symmetric Van ’t Hoff equation and equilibrium temperature gradients. J. Non-Equilib. Thermodyn. 2018, 43, 301. [Google Scholar] [CrossRef]
- Buckingham, E. On physically similar systems; Illustrations of the use of dimensional equations. Phys. Rev. 1914, 4, 345. [Google Scholar] [CrossRef]
- Sweeney, M.; (Santa Clara University, Santa Clara, CA, USA). A Strong Acid Is Like a Mugger Who Corners You in An Alley, Puts a Gun to Your Head, and Barks, Take My Wallet. Personal communication, 1980. [Google Scholar]
- Snyder, L.R.; Kirkland, J.J.; Dolan, J.W. Introduction to Modern Liquid Chromatography, 3rd ed.; Wiley: Hoboken, NJ, USA, 2010. [Google Scholar]
- Vitha, M.F. Chromatography: Principles and Instrumentation; Wiley: Hoboken, NJ, USA, 2017. [Google Scholar]
- Ahmad, Z. Principles of Corrosion: Engineering and Corrosion Control; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- McCafferty, E. Introduction to Corrosion Science; Springer: New York, NY, USA, 2010. [Google Scholar]
- Roberge, P.K. Handbook of Corrosion Engineering, 3rd ed.; McGraw Hill: New York, NY, USA, 2019. [Google Scholar]
- Vermaas, D.A.; Wiegman, S.; Nagaki, T.; Smith, W.A. Ion transport mechanisms in bipolar membranes for (photo)electrochemical water splitting. Sust. Energy Fuels 2018, 2, 2006. [Google Scholar] [CrossRef]
- Reiter, R.S.; White, W.; Ardo, S.J. Communication—Electrochemical characterization of commercial bipolar membranes under electrolyte conditions relevant to solar fuels technologies. Electrochem. Soc. 2016, 163, H3132. [Google Scholar] [CrossRef]
- Sun, K.; Liu, R.; Chen, Y.; Verlage, E.; Lewis, N.S.; Xiang, C. A stabilized, intrinsically safe, 10% efficient, solar-driven water-splitting cell incorporating earth-abundant electrocatalysts with steady-state pH gradients and product separation enabled by a bipolar membrane. Adv. Energy Mater. 2016, 6, 1600379. [Google Scholar] [CrossRef] [Green Version]
- Vermaas, D.A.; Sassenburg, M.; Smith, W.A. photo-assisted water splitting with bipolar membrane induced pH gradients for practical solar fuel devices. J. Mater. Chem. A 2015, 3, 19556. [Google Scholar] [CrossRef] [Green Version]
- Ashrafi, A.M.; Gupta, N.; Neděla, D. An investigation through the validation of the electrochemical methods used for bipolar membranes characterization. J. Membr. Sci. 2017, 544, 195. [Google Scholar] [CrossRef]
- Moussaoui, R.E.; Pourcelly, G.; Maeck, M.; Hurwitz, H.D.; Gavach, C. Co-ion leakage through bipolar membranes Influence on I–V responses and water-splitting efficiency. J. Membr. Sci. 1994, 90, 283. [Google Scholar] [CrossRef]
- Strathmann, H. Ion Exchange Membrane Separation Processes; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Mafe, S.; Ramirez, P. Electrochemical characterization of polymer ion-exchange bipolar membranes. Acta Polym. 1997, 48, 234. [Google Scholar] [CrossRef]
- Volkov, A.V.; Tybrandt, K.; Berggren, M.; Zozoulenko, I.V. Modeling of charge transport in ion bipolar junction transistors. Langmuir 2014, 30, 6999. [Google Scholar] [CrossRef] [Green Version]
- Tybrandt, K.; Gabrielsson, E.O.; Berggren, M. Toward complementary ionic circuits: The npn ion bipolar junction transistor. J. Am. Chem. Soc. 2011, 133, 10141. [Google Scholar] [CrossRef] [Green Version]
- Karnik, R.; Fan, R.; Yue, M.; Li, D.; Yang, P.; Majumdar, A. Electrostatic control of ions and molecules in nanofluidic transistors. Nano Lett. 2005, 5, 943. [Google Scholar] [CrossRef] [Green Version]
- Kim, K.B.; Han, J.H.; Kim, H.C.; Chung, T.D. Polyelectrolyte junction field effect transistor based on microfluidic chip. Appl. Phys. Lett. 2010, 96, 143506. [Google Scholar] [CrossRef]
- Tybrandt, K.; Forchheimer, R.; Berggren, M. Logic gates based on ion transistors. Nat. Comm. 2012, 3, 871. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sun, G.; Senapati, S.; Chang, H.-S. High-flux ionic diodes, ionic transistors and ionic amplifiers based on external ion concentration polarization by an ion exchange membrane: A new scalable ionic circuit platform. Lab Chip 2016, 16, 1171. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pierret, R.F.; Neudeck, G.W. (Eds.) Modular Series on Solid State Devices, 2nd ed.; Addison-Wesley: Reading, MA, USA, 1989; Volumes 1–2. [Google Scholar]
- Mouthaan, T. Semiconductor Devices Explained; Wiley: Chichester, UK, 1999. [Google Scholar]
- Sheehan, D.P.; Putnam, A.R.; Wright, J.H. A solid-state Maxwell demon. Found. Phys. 2002, 32, 1557. [Google Scholar] [CrossRef]
- Sheehan, D.P.; Wright, J.H.; Putnam, A.R.; Perttu, E.K. Intrinsically-biased resonant NEMS-MEMS oscillator and the second law of thermodynamics. Phys. E 2005, 29, 87. [Google Scholar] [CrossRef]
- Fick, A. Ueber diffusion. Ann. Phys. 1855, 94, 59. [Google Scholar] [CrossRef]
- Sheehan, D.P.; (University of San Diego, San Diego, CA, USA); Miller, D.W.; (University of San Diego, San Diego, CA, USA); Gibson, C.C.; (University of San Diego, San Diego, CA, USA). Unpublished results, 2023.
- Voutchkov, N. Desalination Engineering: Planning and Design; McGraw-Hill: New York, NY, USA, 2013. [Google Scholar]
- Wu, J.; Wang, J.; Liu, Y.; Rao, U. Sustainable Desalination and Water Reuse; Hoek, E.M., Jassby, D., Kaner, R.B., Eds.; Morgan and Claypool Publishers: San Rafael, CA, USA, 2021. [Google Scholar]
- Gude, V.G. (Ed.) Resource Recovery from Wastewater: Toward Sustainability; Apple Academic: Moonachie, NJ, USA, 2022. [Google Scholar]
- Čápek, V.; Sheehan, D.P. Challenges to the Second Law of Thermodynamics: Theory and Experiment; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Newman, J.; Balsara, N.P. Electrochemical Systems, 4th ed.; John Wiley and Sons: Hoboken, NJ, USA, 2021. [Google Scholar]
- Bard, A.J.; Falkner, L.R. Electrochemical Methods: Fundamentals and Applications, 2nd ed.; John Wiley and Sons: Hoboken, NJ, USA, 2001. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sheehan, D.P. A Self-Charging Concentration Cell: Theory. Batteries 2023, 9, 372. https://doi.org/10.3390/batteries9070372
Sheehan DP. A Self-Charging Concentration Cell: Theory. Batteries. 2023; 9(7):372. https://doi.org/10.3390/batteries9070372
Chicago/Turabian StyleSheehan, D.P. 2023. "A Self-Charging Concentration Cell: Theory" Batteries 9, no. 7: 372. https://doi.org/10.3390/batteries9070372
APA StyleSheehan, D. P. (2023). A Self-Charging Concentration Cell: Theory. Batteries, 9(7), 372. https://doi.org/10.3390/batteries9070372




