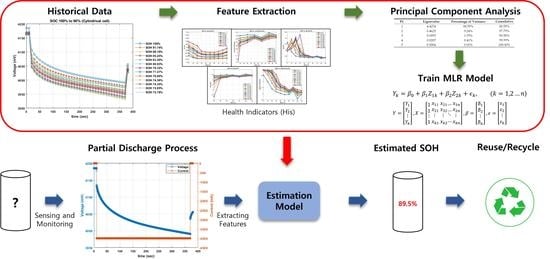
Rapid Estimation of Battery Storage Capacity through Multiple Linear Regression
Abstract
:1. Introduction
1.1. A Brief Review of Battery Storage Capacity Evaluation Methods
1.2. Organization of Paper
2. Experimental Setups and Methodologies
2.1. Description of Experimental Setup and Battery Cell Data
2.1.1. Definition of State of Charge (SOC)
2.1.2. Definition of State of Health (SOH)
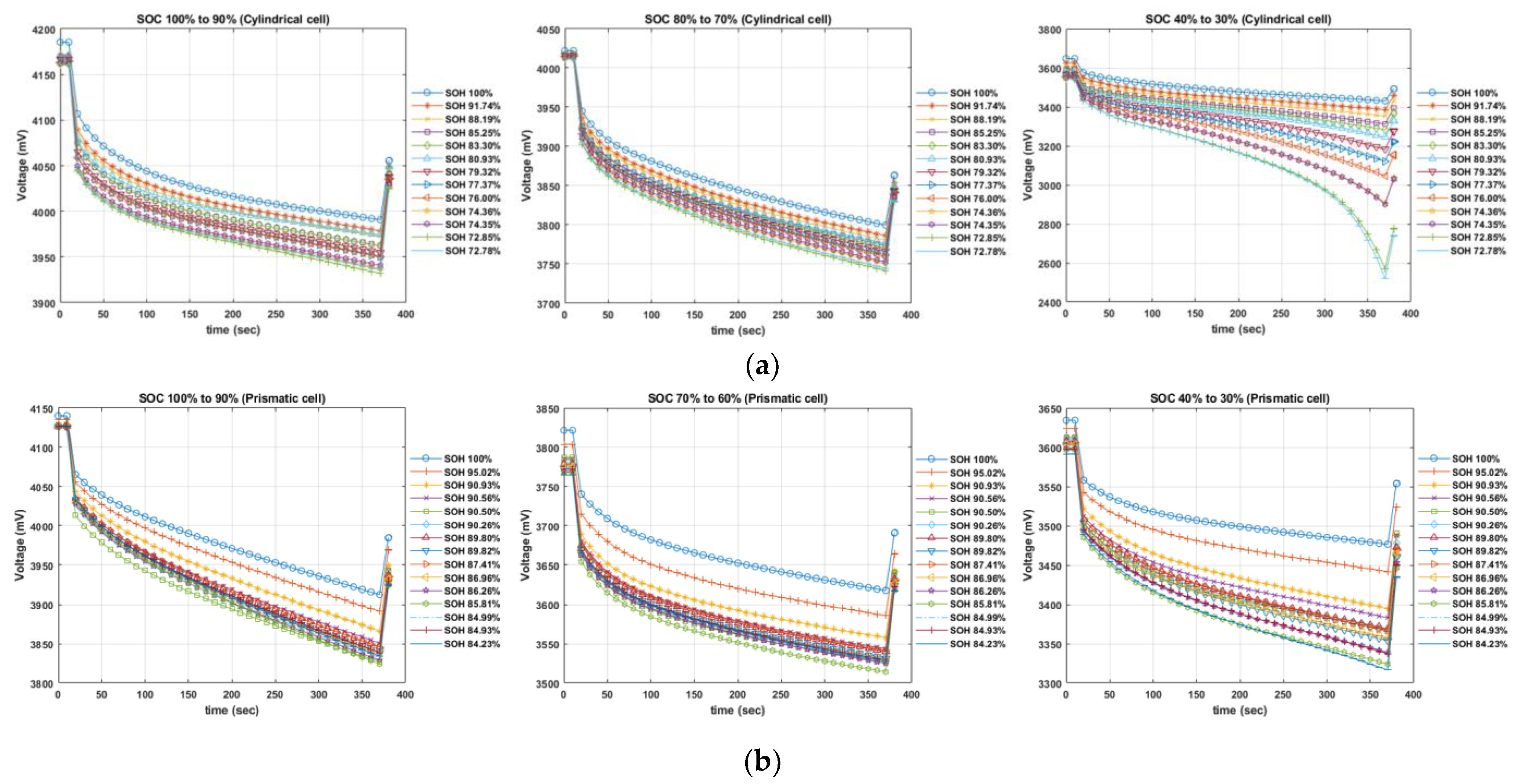
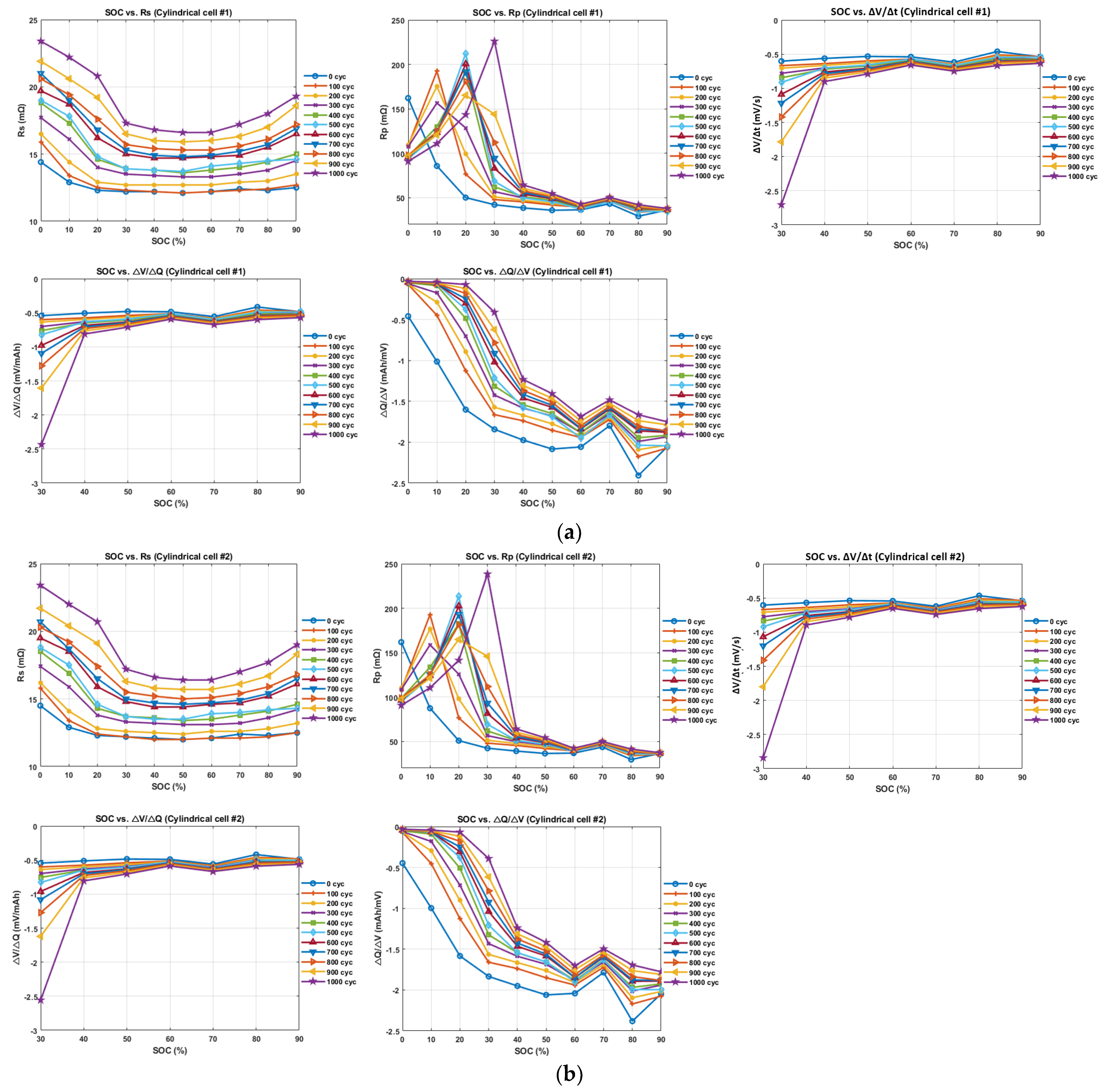
2.2. Transient Response Analysis (TRA) of Voltage
2.3. Feature Extraction and Correlation Analysis
2.3.1. Feature Extraction Based on Transient Response of Voltage Curve
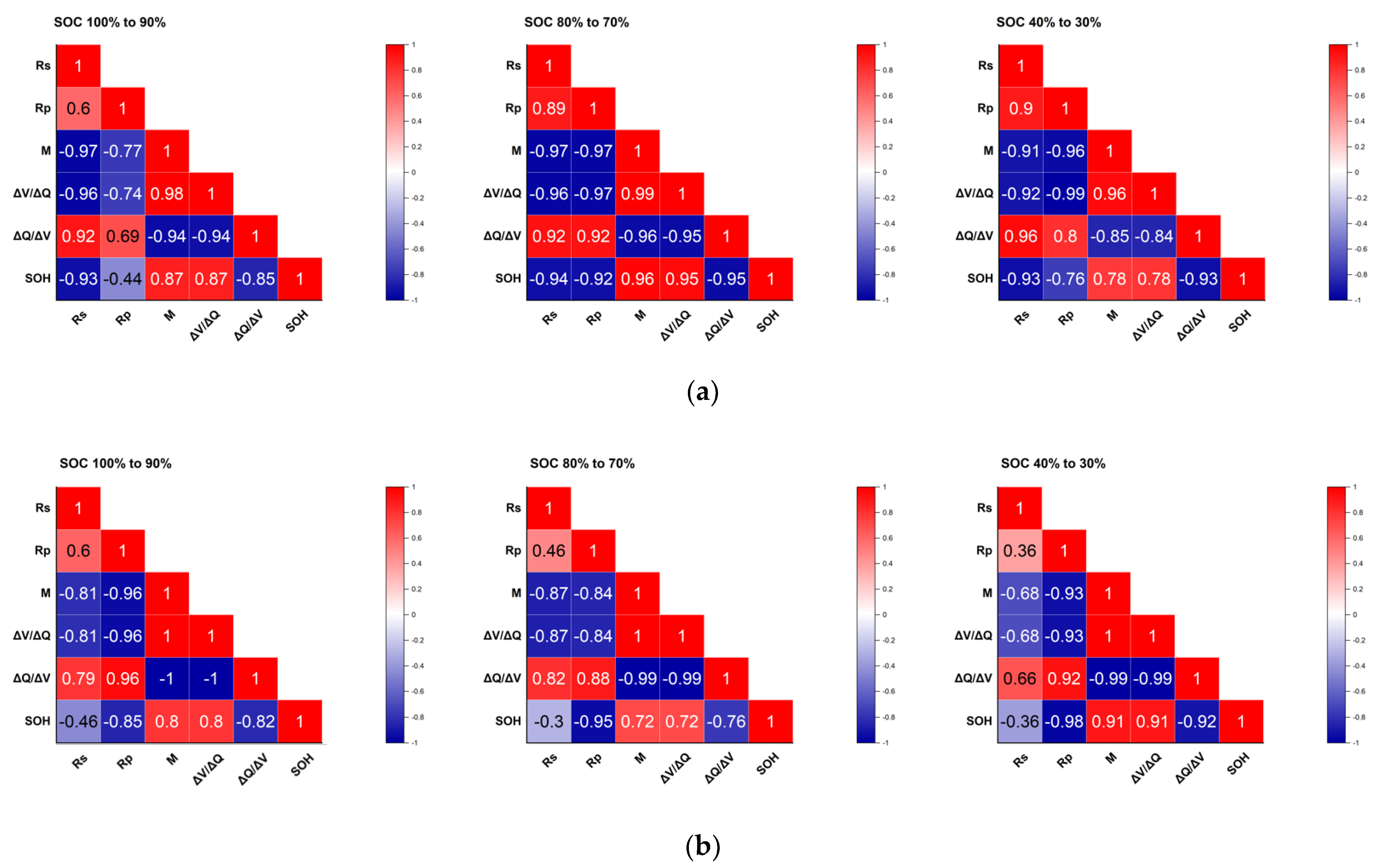
2.3.2. Correlation Analysis
2.4. Feature Reduction
2.5. Multiple Linear Regression Model
3. Estimated Battery Storage Capacity and Comparison with the Measured Capacities
3.1. Case Study1: Cylindrical Cells
3.2. Case Study2: Prismatic Cells
4. Discussion and Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhu, J.; Mathews, I.; Ren, D.; Li, W.; Cogswell, D.; Xing, B.; Sedlatschek, T.; Kantareddy, S.N.R.; Yi, M.; Gao, T.; et al. End-of-life or second-life options for retired electric vehicle batteries. Cell Rep. Phys. Sci. 2021, 2, 100537. [Google Scholar] [CrossRef]
- Hua, Y.; Liu, X.; Zhou, S.; Huang, Y.; Ling, H.; Yang, S. Toward Sustainable Reuse of Retired Lithium-ion Batteries from Electric Vehicles. Resour. Conserv. Recycl. 2021, 168, 105249. [Google Scholar] [CrossRef]
- Shahjalal, M.; Roy, P.K.; Shams, T.; Fly, A.; Chowdhury, J.I.; Ahmed, M.R.; Liu, K. A review on second-life of Li-ion batteries: Prospects, challenges, and issues. Energy 2021, 241, 122881. [Google Scholar] [CrossRef]
- Hu, X.; Deng, X.; Wang, F.; Deng, Z.; Lin, X.; Teodorescu, R.; Pecht, M.G. A Review of Second-Life Lithium-Ion Batteries for Stationary Energy Storage Applications. Proc. IEEE 2022, 110, 735–753. [Google Scholar] [CrossRef]
- Martinez-Laserna, E.; Gandiaga, I.; Sarasketa-Zabala, E.; Badeda, J.; Stroe, D.-I.; Swierczynski, M.; Goikoetxea, A. Battery second life: Hype, hope or reality? A critical review of the state of the art. Renew. Sustain. Energy Rev. 2018, 93, 701–718. [Google Scholar] [CrossRef]
- Steckel, T.; Kendall, A.; Ambrose, H. Applying levelized cost of storage methodology to utility-scale second-life lithium-ion battery energy storage systems. Appl. Energy 2021, 300, 117309. [Google Scholar] [CrossRef]
- Yao, L.; Xu, S.; Tang, A.; Zhou, F.; Hou, J.; Xiao, Y.; Fu, Z. A Review of Lithium-Ion Battery State of Health Estimation and Prediction Methods. World Electr. Veh. J. 2021, 12, 113. [Google Scholar] [CrossRef]
- Lin, Q.; Li, H.; Chai, Q.; Cai, F.; Zhan, Y. Simultaneous and rapid estimation of state of health and state of charge for lithium-ion battery based on response characteristics of load surges. J. Energy Storage 2022, 55, 105495. [Google Scholar] [CrossRef]
- Ren, P.; Wang, S.; He, M.; Cao, W. Novel strategy based on improved Kalman filter algorithm for state of health evaluation of hybrid electric vehicles Li-ion batteries during short and long term operating conditions. J. Power Electron. 2021, 21, 1190–1199. [Google Scholar] [CrossRef]
- Wang, S.; Yin, Z.; Lu, X.; Yang, D.; Tian, S.; Han, Y.; Zheng, Z. Research on the Influence of Battery Cell Static Parameters on the Capacity of Different Topology Battery Packs. Energies 2021, 14, 1610. [Google Scholar] [CrossRef]
- Edge, J.S.; O’KaneKane, S.; Prosser, R.; Kirkaldy, N.D.; Patel, A.N.; Hales, A.; Ghosh, A.; Ai, W.; Chen, J.; Yang, J.; et al. Lithium ion battery degradation: What you need to know. Phys. Chem. Chem. Phys. 2021, 23, 8200. [Google Scholar] [CrossRef]
- Han, X.; Lu, L.; Zheng, Y.; Feng, X.; Li, Z.; Li, J.; Ouyang, M. A review on the key issues of the lithium ion battery degradation among the whole life cycle. eTransportation 2019, 1, 100005. [Google Scholar] [CrossRef]
- Cao, J.; Harrold, D.; Fan, Z.; Morstyn, T.; Healey, D.; Li, K. Deep Reinforcement Learning-Based Energy Storage Arbitrage With Accurate Lithium-Ion Battery Degradation Model. IEEE Trans. Smart Grid 2020, 11, 4513–4521. [Google Scholar] [CrossRef]
- Li, Y.; Stroe, D.; Cheng, Y.; Sheng, H.; Sui, X.; Teodorescu, R. On the feature selection for battery state of health estimation based on charging–discharging profiles. J. Energy Storage 2021, 33, 102122. [Google Scholar] [CrossRef]
- Li, Q.; Li, D.; Zhao, K.; Wang, L.; Wang, K. State of health estimation of lithium-ion battery based on improved ant lion optimization and support vector regression. J. Energy Storage 2022, 50, 104215. [Google Scholar] [CrossRef]
- Chang, C.; Wang, Q.; Jiang, J.; Wu, T. Lithium-ion battery state of health estimation using the incremental capacity and wavelet neural networks with genetic algorithm. J. Energy Storage 2021, 38, 102570. [Google Scholar] [CrossRef]
- Granato, D.; Santos, J.S.; Escher, G.B.; Ferreira, B.L.; Maggio, R.M. Use of principal component analysis (PCA) and hierarchical cluster analysis (HCA) for multivariate association between bioactive compounds and functional properties in foods: A critical perspective. Trends Food Sci. Technol. 2018, 72, 83–90. [Google Scholar] [CrossRef]
- Lyu, Z.; Wang, G.; Tan, C. A novel Bayesian multivariate linear regression model for online state-of-health estimation of Lithium-ion battery using multiple health indicators. Microelectron. Reliab. 2022, 131, 114500. [Google Scholar] [CrossRef]
- Wei, Z.; He, Q.; Zhao, Y. Machine learning for battery research. J. Power Sources 2022, 549, 232125. [Google Scholar] [CrossRef]
- Vilsen, S.B.; Stroe, D. Battery state-of-health modelling by multiple linear regression. J. Clean. Prod. 2021, 290, 125700. [Google Scholar] [CrossRef]
- Tamilselvi, S.; Gunasundari, S.; Karuppiah, N.; Razak RK, A.; Madhusudan, S.; Nagarajan, V.M.; Sathish, T.; Shamim, M.Z.M.; Saleel, C.A.; Afzal, A. A Review on Battery Modelling Techniques. Sustainability 2021, 13, 10042. [Google Scholar] [CrossRef]
- Gong, D.; Gao, Y.; Kou, Y.; Wang, Y. State of health estimation for lithium-ion battery based on energy features. Energy 2022, 257, 124812. [Google Scholar] [CrossRef]
- Driscoll, L.; de la Torre, S.; Gomez-Ruiz, J.A. Feature-based lithium-ion battery state of health estimation with artificial neural networks. J. Energy Storage 2022, 50, 104584. [Google Scholar] [CrossRef]



| PC | Eigenvalue | Percentage of Variance | Cumulative |
|---|---|---|---|
| 1 | 4.4274 | 88.55% | 88.55% |
| 2 | 0.4623 | 9.24% | 97.79% |
| 3 | 0.0893 | 1.79% | 99.58% |
| 4 | 0.0207 | 0.41% | 99.99% |
| 5 | 0.0004 | 0.01% | 100.00% |
| PC | Eigenvalue | Percentage of Variance | Cumulative |
|---|---|---|---|
| 1 | 4.5590 | 91.18% | 91.18% |
| 2 | 0.4117 | 8.23% | 99.41% |
| 3 | 0.0244 | 0.49% | 99.90% |
| 4 | 0.0049 | 0.10% | 100.00% |
| 5 | 0.0001 | 0.00% | 100.00% |
| Cell No. | SOC | Estimated SOH (%) | Measured SOH (%) | Error (%) | |||||
|---|---|---|---|---|---|---|---|---|---|
| C1 | 100% to 90% | 0.3325 | 0.3524 | 0.5194 | 0.8788 | 0.8654 | 71.47 | 72.85 | 1.90 |
| 90% to 80% | 0.3325 | −0.4384 | 0.1065 | 0.9356 | 0.9284 | 70.35 | 3.43 | ||
| 80% to 70% | 0.3325 | −0.4301 | 0.0037 | 0.9274 | 0.9194 | 69.97 | 3.96 | ||
| 70% to 60% | 0.3325 | 0.4264 | 0.4695 | 0.9072 | 0.8969 | 69.99 | 3.92 | ||
| 60% to 50% | 0.3325 | −0.4382 | 0.2635 | 0.9684 | 0.9649 | 71.44 | 1.94 | ||
| 50% to 40% | 0.3325 | −0.4212 | −0.4515 | 0.9498 | 0.9442 | 71.13 | 2.37 | ||
| 40% to 30% | 0.3325 | 0.3457 | −0.5935 | 0.8934 | 0.8816 | 71.57 | 1.76 | ||
| C2 | 100% to 90% | 0.3325 | 0.3524 | 0.5194 | 0.8788 | 0.8654 | 71.53 | 72.78 | 1.72 |
| 90% to 80% | 0.3325 | −0.4384 | 0.1065 | 0.9356 | 0.9284 | 71.65 | 1.55 | ||
| 80% to 70% | 0.3325 | −0.4301 | 0.0037 | 0.9274 | 0.9194 | 71.09 | 2.32 | ||
| 70% to 60% | 0.3325 | 0.4264 | 0.4695 | 0.9072 | 0.8969 | 71.05 | 2.38 | ||
| 60% to 50% | 0.3325 | −0.4382 | 0.2635 | 0.9684 | 0.9649 | 72.20 | 1.04 | ||
| 50% to 40% | 0.3325 | −0.4212 | −0.4515 | 0.9498 | 0.9442 | 71.34 | 1.98 | ||
| 40% to 30% | 0.3325 | 0.3457 | −0.5935 | 0.8934 | 0.8816 | 71.83 | 1.30 |
| Cell No. | SOC | Estimated SOH (%) | Measured SOH (%) | Error (%) | |||||
|---|---|---|---|---|---|---|---|---|---|
| P1 | 100% to 90% | 0.3150 | −0.3695 | 0.4582 | 0.7291 | 0.7044 | 88.7724 | 84.93 | 4.52 |
| 90% to 80% | 0.3150 | 0.3883 | 0.7084 | 0.8955 | 0.8860 | 87.2357 | 2.71 | ||
| 80% to 70% | 0.3150 | −0.3787 | −0.8117 | 0.8564 | 0.8433 | 88.3708 | 4.05 | ||
| 70% to 60% | 0.3150 | −0.3062 | −0.8693 | 0.6577 | 0.6265 | 85.2296 | 0.35 | ||
| 60% to 50% | 0.3150 | −0.3486 | −0.3250 | 0.6882 | 0.6598 | 86.2033 | 1.50 | ||
| 50% to 40% | 0.3150 | 0.4128 | 0.5551 | 0.9430 | 0.9378 | 86.6941 | 2.08 | ||
| 40% to 30% | 0.3150 | 0.3995 | 0.4877 | 0.9598 | 0.9561 | 86.8859 | 2.30 | ||
| P2 | 100% to 90% | 0.3150 | −0.3695 | 0.4582 | 0.7291 | 0.7044 | 85.9919 | 84.23 | 2.09 |
| 90% to 80% | 0.3150 | 0.3883 | 0.7084 | 0.8955 | 0.8860 | 86.5929 | 2.81 | ||
| 80% to 70% | 0.3150 | −0.3787 | −0.8117 | 0.8564 | 0.8433 | 85.4828 | 1.49 | ||
| 70% to 60% | 0.3150 | −0.3062 | −0.8693 | 0.6577 | 0.6265 | 89.1034 | 5.79 | ||
| 60% to 50% | 0.3150 | −0.3486 | −0.3250 | 0.6882 | 0.6598 | 85.3956 | 1.39 | ||
| 50% to 40% | 0.3150 | 0.4128 | 0.5551 | 0.9430 | 0.9378 | 84.0964 | 0.16 | ||
| 40% to 30% | 0.3150 | 0.3995 | 0.4877 | 0.9598 | 0.9561 | 83.9711 | 0.30 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jung, C.; Choi, W. Rapid Estimation of Battery Storage Capacity through Multiple Linear Regression. Batteries 2023, 9, 424. https://doi.org/10.3390/batteries9080424
Jung C, Choi W. Rapid Estimation of Battery Storage Capacity through Multiple Linear Regression. Batteries. 2023; 9(8):424. https://doi.org/10.3390/batteries9080424
Chicago/Turabian StyleJung, Chulwon, and Woongchul Choi. 2023. "Rapid Estimation of Battery Storage Capacity through Multiple Linear Regression" Batteries 9, no. 8: 424. https://doi.org/10.3390/batteries9080424
APA StyleJung, C., & Choi, W. (2023). Rapid Estimation of Battery Storage Capacity through Multiple Linear Regression. Batteries, 9(8), 424. https://doi.org/10.3390/batteries9080424