Investigating the Effect of Different Bidirectional Pulsed Current Parameters on the Heat Generation of Lithium-Ion Battery at Low Temperatures

Abstract

Bidirectional pulsed current (BPC) heating has proven to be an effective method for internal heating. However, current research has primarily focused on the impact of symmetrical BPC on battery heat generation, while neglecting the influence of different BPC parameters. To address this gap, this paper investigates the effects of various BPC parameters on battery heat generation. Initially, an electro-thermal coupled model of the battery is constructed based on the results of electrochemical impedance spectroscopy (EIS) tests conducted at different temperatures and amplitudes at 20% state of charge (SOC). The validation results of the model demonstrate that the absolute errors of voltage and temperature are generally less than 50 mV and 1.2 °C. Subsequently, the influence of BPC parameters on battery heat generation is examined under different terminal voltage constraints, temperatures, and frequencies. The findings at 20% SOC reveal that symmetrical BPC does not consistently correspond to the maximum heating power. The proportion of charge time and discharge time in one cycle, corresponding to the maximum heating power, varies depending on the charge and discharge cut-off voltages. Moreover, these variations differ across frequencies and temperatures. When the terminal voltage is constrained between 3 V and 4.2 V, the maximum heat power corresponds to a discharge time share of 0.55 in one cycle. In conclusion, the results underscore the complex relationship between BPC parameters and battery heat generation, which can further enhance our understanding of effective heating strategies for batteries.

1. Introduction

Due to their high energy and power density, long cycle life, and low self-discharge, lithium-ion batteries (LIBs) have been widely used in electric vehicles (EVs), energy storage systems (ESSs), and electronic products [1,2]. However, at low temperatures, LIBs suffer from problems such as a decrease in discharge capacity [3], a decline in cycle performance [4], and difficulty in charging [5]. These problems seriously affect the performance of EVs, ESSs, and electronic products at low temperatures. Moreover, lithium plating may occur during the low-temperature charging process [5]. On the one hand, lithium plating will reduce the number of available lithium ions in the battery, which will reduce the life of the battery. On the other hand, the deposited lithium dendrites will pierce the separator and lead to an internal short circuit, further threatening the safety of the battery. Therefore, LIBs need to be heated in advance before use at low temperatures.

The heating methods for LIBs can be divided into external heating and internal heating [6]. External heating uses an external heat source to heat the battery by conductive heating or convective heating [7]. Internal heating uses the internal resistance, or the heat-generating device embedded inside the battery to heat the battery. Compared with external heating, internal heating has the advantages of uniform temperature rise, high heating efficiency, and low energy consumption [8]. Therefore, internal heating has gained the attention of many researchers. Wang et al. [9] proposed a self-heating battery design by integrating nickel foil inside the battery. The new battery can be heated from −20 °C to 0 °C within 20 s. Although this method exhibited high heating efficiency, it required substantial structural modifications, resulting in increased costs and potential safety concerns. In contrast to the embedded nickel foil in the battery, the internal resistance heating method relies on the heat generated by the charging or discharging processes. Internal resistance heating can be further categorized into discharge heating and AC heating [10,11]. Discharge heating employs the discharge current to generate heat in the battery, while AC heating utilizes alternating currents of specific frequencies. Since AC heating includes both charging and discharging phases, it generally exhibits higher heating efficiency and lower energy consumption compared to discharge heating methods.

Although AC heating methods encompass a variety of waveforms [12,13,14,15,16,17], sinusoidal alternating current (SAC) and BPC are the most commonly utilized. Zhang et al. [18] employed an SAC with a frequency of 1 Hz to heat the battery from −20 °C to 5 °C in 900 s. Guo et al. [19] devised an SAC heating method without lithium plating using a three-electrode battery. Ruan et al. [20] optimized the frequency of SAC heating and identified the optimal heating frequency for different temperatures. At this frequency, the battery could be heated from −15.4 °C to 5.6 °C in 338 s. In contrast to frequency optimization, Zhang et al. [21] adjusted the amplitude of SAC heating for various temperatures at the predetermined heating frequency and achieved a temperature increase from −20 °C to 0 °C in 300 s. The advantages of BPC heating over SAC heating have been noticed and studied in recent years. Both Zhu et al. [22] and Zhang et al. [23] conducted comparative analyses of SAC heating and BPC heating. They observed that BPC heating exhibited higher heating power than SAC heating under the same voltage constraint. Wu et al. [24] proposed a BPC heating strategy with temperature-dependent amplitude and heated the battery from −20 °C to 5 °C within 308 s. Li et al. [16] achieved BPC heating by reconfiguring the battery pack structure and traction motor drive system, which can heat the battery from −7 °C to 29.1 °C in 300 s. Qin et al. [25] investigated various types of BPC heating methods and found that the battery can be heated from −8 °C to 25 °C in 250 s.

Despite the evident advantages of BPC heating, the existing studies on BPC heating have primarily focused on using the same charge and discharge time and the same charge and discharge amplitude in one waveform cycle [16,22,23,24,25]. Little attention has been given to investigating the impact of different BPC parameters, such as varying charge and discharge times and amplitudes within a waveform cycle, on battery heat generation. In addition, the relationship between BPC parameters and battery heat generation under different charge and discharge cut-off voltages, temperatures, and frequencies remains unclear. To address these knowledge gaps, this study presents an electro-thermal coupled model for a 1 Ah pouch battery at 20% state of charge (SOC), which is constructed based on the fractional-order equivalent circuit model. The electro-thermal coupled model serves two purposes. Firstly, it is employed to calculate the battery heating power. Secondly, it determines the battery’s terminal voltage and temperature rise. The parameters of the electro-thermal coupled model are determined through electrochemical impedance spectroscopy (EIS) tests conducted at different temperatures and current amplitudes. To indirectly validate the accuracy of the calculated battery heating power, the temperature rise experiments of the battery are conducted. Finally, the electro-thermal coupled model is utilized to comprehensively analyze the relationship between BPC parameters and battery heating power under different charge and discharge cut-off voltages, temperatures, and frequencies.

2. Experiments

2.1. Experiment Platform

The experimental platform and tests in this paper are shown in Figure 1. The battery test platform includes a temperature acquisition recorder (Hongrun OHR-XH710), a temperature chamber (Binder MK56), a host computer, an electrochemical workstation (EnergyLab XM), and a power booster (Solartron analytical, 24 V/10 A). The sample lithium-ion battery is a nickel–cobalt–manganese (NCM)/graphite battery with a nominal capacity of 1 Ah. The operating voltage range is 3 V–4.2 V. The temperature acquisition recorder is used to obtain the surface temperature of the battery. The EnergyLab XM is used to perform the EIS test as well as the BPC test. Due to the small current range of the EnergyLab XM, the power booster is used to increase the range.

2.2. EIS Test at Different Temperatures and AC Amplitude

Given that the impedance of the battery is influenced by both temperature and current amplitude, EIS tests are conducted on the battery at various temperatures and AC amplitudes to determine the parameters of the fractional-order equivalent circuit model. In addition, the SOC of the battery studied is set at 20% before conducting the EIS test. According to [26,27], lithium plating is more likely to occur under large-rate charging and low-temperature conditions. In addition, a high SOC increases the risk of lithium plating [28]. Since the EIS test includes the charging process, lithium plating may occur during the large-current EIS test. To mitigate this risk, a low SOC is chosen here. However, an excessively low SOC may expose the battery to the danger of over-discharge during the EIS test. Consequently, an SOC of 20% is chosen as a balanced compromise. The specific procedure involved initially charging the battery to full capacity using Constant Current Constant Voltage (CCCV) charging, with a charge current of 1 A and a charge cut-off current of 0.02 A. The constant voltage is 4.2 V. Subsequently, the battery is discharged with a constant current of 1 A after a resting period of 30 min. Discharging is terminated once the discharged capacity reached 0.8 Ah. At this time, the SOC of the battery is 20%. Considering the actual capacity of the battery is 1.05 A, the actual SOC of the battery is 23.8%. The effect of SOC is not discussed in this paper, and the error in SOC is only 3.8%. Therefore, the error is ignored. The impedance test is in galvanostatic mode, and the frequency range is 0.1 Hz to 10⁶ Hz. Numerous studies [19,22,23,29,30] have focused on low-temperature AC heating strategies. In these investigations, the battery’s maximum heating temperature typically hovers around 10 °C. The minimum temperature is usually determined based on the temperature range in which the battery will be used. In addition, the literature calibrates the parameters of the battery every 5 °C. The minimum discharge temperature of the battery used in this paper is −15 °C. Therefore, the test temperatures chosen for this paper are 10 °C, 5 °C, 0 °C, −5 °C, −10 °C, and −15 °C. After each temperature adjustment, the battery needs to be left for 2 h before the impedance test. The impedance tests are performed at different amplitudes of 0.25 A, 0.65 A, 1 A, 1.5 A, 2 A, and 2.5 A. The time interval between successive impedance tests with varying amplitudes at the same temperature is 1 h.

2.3. BPC Test

Before conducting the BPC test, it is necessary to predefine the relevant parameters. Figure 1 illustrates the key parameters of the BPC, which encompass charge time t_cha, discharge time t_dis, charge amplitude A_cha, and discharge amplitude A_dis, period T_pulse, frequency f_pulse, and ratio R_pulse. T_pulse and f_pulse have straightforward interpretations. t_cha and t_dis signify the duration of the charging and discharging within one cycle of the waveform, respectively. A_cha and A_dis indicate the magnitude of charging and discharging within one cycle of the waveform, respectively. In addition, R_pulse represents the ratio of t_dis to T_pulse within one cycle of the waveform. An accurate electro-thermal coupled model is crucial for precise calculations of heating power in the battery. The accuracy of the equivalent circuit model can be assessed by comparing the discrepancy between the terminal voltage calculated by the model and the terminal voltage obtained through experimental measurement. Furthermore, the accuracy of the heat generation calculation is evaluated by comparing the temperature rise calculated by the electro-thermal coupled model with the temperature rise measured experimentally. Consequently, the BPC test consists of two types: voltage testing and temperature testing. For voltage testing, the test temperatures include 10 °C, −5 °C, and −15 °C. The specific parameters of different BPCs at each temperature are presented in

Table 1. The BPCs for voltage testing.

Frequency fpulse (Hz)	Ratio Rpulse	Discharge Amplitude Adis (A)	Charge Amplitude Acha (A)	Abbreviation
1	0.5	3.5	1.5	I@1 Hz
	0.7	2.5	2.5	II@1 Hz
50	0.5	3.5	1.5	I@50 Hz
	0.7	2.5	2.5	II@50 Hz
100	0.5	3.5	1.5	I@100 Hz
	0.7	2.5	2.5	II@100 Hz

. The frequencies of the BPCs include three kinds of 1 Hz, 50 Hz, and 100 Hz. Each frequency includes two BPCs with different parameters, denoted as BPC I and BPC II, respectively. BPC I has a discharge amplitude of 3.5 A and a charge amplitude of 1.5 A. The ratio is 0.5. For BPC II, both discharge amplitude and charge amplitude are 2.5 A. The ratio is 0.7. During the voltage testing, both current and voltage are collected by the EnergyLab XM. The sampling frequency is 100 times the corresponding BPC frequency. Moreover, a 2 h stabilization period is set after each temperature adjustment, and the time interval between BPC tests conducted at the same temperature is set to 30 min. As an example of the test procedure at 10 °C, the battery is initially placed in a 10 °C environment for 2 h to reach the desired temperature. Subsequently, the BPC I@1 Hz test is performed using the EnergyLab XM and the power booster. Since the EnergyLab XM has a high sampling frequency, a sufficient amount of current and voltage data can be obtained in just a few seconds. After the BPC I@1 Hz test, the battery is allowed to stand for 30 min to stabilize. The BPC II@1 Hz test is then conducted following the same methodology. Similar procedures are followed for the other BPCs listed in Table 1. Upon completing the BPC II@100 Hz test, it signifies the completion of the voltage testing at 10 °C. Subsequently, the temperature is adjusted to other specified values to continue the testing. Once all the measurements at −5 °C and −15 °C are completed, the voltage testing is considered finished. For temperature testing, unlike voltage testing, it is only necessary to obtain the temperature rise data of the battery under different BPCs in

Table 2. The BPCs for temperature testing.

Frequency fpulse (Hz)	Ratio Rpulse	Discharge Amplitude Adis (A)	Charge Amplitude Acha (A)	Abbreviation
1	0.5	2.5	2.5	III@1 Hz
	0.7	1.5	3.5	IV@1 Hz
10	0.5	2.5	2.5	III@10 Hz
	0.7	1.5	3.5	IV@10 Hz
100	0.5	2.5	2.5	III@100 Hz
	0.7	1.5	3.5	IV@100 Hz

without the need for high-frequency sampling of current and voltage. The BPCs for temperature testing consist of three different frequencies. There are two types of BPCs at each frequency, BPC III and BPC IV. The ratios of BPC III and BPC IV are 0.5 and 0.7, respectively. For BPC III, both the discharge amplitude and charge amplitude are 2.5 A. The discharge amplitude and charge amplitude of BPC IV are 1.5 A and 3.5 A, respectively. The temperature testing is performed according to the following procedure. The battery is first placed at −13 °C for 2 h. Subsequently, the BPC III@1 Hz is applied to the battery using the EnergyLab XM and the power booster, while the temperature of the battery surface is measured simultaneously. After a 30 min duration, the heating of the battery is discontinued. The battery is left for 1 h and then subjected to BPC IV@1 Hz. The other BPCs are conducted following the same procedure. Upon completion of the BPC IV@100 Hz, it indicates the conclusion of the temperature testing.

3. Mathematic Model

3.1. Calculation of Heating Power

The heat generation of the battery can be quantified by the heating power. Without considering the heat of mixing and side reactions, the heat generation of the battery consists mainly of reaction heat and Joule heat [31]. The reaction heat is determined by the effective entropy potential of the battery and is reversible heat for the electrochemical reaction [32]. For AC heating, the reaction heat generated by the charging and discharging process can cancel each other. Therefore, AC heating can be used to consider only Joule heat [33]. Joule heat includes ohmic internal resistance heat generation and polarization internal resistance heat generation [25]. Therefore, based on the parameter definitions of the BPC in Figure 1, the heating power q of the battery under BPC conditions can be expressed as

$$q=q_{dis}+q_{cha}=\frac{A_{dis}^2{Z^{\prime }}_{dis}^{}{t}_{dis}}{T_{pulse}}+\frac{A_{cha}^2{Z^{\prime }}_{cha}^{}{t}_{cha}}{T_{pulse}}$$

(1)

where q_dis and q_cha denote the discharge heating power and charge heating power, respectively. ${Z^{\prime }}_{dis}$ and ${Z^{\prime }}_{cha}$ represent the real part of the impedance corresponding to the discharge and the real part of the impedance corresponding to the charge, respectively. They can be calculated by the fractional-order equivalent circuit model. In addition, the accuracy of the heating power calculation cannot be directly verified. Indirect validation is performed by comparing experimental measurements of cell temperature with calculated values from the thermal model. Therefore, an accurate electro-thermal coupled model is necessary for the calculation and verification of the heating power.

3.2. Electro-Thermal Coupled Model

The fractional-order equivalent circuit model can accurately describe the impedance variation of the battery at different frequencies [34]. Hence, the electrical model in the electro-thermal coupled model is constructed using a fractional-order equivalent circuit model. The fractional-order equivalent circuit model is shown in Figure 2. The constant voltage source U_oc represents the open circuit voltage (OCV) of the battery. The resistance R₀ represents the ohmic resistance of the battery. The remaining polarization process inside the battery is described by two parallel structures of resistance and constant phase element (CPE). In addition, the battery in this paper is a 1 Ah pouch cell. Considering the relatively small size of the battery, the temperature distribution gradient of the battery is neglected. Therefore, the lumped thermal model is used to describe the temperature rise variation of the battery.

For the fractional-order equivalent circuit model, the real part of the impedance $Z^{\prime }$ can be calculated as [21]

$$Z^{\prime }=R_0+\frac{R_1+{\omega }^{n_1}{R}_1^2{Q}_1\cos \frac{n_1\pi }{2}}{1+2{\omega }^{n_1}{R}_1{Q}_1\cos \frac{n_1\pi }{2}+{\omega }^{2n_1}{R}_1^2{Q}_1}+\frac{R_2+{\omega }^{n_2}{R}_2^2{Q}_2\cos \frac{n_2\pi }{2}}{1+2{\omega }^{n_2}{R}_2{Q}_2\cos \frac{n_2\pi }{2}+{\omega }^{2n_2}{R}_2^2{Q}_2}$$

(2)

where ω is the angular frequency of the current. Q and n are the generalized capacitor and depression factors of CPE. The terminal voltage $U_t$ of the battery can be expressed as

$$U_t=U_{oc}+U_p$$

(3)

where $U_p$ is the polarization voltage, which can be expressed as [34]

$$U_p(s)=Z(s)I(s)=\left(\frac{{\displaystyle {\sum }_{k=1}^4{a}_k{s}^{{\alpha }_k}}}{{\displaystyle {\sum }_{k=1}^4{b}_k{s}^{{\beta }_k}}}+R_0\right)I(s)=\left(\frac{R_1}{R_1{Q}_1{s}^{n_1}+1}+\frac{R_2}{R_2{Q}_2{s}^{n_2}+1}+R_0\right)I(s)$$

(4)

the coefficients are expressed as

$$\{\begin{array}{l}[\begin{array}{cccc}{a}_1& a_2& a_3& a_4\end{array}]=[\begin{array}{cccc}{R}_1{R}_2{Q}_2& R_1& R_1{R}_2{Q}_1& R_2\end{array}]\hfill \\ [\begin{array}{cccc}{\alpha }_1& {\alpha }_2& {\alpha }_3& {\alpha }_4\end{array}]=[\begin{array}{cccc}{n}_2& 0& n_1& 0\end{array}]\hfill \\ [\begin{array}{cccc}{b}_1& b_2& b_3& b_4\end{array}]=[\begin{array}{cccc}{R}_1{R}_2{Q}_1{Q}_2& R_1{Q}_1& R_2{Q}_2& 1\end{array}]\hfill \\ [\begin{array}{cccc}{\beta }_1& {\beta }_2& {\beta }_3& {\beta }_4\end{array}]=[\begin{array}{cccc}{n}_1+n_2& n_1& n_2& 0\end{array}]\hfill \end{array}$$

(5)

Fractional calculus is difficult to solve directly. The Grünwald–Letnikov (GL) definition can discretize fractional calculus and realize the solution of fractional-order equations [35,36]. Then, the solution for the polarization voltage is

$$\begin{array}{l}{U}_p(t)=\frac{1}{{\displaystyle {\sum }_{k=1}^4\frac{b_k}{\Delta t^{{\beta }_k}}}}[{\displaystyle {\sum }_{k=1}^4{\displaystyle {\sum }_{g=0}^{[t/\Delta t]}\frac{a_k}{\Delta t^{{\alpha }_k}}}}{(-1)}^g\left(\begin{array}{c}{\alpha }_k\\ g\end{array}\right)I(t-g\Delta t)+\\ {\displaystyle {\sum }_{k=1}^4{\displaystyle {\sum }_{g=0}^{[t/\Delta t]}\frac{b_k}{\Delta t^{{\beta }_k}}}}{(-1)}^g\left(\begin{array}{c}{\beta }_k\\ g\end{array}\right)I(t-g\Delta t)R_0-{\displaystyle {\sum }_{k=1}^4{\displaystyle {\sum }_{g=0}^{[t/\Delta t]}\frac{b_k}{\Delta t^{{\beta }_k}}}}{(-1)}^g\left(\begin{array}{c}{\beta }_k\\ g\end{array}\right)U_p(t-g\Delta t)]\end{array}$$

(6)

where Δt is the sampling time interval. [t/Δt] is the integer part of t/Δt. $\left(\begin{array}{c}\mu \\ g\end{array}\right)$ is the Newton binomial term and can be expressed as

$$\left(\begin{array}{c}\mu \\ g\end{array}\right)=\{\begin{array}{ll}\frac{\mu (\mu -1)\cdots (\mu -g+1)}{g!}\hfill & (g>0)\hfill \\ 1\hfill & (g=0)\hfill \end{array}$$

(7)

where μ represents the non-integer order of fractional calculus, representing α_k and β_k.

The lumped thermal model is expressed as [18]

$$mc\frac{dT}{dt}=q-hS(T-T_{am})$$

(8)

where m is the battery mass, which is 22 g. c is the specific heat capacity. The value provided by the battery manufacturer is 1.1 Jg⁻¹K⁻¹. T and T_am represent battery temperature and ambient temperature, respectively. S is the surface area of the battery, and the value is 73.05 cm². h is the equivalent heat transfer coefficient, which needs to be identified by experiment. The procedure begins by placing the battery in a −15 °C environment for 2 h. Subsequently, the battery is heated to approximately 10 °C using the BPC heating method. The battery is then left to rest for 1.5 h. The temperature change during the resting phase of the battery is used to calculate h.

3.3. Determinations of Model Parameters

3.3.1. Electrical Model Parameters

Figure 3 displays the EIS test results conducted at different temperatures and current amplitudes. It is evident from the figure that the high-frequency impedance arc is minimally influenced by the current amplitude. However, the low- and medium-frequency impedance arcs gradually diminish in size as the current amplitude increases. Moreover, these characteristic frequencies are 8 Hz, 6.3 Hz, 5 Hz, 20 Hz, 25 Hz, and 63 Hz with decreasing temperature. These characteristic frequencies remain relatively stable around 6 Hz at temperatures above 0 °C. However, as the temperature drops below 0 °C, this characteristic frequency increases. These characteristic frequencies are determined based on the degree of impedance variation with current amplitude. Furthermore, as the temperature decreases, the reduction in impedance arc becomes more pronounced. Firstly, at the same temperature, the impedance arcs contract with increasing current amplitude, which is related to the solid electrolyte interphase (SEI)/cathode electrolyte interphase (CEI) processes and the charge transfer process. According to our previous research [37], the resistances of the SEI/CEI processes and the charge transfer process decrease with increasing current amplitude at low temperatures, which leads to the contraction of the impedance arc. Secondly, as the temperature decreases, the SEI/CEI processes and the charge transfer process slow down, causing the corresponding frequencies to decrease. However, in Figure 3, the characteristic frequency decreases with decreasing temperature only at temperatures above 0 °C. For temperatures below 0 °C, the characteristic frequency increases. This phenomenon may be related to the conduction process. The conduction process is the contact impedance of particle/particle and particle/current-collector, and it usually occurs more quickly than SEI/CEI processes and the charge transfer process [38]. At relatively high temperatures, the conduction process is less affected by current, with only the SEI/CEI processes and the charge transfer processes being influenced. However, once the temperature drops to a certain level, the conduction process may also be affected by the current. Furthermore, the conduction process exhibits a relatively broad frequency distribution. As the temperature decreases, the influence of the current on this process becomes increasingly pronounced. Consequently, the characteristic frequency progressively increases when the temperature drops below 0 °C.

Figure 4a illustrates the correlation between each parameter of the fractional-order equivalent circuit model and the impedance arc. The calculation of each parameter is fitted using Zview software [39]. The calculated results correspond to the experimental values as depicted in Figure 4b–h. These results demonstrate that the parameters of the fractional-order model are influenced not only by temperature but also by current amplitude. It should be noted that the effect of current amplitude on R₀ seems to be negligible in Figure 3. This is due to R₀ being relatively small and its influence being negligible compared to temperature. Despite this, both temperature and current are taken into consideration when considering the fractional-order equivalent circuit model parameters to ensure accuracy.

Referring to [22,37], relationship between R₁ and the current and temperature and relationship between R₂ and the current and temperature can be expressed as

$$R(I,T)=\frac{\ln \left\{\frac{1}{2M}{e}^{KT}I+{\left[{\left(\frac{1}{2M}{e}^{KT}I\right)}^2+1\right]}^{0.5}\right\}}{\frac{1}{2M}XI}$$

(9)

where R represents R₁ or R₂. M, X, and K denote the coefficients of the equation. For R₀ and the parameters of CPE, the polynomial is used to represent the relationship between them and the current and temperature in this paper, which can be expressed as

$$A(I,T)=d_0+d_{1}T+d_{2}I+d_3{T}^2+d_{4}TI+d_6{T}^3+d_7{T}^{2}I$$

(10)

where A refers to R₀ and the parameters of CPE. d denotes the coefficients of the polynomial. The fitting results for each parameter of the fractional-order equivalent circuit model are presented in Figure 4b–h. The coefficient of determination R² reflects the goodness of fit. The closer R² is to 1, the better the fit is demonstrated. The coefficient of determination R² for R₁ and R₂ are 0.97838 and 0.97143, respectively, indicating the accuracy of Equation (9). Furthermore, the coefficient of determination R² for R₀, n₁, Q₁, n₂, and Q₂ are 0.99343, 0.99177, 0.9814, 0.97443, and 0.98933. Among the R₀ and the parameters of CPE, n₂ exhibits the smallest R² value of 0.97443, supporting the accuracy of Equation (10). Consequently, Equations (9) and (10) effectively capture the relationship between the parameters of the fractional-order equivalent circuit model and the temperature and current, which provides a reliable foundation for the calculation of battery heating power.

3.3.2. Calculation of Equivalent Heat Transfer Coefficient h

Another important parameter is the equivalent heat transfer coefficient h of the thermal model. h can be calculated by the temperature change of the battery during resting. The solution of Equation (8) is

$$T=\frac{q+hS{T}_{am}}{hS}\left(1-e^{-\frac{hS}{mc}t}\right)+T_{t=0}{e}^{-\frac{hS}{mc}t}$$

(11)

where T_t=0 indicates the temperature of the battery at the start moment. When q is 0, Equation (11) becomes

$$T=T_{am}+\left(T_{t=0}-T_{am}\right)e^{-\frac{hS}{mc}t}$$

(12)

Figure 5 shows the fitting result of the battery cooling curve. The maximum absolute temperature error is less than 0.5 °C. The calculated value for h is 7.0993 Wm⁻²K⁻¹.

4. Results and Discussions

4.1. Validation of the Electro-Thermal Coupled Model

Figure 6 shows the measured voltages and the calculated voltages of BPCs I and II at different frequencies (1 Hz, 50 Hz, 100 Hz) and temperatures (10 °C, −5 °C, −10 °C). In the error plots, the gray areas indicate the absolute value of error is less than 0.05 V. The error of the terminal voltage calculated by the electro-thermal coupled model is larger at the frequency of 1 Hz and the temperature of −15 °C. Some voltage errors are even greater than 0.1 V. Nevertheless, the absolute value of the voltage error is in general within 0.05 V in others. Only a few errors are outside the gray area. Therefore, the results indicate that the electro-thermal coupled model can calculate the voltages of BPCs at different temperatures and frequencies relatively accurately. This ensures the accuracy of the BPC heating power calculation under various voltage constraints in the subsequent analysis.

The accuracy of the battery heating power calculation is validated through battery temperature rise experiments. Figure 7 illustrates the temperature variations of the battery under BPCs III and IV at different frequencies (1 Hz, 10 Hz, 100 Hz) and the temperature values computed by the electro-thermal coupled model. For BPC III, the absolute temperature error remains within 1.2 °C, while for BPC IV, it is within 1 °C. These results demonstrate that the developed electro-thermal coupled model accurately predicts the temperature changes in the battery. Furthermore, it confirms the capability of the electro-thermal coupled model to accurately calculate the heating power of BPC with different parameters at various temperatures. Additionally, it is observed that for both BPC III and BPC IV, a lower frequency corresponds to a higher balanced temperature. This can be attributed to the larger real part of the impedance at a lower frequency, resulting in higher heating power.

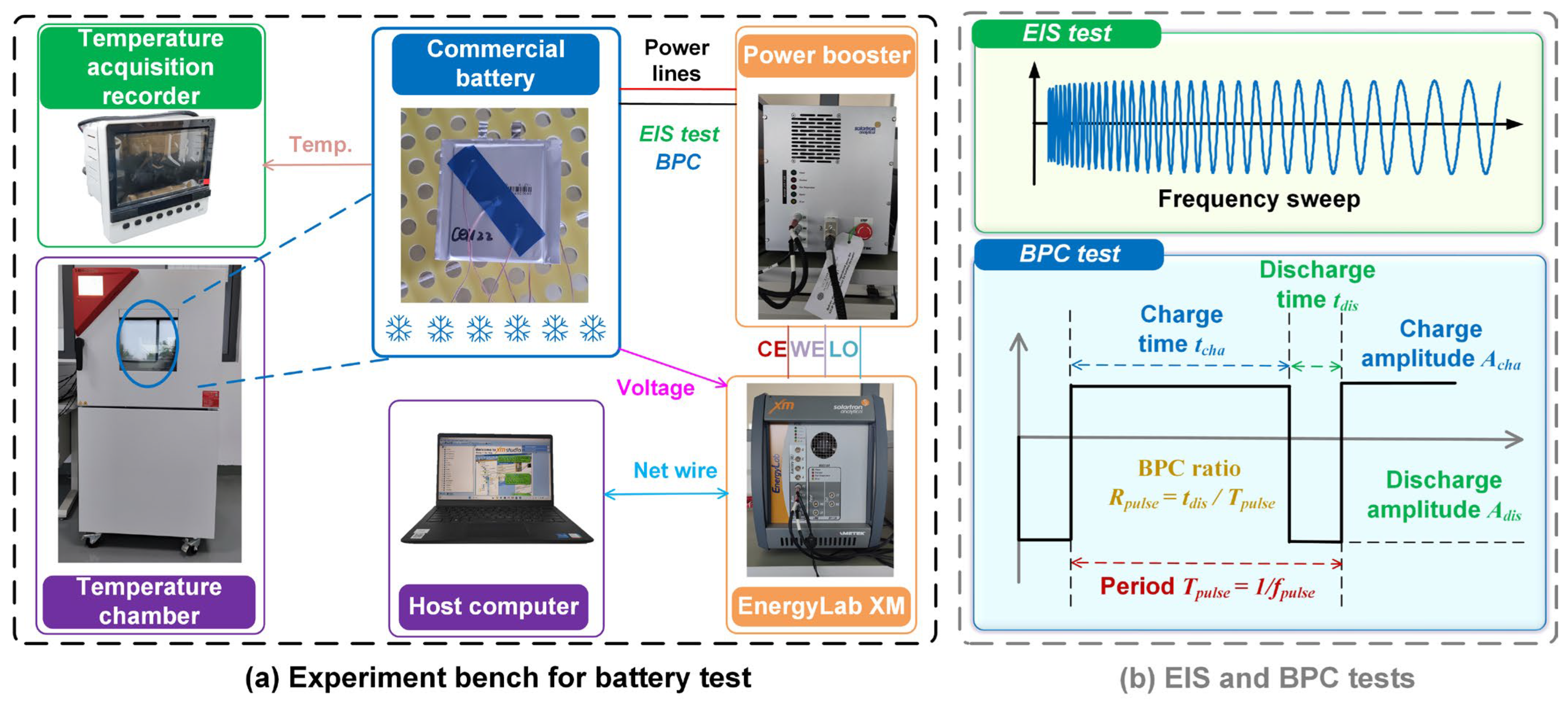
4.2. Determination of BPC Parameters

The definition of BPC in Figure 1 contains several parameters, which makes it difficult to study the heating power variation of the BPC with different parameters. In practical scenarios of AC heating applications, there are two primary types of AC heating schemes. One category encompasses the AC heating scheme with energy injection, as seen in instances where battery packs are heated through charge devices [40,41,42,43]. The second type involves the AC heating scheme without energy injection. In the latter approach, the design of the AC heating scheme commonly leverages circuit elements to configure heating systems, effectively employing controlled switching elements to induce AC heating in batteries [13,14,16,44]. For the AC heating scheme with energy injection, adhering to an equilibrium between discharge and charge ampere-hours in a single cycle may not be theoretically essential. In contrast, for the AC heating schemes without energy injection, it is preferable to uphold parity between discharge and charge ampere-hours in a single cycle, thereby mitigating energy consumption. Given the context of EV applications, the AC heating scheme without energy injection proves more expedient for implementation. Furthermore, the AC heating scheme with energy injection can also embrace the strategy of equalizing the charge and discharge ampere-hours. Consequently, this paper delves into an analysis of the influence exerted by varying BPC parameters on heating power under the stipulation of maintaining equal charge and discharge ampere-hours. This can be expressed as

$$A_{dis}{t}_{dis}=A_{cha}{t}_{cha}$$

(13)

Subject to the constraints outlined in Equation (13), the BPC can be uniquely determined by the three parameters: frequency f_pulse, ratio R_pulse, and discharge amplitude A_dis. In addition, the failure boundary of the battery also needs to be considered during the design of AC heating strategies. Therefore, in this study, the heating power corresponding to different BPC parameters must satisfy the failure boundary constraints. Although various approaches have been proposed by researchers for the development of AC heating strategies, the determination of constraint boundaries remains a topic of controversy. Currently, recognized failure modes of low-temperature AC heating include lithium plating, overcharge, and over-discharge [25,30,45], which have been the focal points of recent research. Controlling the polarization voltage of the battery, specifically the charge and discharge cut-off voltages, is one way to mitigate these failure modes. However, the relationships between lithium plating and terminal voltage, overcharge and terminal voltage, and over-discharge and terminal voltage under high-frequency AC conditions remain unclear. Thus, to encompass a wide range of terminal voltage, this paper considers charge cut-off voltage constraints within the range of 4.2 V–5 V and discharge cut-off voltage constraints within the range of 2 V–3 V. In addition, although the parameters determining the BPC include frequency f_pulse, ratio R_pulse, and discharge amplitude A_dis, A_dis is determined by the voltage constraint. When the frequency f_pulse and ratio R_pulse are determined, there is a maximum amplitude A_dis so that the terminal voltage is exactly at the constraint boundary and the corresponding heating power is maximum. This heating power is the object of the subsequent study in this paper.

In addition to the discharge amplitude A_dis, two other parameters that require attention are frequency f_pulse and ratio R_pulse. The ratio R_pulse takes values between 0 and 1. The values of 0 and 1 represent complete charging and complete discharging, respectively. Therefore, 0 and 1 cannot be taken. For this research, the ratio analysis ranges from 0.05 to 0.95 and the calculation of the heating power is conducted at an interval of 0.05. Moreover, the selection of frequency range is based on the EIS test results of the battery. Four frequencies (0.5 Hz, 5 Hz, 100 Hz, and 10,000 Hz) are chosen to ensure the coverage of the entire impedance distribution as extensively as possible. Figure 8 illustrates the distribution of these four frequencies over the EIS at different temperatures. The current amplitude corresponding to each impedance is 0.25 A.

4.3. Heating Power of the Battery with Different BPC Parameters

Figure 9 shows the variation of the relationship between R_pulse and heating power with frequency and temperature at different discharge cut-off voltages. The legends for the 0.5 Hz, 5 Hz, and 100 Hz results in the figure range from 0 W to 150 W, while the legends for the 10,000 Hz results range from 0 W to 300 W. The black areas in the plots indicate that the heating power exceeds the maximum value in the legend. For further analysis of the heating power distribution, Figure A1 provides detailed information for each case. The heating power falling in the black area can be examined and analyzed in Figure A1. In each subplot of Figure 9 and Figure A1, it is evident that the heating power gradually increases as the discharge cut-off voltage decreases at the same R_pulse. When the discharge cut-off voltage is set to a smaller value, a higher discharge current is required to reach the discharge cut-off voltage. Additionally, based on Equation (13), the charge current also increases accordingly. Consequently, the battery heating power increases. Then, under the same discharge cut-off voltage constraint, the battery heating power becomes larger first and then smaller as R_pulse increases in most cases. The heating power variation can be attributed to the combined effects of currents and time of discharge and charge. To illustrate this phenomenon, the results for 100 Hz@−5 °C with the discharge cut-off voltage of 2.7 V as shown in

Table 3. Parameter variations in Equation (1) at −5 °C with different R_pulse values under the discharge cut-off voltage of 2.7 V when the BPC frequency is 100 Hz.

Rpulse	0.05	0.10	0.15	0.20	0.25	0.30	0.35	0.40	0.45	0.50	0.55	0.60	0.65	0.70	0.75	0.80	0.85	0.90	0.95
Adis (A)	14.49	13.80	13.89	13.07	12.81	12.58	12.38	12.20	12.04	11.88	11.74	11.61	11.48	11.36	11.25	11.14	9.21	6.49	3.44
${Z^{\prime }}_{dis}$ (Ω)	0.0619	0.0624	0.0628	0.0631	0.0633	0.0635	0.0637	0.0638	0.0640	0.0641	0.0643	0.0644	0.0645	0.0647	0.0648	0.0649	0.0672	0.0715	0.079
qdis (W)	0.65	1.19	1.69	2.15	2.60	3.02	3.42	3.80	4.17	4.53	4.87	5.21	5.53	5.84	6.15	6.45	4.84	2.71	0.89
Acha (A)	0.76	1.53	2.36	3.27	4.27	5.39	6.67	8.13	9.84	11.88	14.35	17.41	21.32	26.51	33.75	44.57	52.18	58.43	65.33
${Z^{\prime }}_{cha}$ (Ω)	0.0841	0.0827	0.0823	0.0796	0.0766	0.0738	0.0711	0.0687	0.0664	0.0641	0.0620	0.0600	0.0580	0.0560	0.0541	0.0522	0.0513	0.0506	0.0501
qcha (W)	0.047	0.18	0.39	0.68	1.05	1.50	2.06	2.73	3.54	4.53	5.75	7.27	9.22	11.82	15.41	20.74	20.93	17.29	10.68
q (W)	0.70	1.36	2.08	2.83	3.64	4.52	5.47	6.53	7.71	9.06	10.62	12.48	14.75	17.66	21.56	27.19	25.77	20.00	11.57

. Combined with Equation (1), currents and the time of discharge and charge are relatively large in terms of magnitude. (In calculating the heating power, the discharge time is t_dis/T_pulse and the charge time is t_cha/T_pulse according to Equation (1)) Although ${Z^{\prime }}_{dis}$ and ${Z^{\prime }}_{cha}$ exhibit variation, their impact on heating power is comparatively minor. Therefore, currents and the time of discharge and charge are the main factors affecting the battery heating power. When R_pulse increases, the discharge current diminishes while the discharge heating power initially rises and subsequently declines. Notably, the discharge heating power reaches its peak when R_pulse is 0.8. When R_pulse is less than 0.8, although the discharge current decreases, the degree of decrease is not large. In addition, the discharge time in one cycle increases. Therefore, the discharge heating power increases. When R_pulse exceeds 0.8, although the discharge time increases, the discharge current is significantly smaller. Therefore, the discharge heating power decreases. Combined with the above analysis, the reason for the increase in the discharge heating power is attributed to the elevation in the discharge time, while the reason for the decline in the discharge heating power is the reduction in the discharge current. In addition, when R_pulse increases, it can be seen from Table 3 that the charge current increases, and the charge heating power initially rises and subsequently declines. When R_pulse is 0.85, the charge heating power has the maximum value. In the same way as the analysis of the discharge heating power, the reason for the increase in the charge heating power can be attributed to the elevation in the charge current. The decrease in the charge heating power can be attributed to the reduction in charge time. Finally, the changes in the discharge heating power and the charge heating power together determine the changes in the battery heating power.

Furthermore, the relationship between heating power and frequency and the relationship between heating power and temperature exhibit variability across different R_pulse values and discharge cutoff voltages. Figure 9 demonstrates that the area covered in white and red becomes larger as the temperature increases at the same frequency, which shows that the area covered by the high heating power is increasing. Therefore, at the same discharge cut-off voltage and R_pulse, the battery heating power may become larger with the increase in temperature. This phenomenon can be explained by the variation of battery resistance with temperature. In Figure 8, the resistance becomes small as the temperature increases. Thus, at the same discharge cut-off voltage, the battery needs a larger current to reach the constraint. From the above analysis, it is clear that the battery heating power is mainly affected by the current. Therefore, the battery heating power becomes large as the current increases. In addition, Figure A1 shows that the relationship between the maximum heating power and temperature is not certain. For example, at a frequency of 0.5 Hz, the R_pulse value corresponding to the maximum heating power remains at 0.9 within the temperature range of −15 °C to 0 °C. However, when temperatures are 5 °C and 10 °C, the R_pulse value associated with the maximum heating power increases to 0.95. Moreover, the maximum heating power gradually increases with rising temperature. Conversely, when the frequency is 100 Hz, the R_pulse value linked to the maximum heating power tends to decrease with the increase in temperature. The difference in the maximum heating power is not significant. Additionally, the variations of R_pulse corresponding to the maximum heating power with frequency at the same discharge cut-off voltage are not the same at temperatures of −15 °C and 5 °C. When the temperature is below 0 °C, Figure 9 demonstrates that the area covered in white and red becomes large as the frequency increases at the same temperature, which shows that the area covered by the high heating power is increasing. However, when the temperature exceeds 0 °C, this phenomenon is not obvious. At the same temperature, the area covered in white and red seems to first diminish and then grow large with increasing frequency. At a frequency of 100 Hz, the region is the smallest and the heating power in this region is significantly small. The reason for the difference can be attributed to variations in battery resistance. For example,

Table 4. Parameter variations in Equation (1) at −15 °C and 10 °C with different BPC frequencies under the discharge cut-off voltage of 2.2 V when the R_pulse is 0.85.

Temperature (°C)	−15				10
fpulse (Hz)	0.5	5	100	10,000	0.5	5	100	10,000
Adis (A)	6.13	7.12	10.91	18.89	17.74	18.14	18.26	28.37
${Z^{\prime }}_{dis}$ (Ω)	0.2085	0.1578	0.0956	0.0637	0.0765	0.0652	0.0522	0.0435
qdis (W)	6.66	6.79	9.67	19.31	20.47	18.24	14.79	29.74
Acha (A)	34.73	40.34	61.81	107.04	100.54	102.81	103.49	160.79
${Z^{\prime }}_{cha}$ (Ω)	0.1062	0.0960	0.0742	0.0589	0.0587	0.0536	0.0433	0.0414
qcha (W)	19.21	23.44	42.52	101.30	89.03	85.05	69.54	160.71
q (W)	25.87	30.24	52.19	120.61	109.51	103.29	84.33	190.45

demonstrates the parameter variations in Equation (1) with different BPC frequencies at −15 °C and 10 °C when the discharge cut-off voltage is 2.2 V and R_pulse is 0.85. Both ${Z^{\prime }}_{dis}$ and ${Z^{\prime }}_{cha}$ decrease gradually with increasing frequency at −15 °C and 10 °C. However, compared to the results at 10 °C, ${Z^{\prime }}_{dis}$ and ${Z^{\prime }}_{cha}$ decrease more significantly at −15 °C, which also leads to a greater increase in discharge and charge currents at −15 °C. Thus, the battery heating power at −15 °C becomes large with the increase in frequency. When the temperature is 10 °C, the increase in discharge and charge currents from 0.5 Hz to 100 Hz is not obvious and ${Z^{\prime }}_{dis}$ and ${Z^{\prime }}_{cha}$ decrease, thus causing the battery heating power to reduce. When the frequency is 10,000 Hz, ${Z^{\prime }}_{dis}$ and ${Z^{\prime }}_{cha}$ are significantly smaller, which makes a significant increase in the discharge and charge currents. Consequently, the battery heating power becomes large again. Comprehensive analysis of the above shows that, when the temperature is less than 0 °C, because the battery resistance reduces more obviously with the increase in frequency, the battery heating power is mainly dominated by the discharge and charge currents. Therefore, the battery heating power gradually becomes large with the increase in frequency. When the temperature is equal to or greater than 0 °C, as the battery resistance decreases less with the increase of frequency, the battery heating power is dominated by the discharge and charge currents, in conjunction with ${Z^{\prime }}_{dis}$ and ${Z^{\prime }}_{cha}$. Therefore, the battery heating power changes uncertainly with the increase in frequency. In addition, the variation of the maximum heating power with different frequencies is similar to the variation of the maximum heat production power with different temperatures. There is no obvious pattern as can be seen in Figure A1.

Figure 10 shows the variation of the relationship between R_pulse and heating power with frequency and temperature at different charge cut-off voltages. The legends in the figure range from 0 W to 130 W. The black areas in the plots indicate that the heating power exceeds the maximum value in the legend. Figure A2 demonstrates detailed information for each case. In each subplot of Figure 10 and Figure A2, the battery heating power at the same R_pulse increases gradually as the charge cut-off voltage becomes larger. This is similar to the results for the discharge cut-off voltage. A larger charge cut-off voltage needs a higher current to reach the constraint boundary. The heating power will also become larger. Similar to the discharge cut-off voltage, the battery heating power becomes large first and then smaller as R_pulse increases in most cases under the same charge cut-off voltage. Unlike the discharge cut-off voltage, the large heating power is mainly concentrated in the interval where R_pulse is small. To illustrate this phenomenon,

Table 5. Parameter variations in Equation (1) at −5 °C with different R_pulse values under the charge cut-off voltage of 4.8 V when the BPC frequency is 100 Hz.

Rpulse	0.05	0.10	0.15	0.20	0.25	0.30	0.35	0.40	0.45	0.50	0.55	0.60	0.65	0.70	0.75	0.80	0.85	0.90	0.95
Adis (A)	43.79	48.18	51.54	48.93	42.83	37.02	31.83	27.30	23.35	19.88	16.83	14.12	11.69	9.51	7.53	5.73	4.08	2.58	1.21
${Z^{\prime }}_{dis}$ (Ω)	0.0523	0.0517	0.0513	0.0516	0.0525	0.0534	0.0546	0.0558	0.0571	0.0586	0.0603	0.0622	0.0643	0.0668	0.0696	0.0730	0.0771	0.0820	0.0832
qdis (W)	5.02	12.01	20.45	24.72	24.06	21.97	19.35	16.63	14.02	11.59	9.40	7.44	5.72	4.23	2.96	1.92	1.09	0.49	0.12
Acha (A)	2.31	5.35	9.10	12.23	14.28	15.86	17.14	18.20	19.10	19.88	20.57	21.18	21.72	22.19	22.59	22.91	23.14	23.22	22.93
${Z^{\prime }}_{cha}$ (Ω)	0.0823	0.0739	0.0673	0.0638	0.0621	0.0609	0.0601	0.0595	0.0590	0.0586	0.0583	0.0580	0.0578	0.0576	0.0574	0.0573	0.0572	0.0572	0.0573
qcha (W)	0.42	1.91	4.73	7.64	9.49	10.74	11.48	11.83	11.85	11.59	11.10	10.41	9.54	8.51	7.33	6.02	4.60	3.08	1.51
q (W)	5.43	13.91	25.19	32.36	33.55	32.71	30.83	28.46	25.87	23.19	20.50	17.85	15.26	12.73	10.29	7.94	5.69	3.58	1.62

shows the results for 100 Hz@−5 °C with the charge cut-off voltage of 4.8 V. It can be seen that the battery heating power first increases and then decreases with the increase of R_pulse, which is the same as the changes of discharge heating power and charge heating power. Moreover, the maximum values of the battery heating power, discharge heating power, and charge heating power correspond to R_pulse of 0.25, 0.2, and 0.45, respectively. Similar to the analysis of the discharge cut-off voltage, due to the small influence of ${Z^{\prime }}_{dis}$ and ${Z^{\prime }}_{cha}$ on the battery heating power, the discussion will exclusively focus on the currents and time of charge and discharge. For the discharge heating power, with the increase of R_pulse, the variation of the discharge heating power is the same as the variation of the discharge current. Therefore, the change in the discharge heating power is mainly dominated by the discharge current. For the charge heating power, with the increase of R_pulse, the charge current gradually increases, while the charge time gradually decreases. The initial increase in charge heating power can be attributed to the increase in charge current. As the charge time decreases sharply afterward, the dominant factor of the charge heating power changes from the charge current to the charge time. As a result, the charge heating power becomes small with the increase in R_pulse.

Similar to the discharge cut-off voltage, the effect of temperature and frequency on the heating power is also diverse. First, it can be seen from Figure 10 that at the same frequency, the area covered by high heating power becomes larger as the temperature increases. Therefore, at the same charge cut-off voltage and R_pulse, the battery heating power may become large with the increase in temperature. The reason is the same as that for the discharge cut-off voltage, which is caused by the decrease in battery resistance due to the increase in temperature. When the battery resistance decreases, the current increases at the same charge cut-off voltage. Thus, the battery heating power becomes large. In addition, the relationship between the maximum heating power and temperature is not clear in Figure A2. For example, at 0.5 Hz, the R_pulse corresponding to the maximum heating power at the same charge cut-off voltage is 0.1 when the temperature is less than 5 °C. When the temperature is 10 °C, the R_pulse becomes 0.05 and the maximum heating power becomes larger as the temperature increases. At 10 kHz, the R_pulse of the maximum heating power at the same charge cut-off voltage becomes larger as the temperature increases. Then, at the same temperature, the result of high heating power distribution with frequency is similar to that of discharge cut-off voltage. When the temperature is less than 0 °C, the region of high heating power distribution increases with frequency. When the temperature is equal to or greater than 0 °C, the region of high heating power distribution decreases and then increases with frequency. To explain this phenomenon,

Table 6. Parameter variations in Equation (1) at −15 °C and 10 °C with different BPC frequencies under the charge cut-off voltage of 4.8 V when the R_pulse is 0.2.

Temperature (°C)	−15				10
fpulse (Hz)	0.5	5	100	10,000	0.5	5	100	10,000
Adis (A)	19.59	23.44	35.59	59.85	61.52	63.33	64.69	84.00
${Z^{\prime }}_{dis}$ (Ω)	0.1294	0.1110	0.0795	0.0608	0.0626	0.0560	0.0449	0.0426
qdis (W)	9.93	12.20	20.13	43.52	47.37	44.93	37.55	60.15
Acha (A)	4.90	5.86	8.90	14.96	15.38	15.83	16.17	21.00
${Z^{\prime }}_{cha}$ (Ω)	0.2292	0.1669	0.0991	0.064	0.0784	0.0665	0.0530	0.0435
qcha (W)	4.40	4.59	6.27	11.47	14.84	13.34	11.10	15.35
q (W)	14.32	16.78	26.41	54.99	62.21	58.27	48.65	75.50

shows the parameter variations in Equation (1) with different BPC frequencies at −15 °C and 10 °C when the charge cut-off voltage is 4.8 V and R_pulse is 0.2. Whether the temperature is −15 °C or 10 °C, the battery resistance gradually gets small as the frequency increases. However, at −15 °C, the resistance decreases more significantly, which makes the increase in current at −15 °C more pronounced. Therefore, the battery heating power becomes progressively larger with increasing frequency at −15 °C. When the temperature is 10 °C, the current does not increase much from 0.5 Hz to 100 Hz, while the resistance decreases. Therefore, the battery heating power decreases. When the frequency is 10,000 Hz, the current is a little larger. Therefore, the battery heating power becomes large again. Comprehensive analysis of the above shows that at −15 °C, the battery heating power becomes larger with the increase of frequency, which is determined by the current. The change of battery heating power at 10 °C is determined by the current and resistance together. In addition, the variation of the maximum heating power with different frequencies in Figure A2 is similar to the result of discharge cut-off voltage. Neither of them has a clear pattern.

The variations of the relationship between R_pulse and heating power with frequency and temperature for different discharge and charge cut-off voltages are analyzed in Figure 9 and Figure 10, respectively. However, when the AC heating strategy in practice is designed, the charge and discharge cut-off voltages should be considered simultaneously. Figure 11 shows the variation of the relationship between R_pulse and heating power with charge and discharge cut-off voltages at −5 °C and 100 Hz. The curves in the figure represent the maximum heating power that can be achieved at the corresponding charge and discharge cut-off voltages. When both charge and discharge cut-off voltages are considered, the battery heating power is determined by the smaller one. Therefore, the intersection of the heating power curves for the charge and discharge cut-off voltages is the maximum heating power under the constraints of charge and discharge terminal voltages, such as the green dots in Figure 11. If the value of R_pulse is smaller than the R_pulse value of the intersection, the maximum heating power is determined by the discharge cut-off voltage. Conversely, if the value of R_pulse is larger than the R_pulse value of the intersection, the maximum heating power is determined by the charge cut-off voltage. The two figures on the right in Figure 11 demonstrate the influences of the discharge cut-off voltage and the charge cut-off voltage on the position of the intersection, respectively. As the discharge cut-off voltage increases, the intersection gradually shifts towards a larger R_pulse value. Conversely, as the charge cut-off voltage decreases, the intersection gradually shifts towards a smaller R_pulse value. Moreover, the heating power corresponding to R_pulse of 0.5 is not the maximum heating power. For example, when the charge cut-off voltage and the discharge cut-off voltage are 5 V and 3 V, the maximum heating power corresponds to R_pulse of about 0.8.

The intersection of the heating power curves for the charge and discharge cut-off voltages corresponds to the maximum heating power. Thus, the impact of different frequencies and temperatures on the heating power under the constraints of both charge and discharge cut-off voltage can be assessed through the intersection. In this study, the charge and discharge cut-off voltages of the battery are 4.2 V and 3 V, respectively. Therefore, the maximum heating power at these voltage constraints serves as the basis for analyzing the effects of frequency and temperature, and the results are presented in Figure 12. Figure 12a,b depict the variations in maximum heating power with frequency and temperature and the distribution of the corresponding R_pulse value, respectively. Notably, the maximum heating power increases with temperature for a given frequency. Similarly, at a constant temperature, the maximum heating power exhibits continuous growth with the increase in frequency. Figure 12b reveals that the value of R_pulse corresponding to the maximum heating power is predominantly 0.55. The value of R_pulse corresponding to the maximum heating power is 0.5 only when the frequency is 0.5 Hz and the temperatures are 5 °C and 10 °C.

5. Conclusions

This paper investigates the impact of various BPC parameters on the heat generation of the battery by the electro-thermal coupled model under the premise that the charge capacity and discharge capacity are equal. The main conclusions of this study can be summarized as follows:

(1)

The heating power of the battery increases with a decrease in the discharge cut-off voltage and an increase in the charge cut-off voltage. Under the discharge cut-off voltage constraint, higher heating powers are observed in the range of larger R_pulse values. Conversely, the higher heating powers are mainly concentrated in the range of smaller R_pulse values for the charge cut-off voltage constraint.

(2)

The symmetrical BPC approach does not result in maximum heating power. The relationship between the maximum heating power and R_pulse is influenced by both the charge cut-off voltage and the discharge cut-off voltage. Specifically, the R_pulse of the maximum heating power increases with an increase in the discharge cut-off voltage, while it decreases with a decrease in the charge cut-off voltage.

(3)

When the voltage constraint range is set between 3 V and 4.2 V, the R_pulse of the maximum heating power is primarily 0.55. Moreover, under the same frequency, the maximum heating power gradually increases with rising temperatures. At frequencies of 0.5 Hz, 5 Hz, 100 Hz, and 10,000 Hz, the maximum heating power exhibits a progressive increase with higher frequencies at a constant temperature.

BPC heating offers higher heating efficiency compared to SAC heating. However, BPC involves multiple parameters, making it challenging to optimize the BPC heating strategy. The research approach in this paper provides the possibility of optimizing the BPC heating strategy. Moreover, the findings of this study demonstrate that the widely used symmetrical BPC heating is not the most efficient strategy. To enhance heating efficiency when designing BPC heating, intervals with higher frequencies should be considered. Additionally, the optimization of the BPC heating strategy should not only consider amplitude and frequency, but also the BPC ratio. In future work, the terminal voltages corresponding to lithium plating, overcharge, and over-discharge of the battery will be determined. Under these constraints, the frequency, the ratio, and the amplitude of BPC heating will be optimized.