How the Structure and Wettability Properties of Morpho peleides Butterfly Wings Can Be a Source of Inspiration
Abstract
:1. Introduction
- o The contact line density Λ, defined using the following equation:
- o The critical contact line density Λc, which is expressed as follows:
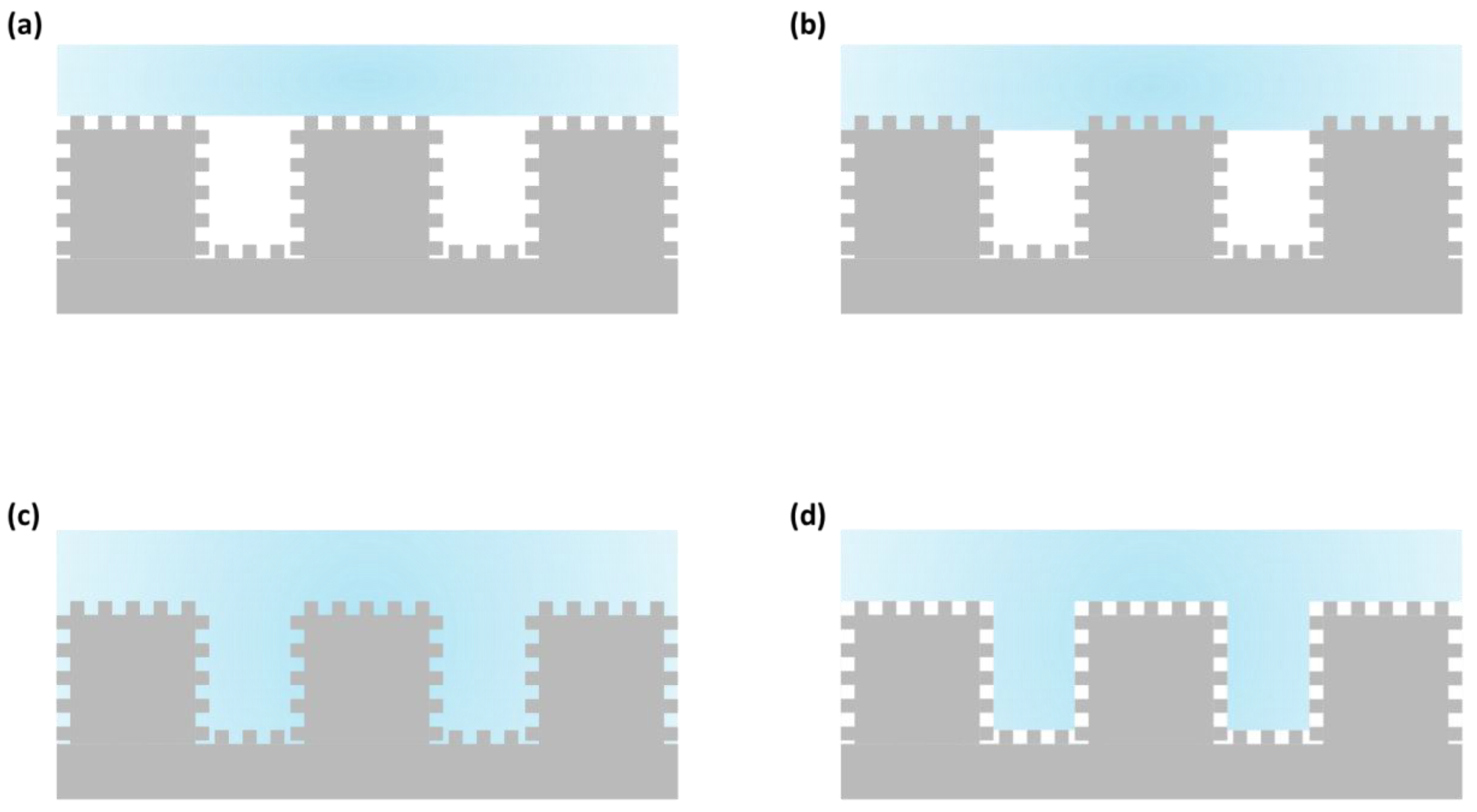
- o The pure Cassie–Baxter state: both scales are wet in the Cassie–Baxter condition, and the associated apparent contact angle is:
- o The pure Wenzel state: both scales are wet in the Wenzel condition, and the associated contact angle is:
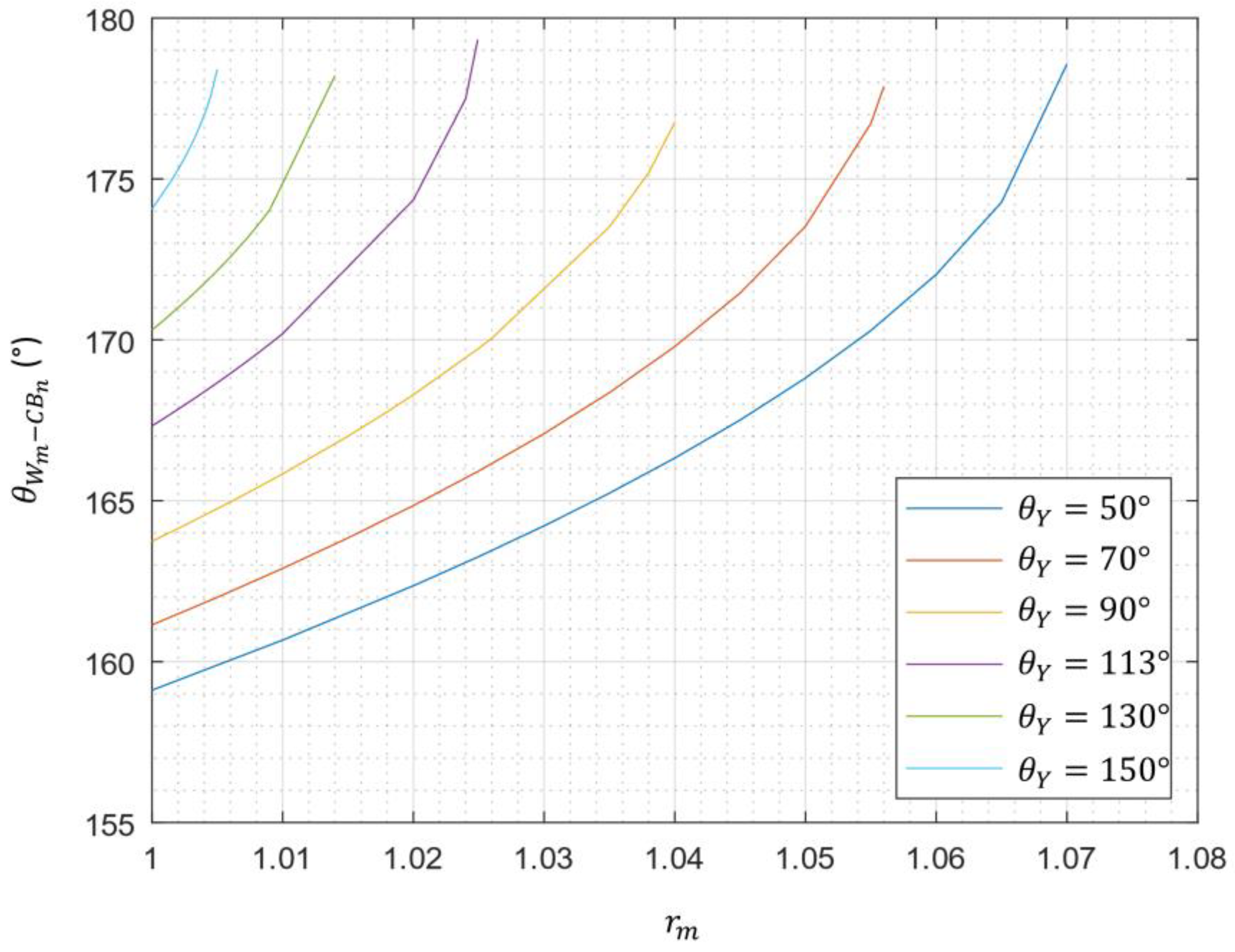
- o The Cassie–Wenzel mixed state: the principal ridged stripes are wet in Cassie–Baxter and the cross-ribs are wet in Wenzel; the associated apparent contact angle is:
- o The Wenzel–Cassie mixed state: the principal ridged stripes are wet in Wenzel and the cross-ribs are wet in Cassie–Baxter; the associated apparent contact angle is:
2. Materials and Methods
2.1. M. peleides Butterfly
2.2. Topography Characterization
2.3. Wettability
3. Results
3.1. Topography
3.1.1. Topography of M. peleides Butterfly’s Wings
3.1.2. Simplified Topography for Modeling
3.2. Wettability Behavior
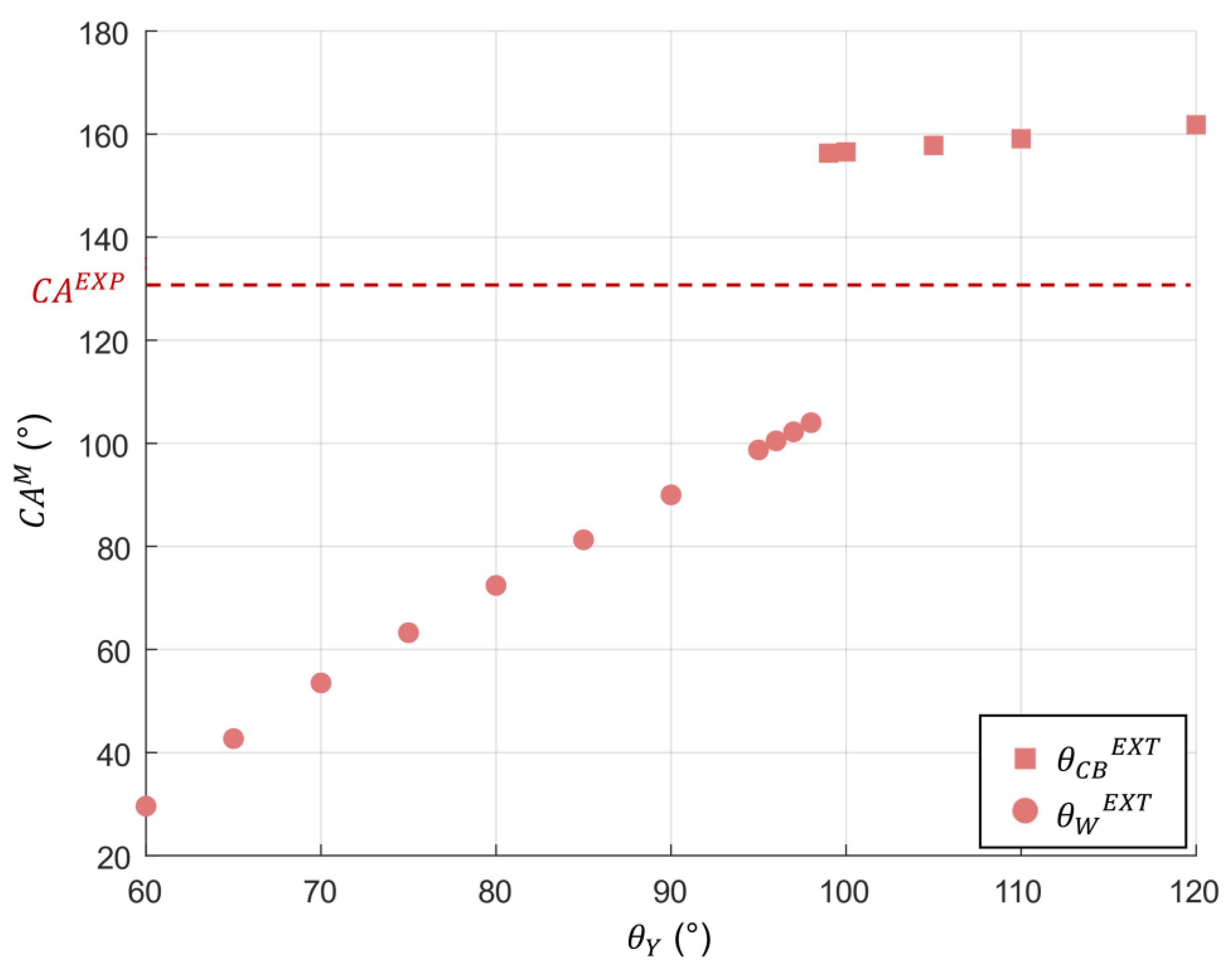
3.2.1. Static Contact Angle of M. peleides Butterfly Wings
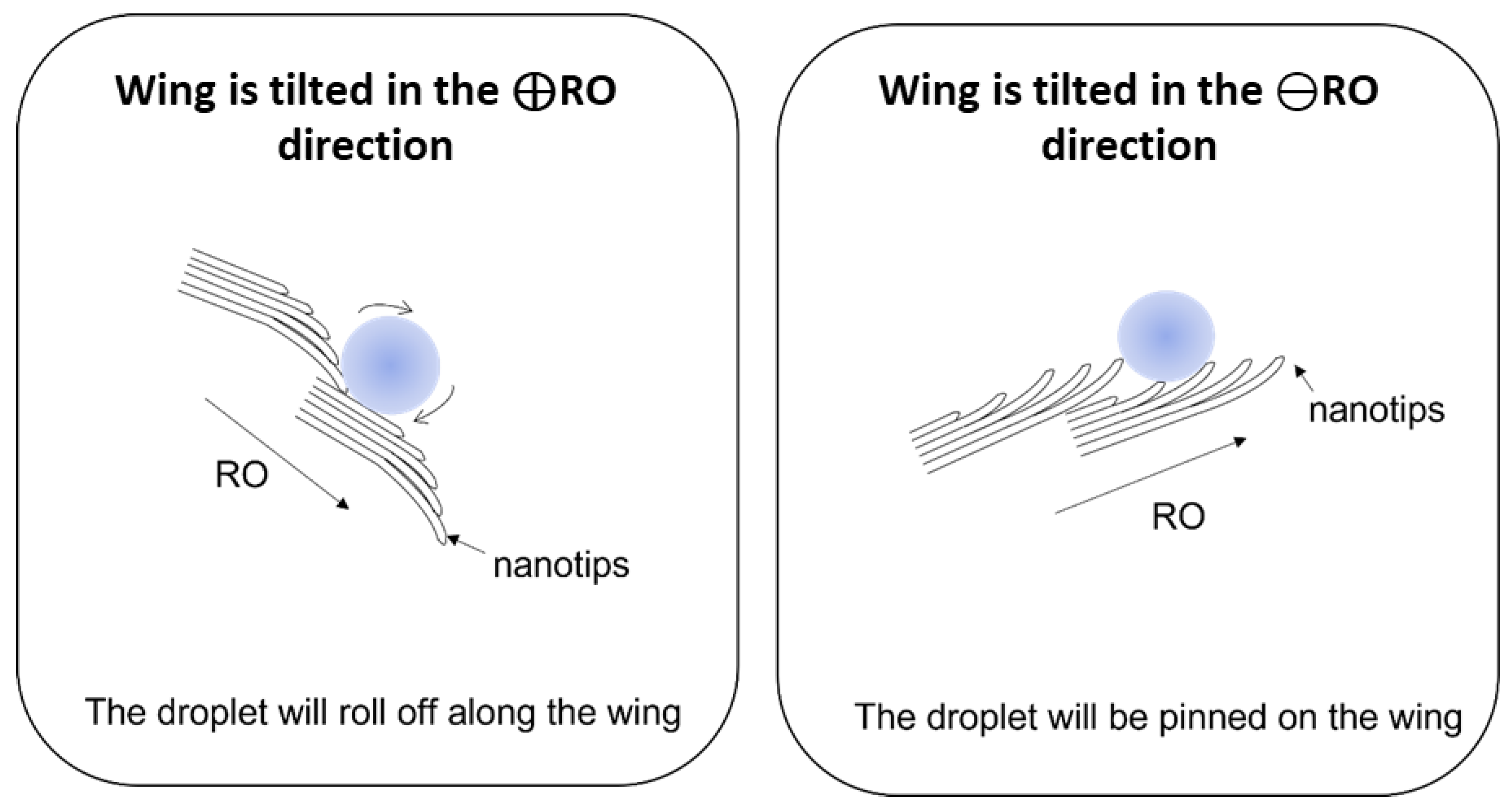
3.2.2. Sliding Angle of Morpho peleides Butterfly’s Wings
4. Discussions
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, D.; Wang, L.; Qian, H.; Li, X. Superhydrophobic surfaces for corrosion protection: A review of recent progresses and future directions. J. Coat. Technol. Res. 2016, 13, 11–29. [Google Scholar] [CrossRef]
- Li, X.; Jiang, Y.; Jiang, Z.; Li, Y.; Wen, C.; Zhang, D.; Lian, J.; Zhang, Z. Improvement of corrosion resistance of H59 brass through fabricating superhydrophobic surface using laser ablation and heating treatment. Corros. Sci. 2021, 180, 109186. [Google Scholar] [CrossRef]
- Zhou, P.; Zhu, Z.; She, W. A superhydrophobic mortar with ultra-robustness for self-cleaning, anti-icing, and anti-corrosion. Chem. Eng. J. 2024, 495, 153488. [Google Scholar] [CrossRef]
- Yang, C.; Sun, Z.; Wang, C.; Huang, A.; Ye, Z.; Ying, T.; Zhou, L.; Xiao, S.; Chu, P.K.; Zeng, X. A self-sealing and self-healing MAO corrosion-resistant coating on aluminum alloy by in situ growth of CePO4/Al2O3. Corros. Sci. 2025, 245, 112706. [Google Scholar] [CrossRef]
- Farhadi, S.; Farzaneh, M.; Kulinich, S.A. Anti-icing performance of superhydrophobic surfaces. Appl. Surf. Sci. 2011, 257, 6264–6269. [Google Scholar] [CrossRef]
- Karapanagiotis, I.; Grosu, D.; Aslanidou, D.; Aifantis, K.E. Facile Method to Prepare Superhydrophobic and Water Repellent Cellulosic Paper. J. Nanomater. 2015, 2015, 219013. [Google Scholar] [CrossRef]
- Neinhuis, C. Characterization and Distribution of Water-repellent, Self-cleaning Plant Surfaces. Ann. Bot. 1997, 79, 667–677. [Google Scholar] [CrossRef]
- Berthier, S. L’éveil du Morpho; Flammarion: Paris, France, 2021; p. 50. [Google Scholar]
- Kinoshita, S.; Yoshioka, S.; Kawagoe, K. Mechanisms of structural colour in the Morpho butterfly: Cooperation of regularity and irregularity in an iridescent scale. Proc. R. Soc. B Biol. Sci. 2002, 269, 1417–1421. [Google Scholar] [CrossRef] [PubMed]
- Ding, Y.; Xu, S.; Wang, Z.L. Structural colors from Morpho peleides butterfly wing scales. J. Appl. Phys. 2009, 106, 074702. [Google Scholar] [CrossRef]
- Chung, K.; Yu, S.; Heo, C.; Shim, J.W.; Yang, S.; Han, M.G.; Lee, H.; Jin, Y.; Lee, S.Y.; Park, N.; et al. Flexible, Angle-Independent, Structural Color Reflectors Inspired by Morpho Butterfly Wings. Adv. Mater. 2012, 24, 2375–2379. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Shi, F.; Niu, J.; Jiang, Y.; Wang, Z. Superhydrophobic surfaces: From structural control to functional application. J. Mater. Chem. 2008, 18, 621–633. [Google Scholar] [CrossRef]
- Siddique, R.H.; Diewald, S.; Leuthold, J.; Hölscher, H. Theoretical and experimental analysis of the structural pattern responsible for the iridescence of Morpho butterflies. Opt. Express 2013, 21, 14351. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Y.; Gao, X.; Jiang, L. Directional adhesion of superhydrophobic butterfly wings. Soft Matter 2007, 3, 178–182. [Google Scholar] [CrossRef]
- Pris, A.D.; Utturkar, Y.; Surman, C.; Morris, W.G.; Vert, A.; Zalyubovskiy, S.; Deng, T.; Ghiradella, H.T.; Potyrailo, R.A. Towards high-speed imaging of infrared photons with bio-inspired nanoarchitectures. Nat. Photonics 2012, 6, 195–200. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, D.; Fan, T.; Gu, J.; Ding, J.; Wang, H.; Guo, Q.; Ogawa, H. Novel Photoanode Structure Templated from Butterfly Wing Scales. Chem. Mater. 2009, 21, 33–40. [Google Scholar] [CrossRef]
- Wagner, T.; Neinhuis, C.; Barthlott, W. Wettability and Contaminability of Insect Wings as a Function of Their Surface Sculptures. Acta Zool. 1996, 77, 213–225. [Google Scholar] [CrossRef]
- Wenzel, R.N. Resistance of Solid Surfaces to Wetting by Water. Ind. Eng. Chem. 1936, 28, 988–994. [Google Scholar] [CrossRef]
- Cassie, A.B.D.; Baxter, S. Wettability of porous surfaces. Trans. Faraday Soc. 1944, 40, 546. [Google Scholar] [CrossRef]
- Extrand, C.W.; Kumagai, Y. An Experimental Study of Contact Angle Hysteresis. J. Colloid Interface Sci. 1997, 191, 378–383. [Google Scholar] [CrossRef] [PubMed]
- Dettre, R.H.; Johnson, R.E. Contact Angle Hysteresis—Contact Angle Measurements on Rough Surfaces; Advances in Chemistry; American Chemical Society: Washington, DC, USA, 1964; Volume 43. [Google Scholar] [CrossRef]
- Extrand, C.W. Criteria for Ultralyophobic Surfaces. Langmuir 2004, 20, 5013–5018. [Google Scholar] [CrossRef] [PubMed]
- Feng, L.; Zhang, Y.; Xi, J.; Zhu, Y.; Wang, N.; Xia, F.; Jiang, L. Petal Effect: A Superhydrophobic State with High Adhesive Force. Langmuir 2008, 24, 4114–4119. [Google Scholar] [CrossRef] [PubMed]
- Rahmawan, Y.; Moon, M.-W.; Kim, K.-S.; Lee, K.-R.; Suh, K.-Y. Wrinkled, Dual-Scale Structures of Diamond-Like Carbon (DLC) for Superhydrophobicity. Langmuir 2010, 26, 484–491. [Google Scholar] [CrossRef] [PubMed]
- Mountains® Surface Analysis & Metrology Software. Digital Surf. Available online: https://www.digitalsurf.com/mountains-surface-analysis-metrology-software/ (accessed on 31 August 2023).
- ISO 25178-2:2021(en); Geometrical Product Specifications (GPS)—Surface Texture: Areal—Part 2: Terms, Definitions and Surface Texture Parameters. Available online: https://www.iso.org/obp/ui/#iso:std:iso:25178:-2:ed-2:v1:en (accessed on 24 October 2023).
- Legrand, Q.; Benayoun, S.; Valette, S. Biomimetic Approach for the Elaboration of Highly Hydrophobic Surfaces: Study of the Links between Morphology and Wettability. Biomimetics 2021, 6, 38. [Google Scholar] [CrossRef]
- Extrand, C.W. Uncertainty in contact angle measurements from the tangent method. J. Adhes. Sci. Technol. 2016, 30, 1597–1601. [Google Scholar] [CrossRef]
- Zheng, Y. Bio-Inspired Wettability Surfaces: Developments in Micro- and Nanostructures; Pan Stanford Publishing: Singapore, 2016. [Google Scholar]
- Sun, G.; Fang, Y.; Cong, Q.; Ren, L. Anisotropism of the Non-Smooth Surface of Butterfly Wing. J. Bionic Eng. 2009, 6, 71–76. [Google Scholar] [CrossRef]
- Marmur, A. The Lotus Effect: Superhydrophobicity and Metastability. Langmuir 2004, 20, 3517–3519. [Google Scholar] [CrossRef] [PubMed]
- Patankar, N.A. On the Modeling of Hydrophobic Contact Angles on Rough Surfaces. Langmuir 2003, 19, 1249–1253. [Google Scholar] [CrossRef]
- Zheng, L. Superhydrophobicity from microstructured surface. Chin. Sci. Bull. 2004, 49, 1779. [Google Scholar] [CrossRef]
- Kusumaatmaja, H.; Yeomans, J.M. Anisotropic hysteresis on ratcheted superhydrophobic surfaces. Soft Matter 2009, 5, 2704. [Google Scholar] [CrossRef]
- Elbaz, A.; Lu, J.; Gao, B.; Zheng, F.; Mu, Z.; Zhao, Y.; Gu, Z. Chitin-Based Anisotropic Nanostructures of Butterfly Wings for Regulating Cells Orientation. Polymers 2017, 9, 386. [Google Scholar] [CrossRef]
- Greca, L.G.; Azpiazu, A.; Reyes, G.; Rojas, O.J.; Tardy, B.L.; Lizundia, E. Chitin-based pulps: Structure-property relationships and environmental sustainability. Carbohydr. Polym. 2024, 325, 121561. [Google Scholar] [CrossRef] [PubMed]

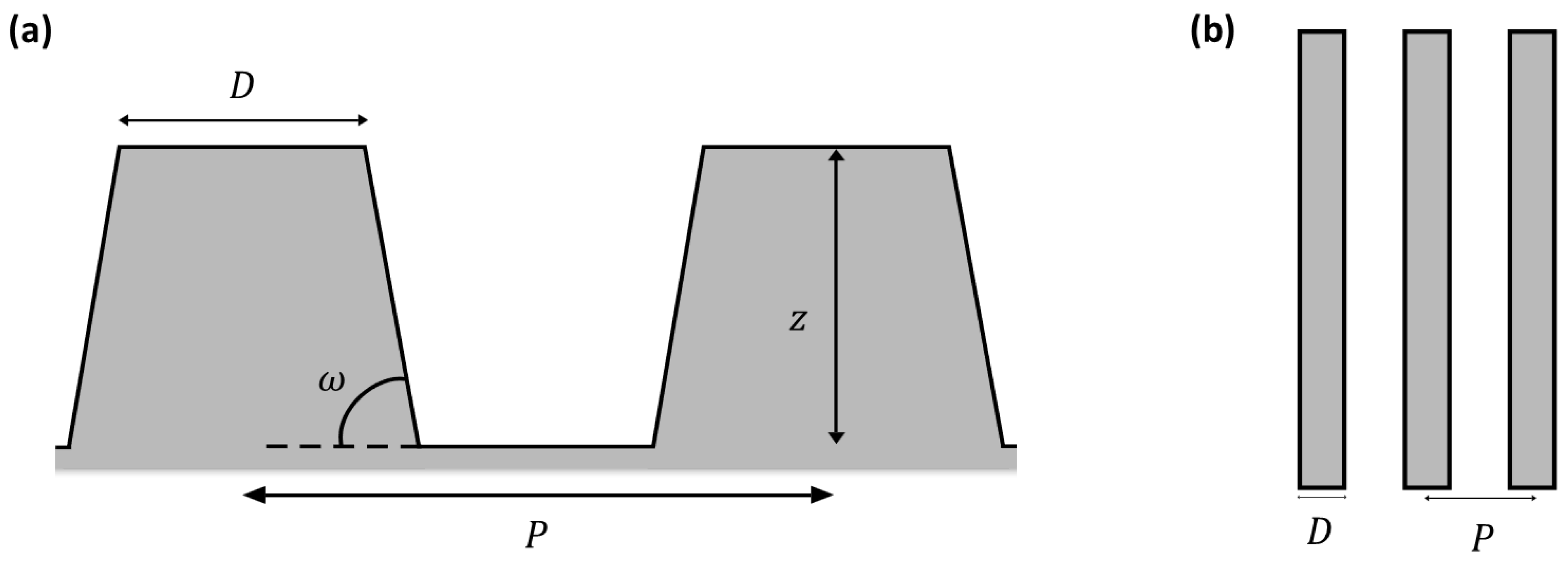






| D (µm) | H (µm) | P (µm) | ꙍ (°) |
|---|---|---|---|
| 0.20 ± 0.05 | 1.71 ± 0.03 | 2.01 ± 0.02 | 71.50 ± 0.75 |
| Dorsal Wing | Ventral Wing | Damaged Wing |
|---|---|---|
| 136 ± 1° | 130 ± 1° | 108 ± 1° |
| ⊖RO Direction | ⊕RO Direction |
|---|---|
| 29 ± 3° | 7 ± 1° |
| λCO (μm) | Sdr (%) | r (According to Equation (1)) | ||
|---|---|---|---|---|
| Principal ridged stripes (m) | 2.50 | 17.6 | rm = 1.176 | 0.12 |
| Cross-ribs (n) | 0.08 | 0.521 | rn = 1.005 | 0.04 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Burdin, L.; Brulez, A.-C.; Mazurczyk, R.; Leclercq, J.-L.; Benayoun, S. How the Structure and Wettability Properties of Morpho peleides Butterfly Wings Can Be a Source of Inspiration. Biomimetics 2025, 10, 89. https://doi.org/10.3390/biomimetics10020089
Burdin L, Brulez A-C, Mazurczyk R, Leclercq J-L, Benayoun S. How the Structure and Wettability Properties of Morpho peleides Butterfly Wings Can Be a Source of Inspiration. Biomimetics. 2025; 10(2):89. https://doi.org/10.3390/biomimetics10020089
Chicago/Turabian StyleBurdin, Louise, Anne-Catherine Brulez, Radoslaw Mazurczyk, Jean-Louis Leclercq, and Stéphane Benayoun. 2025. "How the Structure and Wettability Properties of Morpho peleides Butterfly Wings Can Be a Source of Inspiration" Biomimetics 10, no. 2: 89. https://doi.org/10.3390/biomimetics10020089
APA StyleBurdin, L., Brulez, A.-C., Mazurczyk, R., Leclercq, J.-L., & Benayoun, S. (2025). How the Structure and Wettability Properties of Morpho peleides Butterfly Wings Can Be a Source of Inspiration. Biomimetics, 10(2), 89. https://doi.org/10.3390/biomimetics10020089






