Electrical Equivalent Circuit Parameter Estimation of Commercial Induction Machines Using an Enhanced Grey Wolf Optimization Algorithm
Abstract
1. Introduction
1.1. Basic Concepts
1.2. Related Works
1.3. Advanced Techniques for IM Parameter Estimation
1.4. Motivation
- The study introduces the GWO algorithm with an adaptive weight mechanism to dynamically balance exploration and exploitation and address the limitations of existing algorithms in parameter estimation of the IM.
- The AWGWO enhances the accuracy of IM parameter estimation by handling multimodal and nonlinear optimization search space, reducing premature convergence.
- The proposed AMGWO is validated using the numerical benchmark problems, which include different features like unimodal and multimodal with variable dimensions.
- The proposed AWGWO is also validated using the IM benchmark model and eight commercial motors to demonstrate the performance compared to other algorithms.
2. Problem Formulation
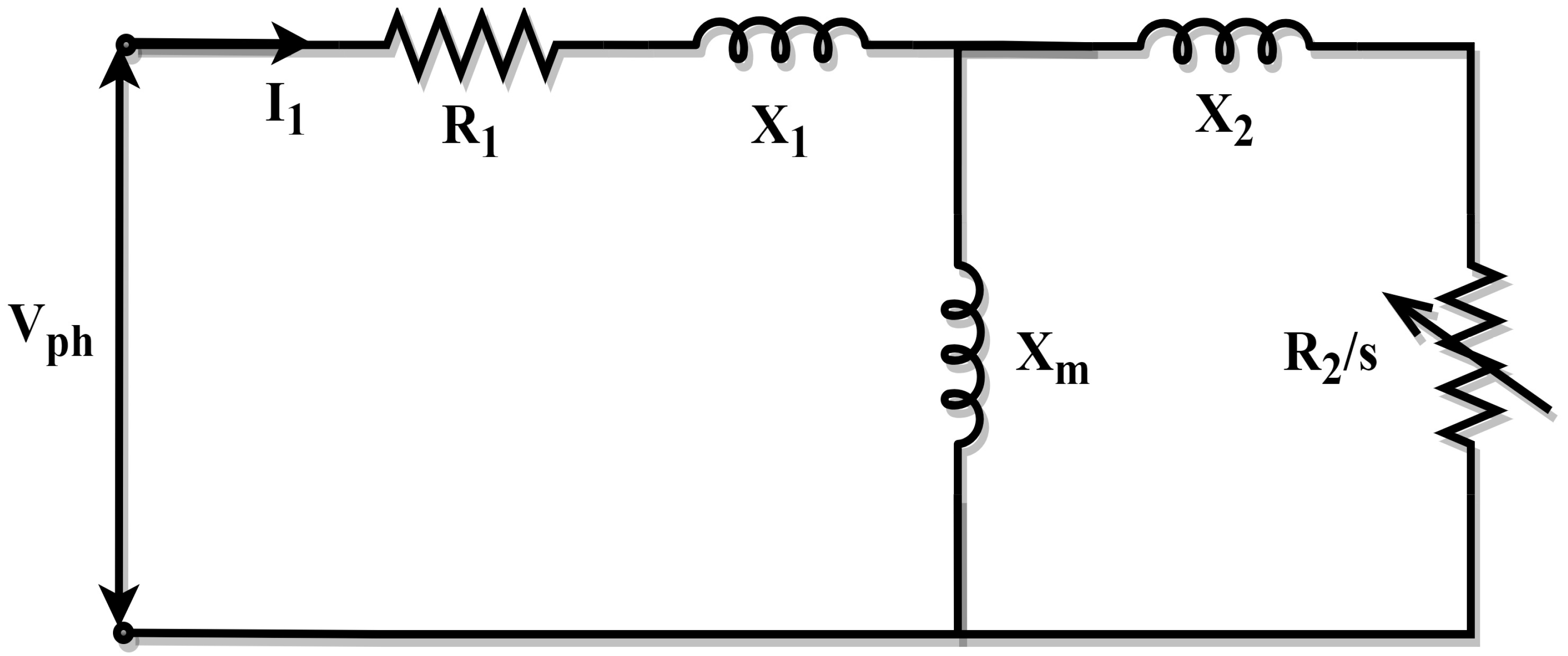
2.1. Approximate Model of the Induction Machine
2.2. Exact Model of the Induction Machine
3. Proposed Algorithm
3.1. Grey Wolf Algorithm
3.2. Defects of Grey Wolf Optimizer
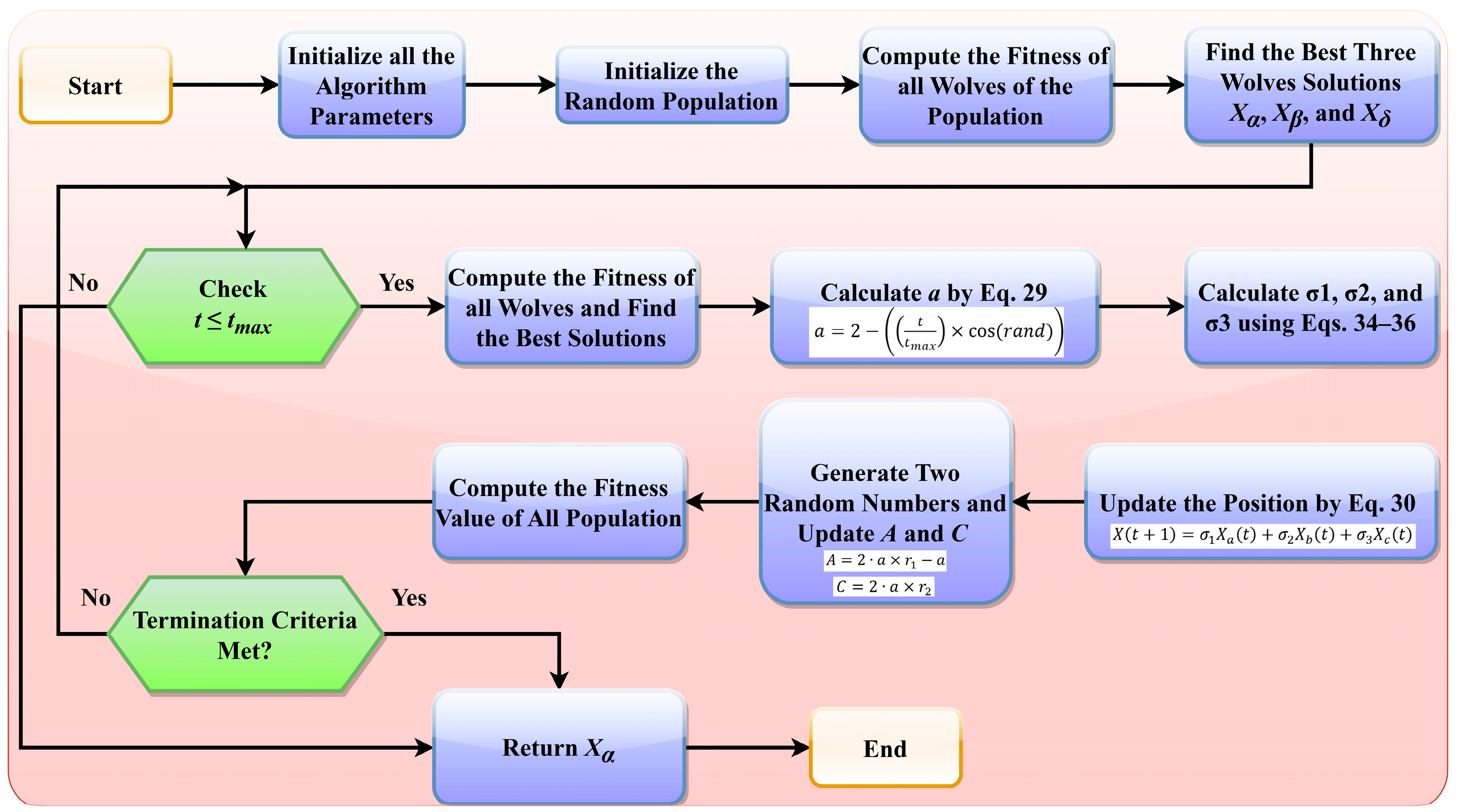
3.3. Proposed Adaptive Weighted Grey Wolf Optimizer
| Algorithm 1: Pseudocode of the proposed AWGWO | |
| 1: 2: 3: 4: 5: 6: 7: 8: 9: 10: 11: 12: 13: 14: | Initialize the and population size Initialize the random population and random population solution Initialize the GWO parameters, such as , , and Identify the best three individuals, such as , , and For do For do The position of the current search agent is updated using Equation (30) End For Update the value of using Equation (29) and and using Equations (22) and (23) Find the fitness of all the search agents Position of , , and is updated using Equations (25)–(27) End For Return the best solution |
3.4. Computational Complexity
4. Results and Discussions
4.1. Results Obtained for Benchmark Problems
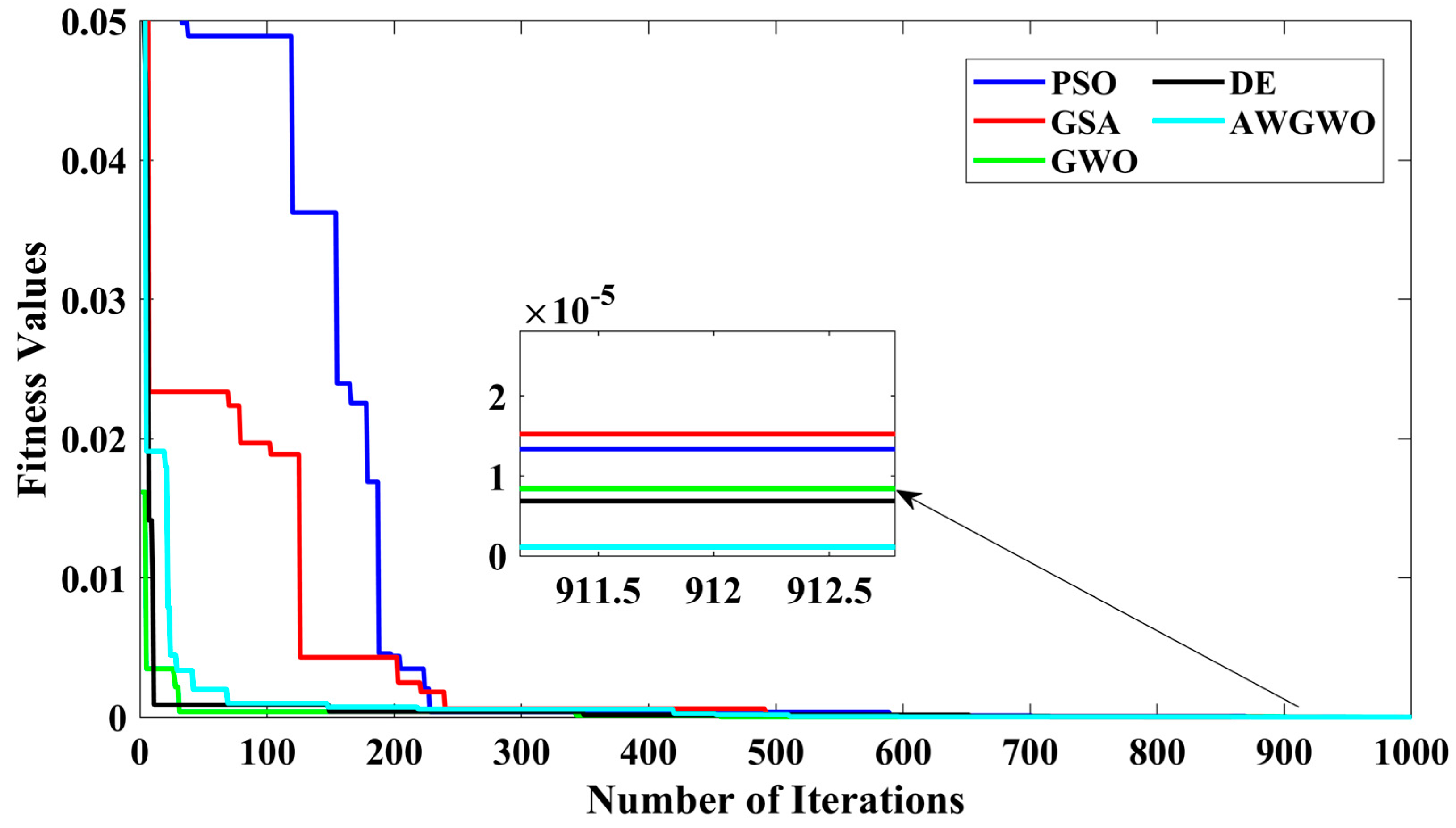
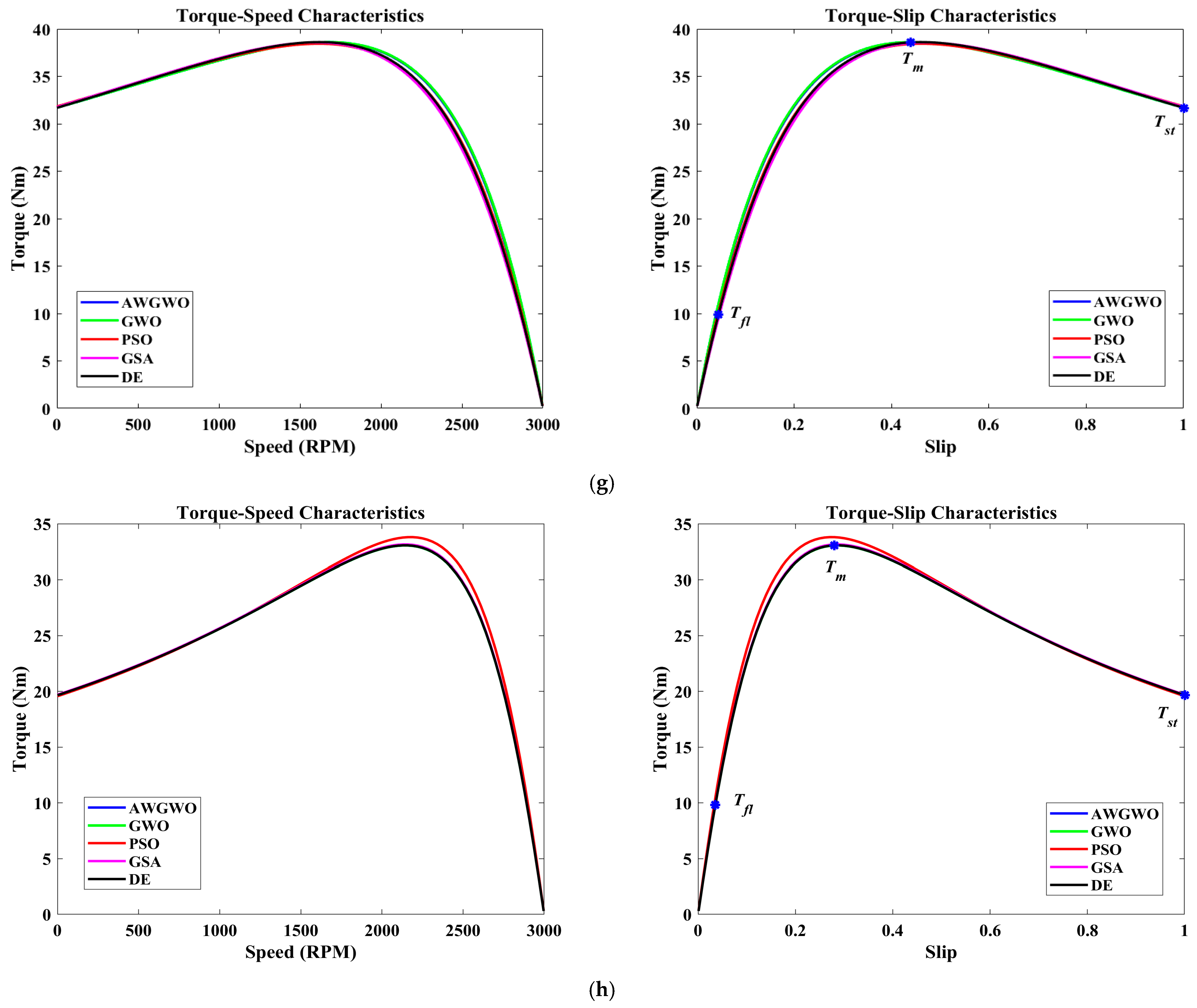
4.2. Results Obtained for Parameter Estimation Problem
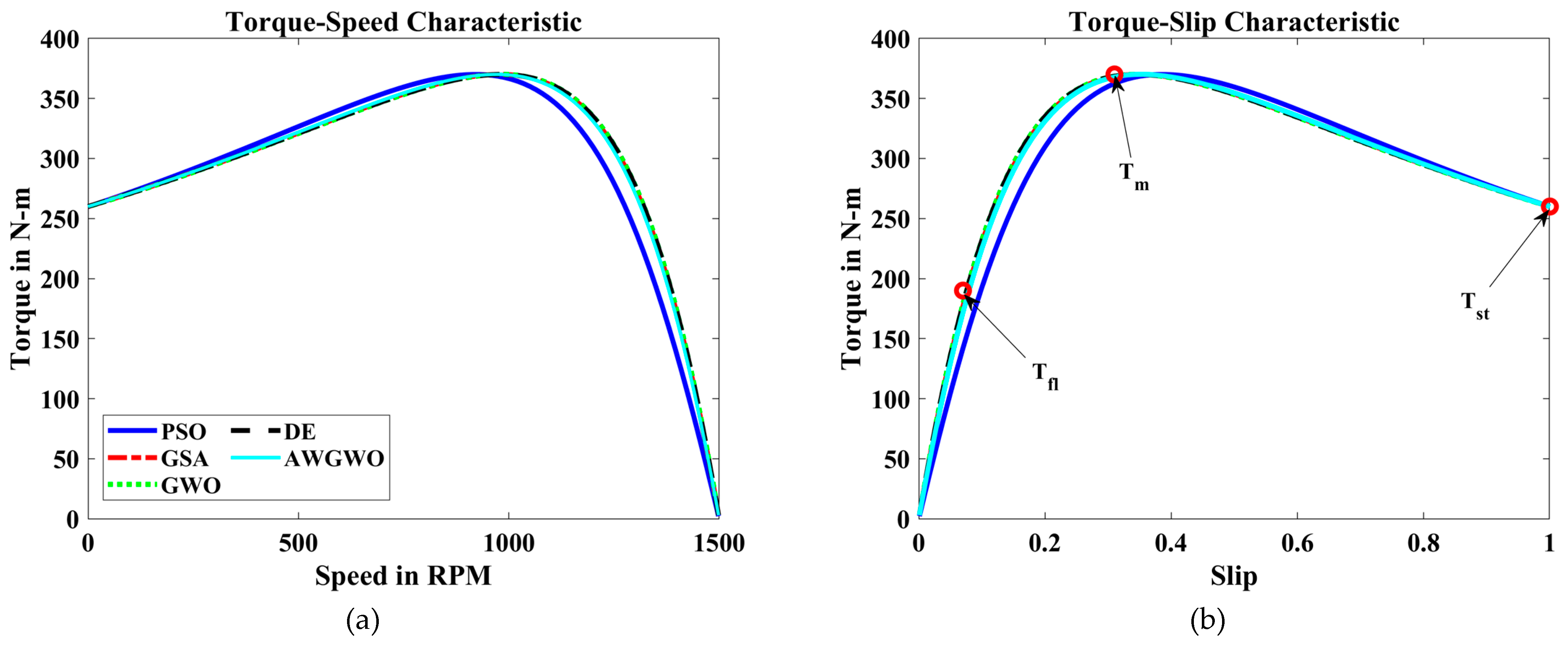
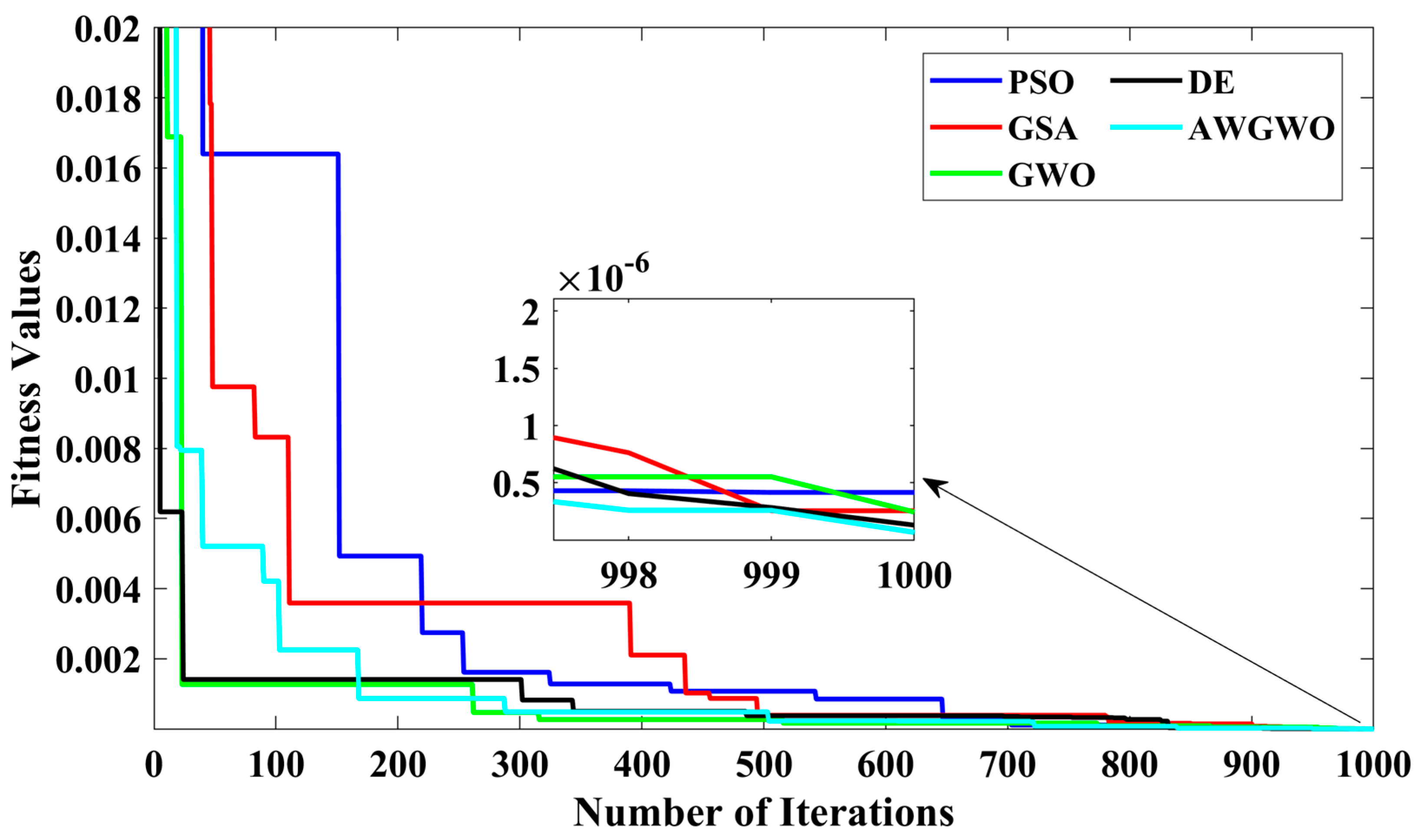
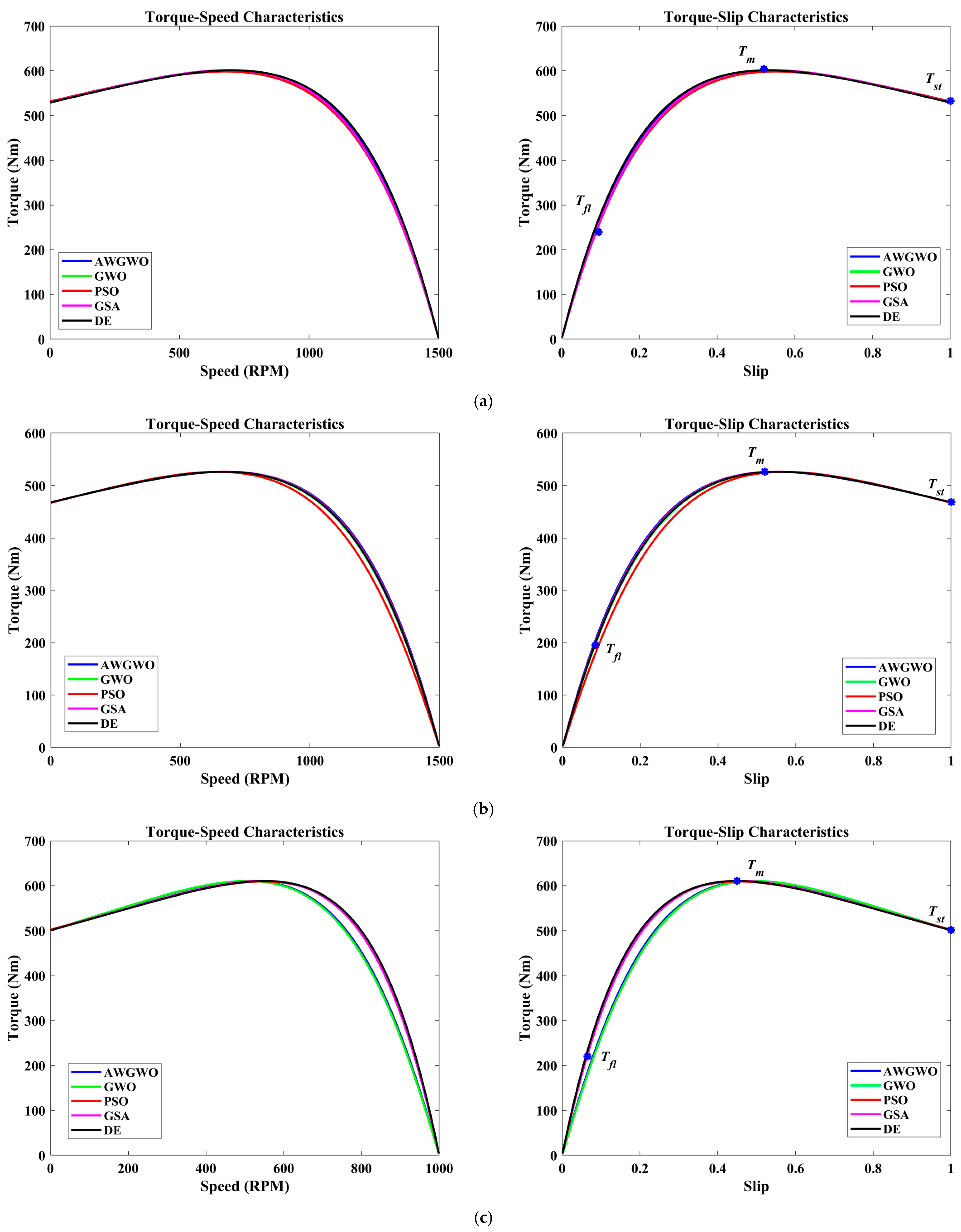
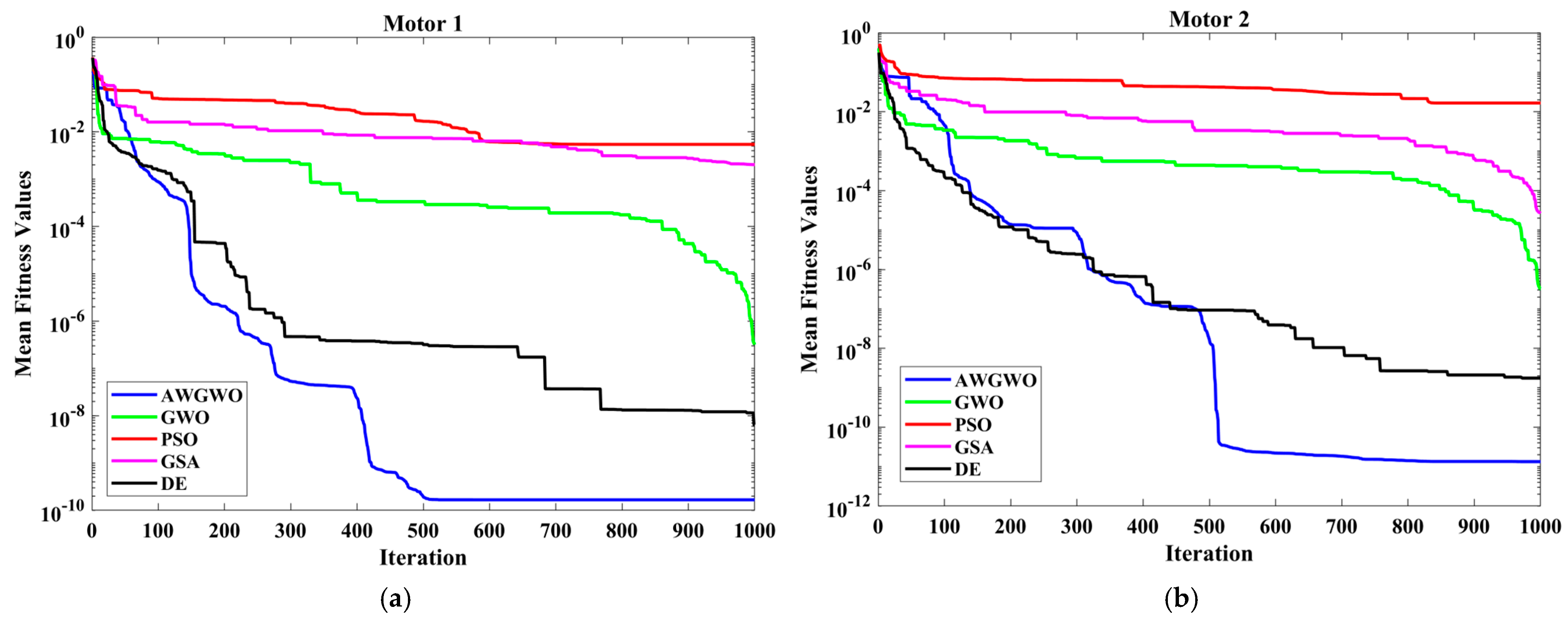
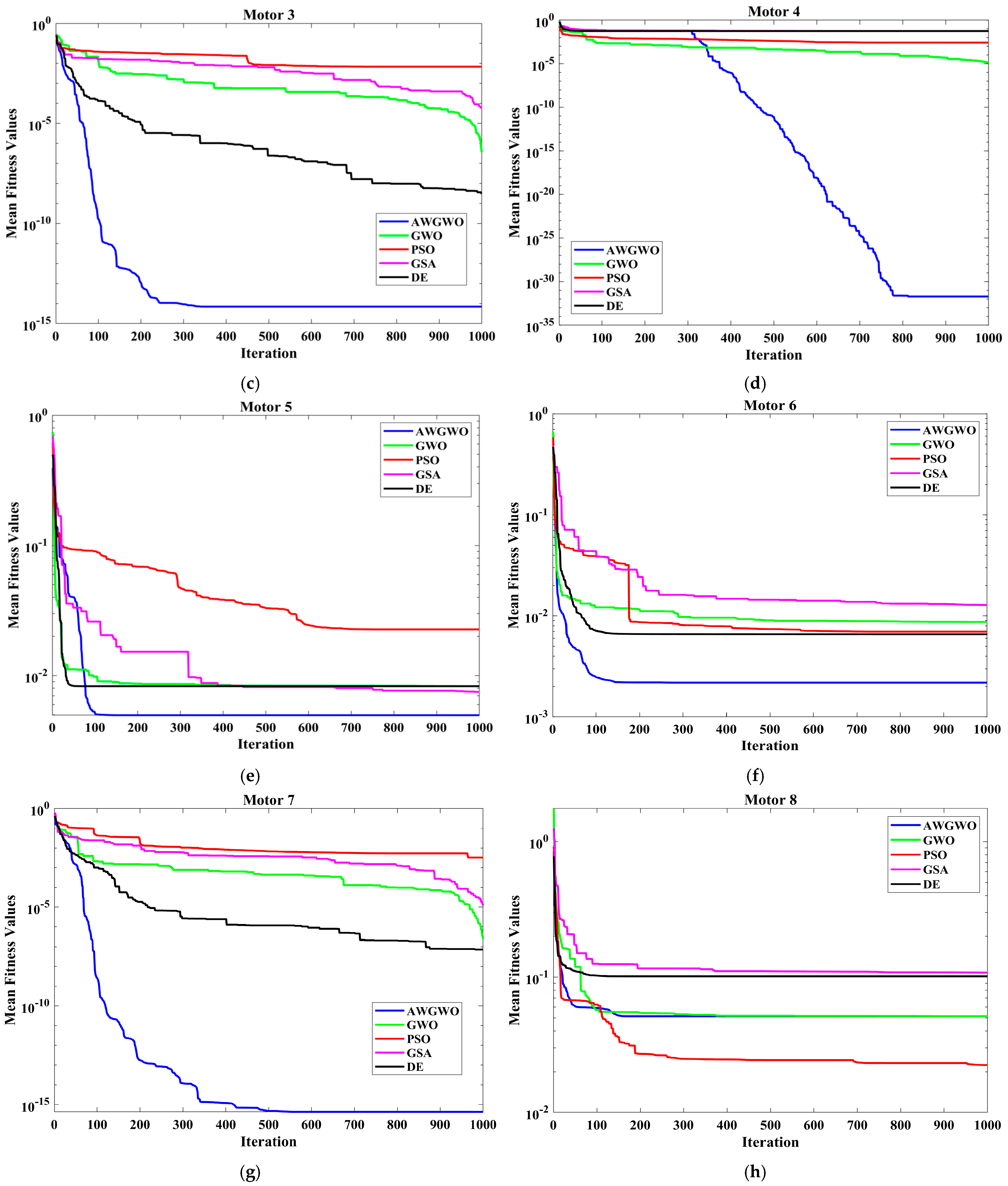
4.2.1. Results on Approximate Circuit Model
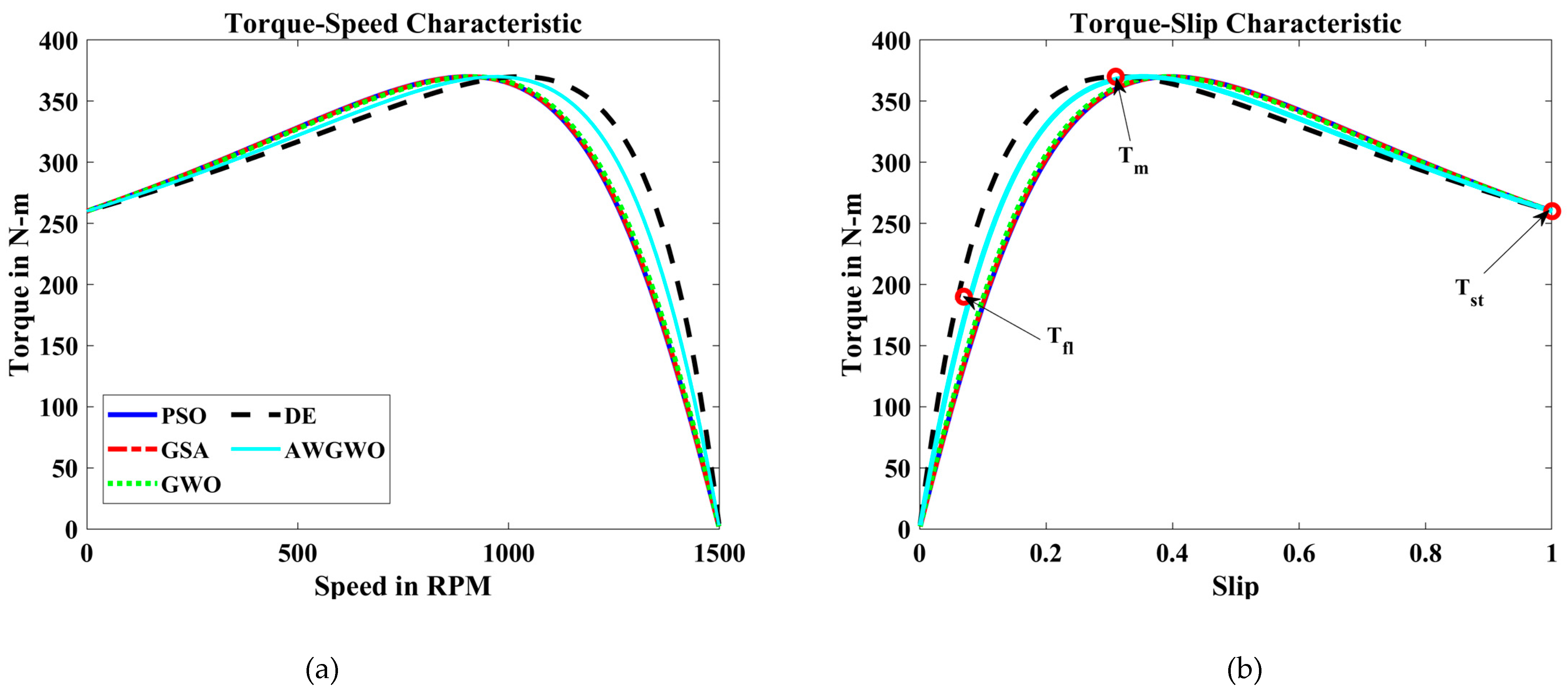
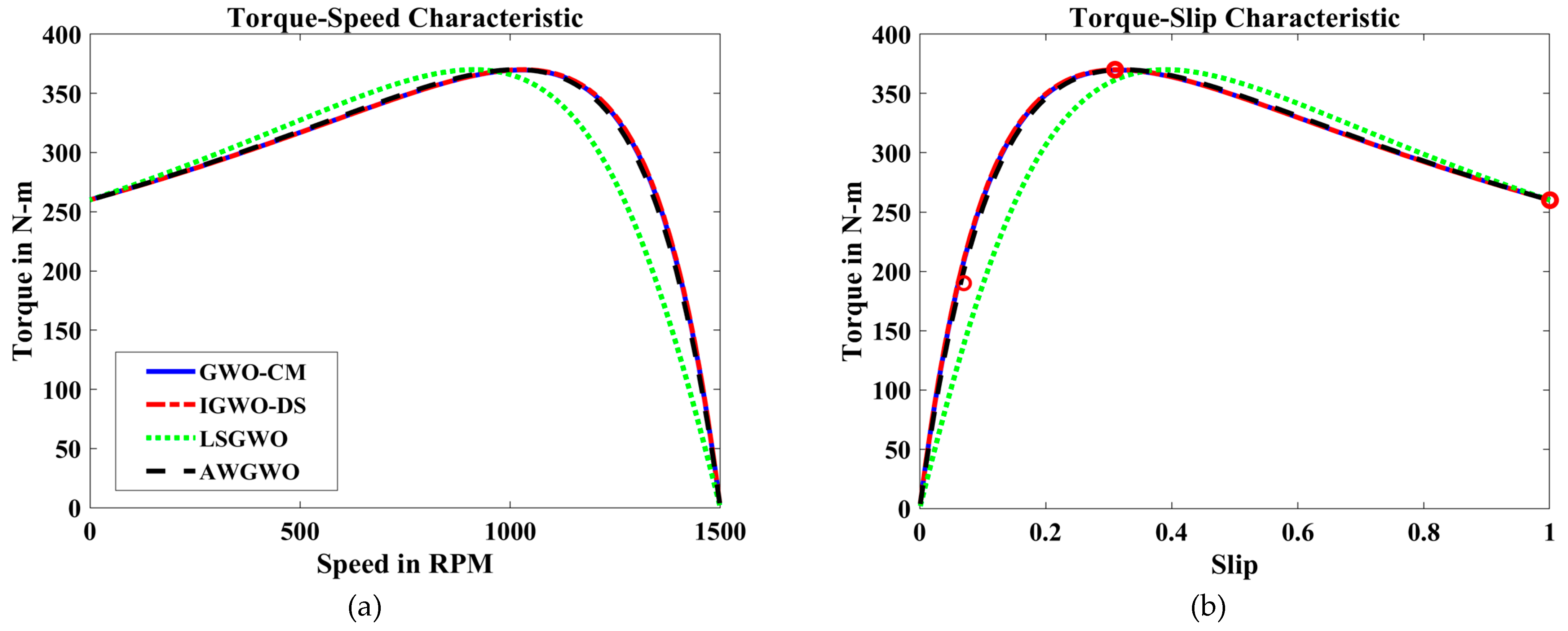
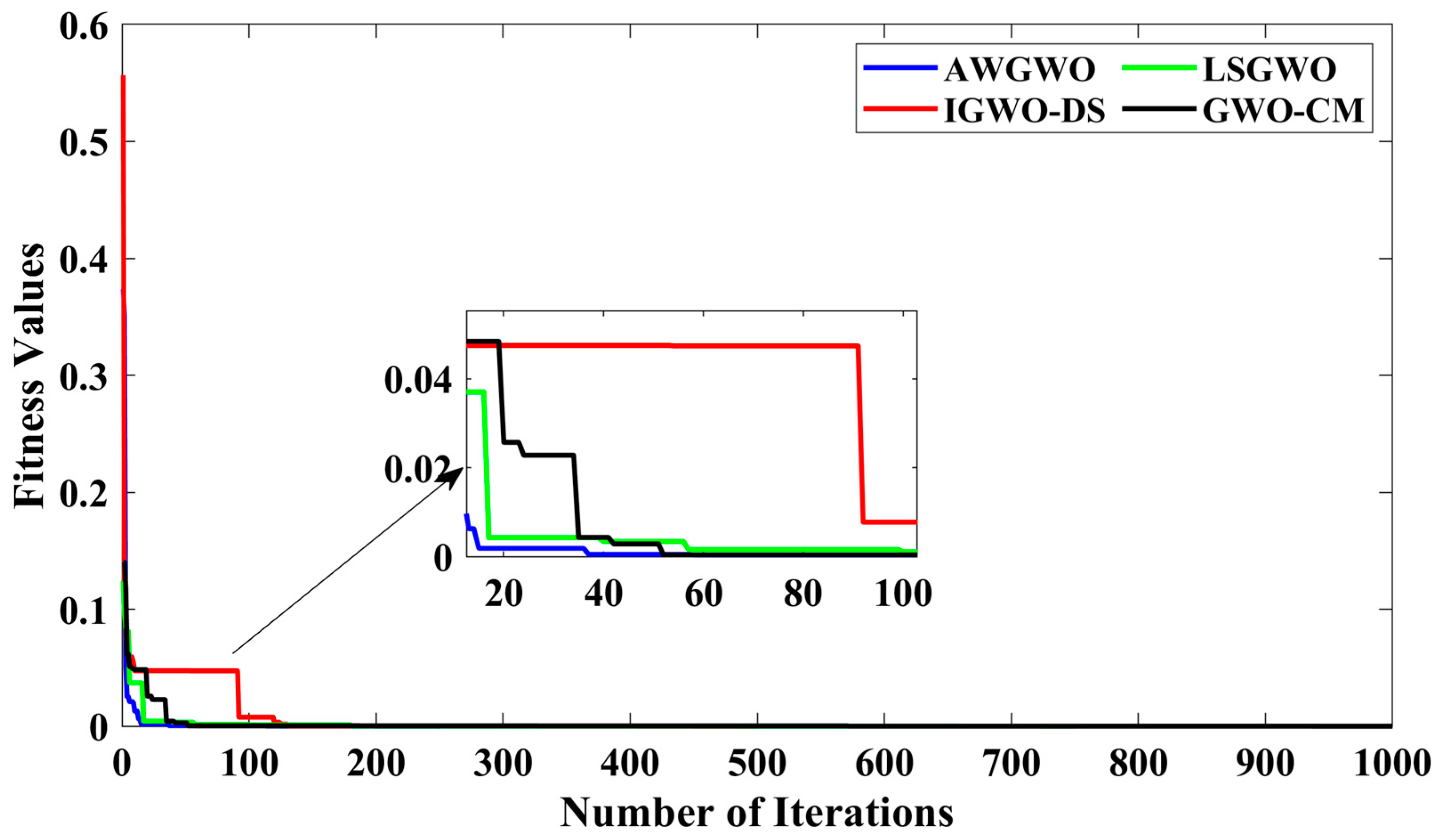
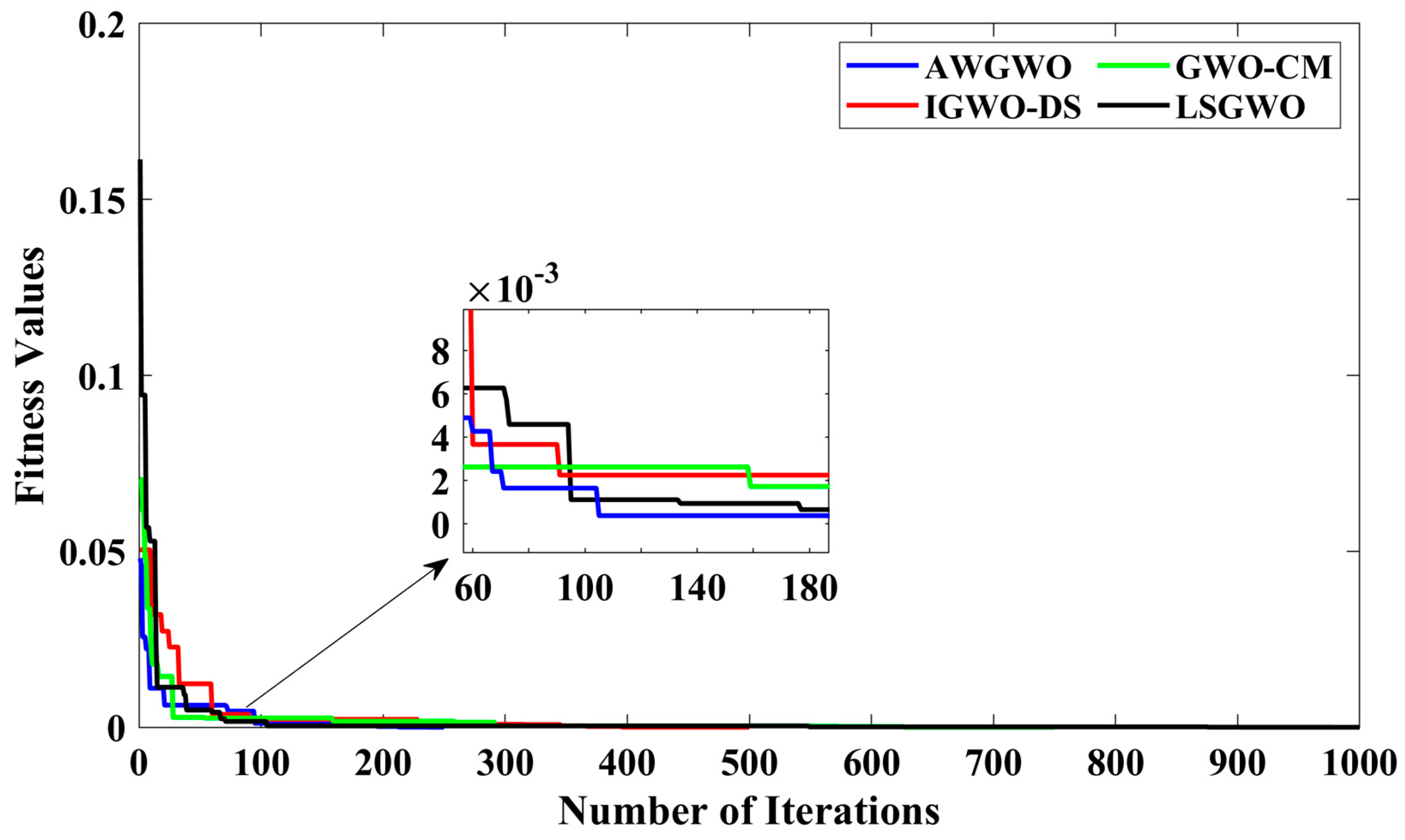
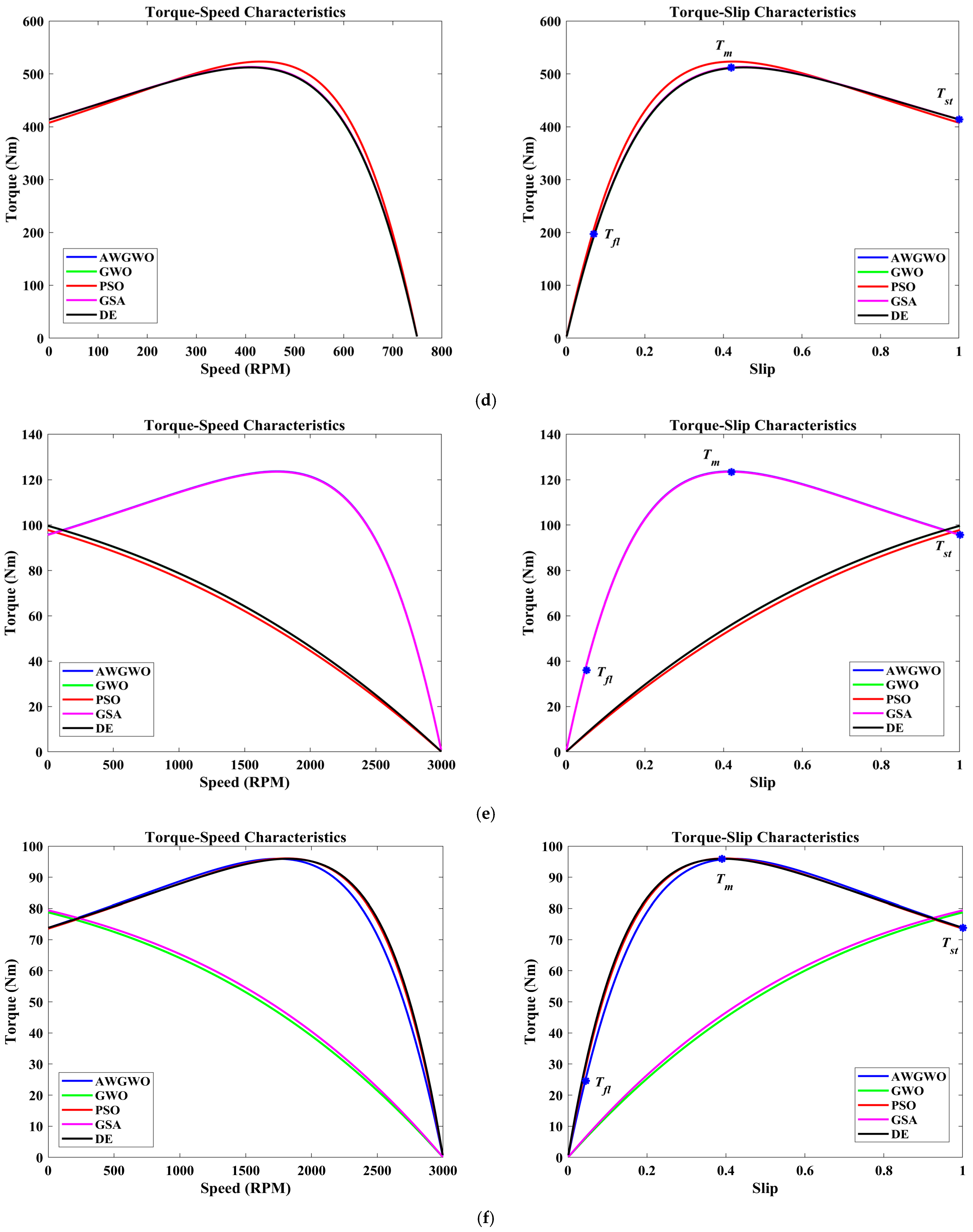
4.2.2. Results for Exact Circuit Model
4.3. Limitations and Challenges
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bhowmick, D.; Manna, M.; Chowdhury, S.K. Estimation of Equivalent Circuit Parameters of Transformer and Induction Motor from Load Data. IEEE Trans. Ind. Appl. 2018, 54, 2784–2791. [Google Scholar] [CrossRef]
- Koubaa, Y. Recursive Identification of Induction Motor Parameters. Simul. Model. Pract. Theory 2004, 12, 363–381. [Google Scholar] [CrossRef]
- Mossad, M.I.; Azab, M.; Abu-Siada, A. Transformer Parameters Estimation from Nameplate Data Using Evolutionary Programming Techniques. IEEE Trans. Power Deliv. 2014, 29, 2118–2123. [Google Scholar] [CrossRef]
- Al-Badri, M.; Pillay, P.; Angers, P. A Novel In Situ Efficiency Estimation Algorithm for Three-Phase IM Using GA, IEEE Method F1 Calculations, and Pretested Motor Data. IEEE Trans. Energy Convers. 2015, 30, 1092–1102. [Google Scholar] [CrossRef]
- Pedra, J.; Sainz, L. Parameter Estimation of Squirrel-Cage Induction Motors without Torque Measurements. IEE Proc. Electr. Power Appl. 2006, 153, 263–270. [Google Scholar] [CrossRef]
- Feyzi, M.R.; Sabahi, M. Online Dynamic Parameter Estimation of Transformer Equivalent Circuit. In Proceedings of the 2006 CES/IEEE 5th International Power Electronics and Motion Control Conference, Shanghai, China, 14–16 August 2006; pp. 1–5. [Google Scholar] [CrossRef]
- Zhang, H.; Gong, S.J.; Dong, Z.Z. On-Line Parameter Identification of Induction Motor Based on RLS Algorithm. In Proceedings of the 2013 International Conference on Electrical Machines and Systems (ICEMS), Busan, Republic of Korea, 26–29 October 2013; pp. 2132–2137. [Google Scholar] [CrossRef]
- Dineva, A.; Mosavi, A.; Ardabili, S.F.; Vajda, I.; Shamshirband, S.; Rabczuk, T.; Chau, K.W. Review of Soft Computing Models in Design and Control of Rotating Electrical Machines. Energies 2019, 12, 1049. [Google Scholar] [CrossRef]
- Peretti, L.; Zigliotto, M. Automatic Procedure for Induction Motor Parameter Estimation at Standstill. IET Electr. Power Appl. 2012, 6, 214–224. [Google Scholar] [CrossRef]
- Tang, J.; Yang, Y.; Blaabjerg, F.; Chen, J.; Diao, L.; Liu, Z. Parameter Identification of Inverter-Fed Induction Motors: A Review. Energies 2018, 11, 2194. [Google Scholar] [CrossRef]
- Odhano, S.A.; Pescetto, P.; Awan, H.A.A.; Hinkkanen, M.; Pellegrino, G.; Bojoi, R. Parameter Identification and Self-Commissioning in AC Motor Drives: A Technology Status Review. IEEE Trans. Power Electron. 2019, 34, 3603–3614. [Google Scholar] [CrossRef]
- Lindenmeyer, D.; Dommel, H.W.; Moshref, A.; Kundur, P. An Induction Motor Parameter Estimation Method. Int. J. Electr. Power Energy Syst. 2001, 23, 251–262. [Google Scholar] [CrossRef]
- Al-Jufout, S.A.; Al-Rousan, W.H.; Wang, C. Optimization of Induction Motor Equivalent Circuit Parameter Estimation Based on Manufacturer’s Data. Energies 2018, 11, 1792. [Google Scholar] [CrossRef]
- Haque, M.H. Determination of NEMA Design Induction Motor Parameters from Manufacturer Data. IEEE Trans. Energy Convers. 2008, 23, 997–1004. [Google Scholar] [CrossRef]
- Pedra, J.; Córcoles, F. Estimation of Induction Motor Double-Cage Model Parameters from Manufacturer Data. IEEE Trans. Energy Convers. 2004, 19, 310–317. [Google Scholar] [CrossRef]
- Helonde, A.R.; Mankar, M. Identifying Three Phase Induction Motor Equivalent Circuit Parameters from Nameplate Data by Different Analytical Methods. Int. J. Trend Sci. Res. Dev. 2019, 3, 642–645. [Google Scholar] [CrossRef]
- Pereira, L.A.; Perin, M.; Pereira, L.F.A. A New Method to Estimate Induction Machine Parameters from the No-Load Startup Transient. J. Control. Autom. Electr. Syst. 2019, 30, 41–53. [Google Scholar] [CrossRef]
- Mohammadi, H.R.; Akhavan, A. Parameter Estimation of Three-Phase Induction Motor Using Hybrid of Genetic Algorithm and Particle Swarm Optimization. J. Eng. 2014, 2014, 148204. [Google Scholar] [CrossRef]
- Zhu, H.Y.; Cheng, W.S.; Jia, Z.Z.; Hou, W.G. Parameter Estimation of Induction Motor Based on Chaotic Ant Swarm Algorithm. In Proceedings of the 2nd International Conference on Information Science and Engineering, Hangzhou, China, 4–6 December 2010; pp. 1370–1373. [Google Scholar] [CrossRef]
- Tekgun, B.; Sozer, Y.; Tsukerman, I. Modeling and Parameter Estimation of Split-Phase Induction Motors. IEEE Trans. Ind. Appl. 2016, 52, 1431–1440. [Google Scholar] [CrossRef]
- Sakthivel, V.P.; Bhuvaneswari, R.; Subramanian, S. Multi-Objective Parameter Estimation of Induction Motor Using Particle Swarm Optimization. Eng. Appl. Artif. Intell. 2010, 23, 302–312. [Google Scholar] [CrossRef]
- Ćalasan, M.; Micev, M.; Ali, Z.M.; Zobaa, A.F.; Aleem, S.H.E.A. Parameter Estimation of Induction Machine Single-Cage and Double-Cage Models Using a Hybrid Simulated Annealing–Evaporation Rate Water Cycle Algorithm. Mathematics 2020, 8, 1024. [Google Scholar] [CrossRef]
- Huynh, D.C.; Dunnigan, M.W. Parameter Estimation of An Induction Machine Using Advanced Particle Swarm Optimisation Algorithms. IET Electric Power Applications 2010, 4, 748–760. [Google Scholar] [CrossRef]
- Çanakoǧlu, A.I.; Yetgin, A.G.; Temurtaş, H.; Turan, M. Induction Motor Parameter Estimation Using Metaheuristic Methods. Turk. J. Electr. Eng. Comput. Sci. 2014, 22, 1177–1192. [Google Scholar] [CrossRef]
- Arslan, M.; Çunkaş, M.; Saǧ, T. Determination of Induction Motor Parameters with Differential Evolution Algorithm. Neural Comput. Appl. 2012, 21, 1995–2004. [Google Scholar] [CrossRef]
- Guedes, J.J.; Castoldi, M.F.; Goedtel, A.; Agulhari, C.M.; Sanches, D.S. Parameters Estimation of Three-Phase Induction Motors Using Differential Evolution. Electr. Power Syst. Res. 2018, 154, 204–212. [Google Scholar] [CrossRef]
- Wang, L.; Liu, Y. Application of Simulated Annealing Particle Swarm Optimization Based on Correlation in Parameter Identification of Induction Motor. Math. Probl. Eng. 2018, 2018, 1869232. [Google Scholar] [CrossRef]
- Accetta, A.; Alonge, F.; Cirrincione, M.; D’Ippolito, F.; Pucci, M.; Sferlazza, A. GA-Based off-Line Parameter Estimation of the Induction Motor Model Including Magnetic Saturation and Iron Losses. IEEE Open J. Ind. Appl. 2020, 1, 135–147. [Google Scholar] [CrossRef]
- Cuevas, E.; Barocio Espejo, E.; Conde Enríquez, A. Metaheuristic Schemes for Parameter Estimation in Induction Motors. Stud. Comput. Intell. 2019, 822, 9–22. [Google Scholar] [CrossRef]
- Aminu, M. A Parameter Estimation Algorithm for Induction Machines Using Artificial Bee Colony (ABC) Optimization. Niger. J. Technol. 2019, 38, 193–201. [Google Scholar] [CrossRef]
- Sharma, F.B.; Kapoor, S.R. Induction Motor Parameter Estimation Using Disrupted Black Hole Artificial Bee Colony Algorithm. Int. J. Metaheuristics 2017, 6, 85. [Google Scholar] [CrossRef]
- Rezk, H.; Elghany, A.A.; Al-Dhaifallah, M.; El Sayed, A.H.M.; Ibrahim, M.N. Numerical Estimation and Experimental Verification of Optimal Parameter Identification Based on Modern Optimization of a Three Phase Induction Motor. Mathematics 2019, 7, 1135. [Google Scholar] [CrossRef]
- Montano, J.; Garzón, O.D.; Herrera-Jaramillo, D.A.; Montoya, O.D.; Andrade, F.; Tobon, A. Estimating the Parameters of a Three-Phase Induction Motor Using the Vortex Search Algorithm. Iran. J. Sci. Technol. Trans. Electr. Eng. 2024, 48, 337–347. [Google Scholar] [CrossRef]
- Zorig, A.; Belkheiri, A.; Bendjedia, B.; Kouzi, K.; Belkheiri, M. New Identification of Induction Machine Parameters with a Meta-Heuristic Algorithm Based on Least Squares Method. COMPEL-Int. J. Comput. Math. Electr. Electron. Eng. 2023, 42, 1852–1866. [Google Scholar] [CrossRef]
- Abdelwanis, M.I.; Sehiemy, R.A.; Hamida, M.A. Hybrid Optimization Algorithm for Parameter Estimation of Poly-Phase Induction Motors with Experimental Verification. Energy AI 2021, 5, 100083. [Google Scholar] [CrossRef]
- Vukašinović, J.; Štatkić, S.; Milovanović, M.; Arsić, N.; Perović, B. Combined Method for the Cage Induction Motor Parameters Estimation Using Two-Stage PSO Algorithm. Electr. Eng. 2023, 105, 2703–2714. [Google Scholar] [CrossRef]
- Gutierrez-Villalobos, J.M.; Rodriguez-Resendiz, J.; Rivas-Araiza, E.A.; Mucino, V.H. A Review of Parameter Estimators and Controllers for Induction Motors Based on Artificial Neural Networks. Neurocomputing 2013, 118, 87–100. [Google Scholar] [CrossRef]
- Qi, X. Rotor Resistance and Excitation Inductance Estimation of an Induction Motor Using Deep-Q-Learning Algorithm. Eng. Appl. Artif. Intell. 2018, 72, 67–79. [Google Scholar] [CrossRef]
- Chaturvedi, D.K.; Singh, M.P.; Iqbal, M.S.; Singh, V.P. Estimation of Induction Motor Parameters: An Overview. Power Res.-A J. CPRI 2014, 10, 755–764. [Google Scholar]
- Cui, M.; Khodayar, M.; Chen, C.; Wang, X.; Zhang, Y.; Khodayar, M.E. Deep Learning-Based Time-Varying Parameter Identification for System-Wide Load Modeling. IEEE Trans. Smart Grid. 2019, 10, 6102–6114. [Google Scholar] [CrossRef]
- Drakaki, M.; Karnavas, Y.L.; Tziafettas, I.A.; Linardos, V.; Tzionas, P. Machine Learning and Deep Learning Based Methods toward Industry 4.0 Predictive Maintenance in Induction Motors: State of the Art Survey. J. Ind. Eng. Manag. 2022, 15, 31–57. [Google Scholar] [CrossRef]
- Laadjal, K.; Amaral, A.M.R.; Sahraoui, M.; Cardoso, A.J.M. Machine Learning Based Method for Impedance Estimation and Unbalance Supply Voltage Detection in Induction Motors. Sensors 2023, 23, 7989. [Google Scholar] [CrossRef]
- Jirdehi, M.A.; Rezaei, A. Parameters Estimation of Squirrel-Cage Induction Motors Using ANN and ANFIS. Alex. Eng. J. 2016, 55, 357–368. [Google Scholar] [CrossRef]
- Chaturvedi, D.K.; Singh, M.P. Online Equivalent Circuit Parameter Estimation of Three-Phase Induction Motor Using ANN. J. Inst. Eng. (India) Ser. B 2019, 100, 343–347. [Google Scholar] [CrossRef]
- Ipek, S.N.; Taskiran, M.; Bekiroglu, N.; Aycicek, E. Optimal Induction Machine Parameter Estimation Method with Artificial Neural Networks. Electr. Eng. 2024, 106, 1959–1975. [Google Scholar] [CrossRef]
- Lourenco, G.; De Arruda, G.T.; Correia De La Rosa, V.E.; Castoldi, M.F.; Goedtel, A.; De Souza, W.A. Three-Phase Induction Motor Electrical Parameter Estimation Using Artificial Neural Networks. In Proceedings of the 2024 International Symposium on Power Electronics, Electrical Drives, Automation and Motion, SPEEDAM, Napoli, Italy, 19–21 June 2024; pp. 883–888. [Google Scholar] [CrossRef]
- Montoya, O.D.; De Angelo, C.H.; Bossio, G. Parametric Estimation in Three-Phase Induction Motors Using Torque Data via the Generalized Normal Distribution Optimizer. Results Eng. 2024, 23, 102446. [Google Scholar] [CrossRef]
- Elkholy, M.M.; El-Hay, E.A.; El-Fergany, A.A. Synergy of Electrostatic Discharge Optimizer and Experimental Verification for Parameters Estimation of Three Phase Induction Motors. Eng. Sci. Technol. Int. J. 2022, 31, 101067. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Premkumar, M.; Sowmya, R.; Umashankar, S.; Jangir, P. Extraction of Uncertain Parameters of Single-Diode Photovoltaic Module Using Hybrid Particle Swarm Optimization and Grey Wolf Optimization Algorithm. Mater. Today Proc. 2021, 46, 5315–5321. [Google Scholar] [CrossRef]
- Xavier, F.J.; Pradeep, A.; Premkumar, M.; Kumar, C. Orthogonal Learning-Based Gray Wolf Optimizer for Identifying the Uncertain Parameters of Various Photovoltaic Models. Optik 2021, 247, 167973. [Google Scholar] [CrossRef]
- Premkumar, M.; Jangir, P.; Kumar, B.S.; Alqudah, M.A.; Nisar, K.S. Multi-Objective Grey Wolf Optimization Algorithm for Solving Real-World Bldc Motor Design Problem. Comput. Mater. Contin. 2022, 70, 2435–2452. [Google Scholar] [CrossRef]
- Wang, Z.; Fang, X.; Gao, F.; Xie, L.; Meng, X. An Adaptive Grey Wolf Optimization with Differential Evolution Operator for Solving the Discount {0-1} Knapsack Problem. Neural Comput. Appl. 2023, 1–17. [Google Scholar] [CrossRef]
- Asghari, K.; Masdari, M.; Gharehchopogh, F.S.; Saneifard, R. A Chaotic and Hybrid Gray Wolf-Whale Algorithm for Solving Continuous Optimization Problems. Prog. Artif. Intell. 2021, 10, 349–374. [Google Scholar] [CrossRef]
- Gu, W.; Zhou, B. Improved Grey Wolf Optimization Based on the Quantum-Behaved Mechanism. In Proceedings of the 2019 IEEE 4th Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), Chengdu, China, 20–22 December 2019; pp. 1537–1540. [Google Scholar] [CrossRef]
- Premkumar, M.; Sinha, G.; Ramasamy, M.D.; Sahu, S.; Subramanyam, C.B.; Sowmya, R.; Abualigah, L.; Derebew, B. Augmented Weighted K-Means Grey Wolf Optimizer: An Enhanced Metaheuristic Algorithm for Data Clustering Problems. Sci. Rep. 2024, 14, 5434. [Google Scholar] [CrossRef]
- Dhargupta, S.; Ghosh, M.; Mirjalili, S.; Sarkar, R. Selective Opposition Based Grey Wolf Optimization. Expert Syst. Appl. 2020, 151, 113389. [Google Scholar] [CrossRef]
- Sikkanan, S.; Kumar, C.; Manoharan, P.; Ravichandran, S. Exploring the Potential of 5G Uplink Communication: Synergistic Integration of Joint Power Control, User Grouping, and Multi-Learning Grey Wolf Optimizer. Sci. Rep. 2024, 14, 21406. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, R.; Rangaiah, G.P.; Mahadzir, S.; Mirjalili, S.; Hassan, M.H.; Kamel, S. Memory, Evolutionary Operator, and Local Search Based Improved Grey Wolf Optimizer with Linear Population Size Reduction Technique. Knowl. Based Syst. 2023, 264, 110297. [Google Scholar] [CrossRef]
- Nadimi-Shahraki, M.H.; Taghian, S.; Mirjalili, S. An Improved Grey Wolf Optimizer for Solving Engineering Problems. Expert Syst. Appl. 2021, 166, 113917. [Google Scholar] [CrossRef]
- Heidari, A.A.; Pahlavani, P. An Efficient Modified Grey Wolf Optimizer with Lévy Flight for Optimization Tasks. Appl. Soft Comput. 2017, 60, 115–134. [Google Scholar] [CrossRef]
- Gupta, S.; Deep, K. Hybrid Grey Wolf Optimizer with Mutation Operator. Adv. Intell. Syst. Comput. 2019, 817, 961–968. [Google Scholar] [CrossRef]
- Yue, Z.H.; Zhang, S.; Xiao, W.D. A Novel Hybrid Algorithm Based on Grey Wolf Optimizer and Fireworks Algorithm. Sensors 2020, 20, 2147. [Google Scholar] [CrossRef]
- Liu, X.; Tian, Y.; Lei, X.; Wang, H.; Liu, Z.; Wang, J. An Improved Self-Adaptive Grey Wolf Optimizer for the Daily Optimal Operation of Cascade Pumping Stations. Appl. Soft Comput. 2019, 75, 473–493. [Google Scholar] [CrossRef]
- Avalos, O.; Cuevas, E.; Gálvez, J. Induction Motor Parameter Identification Using a Gravitational Search Algorithm. Computers 2016, 5, 6. [Google Scholar] [CrossRef]




| Function | Dim | Range | fmin |
|---|---|---|---|
| 30 | [−100, 100] | 0 | |
| [−10, 10] | |||
| [−100, 100] | |||
| [−5.12, 5.12] | |||
| [−32, 32] | |||
| [−600, 600] | |||
| 2 | [−5, 5] | −1.0316 | |
| 0.398 | |||
| 4 | [0, 10] | −10.5363 |
| Functions | Metrics | AWGWO | GWO | LSGWO | DE | GSA | IGWO-DS | GWO-CM | PSO |
|---|---|---|---|---|---|---|---|---|---|
| Min | 4.63E-126 | 2.48E-29 | 8.43E-04 | 1.70E-04 | 2.56E-01 | 3.85E-111 | 4.20E-87 | 4.37E+02 | |
| Max | 6.78E-115 | 1.81E-27 | 1.51E+00 | 6.41E-04 | 6.86E+01 | 1.32E-97 | 8.30E-75 | 1.42E+04 | |
| Mean | 6.78E-116 | 7.67E-28 | 5.46E-01 | 3.01E-04 | 1.01E+01 | 1.80E-98 | 1.55E-75 | 4.38E+03 | |
| STD | 2.14E-115 | 5.37E-28 | 5.88E-01 | 1.62E-04 | 2.07E+01 | 4.16E-98 | 3.03E-75 | 5.67E+03 | |
| RT | 0.112 | 0.088 | 0.153 | 0.273 | 0.113 | 0.181 | 2.628 | 0.161 | |
| FRT | 1 | 4 | 6 | 5 | 7 | 2 | 3 | 8 | |
| Min | 2.70E-65 | 2.37E-17 | 1.12E-01 | 2.26E-03 | 7.54E-04 | 6.03E-57 | 4.66E-57 | 5.57E+00 | |
| Max | 3.55E-59 | 1.86E-16 | 3.24E+00 | 7.05E-03 | 5.82E-02 | 5.03E-51 | 3.15E-50 | 5.33E+01 | |
| Mean | 4.20E-60 | 1.00E-16 | 1.05E+00 | 4.44E-03 | 1.17E-02 | 6.01E-52 | 3.23E-51 | 2.61E+01 | |
| STD | 1.12E-59 | 6.33E-17 | 1.04E+00 | 1.20E-03 | 1.70E-02 | 1.58E-51 | 9.93E-51 | 1.34E+01 | |
| RT | 0.103 | 0.08 | 0.16 | 0.19 | 0.12 | 0.16 | 2.61 | 0.15 | |
| FRT | 1 | 4 | 7 | 5.4 | 5.6 | 2.5 | 2.5 | 8 | |
| Min | 1.69E-104 | 1.26E-08 | 8.64E-01 | 3.18E+04 | 1.44E+03 | 9.36E-96 | 1.66E+04 | 9.96E+03 | |
| Max | 6.71E-93 | 2.79E-04 | 3.91E+01 | 4.61E+04 | 1.87E+04 | 6.06E-78 | 6.65E+04 | 5.19E+04 | |
| Mean | 6.72E-94 | 3.04E-05 | 2.30E+01 | 3.91E+04 | 7.45E+03 | 7.81E-79 | 4.96E+04 | 2.91E+04 | |
| STD | 2.12E-93 | 8.76E-05 | 1.10E+01 | 4.64E+03 | 5.01E+03 | 1.93E-78 | 1.68E+04 | 1.43E+04 | |
| RT | 0.22 | 0.18 | 0.24 | 0.27 | 0.29 | 0.29 | 2.66 | 0.25 | |
| FRT | 1 | 3 | 4 | 7 | 5.1 | 2 | 7.6 | 6.3 | |
| Min | 2.93E-57 | 1.07E-07 | 7.17E-02 | 5.28E+00 | 2.34E+01 | 1.98E-58 | 6.18E-01 | 5.84E+01 | |
| Max | 4.86E-52 | 3.05E-06 | 1.29E+00 | 1.10E+01 | 5.32E+01 | 2.23E-48 | 8.48E+01 | 8.27E+01 | |
| Mean | 6.27E-53 | 1.05E-06 | 5.40E-01 | 7.66E+00 | 3.96E+01 | 3.00E-49 | 4.29E+01 | 7.08E+01 | |
| STD | 1.55E-52 | 1.11E-06 | 3.27E-01 | 1.80E+00 | 9.86E+00 | 6.89E-49 | 3.49E+01 | 6.46E+00 | |
| RT | 0.15 | 0.09 | 0.17 | 0.18 | 0.21 | 0.27 | 2.53 | 0.26 | |
| FRT | 1.2 | 3 | 4 | 5.3 | 6.4 | 1.8 | 6.6 | 7.7 | |
| Min | 0.00E+00 | 5.68E-14 | 6.98E-03 | 1.40E+02 | 1.11E+01 | 0.00E+00 | 0.00E+00 | 1.07E+02 | |
| Max | 0.00E+00 | 1.10E+01 | 4.89E+01 | 1.67E+02 | 5.87E+01 | 0.00E+00 | 0.00E+00 | 1.74E+02 | |
| Mean | 0.00E+00 | 3.95E+00 | 1.85E+01 | 1.57E+02 | 3.58E+01 | 0.00E+00 | 0.00E+00 | 1.41E+02 | |
| STD | 0.00E+00 | 4.20E+00 | 1.92E+01 | 8.79E+00 | 1.87E+01 | 0.00E+00 | 0.00E+00 | 2.02E+01 | |
| RT | 0.12 | 0.09 | 0.15 | 0.18 | 0.17 | 0.19 | 2.58 | 0.17 | |
| FRT | 1.65 | 4 | 6.1 | 5 | 7.5 | 1.65 | 2.7 | 7.4 | |
| Min | 4.44E-16 | 9.28E-14 | 1.20E-02 | 3.65E-03 | 7.39E-02 | 4.44E-16 | 4.44E-16 | 1.77E+01 | |
| Max | 4.44E-16 | 1.39E-13 | 3.50E+00 | 7.98E-03 | 2.03E+01 | 4.44E-16 | 7.55E-15 | 2.00E+01 | |
| Mean | 4.44E-16 | 1.09E-13 | 1.04E+00 | 5.00E-03 | 1.39E+01 | 4.44E-16 | 3.64E-15 | 1.97E+01 | |
| STD | 0.00E+00 | 1.28E-14 | 1.18E+00 | 1.35E-03 | 9.02E+00 | 0.00E+00 | 2.62E-15 | 7.02E-01 | |
| RT | 0.15 | 0.10 | 0.16 | 0.19 | 0.21 | 0.29 | 2.49 | 0.28 | |
| FRT | 2.4 | 3 | 5.7 | 5.1 | 7 | 2.4 | 2.4 | 8 | |
| Min | 0.00E+00 | 0.00E+00 | 5.27E-06 | 2.88E-04 | 5.67E-01 | 0.00E+00 | 0.00E+00 | 6.31E+00 | |
| Max | 0.00E+00 | 1.76E-02 | 4.39E-02 | 4.64E-02 | 1.21E+00 | 0.00E+00 | 0.00E+00 | 2.31E+01 | |
| Mean | 0.00E+00 | 2.90E-03 | 1.61E-02 | 7.02E-03 | 9.23E-01 | 0.00E+00 | 0.00E+00 | 1.17E+01 | |
| STD | 0.00E+00 | 6.28E-03 | 1.52E-02 | 1.45E-02 | 2.02E-01 | 0.00E+00 | 0.00E+00 | 5.03E+00 | |
| RT | 0.14 | 0.11 | 0.17 | 0.15 | 0.19 | 0.21 | 2.58 | 0.18 | |
| FRT | 1.2 | 5.8 | 4.2 | 3.1 | 7.2 | 1.8 | 4.9 | 7.8 | |
| Min | −1.0316 | −1.0316 | −1.0316 | −1.0316 | −1.0316 | −1.0316 | −1.0316 | −1.0316 | |
| Max | −1.0316 | −1.0316 | −1.0316 | −1.0316 | −1.0315 | −1.0316 | −1.0316 | −1.0316 | |
| Mean | −1.0316 | −1.0316 | −1.0316 | −1.0316 | −1.0316 | −1.0316 | −1.0316 | −1.0316 | |
| STD | 1.05E-16 | 1.05E-08 | 2.22E-16 | 0.00E+00 | 3.21E-05 | 8.18E-10 | 8.11E-10 | 7.40E-17 | |
| RT | 0.09 | 0.02 | 0.11 | 0.14 | 0.13 | 0.17 | 2.51 | 0.12 | |
| FRT | 2.5 | 6.2 | 2.5 | 2.5 | 8 | 5.9 | 5.9 | 2.5 | |
| Min | 0.3979 | 0.3979 | 0.3979 | 0.3979 | 0.3980 | 0.3979 | 0.3979 | 0.3979 | |
| Max | 0.3979 | 0.3979 | 0.3979 | 0.3979 | 0.4056 | 0.3979 | 0.3979 | 0.3979 | |
| Mean | 0.3979 | 0.3979 | 0.3979 | 0.3979 | 0.4004 | 0.3979 | 0.3979 | 0.3979 | |
| STD | 0.00E+00 | 5.23E-06 | 0.00E+00 | 0.00E+00 | 2.46E-03 | 1.31E-05 | 7.24E-06 | 0.00E+00 | |
| RT | 0.07 | 0.01 | 0.09 | 0.11 | 0.11 | 0.15 | 2.60 | 0.11 | |
| FRT | 2.3 | 6.7 | 3.85 | 1.4 | 7.5 | 4.9 | 6.5 | 2.85 | |
| Min | −10.5364 | −10.5360 | −10.5364 | −10.5364 | −7.6146 | −5.1280 | −10.5362 | −10.5364 | |
| Max | −5.1285 | −10.5333 | −5.1285 | −10.5364 | −0.9424 | −5.0997 | −5.1223 | −1.8595 | |
| Mean | −8.3732 | −10.5349 | −8.9235 | −10.5364 | −4.7679 | −5.1222 | −8.6365 | −7.4206 | |
| STD | 2.79E+00 | 8.02E-04 | 2.60E+00 | 1.87E-15 | 2.03E+00 | 8.67E-03 | 2.55E+00 | 4.05E+00 | |
| RT | 0.13 | 0.05 | 0.14 | 0.19 | 0.16 | 0.21 | 2.51 | 0.15 | |
| FRT | 3.45 | 4 | 3.8 | 1.2 | 6.9 | 6.9 | 5.2 | 4.55 | |
| Mean FRT | 1.77 | 4.37 | 4.715 | 4.1 | 6.82 | 3.185 | 4.73 | 6.31 | |
| S. No. | Parameters | Specification |
|---|---|---|
| 1 | Current (Ifl) in A | 45 |
| 2 | Voltage (Vfl) in V | 400 |
| 3 | Power (Pfl) in HP | 40 |
| 4 | Number of poles | 4 |
| 5 | Frequency (F) in Hz | 50 |
| 6 | Starting current (Ist) in A | 180 |
| 7 | Full-load torque (Tfl) in N-m | 190 |
| 8 | Maximum-load torque (Tm) in N-m | 370 |
| 9 | Starting torque (Tst) in N-m | 260 |
| 10 | Full-load slip (sfl) in % | 9 |
| Algorithms | (Ω) | (Ω) | (Ω) | Fitness Function Value | |
|---|---|---|---|---|---|
| PSO | 0.1025 | 0.9874 | 0.5046 | 0.1048 | 1.0495 × 10−7 |
| GSA | 0.1156 | 0.9815 | 0.4988 | 0.1040 | 9.2153 × 10−8 |
| GWO | 0.1502 | 0.9759 | 0.4794 | 0.1011 | 8.8727 × 10−8 |
| DE | 0.5994 | 0.4943 | 0.2439 | 0.0608 | 4.8692 × 10−8 |
| ABC [31] | 1.693 | 0.759 | 1.526 | NA | NA |
| BSFABC [31] | 1.968 | 0.7984 | 1 | NA | NA |
| EABC [31] | 1.403 | 0.823 | 2.033 | NA | NA |
| DBHABC [31] | 1.382 | 0.751 | 1 | NA | NA |
| AWGWO | 0.3919 | 0.9032 | 03480 | 0.0799 | 4.3342 × 10−8 |
| Algorithms | (Nm) | (Nm) | (Nm) | |||
|---|---|---|---|---|---|---|
| PSO | 189.8076 | 0.1924 | 370.1391 | −0.1391 | 260.0900 | −0.09 |
| GSA | 190.0097 | −0.0097 | 369.7911 | 0.2089 | 259.9513 | 0.0487 |
| GWO | 189.9144 | 0.0856 | 369.8451 | 0.1549 | 259.9170 | 0.0830 |
| DE | 189.9132 | 0.0868 | 369.9557 | 0.0443 | 259.9310 | 0.0691 |
| ABC [31] | 194.774 | −2.513 | 360.576 | 2.547 | 260.656 | −0.252 |
| BSFABC [31] | 181.6591 | 4.39 | 343.0155 | 7.293 | 264.3033 | 1.655 |
| EABC [31] | 189.927 | 0.039 | 369.85 | 0.041 | 259.483 | 0.199 |
| DBHABC [31] | 189.953 | 0.0247 | 369.857 | 0.0386 | 260.556 | 0.2138 |
| AWGWO | 190.2889 | −0.2889 | 370.3286 | −0.3286 | 260.3685 | −0.3685 |
| Algorithms | RT | ||||
|---|---|---|---|---|---|
| PSO | 1.049E-07 | 7.093E-06 | 2.573E-07 | 2.799E-06 | 12.1744 |
| GSA | 9.2153E-08 | 2.533E-07 | 1.284E-07 | 7.157E-08 | 14.7143 |
| GWO | 8.8727E-08 | 4.725E-02 | 9.450E-03 | 2.113E-02 | 15.6507 |
| DE | 4.8692E-08 | 8.283E-08 | 6.735E-08 | 7.378E-08 | 15.5205 |
| AWGWO | 4.3342E-08 | 1.884E-07 | 5.485E-08 | 6.202E-08 | 16.7774 |
| Algorithms | (Ω) | (Ω) | (Ω) | Fitness Function Value | |
|---|---|---|---|---|---|
| LSGWO | 0.5964 | 0.5043 | 0.2463 | 0.0613 | 8.7309 × 10−7 |
| GWO-CM | 0.6000 | 0.4927 | 0.2437 | 0.0608 | 5.6671 × 10−8 |
| IGWO-DS | 0.3888 | 0.9149 | 0.3541 | 0.0678 | 4.7220 × 10−8 |
| AWGWO | 0.3919 | 0.9032 | 0.3480 | 0.0799 | 4.3342 × 10−8 |
| Algorithms | (Nm) | (Nm) | (Nm) | |||
|---|---|---|---|---|---|---|
| LSGWO | 189.1575 | 0.8425 | 370.3082 | −0.3082 | 261.4844 | −1.4844 |
| GWO-CM | 189.8839 | 0.1161 | 369.8744 | 0.1256 | 259.8014 | 0.1986 |
| IGWO-DS | 189.8787 | 0.1213 | 370.1823 | −0.1823 | 260.2970 | −0.2970 |
| AWGWO | 190.2889 | −0.2889 | 370.3286 | −0.3286 | 260.2685 | −0.2685 |
| Algorithms | RT | ||||
|---|---|---|---|---|---|
| LSGWO | 8.7309E-07 | 4.725E-02 | 9.451E-03 | 2.113E-02 | 17.0214 |
| GWO-CM | 5.6671E-08 | 3.178E-07 | 1.609E-07 | 1.212E-07 | 23.7065 |
| IGWO-DS | 4.7220E-08 | 4.339E-07 | 1.472E-07 | 1.724E-07 | 35.2150 |
| AWGWO | 4.3342E-08 | 1.884E-07 | 5.485E-08 | 6.202E-08 | 16.7774 |
| Algorithms | (Ω) | (Ω) | (Ω) | (Ω) | (Ω) | (%) | Fitness |
|---|---|---|---|---|---|---|---|
| PSO | 0.1819 | 0.1279 | 0.4413 | 0.9994 | 5.8727 | 0.0983 | 4.1630 × 10−7 |
| GSA | 0.4263 | 0.2841 | 0.3050 | 0.4894 | 7.3919 | 0.0768 | 2.5620 × 10−7 |
| GWO | 0.4387 | 0.2735 | 0.2873 | 0.4437 | 4.7941 | 0.0756 | 2.4504 × 10−7 |
| DE | 0.4372 | 0.2894 | 0.2987 | 0.4632 | 7.1306 | 0.0758 | 1.3056 × 10−7 |
| GA [22] | 0.4875 | 0.3264 | 0.3556 | 0.3556 | 6.6072 | NA | 3.5000 × 10−3 |
| SFLA [22] | 0.3437 | 0.3360 | 0.4345 | 0.4345 | 6.2629 | NA | 1.1000 × 10−3 |
| MSFLA [22] | 0.2707 | 0.3573 | 0.4773 | 0.4773 | 7.5432 | NA | 2.8000 × 10−4 |
| ABC [31] | 1.732 | 0.1 | 0.803 | 1.44 | 400 | NA | NA |
| BSFABC [31] | 1.508 | 1.84 | 0.892 | 0.12 | 400 | NA | NA |
| EABC [31] | 1.403 | 0.1 | 0.824 | 1.93 | 400 | NA | NA |
| DBHABC [31] | 1.217 | 0.10 | 0.773 | 0.10 | 400 | NA | NA |
| AWGWO | 0.3977 | 0.2357 | 0.2981 | 0.5150 | 3.4079 | 0.0794 | 1.1026 × 10−8 |
| Algorithms | (Nm) | (Nm) | (Nm) | |||||
|---|---|---|---|---|---|---|---|---|
| PSO | 189.8591 | 0.1409 | 370.0899 | −0.0899 | 260.2098 | −0.2098 | 0.8004 | −4.1427 × 10−4 |
| GSA | 189.7253 | 0.2747 | 370.0843 | −0.0843 | 260.1523 | −0.1523 | 0.7993 | 6.6217 × 10−4 |
| GWO | 190.1486 | −0.1486 | 370.4367 | −0.4367 | 260.1793 | −0.1793 | 0.8001 | −1.1833 × 10−4 |
| DE | 189.9056 | 0.0944 | 370.0152 | −0.0152 | 260.1370 | −0.1370 | 0.8000 | −4.2484 × 10−5 |
| GA [22] | 192.7880 | 2.7880 | 354.0920 | 15.9080 | 268.0160 | 8.0160 | 0.8170 | 0.0170 |
| SFLA [22] | 195.1060 | 5.1060 | 368.0360 | 1.9640 | 262.4670 | 2.4670 | 0.7860 | 0.0140 |
| MSFLA [22] | 192.1970 | 2.1970 | 373.852 | 3.8520 | 261.6870 | 1.6870 | 0.7995 | 0.0005 |
| ABC [31] | 185.846 | 2.186 | 353.752 | 4.391 | 261.725 | −0.664 | NA | NA |
| BSFABC [31] | 174.979 | 7.906 | 358.528 | 3.101 | 266.194 | −2.382 | NA | NA |
| EABC [31] | 189.752 | 0.131 | 370.075 | −0.02 | 260.013 | −0.005 | NA | NA |
| DBHABC [31] | 190.734 | 0.374 | 369.081 | 0.248 | 259.991 | 0.0034 | NA | NA |
| AWGWO | 189.7910 | 0.2090 | 370.1063 | −0.1063 | 260.2997 | −0.2997 | 0.8003 | −3.1990 × 10−4 |
| Algorithms | RT | ||||
|---|---|---|---|---|---|
| PSO | 4.1630E-07 | 2.812E-06 | 9.313E-07 | 1.055E-06 | 14.1569 |
| GSA | 2.5620E-07 | 9.683E-07 | 3.011E-07 | 1.241E-07 | 18.5698 |
| GWO | 2.4504E-07 | 6.607E-07 | 2.120E-07 | 1.162E-07 | 19.9856 |
| DE | 1.3056E-07 | 3.004E-07 | 1.202E-07 | 4.558E-08 | 16.6944 |
| AWGWO | 1.1026E-08 | 4.582E-07 | 9.453E-07 | 1.906E-09 | 20.2568 |
| Algorithms | (Ω) | (Ω) | (Ω) | (Ω) | (Ω) | Fitness Function Value | |
|---|---|---|---|---|---|---|---|
| LSGWO | 0.3191 | 0.2238 | 0.3699 | 0.7352 | 9.9167 | 0.0866 | 8.8038 × 10−7 |
| GWO-CM | 0.2756 | 0.1129 | 0.3066 | 0.6423 | 0.9465 | 0.0902 | 2.4099 × 10−7 |
| IGWO-DS | 0.1902 | 0.1369 | 0.4437 | 0.9990 | 9.5711 | 0.0976 | 8.0533 × 10−8 |
| AWGWO | 0.3977 | 0.2357 | 0.2981 | 0.5150 | 3.4079 | 0.0794 | 1.1026 × 10−8 |
| Algorithms | (Nm) | (Nm) | (Nm) | |||||
|---|---|---|---|---|---|---|---|---|
| LSGWO | 189.5157 | 0.4843 | 369.8549 | 0.1451 | 259.6347 | 0.3653 | 0.8022 | −0.00220 |
| GWO-CM | 189.3420 | 0.6580 | 369.8387 | 0.1613 | 260.5639 | −0.5639 | 0.7997 | 2.5406 × 10−6 |
| IGWO-DS | 190.2779 | −0.2779 | 370.1230 | −0.1230 | 259.9000 | 0.1000 | 0.8002 | −1.6099 × 10−4 |
| AWGWO | 189.7910 | 0.2090 | 370.1063 | −0.1063 | 260.2997 | −0.2997 | 0.8003 | −3.1990 × 10−4 |
| Algorithm | RT | ||||
|---|---|---|---|---|---|
| LSGWO | 8.089E-07 | 5.553E-06 | 3.040E-06 | 1.871E-06 | 20.4125 |
| GWO-CM | 1.579E-07 | 8.094E-07 | 4.855E-07 | 2.766E-07 | 24.1456 |
| IGWO-DS | 8.053E-08 | 6.094E-07 | 2.713E-07 | 2.105E-07 | 26.7845 |
| AWGWO | 7.505E-08 | 8.158E-07 | 1.037E-07 | 3.092E-08 | 20.2568 |
| Specifications | Motor 1 | Motor 2 | Motor 3 | Motor 4 | Motor 5 | Motor 6 | Motor 7 | Motor 8 |
|---|---|---|---|---|---|---|---|---|
| Vfl in V | 400 | 415 | 415 | 415 | 230 | 230 | 230 | 230 |
| Pfl in kW | 37 | 30 | 22 | 15 | 11 | 7.5 | 3 | 3 |
| F in Hz | 50 | 50 | 50 | 50 | 50 | 50 | 50 | 50 |
| ηfl | 0.962 | 0.925 | 0.912 | 0.85 | 0.912 | 0.901 | 0.871 | 0.871 |
| Ifl in A | 64 | 52.8 | 42 | 31.2 | 19.2 | 13.1 | 9.3 | 10.2 |
| cosφ | 0.87 | 0.87 | 0.83 | 0.81 | 0.91 | 0.9 | 0.9 | 0.85 |
| Speed in RPM | 1470 | 1470 | 970 | 730 | 2943 | 2909 | 2896 | 2915 |
| Tfl in Nm | 240.46 | 195 | 218 | 197 | 36 | 24.6 | 9.9 | 9.83 |
| Ist/Ifl | 6 | 6.8 | 6.4 | 6 | 8 | 8.3 | 8.4 | 8.3 |
| Tm/Tfl | 2.5 | 2.7 | 2.8 | 2.6 | 3.6 | 3.9 | 3.9 | 3.3 |
| Tst/Tfl | 2.2 | 2.4 | 2.3 | 2.1 | 2.6 | 3 | 3.2 | 2 |
| Motor No. | Algorithms | (Ω) | (Ω) | (Ω) | (Ω) | (Ω) | Best Fitness | |
|---|---|---|---|---|---|---|---|---|
| Motor 1 | AWGWO | 0.2656 | 0.1275 | 0.2913 | 0.3417 | 3.7763 | 0.0866 | 8.85E-24 |
| GWO | 0.2490 | 0.1213 | 0.3036 | 0.3771 | 3.8691 | 0.0891 | 7.58E-08 | |
| PSO | 0.2683 | 0.1272 | 0.2982 | 0.3411 | 3.7393 | 0.0887 | 4.60E-05 | |
| GSA | 0.2539 | 0.1290 | 0.3049 | 0.3725 | 5.3651 | 0.0883 | 1.70E-06 | |
| DE | 0.2903 | 0.1547 | 0.2872 | 0.3020 | 11.0000 | 0.0828 | 4.21E-17 | |
| Motor 2 | AWGWO | 0.3372 | 0.1644 | 0.3623 | 0.3999 | 5.2755 | 0.0798 | 3.310E-12 |
| GWO | 0.3061 | 0.1528 | 0.3863 | 0.4680 | 5.6533 | 0.0834 | 2.513E-07 | |
| PSO | 0.2215 | 0.1000 | 0.4199 | 0.5914 | 1.9850 | 0.0929 | 7.086E-05 | |
| GSA | 0.3202 | 0.1274 | 0.3497 | 0.4086 | 2.2396 | 0.0816 | 2.530E-06 | |
| DE | 0.3137 | 0.1651 | 0.3900 | 0.4626 | 9.9066 | 0.0826 | 3.737E-12 | |
| Motor 3 | AWGWO | 0.2471 | 0.1533 | 0.5137 | 0.8643 | 6.6287 | 0.0783 | 1.580E-22 |
| GWO | 0.2189 | 0.1359 | 0.5313 | 0.9157 | 5.8951 | 0.0804 | 7.973E-08 | |
| PSO | 0.4901 | 0.1447 | 0.3087 | 0.3260 | 1.7213 | 0.0598 | 9.839E-04 | |
| GSA | 0.4390 | 0.2538 | 0.3795 | 0.4583 | 6.2687 | 0.0630 | 2.320E-06 | |
| DE | 0.4811 | 0.2814 | 0.3594 | 0.3668 | 7.4043 | 0.0601 | 1.502E-10 | |
| Motor 4 | AWGWO | 0.5997 | 0.3344 | 0.6000 | 0.8473 | 4.7252 | 0.0720 | 0.000E+00 |
| GWO | 0.5974 | 0.3179 | 0.5886 | 0.8336 | 3.9921 | 0.0721 | 9.837E-08 | |
| PSO | 0.5661 | 0.3631 | 0.6000 | 0.9318 | 9.3455 | 0.0665 | 6.946E-04 | |
| GSA | 0.5973 | 0.3231 | 0.5901 | 0.8372 | 4.2305 | 0.0718 | 3.497E-06 | |
| DE | 0.5995 | 0.3341 | 0.6000 | 0.8475 | 4.7147 | 0.0720 | 4.386E-14 | |
| Motor 5 | AWGWO | 0.1921 | 0.1000 | 0.2000 | 0.3377 | 10.0000 | 0.0482 | 3.857E-03 |
| GWO | 0.2142 | 0.1000 | 1.0000 | 0.3000 | 4.7803 | 0.2489 | 8.289E-03 | |
| PSO | 0.1981 | 0.1000 | 1.0000 | 0.3000 | 2.1635 | 0.2622 | 1.033E-02 | |
| GSA | 0.1916 | 0.1000 | 0.2000 | 0.3376 | 8.5397 | 0.0484 | 4.076E-03 | |
| DE | 0.2145 | 0.1000 | 1.0000 | 0.3000 | 4.8941 | 0.2487 | 8.289E-03 | |
| Motor 6 | AWGWO | 0.2194 | 0.1004 | 0.2710 | 0.5039 | 9.9975 | 0.0436 | 1.671E-16 |
| GWO | 0.3122 | 0.1000 | 1.0000 | 0.3000 | 1.4261 | 0.1937 | 8.718E-03 | |
| PSO | 0.2927 | 0.1000 | 0.2000 | 0.3000 | 1.6483 | 0.0374 | 5.155E-04 | |
| GSA | 0.3353 | 0.1044 | 1.0000 | 0.3000 | 2.1043 | 0.1841 | 9.982E-03 | |
| DE | 0.3165 | 0.1410 | 0.2140 | 0.3010 | 9.7443 | 0.0358 | 3.456E-12 | |
| Motor 7 | AWGWO | 0.8018 | 0.2887 | 0.5615 | 0.6710 | 7.2870 | 0.0402 | 6.353E-29 |
| GWO | 0.8173 | 0.1986 | 0.5185 | 0.5971 | 3.5970 | 0.0396 | 9.665E-08 | |
| PSO | 0.7424 | 0.1916 | 0.6078 | 0.8508 | 5.0526 | 0.0433 | 7.374E-04 | |
| GSA | 0.6341 | 0.2134 | 0.6541 | 0.9984 | 4.8126 | 0.0465 | 7.619E-06 | |
| DE | 0.6724 | 0.2725 | 0.6548 | 0.9660 | 9.9047 | 0.0447 | 5.194E-12 | |
| Motor 8 | AWGWO | 0.6000 | 0.1000 | 0.3870 | 1.0000 | 1.1774 | 0.0354 | 1.394E-03 |
| GWO | 0.6000 | 0.1000 | 0.3872 | 1.0000 | 1.1760 | 0.0355 | 1.395E-03 | |
| PSO | 0.6000 | 0.1894 | 0.3797 | 1.0000 | 1.6755 | 0.0330 | 3.442E-03 | |
| GSA | 0.6000 | 0.1194 | 0.3880 | 0.9998 | 1.2558 | 0.0353 | 1.660E-03 | |
| DE | 0.6000 | 0.1000 | 0.3870 | 1.0000 | 1.1774 | 0.0354 | 1.394E-03 |
| Motor No. | Algorithms | (Nm) | (Nm) | (Nm) | |||||
|---|---|---|---|---|---|---|---|---|---|
| Motor 1 | AWGWO | 240.4615 | 1.48E-03 | 601.1370 | 1.30E-02 | 529.0188 | 6.80E-03 | 0.8700 | 1.34E-09 |
| GWO | 240.2838 | 1.76E-01 | 600.7601 | 3.90E-01 | 528.2561 | 7.56E-01 | 0.8697 | 2.93E-04 | |
| PSO | 240.2162 | 2.44E-01 | 598.4854 | 2.66E+00 | 531.4233 | 2.41E+00 | 0.8719 | 1.86E-03 | |
| GSA | 244.4188 | 3.96E+00 | 598.7888 | 2.36E+00 | 526.4271 | 2.58E+00 | 0.8723 | 2.30E-03 | |
| DE | 240.4639 | 3.88E-03 | 601.1588 | 8.76E-03 | 529.0209 | 8.94E-03 | 0.8700 | 5.21E-06 | |
| Motor 2 | AWGWO | 195.0000 | 4.42E-05 | 526.4983 | 1.65E-03 | 468.0011 | 1.14E-03 | 0.8700 | 6.61E-07 |
| GWO | 194.9206 | 7.94E-02 | 526.3572 | 1.43E-01 | 467.5901 | 4.10E-01 | 0.8701 | 1.20E-04 | |
| PSO | 195.0978 | 9.78E-02 | 526.2919 | 2.08E-01 | 467.1433 | 8.57E-01 | 0.8629 | 7.13E-03 | |
| GSA | 197.5206 | 2.52E+00 | 528.4356 | 1.94E+00 | 469.5004 | 1.50E+00 | 0.8725 | 2.52E-03 | |
| DE | 194.9999 | 6.13E-05 | 526.8172 | 3.17E-01 | 468.4592 | 4.59E-01 | 0.8697 | 2.52E-04 | |
| Motor 3 | AWGWO | 218.0000 | 3.79E-09 | 610.3999 | 7.60E-05 | 501.4001 | 5.56E-05 | 0.8300 | 7.97E-09 |
| GWO | 217.8997 | 1.00E-01 | 610.8046 | 4.05E-01 | 502.0696 | 6.70E-01 | 0.8295 | 4.65E-04 | |
| PSO | 217.0364 | 9.64E-01 | 609.3855 | 1.01E+00 | 502.5774 | 1.18E+00 | 0.8557 | 2.57E-02 | |
| GSA | 217.0041 | 9.96E-01 | 610.4461 | 4.61E-02 | 500.2396 | 1.16E+00 | 0.8303 | 3.21E-04 | |
| DE | 218.5128 | 5.13E-01 | 610.5979 | 1.98E-01 | 501.1453 | 2.55E-01 | 0.8309 | 8.96E-04 | |
| Motor 4 | AWGWO | 197.0000 | 0.00E+00 | 512.2000 | 0.00E+00 | 413.7000 | 0.00E+00 | 0.8100 | 0.00E+00 |
| GWO | 196.9198 | 8.02E-02 | 512.1304 | 6.96E-02 | 413.6990 | 1.04E-03 | 0.8096 | 3.77E-04 | |
| PSO | 196.7801 | 2.20E-01 | 523.2646 | 1.11E+01 | 407.4978 | 6.20E+00 | 0.8089 | 1.13E-03 | |
| GSA | 195.4200 | 1.58E+00 | 513.2434 | 1.04E+00 | 413.9373 | 2.37E-01 | 0.8103 | 3.09E-04 | |
| DE | 196.9996 | 4.48E-04 | 512.1962 | 3.80E-03 | 413.6958 | 4.23E-03 | 0.8100 | 4.31E-07 | |
| Motor 5 | AWGWO | 36.0001 | 1.00E-04 | 123.6633 | 5.94E+00 | 95.7570 | 2.16E+00 | 0.8781 | 3.19E-02 |
| GWO | 35.9873 | 1.27E-02 | 122.0890 | 7.51E+00 | 99.7156 | 6.12E+00 | 0.8865 | 2.35E-02 | |
| PSO | 36.1292 | 1.29E-01 | 121.4679 | 8.13E+00 | 97.8295 | 4.23E+00 | 0.8500 | 6.00E-02 | |
| GSA | 35.8029 | 1.97E-01 | 123.5587 | 6.04E+00 | 95.6348 | 2.03E+00 | 0.8749 | 3.51E-02 | |
| DE | 36.0000 | 5.32E-09 | 122.0063 | 7.59E+00 | 99.6937 | 6.09E+00 | 0.8874 | 2.26E-02 | |
| Motor 6 | AWGWO | 24.6000 | 2.72E-07 | 95.9400 | 5.65E-07 | 73.8000 | 2.31E-07 | 0.9000 | 8.38E-10 |
| GWO | 24.6049 | 4.95E-03 | 90.6112 | 5.33E+00 | 78.8339 | 5.03E+00 | 0.8718 | 2.82E-02 | |
| PSO | 24.6489 | 4.89E-02 | 96.0609 | 1.21E-01 | 73.5365 | 2.64E-01 | 0.8799 | 2.01E-02 | |
| GSA | 24.6442 | 4.42E-02 | 90.0774 | 5.86E+00 | 79.6408 | 5.84E+00 | 0.8986 | 1.37E-03 | |
| DE | 24.5963 | 3.71E-03 | 95.9354 | 4.58E-03 | 73.8004 | 3.82E-04 | 0.9000 | 8.86E-06 | |
| Motor 7 | AWGWO | 9.9000 | 3.55E-15 | 38.6100 | 1.71E-13 | 31.6800 | 1.74E-13 | 0.9000 | 3.33E-15 |
| GWO | 9.9086 | 8.63E-03 | 38.5871 | 2.29E-02 | 31.6408 | 3.92E-02 | 0.9003 | 2.69E-04 | |
| PSO | 9.8762 | 2.38E-02 | 38.4415 | 1.68E-01 | 31.8248 | 1.45E-01 | 0.9237 | 2.37E-02 | |
| GSA | 9.7641 | 1.36E-01 | 38.5272 | 8.28E-02 | 31.6977 | 1.77E-02 | 0.8997 | 2.71E-04 | |
| DE | 9.8990 | 9.58E-04 | 38.6100 | 1.06E-05 | 31.6956 | 1.56E-02 | 0.9000 | 3.32E-06 | |
| Motor 8 | AWGWO | 9.8300 | 3.21E-07 | 33.0709 | 6.32E-01 | 19.6600 | 4.04E-07 | 0.8229 | 7.08E-03 |
| GWO | 9.8488 | 1.88E-02 | 33.0906 | 6.52E-01 | 19.6623 | 2.27E-03 | 0.8231 | 6.93E-03 | |
| PSO | 9.8031 | 2.69E-02 | 33.8048 | 1.37E+00 | 19.5684 | 9.16E-02 | 0.8156 | 1.44E-02 | |
| GSA | 9.8129 | 1.71E-02 | 33.1536 | 7.15E-01 | 19.6750 | 1.50E-02 | 0.8209 | 9.09E-03 | |
| DE | 9.8300 | 7.25E-09 | 33.0709 | 6.32E-01 | 19.6600 | 7.99E-09 | 0.8229 | 7.08E-03 |
| Motor No. | Algorithms | |||||
|---|---|---|---|---|---|---|
| Motor 1 | AWGWO | 8.846E-24 | 6.676E-10 | 1.672E-10 | 3.336E-10 | 9.25 |
| GWO | 7.582E-08 | 5.956E-07 | 3.186E-07 | 2.133E-07 | 8.86 | |
| PSO | 4.603E-05 | 8.836E-03 | 5.431E-03 | 3.880E-03 | 11.03 | |
| GSA | 1.704E-06 | 7.986E-03 | 2.023E-03 | 3.975E-03 | 9.62 | |
| DE | 4.205E-17 | 2.550E-08 | 6.485E-09 | 1.268E-08 | 10.10 | |
| Motor 2 | AWGWO | 3.310E-12 | 2.680E-11 | 1.335E-11 | 1.054E-11 | 8.82 |
| GWO | 2.513E-07 | 3.798E-07 | 3.290E-07 | 5.817E-08 | 8.11 | |
| PSO | 7.086E-05 | 5.525E-02 | 1.667E-02 | 2.586E-02 | 9.41 | |
| GSA | 2.530E-06 | 9.289E-05 | 2.658E-05 | 4.427E-05 | 9.56 | |
| DE | 3.737E-12 | 4.657E-09 | 1.759E-09 | 2.041E-09 | 9.12 | |
| Motor 3 | AWGWO | 1.580E-22 | 2.793E-14 | 6.988E-15 | 1.396E-14 | 10.75 |
| GWO | 7.973E-08 | 7.800E-07 | 3.757E-07 | 3.084E-07 | 10.36 | |
| PSO | 9.839E-04 | 2.017E-02 | 6.861E-03 | 8.995E-03 | 12.74 | |
| GSA | 2.320E-06 | 2.071E-04 | 5.787E-05 | 9.958E-05 | 11.17 | |
| DE | 1.502E-10 | 5.969E-09 | 3.135E-09 | 2.863E-09 | 11.37 | |
| Motor 4 | AWGWO | 0.000E+00 | 3.969E-32 | 1.932E-32 | 1.622E-32 | 6.41 |
| GWO | 9.837E-08 | 5.483E-05 | 1.407E-05 | 2.717E-05 | 5.96 | |
| PSO | 6.946E-04 | 6.841E-03 | 2.627E-03 | 2.847E-03 | 7.12 | |
| GSA | 3.497E-06 | 2.237E-01 | 5.596E-02 | 1.118E-01 | 7.08 | |
| DE | 4.386E-14 | 2.237E-01 | 5.591E-02 | 1.118E-01 | 6.45 | |
| Motor 5 | AWGWO | 3.857E-03 | 8.289E-03 | 4.965E-03 | 2.216E-03 | 6.23 |
| GWO | 8.289E-03 | 8.306E-03 | 8.297E-03 | 7.071E-06 | 5.77 | |
| PSO | 1.033E-02 | 3.703E-02 | 2.265E-02 | 1.172E-02 | 7.62 | |
| GSA | 4.076E-03 | 8.904E-03 | 7.489E-03 | 2.284E-03 | 6.90 | |
| DE | 8.289E-03 | 8.289E-03 | 8.289E-03 | 5.925E-18 | 7.18 | |
| Motor 6 | AWGWO | 1.671E-16 | 8.742E-03 | 2.186E-03 | 4.371E-03 | 6.02 |
| GWO | 8.718E-03 | 8.719E-03 | 8.719E-03 | 5.621E-07 | 5.56 | |
| PSO | 5.155E-04 | 1.426E-02 | 6.988E-03 | 7.021E-03 | 7.80 | |
| GSA | 9.982E-03 | 1.397E-02 | 1.285E-02 | 1.915E-03 | 6.50 | |
| DE | 3.456E-12 | 8.902E-03 | 6.590E-03 | 4.394E-03 | 6.86 | |
| Motor 7 | AWGWO | 6.353E-29 | 1.656E-15 | 4.305E-16 | 8.169E-16 | 6.17 |
| GWO | 9.665E-08 | 4.159E-07 | 2.432E-07 | 1.318E-07 | 5.74 | |
| PSO | 7.374E-04 | 7.423E-03 | 3.281E-03 | 3.047E-03 | 7.32 | |
| GSA | 7.619E-06 | 1.979E-05 | 1.202E-05 | 5.538E-06 | 6.81 | |
| DE | 5.194E-12 | 2.724E-07 | 7.235E-08 | 1.335E-07 | 6.21 | |
| Motor 8 | AWGWO | 1.394E-03 | 2.014E-01 | 5.139E-02 | 1.000E-01 | 9.66 |
| GWO | 1.395E-03 | 2.014E-01 | 5.140E-02 | 1.000E-01 | 8.82 | |
| PSO | 3.442E-03 | 3.355E-02 | 2.239E-02 | 1.322E-02 | 20.62 | |
| GSA | 1.660E-03 | 2.073E-01 | 1.081E-01 | 1.114E-01 | 8.79 | |
| DE | 1.394E-03 | 2.014E-01 | 1.014E-01 | 1.155E-01 | 9.62 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Manoharan, P.; Ravichandran, S.; Siva Kumar, J.S.V.; Abdullah, M.; Ching Sin, T.; Tengku Hashim, T.J. Electrical Equivalent Circuit Parameter Estimation of Commercial Induction Machines Using an Enhanced Grey Wolf Optimization Algorithm. Biomimetics 2025, 10, 228. https://doi.org/10.3390/biomimetics10040228
Manoharan P, Ravichandran S, Siva Kumar JSV, Abdullah M, Ching Sin T, Tengku Hashim TJ. Electrical Equivalent Circuit Parameter Estimation of Commercial Induction Machines Using an Enhanced Grey Wolf Optimization Algorithm. Biomimetics. 2025; 10(4):228. https://doi.org/10.3390/biomimetics10040228
Chicago/Turabian StyleManoharan, Premkumar, Sowmya Ravichandran, Jagarapu S. V. Siva Kumar, Mustafa Abdullah, Tan Ching Sin, and Tengku Juhana Tengku Hashim. 2025. "Electrical Equivalent Circuit Parameter Estimation of Commercial Induction Machines Using an Enhanced Grey Wolf Optimization Algorithm" Biomimetics 10, no. 4: 228. https://doi.org/10.3390/biomimetics10040228
APA StyleManoharan, P., Ravichandran, S., Siva Kumar, J. S. V., Abdullah, M., Ching Sin, T., & Tengku Hashim, T. J. (2025). Electrical Equivalent Circuit Parameter Estimation of Commercial Induction Machines Using an Enhanced Grey Wolf Optimization Algorithm. Biomimetics, 10(4), 228. https://doi.org/10.3390/biomimetics10040228






