Structural Sizing and Topology Optimization Based on Weight Minimization of a Variable Tapered Span-Morphing Wing for Aerodynamic Performance Improvements
Abstract
1. Introduction
2. Parametric Layout of the Optimized VSMTW
2.1. Wing Design Configurations
2.2. Material Choice
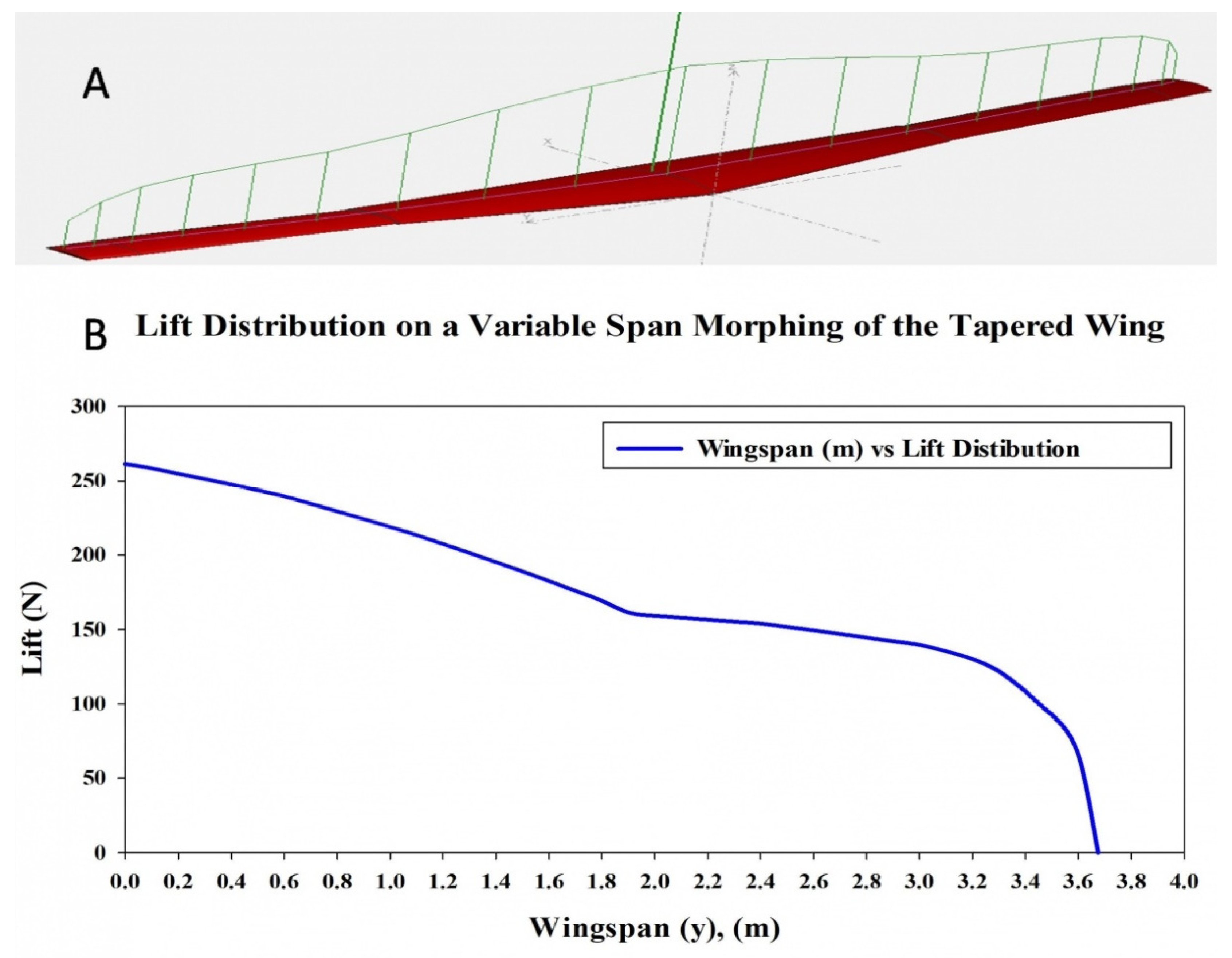
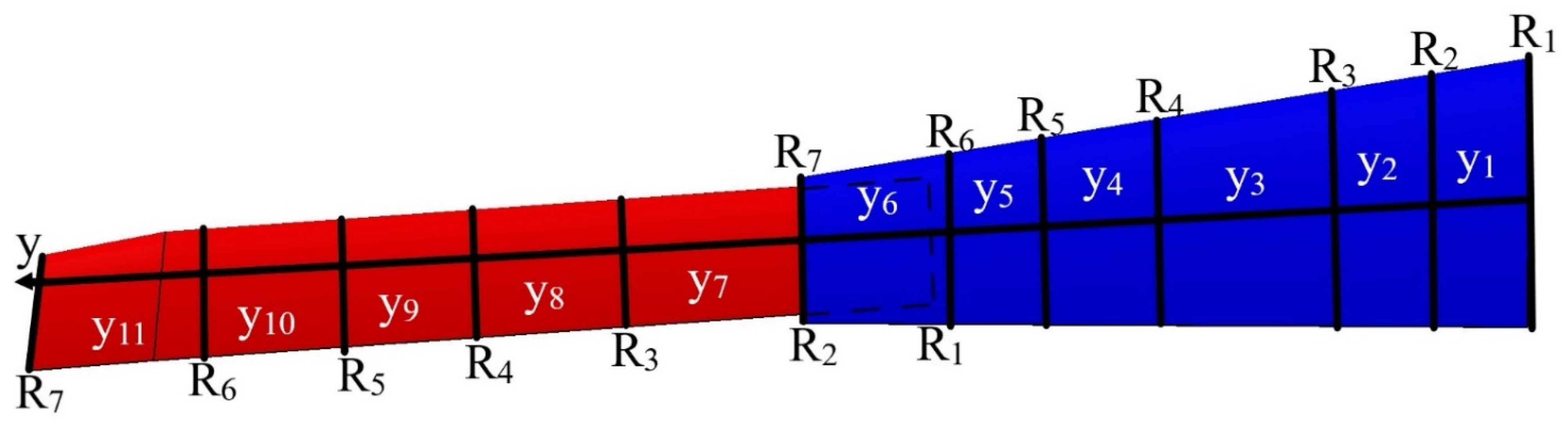
3. Load Cases
4. Optimization Mathematical Model
4.1. Topology Optimization Methodology
4.2. Formulation of the Stiffness and Topology Optimization Problem
5. Wing Component Structure Design Optimization Process
5.1. Wing Skin Thickness Size Optimization
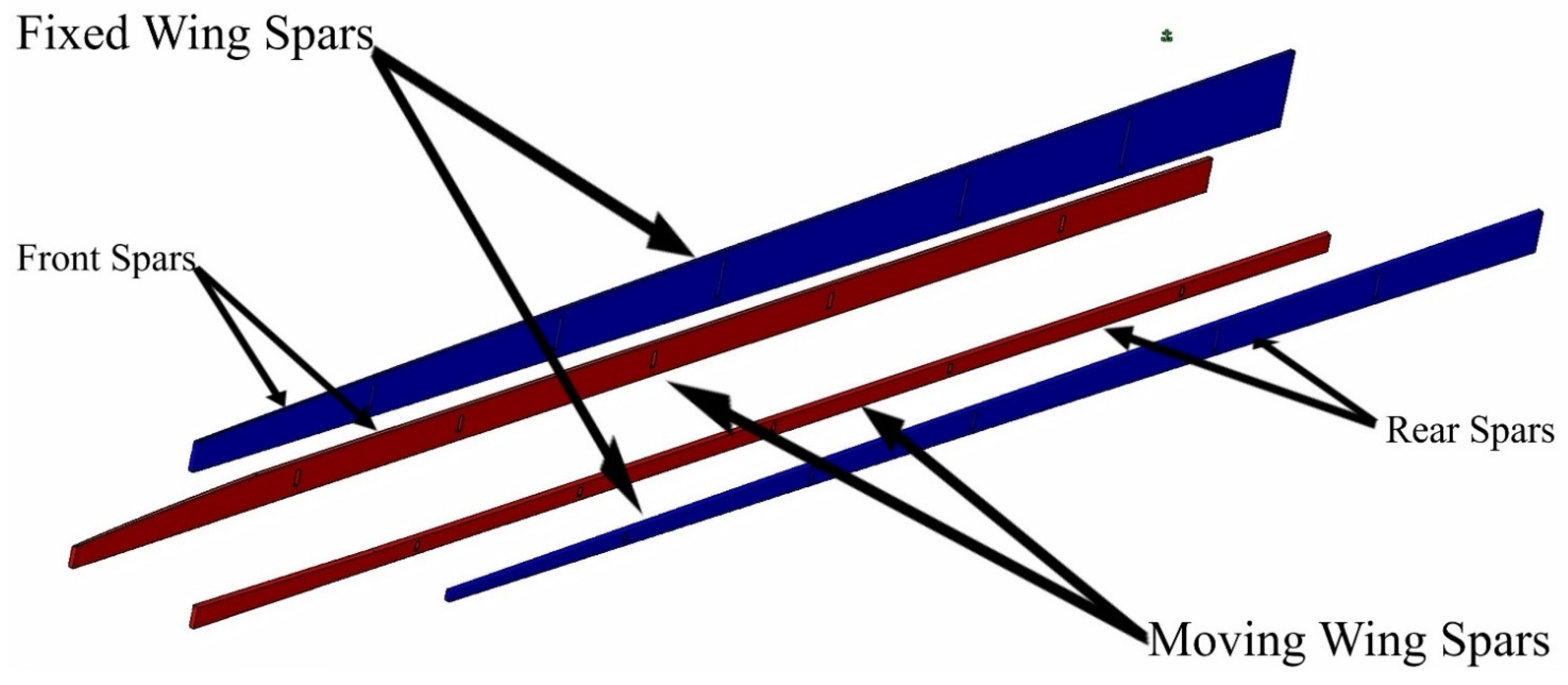
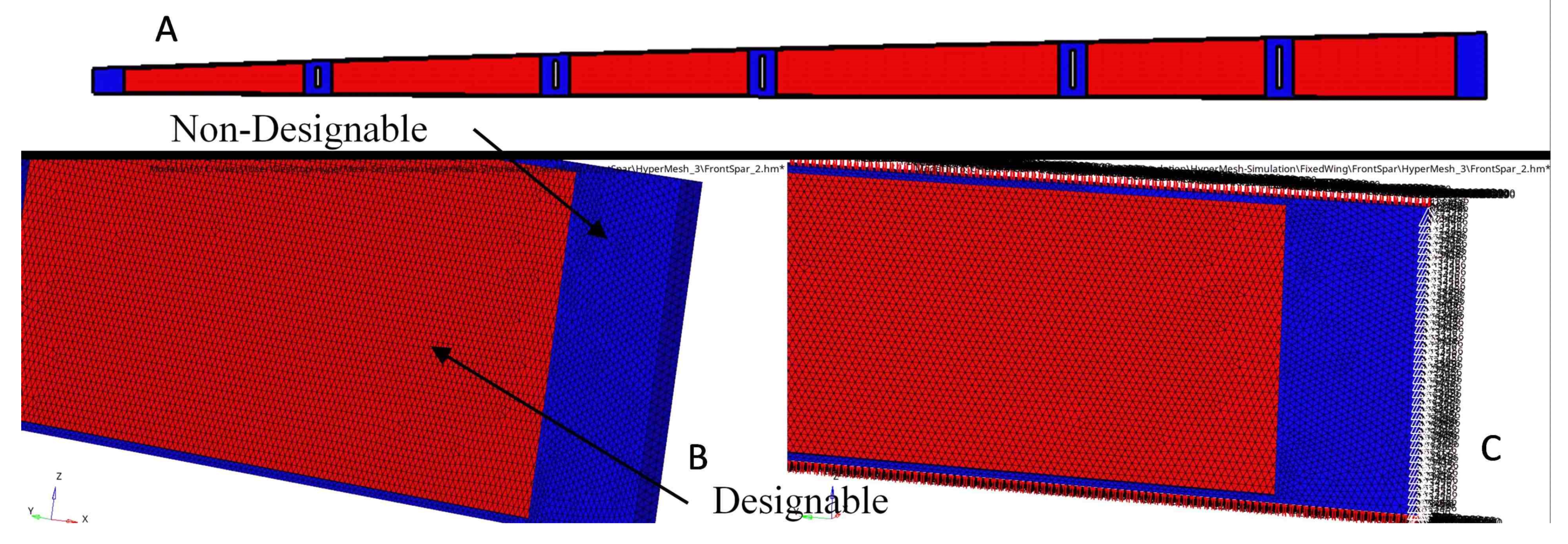
5.2. Spar Structure Topology Optimization
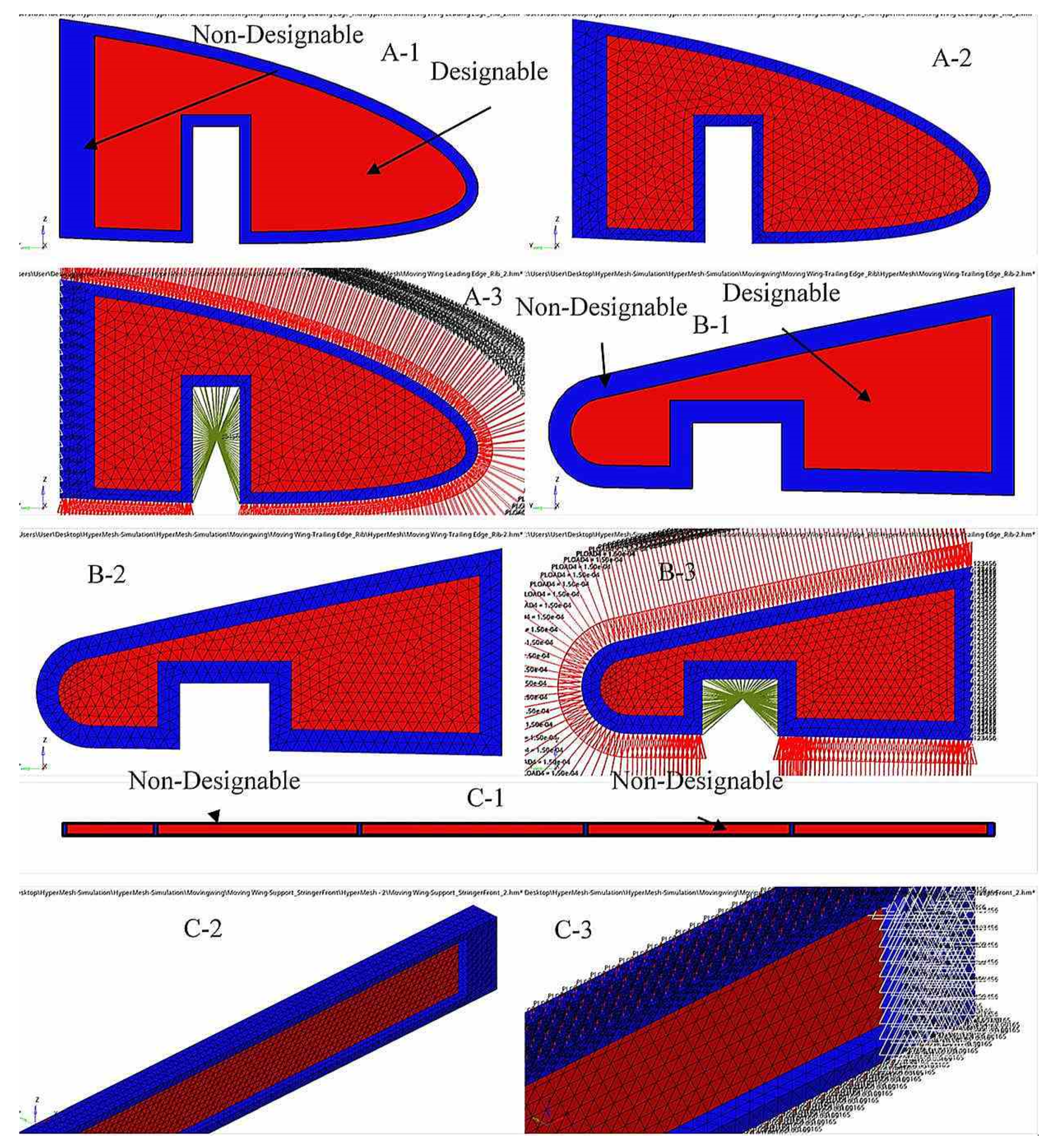
5.3. Rib Structure Topology Optimization
5.4. Topology Optimization (TO) of the Support Element’s Structure
6. Results and Discussion
7. Remodeling of the Optimized Wing Components and Their Final Design
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| CAE | Computer-Aided Engineering |
| CFD | Computational Fluid Dynamics |
| E(xi) | Young’s modulus of each element |
| Esolid | Young’s modulus of solid regions |
| Evoid | Very low Young’s modulus |
| f | Distributed body force |
| F | Force vector |
| FAA | Federal Aviation Regulations |
| FEM | Finite Element Method |
| Fi | Point load on the ith node |
| K | Global stiffness matrix |
| k0 | Elemental stiffness matrix |
| MVSTW | morphing variable span of tapered wing |
| S | Surface area of the continuum |
| SO | sizing optimization |
| STO | sizing and topology optimization |
| SIMP | Solid Isotropic Material with the Penalization |
| t | Traction force |
| TO | topology optimization |
| u | Displacement area |
| U | Global displacement |
| Ui | ith displacement degree of freedom |
| V | Total volume |
| V0 | Initial volume |
| Vi | Volume of the ith element |
| Γ(y) | Circulation distribution |
| Xi | Pseudo density |
| p0 | Density of the base material |
| pi | Density of the ith element |
References
- Ameduri, S.; Concilio, A. Morphing wings review: Aims, challenges, and current open issues of a technology. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2020. [Google Scholar] [CrossRef]
- Concilio, A.; Dimino, I.; Pecora, R. SARISTU: Adaptive Trailing Edge Device (ATED) design process review. Chin. J. Aeronaut. 2020, 34, 187–210. [Google Scholar] [CrossRef]
- Dimino, I.; Lecce, L.; Pecora, R. Morphing Wing Technologies: Large Commercial Aircraft and Civil Helicopters; Butterworth-Heinemann: Oxford, UK, 2017. [Google Scholar]
- Armendáriz, I.; Millán, J.S.; Encinas, J.M.; Olarrea, J. Chapter 2—Strategies for dynamic failure analysis on aerospace structures. In Handbook of Materials Failure Analysis with Case Studies from the Aerospace and Automotive Industries; Makhlouf, A.S.H., Aliofkhazraei, M., Eds.; Butterworth-Heinemann: Oxford, UK, 2016; pp. 29–55. [Google Scholar]
- Muneiah, T.; Bhaskar, E.; Rajesh, C.V. Design and Developemnt of Aircraft Droop Nose Ribs by Using Optistruct. Int. J. Adv. Eng. Res. Stud. 2014, 3, 18–21. [Google Scholar]
- Rao, J.; Kiran, S.; Kamesh, J.; Padmanabhan, M.A.; Chandra, S. Topology optimization of aircraft wing. J. Aerosp. Sci. Technol. 2009, 61, 402. [Google Scholar]
- Liu, Q.; Mulani, S.B.; Kapania, R.K. Global/Local Multidisciplinary Design Optimization of Subsonic Wing. In Proceedings of the 10th AIAA Multidisciplinary Design Optimization Conference, National Harbor, MY, USA, 13–17 January 2014. [Google Scholar] [CrossRef]
- Zhu, J.; Zhang, W.-H.; Xia, L. Topology Optimization in Aircraft and Aerospace Structures Design. Arch. Comput. Methods Eng. 2015, 23, 595–622. [Google Scholar] [CrossRef]
- Mitropoulou, C.C.; Fourkiotis, Y.; Lagaros, N.D.; Karlaftis, M.G. Evolution Strategies-Based Metaheuristics in Structural Design Optimization. Metaheuristic Appl. Struct. Infrastruct. 2013, 79–102. [Google Scholar] [CrossRef]
- Michaud, F.; Joncas, S.; Botez, R. Design, manufacturing and testing of a small-scale composite morphing wing. In Proceedings of the 19th International Conference on Composite Materials-ICCM19, Montreal, QC, Canada, 28 July–4 August 2013; Available online: https://espace2.etsmtl.ca/id/eprint/8930/ (accessed on 23 August 2013).
- Krog, L.; Tucker, A.; Kemp, M.; Boyd, R. Topology optimisation of aircraft wing box ribs. In Proceedings of the 10th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Albany, NY, USA, 30 August–1 September 2004; p. 4481. [Google Scholar]
- Eves, J.; Toropov, V.; Thompson, H.; Gaskell, P.; Doherty, J.; Harris, J. Topology optimization of aircraft with non-conventional configurations. In Proceedings of the 8th World Congress on Structural and Multidisciplinary Optimization, Lisbon, Portugal, 1–5 June 2009. [Google Scholar]
- Rinku, A.; Ananthasuresh, G. Topology and Size Optimization of Modular Ribs in Aircraft Wings. In Proceedings of the 11th World Congress on Structural and Multidisciplinary Optimisation, Sydney, Australia, 7–12 June 2015. [Google Scholar]
- Grihon, S.; Krog, L.; Hertel, K. A380 weight savings using numerical structural optimization. In Proceedings of the 20th AAAF Colloqium “Material for Aerospace Application”, Paris, France, 9–12 November 2004. [Google Scholar]
- Wang, Q.; Lu, Z.; Zhou, C.; Qi, W. New Topology Optimization Method for Wing Leading-Edge Ribs. J. Aircr. 2011, 48, 1741–1748. [Google Scholar] [CrossRef]
- James, K.A.; Kennedy, G.J.; Martins, J. Concurrent aerostructural topology optimization of a wing box. Comput. Struct. 2014, 134, 1–17. [Google Scholar] [CrossRef]
- Oktay, E.; Akay, H.U.; Merttopcuoglu, O. Parallelized structural topology optimization and CFD coupling for design of aircraft wing structures. Comput. Fluids 2011, 49, 141–145. [Google Scholar] [CrossRef]
- Oktay, E.; Akay, H.U.; Sehitoglu, O.T. Three-dimensional structural topology optimization of aerial vehicles under aerodynamic loads. Comput. Fluids 2014, 92, 225–232. [Google Scholar] [CrossRef]
- Tang, J.; Xi, P.; Zhang, B.; Hu, B. A finite element parametric modeling technique of aircraft wing structures. Chin. J. Aeronaut. 2013, 26, 1202–1210. [Google Scholar] [CrossRef]
- Gawel, D.; Nowak, M.; Hausa, H.; Roszak, R. New biomimetic approach to the aircraft wing structural design based on aeroelastic analysis. Bull. Pol. Acad. Sci. Tech. Sci. 2017, 65, 741–750. [Google Scholar] [CrossRef][Green Version]
- Morlier, J.; Charlotte, M. Structural wingbox optimization in a coupled FSI problem of a flexible wing: FEA sol200 versus surrogate models. In Proceedings of the Eighth International Conference on Engineering Computational Technology, Dubrovnik, Croatia, 4–7 September 2012; Available online: https://oatao.univ-toulouse.fr/7908/ (accessed on 23 September 2012).
- Botez, R.M. Morphing Wing, UAV and Aircraft Multidisciplinary Studies at the Laboratory of Applied Research in Active Controls, Avionics and AeroServoElasticity LARCASE. Aerosp. Lab 2018, 14, 1–11. (In English) [Google Scholar] [CrossRef]
- Kuitche, M.A.J.; Botez, R.M.; Viso, R.; Maunand, J.C.; Moyao, O.C. Blade element momentum new methodology and wind tunnel test performance evaluation for the UAS-S45 Bàlaam propeller. CEAS Aeronaut. J. 2020, 11, 937–953. [Google Scholar] [CrossRef]
- Kuitche, M.A.J.; Botez, R.M.; Guillemin, A.; Communier, D. Aerodynamic Modelling of Unmanned Aerial System through Nonlinear Vortex Lattice Method, Computational Fluid Dynamics and Experimental Validation—Application to the UAS-S45 Bàlaam: Part 1. INCAS Bull. 2020, 12, 91–103. [Google Scholar] [CrossRef]
- Tondji, Y.; Botez, R.M. Semi-empirical estimation and experimental method for determining inertial properties of the Unmanned Aerial System—UAS-S4 of Hydra Technologies. Aeronaut. J. 2017, 121, 1648–1682. [Google Scholar] [CrossRef]
- Liauzun, C.; Mortchéléwicz, G.D.; Lepage, A. Assessment of CFD methods taking into account laminar-turbulent transition for aeroelasticity of laminar wings. Evaluation de méthodes CFD avec prise en compte de la transition laminaire-turbulent pour l’aéroélasticité des voilures luminaires. In Proceedings of the IFASD 2019, Savannah, GA, USA, 10–13 June 2019; Available online: https://hal.archives-ouvertes.fr/hal-02339721 (accessed on 12 October 2019).
- Communier, D.; Salinas, M.F.; Moyao, O.C.; Botez, R.M. Aero structural modeling of a wing using CATIA V5 and XFLR5 software and experimental validation using the Price- Païdoussis wing tunnel. In Proceedings of the AIAA Atmospheric Flight Me-Chanics Conference, Dallas, TX, USA, 22–26 June 2015. [Google Scholar] [CrossRef]
- Elelwi, M.; Kuitche, M.; Botez, R.; Dao, T. Comparison and analyses of a variable span-morphing of the tapered wing with a varying sweep angle. Aeronaut. J. 2020, 124, 1146–1169. [Google Scholar] [CrossRef]
- Elelwi, M.; Calvet, T.; Botez, R.; Dao, T.-M. Wing component allocation for a morphing variable span of tapered wing using finite element method and topology optimization—application to the UAS-S4. Aeronaut. J. 2021, 125, 1313–1336. [Google Scholar] [CrossRef]
- Zhao, L.; Li, K.; Chang, Y.; Li, J. Topology Optimization Design of Compliant Mechanism of Composite Wing Leading Edge. J. Phys. Conf. Ser. 2019, 1215, 012002. [Google Scholar] [CrossRef]
- Zhao, Y.-B.; Guo, W.-J.; Duan, S.-H.; Xing, L.-G. A novel substructure-based topology optimization method for the design of wing structure. Int. J. Simul. Multidiscip. Des. Optim. 2017, 8, A5. [Google Scholar] [CrossRef]
- Kammegne, M.J.T.; Botez, R.M.; Grigorie, T.L.; Manou, M.; Mebarki, Y. A fuel saving way in aerospace engineering based on morphing wing technology: A new multidisciplinary experimental model. Int. J. Contemp. Energy 2016, 2. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, H.H.T. Aerodynamics Modeling and Analysis of Close Formation Flight. J. Aircr. 2017, 54, 2192–2204. [Google Scholar] [CrossRef]
- Gross, A.; Fasel, H.; Gaster, M. Criterion for Spanwise Spacing of Stall Cells. AIAA J. 2015, 53, 272–274. [Google Scholar] [CrossRef]
- Jensen, F. Topology Optimization of Turbine Manifold in the Rocket Engine Demonstrator Prometheus ed. Master’s Thesis, Luleå University of Technology, Luleå, Swenden, 29 June 2018. [Google Scholar]
- Raheel, M.; Toropov, V. Topology Optimization of an Aircraft Wing with an Outboard X-Stabilizer. In Proceedings of the 2018 Multi-Disciplinary Analysis and Optimization Conference, Atlanta, GA, USA, 25–29 June 2018. [Google Scholar] [CrossRef]
- Gunwant, D.; Misra, A. Topology Optimization of sheet metal brackets using ANSYS. MIT Int. J. Mech. Eng. 2012, 2, 120–126. [Google Scholar]
- Aage, N.; Andreassen, E.; Lazarov, B.S.; Sigmund, O. Giga-voxel computational morphogenesis for structural design. Nature 2017, 550, 84–86. [Google Scholar] [CrossRef]
- Bendsøe, M.P.; Sigmund, O. Material interpolation schemes in topology optimization. Arch. Appl. Mech. 1999, 69, 635–654. [Google Scholar] [CrossRef]
- Höke, Ö.; Bozca, M. Topology Optimisation of Engine Cross Members for Lightweight Structure in Light Commercial Vehicles. Int. J. Precis. Eng. Manuf. 2019, 21, 465–482. [Google Scholar] [CrossRef]
- Bakhtiarinejad, M. Topology Optimization Based on Morphing Mesh for Simultaneous Component Relocation and Frame Structure Design; University of Maryland: Baltimore County, MY, USA, 2015. [Google Scholar]
- Daynes, S.; Feih, S.; Lu, W.F.; Wei, J. Optimisation of functionally graded lattice structures using isostatic lines. Mater. Des. 2017, 127, 215–223. [Google Scholar] [CrossRef]
- Mou, B.; He, B.-J.; Zhao, D.-X.; Chau, K.-W. Numerical simulation of the effects of building dimensional variation on wind pressure distribution. Eng. Appl. Comput. Fluid Mech. 2017, 11, 293–309. [Google Scholar] [CrossRef]
- Vasista, S.; De Gaspari, A.; Ricci, S.; Riemenschneider, J.; Monner, H.P.; Van De Kamp, B. Compliant structures-based wing and wingtip morphing devices. Aircr. Eng. Aerosp. Technol. 2016, 88, 311–330. [Google Scholar] [CrossRef]
- Coroian, A.; Lupea, I. Improving the sound pressure level for a simplified passenger cabin by using modal participation and size optimization. Rom. J. Acoust. Vib. 2013, 10, 47. [Google Scholar]
- Girennavar, M.; Soumya, H.; Subodh, H.; Heraje, T.J.; P.Y, D.R. Design, Analysis and Testing of Wing Spar for Optimum Weight. Int. J. Res. Sci. Innov. (IJRSI) 2017, 4, 104–112. [Google Scholar]
- Grbović, A.; Kastratović, G.; Sedmak, A.; Balać, I.; Popović, M.D. Fatigue crack paths in light aircraft wing spars. Int. J. Fatigue 2019, 123, 96–104. [Google Scholar] [CrossRef]
- Grisval, J.-P.; Liauzun, C. Application of the finite element method to aeroelasticity. Rev. Eur. Éléments Finis 1999, 8, 553–579. [Google Scholar] [CrossRef]
- Li, C.; Kim, I.Y.; Jeswiet, J. Conceptual and detailed design of an automotive engine cradle by using topology, shape, and size optimization. Struct. Multidiscip. Optim. 2014, 51, 547–564. [Google Scholar] [CrossRef]
- Bashir, M.; Longtin-Martel, S.; Botez, R.; Wong, T. Aerodynamic Design Optimization of a Morphing Leading Edge and Trailing Edge Airfoil–Application on the UAS-S45. Appl. Sci. 2021, 11, 1664. [Google Scholar] [CrossRef]
- Kuitche, M.A.J.; Botez, R.M. Modeling novel methodologies for unmanned aerial systems—Applications to the UAS-S4 Ehecatl and the UAS-S45 Bálaam. Chin. J. Aeronaut. 2018, 32, 58–77. [Google Scholar] [CrossRef]



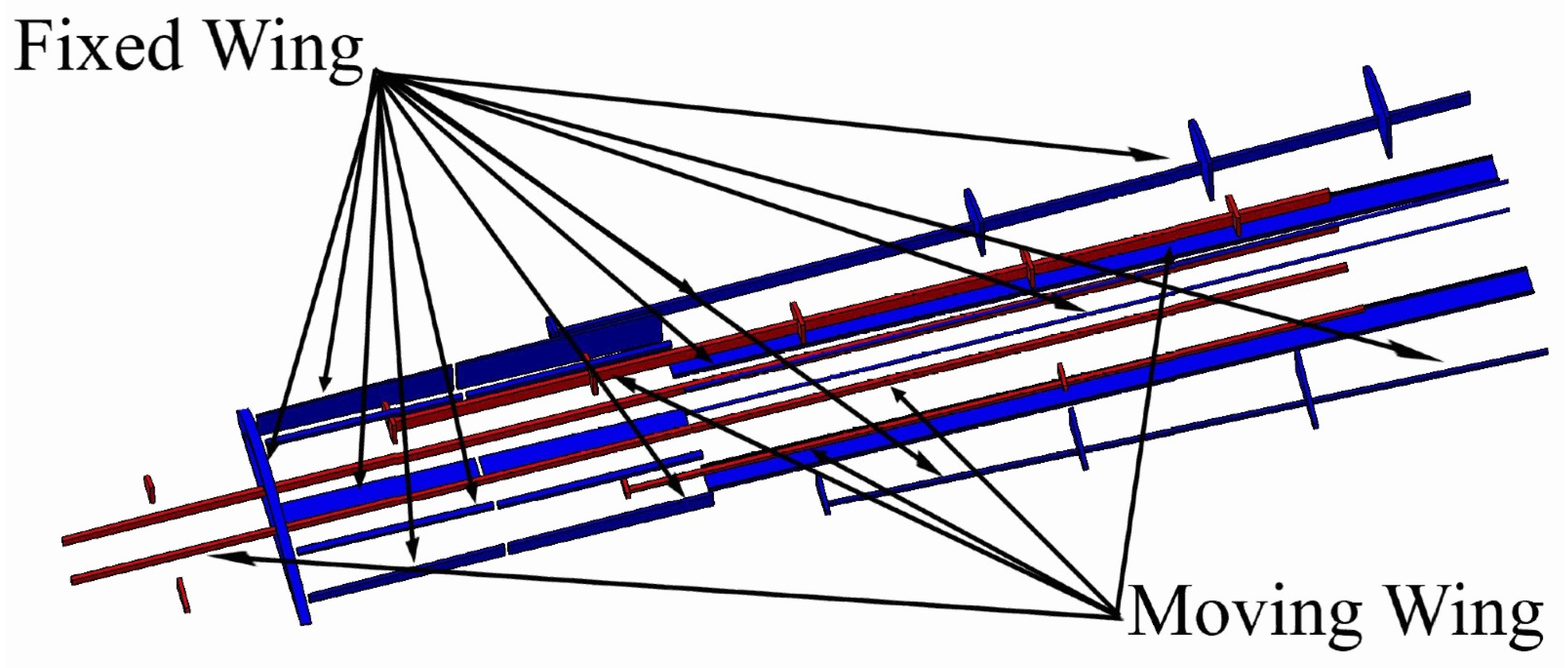







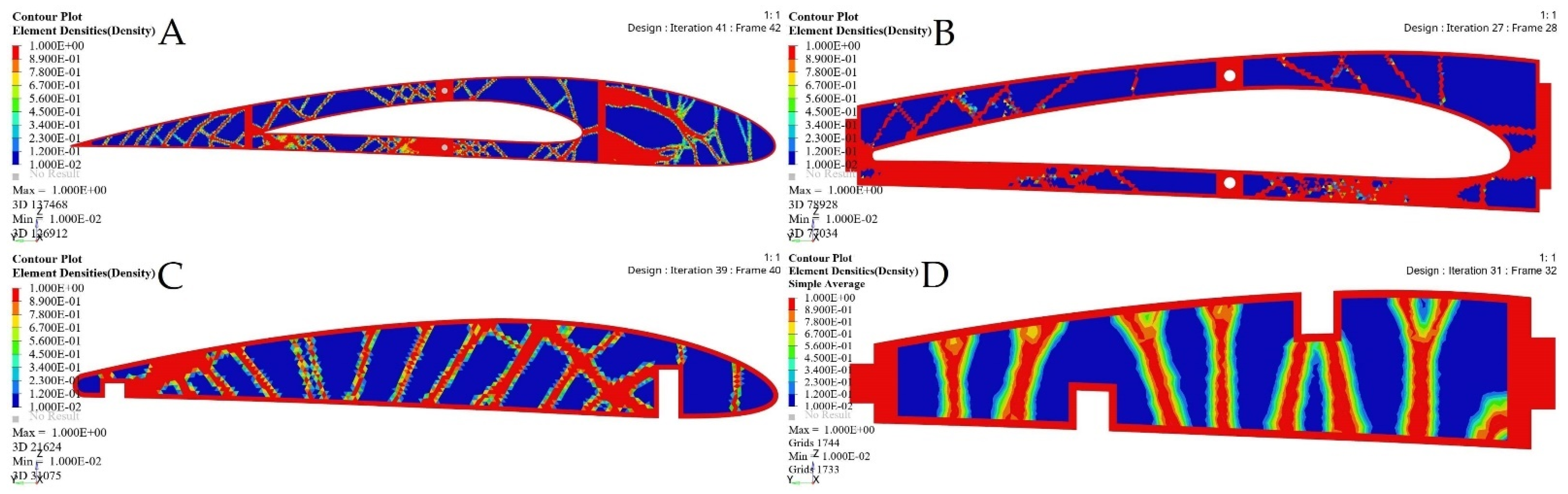

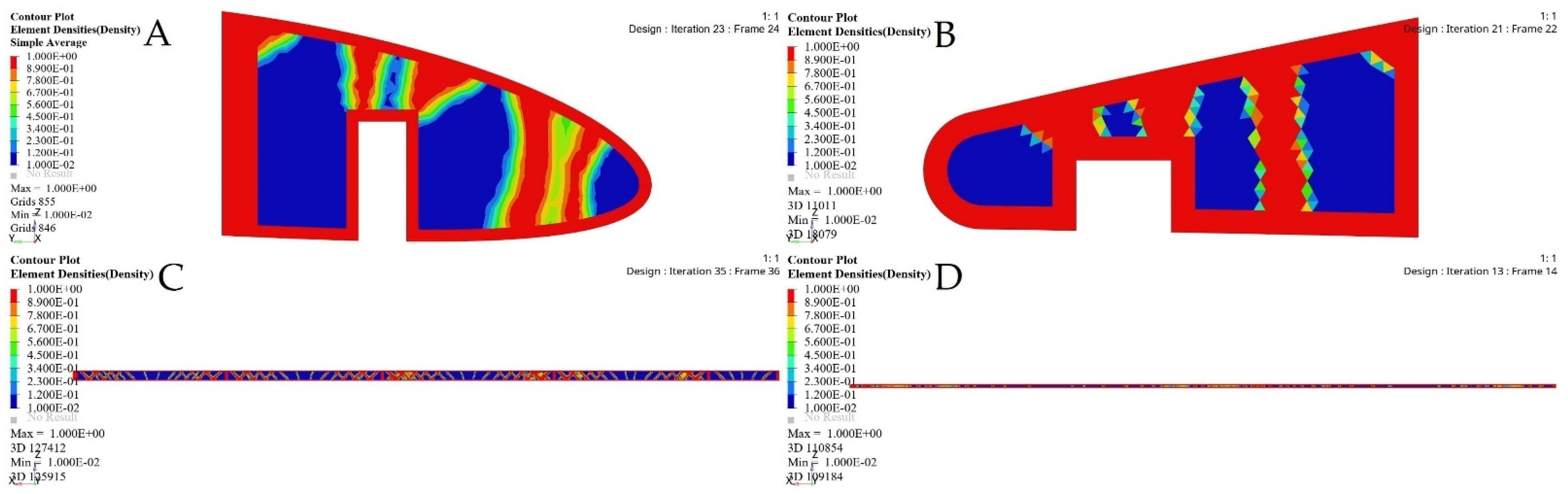
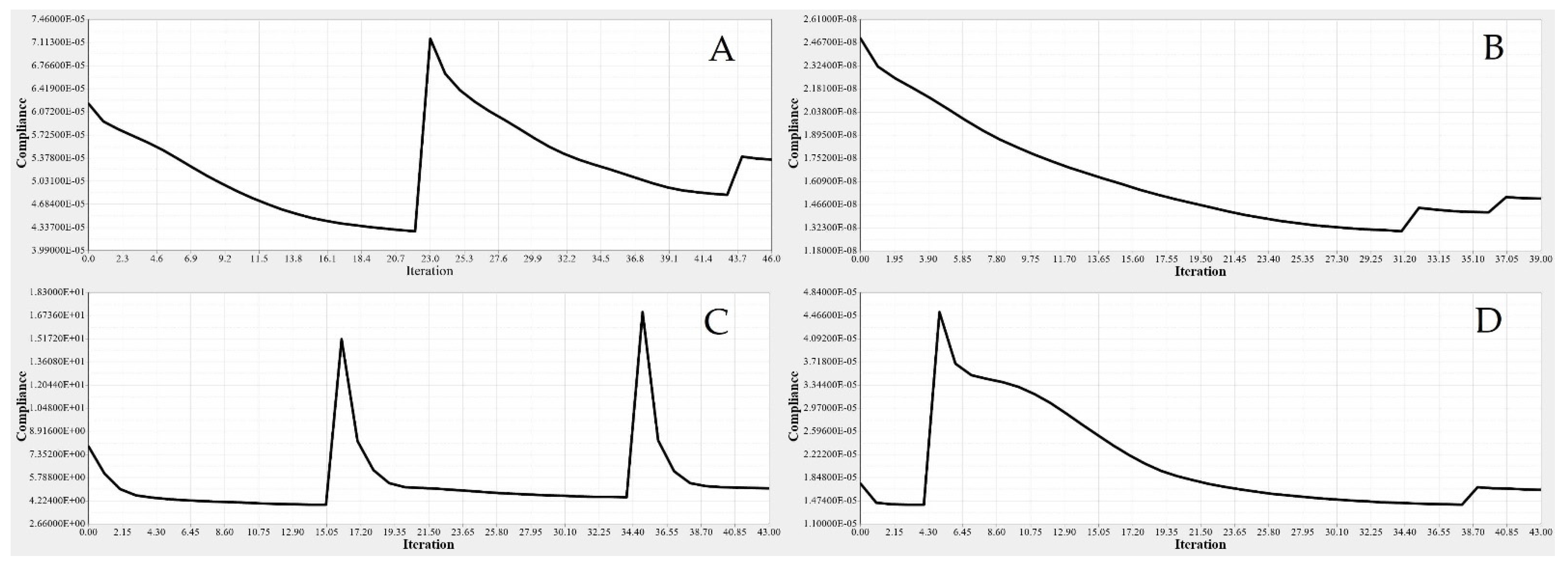
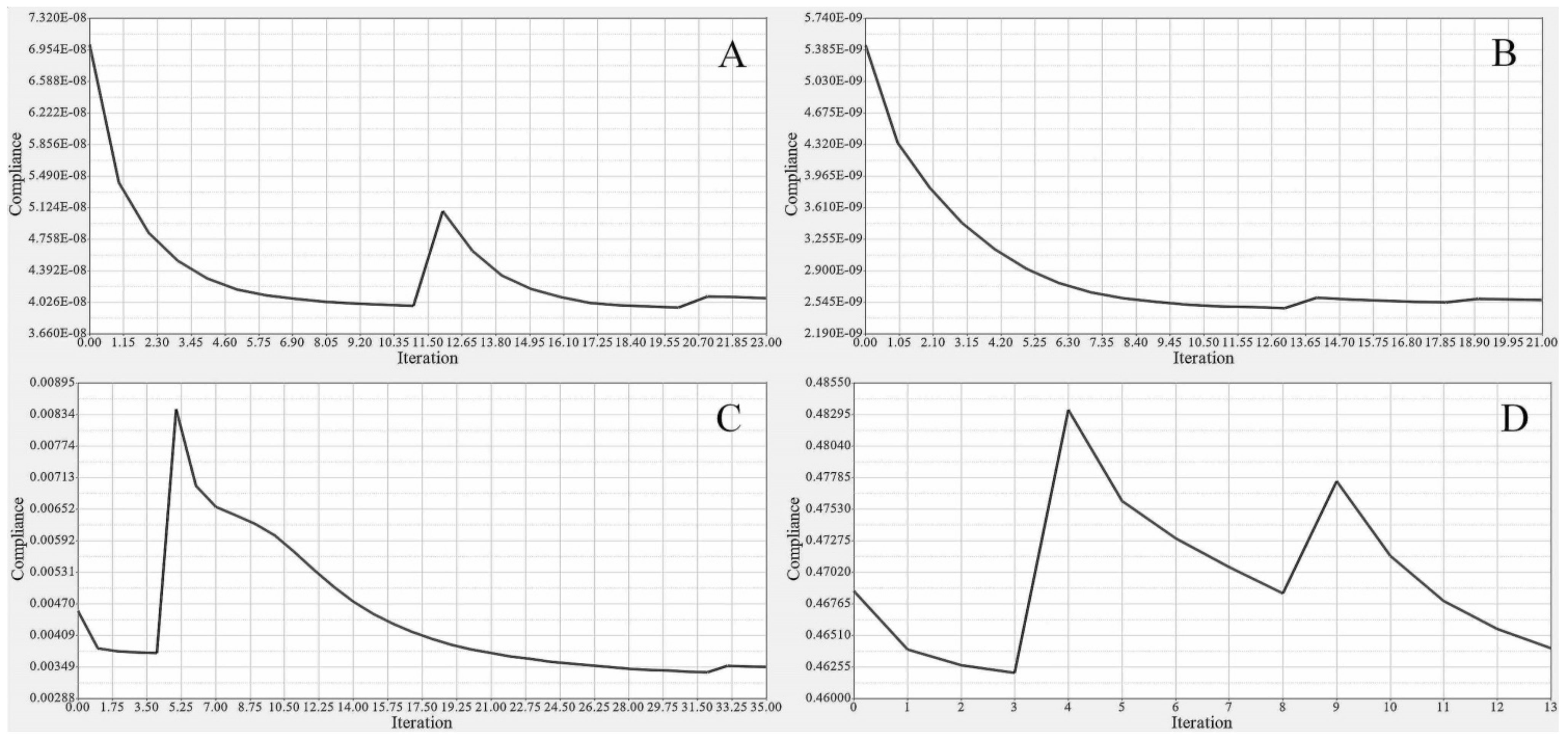

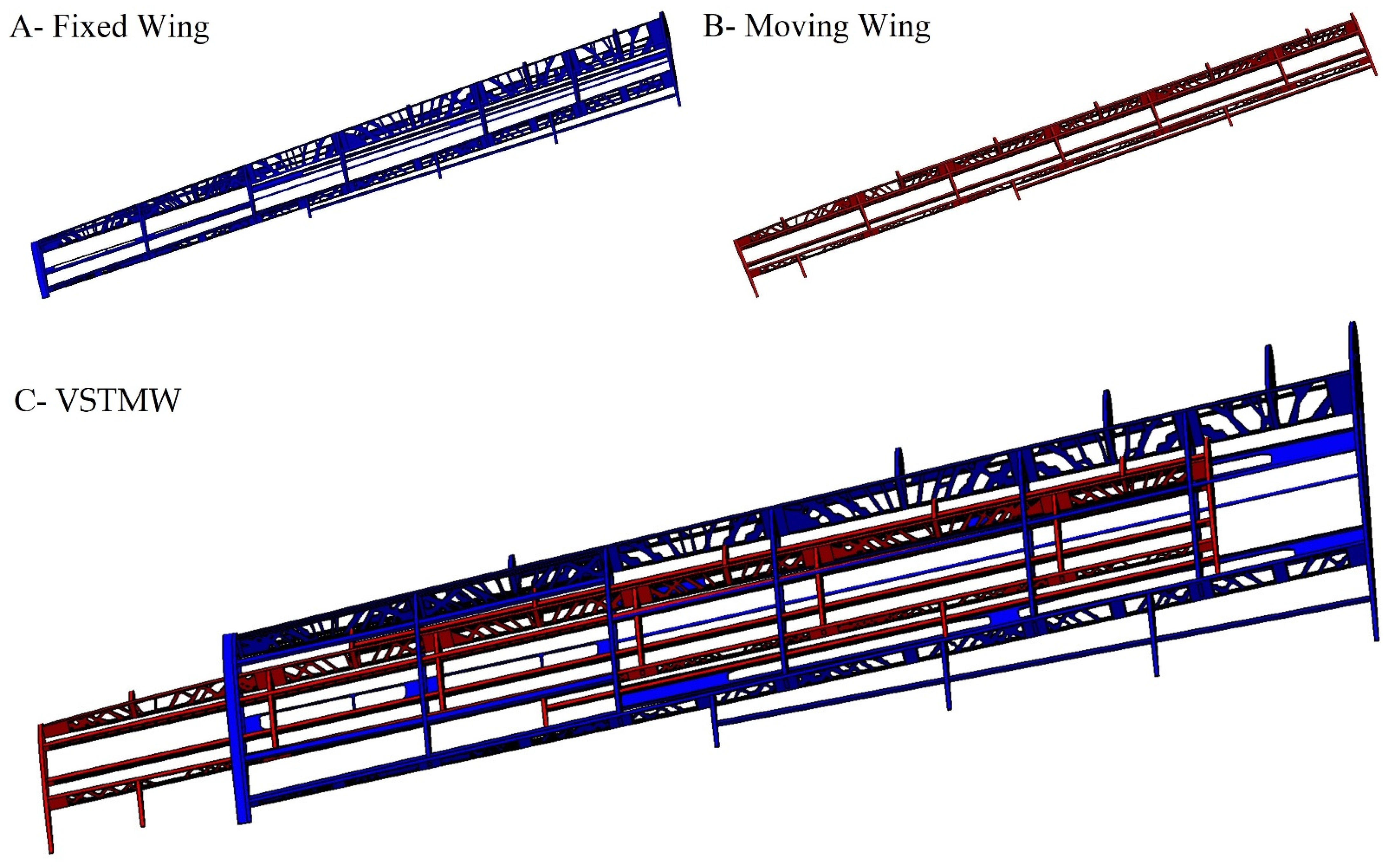
| Rib No. | Fixed Wing | Moving Wing |
|---|---|---|
| 1. | 0 mm Reference | 0 mm Reference |
| 2. | 269 mm | 245 mm |
| 3. | 534 mm | 626 mm |
| 4. | 932 mm | 919 mm |
| 5. | 1198 mm | 1234 mm |
| 6. | 1503 mm | 1502 mm |
| 7. | 1800 mm | 1875 mm |
| Physical and Mechanical Properties | |
|---|---|
| Density | 2780 kg/m3 |
| Ultimate Tensile Strength | 483 MPa |
| Tensile Yield Strength | 345 MPa |
| Modulus of Elasticity | 73,100 MPa |
| Poisson’s Ratio | 0.33 |
| Fatigue Strength | 138 MPa |
| Shear Modulus | 28,000 MPa |
| Shear Strength | 283 MPa |
| Section Number | Lift Load (N) | Ultimate Load |
|---|---|---|
| y1 | 257.36 | 1158.1 |
| y2 | 243.77 | 1096.97 |
| y3 | 232.15 | 1044.65 |
| y4 | 213.325 | 959.96 |
| y5 | 198.29 | 892.28 |
| y6 | 175.96 | 791.8 |
| y7 | 158.62 | 713.77 |
| y8 | 152.7 | 687.15 |
| y9 | 147.12 | 662.04 |
| y10 | 134.61 | 605.75 |
| y11 | 79.11 | 355.995 |
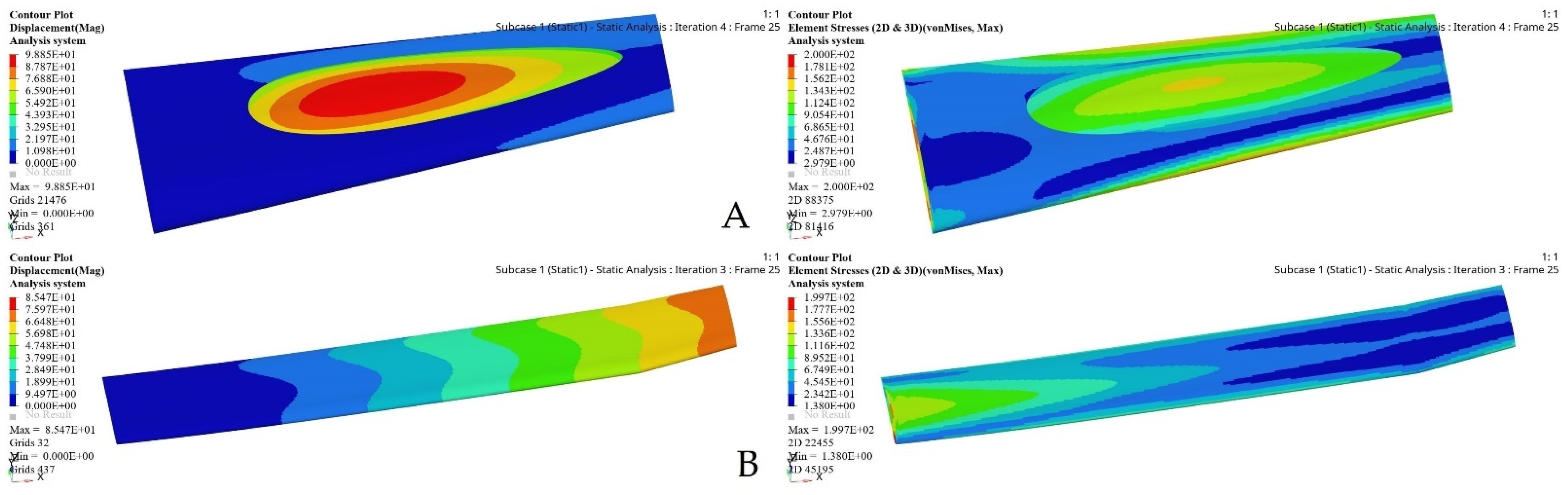
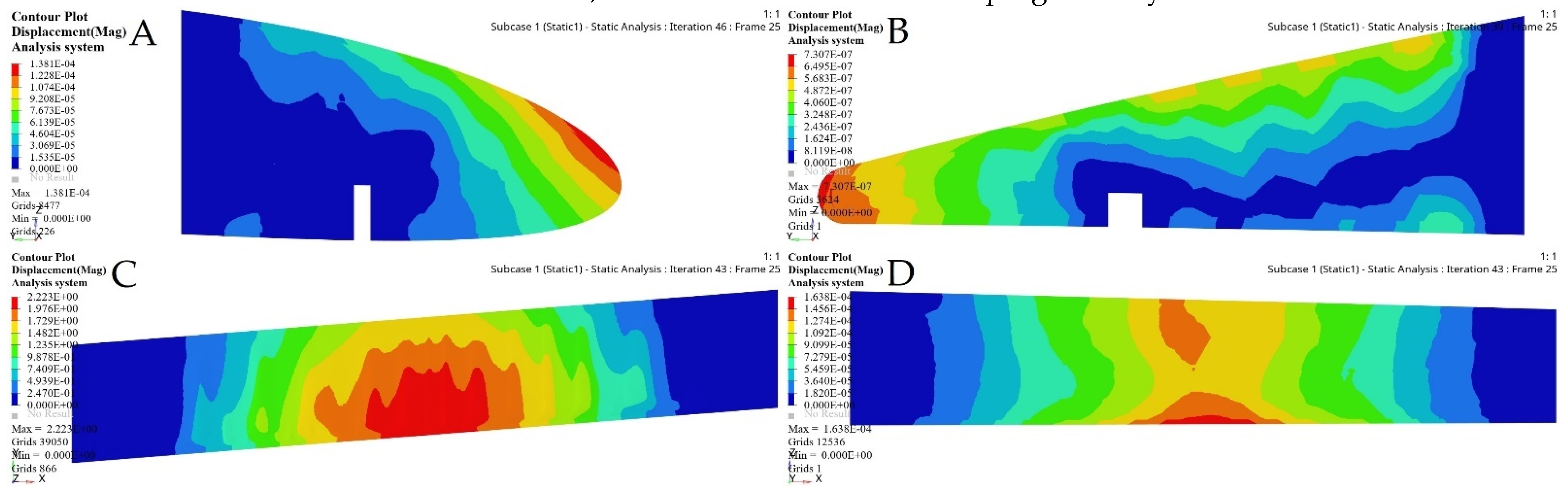
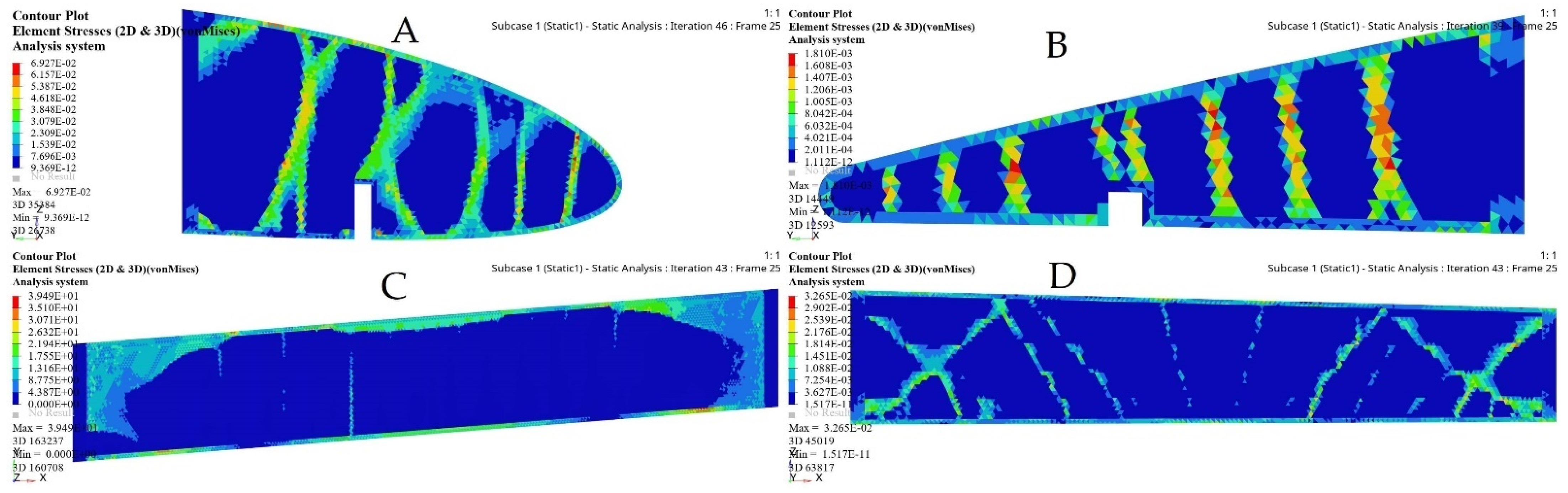
| Iterations | Deformation | Stress | Original Skin Thickness | Optimized Skin Thickness | Weight Reduction Ratio | |
|---|---|---|---|---|---|---|
| Fixed Wing | 4 | 98.85 mm | 200 MPa | 2 mm | 0.995 mm | 52.4% |
| Moving Wing | 3 | 85.47 mm | 199.7MPa | 2 mm | 0.84mm | 58.3% |
| Fixed Wing | Moving Wing | |||
|---|---|---|---|---|
| Front Spar | Rear Spar | Front Spar | Rear Spar | |
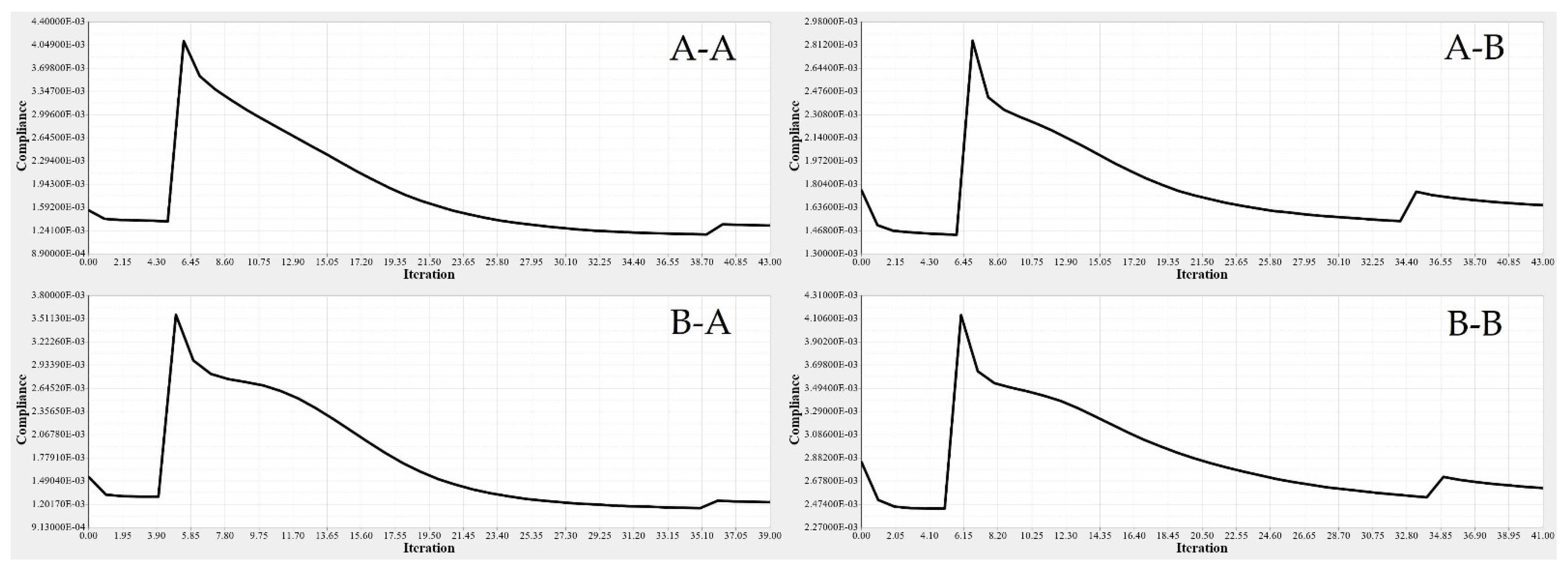
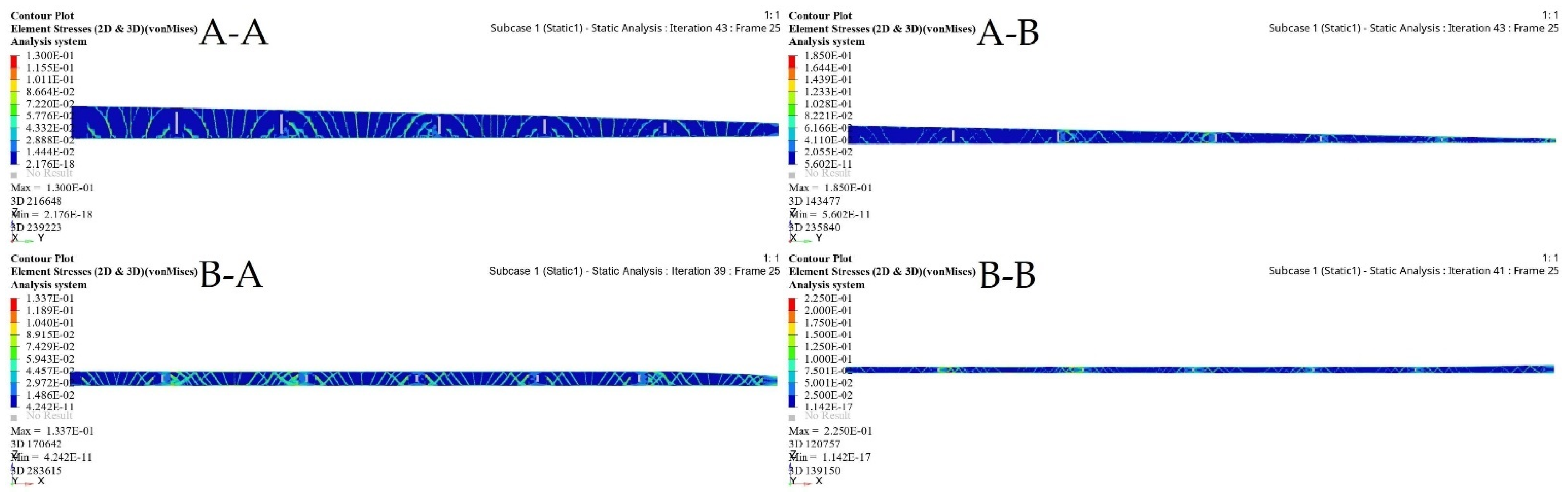
| Iterations | 43 | 43 | 39 | 41 |
| Initial Weight | 1.79 kg | 0.82 kg | 1.1 kg | 0.59 kg |
| Optimized Weight | 0.58 kg | 0.37 kg | 0.43 kg | 0.29 kg |
| Weight reduction Ratio | 67.6% | 54.9% | 60.9% | 50.9% |
| Deformation | 0.00064 mm | 0.00117 mm | 0.00073 mm | 0.00227 mm |
| Stress | 0.13MPa | 0.185 MPa | 0.134 MPa | 0.225 MPa |
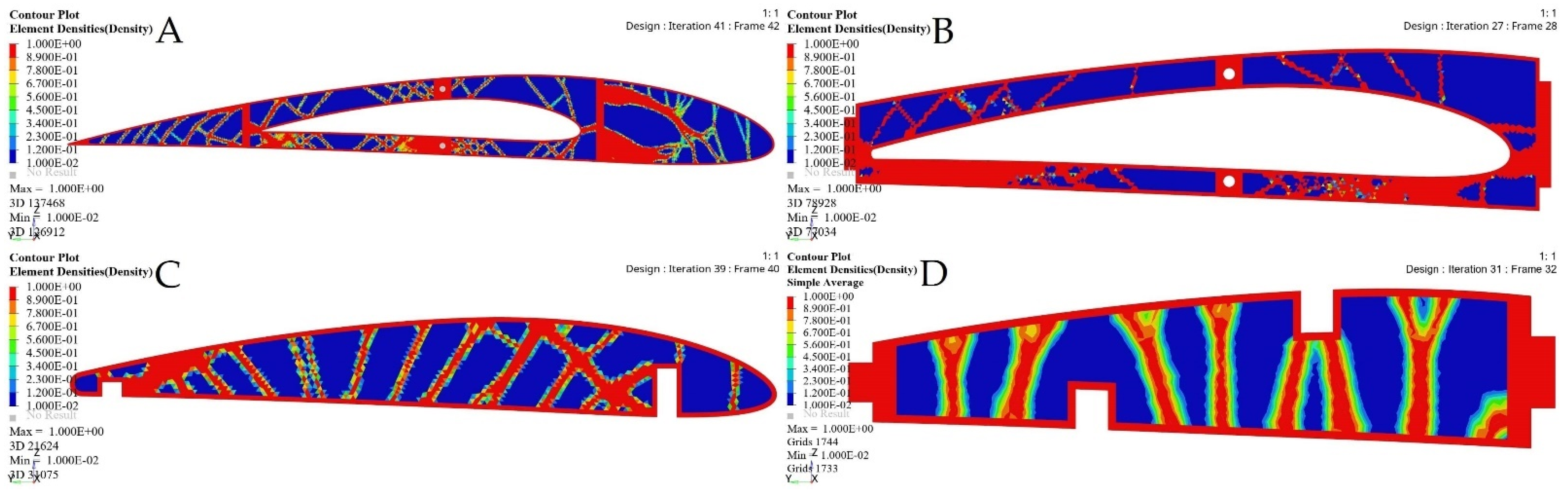
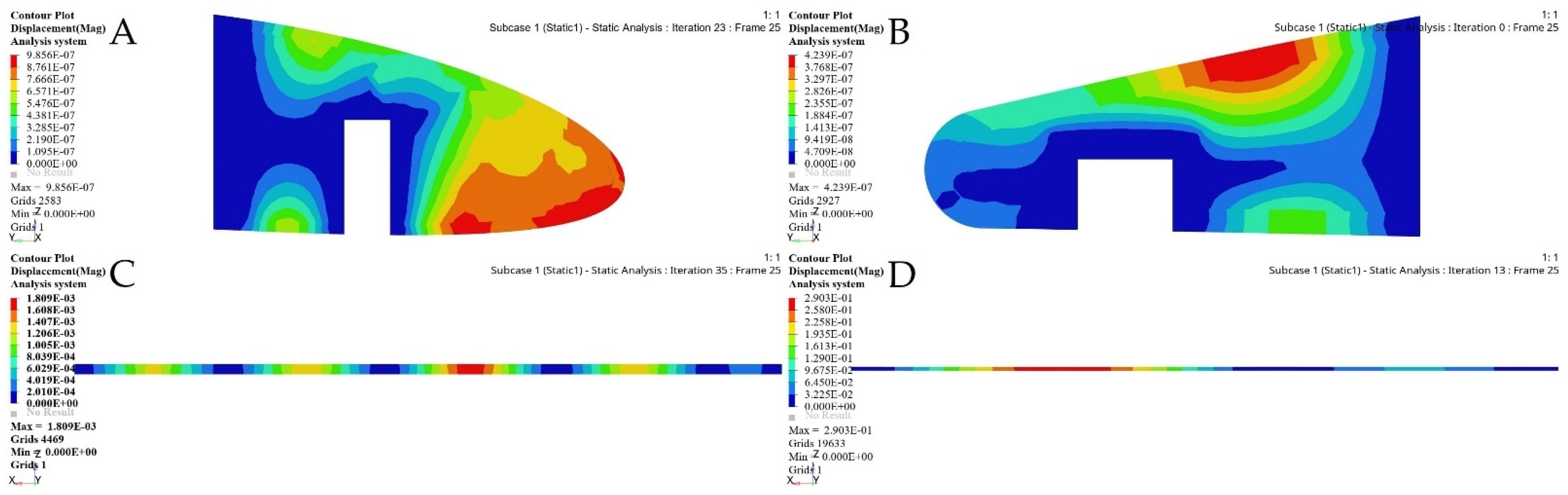
| Iteration | Initial Weight | Optimized Weight | Weight Reduction Ratio | Deformation | Stress | ||
|---|---|---|---|---|---|---|---|
| Fixed Wing | Rib 1 | 41 | 0.539 kg | 0.279 kg | 48.2% | 0.024 mm | 0.85 MPa |
| Rib 2 | 27 | 0.237 kg | 0.1 kg | 57.8% | 0.0088 mm | 2.26 MPa | |
| Rib 3 | 26 | 0.209 kg | 0.095 kg | 54.5% | 0.003 mm | 1.11 MPa | |
| Rib 4 | 24 | 0.167 kg | 0.09 kg | 46.1% | 0.023 mm | 3.813 MPa | |
| Rib 5 | 20 | 0.137 kg | 0.086 kg | 37.2% | 0.04mm | 5.462 MPa | |
| Rib 6 | 9 | 0.107 kg | 0.086 kg | 19.6% | 0.082 mm | 5.737 MPa | |
| Rib 7 | 0 | 0.086 kg | 0.086 kg | 0 | 0 | 0 | |
| Moving Wing | Rib 1 | 40 | 0.134 kg | 0.04 kg | 70.1% | 0.00034 mm | 0.19 MPa |
| Rib 2 | 30 | 0.086 kg | 0.028 kg | 67.4% | 0.00002 mm | 0.047 MPa | |
| Rib 3 | 30 | 0.086 kg | 0.028 kg | 67.4% | 0.00002 mm | 0.047 MPa | |
| Rib 4 | 29 | 0.086 kg | 0.028 kg | 67.4% | 0.00002 mm | 0.045 MPa | |
| Rib 5 | 32 | 0.086 kg | 0.028 kg | 67.4% | 0.00001 mm | 0.032 MPa | |
| Rib 6 | 31 | 0.086 kg | 0.028 kg | 67.4% | 0.00001 mm | 0.027 MPa | |
| Rib 7 | 0 | 0.113 kg | 0.113 kg | 0 | 0 | 0 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elelwi, M.; Botez, R.M.; Dao, T.-M. Structural Sizing and Topology Optimization Based on Weight Minimization of a Variable Tapered Span-Morphing Wing for Aerodynamic Performance Improvements. Biomimetics 2021, 6, 55. https://doi.org/10.3390/biomimetics6040055
Elelwi M, Botez RM, Dao T-M. Structural Sizing and Topology Optimization Based on Weight Minimization of a Variable Tapered Span-Morphing Wing for Aerodynamic Performance Improvements. Biomimetics. 2021; 6(4):55. https://doi.org/10.3390/biomimetics6040055
Chicago/Turabian StyleElelwi, Mohamed, Ruxandra Mihaela Botez, and Thien-My Dao. 2021. "Structural Sizing and Topology Optimization Based on Weight Minimization of a Variable Tapered Span-Morphing Wing for Aerodynamic Performance Improvements" Biomimetics 6, no. 4: 55. https://doi.org/10.3390/biomimetics6040055
APA StyleElelwi, M., Botez, R. M., & Dao, T.-M. (2021). Structural Sizing and Topology Optimization Based on Weight Minimization of a Variable Tapered Span-Morphing Wing for Aerodynamic Performance Improvements. Biomimetics, 6(4), 55. https://doi.org/10.3390/biomimetics6040055







