Asymmetric Airfoil Morphing via Deep Reinforcement Learning
Abstract
:1. Introduction
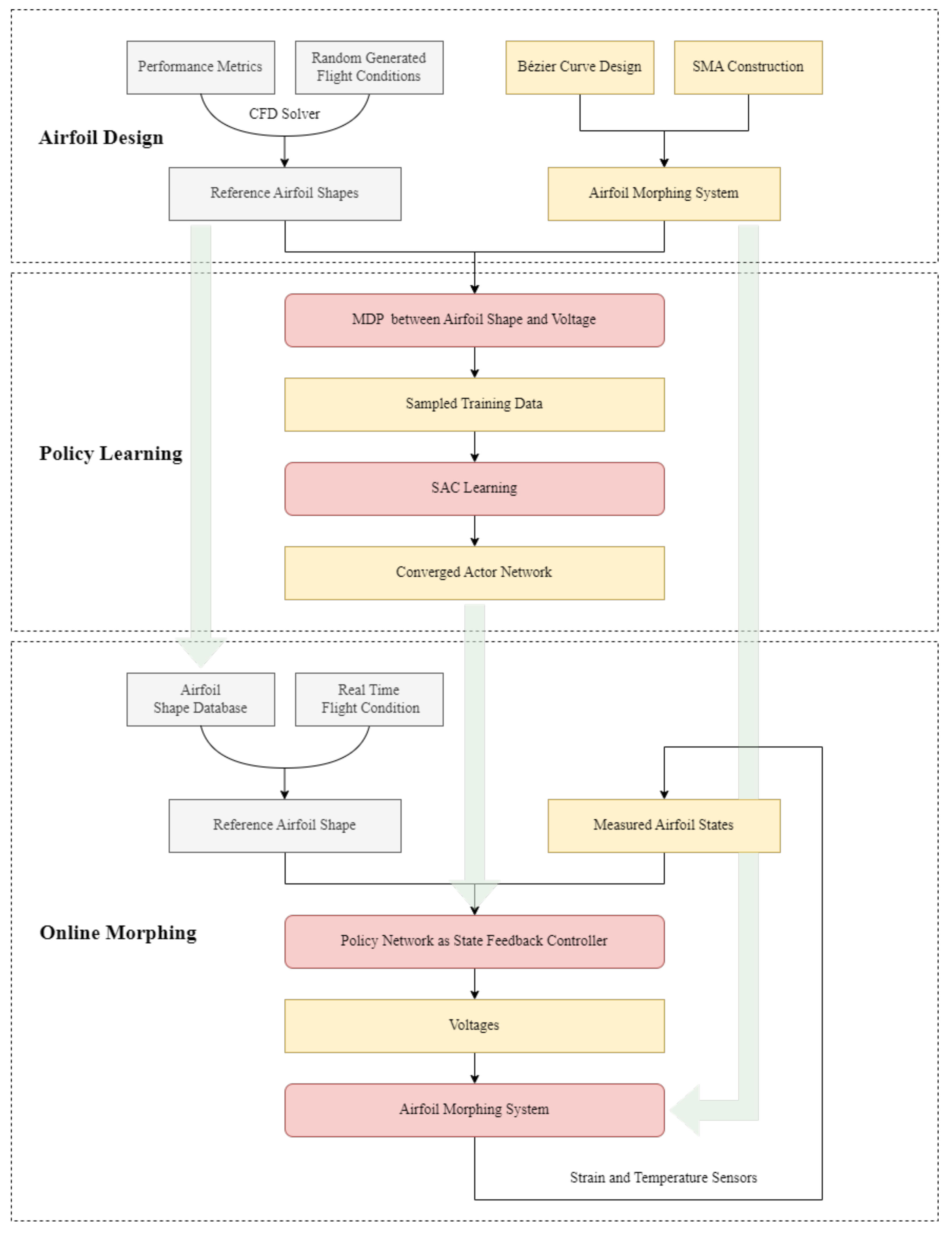
2. Materials and Methods
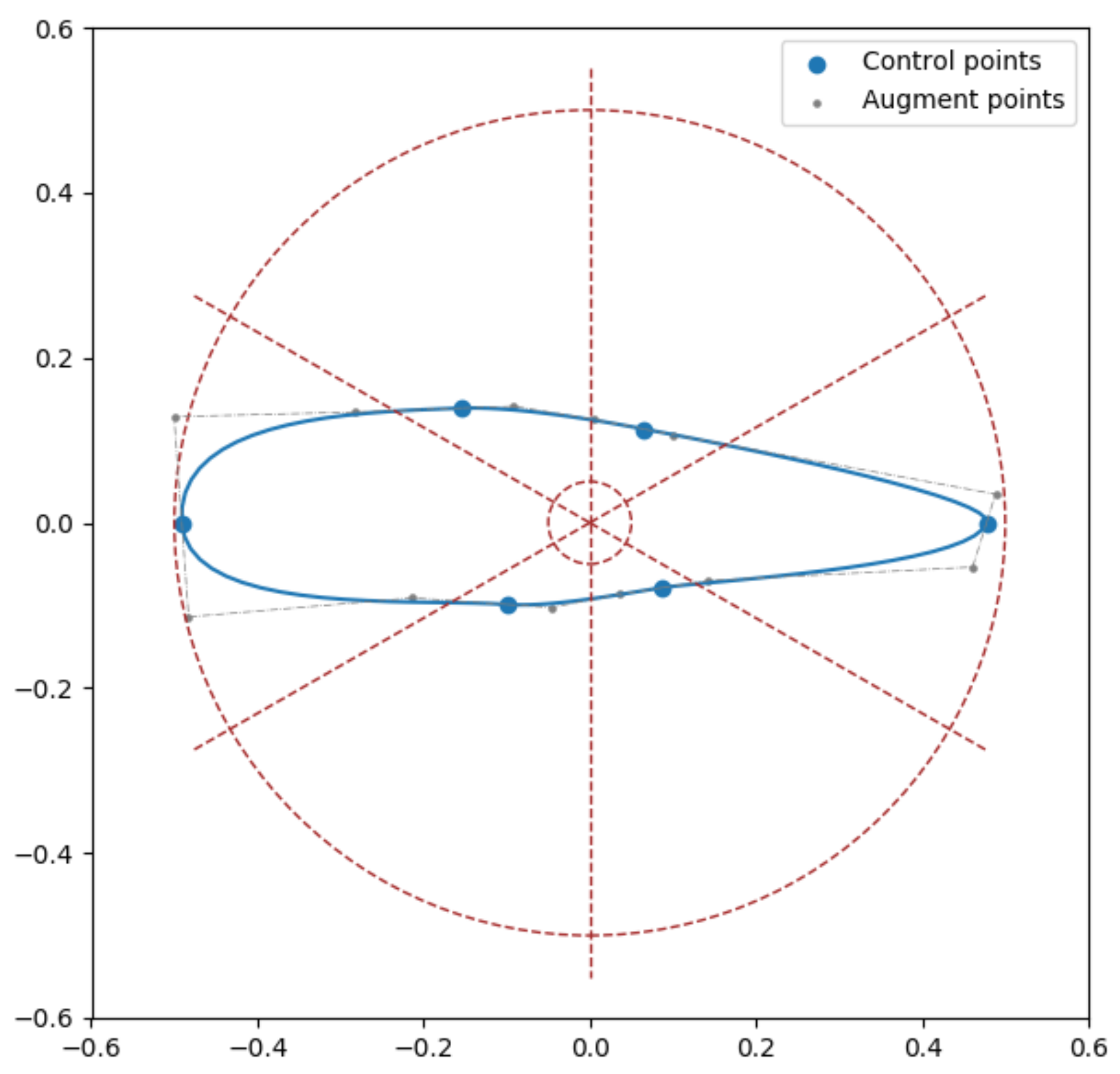
2.1. Asymmetric Airfoil Shape Modeling
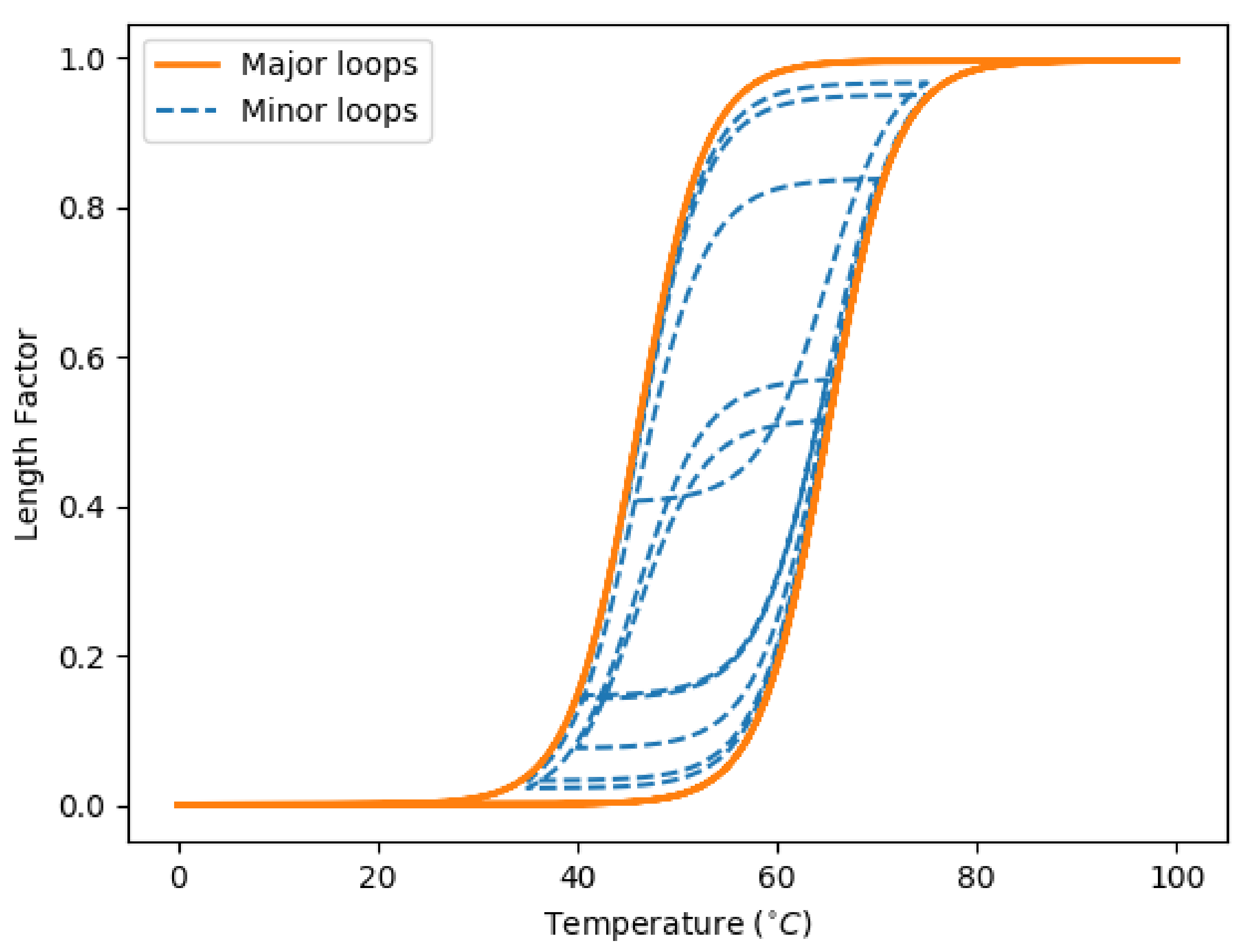
2.2. Dynamic System of Airfoil Morphing
2.3. Reinforcement Learning based Morphing Control
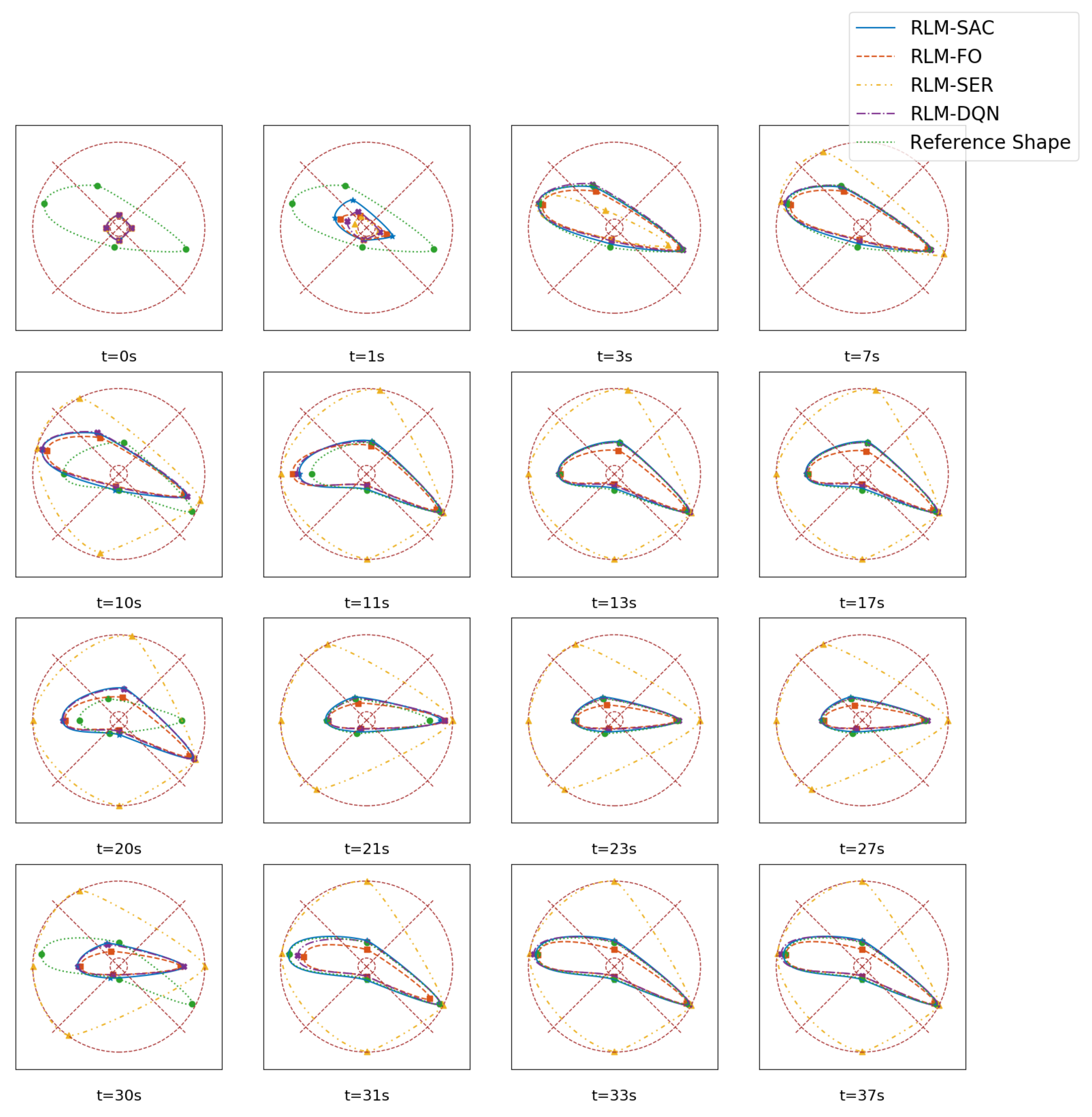
3. Results
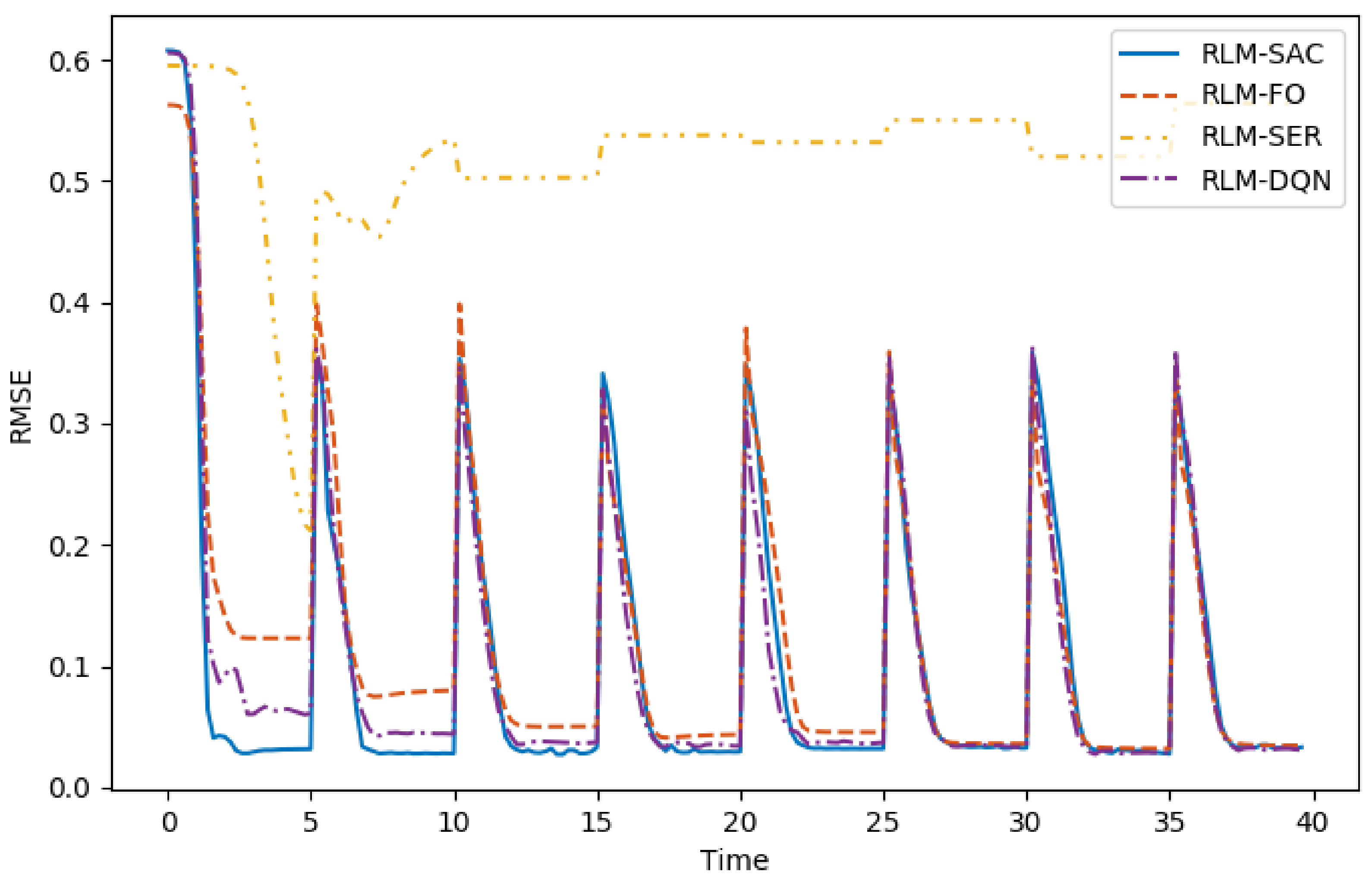
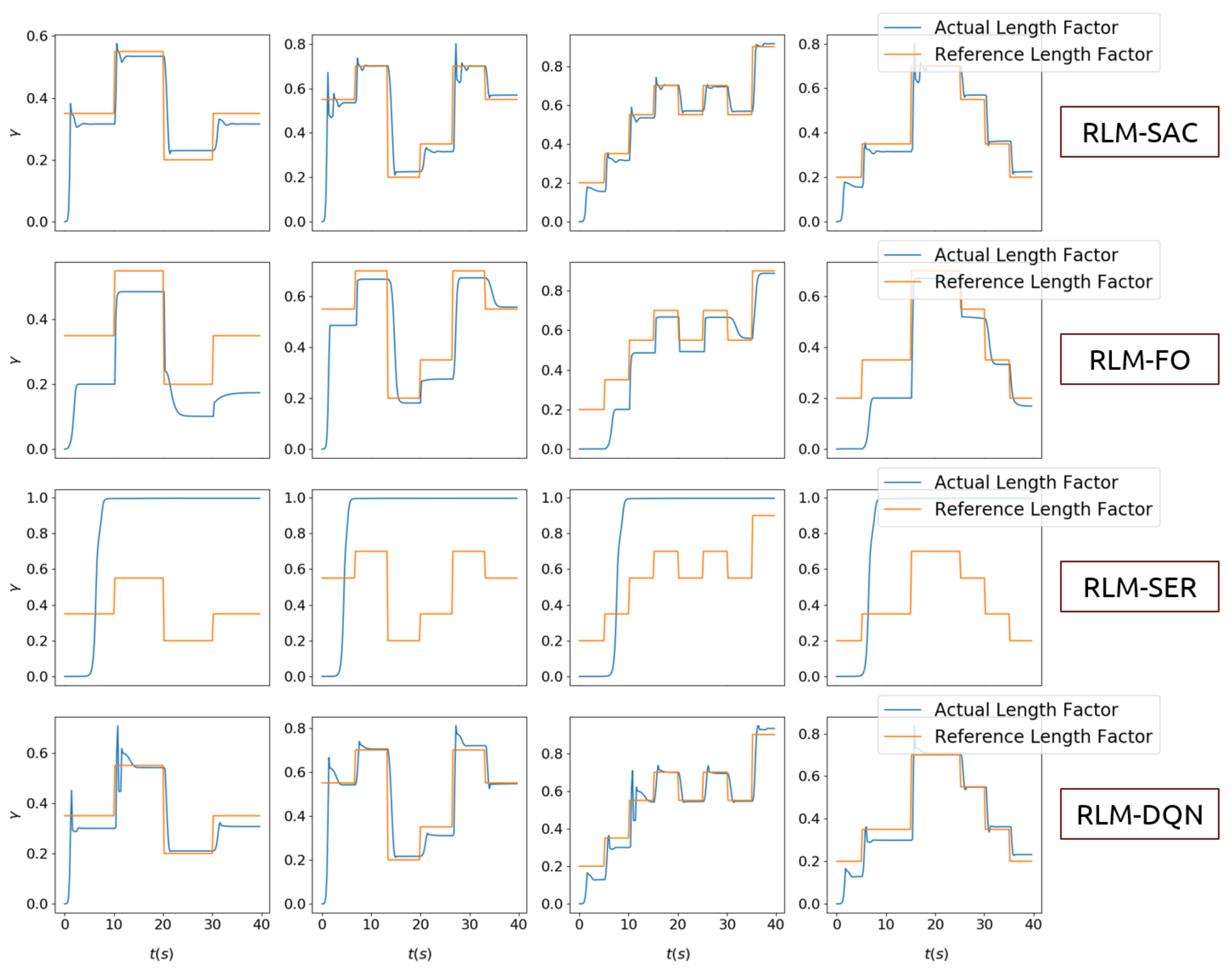
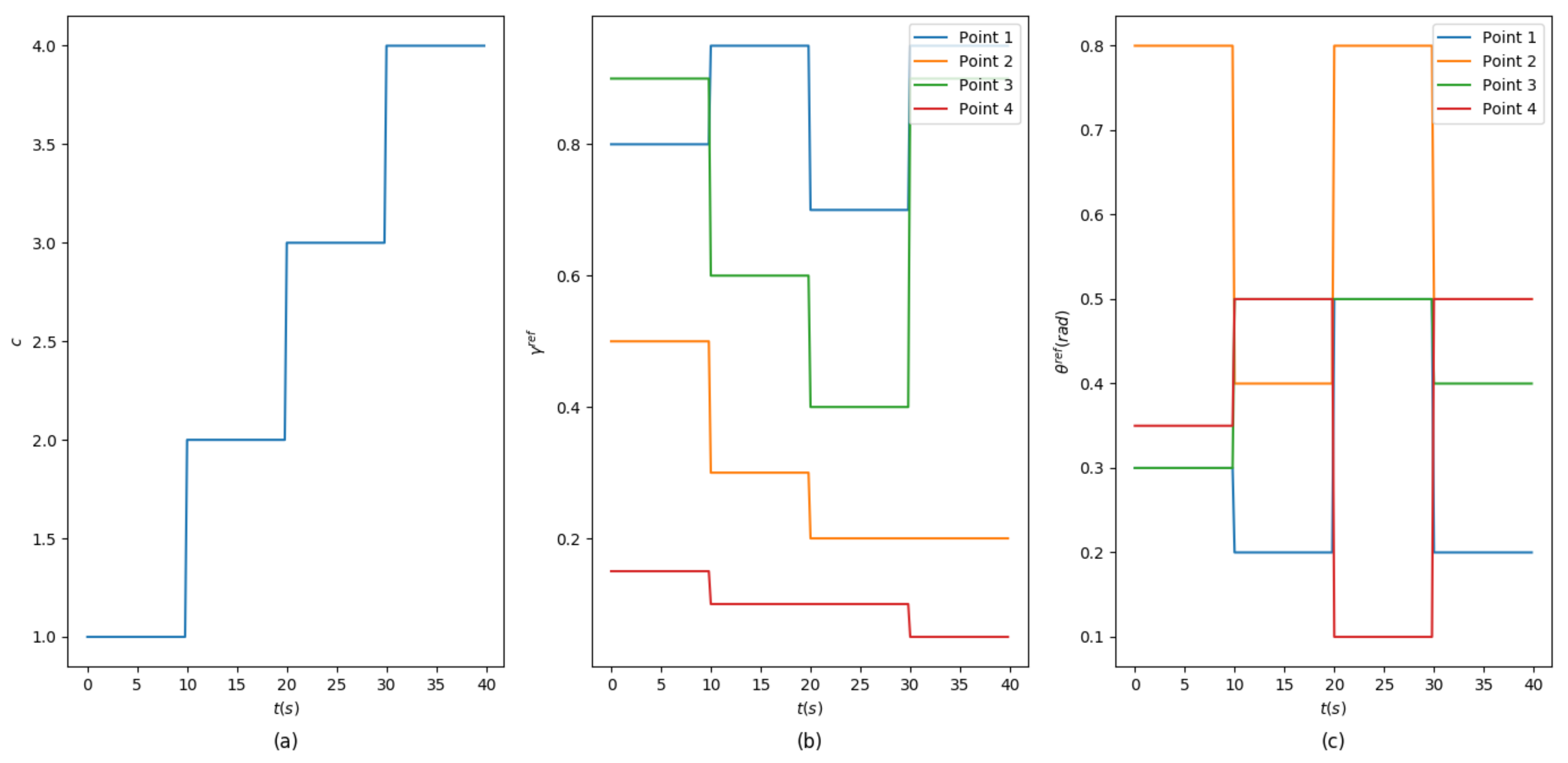
3.1. Tracking Random Shapes
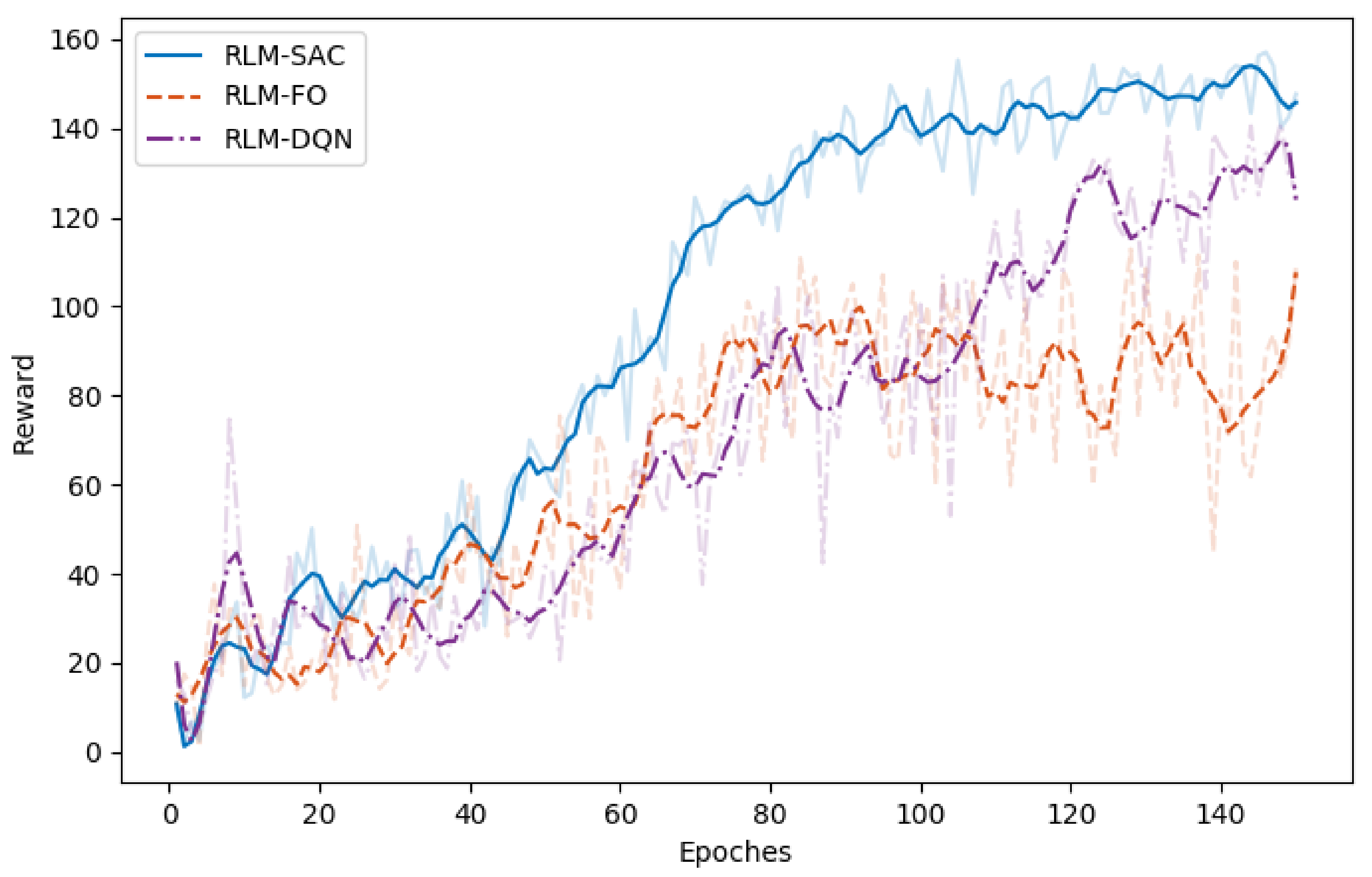
- Second-order state/action versus first-order state/actionIn Section 2, second-order MDP is adopted to model the hysteresis characteristics of the morphing system. Therefore, we chose the states and actions as combinations of that in current step and previous step. We compared the performance with RL algorithms where the policy is generated according to only current states, and the value function was also evaluated with only current states and actions as inputs that are applied in existing investigations on controling SMA wires. We refer to this as RLM-FO.
- Sparse reward versus squared error rewardWe designed a sparse reward taking value in , which is different from traditional RL-based morphing research. We compared that with the square error rewards, which is given bywhich is named RLM-SER.
- SAC versus DQNThe entropy regularization improves the capability of exploration in our algorithm. A modified deep Q learning method was implemented as a comparison, where only the entropy loss was removed, and both the double-Q setting and reparameterization trick remained. We denote this as RLM-DQN.
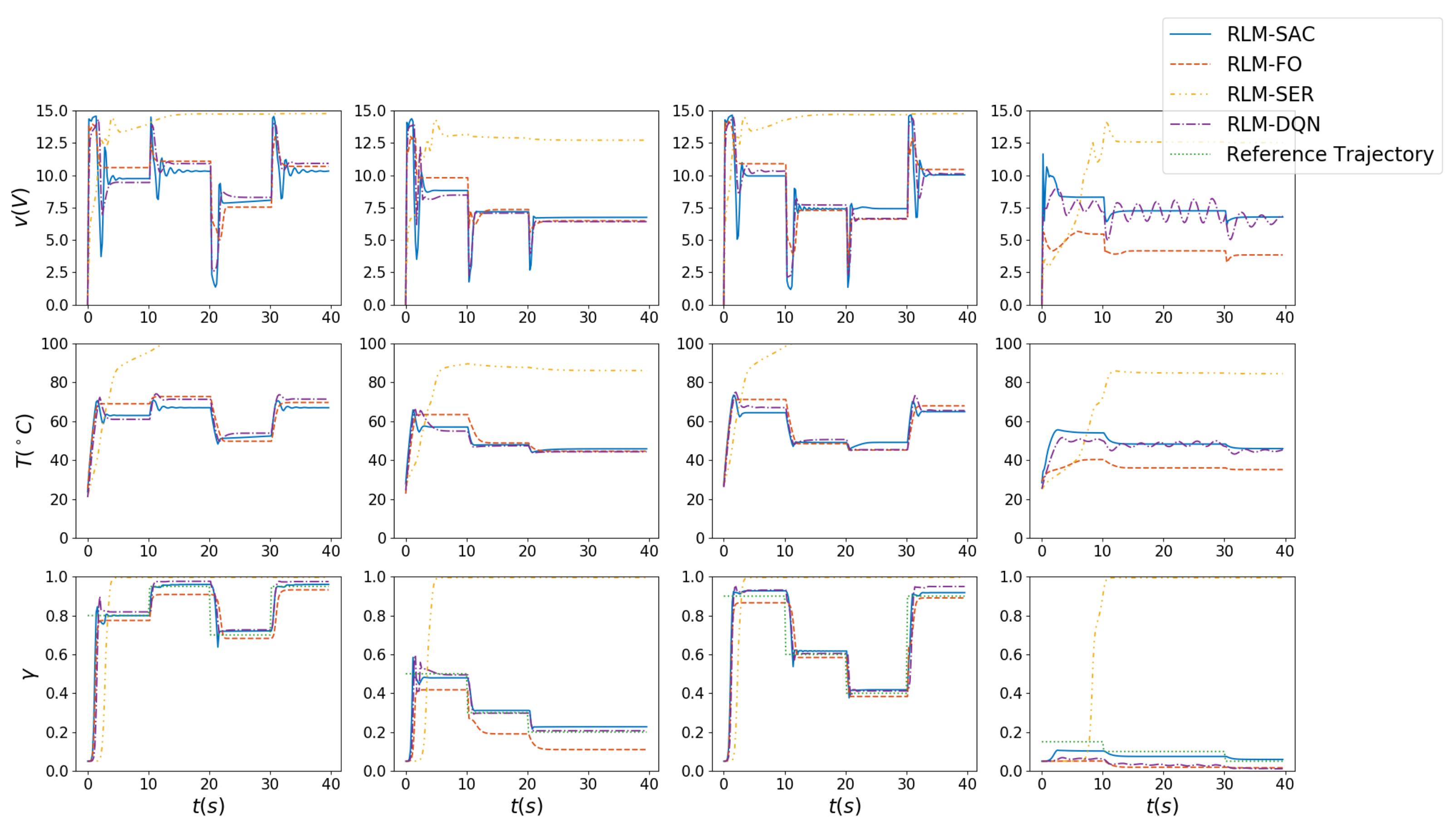
3.2. Morphing Procedure Simulation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CFD | Computational Fluid Dynamics |
| MDP | Markov Decision Process |
| NACA | National Advisory Committee for Aeronautics |
| RL | Reinforcement Learning |
| RMSE | Root-Mean-Squared Error |
| SAC | Soft Actor-Critic |
| SMA | Shape Memory Alloy |
| UAV | Unmanned Aerial Vehicle |
References
- Floreano, D.; Wood, R.J. Science, technology and the future of small autonomous drones. Nature 2015, 521, 460–466. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Harvey, C.; Gamble, L.L.; Bolander, C.R.; Hunsaker, D.F.; Joo, J.J.; Inman, D.J. A review of avian-inspired morphing for UAV flight control. Prog. Aerosp. Sci. 2022, 132, 100825. [Google Scholar] [CrossRef]
- Gerdes, J.W.; Gupta, S.K.; Wilkerson, S.A. A review of bird-inspired flapping wing miniature air vehicle designs. J. Mech. Robot. 2012, 4, 021003. [Google Scholar] [CrossRef] [Green Version]
- Ajanic, E.; Feroskhan, M.; Mintchev, S.; Noca, F.; Floreano, D. Bioinspired wing and tail morphing extends drone flight capabilities. Sci. Robot. 2020, 5, eabc2897. [Google Scholar] [CrossRef]
- Harvey, C.; Baliga, V.; Goates, C.; Hunsaker, D.; Inman, D. Gull-inspired joint-driven wing morphing allows adaptive longitudinal flight control. J. R. Soc. Interface 2021, 18, 20210132. [Google Scholar] [CrossRef]
- Derrouaoui, S.H.; Bouzid, Y.; Guiatni, M.; Dib, I. A comprehensive review on reconfigurable drones: Classification, characteristics, design and control technologies. Unmanned Syst. 2022, 10, 3–29. [Google Scholar] [CrossRef]
- Barbarino, S.; Bilgen, O.; Ajaj, R.M.; Friswell, M.I.; Inman, D.J. A review of morphing aircraft. J. Intell. Mater. Syst. Struct. 2011, 22, 823–877. [Google Scholar] [CrossRef]
- Carruthers, A.C.; Walker, S.M.; Thomas, A.L.; Taylor, G.K. Aerodynamics of aerofoil sections measured on a free-flying bird. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2010, 224, 855–864. [Google Scholar] [CrossRef]
- Liu, T.; Kuykendoll, K.; Rhew, R.; Jones, S. Avian wing geometry and kinematics. AIAA J. 2006, 44, 954–963. [Google Scholar] [CrossRef]
- Li, D.; Zhao, S.; Da Ronch, A.; Xiang, J.; Drofelnik, J.; Li, Y.; Zhang, L.; Wu, Y.; Kintscher, M.; Monner, H.P.; et al. A review of modelling and analysis of morphing wings. Prog. Aerosp. Sci. 2018, 100, 46–62. [Google Scholar] [CrossRef]
- Vasista, S.; Riemenschneider, J.; Monner, H.P. Design and testing of a compliant mechanism-based demonstrator for a droop-nose morphing device. In Proceedings of the 23rd AIAA/AHS Adaptive Structures Conference, Kissimmee, FL, USA, 5–9 January 2015; p. 1049. [Google Scholar]
- Monner, H.P. Realization of an optimized wing camber by using formvariable flap structures. Aerosp. Sci. Technol. 2001, 5, 445–455. [Google Scholar] [CrossRef]
- Skinner, S.N.; Zare-Behtash, H. State-of-the-art in aerodynamic shape optimisation methods. Appl. Soft Comput. 2018, 62, 933–962. [Google Scholar] [CrossRef]
- Wang, Y.; Shimada, K.; Farimani, A.B. Airfoil gan: Encoding and synthesizing airfoils foraerodynamic-aware shape optimization. arXiv 2021, arXiv:2101.04757. [Google Scholar]
- Achour, G.; Sung, W.J.; Pinon-Fischer, O.J.; Mavris, D.N. Development of a conditional generative adversarial network for airfoil shape optimization. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020; p. 2261. [Google Scholar]
- He, X.; Li, J.; Mader, C.A.; Yildirim, A.; Martins, J.R. Robust aerodynamic shape optimization—From a circle to an airfoil. Aerosp. Sci. Technol. 2019, 87, 48–61. [Google Scholar] [CrossRef]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal policy optimization algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
- Viquerat, J.; Rabault, J.; Kuhnle, A.; Ghraieb, H.; Larcher, A.; Hachem, E. Direct shape optimization through deep reinforcement learning. J. Comput. Phys. 2021, 428, 110080. [Google Scholar] [CrossRef]
- Syed, A.A.; Khamvilai, T.; Kim, Y.; Vamvoudakis, K.G. Experimental Design and Control of a Smart Morphing Wing System using a Q-learning Framework. In Proceedings of the 2021 IEEE Conference on Control Technology and Applications (CCTA), San Diego, CA, USA, 9–11 August 2021; pp. 354–359. [Google Scholar]
- Bhola, S.; Pawar, S.; Balaprakash, P.; Maulik, R. Multi-fidelity reinforcement learning framework for shape optimization. arXiv 2022, arXiv:2202.11170. [Google Scholar]
- Liu, J.; Shan, J.; Hu, Y.; Rong, J. Optimal switching control for Morphing aircraft with Aerodynamic Uncertainty. In Proceedings of the 2020 IEEE 16th International Conference on Control & Automation (ICCA), Sapporo, Japan, 6–9 July 2020; pp. 1167–1172. [Google Scholar]
- Valasek, J.; Tandale, M.D.; Rong, J. A reinforcement learning-adaptive control architecture for morphing. J. Aerosp. Comput. Inf. Commun. 2005, 2, 174–195. [Google Scholar] [CrossRef]
- Valasek, J.; Doebbler, J.; Tandale, M.D.; Meade, A.J. Improved adaptive–reinforcement learning control for morphing unmanned air vehicles. IEEE Trans. Syst. Man, Cybern. Part B 2008, 38, 1014–1020. [Google Scholar] [CrossRef]
- Lampton, A.; Niksch, A.; Valasek, J. Reinforcement learning of a morphing airfoil-policy and discrete learning analysis. J. Aerosp. Comput. Inf. Commun. 2010, 7, 241–260. [Google Scholar] [CrossRef]
- Niksch, A.; Valasek, J.; Carlson, L.; Strganac, T. Morphing Aircaft Dynamical Model: Longitudinal Shape Changes. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference and Exhibit, Honolulu, HI, USA, 18–21 August 2008; p. 6567. [Google Scholar]
- Júnior, J.M.M.; Halila, G.L.; Kim, Y.; Khamvilai, T.; Vamvoudakis, K.G. Intelligent data-driven aerodynamic analysis and optimization of morphing configurations. Aerosp. Sci. Technol. 2022, 121, 107388. [Google Scholar] [CrossRef]
- Paranjape, A.A.; Chung, S.J.; Selig, M.S. Flight mechanics of a tailless articulated wing aircraft. Bioinspir. Biomimetics 2011, 6, 026005. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chang, E.; Matloff, L.Y.; Stowers, A.K.; Lentink, D. Soft biohybrid morphing wings with feathers underactuated by wrist and finger motion. Sci. Robot. 2020, 5, eaay1246. [Google Scholar] [CrossRef] [PubMed]
- Di Luca, M.; Mintchev, S.; Heitz, G.; Noca, F.; Floreano, D. Bioinspired morphing wings for extended flight envelope and roll control of small drones. Interface Focus 2017, 7, 20160092. [Google Scholar] [CrossRef] [Green Version]
- Hetrick, J.; Osborn, R.; Kota, S.; Flick, P.; Paul, D. Flight testing of mission adaptive compliant wing. In Proceedings of the 48th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Palm Springs, CA, USA, 4–7 May 2007; p. 1709. [Google Scholar]
- Gilbert, W.W. Mission adaptive wing system for tactical aircraft. J. Aircr. 1981, 18, 597–602. [Google Scholar] [CrossRef]
- Alulema, V.H.; Valencia, E.A.; Pillajo, D.; Jacome, M.; Lopez, J.; Ayala, B. Degree of deformation and power consumption of compliant and rigid-linked mechanisms for variable-camber morphing wing UAVs. In Proceedings of the AIAA Propulsion and Energy 2020 Forum, Online, 24–28 August 2020; p. 3958. [Google Scholar]
- Vasista, S.; Riemenschneider, J.; Van de Kamp, B.; Monner, H.P.; Cheung, R.C.; Wales, C.; Cooper, J.E. Evaluation of a compliant droop-nose morphing wing tip via experimental tests. J. Aircr. 2017, 54, 519–534. [Google Scholar] [CrossRef] [Green Version]
- Barbarino, S.; Flores, E.S.; Ajaj, R.M.; Dayyani, I.; Friswell, M.I. A review on shape memory alloys with applications to morphing aircraft. Smart Mater. Struct. 2014, 23, 063001. [Google Scholar] [CrossRef]
- Sun, J.; Guan, Q.; Liu, Y.; Leng, J. Morphing aircraft based on smart materials and structures: A state-of-the-art review. J. Intell. Mater. Syst. Struct. 2016, 27, 2289–2312. [Google Scholar] [CrossRef]
- Brailovski, V.; Terriault, P.; Georges, T.; Coutu, D. SMA actuators for morphing wings. Phys. Procedia 2010, 10, 197–203. [Google Scholar] [CrossRef] [Green Version]
- DiPalma, M.; Gandhi, F. Autonomous camber morphing of a helicopter rotor blade with temperature change using integrated shape memory alloys. J. Intell. Mater. Syst. Struct. 2021, 32, 499–515. [Google Scholar] [CrossRef]
- Lv, B.; Wang, Y.; Lei, P. Effects of Trailing Edge Deflections Driven by Shape Memory Alloy Actuators on the Transonic Aerodynamic Characteristics of a Super Critical Airfoil. Actuators 2021, 10, 160. [Google Scholar] [CrossRef]
- Elahinia, M.H.; Ashrafiuon, H. Nonlinear control of a shape memory alloy actuated manipulator. J. Vib. Acoust. 2002, 124, 566–575. [Google Scholar] [CrossRef]
- Kirkpatrick, K.; Valasek, J. Active length control of shape memory alloy wires using reinforcement learning. J. Intell. Mater. Syst. Struct. 2011, 22, 1595–1604. [Google Scholar] [CrossRef]
- Kirkpatrick, K.; Valasek, J.; Haag, C. Characterization and control of hysteretic dynamics using online reinforcement learning. J. Aerosp. Inf. Syst. 2013, 10, 297–305. [Google Scholar] [CrossRef] [Green Version]
- Chen, W.; Fuge, M. B∖’ezierGAN: Automatic Generation of Smooth Curves from Interpretable Low-Dimensional Parameters. arXiv 2018, arXiv:1808.08871. [Google Scholar]
- Lepine, J.; Guibault, F.; Trepanier, J.Y.; Pepin, F. Optimized nonuniform rational B-spline geometrical representation for aerodynamic design of wings. AIAA J. 2001, 39, 2033–2041. [Google Scholar] [CrossRef]
- Yasong, Q.; Junqiang, B.; Nan, L.; Chen, W. Global aerodynamic design optimization based on data dimensionality reduction. Chin. J. Aeronaut. 2018, 31, 643–659. [Google Scholar]
- Grey, Z.J.; Constantine, P.G. Active subspaces of airfoil shape parameterizations. AIAA J. 2018, 56, 2003–2017. [Google Scholar] [CrossRef]
- Abbott, I.H.; Von Doenhoff, A.E.; Stivers, L., Jr. Summary of Airfoil Data; No. NACA-TR-824; National Advisory Committee for Aeronautics, Langley Memorial Aeronautical Laboratory: Langley Field, VA, USA, 1945. Available online: https://ntrs.nasa.gov/citations/19930090976 (accessed on 6 September 2013).
- Silisteanu, P.D.; Botez, R.M. Two-dimensional airfoil design for low speed airfoils. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference, Monterey, CA, USA, 5–8 August 2012. [Google Scholar]
- Thomas, N.; Poongodi, D.P. Position control of DC motor using genetic algorithm based PID controller. In Proceedings of the World Congress on Engineering, London, UK, 1–3 July 2009; Volume 2, pp. 1–3. [Google Scholar]
- Hassani, V.; Tjahjowidodo, T.; Do, T.N. A survey on hysteresis modeling, identification and control. Mech. Syst. Signal Process. 2014, 49, 209–233. [Google Scholar] [CrossRef]
- Ma, J.; Huang, H.; Huang, J. Characteristics analysis and testing of SMA spring actuator. Adv. Mater. Sci. Eng. 2013, 2013, 823594. [Google Scholar] [CrossRef] [Green Version]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Haarnoja, T.; Zhou, A.; Abbeel, P.; Levine, S. Soft actor-critic: Off-policy maximum entropy deep reinforcement learning with a stochastic actor. In Proceedings of the International Conference on Machine Learning, PMLR, Stockholm, Sweden, 10–15 July 2018; pp. 1861–1870. [Google Scholar]
- Van Hasselt, H.; Guez, A.; Silver, D. Deep reinforcement learning with double q-learning. In Proceedings of the AAAI Conference on Artificial Intelligence, Phoenix, AZ, USA, 12–17 February 2016; Volume 30. [Google Scholar]
- Kingma, D.P.; Welling, M. Auto-encoding variational bayes. arXiv 2013, arXiv:1312.6114. [Google Scholar]
- Papamakarios, G.; Nalisnick, E.T.; Rezende, D.J.; Mohamed, S.; Lakshminarayanan, B. Normalizing Flows for Probabilistic Modeling and Inference. J. Mach. Learn. Res. 2021, 22, 1–64. [Google Scholar]
- Savitzky, A.; Golay, M.J. Smoothing and differentiation of data by simplified least squares procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]


| Parameter | Value | Parameter | Value |
|---|---|---|---|
| 837.4 | 50.8 | ||
| 20 | 120 | ||
| H | 0.995 | 0.147 | |
| 0.001 | |||
| 46 | 65 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| 0.98 | 0.2 | ||
| 0.995 | 15 | ||
| 1 | 0.02 | ||
| 0.1 |
| RLM-SAC | RLM-FO | RLM-SER | RLM-DQN | |
|---|---|---|---|---|
| 14.04% | 31.44% | 323.6% | 23.24% | |
| 0.0533 | 0.0645 | 0.2202 | 0.0601 | |
| 0.0019 | 0.0055 | 0.0494 | 0.0031 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, K.; Fu, Q.; Cao, R.; Peng, J.; Wang, Q. Asymmetric Airfoil Morphing via Deep Reinforcement Learning. Biomimetics 2022, 7, 188. https://doi.org/10.3390/biomimetics7040188
Lu K, Fu Q, Cao R, Peng J, Wang Q. Asymmetric Airfoil Morphing via Deep Reinforcement Learning. Biomimetics. 2022; 7(4):188. https://doi.org/10.3390/biomimetics7040188
Chicago/Turabian StyleLu, Kelin, Qien Fu, Rui Cao, Jicheng Peng, and Qianshuai Wang. 2022. "Asymmetric Airfoil Morphing via Deep Reinforcement Learning" Biomimetics 7, no. 4: 188. https://doi.org/10.3390/biomimetics7040188
APA StyleLu, K., Fu, Q., Cao, R., Peng, J., & Wang, Q. (2022). Asymmetric Airfoil Morphing via Deep Reinforcement Learning. Biomimetics, 7(4), 188. https://doi.org/10.3390/biomimetics7040188




