The Limb Kinetics of Goat Walking on the Slope with Different Angles
Abstract
:1. Introduction
2. Materials and Methods
2.1. Animal
2.2. Experimental Scheme Design
2.3. Data Collection
2.4. Data Analysis and Outcome Parameters
2.5. Statistical Analysis
3. Results
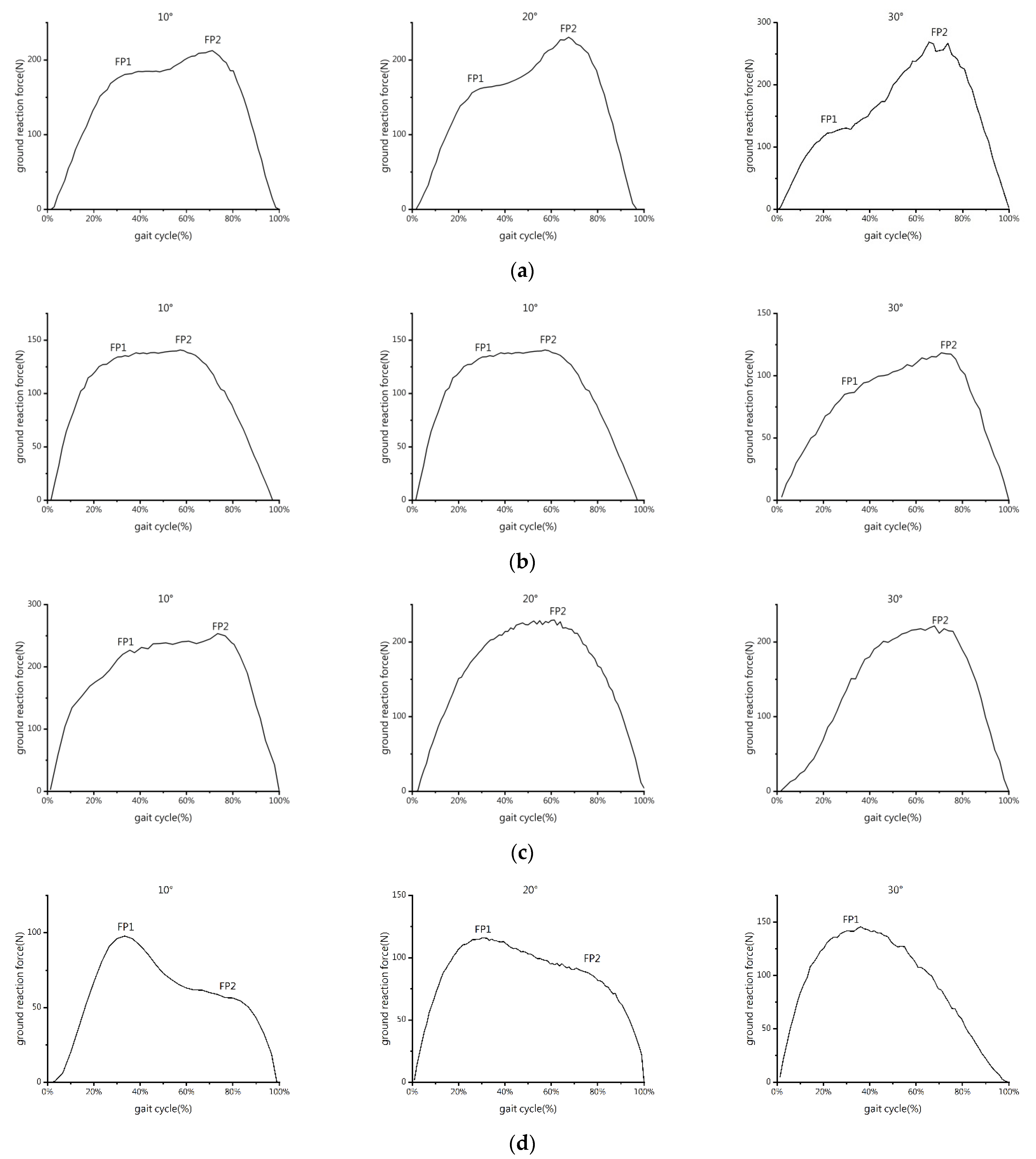
3.1. GRF-Time Curve
3.2. Included Angle between the Propulsive Force and Slope
3.3. Propulsive Force-Time Curve, GRF-Time Curve and Impulse
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Sherrod, V.; Johnson, C.C.; Killpack, M.D. Design Optimization for Rough Terrain Traversal Using a Compliant, Continuum-Joint, Quadruped Robot. Front. Robot. AI 2022, 9, 860020. [Google Scholar] [CrossRef] [PubMed]
- Zhao, X.; Wu, Y.; You, Y.; Laurenzi, A.; Tsagarakis, N. Variable stiffness locomotion with guaranteed stability for quadruped robots traversing uneven terrains. Front. Robot. AI 2022, 9, 874290. [Google Scholar] [CrossRef] [PubMed]
- Uno, K.; Valsecchi, G.; Hutter, M.; Yoshida, K. Simulation-Based Climbing Capability Analysis for Quadrupedal Robots. In Proceedings of the Climbing and Walking Robots Conference, Virtual Event, Japan, 30 August–1 September 2021; Springer: Cham, Switzerland; pp. 179–191. [Google Scholar]
- Zheng, Y.; Xu, K.; Tian, Y.; Deng, H.; Ding, X. Bionic Design and Analysis of a Novel Quadruped Robot with a Multistage Buffer System. Chin. J. Mech. Eng. 2022, 35, 32. [Google Scholar] [CrossRef]
- Torres-Pardo, A.; Pinto-Fernández, D.; Garabini, M.; Angelini, F.; Rodriguez-Cianca, D.; Massardi, S.; Tornero-López, J.; Moreno, J.C.; Torricelli, D. Legged locomotion over irregular terrains: State of the art of human and robot performance. Bioinspiration Biomim. 2022, 17, 061002. [Google Scholar] [CrossRef] [PubMed]
- Full, R.J.; Kubow, T.; Schmitt, J.; Holmes, P.; Koditschek, D. Quantifying Dynamic Stability and Maneuverability in Legged Locomotion. Integr. Comp. Biol. 2002, 42, 149–157. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wilshin, S.; Reeve, M.A.; Spence, A.J. Dog galloping on rough terrain exhibits similar limb co-ordination patterns and gait variability to that on flat terrain. Bioinspiration Biomim. 2020, 16, 015001. [Google Scholar] [CrossRef] [PubMed]
- Holmes, P.; Full, R.J.; Koditschek, D.; Guckenheimer, J. The Dynamics of Legged Locomotion: Models, Analyses, and Challenges. SIAM Rev. 2006, 48, 207–304. [Google Scholar] [CrossRef] [Green Version]
- Wilshin, S.; Reeve, M.A.; Haynes, G.C.; Revzen, S.; Koditschek, D.E.; Spence, A.J. Longitudinal quasi-static stability predicts changes in dog gait on rough terrain. J. Exp. Biol. 2017, 220, 1864–1874. [Google Scholar] [CrossRef] [Green Version]
- Daley, M.A.; Biewener, A.A. Running over rough terrain reveals limb control for intrinsic stability. Proc. Natl. Acad. Sci. USA 2006, 103, 15681–15686. [Google Scholar] [CrossRef] [Green Version]
- McLaughlin, R.M. Kinetic and Kinematic Gait Analysis in Dogs. Vet. Clin. N. Am. Small Anim. Pract. 2001, 31, 193–201. [Google Scholar] [CrossRef]
- Gillette, R.L.; Angle, T.C. Recent developments in canine locomotor analysis: A review. Vet. J. 2008, 178, 165–176. [Google Scholar] [CrossRef] [PubMed]
- Anzuino, K.; Bell, N.J.; Bazeley, K.J.; Nicol, C.J. Assessment of welfare on 24 commercial UK dairy goat farms based on direct observations. Vet. Rec. 2010, 167, 774–780. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vieira, A.; Oliveira, M.D.; Nunes, T.; Stilwell, G. Making the case for developing alternative lameness scoring systems for dairy goats. Appl. Anim. Behav. Sci. 2015, 171, 94–100. [Google Scholar] [CrossRef]
- Hunt, W.F.; Thomas, V.G.; Stiefel, W. Analysis of video-recorded images to determine linear and angular dimensions in the growing horse. Equine Vet. J. 1999, 31, 402–410. [Google Scholar] [CrossRef]
- Bosch, S.; Serra Bragança, F.; Marin-Perianu, M.; Marin-Perianu, R.; Van Der Zwaag, B.J.; Voskamp, J.; Back, W.; Van Weeren, R.; Havinga, P. EquiMoves: A Wireless Networked Inertial Measurement System for Objective Examination of Horse Gait. Sensors 2018, 18, 850. [Google Scholar] [CrossRef] [Green Version]
- Bragança, F.M.S.; Rhodin, M.; Wiestner, T.; Hernlund, E.; Pfau, T.; Van Weeren, P.; Weishaupt, M.A. Quantification of the effect of instrumentation error in objective gait assessment in the horse on hindlimb symmetry parameters. Equine Vet. J. 2017, 50, 370–376. [Google Scholar] [CrossRef] [Green Version]
- Biknevicius, A.R.; Mullineaux, D.R.; Clayton, H.M. Ground reaction forces and limb function in tölting Icelandic horses. Equine Vet. J. 2010, 36, 743–747. [Google Scholar] [CrossRef]
- Hobbs, S.J.; Clayton, H.M. Sagittal plane ground reaction forces, centre of pressure and centre of mass in trotting horses. Vet. J. 2013, 198, e14–e19. [Google Scholar] [CrossRef]
- Munoz-Nates, F.; Chateau, H.; Pourcelot, P.; Camus, M.; Ravary-Plumioen, B.; Denoix, J.M.; Crevier-Denoix, N. Ground reaction force and impulses of fore and hindlimbs in horses at trot on an asphalt track: Effects of an inclined (uphill) compared to a flat surface. Comput. Methods Biomech. Biomed. Eng. 2017, 20, S143–S144. [Google Scholar] [CrossRef] [Green Version]
- Walker, A.; Pfau, T.; Channon, A.; Wilson, A. Assessment of dairy cow locomotion in a commercial farm setting: The effects of walking speed on ground reaction forces and temporal and linear stride characteristics. Res. Vet. Sci. 2010, 88, 179–187. [Google Scholar] [CrossRef]
- Waldern, N.M.; Weishaupt, M.A.; Wiestner, T.; Nuss, K. Kinetische Auswertung des Schrittes von Jungrindern und Kühen auf einem instrumentierten Laufband. Tierarztl. Prax. Ausg. G 2015, 43, 73–80. [Google Scholar] [CrossRef] [PubMed]
- Oehme, B.; Grund, S.; Munzel, J.; Mülling, C. Kinetic effect of different ground conditions on the sole of the claws of standing and walking dairy cows. J. Dairy Sci. 2019, 102, 10119–10128. [Google Scholar] [CrossRef] [PubMed]
- Rifkin, R.E.; Grzeskowiak, R.; Mulon, P.-Y.; Adair, H.S.; Biris, A.S.; Dhar, M.; Anderson, D.E. Use of a pressure-sensing walkway system for biometric assessment of gait characteristics in goats. PLoS ONE 2019, 14, e0223771. [Google Scholar] [CrossRef] [PubMed]
- Schnabl-Feichter, E.; Tichy, A.; Bockstahler, B. Coefficients of variation of ground reaction force measurement in cats. PLoS ONE 2017, 12, e0171946. [Google Scholar] [CrossRef]
- Liu, C.; Wang, G.; Zhou, H.; Mei, Y.; Asafo-Duho, B.M.K. Adaptability of Kinetic Parameters to a Narrow Speed Range in Healthy Free-Moving Cats. Math. Probl. Eng. 2020, 2020, 2954329. [Google Scholar] [CrossRef]
- Corbee, R.; Maas, H.; Doornenbal, A.; Hazewinkel, H. Forelimb and hindlimb ground reaction forces of walking cats: Assessment and comparison with walking dogs. Vet. J. 2014, 202, 116–127. [Google Scholar] [CrossRef]
- Schnabl, E.; Bockstahler, B. Systematic review of ground reaction force measurements in cats. Vet. J. 2015, 206, 83–90. [Google Scholar] [CrossRef]
- Glyde, M.R.; Hosgood, G.; Dempsey, A.R.; Wickham, S.; Appelgrein, C. Kinetic Gait Analysis of Agility Dogs Entering the A-Frame. Vet. Comp. Orthop. Traumatol. 2019, 32, 097–103. [Google Scholar] [CrossRef]
- Gündemir, O.; Duro, S.; Kaya, D.A.; Yazgan, Y.Z. Temporo-spatial and kinetic gait parameters in English setter dogs. Anat. Histol. Embryol. 2020, 49, 763–769. [Google Scholar] [CrossRef]
- Schnabl-Feichter, E.; Tichy, A.; Gumpenberger, M.; Bockstahler, B. Comparison of ground reaction force measurements in a population of Domestic Shorthair and Maine Coon cats. PLoS ONE 2018, 13, e0208085. [Google Scholar] [CrossRef]
- Wiestner, T.; Galeandro, L.; Hässig, M.; Montavon, P.M.; Voss, K. Effect of dog breed and body conformation on vertical ground reaction forces, impulses, and stance times. Vet. Comp. Orthop. Traumatol. 2011, 24, 106–112. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Verdugo, M.R.; Rahal, S.C.; Agostinho, F.S.; Govoni, V.M.; Mamprim, M.J.; Monteiro, F.O. Kinetic and temporospatial parameters in male and female cats walking over a pressure sensing walkway. BMC Vet. Res. 2013, 9, 129. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lascelles, B.D.X.; Findley, K.; Correa, M.; Marcellin-Little, D.; Roe, S. Kinetic evaluation of normal walking and jumping in cats, using a pressure-sensitive walkway. Vet. Rec. 2007, 160, 512–516. [Google Scholar] [CrossRef] [PubMed]
- Agostinho, F.S.; Rahal, S.C.; Araújo, F.A.P.; Conceição, R.T.; Hussni, C.A.; El-Warrak, A.O.; Monteiro, F.O.B. Gait analysis in clinically healthy sheep from three different age groups using a pressure-sensitive walkway. BMC Vet. Res. 2012, 8, 87. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kim, J.; Breur, G.J. Temporospatial and kinetic characteristics of sheep walking on a pressure sensing walkway. Can. J. Vet. Res. 2008, 72, 50–55. [Google Scholar]
- Lee, D.V. Effects of grade and mass distribution on the mechanics of trotting in dogs. J. Exp. Biol. 2011, 214, 402–411. [Google Scholar] [CrossRef] [Green Version]
- Arnold, A.S.; Lee, D.V.; Biewener, A.A. Modulation of joint moments and work in the goat hindlimb with locomotor speed and surface grade. J. Exp. Biol. 2013, 216, 2201–2212. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.; Kui, H.; Qian, Z.; Ren, L. Hoof Pressure Distribution Pattern of Blue Sheep During Walking on Different Slopes: A Subject-Specific Analysis. Front. Vet. Sci. 2021, 8, 633509. [Google Scholar] [CrossRef]
- Lee, D.V.; Biewener, A.A. BigDog-Inspired Studies in the Locomotion of Goats and Dogs. Integr. Comp. Biol. 2011, 51, 190–202. [Google Scholar] [CrossRef] [Green Version]
- Lewinson, R.T.; Stefanyshyn, D.J. A descriptive analysis of the climbing mechanics of a mountain goat (Oreamnos americanus). Zoology 2016, 119, 541–546. [Google Scholar] [CrossRef]
- Lee, D.V.; McGuigan, M.P.; Yoo, E.H.; Biewener, A.A. Compliance, actuation, and work characteristics of the goat foreleg and hindleg during level, uphill, and downhill running. J. Appl. Physiol. 2008, 104, 130–141. [Google Scholar] [CrossRef] [PubMed]
- Chevallereau, C.; Boyer, F.; Porez, M.; Mauny, J.; Aoustin, Y. Morphological self stabilization of locomotion gaits: Illustration on a few examples from bio-inspired locomotion. Bioinspiration Biomim. 2017, 12, 046006. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kazakidi, A.; Vavourakis, V.; Tsakiris, D.; Ekaterinaris, J. A numerical investigation of flow around octopus-like arms: Near-wake vortex patterns and force development. Comput. Methods Biomech. Biomed. Eng. 2014, 18, 1321–1339. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Reynolds, A.M.; Bartumeus, F.; Kölzsch, A.; van de Koppel, J. Signatures of chaos in animal search patterns. Sci. Rep. 2016, 6, 23492. [Google Scholar] [CrossRef] [Green Version]
- Chu, K.M.I.; Seto, S.H.; Beloozerova, I.N.; Marlinski, V. Strategies for obstacle avoidance during walking in the cat. J. Neurophysiol. 2017, 118, 817–831. [Google Scholar] [CrossRef] [Green Version]
- Ma, W.-L.; Ames, A.D. From Bipedal Walking to Quadrupedal Locomotion: Full-Body Dynamics Decomposition for Rapid Gait Generation. In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May–31 August 2020; IEEE: Piscataway, NC, USA; pp. 4491–4497. [Google Scholar] [CrossRef]
- Ma, W.-L.; Csomay-Shanklin, N.; Ames, A.D. Quadrupedal Robotic Walking on Sloped Terrains via Exact Decomposition into Coupled Bipedal Robots. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 24 October 2020–24 January 2022; IEEE: Piscataway, NC, USA; pp. 4006–4011. [Google Scholar]




| Angle of Slope | Propulsive Force Impulse | Ground Reaction Force Impulse | ||||||
|---|---|---|---|---|---|---|---|---|
| Uphill | Downhill | Uphill | Downhill | |||||
| Forelimb | Hindlimb | Forelimb | Hindlimb | Forelimb | Hindlimb | Forelimb | Hindlimb | |
| 10° | 148.42 ± 0.54 | 126.00 ± 1.79 | 215.64 ± 1.61 | 67.97 ± 1.12 | 142.67 ± 0.70 | 98.57 ± 1.44 | 184.48 ± 1.61 | 57.39 ± 1.50 |
| 20° | 144.12 ± 0.90 | 148.94 ± 1.14 | 177.62 ± 1.74 | 96.93 ± 1.59 | 138.52 ± 0.65 | 121.39 ± 1.94 | 155.24 ± 0.75 | 84.80 ± 0.78 |
| 30° | 204.67 ± 1.37 | 89.18 ± 0.24 | 151.02 ± 1.43 | 99.93 ± 0.50 | 138.91 ± 1.09 | 76.35 ± 0.96 | 134.50 ± 1.16 | 90.83 ± 0.66 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tian, W.; Zhang, J.; Zhou, K.; Wang, Z.; Dang, R.; Jiang, L.; Wang, J.; Cong, Q. The Limb Kinetics of Goat Walking on the Slope with Different Angles. Biomimetics 2022, 7, 220. https://doi.org/10.3390/biomimetics7040220
Tian W, Zhang J, Zhou K, Wang Z, Dang R, Jiang L, Wang J, Cong Q. The Limb Kinetics of Goat Walking on the Slope with Different Angles. Biomimetics. 2022; 7(4):220. https://doi.org/10.3390/biomimetics7040220
Chicago/Turabian StyleTian, Weijun, Jinhua Zhang, Kuiyue Zhou, Zhirui Wang, Ruina Dang, Lei Jiang, Ju Wang, and Qian Cong. 2022. "The Limb Kinetics of Goat Walking on the Slope with Different Angles" Biomimetics 7, no. 4: 220. https://doi.org/10.3390/biomimetics7040220
APA StyleTian, W., Zhang, J., Zhou, K., Wang, Z., Dang, R., Jiang, L., Wang, J., & Cong, Q. (2022). The Limb Kinetics of Goat Walking on the Slope with Different Angles. Biomimetics, 7(4), 220. https://doi.org/10.3390/biomimetics7040220





