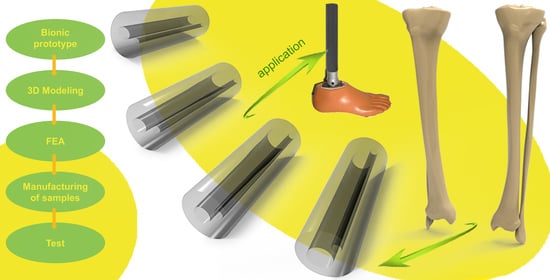
Development of a Bionic Tube with High Bending-Stiffness Properties Based on Human Tibiofibular Shapes
Abstract
:1. Introduction
2. Materials and Methods
2.1. Human Tibiofibular Reconstruction
2.2. Design of Bionic Tubes
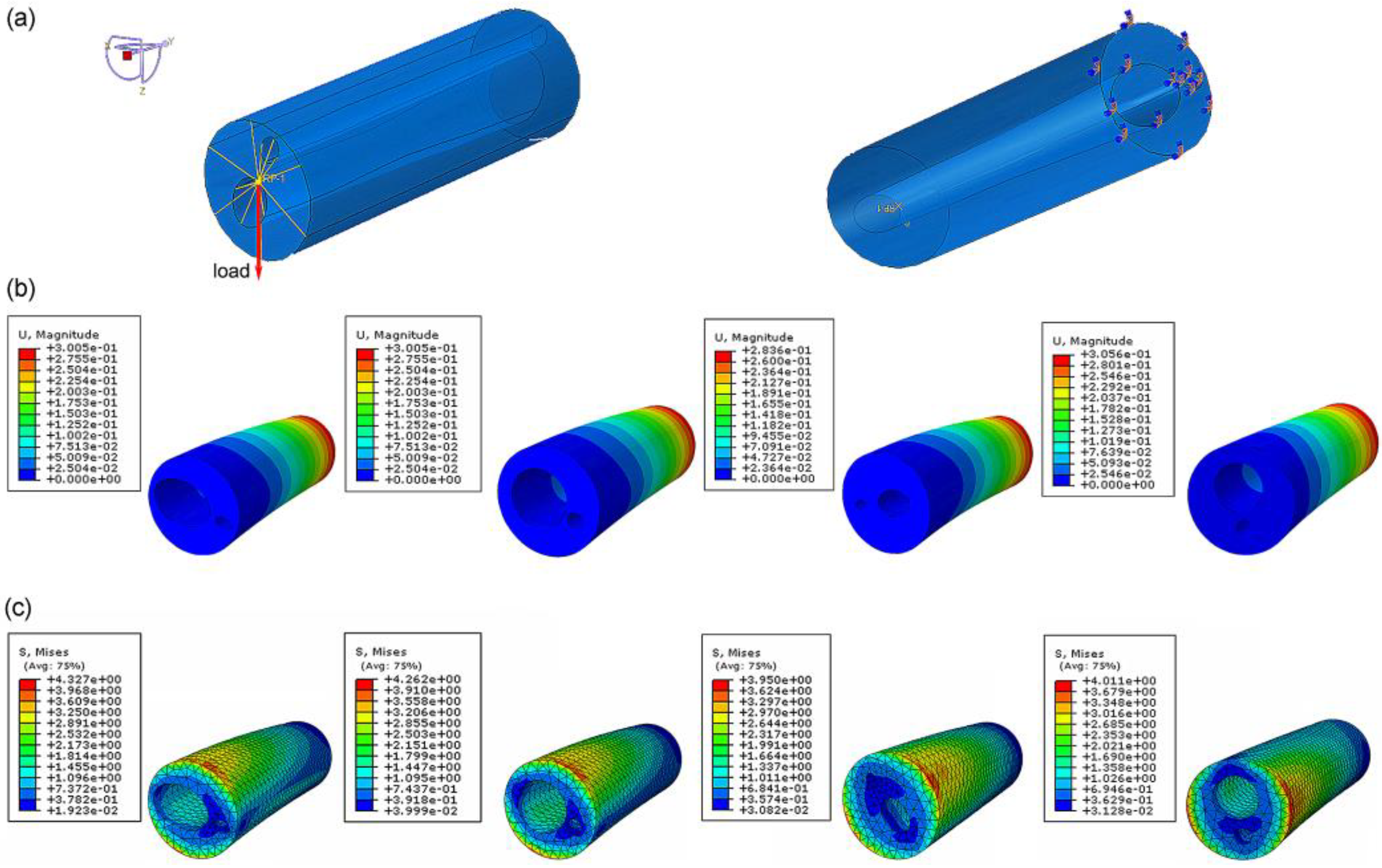
2.3. Finite-Element Simulation
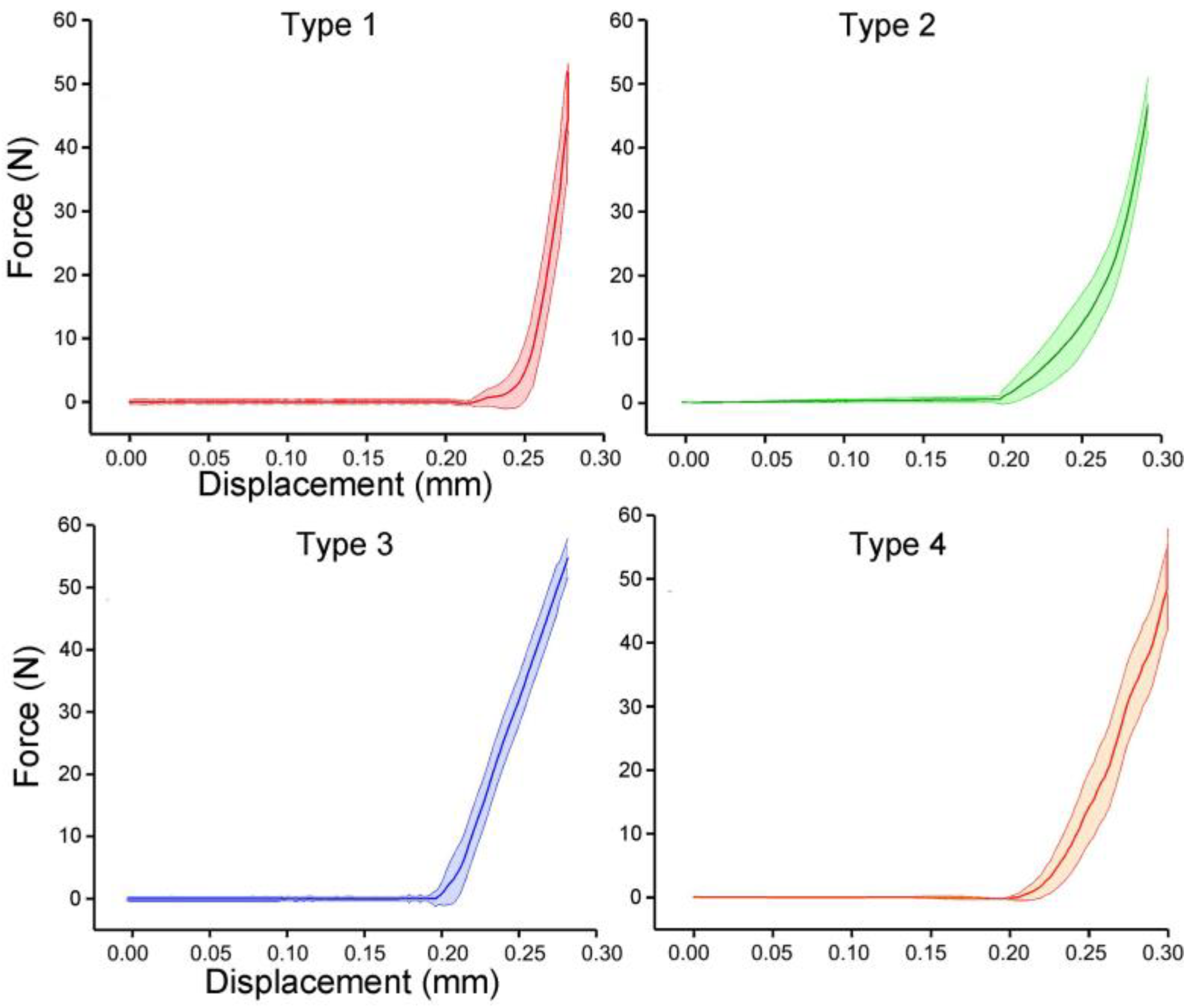
2.4. Bending Test of Bionic Tubes
2.5. Statistical Analysis
3. Results
3.1. Division of Bone Parameters and Design of the Bionic Tubes
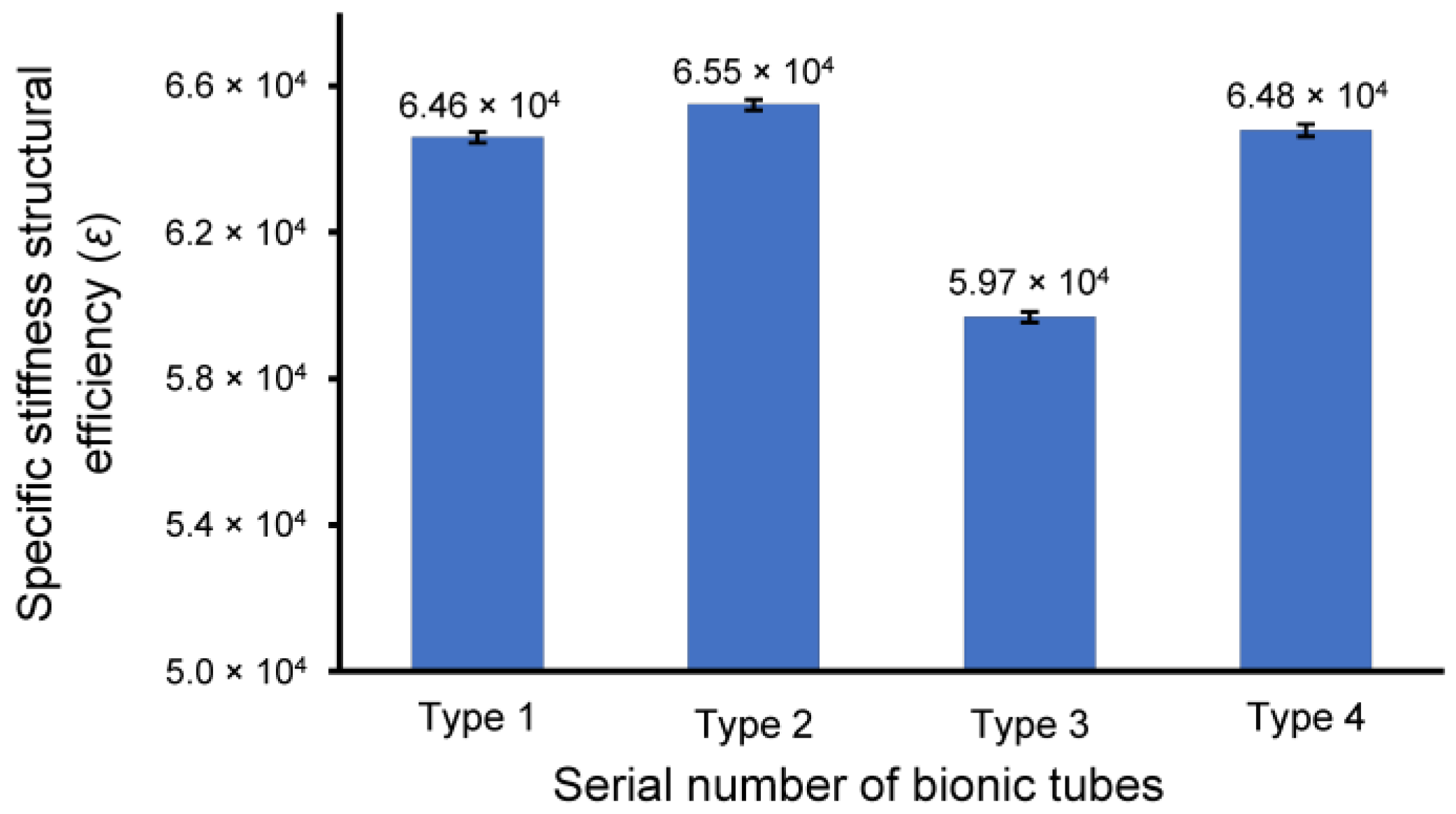
3.2. Specifi cStiffness of Bionic Tubes
3.3. Bending Tests of Bionic Tubes
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, R.; Pang, H.; Han, D.; Xue, S.; Jiang, L.; Li, D.; Wen, L.; Li, J. Bionic design in anti-bending and lightweight tube based on the tarsometatarsus of ostrich. Rend. Lincei Sci. Fis. Nat. 2020, 31, 189–201. [Google Scholar] [CrossRef]
- Wang, S.; Ren, L.; Liu, Y.; Han, Z.; Yang, Y. Mechanical characteristics of typical plant leaves. J. Bionic Eng. 2010, 7, 294–300. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, H.; Yu, X.; Chen, F.; Wu, J. Microscopic Observations of the Lotus Leaf for Explaining the Outstanding Mechanical Properties. J. Bionic Eng. 2012, 9, 84–90. [Google Scholar] [CrossRef]
- Zhao, L.; Chen, W.-Y.; Ma, J.-F.; Yang, Y.-B. Structural Bionic Design and Experimental Verification of a Machine Tool Column. J. Bionic Eng. 2008, 5, 46–52. [Google Scholar] [CrossRef]
- Zou, M.; Xu, S.; Wei, C.; Wang, H.; Liu, Z. A bionic method for the crashworthiness design of thin-walled structures inspired by bamboo. Thin-Walled Struct. 2016, 101, 222–230. [Google Scholar] [CrossRef]
- Khalil, H.P.S.A.; Bhat, I.U.H.; Jawaid, M.; Zaidon, A.; Hermawan, D.; Hadi, Y.S. Bamboo fibre reinforced biocomposites: A review. Mater. Des. 2012, 42, 353–368. [Google Scholar] [CrossRef]
- Zhou, A.; Huang, D.; Li, H.; Su, Y. Hybrid approach to determine the mechanical parameters of fibers and matrixes of bamboo. Constr. Build. Mater. 2012, 35, 191–196. [Google Scholar] [CrossRef]
- Wegst, U.G.K. Bending efficiency through property gradients in bamboo, palm, and wood-based composites. J. Mech. Behav. Biomed. Mater. 2011, 4, 744–755. [Google Scholar] [CrossRef]
- Xiao, Y.; Yin, H.; Fang, H.; Wen, G. Crashworthiness design of horsetail-bionic thin-walled structures under axial dynamic loading. Int. J. Mech. Mater. Des. 2016, 12, 563–576. [Google Scholar] [CrossRef]
- Yin, H.; Wen, G.; Hou, S.; Chen, K. Crushing analysis and multiobjective crashworthiness optimization of honeycomb-filled single and bitubular polygonal tubes. Mater. Des. 2011, 32, 4449–4460. [Google Scholar] [CrossRef]
- Tasdemirci, A.; Akbulut, E.F.; Guzel, E.; Tuzgel, F.; Yucesoy, A.; Sahin, S.; Guden, M. Crushing behavior and energy absorption performance of a bio-inspired metallic structure: Experimental and numerical study. Thin-Walled Struct. 2018, 131, 547–555. [Google Scholar] [CrossRef]
- Nia, A.A.; Parsapour, M. Comparative analysis of energy absorption capacity of simple and multi-cell thin-walled tubes with triangular, square, hexagonal and octagonal sections. Thin-Walled Struct. 2014, 74, 155–165. [Google Scholar] [CrossRef]
- Goel, M.D. Deformation, energy absorption and crushing behavior of single-, double-and multi-wall foam filled square and circular tubes. Thin-Walled Struct. 2015, 90, 1–11. [Google Scholar] [CrossRef]
- Kashani, M.H.; Alavijeh, H.S.; Akbarshahi, H.; Shakeri, M. Bitubular square tubes with different arrangements under quasi-static axial compression loading. Mater. Des. 2013, 51, 1095–1103. [Google Scholar] [CrossRef]
- Smith, D.; Graciano, C.; Martínez, G. Quasi-static axial compression of concentric expanded metal tubes. Thin-Walled Struct. 2014, 84, 170–176. [Google Scholar] [CrossRef]
- Fung, Y.C. Biomechanics: Motion, Flow, Stress, and Growth; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Roux, W. Der Kampf der Theile im Organismu; Engelmann, W., Ed.; Biodiversity Heritage Library: Washington, DC, USA, 1881. [Google Scholar]
- Wolff, J. Das Gesetz der Transformation der Knochen. DMW-Dtsch. Med. Wochenschr. 1893, 19, 1222–1224. [Google Scholar] [CrossRef] [Green Version]
- Cristofolini, L.; Angeli, E.; Juszczyk, J.M.; Juszczyk, M.M. Shape and function of the diaphysis of the human tibia. J. Biomech. 2013, 46, 1882–1892. [Google Scholar] [CrossRef] [PubMed]
- Cristofolini, L.; Viceconti, M. Mechanical validation of whole bone composite tibia models. J. Biomech. 2000, 33, 279–288. [Google Scholar] [CrossRef]
- Al Nazer, R.; Lanovaz, J.; Kawalilak, C.; Johnston, J.; Kontulainen, S. Direct in vivo strain measurements in human bone—A systematic literature review. J. Biomech. 2012, 45, 27–40. [Google Scholar] [CrossRef]
- Conti, G.; Cristofolini, L.; Juszczyk, M.; Leardini, A.; Viceconti, M. Comparison of three standard anatomical reference frames for the tibia–fibula complex. J. Biomech. 2008, 41, 3384–3389. [Google Scholar] [CrossRef]
- Koch, J.C. The laws of bone architecture. Am. J. Anat. 1917, 21, 177–298. [Google Scholar] [CrossRef]
- Gosman, J.H.; Hubbell, Z.R.; Shaw, C.N.; Ryan, T.M. Development of Cortical Bone Geometry in the Human Femoral and Tibial Diaphysis. Anat. Rec. 2013, 296, 774–787. [Google Scholar] [CrossRef]
- Tiwari, A.; Wahi, P.; Sinha, N. Finite Element Analysis of Human Tibia Modeled as a Functionally Graded Material. J. Eng. Sci. Med. Diagn. Ther. 2019, 2, 031007. [Google Scholar] [CrossRef]
- Goliath, J.R.; Gosman, J.H.; Stout, S.D.; Ryan, T.M. Ontogenetic Patterning of Human Subchondral Bone Microarchitecture in the Proximal Tibia. Biology 2022, 11, 1002. [Google Scholar] [CrossRef]
- Miszkiewicz, J.J.; Stewart, T.J.; Naseri, R.; Sołtysiak, A. The lifestyles of Bronze Age Zagros highlanders at Deh Dumen, Iran: Insights from midshaft femur cross-sectional geometry and histology. Archaeometry 2022, 64, 1270–1287. [Google Scholar] [CrossRef]
- Martens, M.; Van Audekercke, R.; De Meester, P.; Mulier, J.C. The geometrical properties of human femur and tibia and their importance for the mechanical behaviour of these bone structures. Arch. Orthop. Trauma. Surg. Arch. Fur Orthop. Unf.-Chir. 1981, 98, 113–120. [Google Scholar] [CrossRef]
- Demes, B. In vivo bone strain and bone functional adaptation. Am. J. Phys. Anthr. 2007, 133, 717–722. [Google Scholar] [CrossRef]
- Minns, R.J.; Campbell, J.; Bremble, G.R. The bending stiffness of the human tibia. Calcif. Tissue Res. 1975, 17, 165–168. [Google Scholar] [CrossRef]
- Gray, H.A.; Taddei, F.; Zavatsky, A.B.; Cristofolini, L.; Gill, H.S. Experimental Validation of a Finite Element Model of a Human Cadaveric Tibia. J. Biomech. Eng. 2008, 130, 031016. [Google Scholar] [CrossRef]
- Gray, H.A.; Zavatsky, A.B.; Taddei, F.; Cristofolini, L.; Gill, H.S. Experimental validation of a finite element model of a composite tibia. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2007, 221, 315–324. [Google Scholar] [CrossRef]
- Cristofolini, L.; Conti, G.; Juszczyk, M.; Cremonini, S.; Jan, S.V.S.; Viceconti, M. Structural behaviour and strain distribution of the long bones of the human lower limbs. J. Biomech. 2010, 43, 826–835. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lambert, K.L. The Weight-Bearing Function of the Fibula. J. Bone Jt. Surg. 1971, 53, 507–513. [Google Scholar] [CrossRef]
- Gardner, E.; Gray, D.J.; O’Rahilly, R. Anatomy: A Regional Study of Human Structure; WB Saunders: Philadelphia, PA, USA, 1963. [Google Scholar]
- Minns, R.; Bremble, G.; Campbell, J. The geometrical properties of the human tibia. J. Biomech. 1975, 8, 253–255. [Google Scholar] [CrossRef]
- Wuyi, Y.Y.C.; Dahai, Z. Bionic design of column structure of machine tool for high specific stiffness. J. Beijing Univ. Aeronaut. Astronaut. 2008, 34, 991. [Google Scholar]

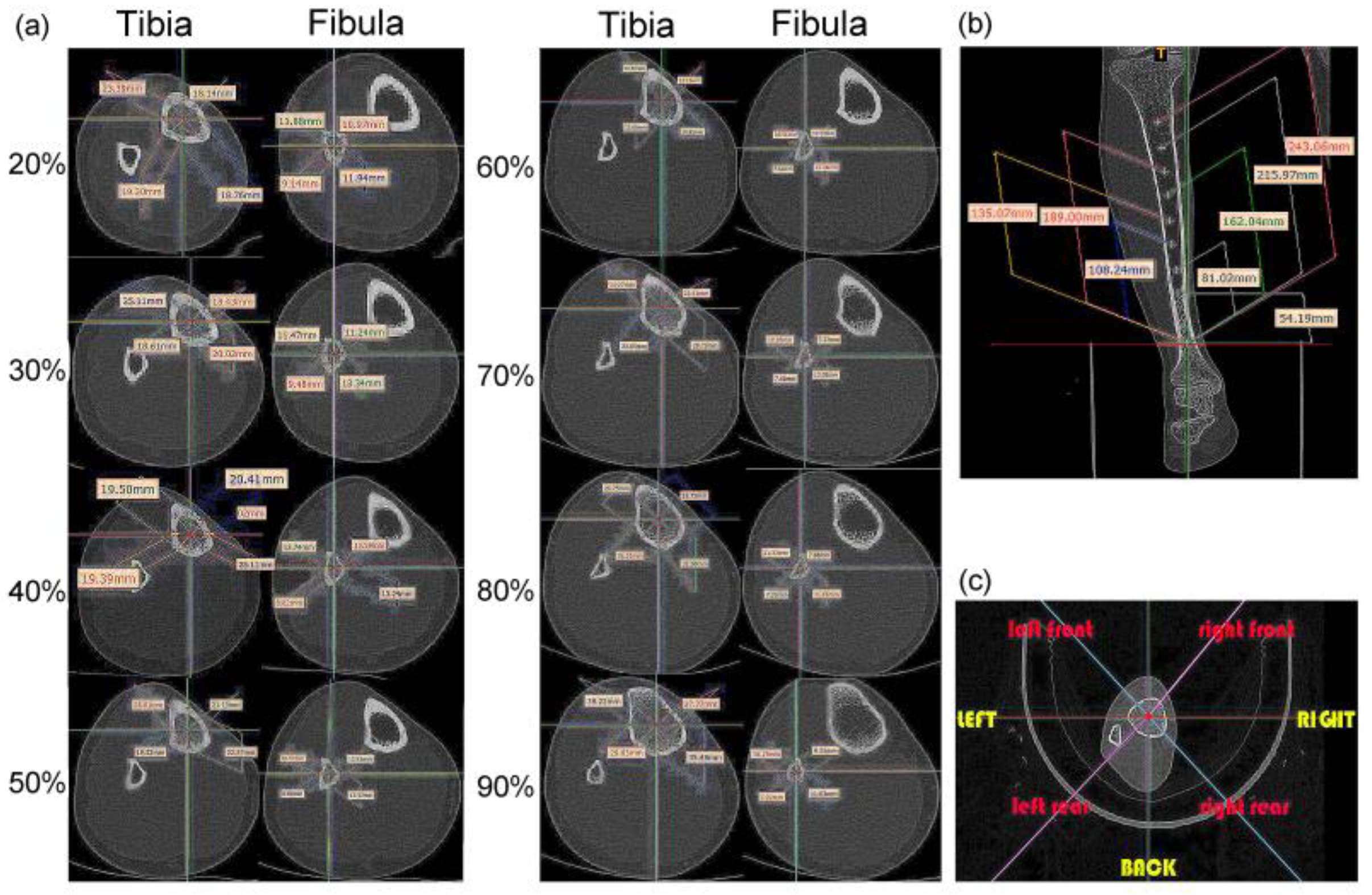


| Type | Fitting Parameter | Cross-Sectional Position | |||||||
|---|---|---|---|---|---|---|---|---|---|
| 20% | 30% | 40% | 50% | 60% | 70% | 80% | 90% | ||
| 1 | long axis of the tibia (mm) | 23.39 | 25.11 | 25.01 | 28.61 | 29.56 | 34.27 | 33.75 | 39.22 |
| short axis of the tibia (mm) | 18.14 | 18.43 | 19.39 | 19.52 | 20.92 | 23.05 | 24.75 | 27.77 | |
| long axis of the fibula (mm) | 11.94 | 11.94 | 13.24 | 13.42 | 14.26 | 13.02 | 11.66 | 11.03 | |
| short axis of the fibula (mm) | 9.14 | 9.14 | 8.82 | 8.84 | 7.61 | 7.33 | 7.33 | 7.92 | |
| 2 | radius of the tibia (mm) | 20.02 | 21.51 | 22.02 | 23.63 | 24.87 | 28.11 | 28.90 | 33.01 |
| radius of the fibula (mm) | 10.45 | 11.25 | 10.81 | 10.89 | 10.42 | 9.77 | 9.24 | 9.35 | |
| 3 | long axis of the tibia (mm) | 31.31 | |||||||
| short axis of the tibia (mm) | 22.96 | ||||||||
| long axis of the fibula (mm) | 12.65 | ||||||||
| short axis of the fibula (mm) | 8.41 | ||||||||
| 4 | radius of the tibia (mm) | 26.51 | |||||||
| radius of the fibula (mm) | 10.25 | ||||||||
| Bionic Tube | Axial Displacement in the Distal End (mm) | Mass (kg) | Specific Stiffness ε |
|---|---|---|---|
| type 1 | 2.96 × 10−1 | 5.32 × 10−2 | 6.39 × 104 |
| type 2 | 2.94 × 10−1 | 5.31 × 10−2 | 6.46 × 104 |
| type 3 | 2.78 × 10−1 | 5.98 × 10−2 | 6.07 × 104 |
| type 4 | 3.05 × 10−1 | 5.16 × 10−2 | 6.40 × 104 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, J.; Wang, K.; Ren, L.; Qian, Z.; Lu, X.; Liang, W.; Xu, X.; Zhao, S.; Zhao, D.; Wang, X.; et al. Development of a Bionic Tube with High Bending-Stiffness Properties Based on Human Tibiofibular Shapes. Biomimetics 2023, 8, 18. https://doi.org/10.3390/biomimetics8010018
Jin J, Wang K, Ren L, Qian Z, Lu X, Liang W, Xu X, Zhao S, Zhao D, Wang X, et al. Development of a Bionic Tube with High Bending-Stiffness Properties Based on Human Tibiofibular Shapes. Biomimetics. 2023; 8(1):18. https://doi.org/10.3390/biomimetics8010018
Chicago/Turabian StyleJin, Jianqiao, Kunyang Wang, Lei Ren, Zhihui Qian, Xuewei Lu, Wei Liang, Xiaohan Xu, Shun Zhao, Di Zhao, Xu Wang, and et al. 2023. "Development of a Bionic Tube with High Bending-Stiffness Properties Based on Human Tibiofibular Shapes" Biomimetics 8, no. 1: 18. https://doi.org/10.3390/biomimetics8010018
APA StyleJin, J., Wang, K., Ren, L., Qian, Z., Lu, X., Liang, W., Xu, X., Zhao, S., Zhao, D., Wang, X., & Ren, L. (2023). Development of a Bionic Tube with High Bending-Stiffness Properties Based on Human Tibiofibular Shapes. Biomimetics, 8(1), 18. https://doi.org/10.3390/biomimetics8010018