1. Introduction
Unmanned vehicles, encompassing unmanned surface vehicles and unmanned underwater vehicles, have received increasing attention over the past several decades. They have found widespread applications in complex, hazardous, and even extreme aquatic environments, such as search and rescue [
1], environmental survey and monitoring [
2], underwater infrastructure inspection and maintenance [
3], sea exploration [
4], and oceanographic observation [
5]. Although traditional propulsion technologies are well-developed and easy-to-use, underwater robots and vehicles powered by rotating propellers are often bulky, noisy, and not sufficiently maneuverable, which hardly meets the ambitious requirements of high maneuverability and stealthiness in marine areas. As is well-known, fish swim with small wakes and low disturbance. Therefore, bionic underwater robots borrowing structural and functional inspiration from aquatic organisms (e.g., fish and dolphins) are advantageous for better maneuverability, adaptability, and quietness in certain cases [
6]. Much of the impetus of the growing interest in biomimetics comes from the appealing promise of being able to learn and utilize optimizations attained over millions of years, as current biological structures and functions are persistently optimized via evolution.
In nature, cetaceans are a mainly aquatic order of mammals including whales, dolphins, and porpoises. Remarkably, in comparison with propeller-driven underwater robots, dolphins can maneuver rapidly in tight space, accelerate and decelerate more swiftly, and even leap out of the water as high as 15 feet, relying on an integrated propulsion and steering system as a whole. In addition to biological relevance, as a typical complex system involving different disciplines, dolphin-inspired robotic research offers vital clues for next-generation innovative underwater robots. To analyse dolphin motions, Tanaka et al. measured the time-varying kinematics of a dolphin in an aquarium by recording the three-dimensional (3D) trajectories of burst-accelerating swimming [
7]. Even though Mendelson et al. explored the water exit dynamics of archerfish with experimental measurements and numerical simulations [
8,
9]. Owing to the limitations of close-up biological observation and on-site motion capture, in reality it is not easy to implement undisturbed kinematic examination of live dolphins’ leaping motions. With the aid of a well-developed robotic dolphin platform, quantification of a dolphin’s leaping motion becomes possible. Thus, bionic robotic dolphins can serve as a useful and multipurpose platform for examining kinematics, dynamics, control, and extensive aquatic applications.
Up to now, the majority of dolphin-inspired robotic research has been concentrated on the development and verification of novel dolphin-like robots, ranging from mechanical design [
10,
11] to measurement and hydrodynamic analysis [
12] and control methods [
13]. The first proof-of-concept self-propelled dolphin robot can be traced back to the year of 1999 [
14]. After that, Nakashima’s group developed a second generation of dolphin-like robot and investigated 3D maneuverability through the coordinated movements of caudal, dorsal, and pectoral fins [
15]. Yu’s group concentrated on mechanism design and motion control of diverse robotic dolphins with the capability of dorsoventral swimming, gliding, and even leaping [
16,
17,
18]. In most of the existing literature on dolphin-like swimming mimicry, unfortunately, the self-propelled leaping motion across the water–air interface is rarely replicated. It is generally acknowledged that achieving high speed is the first step towards crossing the water–air interface. Therefore, reducing drag as significantly as possible during the ignition and acceleration phases plays a critical role. When a body moves near the water surface at high speed, the wave-making resistance becomes the primary drag, consuming energy very evidently [
19,
20]. Extensive investigations on the propulsion efficiency of robotic fish, including system design and control optimization, were conducted in [
21,
22,
23,
24,
25]. The influences of wave-making resistance on the propulsion performance of a bionic robotic dolphin has been less analyzed.
The leaping motion with water surface crossing is extremely complicated, as well as fascinating. Korobkin et al. investigated the hydrodynamic forces of a smooth elongated body during exit from the water surface and proposed a simplified model of water exiting motion [
26]. Hu et al. established a motion model of the water-to-air process for an unmanned submersible aerial vehicle with a regular shape [
27]. Moreover, the numerical method was used to validate the motion model. Chang et al. proposed a theoretical model to analyze the vertical height of the axisymmetric body, and a simple spring system used to shoot a body through the water surface was designed for model validation [
28]. The results suggest that the entrained fluid plays a significant role in limiting the maximum jumping height. Jiang et al. developed a miniature water surface jumping robot. A carbon fiber strip was selected as the energy storage component to actuate two wings to flap the water surface, and a simplified mathematical model was built to predict the jumping performance [
29]. In our previous work [
16], a numerical model with the force equilibrium equations was proposed to estimate the minimum exit speed of a robotic dolphin. As mentioned above, these conducted analyses of leaping motion are mainly aimed at simple bodies with regular profiles and specified exiting speeds. The leaping motion for robots with complex shapes and self-propelled bodies is more comprehensive and needs further investigation.
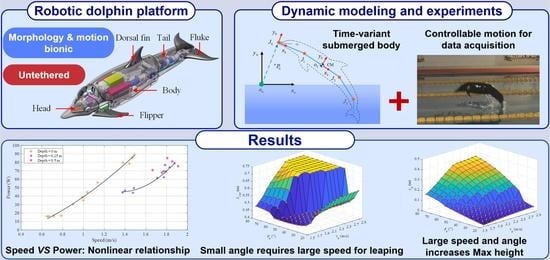
In this paper, we mainly focus on quantifying the leaping motion using a self-propelled bionic robotic dolphin. To this end, aiming at a developed robotic dolphin, a dynamic model of leaping motion with dorsoventral propulsion is established. The Morrison equation is employed to analyze the time-variant hydrodynamic forces acting on the submerged body. In addition, in pursuit of high swimming performance, the effects of wave-making resistance on propulsion performance, including speed and power, are analyzed. The hydrodynamic parameters are identified through the swimming experiments, then a quantitative analysis of leaping motion is provided. This paper provides new insights into the design and control of a novel underwater robot with the capability of leaping motion.
The rest of this paper is organized as follows.
Section 2 introduces the mechanical design and prototype of a robotic dolphin with the capability of leaping. The dynamic model of leaping motion with dorsoventral propulsion is presented in
Section 3. Experiments and motion analyses are offered in
Section 4. Finally,
Section 5 provides the conclusions of this paper.
2. Overview of the Leaping Robotic Dolphin
As illustrated in
Figure 1, a robotic dolphin with the capability of leaping motion was developed in our previous work [
16]. To reduce the hydrodynamic drag, a well-streamlined body profile drawing from a spotted dolphin was adopted. With dorsoventral oscillation, two joints, a waist joint and a tail joint, were configured in the posterior body to ensure powerful propulsion. A neck joint used exclusively for the head-lead nose-up and nose-down is integrated. In addition, a pair of two-degree-of-freedom flippers for realizing the flapping motion and feathering motion is implemented. Combining the flippers and two-joint propulsion body, the 3D swimming motion, including both pitch and yaw maneuverability, can be realized. However, to simplify the analysis of the robotic dolphin’s leaping motion, the flippers’ deflection angles are 0°. A pair of flukes attach to the caudal joint, producing the thrust of swimming. These fins are all made of polypropylene and designed with a NACA 0018 airfoil. Certain materials, such as titanium alloy, aluminum alloy, and nylon, were adopted to meet the requirements of light weight and high strength. A customized elastic skin with a thickness of 1 mm protects the robot from water.
A variety of electronic components including sensors, control units, communication modules, and power supply, are imported into the robotic dolphin. A miniature attitude heading reference system (AHRS, MicroStrain, 3DM-GX3-25) is mounted in the head to provide the attitude data of the robotic dolphin. A pressure sensor (SQsensor, CYG-515A) is utilized to measure the depth information. A control board with various communication interfaces implements the control algorithm and external orders. In addition, dedicated motor controllers (MAXON, EPOS2 50/5) are employed to obtain the state information of the joints, such as their speed and position. With the integration of mechanical structure and electronic modules, the prototype is fabricated with a length of 0.72 m and a mass of 4.7 kg, as shown in
Figure 2. The detailed parameters are tabulated in
Table 1.
3. Dynamic Modeling of Leaping Motion
The complete process of the leaping motion ordinarily contains three phases [
17]. (1) The water-exiting phase: beginning at the penetration of the water surface until achieving complete separation between the flukes and the water surface. During this phase, the robotic dolphin oscillates its body and flukes continuously to provide thrust. (2) The projectile phase: the robotic dolphin enters the air completely and is only dominated by gravity. (3) The water reentry phase: starting from when the tip of the nose touches the water surface until the flukes are submerged in the water. During the water reentry phase, the body and flukes of the robotic dolphin remain still, and its dynamic model including the hydrodynamic analysis and buoyancy analysis is similar to that of the water-exiting phase; therefore, in this paper we primarily concentrate on the dynamic model of the water-exiting phase.
3.1. Kinematic Analysis
To analyze the cross-domain locomotion of a robotic dolphin, a dynamic model was built in detail. As shown in
Figure 3, coordinate frames and notations are defined to describe the dynamic model clearly. The robotic dolphin can be simplified as a four-actuated-link structure in series. The inertial coordinate frame is defined as
and the relative coordinate frames are denoted as
. In particular, a body coordinate frame
which relates to the center of mass (CM) is defined. For the CM of the dolphin located at
, therefore,
is parallel to
. All of the coordinate frames conform to the right-hand rule. The plane
is parallel to the vertical plane. The origin
located at the joint
and axis
is overlapped with link
and points to
. Here,
indicates the tip point of the robotic dolphin’s head, while
,
, and
denote the neck joint, waist joint, and caudal joint, respectively. To simplify the dynamic model, in this paper only the leaping motion in the vertical plane is considered. The length of link
is denoted as
, while
indicates the joint angle of
and
represents the pitch angle of the robotic dolphin. It should be noted that the head of the robotic dolphin, with neck joint
, is mainly designed to provide the pitch moment for posture adjustment in the air, which is not considered in this paper. Therefore, the neck joint
is locked in the water-exiting process.
The kinematics of the robotic dolphin can be derived using a similar method to that for robotic fishes [
30,
31]. The rotation matrix of frame
with respect to
can be provided as follows:
where
represents the angle between axis
and axis
.
Let
represents the position vector of an arbitrary point in the
ith link; it can be calculated as the position vector sum between
and point of link
in frame
:
where
where
is the position vector of
in frame
,
denotes the position vector of
in frame
, and
l denotes the distance of the arbitrary point in
ith link to joint
.
The translational velocity and angular velocity can be obtained by taking the time derivative of the position vector and angular vector in
, and can be formalized through the coordinate transformation as follows:
where
is the angular velocity vector of link
.
The acceleration can be further obtained by taking the time derivative of the velocity as follows:
where
and
is the skew-symmetric matrix of angular velocity vector
.
The velocity and acceleration of an arbitrary point in these links can be obtained with the derivation of the provided kinematic and actuation control of the joints.
3.2. Hydrodynamic Analysis
During the leaping motion, two fluids with strikingly different physical properties are involved. When considering the density of air and the exiting velocity of a robotic dolphin, the aerodynamic forces are neglected. Therefore, only hydrodynamic forces are calculated. It should be noted that the interaction between the robot and surrounding fluid is extremely complicated; in addition, with the increase in leaping height, the length of a body immersed in water varies, which brings about changes in buoyancy and hydrodynamic forces. As only vertical motion is of concern here, the rolling inertia and yaw inertia are not considered in the hydrodynamic analysis, nor is the entrained fluid caused by the exited body is not.
In this paper, the Morrison equation is employed to analyze the hydrodynamic forces acting on the body, which include the added mass force and the drag force [
32]. Note that only the remaining immersed section is subject to hydrodynamic forces.
Figure 4 illustrates the hydrodynamic forces acting on the
ith link which is crossing the water surface with an exiting length of
. For the per unit length of the body with a distance of
l to
, the hydrodynamic forces are considered to act on the cross-section
. The added mass forces are due to the response of the surrounding water, which is accelerated by the oscillation of the robotic dolphin. To account for the decrease in the submerged length of each link, the added mass in the longitudinal and transverse direction of the link are all considered. For simplicity, we directly calculate the added mass force expressed in inertial frame
below:
where
is the added mass of
,
indicates the dimensionless coefficient,
denotes the density of the fluid, and
denotes the immersed height. By integrating
along axis
, the added mass force acting on the link
can be calculated.
The drag force generated by the fluid slice in a cross-section
can be obtained as follows:
where
and
are the dimensionless hydrodynamic coefficients,
denotes the perimeter of the cross-section
, and
and
are the velocity in the direction of axes
and
, respectively.
As shown in
Figure 4, the hydrodynamic forces exerted on the immersed segment of link
can be derived by integrating the forces acting on cross-section
along axis
as follows:
where
means the drag force expressed in inertial frame
.
During the leaping motion, the submerged length of link is changing along with time, that is, the integrating range needs to be updated in each step time. For the link which is totally beneath the water surface, the exiting length is zero.
The hydrodynamic forces for a fluke designed with an airfoil profile for high-speed swimming are calculated with the lift and drag model, as follows:
where
is the angle of attack,
and
are the dimensionless lift coefficient and drag coefficient, respectively,
is the linear velocity magnitude of flukes, and
means the wetted area of flukes.
The moment
generated by the hydrodynamic force
acting on the CM of the robotic dolphin can be calculated as follows:
where
indicates the position vector of CM in inertial frame
.
3.3. Buoyancy Analysis
In addition to the analyzed hydrodynamic forces, the robotic dolphin is affected by the forces of gravity and buoyancy, as illustrated in
Figure 5. To simplify the analysis, the positions of CM and CB are defined as
m and
, which indicate the respective distances to the CM and CB from the top point of the robot along the longitudinal axis of the body. During the leaping motion of the robotic dolphin, the volume of the submerged portion
and the location of the submerged body’s center of buoyancy (CB) vary with the exiting length
, which is defined as the distance between head to the water surface along the body. Considering the irregular shape of the robotic dolphin, it is difficult to describe the changes in volume and CB position accurately. Therefore, we assume that the slight variation in the position of the CM and CB during oscillation of the robotic dolphin can be ignored. In addition, the density of the robotic dolphin is considered to be the same as that of water. Taking advantage of SolidWorks, the volume and location of the CB under different exiting lengths
are measured, then the fitting method is utilized to acquire the function of
and
, as shown in
Figure 6. The change in the buoyancy force and moment with the exiting length
can be provided as follows:
Finally according to the analysis mentioned above, the dynamic model takes the following form:
where
is the total inertia matrix, including the inertial matrix and added mass matrix,
is the total hydrodynamic force acting on each link, and
is the total torque generated by the fluid relative to the CM.
5. Discussion
In this paper, we have analyzed the leaping motion with the built dynamic model. In nature, the leaping motion for a robotic dolphin includes two modes, namely, exiting out of the water surface straightly or with posture adjustment. The first mode considered in this paper requires higher velocity to realize the complete water-exiting motion, and usually pursues the leaping height. Concerning the second mode of the robotic dolphin, achieving complete separation from the water surface requires a lower leaping height, which is easier to achieve and ordinarily pursues the leaping distance. The conducted experiments in our previous study achieved the second mode; therefore, in the present research, we mainly focus on the mode involving a straight exiting from the water surface.
In dynamic modeling, many assumptions have been made to simplify the hydrodynamic analysis. In [
33,
34,
35], the robotic fish body or tail is taken as a slender body or flat plates. Therefore, the added mass coefficient in the longitudinal axis is usually very small and can be neglected, and the added mass force is calculated with the only the transverse acceleration. For our robotic dolphin, the length
of each link is larger than the body height
with a limiting ratio of
. In addition, during the leaping motion, the submerged length of each link gradually decreases with time, causing a decreasing ratio. Thus, we did not ignore the added mass in the direction of each link’s longitudinal axis. In [
21], the added mass in the longitudinal axis of body was considered. Therefore, we directly calculate the added mass force expressed in the inertial frame with the absolute acceleration. When the robotic dolphin moves in the fluid with the oscillation of body, the surrounding water is accelerated in the two axial directions of the inertial frame. Then, we calculate the added mass forces produced by the reaction of the surrounding fluid with the added mass and accelerations. In order to improve the accuracy of our simplified dynamic model, we identify these hydrodynamic parameters with experimental swimming speed, which reshapes the dynamic model with data-driven feature. Even though many simplifications have been made in our hydrodynamic model, the experimental results in swimming speed and leaping height demonstrate its effectiveness.
Unlike our previous analysis of the water-exiting motion, the self-propelled propulsion at different velocities corresponds to different oscillation frequencies of the body, causing the leaping motion to be more sensitive to the pitch angle. For smaller exit angles, the vertical velocity component limits the maximum height of the CM, causing extremely short leaping times and making it more difficult to exit the water completely. In our experiments, the effects of the wave-making resistance are only explored with respect to the speed and power, which are essential for the leaping motion. In future work, further theoretical analysis needs to be conducted. Moreover, further optimization of the design and control system needs to be considered in order to achieve better leaping motion performance.